A.2：tanh関数【ゼロつく2のノート(実装)】

はじめに

　『ゼロから作るDeep Learning 2――自然言語処理編』の初学者向け【実装】攻略ノートです。『ゼロつく2』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。

　本の内容を1つずつ確認しながらゆっくりと組んでいきます。

　この記事は、A.2節「tanh関数」の内容です。tanh関数についてグラフで確認して、tanh関数の微分を導出します。

【他の節の内容】

www.anarchive-beta.com

【この節の内容】

A.2 tanh関数

　tanh関数とは、次の式で定義される関数で双曲線正接関数とも呼ばれます。

$$ \mathrm{tanh}(x) = \frac{ \exp(x) - \exp(-x) }{ \exp(x) + \exp(-x) } \tag{A.5} $$

　ここで$\exp(x) = e^x$です。tanh関数の出力は、-1から1の値をとります。

・順伝播をグラフで確認

　tanh関数の出力をグラフで確認しましょう。

# A.2節で利用するライブラリ
import numpy as np
import matplotlib.pyplot as plt

　tanh関数は、np.tanh()で計算できます。

# x軸の値を生成(描画範囲を指定)
x = np.arange(-5.0, 5.0, 0.01)

# tanh関数による変換
y = np.tanh(x)

# 作図
plt.plot(x, y, color='purple', label='tanh(x)')
plt.xlabel('x')
plt.ylabel('y')
plt.title('tanh function', fontsize=20)
plt.grid()
plt.show()

tanh関数

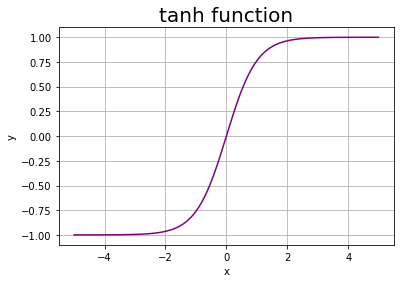
　出力が-1から1の値をとるのを確認できます。また$x = 0$のとき$\mathrm{tanh}(0) = 0$となります。

　式(A.5)について細かく確認してみましょう。まずは$\exp(x)$と$\exp(-x)$をプロットします。

# x軸の値を生成(描画範囲を指定)
x = np.arange(-2.0, 2.0, 0.01)

# ネイピア数を用いた指数関数の計算
exp_x = np.exp(x)
exp_mx = np.exp(-x)

# 作図
plt.plot(x, exp_x, color='brown', label='exp(x)')
plt.plot(x, exp_mx, color='blue', label='exp(-x)')
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.legend()
plt.show()

$\exp(x)$と$\exp(-x)$のグラフ

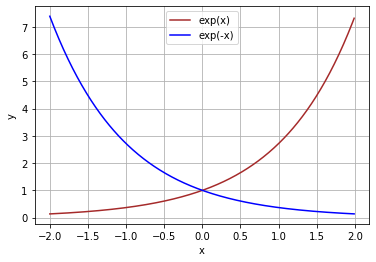
　$x$の値の正負に関わらず、$\exp(\cdot)$は正の値になります。

　次は分子$\exp(x) - \exp(-x)$と分母$\exp(x) + \exp(-x)$をプロットします。

# ネイピア数を用いた指数関数の計算
y_numer = np.exp(x) - np.exp(-x) # 分子
y_denom = np.exp(x) + np.exp(-x) # 分母

# 作図
plt.plot(x, exp_x, color='brown', linestyle='--', label='exp(x)')
plt.plot(x, exp_mx, color='blue', linestyle='--', label='exp(-x)')
plt.plot(x, y_numer, color='green', label='exp(x) - exp(-x)') # 分子
plt.plot(x, y_denom, color='orange', label='exp(x) + exp(-x)') # 分母
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.legend()
plt.show()

tanh関数の分母と分子のグラフ

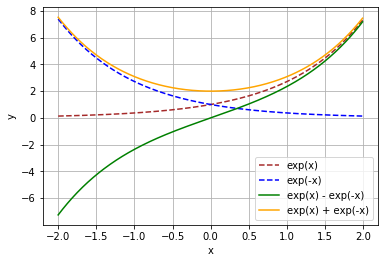
　$\exp(\cdot)$は正の値をとるので、$\exp(x) + \exp(-x)$も常に正の値になります。また分子より分母の方が大きくなります。

　最後にこのグラフとtanh関数のグラフを重ねて表示します。

# ネイピア数を用いた指数関数の計算
y_numer = np.exp(x) - np.exp(-x)
y_denom = np.exp(x) + np.exp(-x)

# tanh関数
y = y_numer / y_denom

# 作図
plt.plot(x, y, color='purple', label='tanh(x)')
plt.plot(x, y_numer, color='green', linestyle='--', label='exp(x) - exp(-x)') # 分子
plt.plot(x, y_denom, color='orange', linestyle='--', label='exp(x) + exp(-x)') # 分母
plt.xlabel('x')
plt.ylabel('y')
plt.ylim((-5, 5))
plt.grid()
plt.legend()
plt.show()

tanh関数

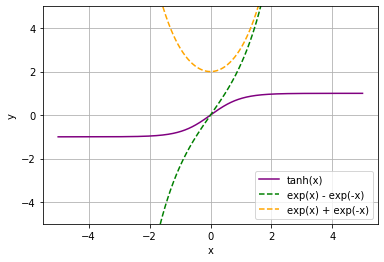
　分母分子の絶対値を比較しても、分子より分母が大きく$|\exp(x) - \exp(-x)| < |\exp(x) + \exp(-x)|$なります。よって$\mathrm{tanh(x)}$の絶対値は1より小さく$\Bigl|\frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)}\Bigr| < 1$なります。これにより$\mathrm{tanh}(x)$が-1から1の値になります。

　今度は、1つの値に注目してこのことを確認してみましょう。

# 値を指定
x = 1.5

print('x = ' + str(x))
print('exp(x) = ' + str(np.round(np.exp(x), 2)))
print('exp(-x) = ' + str(np.round(np.exp(-x), 2)))
print('exp(x) - exp(-x) = ' + str(np.round(np.exp(x) - np.exp(-x), 2)))
print('exp(x) + exp(-x) = ' + str(np.round(np.exp(x) + np.exp(-x), 2)))
print('tanh(x) = ' + str((np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))))

x = 1.5
exp(x) = 4.48
exp(-x) = 0.22
exp(x) - exp(-x) = 4.26
exp(x) + exp(-x) = 4.7
tanh(x) = 0.9051482536448664

　他の値でも試してみましょう(コードは省略)。

x = -4
exp(x) = 0.02
exp(-x) = 54.6
exp(x) - exp(-x) = -54.58
exp(x) + exp(-x) = 54.62
tanh(x) = -0.9993292997390669

　以上が順伝播の計算です。次は逆伝播について考えましょう。

・逆伝播の導出

　続いて、tanh関数の微分(逆伝播)を導出します。

　tanh関数の出力を$y$として

$$ y = \mathrm{tanh}(x) $$

$y$を$x$で微分します。

　tanh関数の定義式(A.5)に関して分子$\exp(x) - \exp(-x)$を$f(x)$、分母$\exp(x) + \exp(-x)$を$g(x)$とおくと、商の微分より

$$ \begin{align} \frac{\partial \mathrm{tanh}(x)}{\partial x} &= \Bigl\{ \frac{f(x)}{g(-x)} \Bigr\}' \\ &= \frac{ f'(x) g(x) - f(x) g'(x) }{ g(x)^2 } \tag{A.6} \end{align} $$

となります。ネイピア数の性質より、$\frac{\partial \exp(x)}{\partial x} = \exp(x)$、$\frac{\partial \exp(-x)}{\partial x} = - \exp(-x)$なので

$$ \begin{aligned} f'(x) &= \Bigl\{\exp(x) - \exp(-x)\Bigr\}' \\ &= \exp(x) + \exp(-x) \end{aligned} $$

また

$$ \begin{aligned} g'(x) &= \Bigl\{\exp(x) + \exp(-x)\Bigr\}' \\ &= \exp(x) - \exp(-x) \end{aligned} $$

となります。式(A.6)にそれぞれ代入すると

$$ \begin{align} \frac{\partial \mathrm{tanh}(x)}{\partial x} &= \frac{ \Bigl\{\exp(x) + \exp(-x)\Bigr\} \Bigl\{\exp(x) + \exp(-x)\Bigr\} - \Bigl\{\exp(x) - \exp(-x)\Bigr\} \Bigl\{\exp(x) - \exp(-x)\Bigr\} }{ \Bigl\{\exp(x) + \exp(-x)\Bigr\}^2 } \\ &= \frac{ \Bigl\{\exp(x) + \exp(-x)\Bigr\}^2 }{ \Bigl\{\exp(x) + \exp(-x)\Bigr\}^2 } - \frac{ \Bigl\{\exp(x) - \exp(-x)\Bigr\}^2 }{ \Bigl\{\exp(x) + \exp(-x)\Bigr\}^2 } \\ &= 1 - \Bigl\{ \frac{ \exp(x) - \exp(-x) }{ \exp(x) + \exp(-x) } \Bigr\}^2 \end{align} $$

と整理できます。後の項はtanh関数の定義式(A.5)になっているので、tanh関数の出力$y$に置き換えると

$$ \frac{\partial \mathrm{tanh}(x)}{\partial x} = 1 - y^2 \tag{A.9} $$

$x$に関する$\mathrm{tanh}(x)$の微分が得られます。

・逆伝播をグラフで確認

　tanh関数の微分もグラフで確認しましょう。

# x軸の値を生成(描画範囲を指定)
x = np.arange(-5.0, 5.0, 0.01)

# tanh関数
y = np.tanh(x)

# tanh関数の微分
dy = 1 - y**2

# 作図
plt.plot(x, y, color='purple', label='tanh(x)')
plt.plot(x, dy, label='dtanh(x) / dx')
plt.xlabel('x')
plt.ylabel('y')
plt.title('tanh function', fontsize=20)
plt.grid()
plt.legend()
plt.show()

tanh関数の微分

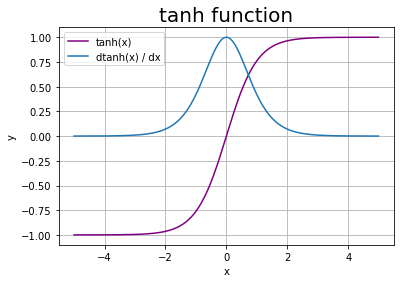
　$y$が-1から1の値をとるので、$\frac{\partial y}{\partial x}$は0から1の値になります。

　最後に、sigmoid関数の微分(A.4)と重ねて比較してみます。

# tanh関数
y_sgm = 1 / (1 + np.exp(-x))

# tanh関数の微分
dy_sgm = y_sgm * (1 - y_sgm)

# 作図
plt.plot(x, dy, label='dtanh(x) / dx')
plt.plot(x, dy_sgm, label='dσ(x) / dx')
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.legend()
plt.show()

tanh関数とsigmoid関数の微分

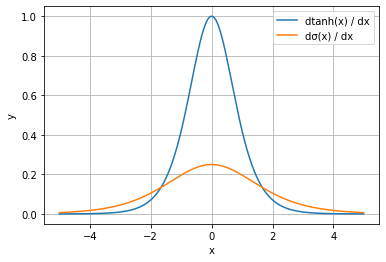
　sigmoid関数は出力が0から1に変化するのに対して、tanh関数は-1から1に変化します。tanh関数の方が変化の度合いが大きいため、微分も大きくなります。これにより、ニューラルネットワークの活性化関数にtanh関数を用いた方が、逆伝播の際に勾配が小さくなりにくくなります。

参考文献

• 斎藤康毅『ゼロから作るDeep Learning 2――自然言語処理編』オライリー・ジャパン,2018年.

おわりに

　(正直このシリーズのためではないですが)tanh関数の微分について記事にしておく必要があったので書きました。