はじめに
この記事は、「R Advent Calendar 2020」の10日目の記事です。
『ベイズ推論による機械学習入門』の学習時のノートです。基本的な内容は「数式の行間を読んでみた」とそれを「RとPythonで組んでみた」になります。「数式」と「プログラム」から理解するのが目標です。
この記事は、4.4.3項の内容です。「観測モデルを多次元ガウス混合分布(多変量正規混合分布)」、「事前分布をガウス・ウィシャート分布とディリクレ分布」とするガウス混合モデルに対する変分推論(変分ベイズ)をRで実装します。
省略してある内容等ありますので、本とあわせて読んでください。初学者な自分が理解できるレベルまで落として書き下していますので、分かる人にはかなりくどくなっています。同じような立場の人のお役に立てれば幸いです。
【数式読解編】
【他の節一覧】
【この節の内容】
・Rでやってみる
人工的に生成したデータを用いて、ベイズ推論を行ってみましょう。アルゴリズム4.6を参考に実装します。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(mvnfast)
mvnfastは、多次元ガウス分布に関するパッケージです。多次元ガウス分布に従う乱数生成関数rmvn()と確率密度関数dmvn()を使います。
・観測モデルの設定
まずは、観測モデルを設定します。この節では、$K$個の観測モデルを多次元ガウス分布$\mathcal{N}(\mathbf{x}_n | \boldsymbol{\mu}_k, \boldsymbol{\Lambda}_k^{-1})$とします。また、各データに対する観測モデルの割り当てをカテゴリ分布$\mathrm{Cat}(\mathbf{s}_n | \boldsymbol{\pi})$によって行います。
観測モデルのパラメータを設定します。この実装例では2次元のグラフで表現するため、$D = 2$のときのみ動作します。
# 次元数を設定:(固定) D <- 2 # クラスタ数を指定 K <- 3 # K個の真の平均を指定 mu_truth_kd <- matrix( c(5, 35, -20, -10, 30, -20), nrow = K, ncol = D, byrow = TRUE ) # K個の真の分散共分散行列を指定 sigma2_truth_ddk <- array( c(250, 65, 65, 270, 125, -45, -45, 175, 210, -15, -15, 250), dim = c(D, D, K) )
$K$の平均パラメータ$\boldsymbol{\mu} = \{\boldsymbol{\mu}_1, \boldsymbol{\mu}_2, \cdots, \boldsymbol{\mu}_K\}$、$\boldsymbol{\mu}_k = (\mu_{k,1}, \mu_{k,2}, \cdots, \mu_{k,D})$をmu_truth_kd、分散共分散行列パラメータ$\boldsymbol{\Sigma} = \{\boldsymbol{\Sigma}_1, \boldsymbol{\Sigma}_2, \cdots, \boldsymbol{\Sigma}_K\}$、$\boldsymbol{\Sigma}_k = (\sigma_{k,1,1}^2, \cdots, \sigma_{k,D,D}^2)$をsigma2_truth_ddkとして、値を指定します。$\boldsymbol{\Sigma}_k$は正定値行列です。また、分散共分散行列の逆行列$\boldsymbol{\Lambda}_k = \boldsymbol{\Sigma}_k^{-1}$を精度行列と呼びます。
mu_true_kdの作成の際に、matrix()の引数にbyrow = TRUEを指定すると行方向に要素を並べるため、値を指定しやすくなります。
設定したパラメータは次のようになります。
# 確認
mu_truth_kd
sigma2_truth_ddk
## [,1] [,2] ## [1,] 5 35 ## [2,] -20 -10 ## [3,] 30 -20 ## , , 1 ## ## [,1] [,2] ## [1,] 250 65 ## [2,] 65 270 ## ## , , 2 ## ## [,1] [,2] ## [1,] 125 -45 ## [2,] -45 175 ## ## , , 3 ## ## [,1] [,2] ## [1,] 210 -15 ## [2,] -15 250
混合比率を設定します。
# 真の混合比率を指定 pi_truth_k <- c(0.45, 0.25, 0.3)
混合比率パラメータ$\boldsymbol{\pi} = (\pi_1, \pi_2, \cdots, \pi_K)$をpi_true_kとして、$\sum_{k=1}^K \pi_k = 1$、$\pi_k \geq 0$の値を指定します。ここで、$\pi_k$は各データがクラスタ$k$となる($s_{n,k} = 1$となる)確率を表します。
この3つのパラメータの値を観測データから求めるのがここでの目的です。
設定した観測モデルをグラフで確認しましょう。作図用の点を作成します。
# 作図用のx軸のxの値を作成 x_1_vec <- seq( min(mu_truth_kd[, 1] - 3 * sqrt(sigma2_truth_ddk[1, 1, ])), max(mu_truth_kd[, 1] + 3 * sqrt(sigma2_truth_ddk[1, 1, ])), length.out = 300) # 作図用のy軸のxの値を作成 x_2_vec <- seq( min(mu_truth_kd[, 2] - 3 * sqrt(sigma2_truth_ddk[2, 2, ])), max(mu_truth_kd[, 2] + 3 * sqrt(sigma2_truth_ddk[2, 2, ])), length.out = 300 ) # 作図用のxの点を作成 x_point_mat <- cbind( rep(x_1_vec, times = length(x_2_vec)), rep(x_2_vec, each = length(x_1_vec)) )
作図用に、2次元ガウス分布に従う変数$\mathbf{x}_n = (x_{n,1}, x_{n,2})$がとり得る点(値の組み合わせ)を作成します。$x_{n,1}$がとり得る値(x軸の値)をseq()で作成してx_1_vecとします。この例では、$K$個のクラスタそれぞれで平均値から標準偏差の3倍を引いた値と足した値を計算して、その最小値から最大値までを範囲とします。length.out引数を使うと指定した要素数で等間隔に切り分けます。by引数を使うと切り分ける間隔を指定できます。処理が重い場合は、この値を調整してください。同様に、$x_{n,2}$がとり得る値(y軸の値)も作成してx_2_vecとします。
x_1_vecとx_2_vecの要素の全ての組み合わせを持つようにマトリクスを作成してx_point_matとします。これは、確率密度を等高線図にする際に格子状の点(2軸の全ての値が直交する点)を渡す必要があるためです。
作成した$\mathbf{x}$の点は次のようになります。
# 確認 x_point_mat[1:5, ]
## [,1] [,2] ## [1,] -53.54102 -67.43416 ## [2,] -53.11622 -67.43416 ## [3,] -52.69142 -67.43416 ## [4,] -52.26662 -67.43416 ## [5,] -51.84182 -67.43416
1列目がx軸の値、2列目がy軸の値に対応しています。
観測モデルの確率密度を計算します。
# 観測モデルを計算 model_density <- 0 for(k in 1:K) { # クラスタkの分布の確率密度を計算 tmp_density <- mvnfast::dmvn( X = x_point_mat, mu = mu_truth_kd[k, ], sigma = sigma2_truth_ddk[, , k] ) # K個の分布の加重平均を計算 model_density <- model_density + pi_truth_k[k] * tmp_density }
$K$個のパラメータmu_truth_kd, sigmga2_truth_ddkを使って、x_point_matの点ごとに、次の混合ガウス分布の式で確率密度を計算します。
$K$個の多次元ガウス分布に対して、$\boldsymbol{\pi}$を使って加重平均をとります。
多次元ガウス分布の確率密度は、mvnfastパッケージのdmvn()で計算できます。$k$番目の分布の場合は、データの引数Xにx_point_mat、平均の引数muにmu_truth_kd[k, ]、分散共分散行列の引数sigmaにsigma2_truth_ddk[, , k]を指定します。
この計算をfor()ループでK回繰り返し行います。各パラメータによって求めた$K$回分の確率密度をそれぞれpi_truth_k[k]で割り引いてmodel_probに加算していきます。
計算結果をデータフレームに格納します。
# 観測モデルをデータフレームに格納 model_df <- tibble( x_1 = x_point_mat[, 1], x_2 = x_point_mat[, 2], density = model_density ) # 確認 head(model_df)
## # A tibble: 6 x 3 ## x_1 x_2 density ## <dbl> <dbl> <dbl> ## 1 -53.5 -67.4 9.07e-13 ## 2 -53.1 -67.4 1.07e-12 ## 3 -52.7 -67.4 1.27e-12 ## 4 -52.3 -67.4 1.50e-12 ## 5 -51.8 -67.4 1.78e-12 ## 6 -51.4 -67.4 2.10e-12
ggplot2パッケージを利用して作図するには、データフレームを渡す必要があります。
観測モデルを作図します。
# 観測モデルを作図 ggplot(model_df, aes(x = x_1, y = x_2, z = density, color = ..level..)) + geom_contour() + # 真の分布 labs(title = "Gaussian Mixture Model", subtitle = paste0("K=", K), x = expression(x[1]), y = expression(x[2]))

等高線グラフはgeom_contour()で描画します。
$K$個の分布を重ねたような分布になります。ただし、積分して1となるようにしているため、$K$個の分布そのものよりも1つ1つの山が小さく(確率密度が小さく)なっています。
・データの生成
続いて、構築した観測モデルに従ってデータを生成します。先に、潜在変数$\mathbf{S} = \{\mathbf{s}_1, \mathbf{s}_2, \cdots, \mathbf{s}_N\}$、$\mathbf{s}_n = (s_{n,1}, s_{n,2}, \cdots, s_{n,K})$を生成し、各データにクラスタを割り当てます。次に、割り当てられたクラスタに従い観測データ$\mathbf{X} = \{\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_N\}$、$\mathbf{x}_n = (x_{n,1}, x_{n,2}, \cdots, x_{n,D})$を生成します。
$N$個の潜在変数$\mathbf{S}$を生成します。
# (観測)データ数を指定 N <- 250 # 潜在変数を生成 s_truth_nk <- rmultinom(n = N, size = 1, prob = pi_truth_k) %>% t()
生成するデータ数$N$をNとして値を指定します。
カテゴリ分布に従う乱数は、多項分布に従う乱数生成関数rmultinom()のsize引数を1にすることで生成できます。また、試行回数の引数nにN、確率(パラメータ)の引数probにpi_truth_kを指定します。生成した$N$個の$K$次元ベクトルをs_truth_nkとします。ただし、クラスタが行でデータが列方向に並んで出力されるので、t()で転置しておきます。
結果は次のようになります。
# 確認 s_truth_nk[1:5, ]
## [,1] [,2] [,3] ## [1,] 0 1 0 ## [2,] 1 0 0 ## [3,] 1 0 0 ## [4,] 1 0 0 ## [5,] 0 0 1
これが本来は観測できない潜在変数であり、真のクラスタです。各行がデータを表し、値が1の列番号が割り当てられたクラスタ番号を表します。
s_truth_nkから各データのクラスタ番号を抽出します。
# クラスタ番号を取得 s_truth_n <- which(t(s_truth_nk) == 1, arr.ind = TRUE) %>% .[, "row"] # 確認 s_truth_n[1:5]
## [1] 2 1 1 1 3
which()を使って行(データ)ごとに要素が1の列番号を抽出します。
各データに割り当てられたクラスタに従い$N$個のデータを生成します。
# (観測)データを生成 x_nd <- matrix(0, nrow = N, ncol = D) for(n in 1:N) { # n番目のデータのクラスタ番号を取得 k <- s_truth_n[n] # n番目のデータを生成 x_nd[n, ] = mvnfast::rmvn(n = 1, mu = mu_truth_kd[k, ], sigma = sigma2_truth_ddk[, , k]) }
各データ$\mathbf{x}_n$に割り当てられたクラスタ($s_{n,k} = 1$である$k$)のパラメータ$\boldsymbol{\mu}_k,\ \boldsymbol{\Sigma}_k$を持つ多次元ガウス分布に従いデータ(値)を生成します。多次元ガウス分布の乱数は、mvnfastパッケージのrmvn()で生成できます。
データごとにクラスタが異なるので、for()で1データずつ処理します。$n$番目のデータのクラスタ番号s_true_n[n]を取り出してkとします。そのクラスタに従ってデータ$\mathbf{x}_n$を生成します。平均の引数muにmu_true_kd[k, ]、分散共分散行列の引数sigmaにsigma2_true_ddk[, , k]を指定します。また1データずつ生成するので、データ数の引数nは1です。
観測データもグラフで確認しましょう。作図用のデータフレームを作成します。
# 観測データと真のクラスタ番号をデータフレームに格納 x_df <- tibble( x_n1 = x_nd[, 1], x_n2 = x_nd[, 2], cluster = as.factor(s_truth_n) ) # 確認 head(x_df)
## # A tibble: 6 x 3 ## x_n1 x_n2 cluster ## <dbl> <dbl> <fct> ## 1 -5.08 -17.2 2 ## 2 1.57 42.4 1 ## 3 19.1 21.2 1 ## 4 -11.8 35.0 1 ## 5 17.7 -17.2 3 ## 6 26.0 -9.53 3
2次元の観測データに1つのクラスタが割り当てられています。
観測データの散布図を観測モデルに重ねて作図します。
# 観測データの散布図を作成 ggplot() + geom_contour(data = model_df, aes(x = x_1, y = x_2, z = density), linetype = "dashed") + # 真の分布 #geom_contour_filled(data = model_df, aes(x = x_1, y = x_2, z = density, fill = ..level..), # alpha = 0.6, linetype = "dashed") + # 真の分布:(塗りつぶし) geom_point(data = x_df, aes(x = x_n1, y = x_n2, color = cluster)) + # 真のクラスタ labs(title = "Gaussian Mixture Model", subtitle = paste0('N=', N, ", pi=(", paste0(pi_truth_k, collapse = ", "), ")"), x = expression(x[1]), y = expression(x[2]))
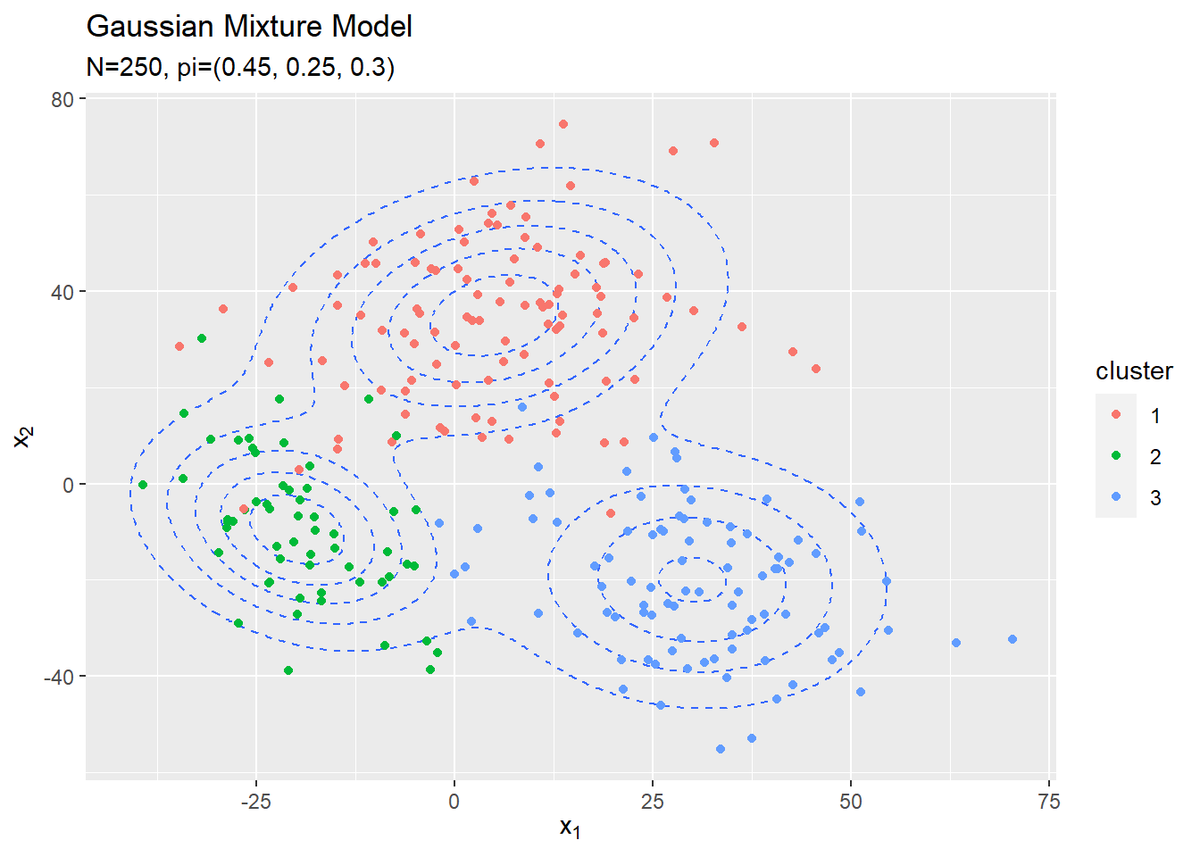
散布図はgeom_point()で描画します。クラスタごとに色分けしています。観測データから各データのクラスタも推定します。
・事前分布の設定
次に、観測モデル(観測データの分布)$p(\mathbf{X} | \mathbf{S}, \boldsymbol{\mu}, \boldsymbol{\Lambda})$と潜在変数の分布$p(\mathbf{S} | \boldsymbol{\pi})$に対する共役事前分布を設定します。多次元ガウス分布のパラメータ$\boldsymbol{\mu},\ \boldsymbol{\Lambda}$に対する事前分布$p(\boldsymbol{\mu}, \boldsymbol{\Lambda})$としてガウス・ウィシャート分布$\mathrm{NW}(\boldsymbol{\mu}, \boldsymbol{\Lambda} | \mathbf{m}, \beta, \nu, \mathbf{W})$、カテゴリ分布のパラメータ$\boldsymbol{\pi}$に対する事前分布$p(\boldsymbol{\pi})$としてディリクレ分布$p(\boldsymbol{\pi} | \boldsymbol{\alpha})$を設定します。
各事前分布のパラメータ(超パラメータ)を設定します。
# muの事前分布のパラメータを指定 beta <- 1 m_d <- rep(0, D) # lambdaの事前分布のパラメータを指定 w_dd <- diag(D) * 0.0005 nu <- D # piの事前分布のパラメータを指定 alpha_k <- rep(2, K)
$K$個の観測モデルの平均パラメータ$\boldsymbol{\mu}$の共通の事前分布(多次元ガウス分布)の平均パラメータ$\mathbf{m} = (m_1, m_2, \cdots, m_D)$をm_d、精度行列パラメータの係数$\beta$をbetaとして値を指定します。
$K$個の観測モデルの精度行列パラメータ$\boldsymbol{\Lambda}$の共通の事前分布(ウィシャート分布)のパラメータ$\mathbf{W} = (w_{1,1}, \cdots, w_{D,D})$をw_dd、自由度$\nu$をnuとして値を指定します。$\mathbf{W}$は正定値行列であり、自由度は$\nu > D - 1$の値をとります。
混合比率パラメータ$\boldsymbol{\pi}$の事前分布(ディリクレ分布)のパラメータ$\boldsymbol{\alpha} = (\alpha_1, \alpha_2, \cdots, \alpha_K)$をalpha_kとして、$\alpha_k > 0$の値を指定します。
パラメータを設定できたので、$\boldsymbol{\mu}$の事前分布をグラフで確認しましょう。作図用の$\boldsymbol{\mu}$の点を作成します。
# muの事前分布の標準偏差を計算 sigma_mu_d <- solve(beta * nu * w_dd) %>% diag() %>% sqrt() # 作図用のx軸のmuの値を作成 mu_1_vec <- seq( min(mu_truth_kd[, 1]) - sigma_mu_d[1], max(mu_truth_kd[, 1]) + sigma_mu_d[1], length.out = 250) # 作図用のy軸のmuの値を作成 mu_2_vec <- seq( min(mu_truth_kd[, 2]) - sigma_mu_d[2], max(mu_truth_kd[, 2]) + sigma_mu_d[2], length.out = 250 ) # 作図用のmuの点を作成 mu_point_mat <- cbind( rep(mu_1_vec, times = length(mu_2_vec)), rep(mu_2_vec, each = length(mu_1_vec)) )
$\mathbf{x}$の点のときと同様に作成します。各軸の描画範囲は、真の平均の最小値から事前分布の標準偏差を引いた値から、真の平均の最大値に標準偏差を足した値までとします。事前分布の標準偏差は$(\beta \boldsymbol{\Lambda}_k)^{-1}$の対角成分の平方根です。ただしこの時点では$\boldsymbol{\Lambda}$が未知の値なので、代わりに$\boldsymbol{\Lambda}$の期待値$\mathbb{E}[\boldsymbol{\Lambda}]$を使うことにします。ウィシャート分布の期待値(2.89)より
です。
また、逆行列の計算はsolve()、対角成分の抽出はdiag()、平方根の計算はsqrt()で行えます。
面倒でしたら適当な値を直接指定してください。
$\boldsymbol{\mu}$の事前分布の確率密度を計算して、作図用のデータフレームを作成します。
# muの事前分布をデータフレームに格納 prior_mu_df <- tibble( mu_1 = mu_point_mat[, 1], mu_2 = mu_point_mat[, 2], density = mvnfast::dmvn(X = mu_point_mat, mu = m_d, sigma = solve(beta * nu * w_dd)) )
観測モデルのときと同様に、多次元ガウス分布の確率密度を計算します。ここでも、$\boldsymbol{\mu}$の事前分布の分散共分散行列を$(\beta \mathbb{E}[\boldsymbol{\Lambda}])^{-1}$とします。
作成したデータフレームは次のようになります。
# 確認 head(prior_mu_df)
## # A tibble: 6 x 3 ## mu_1 mu_2 density ## <dbl> <dbl> <dbl> ## 1 -51.6 -51.6 0.0000111 ## 2 -51.2 -51.6 0.0000113 ## 3 -50.7 -51.6 0.0000116 ## 4 -50.3 -51.6 0.0000119 ## 5 -49.8 -51.6 0.0000121 ## 6 -49.3 -51.6 0.0000124
$\boldsymbol{\mu}$の事前分布を作図します。
# 真の平均をデータフレームに格納 mu_df <- tibble( x_1 = mu_truth_kd[, 1], x_2 = mu_truth_kd[, 2] ) # muの事前分布を作図 ggplot() + geom_contour(data = prior_mu_df, aes(x = mu_1, y = mu_2, z = density, color = ..level..)) + # 事前分布 geom_point(data = mu_df, aes(x = x_1, y = x_2), color = "red", shape = 4, size = 5) + # 真の値 labs(title = "Gaussian Distribution", subtitle = paste0("m=(", paste0(m_d, collapse = ", "), ")", ", sigma2_mu=(", paste0(solve(beta * nu * w_dd), collapse = ", "), ")"), x = expression(mu[1]), y = expression(mu[2]))

真の平均値をプロットしておきます。この真の平均を分布推定します。
$\boldsymbol{\Lambda}$と$\boldsymbol{\pi}$の事前分布(と事後分布)については省略します。詳しくは、3.2.2 項「カテゴリ分布の学習と予測」と3.4.2項「多次元ガウス分布の学習と予測:精度が未知の場合」を参照してください。
・初期値の設定
潜在変数$\mathbf{S}$の近似事後分布$q(\mathbf{S})$の期待値$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$をランダムに生成して初期値とします。また、生成した$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$を用いて各パラメータ$\boldsymbol{\mu},\ \boldsymbol{\Lambda},\ \boldsymbol{\pi}$の近似事後分布$q(\boldsymbol{\mu}),\ q(\boldsymbol{\Lambda}),\ q(\boldsymbol{\pi})$のパラメータ$\hat{\mathbf{m}},\ \hat{\boldsymbol{\beta}},\ \hat{\boldsymbol{\nu}},\ \hat{\mathbf{W}},\ \hat{\boldsymbol{\alpha}}$を計算して初期値とします。
$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$の初期値を生成します。
# 潜在変数の近似事後分布の期待値を初期化 E_s_nk <- runif(n = N * K, min = 0, max = 1) %>% matrix(nrow = N, ncol = K) E_s_nk <- E_s_nk / rowSums(E_s_nk) # 正規化
一様乱数の生成関数runif()を使って0から1の値を生成し、N行K列のマトリクスを作成してE_s_nkとします。ランダムに生成した値を、行ごとの和が1になるように正規化します。(正規化するので乱数の時点で0から1の値である必要はありませんが、確率であることを明示しておきます。)\
生成した潜在変数の期待値は次のようになります。
# 確認 round(E_s_nk[1:5, ], 3) rowSums(E_s_nk[1:5, ])
round(E_s_nk[1:5, ], 3) ## [,1] [,2] [,3] ## [1,] 0.653 0.329 0.018 ## [2,] 0.236 0.490 0.275 ## [3,] 0.356 0.150 0.494 ## [4,] 0.613 0.090 0.297 ## [5,] 0.421 0.467 0.112 ## [1] 1 1 1 1 1
データごとの和が1になります。
s_nkを用いて、$\boldsymbol{\mu}$の近似事後分布のパラメータを計算します。
# 初期値によるmuの近似事後分布のパラメータを計算:式(4.114) beta_hat_k <- colSums(E_s_nk) + beta m_hat_kd <- t(t(x_nd) %*% E_s_nk + beta * m_d) / beta_hat_k
$\boldsymbol{\mu}$の近似事後分布($K$個の多次元ガウス分布)の平均パラメータ$\hat{\mathbf{m}} = \{\hat{\mathbf{m}}_1, \hat{\mathbf{m}}_2, \cdots, \hat{\mathbf{m}}_K\}$、$\hat{\mathbf{m}}_k = (\hat{m}_{k,1}, \hat{m}_{k,2}, \cdots, \hat{m}_{k,D})$、精度行列パラメータの係数$\boldsymbol{\hat{\beta}} = \{\hat{\beta}_1, \hat{\beta}_2, \cdots, \hat{\beta}_K\}$の各項を
で計算して、それぞれbeta_hat_k、m_hat_kdとします。
# 確認
beta_hat_k
m_hat_kd
## [1] 80.29268 88.84880 83.85852 ## [,1] [,2] ## [1,] 8.876976 4.053336 ## [2,] 7.162336 4.543290 ## [3,] 8.700700 3.521244
同様に、$\boldsymbol{\lambda}$の近似事後分布のパラメータを計算します。
# 初期値によるlambdaの近似事後分布のパラメータを計算:式(4.118) w_hat_ddk <- array(0, dim = c(D, D, K)) term_m_dd <- beta * matrix(m_d) %*% t(m_d) for(k in 1:K) { term_x_dd <- t(E_s_nk[, k] * x_nd) %*% x_nd term_m_hat_dd <- beta_hat_k[k] * matrix(m_hat_kd[k, ]) %*% t(m_hat_kd[k, ]) w_hat_ddk[, , k] <- solve(term_x_dd + term_m_dd - term_m_hat_dd + solve(w_dd)) } nu_hat_k <- colSums(E_s_nk) + nu
$\boldsymbol{\lambda}$の近似事後分布($K$個のウィシャート分布)のパラメータ$\hat{\mathbf{W}} = \{\hat{\mathbf{W}}_1, \hat{\mathbf{W}}_2, \cdots, \hat{\mathbf{W}}_K\}$、$\hat{\mathbf{W}}_k = (\hat{w}_{k,1,1}, \cdots, \hat{w}_{k,D,D})$、自由度$\boldsymbol{\hat{\nu}} = \{\hat{\nu}_1, \hat{\nu}_2, \cdots, \hat{\nu}_K\}$を
で計算して、それぞれnu_hat_k、w_hat_ddkとします。
# 確認
w_hat_ddk
nu_hat_k
## , , 1 ## ## [,1] [,2] ## [1,] 2.516190e-05 5.413263e-06 ## [2,] 5.413263e-06 1.562642e-05 ## ## , , 2 ## ## [,1] [,2] ## [1,] 2.263013e-05 3.934521e-06 ## [2,] 3.934521e-06 1.338819e-05 ## ## , , 3 ## ## [,1] [,2] ## [1,] 2.201906e-05 4.063350e-06 ## [2,] 4.063350e-06 1.426164e-05 ## [1] 81.29268 89.84880 84.85852
最後に、$\boldsymbol{\pi}$の近似事後分布のパラメータを計算します。
# 初期値によるpiの近似事後分布のパラメータを計算:式(4.58) alpha_hat_k <- colSums(E_s_nk) + alpha_k
$\boldsymbol{\pi}$の近似事後分布(ディリクレ分布)のパラメータ$\hat{\boldsymbol{\alpha}} = (\hat{\alpha}_1, \hat{\alpha}_2, \cdots, \hat{\alpha}_K)$の各項を
で計算して、alpha_hat_kとします。
# 確認
alpha_hat_k
## [1] 81.29268 89.84880 84.85852
超パラメータの初期値が得られたので、$\boldsymbol{\mu}$の近似事後分布を確認しましょう。$K$個の近似事後分布を計算します。
# 初期値によるmuの近似事後分布をデータフレームに格納 posterior_mu_df <- tibble() for(k in 1:K) { # クラスタkのmuの近似事後分布を計算 tmp_density <- mvnfast::dmvn( X = mu_point_mat, mu = m_hat_kd[k, ], sigma = solve(beta_hat_k[k] * nu_hat_k[k] * w_hat_ddk[, , k]) ) # クラスタkの分布をデータフレームに格納 tmp_df <- tibble( mu_1 = mu_point_mat[, 1], mu_2 = mu_point_mat[, 2], density = tmp_density, cluster = as.factor(k) ) # 結果を結合 posterior_mu_df <- rbind(posterior_mu_df, tmp_df) }
事前分布のときと同様に計算します。ただし、超パラメータが$K$個になったので、多次元ガウス分布も$K$個になります。$K$回分の計算結果をデータフレームに格納していきます。
クラスタ$k$の近似事後分布の平均は$\hat{\mathbf{m}}$で、精度行列として$\hat{\beta}_k \mathbb{E}[\boldsymbol{\Lambda}_k]$を使います。事前分布のときと同様に、$\mathbb{E}[\boldsymbol{\Lambda}_k] = \hat{\nu}_k \hat{\mathbf{W}}_k$です。
作成したデータフレームは次のようになります。
# 確認 head(posterior_mu_df)
## # A tibble: 6 x 4 ## mu_1 mu_2 density cluster ## <dbl> <dbl> <dbl> <fct> ## 1 -51.6 -51.6 2.61e-253 1 ## 2 -51.2 -51.6 5.75e-251 1 ## 3 -50.7 -51.6 1.23e-248 1 ## 4 -50.3 -51.6 2.53e-246 1 ## 5 -49.8 -51.6 5.04e-244 1 ## 6 -49.3 -51.6 9.71e-242 1
$\boldsymbol{\mu}$の近似事後分布を作図します。
# 初期値によるmuの近似事後分布を作図 ggplot() + geom_contour(data = posterior_mu_df, aes(x = mu_1, y = mu_2, z = density, color = cluster)) + # 事後分布 geom_point(data = mu_df, aes(x = x_1, y = x_2), color = "red", shape = 4, size = 5) + # 真の値 labs(title = "Gaussian Distribution", subtitle = paste0("iter:", 0, ", N=", N), x = expression(mu[1]), y = expression(mu[2]))

m_hat_k, beta_hat_kとnu_hat_k, w_hat_ddkから求めた各パラメータの期待値を用いて、混合分布を計算します。
# 初期値による混合分布を計算 init_density <- 0 for(k in 1:K) { # クラスタkの分布の確率密度を計算 tmp_density <- mvnfast::dmvn( X = x_point_mat, mu = m_hat_kd[k, ], sigma = solve(nu_hat_k[k] * w_hat_ddk[, , k]) ) # K個の分布の加重平均を計算 init_density <- init_density + alpha_hat_k[k] / sum(alpha_hat_k) * tmp_density }
観測モデルのときと同様に、多次元ガウス混合分布の確率密度を計算します。ただし、パラメータ$\boldsymbol{\mu},\ \boldsymbol{\Lambda},\ \boldsymbol{\pi}$は未知なので、代わりに各パラメータの期待値$\mathbb{E}[\boldsymbol{\mu}],\ \mathbb{E}[\boldsymbol{\Lambda}],\ \mathbb{E}[\boldsymbol{\pi}]$を使うことにします。
クラスタ$k$における平均パラメータの期待値$\mathbb{E}[\boldsymbol{\mu}_k]$は、多次元ガウス分布の期待値(2.76)より
です。
また、混合比率パラメータの期待値は、ディリクレ分布の期待値(2.51)より
です。
超パラメータの初期値から求めた分布を作図します。
# 初期値による分布をデータフレームに格納 init_df <- tibble( x_1 = x_point_mat[, 1], x_2 = x_point_mat[, 2], density = init_density ) # 初期値による分布を作図 ggplot() + geom_contour(data = model_df, aes(x = x_1, y = x_2, z = density, color = ..level..), alpha = 0.5, linetype = "dashed") + # 真の分布 geom_contour(data = init_df, aes(x = x_1, y = x_2, z = density, color = ..level..)) + # 期待値による分布 labs(title = "Gaussian Mixture Model", subtitle = paste0("iter:", 0, ", K=", K), x = expression(x[1]), y = expression(x[2]))
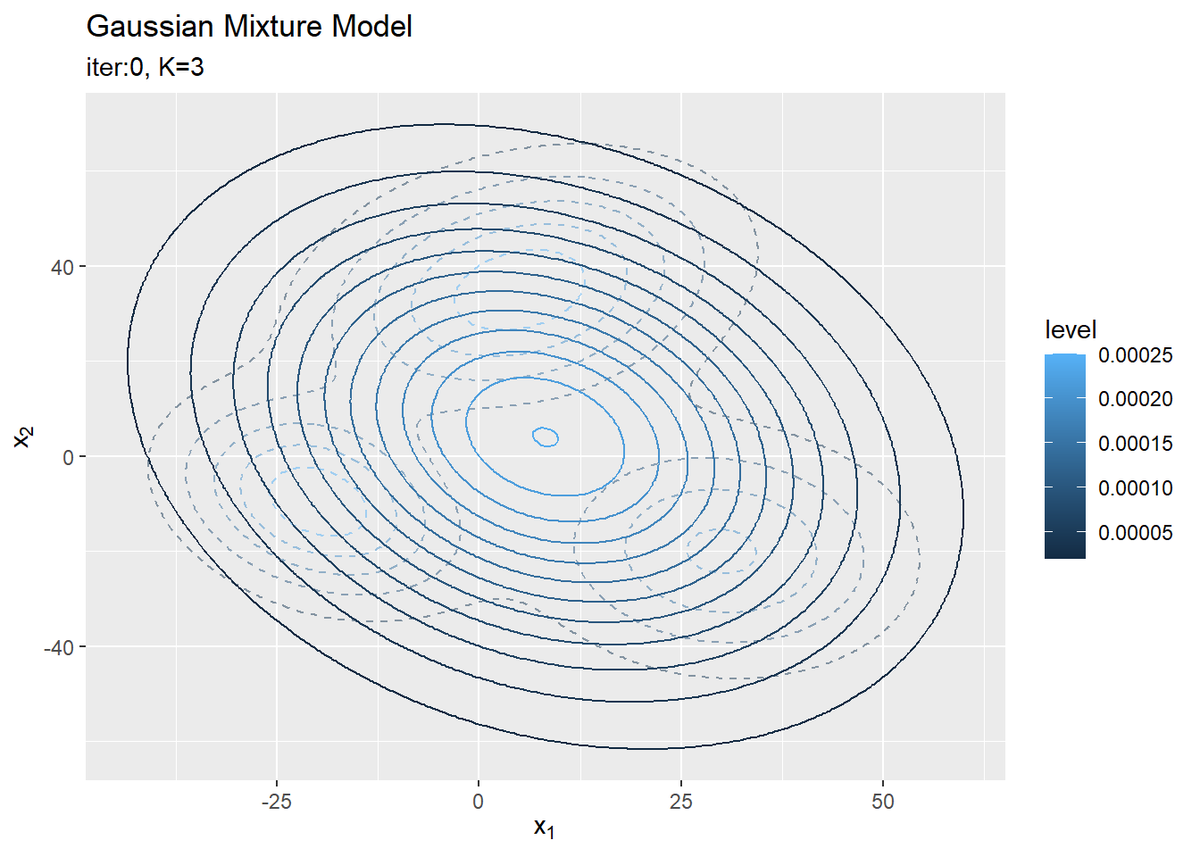
観測モデルのときと同様に作図します。
クラスタの散布図の作成用にデータフレームを作成します。
# 観測データと確率が最大のクラスタ番号をデータフレームに格納 s_df <- tibble( x_n1 = x_nd[, 1], x_n2 = x_nd[, 2], cluster = as.factor(max.col(E_s_nk)), # 確率が最大のクラスタ番号 prob = E_s_nk[cbind(1:N, max.col(E_s_nk))] # 確率の最大値 )
各データにおいて確率が最大のクラスタをそのデータのクラスタとすることにします。max.col()を使って、E_s_nkの行(データ)ごとに確率が最大の列番号(クラスタ番号)を抽出します。これをcluster列とします。
また、その確率をE_s_nk[cbind(1:N, max.col(E_s_nk))]で取り出してprob列とします。添字にマトリクスを指定することで抽出できます。
作成したデータフレームは次のようになります。
# 確認 head(s_df)
## # A tibble: 6 x 4 ## x_n1 x_n2 cluster prob ## <dbl> <dbl> <fct> <dbl> ## 1 -5.08 -17.2 1 0.653 ## 2 1.57 42.4 2 0.490 ## 3 19.1 21.2 3 0.494 ## 4 -11.8 35.0 1 0.613 ## 5 17.7 -17.2 2 0.467 ## 6 26.0 -9.53 3 0.563
クラスタの初期値の散布図を作成します。
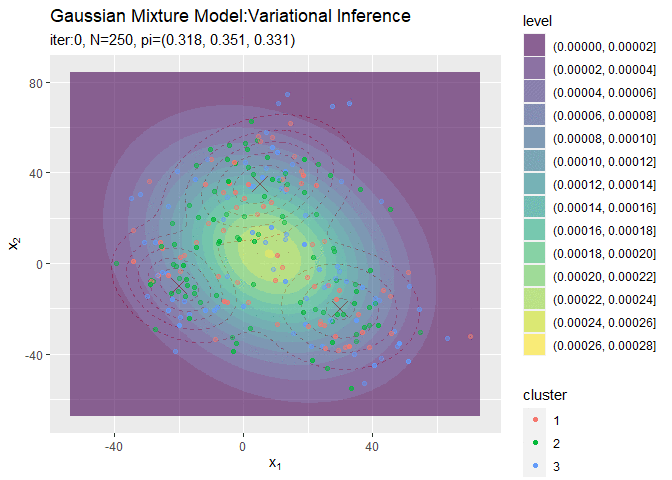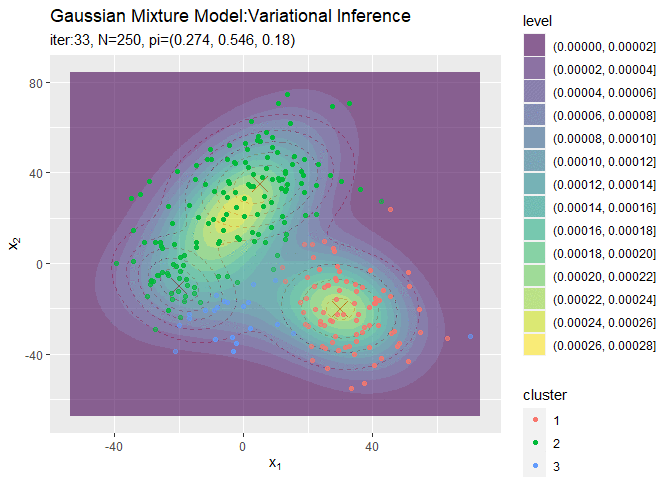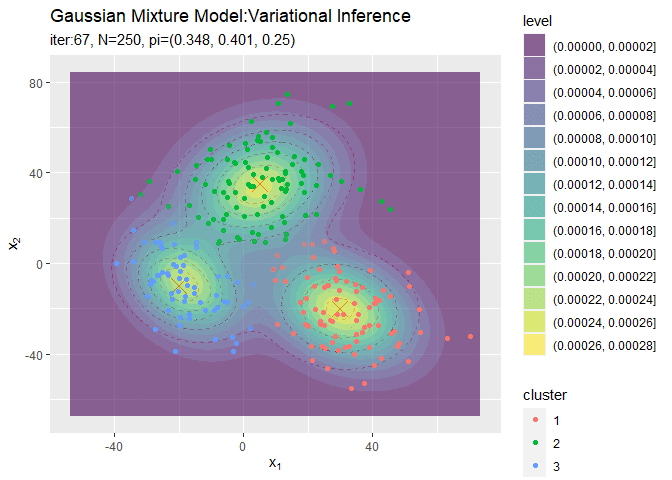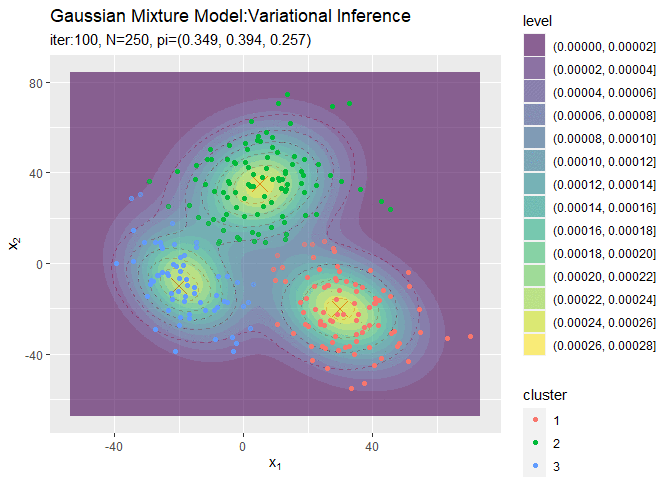
# クラスタの初期値を作図 ggplot() + geom_contour(data = model_df, aes(x = x_1, y = x_2, z = density), color = "red", alpha = 0.5, linetype = "dashed") + # 真の分布 geom_contour_filled(data = init_df, aes(x = x_1, y = x_2, z = density, fill = ..level..), alpha = 0.6) + # 期待値による分布 geom_point(data = s_df, aes(x = x_n1, y = x_n2, color = cluster), alpha = s_df[["prob"]]) + # 確率値によるクラスタ labs(title = "Gaussian Mixture Model", subtitle = paste0("iter:", 0, ", N=", N, ", K=", K), x = expression(x[1]), y = expression(x[2]))
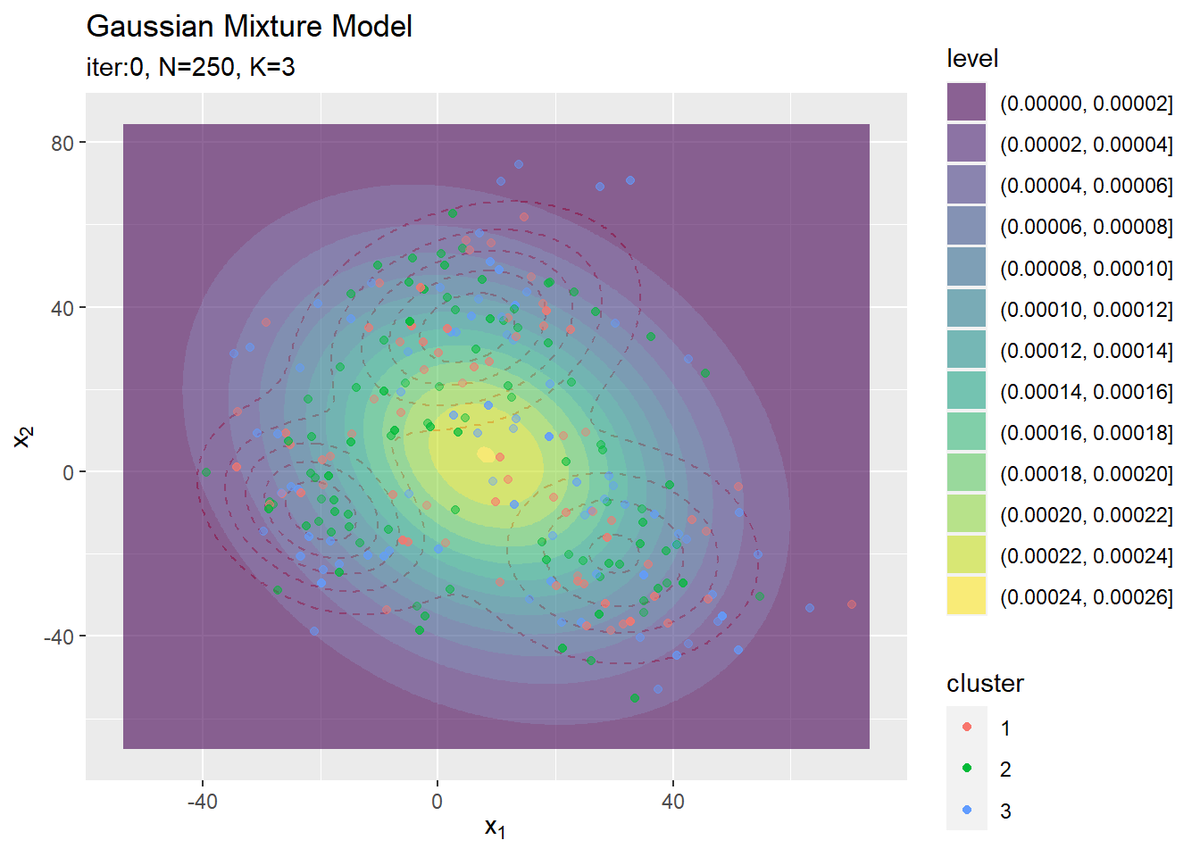
データの生成のときと同様にして作図します。ただしここでは、geom_point()の透過度の引数alphaにs_df[["prob"]]を指定することで、各データに割り当てられたクラスタとなる確率に従って濃淡を付けています。
・変分推論
変分推論では、潜在変数$\mathbf{S}$の近似事後分布$q(\mathbf{S})$の期待値$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$の更新と、各パラメータ$\boldsymbol{\mu},\ \boldsymbol{\Lambda},\ \boldsymbol{\pi}$の近似事後分布$q(\boldsymbol{\mu} | \boldsymbol{\Lambda}),\ q(\boldsymbol{\Lambda}),\ q(\boldsymbol{\pi})$のパラメータ(超パラメータ)$\hat{\mathbf{m}},\ \hat{\boldsymbol{\beta}},\ \hat{\mathbf{W}},\ \hat{\boldsymbol{\nu}},\ \hat{\boldsymbol{\alpha}}$の更新を交互に行います。
まずは、超パラメータの初期値を用いて潜在変数の近似事後分布$q(\mathbf{S})$のパラメータを計算します。得られたパラメータが近似事後分布の期待値$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$になります。次に、求めた$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$を用いて超パラメータを更新します。ここまでが1回の試行です。
さらに次の試行では、前回更新した超パラメータを用いて$\mathbf{S}$の近似事後分布を更新となります。この処理を指定した回数繰り返します。
・コード全体
中間変数ln_eta_nkに関して、添字を使って代入するため予め変数を用意しておく必要があります。
また、後で各パラメータの更新値や分布の推移を確認するために、それぞれ試行ごとにtrace_***に値を保存していきます。関心のあるパラメータを記録してください。
# 試行回数を指定 MaxIter <- 100 # 途中計算に用いる変数を作成 ln_eta_nk <- matrix(0, nrow = N, ncol = K) # 推移の確認用の受け皿を作成 trace_E_s_ink <- array(0, dim = c(MaxIter + 1, N, K)) trace_beta_ik <- matrix(0, nrow = MaxIter + 1, ncol = K) trace_m_ikd <- array(0, dim = c(MaxIter + 1, K, D)) trace_w_iddk <- array(0, dim = c(MaxIter + 1, D, D, K)) trace_nu_ik <- matrix(0, nrow = MaxIter + 1, ncol = K) trace_alpha_ik <- matrix(0, nrow = MaxIter + 1, ncol = K) # 初期値を記録 trace_E_s_ink[1, , ] <- E_s_nk trace_beta_ik[1, ] <- beta_hat_k trace_m_ikd[1, , ] <- m_hat_kd trace_w_iddk[1, , , ] <- w_hat_ddk trace_nu_ik[1, ] <- nu_hat_k trace_alpha_ik[1, ] <- alpha_hat_k # 変分推論 for(i in 1:MaxIter) { # 潜在変数の近似事後分布のパラメータを計算:式(4.109) for(k in 1:K) { # クラスタkの中間変数を計算:式(4.119-4.122,4.62) E_lmd_dd <- nu_hat_k[k] * w_hat_ddk[, , k] E_ln_det_lmd <- sum(digamma(0.5 * (nu_hat_k[k] + 1 - 1:D))) + D * log(2) + log(det(w_hat_ddk[, , k])) E_lmd_mu_d1 <- E_lmd_dd %*% matrix(m_hat_kd[k, ]) E_mu_lmd_mu <- (t(m_hat_kd[k, ]) %*% E_lmd_mu_d1 + D / beta_hat_k[k]) %>% as.vector() E_ln_pi <- digamma(alpha_hat_k[k]) - digamma(sum(alpha_hat_k)) term_x1_n <- - 0.5 * x_nd %*% E_lmd_dd %*% t(x_nd) %>% diag() term_x2_n <- x_nd %*% E_lmd_mu_d1 %>% as.vector() ln_eta_nk[, k] <- term_x1_n + term_x2_n - 0.5 * E_mu_lmd_mu + 0.5 * E_ln_det_lmd + E_ln_pi } tmp_eta_nk <- exp(ln_eta_nk) eta_nk <- (tmp_eta_nk + 1e-7) / rowSums(tmp_eta_nk + 1e-7) # 正規化 # 潜在変数の近似事後分布の期待値を計算:式(4.59) E_s_nk <- eta_nk # 初期値によるmuの近似事後分布のパラメータを計算:式(4.114) beta_hat_k <- colSums(E_s_nk) + beta m_hat_kd <- t(t(x_nd) %*% E_s_nk + beta * m_d) / beta_hat_k # 初期値によるlambdaの近似事後分布のパラメータを計算:式(4.118) w_hat_ddk <- array(0, dim = c(D, D, K)) term_m_dd <- beta * matrix(m_d) %*% t(m_d) for(k in 1:K) { term_x_dd <- t(E_s_nk[, k] * x_nd) %*% x_nd term_m_hat_dd <- beta_hat_k[k] * matrix(m_hat_kd[k, ]) %*% t(m_hat_kd[k, ]) w_hat_ddk[, , k] <- solve(term_x_dd + term_m_dd - term_m_hat_dd + solve(w_dd)) } nu_hat_k <- colSums(E_s_nk) + nu # piの近似事後分布のパラメータを計算:式(4.58) alpha_hat_k <- colSums(E_s_nk) + alpha_k # i回目のパラメータを記録 trace_E_s_ink[i + 1, , ] <- E_s_nk trace_beta_ik[i + 1, ] <- beta_hat_k trace_m_ikd[i + 1, , ] <- m_hat_kd trace_w_iddk[i + 1, , , ] <- w_hat_ddk trace_nu_ik[i + 1, ] <- nu_hat_k trace_alpha_ik[i + 1, ] <- alpha_hat_k # 動作確認 #print(paste0(i, ' (', round(i / MaxIter * 100, 1), '%)')) }
・処理の解説
変分推論で行う処理を確認していきます。
・潜在変数のサンプリング
潜在変数$\mathbf{S}$の近似事後分布(のパラメータ)を計算して、新たな$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$を求めます。
$\mathbf{S}$の近似事後分布のパラメータを計算します。
# 潜在変数の近似事後分布のパラメータを計算:式(4.109) for(k in 1:K) { # クラスタkの中間変数を計算:式(4.119-4.122,4.62) E_lmd_dd <- nu_hat_k[k] * w_hat_ddk[, , k] E_ln_det_lmd <- sum(digamma(0.5 * (nu_hat_k[k] + 1 - 1:D))) + D * log(2) + log(det(w_hat_ddk[, , k])) E_lmd_mu_d1 <- E_lmd_dd %*% matrix(m_hat_kd[k, ]) E_mu_lmd_mu <- (t(m_hat_kd[k, ]) %*% E_lmd_mu_d1 + D / beta_hat_k[k]) %>% as.vector() E_ln_pi <- digamma(alpha_hat_k[k]) - digamma(sum(alpha_hat_k)) term_x1_n <- - 0.5 * x_nd %*% E_lmd_dd %*% t(x_nd) %>% diag() term_x2_n <- x_nd %*% E_lmd_mu_d1 %>% as.vector() ln_eta_nk[, k] <- term_x1_n + term_x2_n - 0.5 * E_mu_lmd_mu + 0.5 * E_ln_det_lmd + E_ln_pi } tmp_eta_nk <- exp(ln_eta_nk) eta_nk <- (tmp_eta_nk + 1e-7) / rowSums(tmp_eta_nk + 1e-7) # 正規化
$n$番目のデータの潜在変数$\mathbf{s}_n$の近似事後分布(カテゴリ分布)のパラメータ$\boldsymbol{\eta}_n = (\eta_{n,1}, \eta_{n,2}, \cdots, \eta_{n,K})$の各項を、次の式で計算します。
$\eta_{n,k}$は、$n$番目の観測データ$\mathbf{x}_n$にクラスタ$k$が割り当てられる($s_{n,k} = 1$となる)確率を表します。また、各項は
で計算できます。
ただし、$\mathbf{x}_n^{\top} \mathbb{E}_{q(\boldsymbol{\Lambda}_k)} [\boldsymbol{\Lambda}_k] \mathbf{x}_n$の計算において、$N$個全てのデータを一度で処理するために1から$N$の全ての組み合わせで行います(term_x1_nの計算時)。この計算結果は、$N \times N$のマトリクスになります。これは例えば、1行$N$列目の要素は$\mathbf{x}_1^{\top} \mathbb{E}_{q(\boldsymbol{\Lambda}_k)} [\boldsymbol{\Lambda}_k] \mathbf{x}_N$の計算結果です。これは不要なので、diag()で対角成分(同じデータによる計算結果)のみを取り出します。
最後に、データごとの和が1となるように
で正規化します。ただし、0除算とならないように、微小な値1e-7($10^{-7} = 0.0000001$)を加えています。
# 確認 eta_nk[1:5, ] rowSums(eta_nk[1:5, ])
## [,1] [,2] [,3] ## [1,] 0.0685830090 0.022472199 0.9089447920 ## [2,] 0.0003925123 0.999378359 0.0002291287 ## [3,] 0.0699756839 0.929733758 0.0002905581 ## [4,] 0.0006705523 0.982364763 0.0169646845 ## [5,] 0.9816656363 0.007535055 0.0107993085 ## [1] 1 1 1 1 1
行(データ)ごとの和が1になるのを確認できます。
eta_nkが$\mathbf{S}$の近似事後分布の期待値です。
# 潜在変数の近似事後分布の期待値を計算:式(4.59) E_s_nk <- eta_nk
$\mathbf{S}$の近似事後分布の期待値$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$の各項は、カテゴリ分布の期待値(2.31)より
です。
これで$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$が得られました。次は、更新した$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$を用いて、超パラメータ$\hat{\mathbf{m}},\ \hat{\boldsymbol{\beta}},\ \hat{\mathbf{W}},\ \hat{\boldsymbol{\nu}},\ \hat{\boldsymbol{\alpha}}$を更新します。
「初期値の設定」のときと同様に計算できます。
以上が変分推論による近似推論で行うの個々の処理です。これを指定した回数繰り返し行うことで、各パラメータの値を徐々に真の値に近付けていきます。
・推論結果の確認
推論結果を確認していきます。
・最後のパラメータの確認
超パラメータm_hat_k, beta_hat_kとnu_hat_k, w_hat_ddkの最後の更新値を用いて、$\boldsymbol{\mu}$の近似事後分布を計算します。
# muの近似事後分布をデータフレームに格納 posterior_mu_df <- tibble() for(k in 1:K) { # クラスタkのmuの近似事後分布を計算 tmp_density <- mvnfast::dmvn( X = mu_point_mat, mu = m_hat_kd[k, ], sigma = solve(beta_hat_k[k] * nu_hat_k[k] * w_hat_ddk[, , k]) ) # クラスタkの分布をデータフレームに格納 tmp_df <- tibble( mu_1 = mu_point_mat[, 1], mu_2 = mu_point_mat[, 2], density = tmp_density, cluster = as.factor(k) ) # 結果を結合 posterior_mu_df <- rbind(posterior_mu_df, tmp_df) } # muの近似事後分布を作図 ggplot() + geom_contour(data = posterior_mu_df, aes(x = mu_1, y = mu_2, z = density, color = cluster)) + # 近似事後分布 geom_point(data = mu_df, aes(x = x_1, y = x_2), color = "red", shape = 4, size = 5) + # 真の値 labs(title = "Gaussian Distribution:Variational Inference", subtitle = paste0("iter:", MaxIter, ", N=", N), x = expression(mu[1]), y = expression(mu[2]))
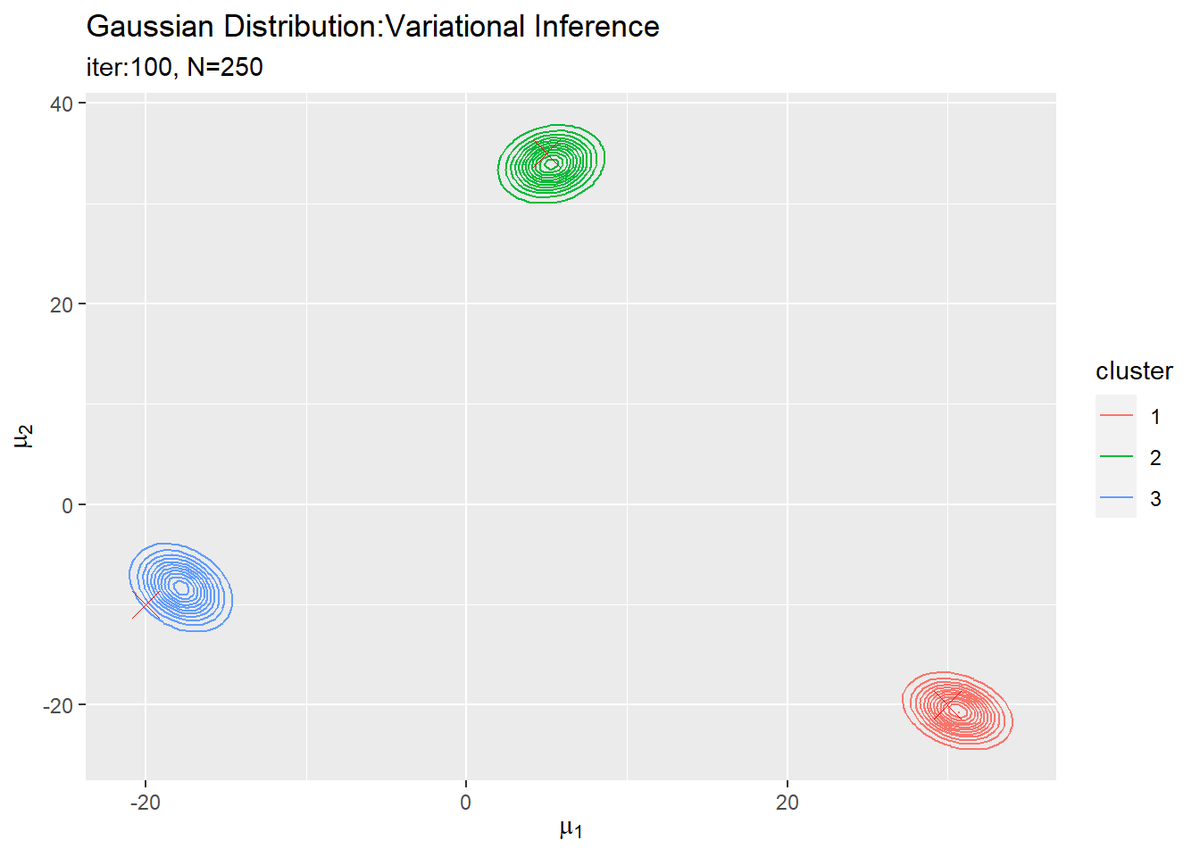
変数名やタイトル以外は「初期値の設定」のときと同じコードです。
$K$個のガウス分布がそれぞれ真の平均付近をピークとする分布を推定できています。
m_hat_k, beta_hat_kとnu_hat_k, w_hat_ddkから求めた各パラメータの期待値$\mathbb{E}[\boldsymbol{\mu}],\ \mathbb{E}[\boldsymbol{\Lambda}],\ \mathbb{E}[\boldsymbol{\pi}]$を用いて、混合分布を計算します。
# 最後に更新したパラメータの期待値による混合分布を計算 res_density <- 0 for(k in 1:K) { # クラスタkの分布の確率密度を計算 tmp_density <- mvnfast::dmvn( X = x_point_mat, mu = m_hat_kd[k, ], sigma = solve(nu_hat_k[k] * w_hat_ddk[, , k]) ) # K個の分布の加重平均を計算 res_density <- res_density + alpha_hat_k[k] / sum(alpha_hat_k) * tmp_density } # 最終的な分布をデータフレームに格納 res_df <- tibble( x_1 = x_point_mat[, 1], x_2 = x_point_mat[, 2], density = res_density ) # 最終的な分布を作図 ggplot() + geom_contour(data = model_df, aes(x = x_1, y = x_2, z = density, color = ..level..), alpha = 0.5, linetype = "dashed") + # 真の分布 geom_point(data = mu_df, aes(x = x_1, y = x_2), color = "red", shape = 4, size = 5) + # 真の平均 geom_contour(data = res_df, aes(x = x_1, y = x_2, z = density, color = ..level..)) + # 期待値による分布 geom_point(data = x_df, aes(x = x_n1, y = x_n2)) + # 観測データ labs(title = "Gaussian Mixture Model:Variational Inference", subtitle = paste0("iter:", MaxIter, ", N=", N, ", K=", K), x = expression(x[1]), y = expression(x[2]))

変数名やタイトル以外は「初期値の設定」のときと同じコードです。
真の分布に近い分布になっています。
最後にサンプルしたクラスタの散布図を作成します。
# 観測データと確率が最大のクラスタ番号をデータフレームに格納 s_df <- tibble( x_n1 = x_nd[, 1], x_n2 = x_nd[, 2], cluster = as.factor(max.col(E_s_nk)), # 確率が最大のクラスタ番号 prob = E_s_nk[cbind(1:N, max.col(E_s_nk))] # 確率の最大値 ) # 最終的なクラスタを作図 ggplot() + geom_contour(data = model_df, aes(x = x_1, y = x_2, z = density), color = "red", alpha = 0.5, linetype = "dashed") + # 真の分布 geom_point(data = mu_df, aes(x = x_1, y = x_2), color = "red", shape = 4, size = 5) + # 真の平均 geom_contour_filled(data = res_df, aes(x = x_1, y = x_2, z = density, fill = ..level..), alpha = 0.6) + # 期待値による分布 geom_point(data = s_df, aes(x = x_n1, y = x_n2, color = cluster), alpha = s_df[["prob"]]) + # 確率値によるクラスタ labs(title = "Gaussian Mixture Model:Variational Inference", subtitle = paste0("iter:", MaxIter, ", N=", N, ", E[pi]=(", paste0(round(alpha_hat_k / sum(alpha_hat_k), 3), collapse = ", "), ")"), x = expression(x[1]), y = expression(x[2]))

タイトル以外は「初期値の設定」のときと同じコードです。
クラスタリングできていることが確認できます。また、(分かりにくいけど)クラスタの境界付近の色が薄く(確率が低く)なっています。ただし、クラスタの番号についてはランダムに決まるため真のクラスタの番号と一致しません。
・超パラメータの推移の確認
超パラメータ$\hat{\mathbf{m}},\ \hat{\boldsymbol{\beta}},\ \hat{\boldsymbol{\nu}}, \hat{\mathbf{W}},\ \hat{\boldsymbol{\alpha}}$の更新値の推移を確認します。
・コード(クリックで展開)
学習ごとの値を格納した各パラメータのマトリクスtrace_***をtidyr::pivot_longer()で縦長のデータフレームに変換して作図します。
# mの推移を作図 dplyr::as_tibble(trace_m_ikd) %>% # データフレームに変換 magrittr::set_names( paste0(rep(paste0("k=", 1:K), D), rep(paste0(", d=", 1:D), each = K)) ) %>% # 列名として次元情報を付与 cbind(iteration = 1:(MaxIter + 1)) %>% # 試行回数列を追加 tidyr::pivot_longer( cols = -iteration, # 変換しない列 names_to = "dim", # 現列名を格納する列名 values_to = "value" # 現要素を格納する列名 ) %>% # 縦持ちに変換 ggplot(aes(x = iteration, y = value, color = dim)) + geom_line() + labs(title = "Variational Inference", subtitle = expression(hat(m)))
# betaの推移を作図 dplyr::as_tibble(trace_beta_ik) %>% # データフレームに変換 cbind(iteration = 1:(MaxIter + 1)) %>% # 試行回数の列を追加 tidyr::pivot_longer( cols = -iteration, # 変換しない列 names_to = "cluster", # 現列名を格納する列名 names_prefix = "V", # 現列名の頭から取り除く文字列 names_ptypes = list(cluster = factor()), # 現列名を値とする際の型 values_to = "value" # 現セルを格納する列名 ) %>% # 縦持ちに変換 ggplot(aes(x = iteration, y = value, color = cluster)) + geom_line() + # 推定値 labs(title = "Variational Inference", subtitle = expression(hat(beta)))
# nuの推移を作図 dplyr::as_tibble(trace_nu_ik) %>% # データフレームに変換 cbind(iteration = 1:(MaxIter + 1)) %>% # 試行回数の列を追加 tidyr::pivot_longer( cols = -iteration, # 変換しない列 names_to = "cluster", # 現列名を格納する列名 names_prefix = "V", # 現列名の頭から取り除く文字列 names_ptypes = list(cluster = factor()), # 現列名を値とする際の型 values_to = "value" # 現セルを格納する列名 ) %>% # 縦持ちに変換 ggplot(aes(x = iteration, y = value, color = cluster)) + geom_line() + # 推定値 labs(title = "Variational Inference", subtitle = expression(hat(nu)))
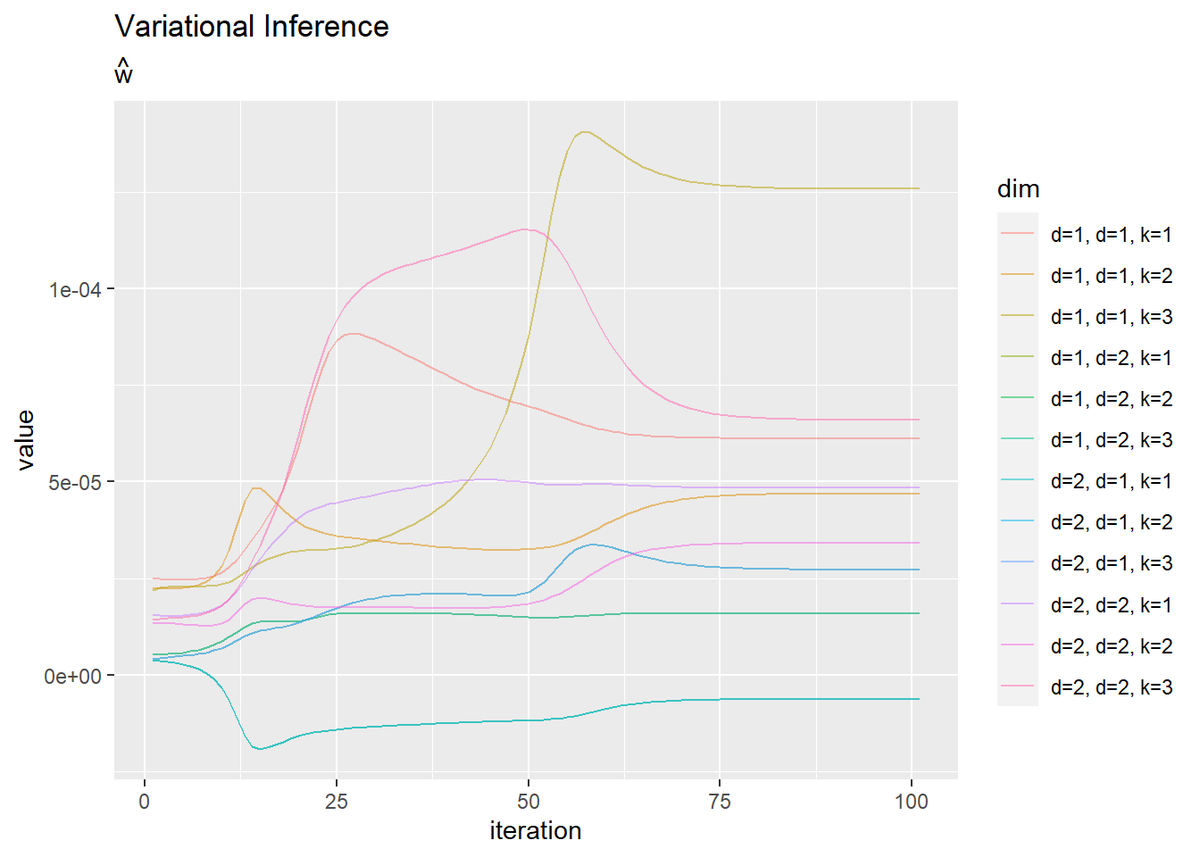
# wの推移を作図 dplyr::as_tibble(trace_w_iddk) %>% # データフレームに変換 magrittr::set_names( paste0( rep(paste0("d=", 1:D), times = D * K), rep(rep(paste0(", d=", 1:D), each = D), times = K), rep(paste0(", k=", 1:K), each = D * D) ) ) %>% # 列名として次元情報を付与 cbind(iteration = 1:(MaxIter + 1)) %>% # 試行回数列を追加 tidyr::pivot_longer( cols = -iteration, # 変換しない列 names_to = "dim", # 現列名を格納する列名 values_to = "value" # 現要素を格納する列名 ) %>% # 縦持ちに変換 ggplot(aes(x = iteration, y = value, color = dim)) + geom_line(alpha = 0.5) + labs(title = "Variational Inference", subtitle = expression(hat(w)))
# alphaの推移を作図 dplyr::as_tibble(trace_alpha_ik) %>% # データフレームに変換 cbind(iteration = 1:(MaxIter + 1)) %>% # 試行回数の列を追加 tidyr::pivot_longer( cols = -iteration, # 変換しない列 names_to = "cluster", # 現列名を格納する列名 names_prefix = "V", # 現列名の頭から取り除く文字列 names_ptypes = list(cluster = factor()), # 現列名を値とする際の型 values_to = "value" # 現セルを格納する列名 ) %>% # 縦持ちに変換 ggplot(aes(x = iteration, y = value, color = cluster)) + geom_line() + # 推定値 labs(title = "Variational Inference", subtitle = expression(hat(alpha)))




・おまけ:アニメーションによる推移の確認
gganimateパッケージを利用して、各分布の推移のアニメーション(gif画像)を作成するためのコードです。
# 追加パッケージ library(gganimate)
・平均パラメータの事後分布の推移
・コード(クリックで展開)
$\boldsymbol{\mu}$の事後分布の推移を確認します。作図用のデータフレームを作成します。
# 作図用のデータフレームを作成 trace_posterior_df <- tibble() for(i in 1:(MaxIter + 1)) { for(k in 1:K) { # クラスタkのmuの近似事後分布を計算 tmp_density <- mvnfast::dmvn( X = mu_point_mat, mu = trace_m_ikd[i, k, ], sigma = solve(trace_beta_ik[i, k] * trace_nu_ik[i, k] * trace_w_iddk[i, , , k]) ) # クラスタkの分布をデータフレームに格納 tmp_df <- tibble( mu_1 = mu_point_mat[, 1], mu_2 = mu_point_mat[, 2], density = tmp_density, cluster = as.factor(k), iteration = as.factor(i - 1) ) # 結果を結合 trace_posterior_df <- rbind(trace_posterior_df, tmp_df) } # 動作確認 #print(paste0(i - 1, ' (', round((i - 1) / MaxIter * 100, 1), '%)')) }
各試行における計算結果を同じデータフレームに格納していく必要があります。処理に時間がかかる場合は、描画するフレーム数(1:(MaxIter + 1))や、mu_point_matの範囲や点の間隔を調整してください。
分布の推移をgif画像で出力します。
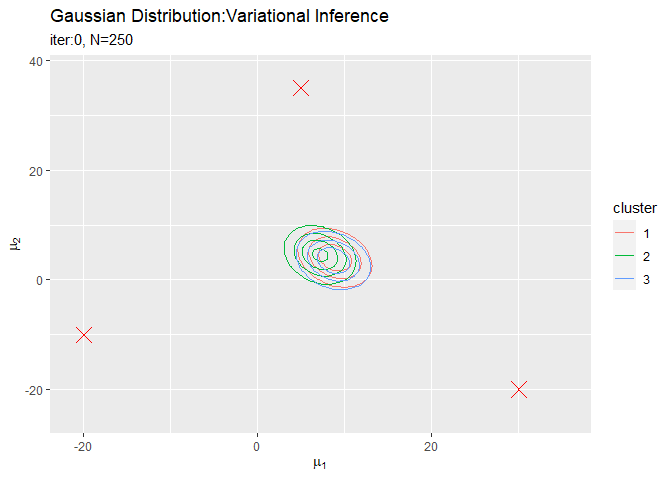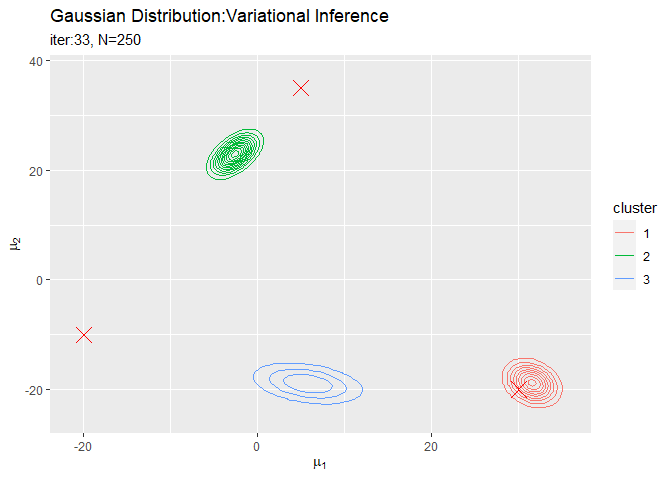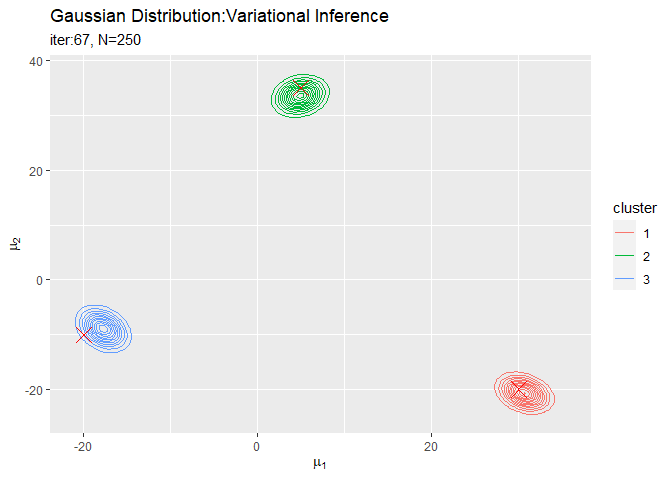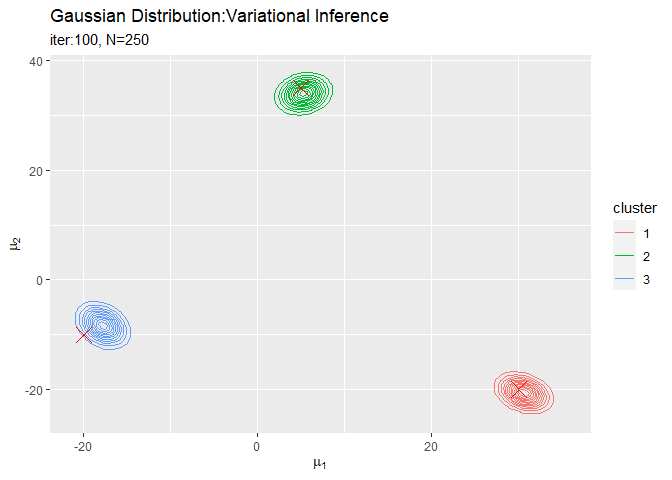
# muの近似事後分布を作図 trace_posterior_graph <- ggplot() + geom_contour(data = trace_posterior_df, aes(x = mu_1, y = mu_2, z = density, color = cluster)) + # 近似事後分布 geom_point(data = mu_df, aes(x = x_1, y = x_2), color = "red", shape = 4, size = 5) + # 真の値 gganimate::transition_manual(iteration) + # フレーム labs(title = "Gaussian Distribution:Variational Inference", subtitle = paste0("iter:{current_frame}", ", N=", N), x = expression(mu[1]), y = expression(mu[2])) # gif画像を作成 gganimate::animate(trace_posterior_graph, nframes = MaxIter + 1, fps = 10)
各フレームの順番を示す列をgganimate::transition_manual()に指定します。初期値を含むため、フレーム数はMaxIter + 1です。
・パラメータの期待値による分布とクラスタの推移
・コード(クリックで展開)
各パラメータの期待値を用いた分布とクラスタのサンプルの推移を確認します。同様に、作図用のデータフレームを作成します。
# 作図用のデータフレームを作成 trace_model_df <- tibble() trace_cluster_df <- tibble() for(i in 1:(MaxIter + 1)) { # i回目の混合分布を計算 res_density <- 0 for(k in 1:K) { # クラスタkの分布の確率密度を計算 tmp_density <- mvnfast::dmvn( X = x_point_mat, mu = trace_m_ikd[i, k, ], sigma = solve(trace_nu_ik[i, k] * trace_w_iddk[i, , , k]) ) # K個の分布の加重平均を計算 res_density <- res_density + trace_alpha_ik[i, k] / sum(trace_alpha_ik[i, ]) * tmp_density } # i回目の分布をデータフレームに格納 res_df <- tibble( x_1 = x_point_mat[, 1], x_2 = x_point_mat[, 2], density = res_density, iteration = as.factor(i - 1), label = paste0( "iter:", i - 1, ", N=", N, ", pi=(", paste0(round(trace_alpha_ik[i, ] / sum(trace_alpha_ik[i, ]), 3), collapse = ", "), ")" ) %>% as.factor() ) # 結果を結合 trace_model_df <- rbind(trace_model_df, res_df) # 観測データとi回目のクラスタ番号をデータフレームに格納 tmp_E_s_nk <- trace_E_s_ink[i, , ] # i回目の結果 s_df <- tibble( x_n1 = x_nd[, 1], x_n2 = x_nd[, 2], cluster = as.factor(max.col(tmp_E_s_nk)), # 確率が最大のクラスタ番号 prob = tmp_E_s_nk[cbind(1:N, max.col(tmp_E_s_nk))], # 確率の最大値 iteration = as.factor(i - 1), label = paste0( "iter:", i - 1, ", N=", N, ", pi=(", paste0(round(trace_alpha_ik[i, ] / sum(trace_alpha_ik[i, ]), 3), collapse = ", "), ")" ) %>% as.factor() ) # 結果を結合 trace_cluster_df <- rbind(trace_cluster_df, s_df) # 動作確認 #print(paste0(i - 1, ' (', round((i - 1) / MaxIter * 100, 1), '%)')) }
・パラメータの期待値による分布の推移
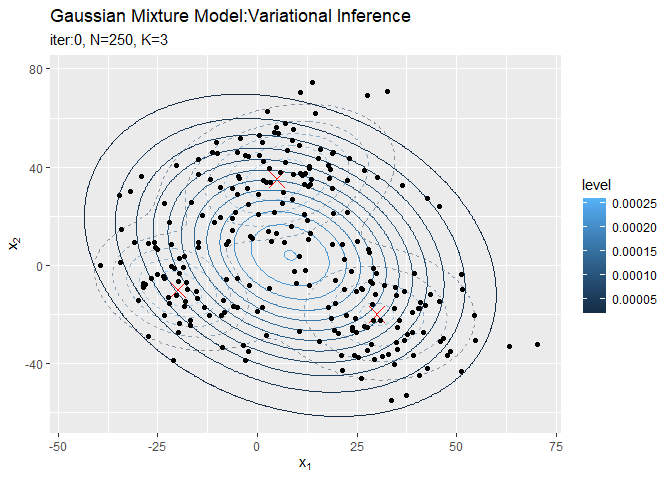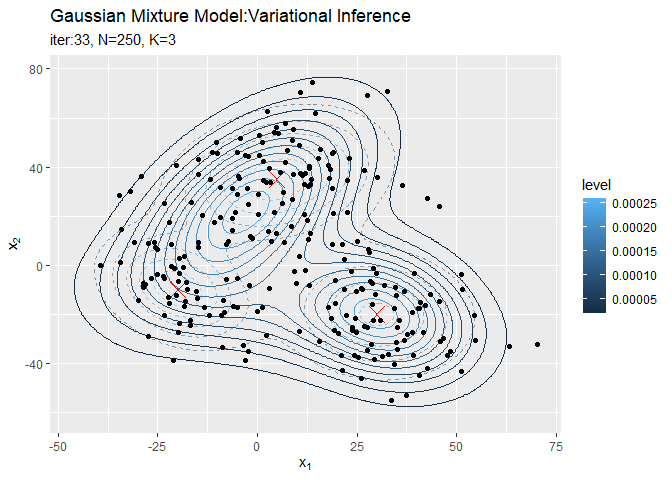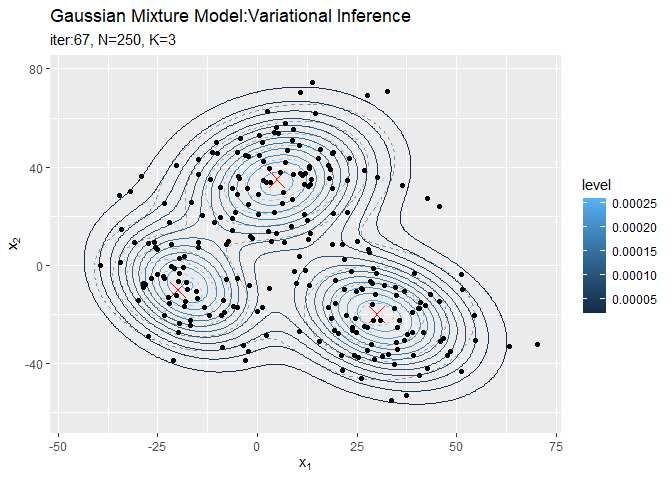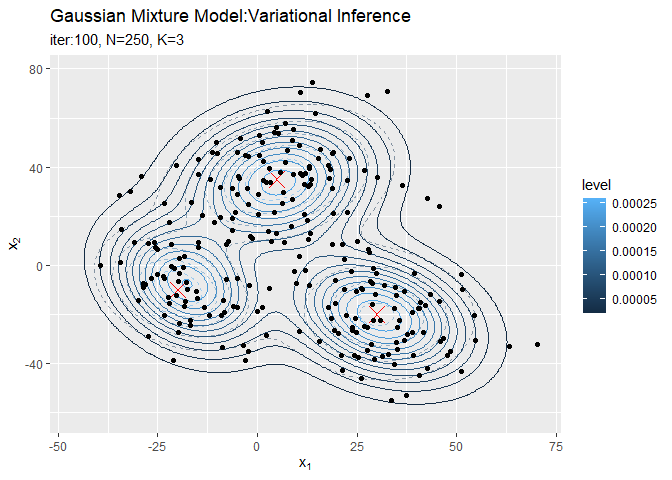
# 分布の推移を作図 trace_model_graph <- ggplot() + geom_contour(data = model_df, aes(x = x_1, y = x_2, z = density, color = ..level..), alpha = 0.5, linetype = "dashed") + # 真の分布 geom_point(data = mu_df, aes(x = x_1, y = x_2), color = "red", shape = 4, size = 5) + # 真の平均 geom_contour(data = trace_model_df, aes(x = x_1, y = x_2, z = density, color = ..level..)) + # 期待値による分布 geom_point(data = trace_cluster_df, aes(x = x_n1, y = x_n2)) + # 観測データ gganimate::transition_manual(iteration) + # フレーム labs(title = "Gaussian Mixture Model:Variational Inference", subtitle = paste0("iter:{current_frame}", ", N=", N, ", K=", K), x = expression(x[1]), y = expression(x[2])) # gif画像を作成 gganimate::animate(trace_model_graph, nframes = MaxIter + 1, fps = 10)
・クラスタの散布図の推移
# クラスタの推移を作図 trace_cluster_graph <- ggplot() + geom_contour(data = model_df, aes(x = x_1, y = x_2, z = density), color = "red", alpha = 0.5, linetype = "dashed") + # 真の分布 geom_point(data = mu_df, aes(x = x_1, y = x_2), color = "red", shape = 4, size = 5) + # 真の平均 geom_contour_filled(data = trace_model_df, aes(x = x_1, y = x_2, z = density), alpha = 0.6) + # 期待値による分布 geom_point(data = trace_cluster_df, aes(x = x_n1, y = x_n2, color = cluster), alpha = trace_cluster_df[["prob"]]) + # 確率が最大のクラスタ gganimate::transition_manual(label) + # フレーム labs(title = "Gaussian Mixture Model:Variational Inference", subtitle = "{current_frame}", x = expression(x[1]), y = expression(x[2])) # gif画像を作成 gganimate::animate(trace_cluster_graph, nframes = MaxIter + 1, fps = 10)
Enjoy!
参考文献
- 須山敦志『ベイズ推論による機械学習入門』(機械学習スタートアップシリーズ)杉山将監修,講談社,2017年.
おわりに
2年ほどROM専だったアドベントカレンダーに初参加しました!
アドカレ経由で初めてこのブログを読む方が増えることを期待して、簡単に自己紹介します。
ここ1年半ほどは、ベイズ推論系の本を読んで、数式の行間を埋め、スクラッチで組み、アルゴリズムを理解することを目指しております。この記事もその内の1つです。よければ他の記事も読んでみてください。そして何か間違い等あったらご指摘ください!よろしくお願いします。
ただ本当は、ハロプロ楽曲の歌詞分析をしたいだけのオタクです。NLPerになるべくトピックモデルを勉強し始めてから何かおかしな方向へ進んでいます。
そんなこんなで今年はベイズ力が少し上がったので、来年はR力を少し上げたいです。
この記事でもイメージしたグラフを描けず悔しいです。クラスタ(潜在変数)を推定した散布図について、左のようにデータごとに確率が最大のクラスタで色分けしましたが、右のように確率値に応じてグラデーションで表現できます。
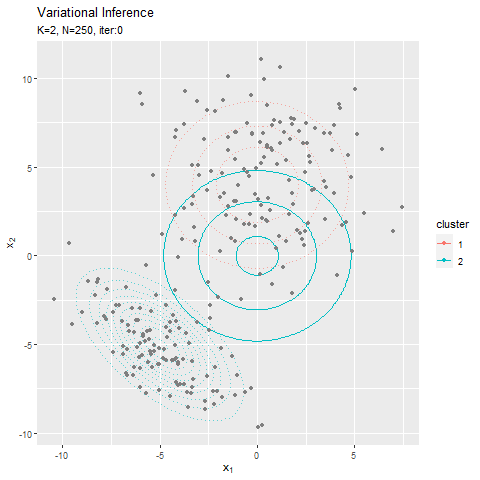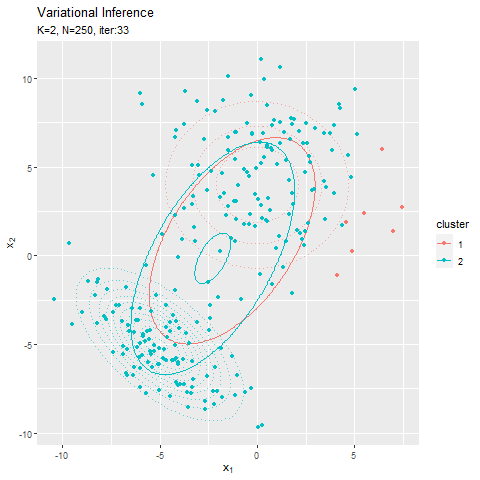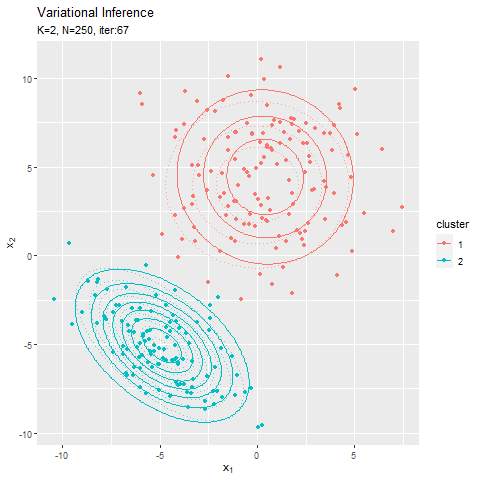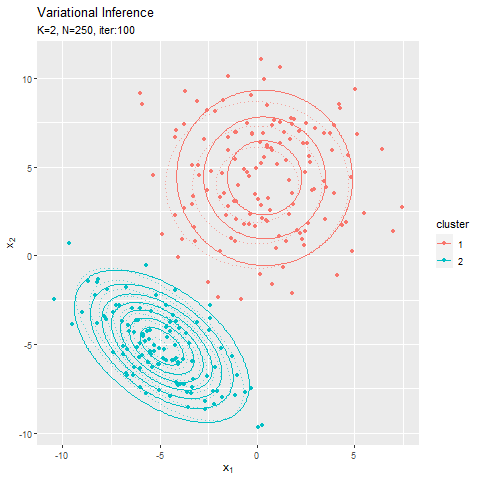
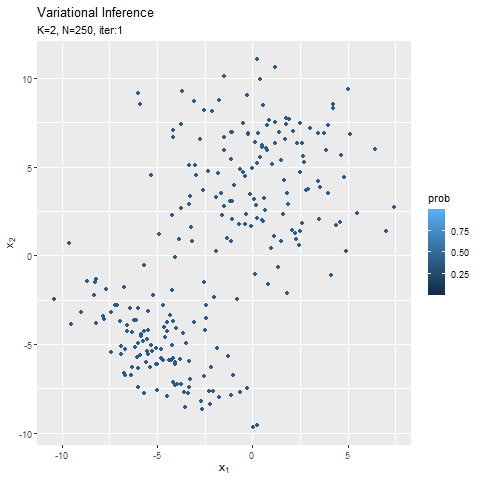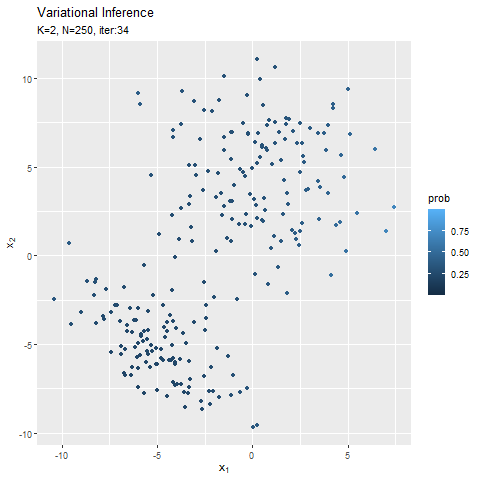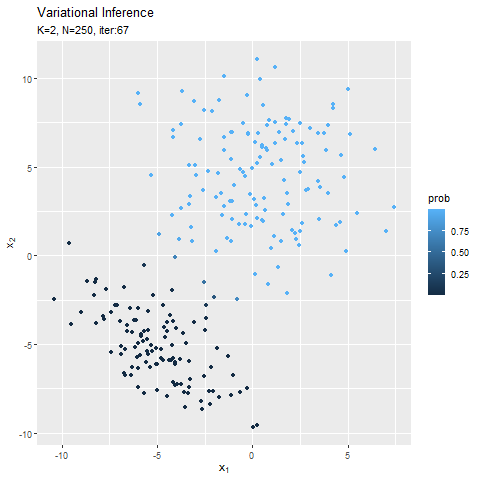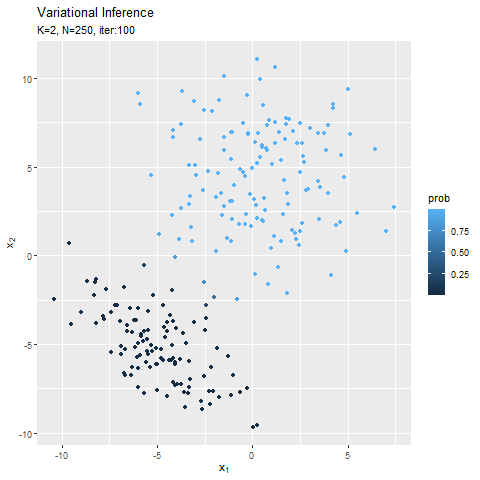
なので本当は、確率が最大のクラスタの色で、確率値に応じてグラデーションにして、確率密度の等高線と重ねたかった。クラスタごとにデータフレームを作って、(何とかできた!でも本当は塗りつぶしじゃない方もクラスタごとに色を付けたかった。geom_point()を重ねて、色も個別に指定すればできそうな気もしましたが、あまりにスマートじゃないので止めました。何かいい方法があるでしょうか?fillとcolorで2つのタイプの色分けはできるけど、geom_point()とgeom_contour()で別のcolorを指定はできないみたい?まぁ自分なりの及第点は越えたので、今回はこれで良しとします。)
あと推論時のは疑似コードに従ってるのでいいとして、作図時の(こちらも少しやっつけられた)。いい加減for()を何とかしたい{purrr}覚えたい(覚えたい)。
そして2020年12月10日は、ハロープロジェクトのグループJuice=Juiceの宮本佳林さんの卒業の日です。
卒業悲しい、ホールツアー観たかった。でもソロデビュー楽しみ、早くアルバム聴きたい。おめでとうございます!
卒コン最高でした!!!卒業おめでとうございます。(追記)
【次節の内容】
- 2021/05/16:加筆修正しました。