はじめに
『ベイズ推論による機械学習入門』の学習時のノートです。基本的な内容は「数式の行間を読んでみた」とそれを「RとPythonで組んでみた」になります。「数式」と「プログラム」から理解するのが目標です。
この記事は、4.3.4項の内容です。「観測モデルをポアソン混合分布」、「事前分布をガンマ分布とディリクレ分布」とするポアソン混合モデルに対する崩壊型ギブスサンプリング(周辺化ギブスサンプリング)をPythonで実装します。
省略してある内容等ありますので、本とあわせて読んでください。初学者な自分が理解できるレベルまで落として書き下していますので、分かる人にはかなりくどくなっています。同じような立場の人のお役に立てれば幸いです。
【数式読解編】
【他の節の内容】
【この節の内容】
・Pythonでやってみる
人工的に生成したデータを用いて、ベイズ推論を行ってみましょう。アルゴリズム4.2を参考に実装します。
利用するライブラリを読み込みます。
# 4.3.4項で利用するライブラリ import numpy as np from scipy.stats import poisson, gamma, nbinom # ポアソン分布, ガンマ分布, 負の二項分布 import matplotlib.pyplot as plt
・モデルの設定
まずは、観測モデルを設定します。この例では、$K$個の観測モデルをポアソン分布$\mathrm{Poi}(x_n | \lambda_k)$とします。また、各データに対する$K$個の観測モデルの割り当てをカテゴリ分布$\mathrm{Cat}(\mathbf{s}_n | \boldsymbol{\pi})$によって行います。
観測モデルのパラメータと混合比率を設定します。
# K個の真のパラメータを指定 lambda_truth_k = np.array([10.0, 25.0, 40.0]) # 真の混合比率を指定 pi_truth_k = np.array([0.35, 0.25, 0.4]) # クラスタ数を取得 K = len(lambda_truth_k)
観測モデルの$K$個のパラメータ$\boldsymbol{\lambda} = \{\lambda_1, \lambda_2, \cdots, \lambda_K\}$をlambda_truth_kとして、$\lambda_k \geq 0$の値を指定します。
混合比率パラメータ$\boldsymbol{\pi} = (\pi_1, \pi_2, \cdots, \pi_K)$をpi_truth_kとして、$\sum_{k=1}^K \pi_k = 1$、$\pi_k \geq 0$の値を指定します。
この2つのパラメータの値を求めるのがここでの目的です。
設定したモデルをグラフで確認しましょう。グラフ用の点を作成します。
# 作図用のxの点を作成 x_line = np.arange(0, 2 * np.max(lambda_truth_k)) # 確認 print(x_line[:10])
[0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]
作図用に、ポアソン分布に従う変数$x_n$がとり得る非負の整数をnp.arange()で作成してx_lineとします。この例では、0から$\boldsymbol{\lambda}$の最大値の2倍を範囲とします。
ポアソン混合分布の確率を計算します。
# 観測モデルを計算 model_prob = 0.0 for k in range(K): # クラスタkの分布の確率を計算 tmp_prob = poisson.pmf(k=x_line, mu=lambda_truth_k[k]) # K個の分布の加重平均を計算 model_prob += pi_truth_k[k] * tmp_prob
$K$個のパラメータlambda_truth_kを使って、x_lineの値ごとに次の式で確率を計算します。
$K$個のポアソン分布に対して、$\boldsymbol{\pi}$を使って加重平均をとります。
ポアソン分布の確率は、SciPyライブラリのstatsモジュールのpoisson.pmf()で計算できます。データの引数kにx_line、パラメータの引数muにlambda_truth_k[k]を指定します。
この計算をfor文でK回繰り返し行います。各パラメータによって求めた$K$回分の確率をpi_truth_k[k]で割り引いてmodel_probに加算していきます。
計算結果は次のようになります。
# 確認 print(np.round(model_prob[:10], 3))
[0. 0. 0.001 0.003 0.007 0.013 0.022 0.032 0.039 0.044]
観測モデルを作図します。
# 観測モデルを作図 plt.figure(figsize=(12, 9)) plt.bar(x=x_line, height=model_prob) # 真の分布 plt.xlabel('x') plt.ylabel('prob') plt.suptitle('Poisson Mixture Model', size = 20) plt.title('$\lambda=[' + ', '.join([str(lmd) for lmd in lambda_truth_k]) + ']' + ', \pi=[' + ', '.join([str(pi) for pi in pi_truth_k])+ ']$', loc='left') plt.show()
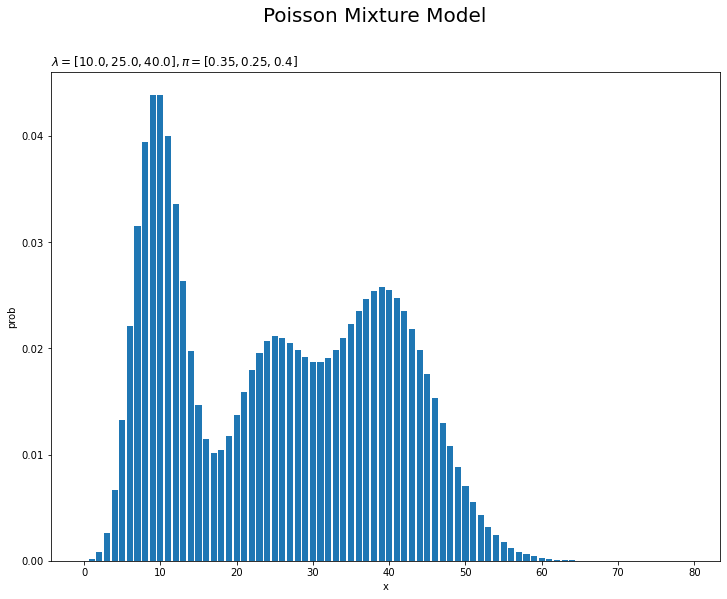
$K$個の分布を重ねたような分布になります。ただし、総和が1となるようにしているため、$K$個の分布そのものよりも1つ1つの山が小さく(確率値が小さく)なっています。
・データの生成
続いて、構築したモデルに従ってデータを生成します。先に、潜在変数$\mathbf{S} = \{\mathbf{s}_1, \mathbf{s}_2, \cdots, \mathbf{s}_N\}$、$\mathbf{s}_n = (s_{n,1}, s_{n,2}, \cdots, s_{n,K})$を生成し、各データに割り当てられたクラスタに従い観測データ$\mathbf{X} = \{x_1, x_2, \cdots, x_N\}$を生成します。
$N$個の潜在変数$\mathbf{S}$を生成します。
# (観測)データ数を指定 N = 250 # 真のクラスタを生成 s_truth_nk = np.random.multinomial(n=1, pvals=pi_truth_k, size=N)
生成するデータ数$N$をNとして値を指定します。
カテゴリ分布に従う乱数は、多項分布に従う乱数生成関数np.random.multinomial()のn引数を1にすることで生成できます。また、確率(パラメータ)の引数pvalsにpi_truth_k、試行回数の引数sizeにNを指定します。生成した$N$個の$K$次元ベクトルをs_truth_nkとします。
結果は次のようになります。
# 確認 print(s_truth_nk[:5])
[[0 1 0]
[0 0 1]
[0 0 1]
[0 1 0]
[1 0 0]]
これが本来は観測できない潜在変数であり、真のクラスタです。各行がデータを表し、値が1の列番号が割り当てられたクラスタ番号を表します。
s_truth_nkから各データのクラスタ番号を抽出します。
# 真のクラスタ番号を抽出 _, s_truth_n = np.where(s_truth_nk == 1) # 確認 print(s_truth_n[:5])
[1 2 2 1 0]
np.where()を使って行(データ)ごとに要素が1の列番号を抽出します。
各データのクラスタに従い$N$個のデータを生成します。
# (観測)データを生成
x_n = np.random.poisson(lam=lambda_truth_k[s_truth_n], size=N)
ポアソン分布に従う乱数は、np.random.poisson()で生成できます。パラメータの引数lamにlambda_truth_k[s_truth_n]、試行回数の引数sizeにNを指定します。各データのクラスタ番号s_truth_nを添字に使うことで、各データのクラスタに対応したパラメータ$\lambda_k$をlambda_truth_kから取り出すことができます。生成した$N$個のデータをx_nとします。式(4.28)を再現して、lamにapply(lambda_truth_k^t(s_truth_nk), 2, prod)を渡しても生成できます。
観測したデータを確認します。
# 確認 print(x_n[:10])
[22 47 50 27 13 10 34 5 10 31]
観測データが非負の整数になっているのを確認できます。
観測データをヒストグラムで確認しましょう。
# 観測データのヒストグラムを作成 plt.figure(figsize=(12, 9)) plt.bar(x=x_line, height=model_prob, label='true model', color='white', alpha=1, edgecolor='red', linestyle='--') # 真の分布 plt.bar(x=x_line, height=[np.sum(x_n == x) / len(x_n) for x in x_line], label='observation data') # 観測データ plt.xlabel('x') plt.ylabel('dens') plt.suptitle('Poisson Mixture Model', fontsize=20) plt.title('$N=' + str(N) + ', \lambda=[' + ', '.join([str(lmd) for lmd in lambda_truth_k]) + ']' + ', \pi=[' + ', '.join([str(pi) for pi in pi_truth_k]) + ']$', loc='left') plt.legend() plt.show()
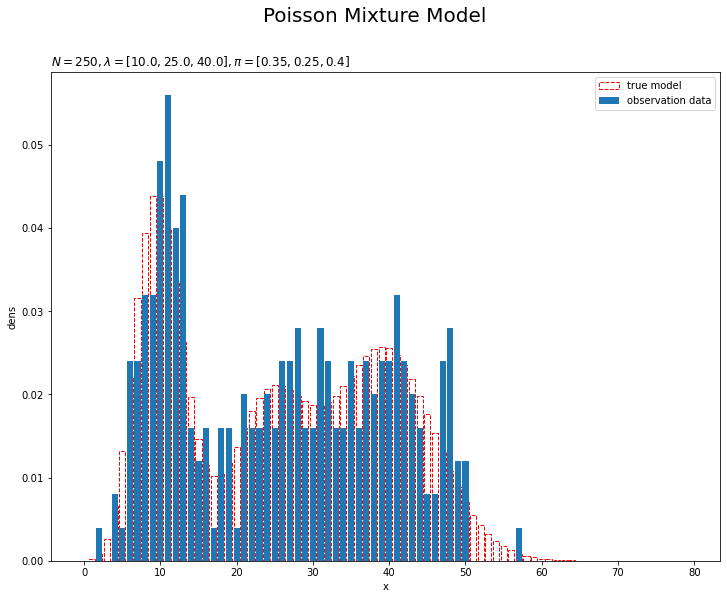
真の分布を重ねて描画しています。
また、クラスタもヒストグラムで確認しましょう。
# 真のクラスタのヒストグラムを作成 plt.figure(figsize=(12, 9)) for k in range(K): plt.bar(x=x_line, height=[np.sum(x_n[s_truth_n == k] == x) for x in x_line], alpha=0.5, label='cluster:' + str(k + 1)) # 真のクラスタ plt.xlabel('x') plt.ylabel('count') plt.suptitle('Poisson Mixture Model', fontsize=20) plt.title('$N=' + str(N) + ', \lambda=[' + ', '.join([str(lmd) for lmd in lambda_truth_k]) + ']' + ', \pi=[' + ', '.join([str(pi) for pi in pi_truth_k]) + ']$', loc='left') plt.legend() plt.show()
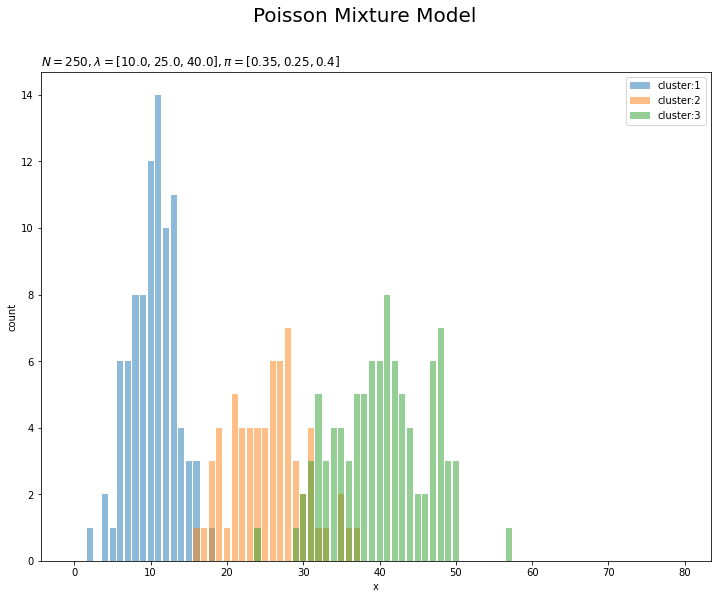
どちらの分布もデータが十分に大きいと真の分布に近づきます。
・事前分布の設定
次に、観測モデル(観測データの分布)$p(\mathbf{X} | \boldsymbol{\lambda})$と潜在変数の分布$p(\mathbf{S} | \boldsymbol{\pi})$に対する共役事前分布を設定します。ポアソン分布のパラメータ$\boldsymbol{\lambda}$に対する事前分布$p(\boldsymbol{\lambda})$としてガンマ分布$\mathrm{Gam}(\boldsymbol{\lambda} | a, b)$、カテゴリ分布のパラメータ$\boldsymbol{\pi}$に対する事前分布$p(\boldsymbol{\pi})$としてディリクレ分布$p(\boldsymbol{\pi} | \boldsymbol{\alpha})$を設定します。
$\boldsymbol{\lambda}$の事前分布と$\boldsymbol{\pi}$の事前分布のパラメータ(超パラメータ)を設定します。
# lambdaの事前分布のパラメータを指定 a = 1.0 b = 1.0 # piの事前分布のパラメータを指定 alpha_k = np.repeat(2.0, K)
ガンマ分布のパラメータ$a,\ b$をそれぞれa, bとして、$a > 0,\ b > 0$の値を指定します。
ディリクレ分布のパラメータ$\boldsymbol{\alpha} = (\alpha_1, \alpha_2, \cdots, \alpha_K)$をalpha_kとして、$\alpha_k > 0$の値を指定します。
超パラメータを設定できたので、$\boldsymbol{\lambda}$の事前分布を確認しましょう。グラフ用の点を作成して、確率密度を計算します。
# 作図用のlambdaの点を作成 lambda_line = np.linspace(0.0, 2.0 * np.max(lambda_truth_k), num=1000) # lambdaの事前分布を計算 prior_lambda = gamma.pdf(x=lambda_line, a=a, scale=1 / b)
ガンマ分布に従う変数$\lambda_k$がとり得る0以上の値をnp.linspace()で作成してlambda_lineとします。この例では、0から$\boldsymbol{\lambda}$の最大値の2倍を範囲とします。np.linspace()を使うと指定した要素数で等間隔に切り分けます。np.arange()を使うと切り分ける間隔を指定できます。処理が重い場合は、この値を調整してください。
作成したlambda_lineの値ごとに確率密度を計算します。ガンマ分布の確率密度は、SciPyライブラリのstatsモジュールのgamma.pdf()で計算できます。データの引数xにlambda_line、a引数にa、scale引数にbを指定します。
計算結果は次のようになります。
# 確認 print(np.round(lambda_line[:10], 2)) print(np.round(prior_lambda[:10], 2))
[0. 0.08 0.16 0.24 0.32 0.4 0.48 0.56 0.64 0.72]
[1. 0.92 0.85 0.79 0.73 0.67 0.62 0.57 0.53 0.49]
$\boldsymbol{\lambda}$の事前分布を作図します。
# lambdaの事前分布を作図 plt.figure(figsize=(12, 9)) plt.plot(lambda_line, prior_lambda, label='prior', color='purple') # 事前分布 plt.vlines(x=lambda_truth_k, ymin=0.0, ymax=np.max(prior_lambda), label='true val', color='red', linestyle='--') # 真の値 plt.xlabel('$\lambda$') plt.ylabel('density') plt.suptitle('Gamma Distribution', fontsize=20) plt.title('a=' + str(a) + ', b=' + str(b), loc='left') plt.legend() plt.show()
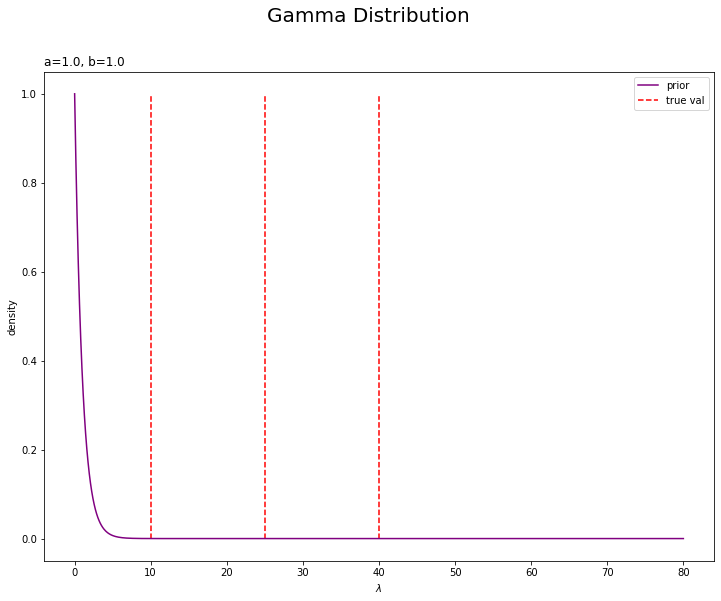
真の値を垂直線plt.vlines()で描画しています。
$\boldsymbol{\pi}$の事前分布(と事後分布)については省略します。詳しくは、3.2.2項「カテゴリ分布の学習と予測」をご参照ください。
・初期値の設定
設定した事前分布に従い、潜在変数$\mathbf{S}$をランダムに生成して初期値とします。
alpha_kを用いて、$\mathbf{S}$の初期値を生成します。
# 潜在変数の初期値をランダムに生成 s_nk = np.random.multinomial(n=1, pvals=alpha_k / np.sum(alpha_k), size=N)
真のクラスタのときと同様に生成してs_nkとします。
ただしここでは、各クラスタとなる確率として、$\boldsymbol{\alpha}$から求めた混合比率の期待値$\mathbb{E}[\boldsymbol{\pi}]$を使うことにします。クラスタ$k$となる確率の期待値$\mathbb{E}[\pi_k]$は、ディリクレ分布の期待値(2.51)より
で計算します。
生成した潜在変数を確認します。
# 確認 print(s_nk[:5])
[[1 0 0]
[1 0 0]
[0 0 1]
[1 0 0]
[1 0 0]]
s_nkを用いて、$\boldsymbol{\lambda}$の事後分布のパラメータの初期値を計算します。
# 初期値によるlambdaの事後分布のパラメータを計算:式(4.24) a_hat_k = np.sum(s_nk.T * x_n, axis=1) + a b_hat_k = np.sum(s_nk, axis=0) + b
$\boldsymbol{\lambda}$の事後分布(ガンマ分布)のパラメータ$\hat{\mathbf{a}} = \{\hat{a}_1, \hat{a}_2, \cdots, \hat{a}_K\}$、$\hat{\mathbf{b}} = \{\hat{b}_1, \hat{b}_2, \cdots, \hat{b}_K\}$の各項は
で計算して、結果をa_hat_k, b_hat_kとします。この時点では、$N$個全てのデータを使っているため(崩壊型ではない)ギブスサンプリング(4.3.2項)の式(4.42)です。
# 確認 print(a_hat_k) print(b_hat_k)
[2564. 1969. 1883.]
[99. 79. 75.]
ちなみに、$\hat{a}_k$の計算式に関して、$s_{n,k} x_n$の計算は
print(x_n[:5]) print((s_nk[:5].T * x_n[:5]).T)
[22 47 50 27 13]
[[22 0 0]
[47 0 0]
[ 0 0 50]
[27 0 0]
[13 0 0]]
各観測データをクラスタごとに仕分ける操作であり、$\sum_{n=1}^N s_{n,k} x_n$は
print(np.sum(s_nk[:5].T * x_n[:5], axis=1))
[109 0 50]
割り当てられたクラスタごとに観測データの値の和をとる操作と言えます。また、$\sum_{n=1}^N s_{n,k}$の計算は
print(s_nk[:5]) print(np.sum(s_nk[:5], axis=0))
[[1 0 0]
[1 0 0]
[0 0 1]
[1 0 0]
[1 0 0]]
[4 0 1]
各クラスタを割り当てられたデータ数です。
同様に、$\boldsymbol{\pi}$の事後分布のパラメータの初期値を計算します。
# 初期値によるpiの事後分布のパラメータを計算:式(4.45) alpha_hat_k = np.sum(s_nk, axis=0) + alpha_k
$\boldsymbol{\pi}$の事後分布(ディリクレ分布)のパラメータ$\hat{\boldsymbol{\alpha}} = (\hat{\alpha}_1, \hat{\alpha}_2, \cdots, \hat{\alpha}_K)$の各項は
で計算して、結果をalpha_hat_kとします。こちらも$N$個全てデータから求めています。
# 確認 print(alpha_hat_k)
[100. 80. 76.]
超パラメータの初期値が得られたので、$\boldsymbol{\lambda}$の事後分布を確認しましょう。$K$個のガンマ分布を計算します。
# 初期値によるlambdaの事後分布を作図 posterior_lambda_kl = np.empty((K, len(lambda_line))) for k in range(K): posterior_lambda_kl[k] = gamma.pdf(x=lambda_line, a=a_hat_k[k], scale=1 / b_hat_k[k])
$K$個のガンマ分布を計算して、2次元配列に格納していきます。
作成した配列は次のようになります。
# 確認 print(posterior_lambda_kl)
[[0. 0. 0. ... 0. 0. 0.]
[0. 0. 0. ... 0. 0. 0.]
[0. 0. 0. ... 0. 0. 0.]]
$\boldsymbol{\lambda}$の事後分布の初期値を作図します。
# 初期値によるlambdaの事後分布を作図 plt.figure(figsize=(12, 9)) for k in range(K): plt.plot(lambda_line, posterior_lambda_kl[k], label='cluster:' + str(k + 1)) # 事後分布 plt.vlines(x=lambda_truth_k, ymin=0.0, ymax=np.max(posterior_lambda_kl), color='red', linestyle='--', label='true val') # 真の値 plt.xlabel('$\lambda$') plt.ylabel('density') plt.suptitle('Gamma Distribution', size=20) plt.title('$iter:' + str(0) + ', N=' + str(N) + ', \hat{a}=[' + ', '.join([str(a) for a in a_hat_k]) + ']' + ', \hat{b}=[' + ', '.join([str(b) for b in b_hat_k]) + ']$', loc='left') plt.legend() plt.show()
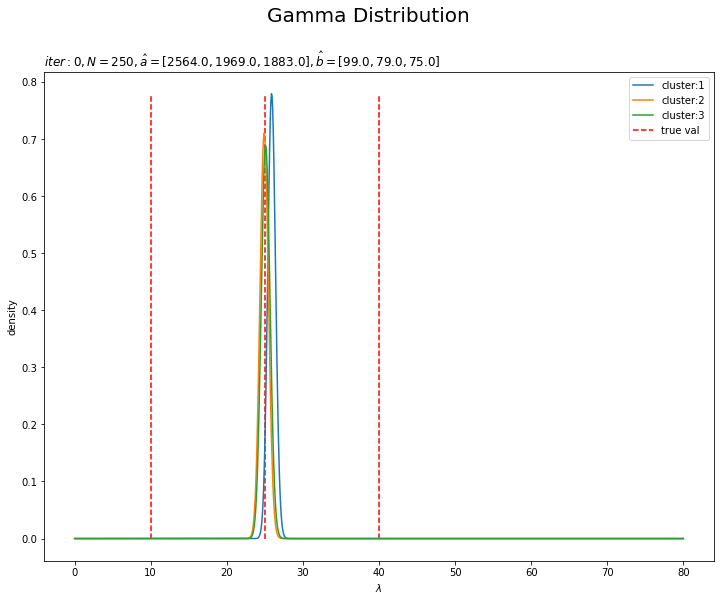
超パラメータ$\hat{a}_k,\ \hat{b}_k,\ \hat{\alpha}_k$からパラメータの期待値$\mathbb{E}[\lambda_k],\ \mathbb{E}[\pi_k]$を求めて、混合分布を計算します。
# lambdaの平均値を計算:式(2.59) E_lambda_k = a_hat_k / b_hat_k # piの平均値を計算:式(2.51) E_pi_k = alpha_hat_k / np.sum(alpha_hat_k) # 初期値による混合分布を計算 init_prob = 0.0 for k in range(K): # クラスタkの分布の確率を計算 tmp_prob = poisson.pmf(k=x_line, mu=E_lambda_k[k]) # K個の分布の加重平均を計算 init_prob += E_pi_k[k] * tmp_prob
$\mathbb{E}[\lambda_k]$は、ガンマ分布の期待値(2.59)より
で計算します。また、$\mathbb{E}[\pi_k]$は、先ほど計算した
です。
超パラメータの初期値から求めた分布を作図します。
# 初期値による分布を作図 plt.figure(figsize=(12, 9)) plt.bar(x=x_line, height=model_prob, label='true model', color='white', alpha=1, edgecolor='red', linestyle='--') # 真の分布 plt.bar(x=x_line, height=init_prob, color='purple') # 初期値による分布 plt.xlabel('x') plt.ylabel('prob') plt.suptitle('Poisson Mixture Model', size = 20) plt.title('$iter:' + str(0) + ', E[\lambda]=[' + ', '.join([str(lmd) for lmd in np.round(E_lambda_k, 2)]) + ']' + ', E[\pi]=[' + ', '.join([str(pi) for pi in np.round(E_pi_k, 2)])+ ']$', loc='left') plt.legend() plt.show()
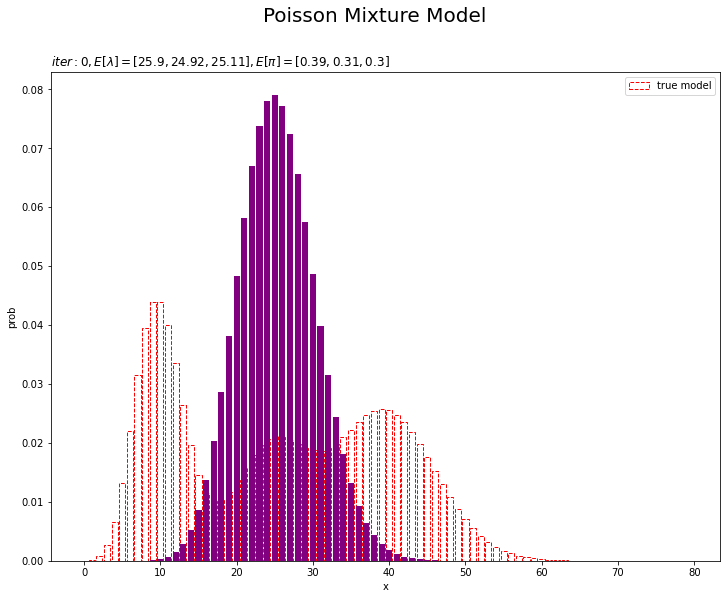
観測モデルのときと同様に作図します。
・崩壊型ギブスサンプリング
崩壊型ギブスサンプリングによりパラメータと潜在変数を推定します。
・コード全体
後で各パラメータの更新値や分布の推移を確認するために、それぞれ試行ごとにtrace_***に値を保存していきます。
# 試行回数を指定 MaxIter = 100 # 推移の確認用の受け皿を作成 _, s_n = np.where(s_nk == 1) # クラスタ番号を抽出 trace_s_in = [list(s_n)] trace_a_ik = [list(a_hat_k)] trace_b_ik = [list(b_hat_k)] trace_alpha_ik = [list(alpha_k)] # 崩壊型ギブスサンプリング for i in range(MaxIter): for n in range(N): # n番目のデータの現在のクラスタ番号を取得 k, = np.where(s_nk[n] == 1)[0] # n番目のデータに関する統計量を除算 a_hat_k[k] = a_hat_k[k] - x_n[n] b_hat_k[k] = b_hat_k[k] - 1 alpha_hat_k[k] = alpha_hat_k[k] - 1 # 負の二項分布(4.81)のパラメータを計算 r_hat_k = a_hat_k p_hat_k = 1 / (b_hat_k + 1) # 負の二項分布の確率を計算:式(4.81) prob_nb_k = nbinom.pmf(k=x_n[n], n=r_hat_k, p=1 - p_hat_k) # カテゴリ分布(4.74)のパラメータを計算:式(4.75) eta_k = alpha_hat_k / np.sum(alpha_hat_k) # n番目のクラスタのサンプリング確率を計算:式(4.66) prob_s_k = (prob_nb_k + 1e-7) * eta_k prob_s_k = prob_s_k / np.sum(prob_s_k) # 正規化 # n番目のクラスタをサンプル:式(4.74) s_nk[n] = np.random.multinomial(n=1, pvals=prob_s_k, size=1) # n番目のデータの新しいクラスタを取得 k, = np.where(s_nk[n] == 1)[0] # n番目のデータに関する統計量を加算:式(4.82-4.83) a_hat_k[k] = a_hat_k[k] + x_n[n] b_hat_k[k] = b_hat_k[k] + 1 alpha_hat_k[k] = alpha_hat_k[k] + 1 # 値を記録 _, s_n = np.where(s_nk == 1) # クラスタ番号を抽出 trace_s_in.append(list(s_n)) trace_a_ik.append(list(a_hat_k)) trace_b_ik.append(list(b_hat_k)) trace_alpha_ik.append(list(alpha_hat_k)) # 動作確認 #print(str(i + 1) + ' (' + str(np.round((i + 1) / MaxIter * 100, 1)) + '%)')
・処理の確認
続いて、変分推論で行う処理を確認していきます。
・潜在変数$\boldsymbol{s}_n$の事後分布$p(\boldsymbol{s}_n | \mathbf{X}, \mathbf{S}_{\backslash n})$のパラメータの計算
崩壊型ギブスサンプリングにおける$\boldsymbol{s}_n$の事後分布パラメータを計算します。
# n番目のデータの現在のクラスタ番号を取得 k, = np.where(s_nk[n] == 1)[0] # n番目のデータに関する統計量を除算 a_hat_k[k] = a_hat_k[k] - x_n[n] b_hat_k[k] = b_hat_k[k] - 1 alpha_hat_k[k] = alpha_hat_k[k] - 1
$n$番目データを除いた超パラメータ$\hat{\mathbf{a}}_{\backslash n},\ \hat{\mathbf{b}}_{\backslash n},\ \hat{\boldsymbol{\alpha}}_{\backslash n}$の各項は次の式で計算できます。
ただし、処理上は次の式のように、$N$個のデータから求めた$\hat{\mathbf{a}},\ \hat{\mathbf{b}},\ \hat{\boldsymbol{\alpha}}$から$n$番目のデータに関して取り除くことにします。
このとき、$n$番目のデータのクラスタが$k$であればそれ以外の$s_{n,1}, \cdots, s_{n,k-1}, s_{n,k+1}, \cdots, s_{n,K}$は0です。よって、$s_{n,k} = 1$である$k$番目の項のみ処理すればいいことが分かります。
which(s_nk[n, ] == 1)で値が1のインデックスを抽出して、kとします。kが、$n$番目のデータに関して割り当てられたクラスタ番号です。a_hat_k、b_hat_k、alpha_hat_kのk番目の要素のみ上の計算をします。
・潜在変数$\mathbf{s}_n$のサンプリング
$\mathbf{s}_n$の事後分布$p(\mathbf{s}_n | \mathbf{X}, \mathbf{S}_{\backslash n})$から$\mathbf{s}_n$をサンプルします。
$\mathbf{s}_n$の事後分布($\mathbf{s}_n$のサンプリング確率)は
を正規化することで求まります。サンプリングに用いるこの2つの分布を計算しましょう。
a_hat_k, b_hat_kを用いて、式(4.66)の前の項のパラメータを計算します。
# 負の二項分布(4.81)のパラメータを計算 r_hat_k = a_hat_k p_hat_k = 1 / (b_hat_k + 1)
負の二項分布のパラメータ$\hat{\mathbf{r}}_{\backslash n} = \{\hat{r}_{1 \backslash n}, \hat{r}_{2 \backslash n}, \cdots, \hat{r}_{K \backslash n}\}$、$\hat{\mathbf{p}}_{\backslash n} = \{\hat{p}_{1 \backslash n}, \hat{p}_{2 \backslash n}, \cdots, \hat{p}_{K \backslash n}\}$の各項は
で計算して、結果をr_hat_k, p_hat_kとします。
# 確認 print(r_hat_k) print(p_hat_k)
[4156. 1397. 863.]
[0.00934579 0.01639344 0.01149425]
r_hat_k, p_hat_kを用いて、負の二項分布の確率を計算します。
# 負の二項分布の確率を計算:式(4.81) prob_nb_k = nbinom.pmf(k=x_n[n], n=r_hat_k, p=1 - p_hat_k)
負の二項分布の確率は、SicPyライブラリのstatsモジュールのnbinom.pmf()で計算できます。データ(試行回数)の引数kに$n$番目の観測データの値x_n[n]、成功回数の引数nにr_hat_k、成功確率の引数pに1 - p_hat_kを指定します。
# 確認 print(np.round(prob_nb_k, 5))
[0.03018 0.02269 0. ]
a_hat_kを用いて、式(4.66)の後の項のパラメータを計算します。
# カテゴリ分布(4.74)のパラメータを計算:式(4.75)
eta_k = alpha_hat_k / np.sum(alpha_hat_k)
カテゴリ分布のパラメータ$\boldsymbol{\eta}_{\backslash n} = (\eta_{1 \backslash n}, \eta_{2 \backslash n}, \cdots, \eta_{K \backslash n})$の各項は
で計算して、結果をeta_kとします。
# 確認 print(np.round(eta_k, 5))
[0.41961 0.23922 0.34118]
式(4.66)の2つの項が得られたので、$\mathbf{s}_n$のサンプリング確率を計算します。
# n番目のクラスタのサンプリング確率を計算:式(4.66) prob_s_k = (prob_nb_k + 1e-7) * eta_k prob_s_k = prob_s_k / np.sum(prob_s_k) # 正規化
負の二項分布とカテゴリ分布のパラメータの積を計算をしてprob_s_kとします。また、総和が1となるように正規化します。
# 確認 print(np.round(prob_s_k, 5))
[0.69994 0.30006 0. ]
以上で潜在変数のサンプリング確率が得られました。
prob_s_kを用いて、$\mathbf{s}_n$をサンプルします。
# n番目のクラスタをサンプル:式(4.74) s_nk[n] = np.random.multinomial(n=1, pvals=prob_s_k, size=1)
データの生成時と同様に、多項分布に従いサンプルします。
新たな$n$番目の潜在変数が得られたので、再度$N$個のデータを用いた超パラメータを計算します。
# n番目のデータの新しいクラスタを取得 k, = np.where(s_nk[n] == 1)[0] # n番目のデータに関する統計量を加算:式(4.82-4.83) a_hat_k[k] = a_hat_k[k] + x_n[n] b_hat_k[k] = b_hat_k[k] + 1 alpha_hat_k[k] = alpha_hat_k[k] + 1
今度は、$n$番目データに関して新たに割り当てられたクラスタに従って加算することで、$N$個のデータから求めた超パラメータを計算します。
この処理をfor文で$N$回繰り返し行うことで、全ての潜在変数のサンプルが得られます。同時に、更新された潜在変数$\mathbf{S}$を用いた超パラメータ$\hat{\mathbf{a}},\ \hat{\mathbf{b}},\ \hat{\boldsymbol{\alpha}}$も得られます。
さらにこの処理を指定した回数繰り返します。
・推論結果の確認
推論結果を確認していきます。
・最後のパラメータの確認
超パラメータa_hat_kとb_hat_kの最後の更新値を用いて、$\boldsymbol{\lambda}$の事後分布を計算します。
# lambdaの事後分布を計算 posterior_lambda_kl = np.empty((K, len(lambda_line))) for k in range(K): posterior_lambda_kl[k] = gamma.pdf(x=lambda_line, a=a_hat_k[k], scale=1 / b_hat_k[k]) # lambdaの事後分布を作図 plt.figure(figsize=(12, 9)) for k in range(K): plt.plot(lambda_line, posterior_lambda_kl[k], label='cluster:' + str(k + 1)) # 事後分布 plt.vlines(x=lambda_truth_k, ymin=0.0, ymax=np.max(posterior_lambda_kl), color='red', linestyle='--', label='true val') # 真の値 plt.xlabel('$\lambda$') plt.ylabel('density') plt.suptitle('Gamma Distribution:Collapsed Gibbs Sampling', size=20) plt.title('$iter:' + str(MaxIter) + ', N=' + str(N) + ', \hat{a}=[' + ', '.join([str(a) for a in a_hat_k]) + ']' + ', \hat{b}=[' + ', '.join([str(b) for b in b_hat_k]) + ']$', loc='left') plt.legend() plt.show()
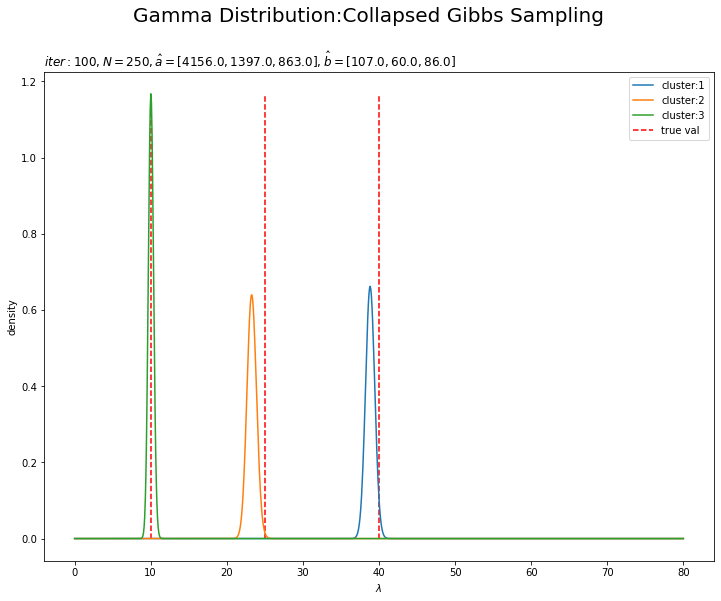
初期値の設定のときと同様にして作図します。
3つのガンマ分布がそれぞれ3つの真の値付近をピークとする分布を推定できています。
また、a_hat_k, b_hat_kとalpha_hat_kを用いて、混合分布を計算します。
# lambdaの平均値を計算:式(2.59) E_lambda_k = a_hat_k / b_hat_k # piの平均値を計算:式(2.51) E_pi_k = alpha_hat_k / np.sum(alpha_hat_k) # 最後の推定値による混合分布を計算 res_prob = 0.0 for k in range(K): # クラスタkの分布の確率を計算 tmp_prob = poisson.pmf(k=x_line, mu=E_lambda_k[k]) # K個の分布の加重平均を計算 res_prob += E_pi_k[k] * tmp_prob # 最後の推定値による分布を作図 plt.figure(figsize=(12, 9)) plt.bar(x=x_line, height=model_prob, label='truth model', color='white', alpha=1, edgecolor='red', linestyle='--') # 真の分布 plt.bar(x=x_line, height=res_prob, color='purple') # 最後の推定値による分布 plt.xlabel('x') plt.ylabel('prob') plt.suptitle('Poisson Mixture Model:Collapsed Gibbs Sampling', size = 20) plt.title('$iter:' + str(MaxIter) + ', N=' + str(N) + ', E[\lambda]=[' + ', '.join([str(lmd) for lmd in np.round(E_lambda_k, 2)]) + ']' + ', E[\pi]=[' + ', '.join([str(pi) for pi in np.round(E_pi_k, 2)])+ ']$', loc='left') plt.legend() plt.show()
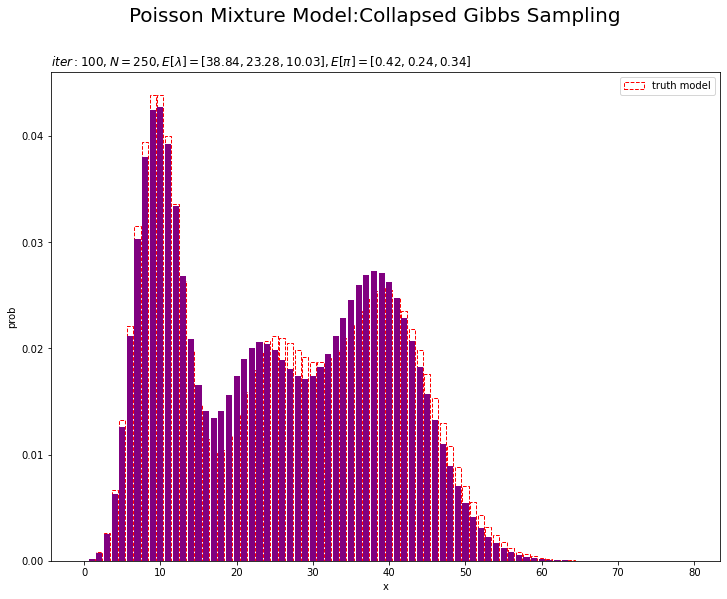
初期値の設定のときと同様にして作図します。
潜在変数s_nkの最後のサンプルを用いて、クラスタのヒストグラムを作成します。
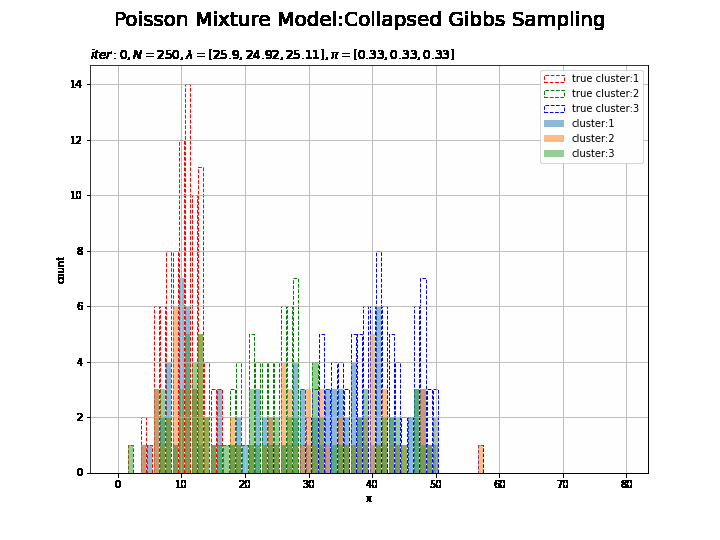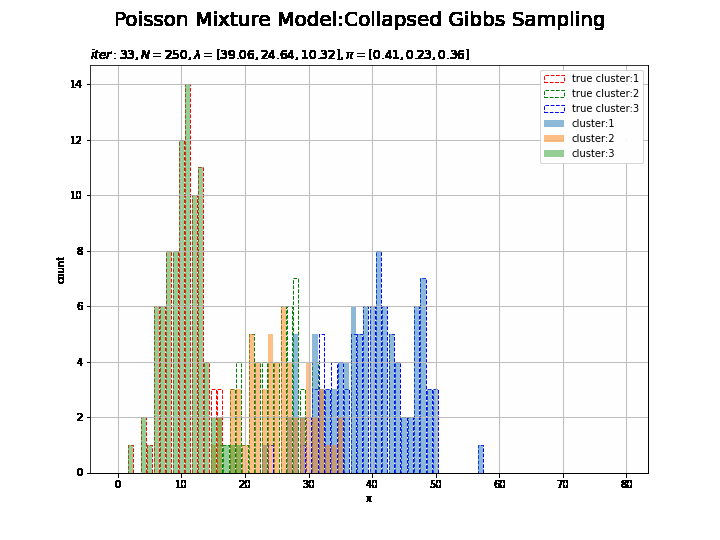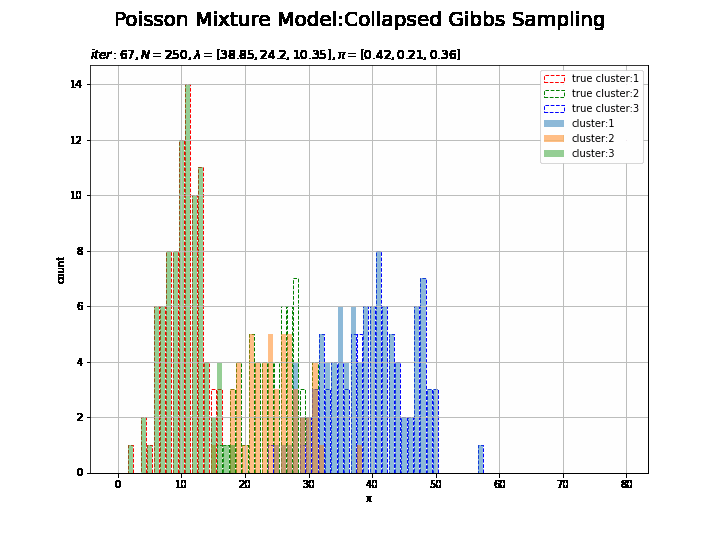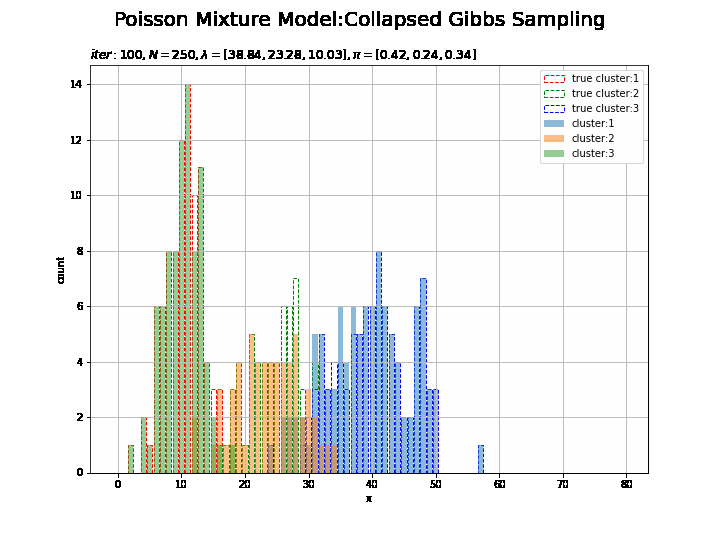
# K個の色を指定 color_list = ['red', 'green', 'blue'] # 最後のクラスタのヒストグラムを作成 plt.figure(figsize=(12, 9)) for k in range(K): plt.bar(x=x_line, height=[np.sum(x_n[s_truth_n == k] == x) for x in x_line], color='white', alpha=1, edgecolor=color_list[k], linestyle='--', label='true cluster:' + str(k + 1)) # 真のクラスタ for k in range(K): plt.bar(x=x_line, height=[np.sum(x_n[s_n == k] == x) for x in x_line], alpha=0.5, label='cluster:' + str(k + 1)) # 最後のクラスタ plt.xlabel('x') plt.ylabel('count') plt.suptitle('Poisson Mixture Model', size=20) plt.title('$N=' + str(N) + ', E[\lambda]=[' + ', '.join([str(lmd) for lmd in np.round(a_hat_k / b_hat_k, 2)]) + ']' + ', E[\pi]=[' + ', '.join([str(pi) for pi in np.round(alpha_hat_k / np.sum(alpha_hat_k), 2)]) + ']$', loc='left') plt.legend() plt.show()
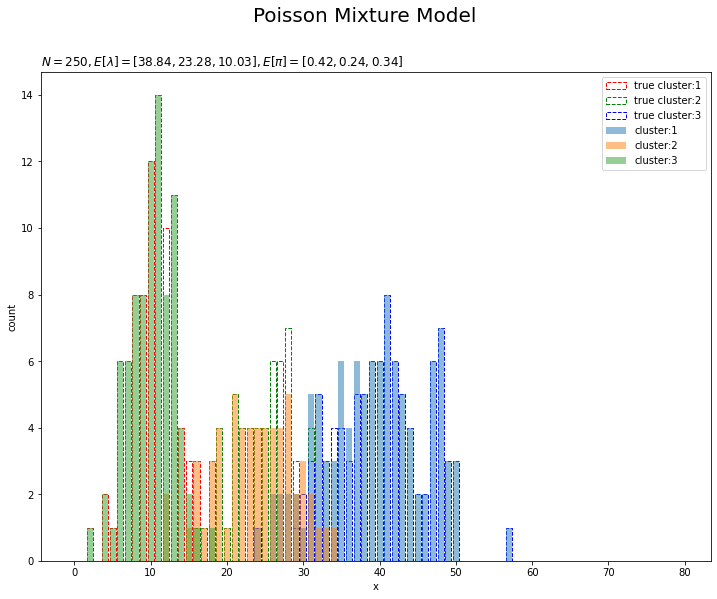
データの生成のときと同様にして作図します。
クラスタはランダムに決まるため、クラスタ番号は一致しません。
・超パラメータの推移の確認
超パラメータの更新値の推移を確認します。
・コード(クリックで展開)
各パラメータの学習ごとの値を格納したリストtrace_***をnp.array()でNumPy配列に変換して作図します。
# aの推移を作図 plt.figure(figsize=(12, 9)) for k in range(K): plt.plot(np.arange(MaxIter + 1), np.array(trace_a_ik).T[k], label='cluster:' + str(k + 1)) plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('Collapsed Gibbs Sampling', size=20) plt.title('$\hat{a}$', loc='left') plt.legend() plt.grid() plt.show()
# bの推移を作図 plt.figure(figsize=(12, 9)) for k in range(K): plt.plot(np.arange(MaxIter + 1), np.array(trace_b_ik).T[k], label='cluster:' + str(k + 1)) plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('Collapsed Gibbs Sampling', size=20) plt.title('$\hat{b}$', loc='left') plt.legend() plt.grid() plt.show()
# alphaの推移を作図 plt.figure(figsize=(12, 9)) for k in range(K): plt.plot(np.arange(MaxIter + 1), np.array(trace_alpha_ik).T[k], label='cluster:' + str(k + 1)) plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('Collapsed Gibbs Sampling', size=20) plt.title('$\hat{\\alpha}$', loc='left') plt.legend() plt.grid() plt.show()
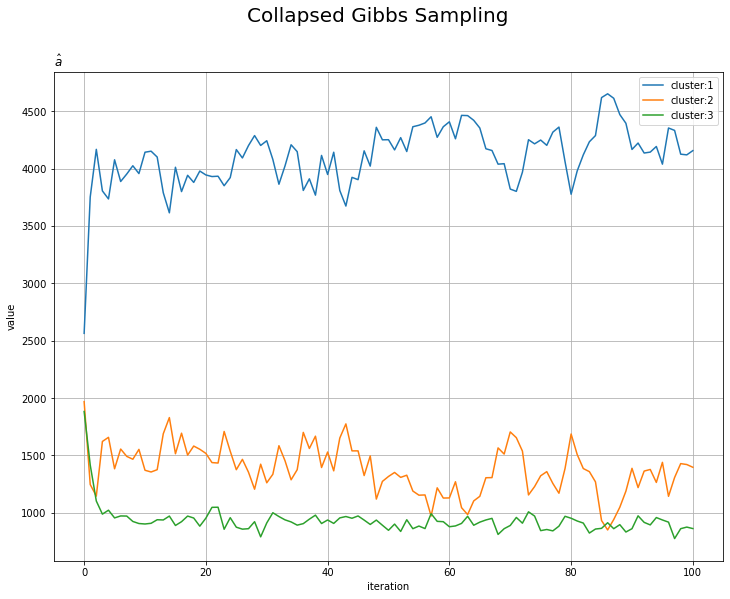
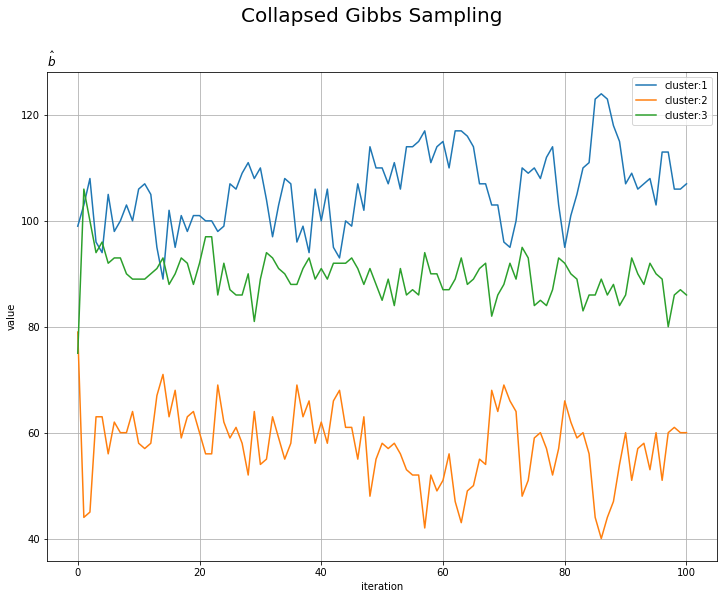
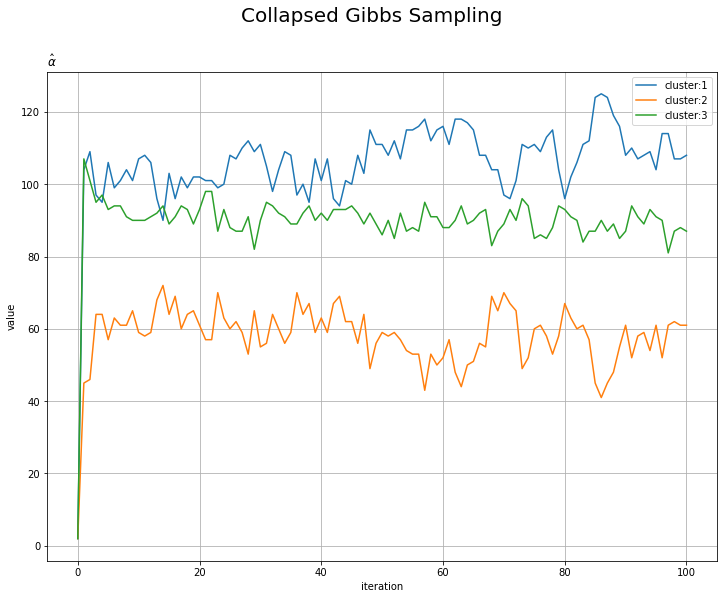
試行回数が増えるに従って真の値に近いているのを確認できます。
・おまけ:アニメーションによる推移の確認
animationモジュールを利用して、各分布の推移のアニメーション(gif画像)を作成するためのコードです。
・コード(クリックで展開)
# 追加ライブラリ import matplotlib.animation as animation
・パラメータの事後分布の推移
# 画像サイズを指定 fig = plt.figure(figsize=(12, 9)) # 作図処理を関数として定義 def update_posterior(i): # 前フレームのグラフを初期化 plt.cla() # i回目のlambdaの事後分布を計算 posterior_lambda_k = np.empty((K, len(lambda_line))) for k in range(K): posterior_lambda_k[k] = gamma.pdf(x=lambda_line, a=trace_a_ik[i][k], scale=1 / trace_b_ik[i][k]) # i回目のlambdaの事後分布を作図 for k in range(K): plt.vlines(x=lambda_truth_k[k], ymin=0.0, ymax=np.max(posterior_lambda_k), color='red', linestyle='--') # 真の値 plt.plot(lambda_line, posterior_lambda_k[k], label='cluster:' + str(k + 1)) # 事後分布 plt.xlabel('$\lambda$') plt.ylabel('density') plt.suptitle('Gamma Distribution:Collapsed Gibbs Sampling', size=20) plt.title('$iter:' + str(i) + ', N=' + str(N) + ', \hat{a}=[' + ', '.join([str(a) for a in trace_a_ik[i]]) + ']' + ', \hat{b}=[' + ', '.join([str(b) for b in trace_b_ik[i]]) + ']$', loc='left') plt.legend() plt.grid() # gif画像を作成 posterior_anime = animation.FuncAnimation(fig, update_posterior, frames=MaxIter + 1, interval=100) posterior_anime.save("ch4_3_4_Posterior.gif")
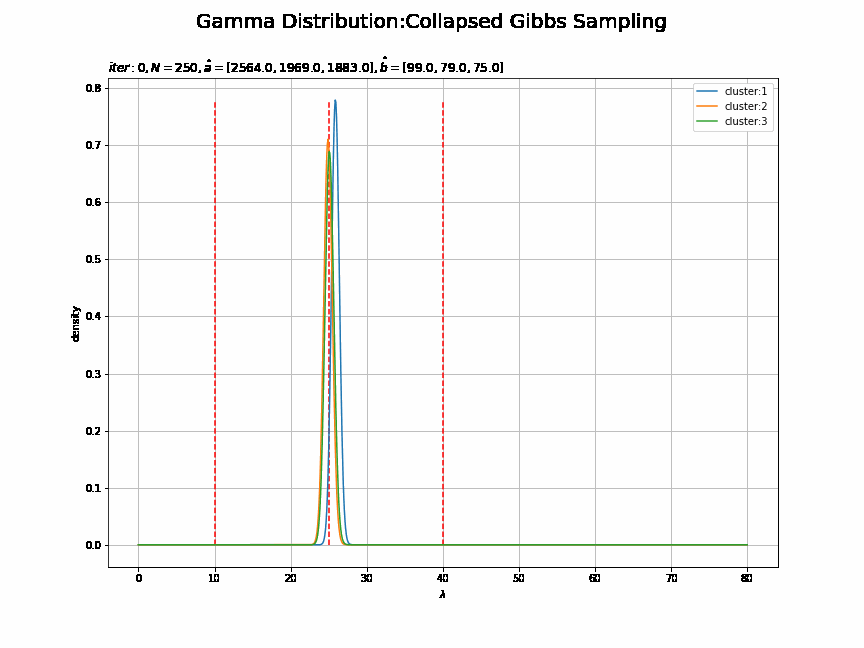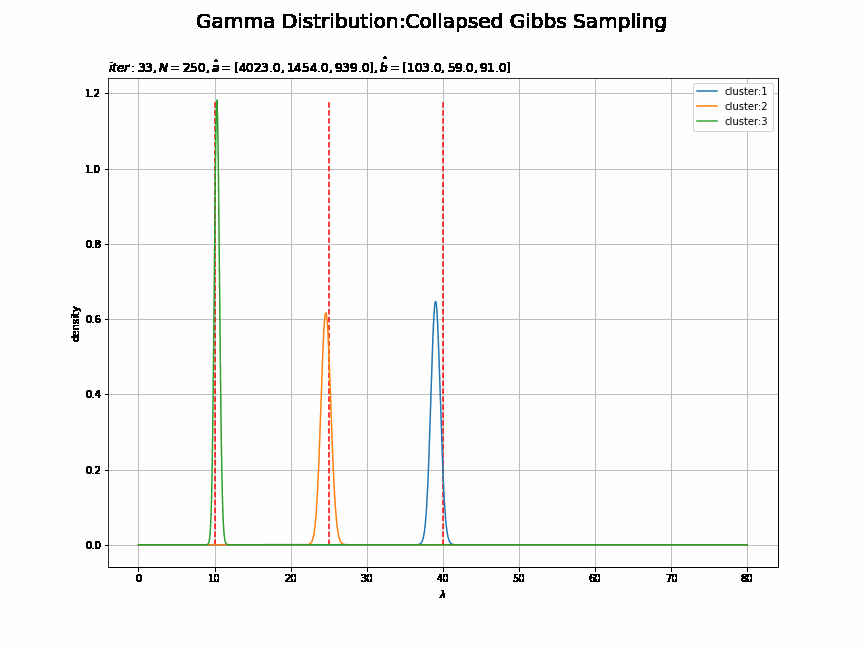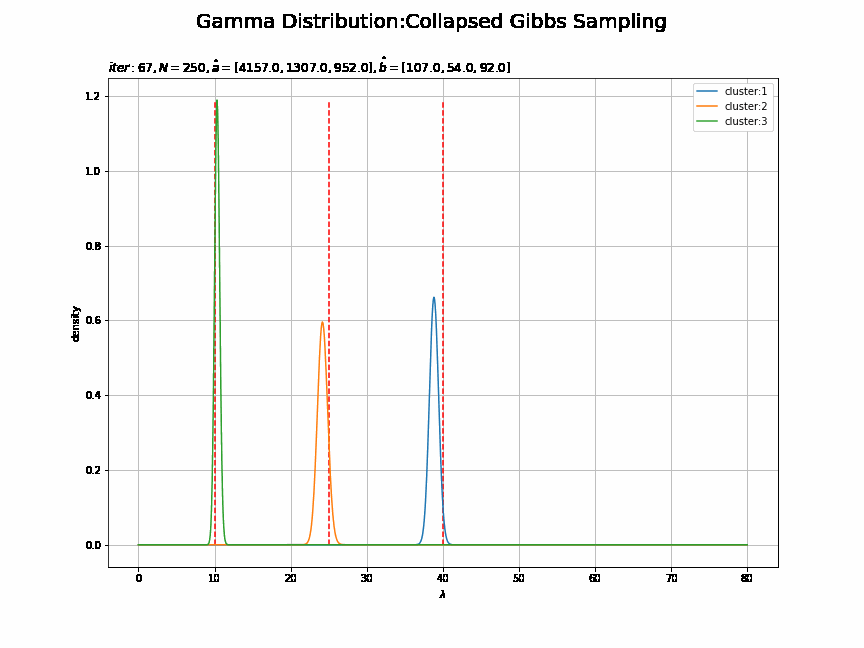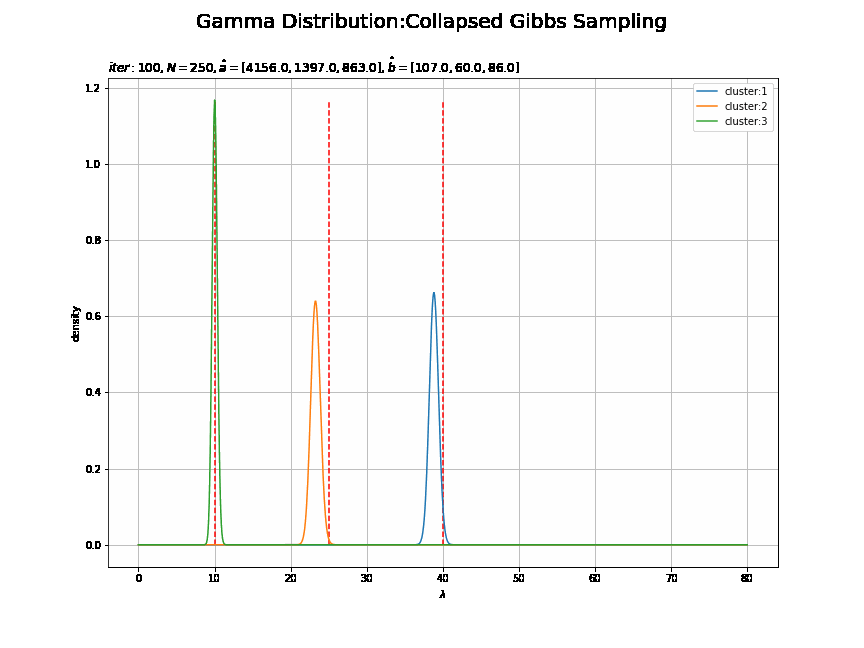
・パラメータの期待値による分布の推移
・コード(クリックで展開)
# 画像サイズを指定 fig = plt.figure(figsize=(12, 9)) # 作図処理を関数として定義 def update_model(i): # 前フレームのグラフを初期化 plt.cla() # i回目のパラメータの平均値を計算:式(2.59,2.51) E_lambda_k = np.array(trace_a_ik[i]) / np.array(trace_b_ik[i]) E_pi_k = np.array(trace_alpha_ik[i]) / np.sum(trace_alpha_ik [i]) # i回目の推定値による混合分布を計算 res_prob = 0.0 for k in range(K): # クラスタkの分布の確率を計算 tmp_prob = poisson.pmf(k=x_line, mu=E_lambda_k[k]) # K個の分布の加重平均を計算 res_prob += E_pi_k[k] * tmp_prob # i回目のサンプルによる分布を作図 plt.bar(x=x_line, height=model_prob, label='true model', color='white', alpha=1, edgecolor='red', linestyle='--') # 真の分布 plt.bar(x=x_line, height=res_prob, color='purple') # 推定値による分布 plt.xlabel('x') plt.ylabel('prob') plt.suptitle('Poisson Mixture Model:Collapsed Gibbs Sampling', size = 20) plt.title('$iter:' + str(i) + ', N=' + str(N) + ', E[\lambda]=[' + ', '.join([str(lmd) for lmd in np.round(E_lambda_k, 2)]) + ']' + ', E[\pi]=[' + ', '.join([str(pi) for pi in np.round(E_pi_k, 2)]) + ']$', loc='left') plt.ylim(0.0, 0.1) plt.legend() plt.grid() # gif画像を作成 model_anime = animation.FuncAnimation(fig, update_model, frames=MaxIter + 1, interval=100) model_anime.save("ch4_3_4_Model.gif")
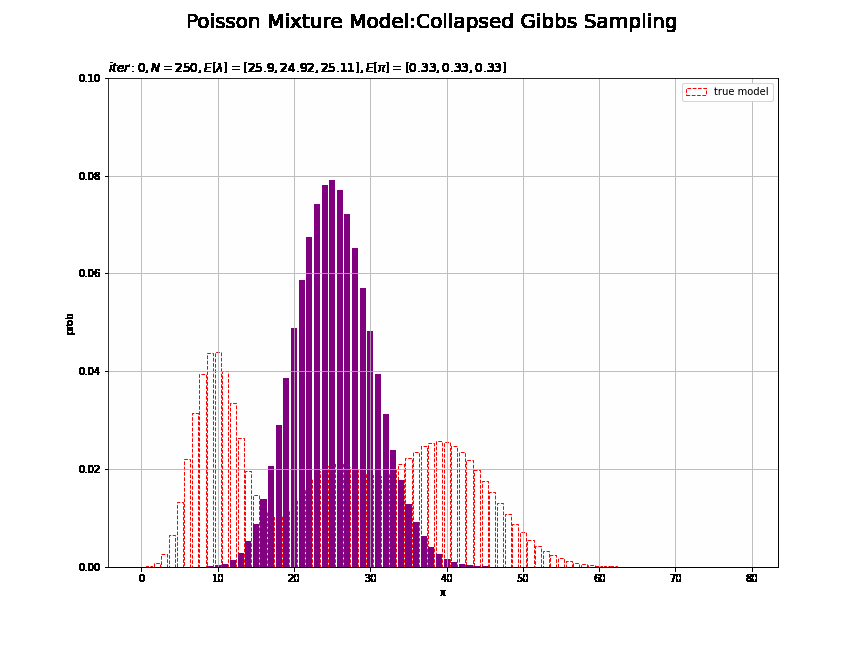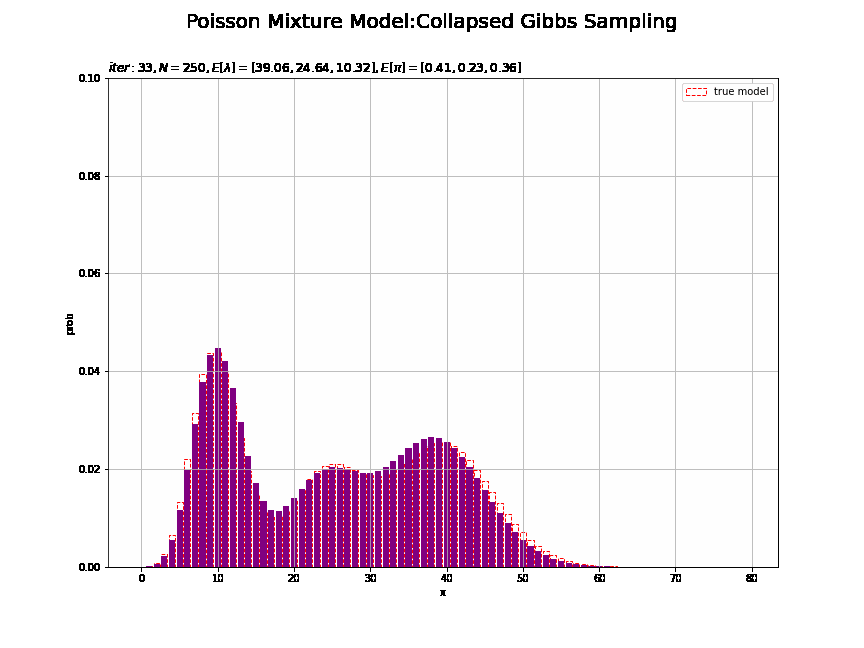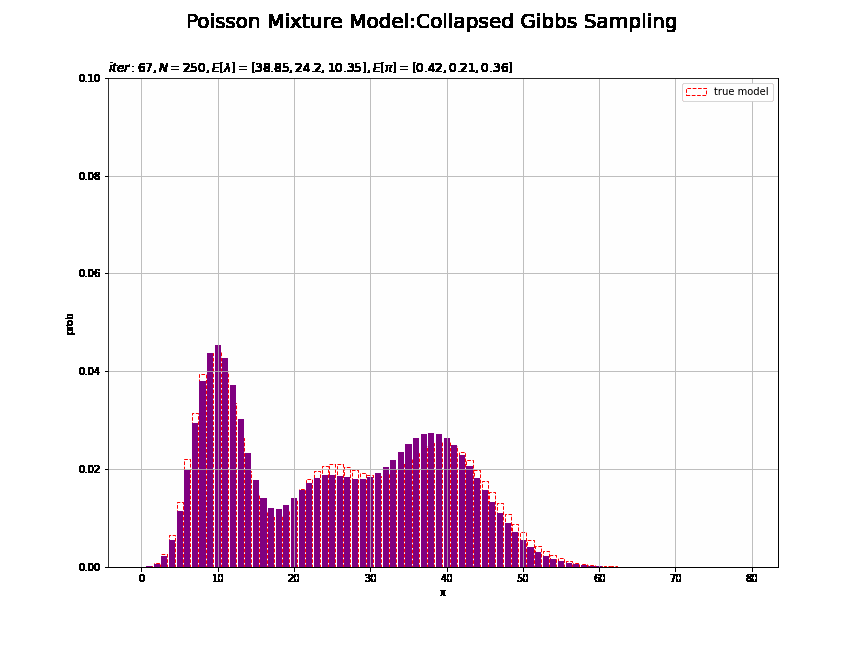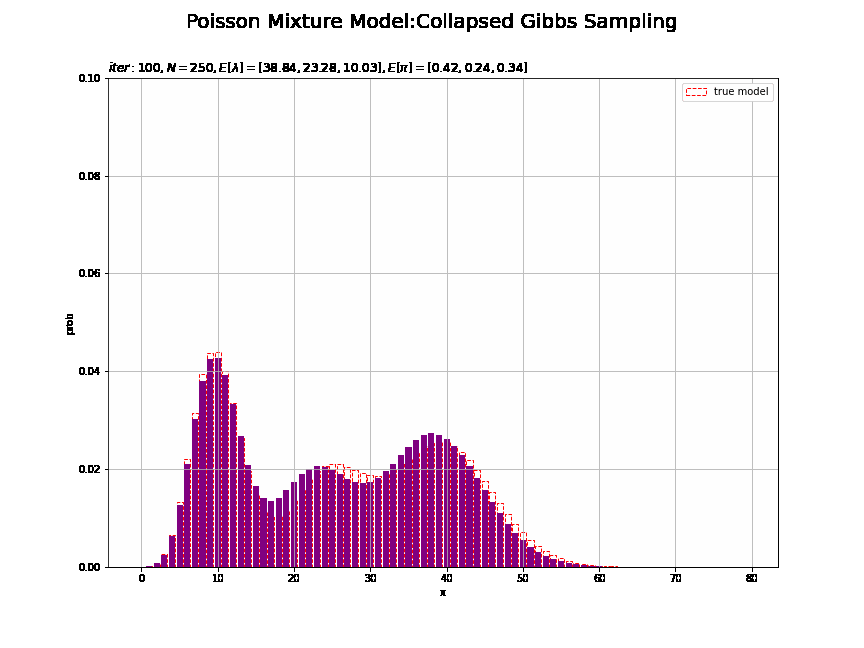
・クラスタのサンプルのヒストグラムの推移
・コード(クリックで展開)
# K個の色を指定 color_list = ['red', 'green', 'blue'] # 作図用のxの点を作成 x_line = np.arange(0, 2 * np.max(lambda_truth_k)) # 画像サイズを指定 fig = plt.figure(figsize=(12, 9)) # 作図処理を関数として定義 def update_cluster(i): # 前フレームのグラフを初期化 plt.cla() # i回目のクラスタの散布図を作成 for k in range(K): plt.bar(x=x_line, height=[np.sum(x_n[s_truth_n == k] == x) for x in x_line], color='white', alpha=1, edgecolor=color_list[k], linestyle='--', label='true cluster:' + str(k + 1)) # 真のクラスタ for k in range(K): plt.bar(x=x_line, height=[np.sum(x_n[np.array(trace_s_in[i]) == k] == x) for x in x_line], alpha=0.5, label='cluster:' + str(k + 1)) # サンプルしたクラスタ plt.xlabel('x') plt.ylabel('count') plt.suptitle('Poisson Mixture Model:Collapsed Gibbs Sampling', size=20) plt.title('$iter:' + str(i) + ', N=' + str(N) + ', \lambda=[' + ', '.join([str(lmd) for lmd in np.round(np.array(trace_a_ik[i]) / np.array(trace_b_ik[i]), 2)]) + ']' + ', \pi=[' + ', '.join([str(pi) for pi in np.round(np.array(trace_alpha_ik[i]) / np.sum(trace_alpha_ik [i]), 2)]) + ']$', loc='left') plt.legend() plt.grid() # gif画像を作成 cluster_anime = animation.FuncAnimation(fig, update_cluster, frames=MaxIter + 1, interval=100) cluster_anime.save("ch4_3_4_Cluster.gif")
(よく理解していないので、animationの解説は省略…とりあえずこれで動きます……)
参考文献
- 須山敦志『ベイズ推論による機械学習入門』(機械学習スタートアップシリーズ)杉山将監修,講談社,2017年.
おわりに
あと1節!疲れた!
【次節の内容】