はじめに
『ベイズ推論による機械学習入門』の学習時のノートです。基本的な内容は「数式の行間を読んでみた」とそれを「RとPythonで組んでみた」になります。「数式」と「プログラム」から理解するのが目標です。
この記事は、4.4.3項の内容です。「観測モデルを多次元ガウス混合分布(多変量正規混合分布)」、「事前分布をガウス・ウィシャート分布とディリクレ分布」とするガウス混合モデルに対する変分推論(変分ベイズ)をPythonで実装します。
省略してある内容等ありますので、本とあわせて読んでください。初学者な自分が理解できるレベルまで落として書き下していますので、分かる人にはかなりくどくなっています。同じような立場の人のお役に立てれば幸いです。
【数式読解編】
【他の節一覧】
【この節の内容】
・Pythonでやってみる
人工的に生成したデータを用いて、ベイズ推論を行ってみましょう。アルゴリズム4.6を参考に実装します。
利用するライブラリを読み込みます。
# 4.4.3項で利用するライブラリ import numpy as np from scipy.stats import multivariate_normal # 多次元ガウス分布 from scipy.special import psi # ディガンマ関数 import matplotlib.pyplot as plt
scipyライブラリのstatsモジュールから、多次元ガウス分布multivariate_normalのクラスを利用します。確率密度の計算にpdf()を使います。また、パラメータの計算に、SciPyライブラリのspecialモジュールからディガンマ関数psiを使います。
・観測モデルの設定
まずは、観測モデルを設定します。この節では、$K$個の観測モデルを多次元ガウス分布$\mathcal{N}(\mathbf{x}_n | \boldsymbol{\mu}_k, \boldsymbol{\Lambda}_k^{-1})$とします。また、各データに対する観測モデルの割り当てをカテゴリ分布$\mathrm{Cat}(\mathbf{s}_n | \boldsymbol{\pi})$によって行います。
観測モデルのパラメータを設定します。この実装例では2次元のグラフで表現するため、$D = 2$のときのみ動作します。
# 次元数を設定:(固定) D = 2 # クラスタ数を指定 K = 3 # K個の真の平均を指定 mu_truth_kd = np.array( [[5.0, 35.0], [-20.0, -10.0], [30.0, -20.0]] ) # K個の真の分散共分散行列を指定 sigma2_truth_kdd = np.array( [[[250.0, 65.0], [65.0, 270.0]], [[125.0, -45.0], [-45.0, 175.0]], [[210.0, -15.0], [-15.0, 250.0]]] )
$K$の平均パラメータ$\boldsymbol{\mu} = \{\boldsymbol{\mu}_1, \boldsymbol{\mu}_2, \cdots, \boldsymbol{\mu}_K\}$、$\boldsymbol{\mu}_k = (\mu_{k,1}, \mu_{k,2}, \cdots, \mu_{k,D})$をmu_truth_kd、分散共分散行列パラメータ$\boldsymbol{\Sigma} = \{\boldsymbol{\Sigma}_1, \boldsymbol{\Sigma}_2, \cdots, \boldsymbol{\Sigma}_K\}$、$\boldsymbol{\Sigma}_k = (\sigma_{k,1,1}^2, \cdots, \sigma_{k,D,D}^2)$をsigma2_truth_ddkとして、値を指定します。$\boldsymbol{\Sigma}_k$は正定値行列です。また、分散共分散行列の逆行列$\boldsymbol{\Lambda}_k = \boldsymbol{\Sigma}_k^{-1}$を精度行列と呼びます。
設定したパラメータは次のようになります。
# 確認 print(mu_truth_kd) print(sigma2_truth_kdd)
[[ 5. 35.]
[-20. -10.]
[ 30. -20.]]
[[[250. 65.]
[ 65. 270.]]
[[125. -45.]
[-45. 175.]]
[[210. -15.]
[-15. 250.]]]
混合比率を設定します。
# 真の混合比率を指定 pi_truth_k = np.array([0.45, 0.25, 0.3])
混合比率パラメータ$\boldsymbol{\pi} = (\pi_1, \pi_2, \cdots, \pi_K)$をpi_true_kとして、$\sum_{k=1}^K \pi_k = 1$、$\pi_k \geq 0$の値を指定します。ここで、$\pi_k$は各データがクラスタ$k$となる($s_{n,k} = 1$となる)確率を表します。
この3つのパラメータの値を観測データから求めるのがここでの目的です。
設定した観測モデルをグラフで確認しましょう。作図用の点を作成します。
# 作図用のx軸のxの値を作成 x_1_line = np.linspace( np.min(mu_truth_kd[:, 0] - 3 * np.sqrt(sigma2_truth_kdd[:, 0, 0])), np.max(mu_truth_kd[:, 0] + 3 * np.sqrt(sigma2_truth_kdd[:, 0, 0])), num=300 ) # 作図用のy軸のxの値を作成 x_2_line = np.linspace( np.min(mu_truth_kd[:, 1] - 3 * np.sqrt(sigma2_truth_kdd[:, 1, 1])), np.max(mu_truth_kd[:, 1] + 3 * np.sqrt(sigma2_truth_kdd[:, 1, 1])), num=300 ) # 作図用の格子状の点を作成 x_1_grid, x_2_grid = np.meshgrid(x_1_line, x_2_line) # 作図用のxの点を作成 x_point = np.stack([x_1_grid.flatten(), x_2_grid.flatten()], axis=1) # 作図用に各次元の要素数を保存 x_dim = x_1_grid.shape print(x_dim)
(300, 300)
作図用に、2次元ガウス分布に従う変数$\mathbf{x}_n = (x_{n,1}, x_{n,2})$がとり得る点(値の組み合わせ)を作成します。$x_{n,1}$がとり得る値(x軸の値)をnp.linspace()で作成してx_1_lineとします。この例では、$K$個のクラスタそれぞれで平均値から標準偏差の3倍を引いた値と足した値を計算して、その最小値から最大値までを範囲とします。
np.linspace()を使うと指定した要素数で等間隔に切り分けます。np.arange()を使うと切り分ける間隔を指定できます。処理が重い場合は、この値を調整してください。
同様に、$x_{n,2}$がとり得る値(y軸の値)も作成してx_2_lineとします。
np.meshgrid()を使って、x_1_lineとx_2_lineの要素の全ての組み合わせを持つような2次元配列に変換してそれぞれx_1_grid, x_2_gridとします。
これは、確率密度を等高線図にする際に格子状の点(2軸の全ての値が直交する点)を渡す必要があるためです。
また、x_1_grid, x_2_gridの要素を列として持つ2次元配列を作成してx_pointとします。これは、確率密度の計算に使います。
計算結果の確率密度は1次元配列になります。作図時にx_1_grid, x_2_gridと同じ形状にする必要があるため、形状をx_dimとして保存しておきます。
作成した$\mathbf{x}$の点は次のようになります。
# 確認 print(x_point[:5])
[[-53.54101966 -67.4341649 ]
[-53.11621983 -67.4341649 ]
[-52.69142 -67.4341649 ]
[-52.26662017 -67.4341649 ]
[-51.84182033 -67.4341649 ]]
1列目がx軸の値、2列目がy軸の値に対応しています。
観測モデルの確率密度を計算します。
# 観測モデルを計算 true_model = 0 for k in range(K): # クラスタkの分布の確率密度を計算 tmp_density = multivariate_normal.pdf( x=x_point, mean=mu_truth_kd[k], cov=sigma2_truth_kdd[k] ) # K個の分布の加重平均を計算 true_model += pi_truth_k[k] * tmp_density
$K$個のパラメータmu_truth_kd, sigmga2_truth_ddkを使って、x_point_matの点ごとに、次の混合ガウス分布の式で確率密度を計算します。
$K$個の多次元ガウス分布に対して、$\boldsymbol{\pi}$を使って加重平均をとります。
多次元ガウス分布の確率密度は、SciPyライブラリのmultivariate_normal.pdf()で計算できます。$k$番目の分布の場合は、データの引数Xにx_point、平均の引数muにmu_truth_kd[k]、分散共分散行列の引数sigmaにsigma2_truth_kdd[k]を指定します。
この計算をfor文でK回繰り返し行います。各パラメータによって求めた$K$回分の確率密度をそれぞれpi_truth_k[k]で割り引いてmodel_probに加算していきます。
計算結果は次のようになります。
# 確認 print(true_model[:5])
[9.06768334e-13 1.07345258e-12 1.27033352e-12 1.50260830e-12
1.77630256e-12]
観測モデルを作図します。
# 観測モデルを作図 plt.figure(figsize=(12, 9)) plt.contour(x_1_grid, x_2_grid, true_model.reshape(x_dim)) # 真の分布 plt.suptitle('Gaussian Mixture Model', fontsize=20) plt.title('K=' + str(K), loc='left') plt.xlabel('$x_1$') plt.ylabel('$x_2$') plt.colorbar() plt.show()
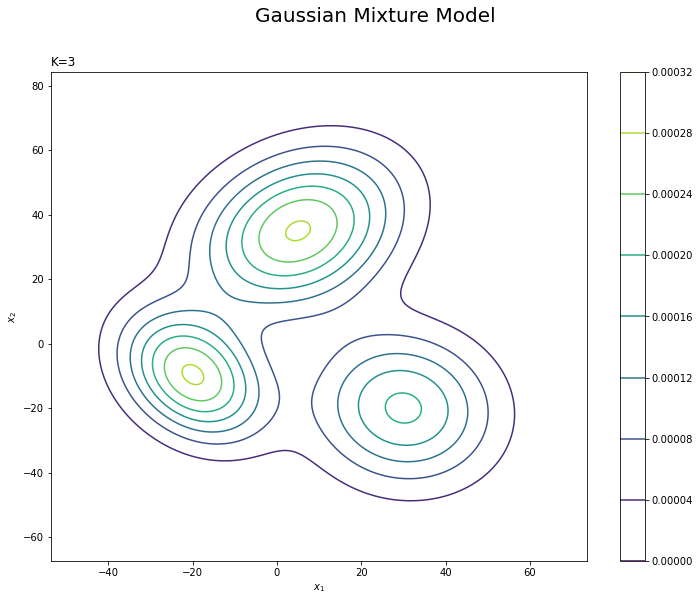
等高線グラフはplt.contour()で描画します。
$K$個の分布を重ねたような分布になります。ただし、積分して1となるようにしているため、$K$個の分布そのものよりも1つ1つの山が小さく(確率密度が小さく)なっています。
・データの生成
続いて、構築した観測モデルに従ってデータを生成します。先に、潜在変数$\mathbf{S} = \{\mathbf{s}_1, \mathbf{s}_2, \cdots, \mathbf{s}_N\}$、$\mathbf{s}_n = (s_{n,1}, s_{n,2}, \cdots, s_{n,K})$を生成し、各データにクラスタを割り当てます。次に、割り当てられたクラスタに従い観測データ$\mathbf{X} = \{\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_N\}$、$\mathbf{x}_n = (x_{n,1}, x_{n,2}, \cdots, x_{n,D})$を生成します。
$N$個の潜在変数$\mathbf{S}$を生成します。
# (観測)データ数を指定 N = 250 # 潜在変数を生成 s_truth_nk = np.random.multinomial(n=1, pvals=pi_truth_k, size=N)
生成するデータ数$N$をNとして値を指定します。
カテゴリ分布に従う乱数は、多項分布に従う乱数生成関数np.random.multinomial()のn引数を1にすることで生成できます。また、確率(パラメータ)の引数probにpi_truth_k、試行回数の引数sizeにNを指定します。生成した$N$個の$K$次元ベクトルをs_truth_nkとします。
結果は次のようになります。
# 確認 print(s_truth_nk[:5])
[[0 1 0]
[0 0 1]
[0 0 1]
[1 0 0]
[0 0 1]]
これが本来は観測できない潜在変数であり、真のクラスタです。各行がデータを表し、値が1の列番号が割り当てられたクラスタ番号を表します。
s_truth_nkから各データのクラスタ番号を抽出します。
# クラスタ番号を抽出 _, s_truth_n = np.where(s_truth_nk == 1) # 確認 print(s_truth_n[:5])
[1 2 2 0 2]
np.where()を使って行(データ)ごとに要素が1の列番号を抽出します。
各データに割り当てられたクラスタに従い$N$個のデータを生成します。
# (観測)データを生成 x_nd = np.array([ np.random.multivariate_normal( mean=mu_truth_kd[k], cov=sigma2_truth_kdd[k], size=1 ).flatten() for k in s_truth_n ])
各データ$\mathbf{x}_n$に割り当てられたクラスタ($s_{n,k} = 1$である$k$)のパラメータ$\boldsymbol{\mu}_k,\ \boldsymbol{\Sigma}_k$を持つ多次元ガウス分布に従いデータ(値)を生成します。多次元ガウス分布の乱数は、np.random.multivariate_normaln()で生成できます。
データごとにクラスタが異なるので、for文(リスト内包表記)で1データずつ処理します。$n$番目のデータのクラスタ番号s_true_n[n]を取り出してkとします。そのクラスタに従ってデータ$\mathbf{x}_n$を生成します。平均の引数meanにmu_true_kd[k]、分散共分散行列の引数covにsigma2_true_kdd[k]を指定します。また1データずつ生成するので、データ数の引数sizeは1です。2次元配列で出力されるため、flatten()で1次元配列に変換しておきます。
生成した観測データは次のようになります。
# 確認 print(x_nd[:5])
[[ 0.89740581 -24.95830061]
[ 21.76837427 -40.19415749]
[ 16.34587795 -30.85479385]
[ 6.92061039 45.78512834]
[ 10.31019784 -17.0872797 ]]
観測データの散布図を観測モデルに重ねて作図します。
# 観測データの散布図を作成 plt.figure(figsize=(12, 9)) for k in range(K): k_idx, = np.where(s_truth_n == k) # クラスタkのデータのインデック plt.scatter(x=x_nd[k_idx, 0], y=x_nd[k_idx, 1], label='cluster:' + str(k + 1)) # 観測データ plt.contour(x_1_grid, x_2_grid, true_model.reshape(x_dim), linestyles='--') # 真の分布 plt.suptitle('Gaussian Mixture Model', fontsize=20) plt.title('$N=' + str(N) + ', K=' + str(K) + ', \pi=[' + ', '.join([str(pi) for pi in pi_truth_k]) + ']$', loc='left') plt.xlabel('$x_1$') plt.ylabel('$x_2$') plt.colorbar() plt.show()
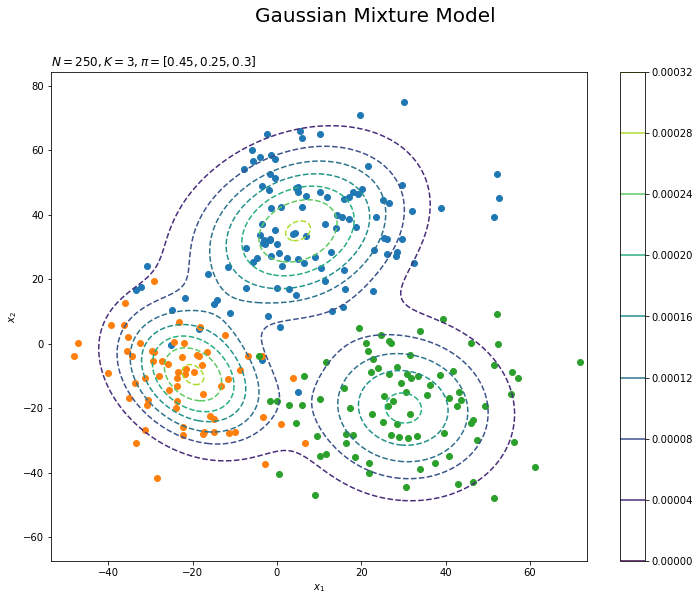
散布図はplt.scatter()で描画します。各クラスタが割り当てられたデータのインデックスをnp.where(s_true_n == k)で抽出してk_idxとします。k_idxを使ってクラスタ$k$が割り当てられたデータを取り出して、クラスタごとに色を変えた散布図を描きます。
観測データから各データのクラスタも推定します。
・事前分布の設定
次に、観測モデル(観測データの分布)$p(\mathbf{X} | \mathbf{S}, \boldsymbol{\mu}, \boldsymbol{\Lambda})$と潜在変数の分布$p(\mathbf{S} | \boldsymbol{\pi})$に対する共役事前分布を設定します。多次元ガウス分布のパラメータ$\boldsymbol{\mu},\ \boldsymbol{\Lambda}$に対する事前分布$p(\boldsymbol{\mu}, \boldsymbol{\Lambda})$としてガウス・ウィシャート分布$\mathrm{NW}(\boldsymbol{\mu}, \boldsymbol{\Lambda} | \mathbf{m}, \beta, \nu, \mathbf{W})$、カテゴリ分布のパラメータ$\boldsymbol{\pi}$に対する事前分布$p(\boldsymbol{\pi})$としてディリクレ分布$p(\boldsymbol{\pi} | \boldsymbol{\alpha})$を設定します。
各事前分布のパラメータ(超パラメータ)を設定します。
# muの事前分布のパラメータを指定 beta = 1.0 m_d = np.repeat(0.0, D) # lambdaの事前分布のパラメータを指定 w_dd = np.identity(D) * 0.0005 nu = D # piの事前分布のパラメータを指定 alpha_k = np.repeat(2.0, K)
$K$個の観測モデルの平均パラメータ$\boldsymbol{\mu}$の共通の事前分布(多次元ガウス分布)の平均パラメータ$\mathbf{m} = (m_1, m_2, \cdots, m_D)$をm_d、精度行列パラメータの係数$\beta$をbetaとして値を指定します。
$K$個の観測モデルの精度行列パラメータ$\boldsymbol{\Lambda}$の共通の事前分布(ウィシャート分布)のパラメータ$\mathbf{W} = (w_{1,1}, \cdots, w_{D,D})$をw_dd、自由度$\nu$をnuとして値を指定します。$\mathbf{W}$は正定値行列であり、自由度は$\nu > D - 1$の値をとります。
混合比率パラメータ$\boldsymbol{\pi}$の事前分布(ディリクレ分布)のパラメータ$\boldsymbol{\alpha} = (\alpha_1, \alpha_2, \cdots, \alpha_K)$をalpha_kとして、$\alpha_k > 0$の値を指定します。
パラメータを設定できたので、$\boldsymbol{\mu}$の事前分布をグラフで確認しましょう。作図用の$\boldsymbol{\mu}$の点を作成します。
# muの事前分布の標準偏差を計算 sigma_mu_d = np.sqrt( np.linalg.inv(beta * nu * w_dd).diagonal() ) # 作図用のx軸のmuの値を作成 mu_0_line = np.linspace( np.min(mu_truth_kd[:, 0]) - sigma_mu_d[0], np.max(mu_truth_kd[:, 0]) + sigma_mu_d[0], num=300 ) # 作図用のy軸のmuの値を作成 mu_1_line = np.linspace( np.min(mu_truth_kd[:, 1]) - sigma_mu_d[1], np.max(mu_truth_kd[:, 1]) + sigma_mu_d[1], num=300 ) # 作図用の格子状の点を作成 mu_0_grid, mu_1_grid = np.meshgrid(mu_0_line, mu_1_line) # 作図用のmuの点を作成 mu_point = np.stack([mu_0_grid.flatten(), mu_1_grid.flatten()], axis=1) # 作図用に各次元の要素数を保存 mu_dim = mu_0_grid.shape print(mu_dim)
(300, 300)
$\mathbf{x}$の点のときと同様に作成します。各軸の描画範囲は、真の平均の最小値から事前分布の標準偏差を引いた値から、真の平均の最大値に標準偏差を足した値までとします。事前分布の標準偏差は$(\beta \boldsymbol{\Lambda}_k)^{-1}$の対角成分の平方根です。ただしこの時点では$\boldsymbol{\Lambda}$が未知の値なので、代わりに$\boldsymbol{\Lambda}$の期待値$\mathbb{E}[\boldsymbol{\Lambda}]$を使うことにします。ウィシャート分布の期待値(2.89)より
です。
また、逆行列の計算はnp.linalg.inv()、対角成分の抽出はdiagonal()、平方根の計算はnp.sqrt()で行えます。
面倒でしたら適当な値を直接指定してください。
$\boldsymbol{\mu}$の事前分布の確率密度を計算します。
# muの事前分布を計算
prior_mu_density = multivariate_normal.pdf(
x=mu_point, mean=m_d, cov=np.linalg.inv(beta * nu * w_dd)
)
観測モデルのときと同様に、多次元ガウス分布の確率密度を計算します。ここでも、$\boldsymbol{\mu}$の事前分布の分散共分散行列を$(\beta \mathbb{E}[\boldsymbol{\Lambda}])^{-1}$とします。
計算結果は次のようになります。
# 確認 print(prior_mu_density[:5])
[1.10780663e-05 1.12959859e-05 1.15165400e-05 1.17397162e-05
1.19655008e-05]
$\boldsymbol{\mu}$の事前分布を作図します。
# muの事前分布を作図 plt.figure(figsize=(12, 9)) plt.scatter(x=mu_truth_kd[:, 0], y=mu_truth_kd[:, 1], label='true val', color='red', s=100, marker='x') # 真の平均 plt.contour(mu_0_grid, mu_1_grid, prior_mu_density.reshape(mu_dim)) # 事前分布 plt.suptitle('Gaussian Mixture Model', fontsize=20) plt.title('iter:' + str(0) + ', K=' + str(K), loc='left') plt.xlabel('$\mu_1$') plt.ylabel('$\mu_2$') plt.colorbar() plt.legend() plt.show()
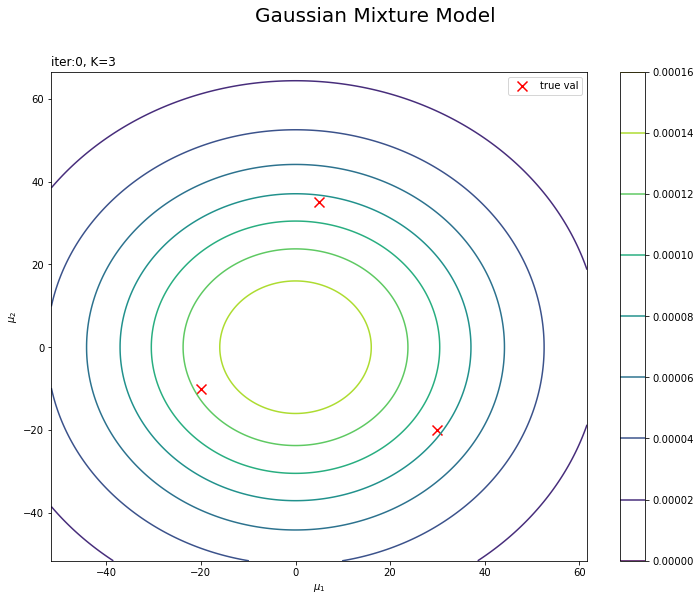
真の平均値をプロットしておきます。この真の平均を分布推定します。
$\boldsymbol{\Lambda}$と$\boldsymbol{\pi}$の事前分布(と事後分布)については省略します。詳しくは、3.2.2 項「カテゴリ分布の学習と予測」と3.4.2項「多次元ガウス分布の学習と予測:精度が未知の場合」を参照してください。
・初期値の設定
潜在変数$\mathbf{S}$の近似事後分布$q(\mathbf{S})$の期待値$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$をランダムに生成して初期値とします。また、生成した$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$を用いて各パラメータ$\boldsymbol{\mu},\ \boldsymbol{\Lambda},\ \boldsymbol{\pi}$の近似事後分布$q(\boldsymbol{\mu} | \boldsymbol{\Lambda}),\ q(\boldsymbol{\Lambda}),\ q(\boldsymbol{\pi})$のパラメータ$\hat{\mathbf{m}},\ \hat{\boldsymbol{\beta}},\ \hat{\boldsymbol{\nu}},\ \hat{\mathbf{W}},\ \hat{\boldsymbol{\alpha}}$を計算して初期値とします。
$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$の初期値を生成します。
# 潜在変数の近似事後分布の期待値を初期化 E_s_nk = np.random.uniform(low=0.0, high=1.0, size=(N, K)) E_s_nk /= np.sum(E_s_nk, axis=1, keepdims=True)
一様乱数の生成関数np.random.uniform()を使って0から1の値を生成し、N行K列の2次元配列を作成してE_s_nkとします。ランダムに生成した値を、行(データ)ごとの和が1になるように正規化します。(正規化するので乱数の時点で0から1の値である必要はありませんが、確率であることを明示しておきます。)
生成した潜在変数の期待値は次のようになります。
# 確認 print(E_s_nk[:5]) print(np.sum(E_s_nk[:5], axis=1))
[[0.14330214 0.63950703 0.21719083]
[0.32561079 0.26345454 0.41093467]
[0.40548386 0.21033534 0.38418081]
[0.60587686 0.04246582 0.35165731]
[0.61461574 0.13147548 0.25390878]]
[1. 1. 1. 1. 1.]
データごとの和が1になります。
s_nkを用いて、$\boldsymbol{\mu}$の近似事後分布のパラメータを計算します。
# 初期値によるmuの近似事後分布のパラメータを計算:式(4.114) beta_hat_k = np.sum(E_s_nk, axis=0) + beta m_hat_kd = (np.dot(E_s_nk.T, x_nd) + beta * m_d) / beta_hat_k.reshape((K, 1))
$\boldsymbol{\mu}$の近似事後分布($K$個の多次元ガウス分布)の平均パラメータ$\hat{\mathbf{m}} = \{\hat{\mathbf{m}}_1, \hat{\mathbf{m}}_2, \cdots, \hat{\mathbf{m}}_K\}$、$\hat{\mathbf{m}}_k = (\hat{m}_{k,1}, \hat{m}_{k,2}, \cdots, \hat{m}_{k,D})$、精度行列パラメータの係数$\boldsymbol{\hat{\beta}} = \{\hat{\beta}_1, \hat{\beta}_2, \cdots, \hat{\beta}_K\}$の各項を
で計算して、それぞれbeta_hat_k、m_hat_kdとします。
# 確認 print(beta_hat_k) print(m_hat_kd)
[90.08594955 82.80360209 80.11044836]
[[6.67256235 5.26793215]
[6.74477897 4.08238381]
[6.91550772 5.96479941]]
同様に、$\boldsymbol{\lambda}$の近似事後分布のパラメータを計算します。
# 初期値によるlambdaの近似後分布のパラメータを計算:式(4.118) w_hat_kdd = np.zeros((K, D, D)) for k in range(K): inv_w_dd = np.dot(E_s_nk[:, k] * x_nd.T, x_nd) inv_w_dd += beta * np.dot(m_d.reshape((D, 1)), m_d.reshape((1, D))) inv_w_dd -= beta_hat_k[k] * np.dot(m_hat_kd[k].reshape((D, 1)), m_hat_kd[k].reshape((1, D))) inv_w_dd += np.linalg.inv(w_dd) w_hat_kdd[k] = np.linalg.inv(inv_w_dd) nu_hat_k = np.sum(E_s_nk, axis=0) + nu
$\boldsymbol{\lambda}$の近似事後分布($K$個のウィシャート分布)のパラメータ$\hat{\mathbf{W}} = \{\hat{\mathbf{W}}_1, \hat{\mathbf{W}}_2, \cdots, \hat{\mathbf{W}}_K\}$、$\hat{\mathbf{W}}_k = (\hat{w}_{k,1,1}, \cdots, \hat{w}_{k,D,D})$、自由度$\boldsymbol{\hat{\nu}} = \{\hat{\nu}_1, \hat{\nu}_2, \cdots, \hat{\nu}_K\}$を
で計算して、それぞれnu_hat_k、w_hat_ddkとします。
# 確認 print(w_hat_kdd) print(nu_hat_k)
[[[1.68853266e-05 1.25076027e-07]
[1.25076027e-07 1.28676082e-05]]
[[1.88902012e-05 7.40906036e-07]
[7.40906036e-07 1.49831772e-05]]
[[1.96880099e-05 1.04385987e-06]
[1.04385987e-06 1.48290062e-05]]]
[91.08594955 83.80360209 81.11044836]
最後に、$\boldsymbol{\pi}$の近似事後分布のパラメータを計算します。
# 初期値によるpiの近似事後分布のパラメータを計算:式(4.58) alpha_hat_k = np.sum(E_s_nk, axis=0) + alpha_k
$\boldsymbol{\pi}$の近似事後分布(ディリクレ分布)のパラメータ$\hat{\boldsymbol{\alpha}} = (\hat{\alpha}_1, \hat{\alpha}_2, \cdots, \hat{\alpha}_K)$の各項を
で計算して、alpha_hat_kとします。
# 確認 print(alpha_hat_k)
[91.08594955 83.80360209 81.11044836]
超パラメータの初期値が得られたので、$\boldsymbol{\mu}$の近似事後分布を確認しましょう。$K$個の近似事後分布を計算します。
# 初期値によるmuの近似事後分布を計算 posterior_density_kg = np.empty((K, mu_point.shape[0])) for k in range(K): # クラスタkのmuの近似事後分布を計算 posterior_density_kg[k] = multivariate_normal.pdf( x=mu_point, mean=m_hat_kd[k], cov=np.linalg.inv(beta_hat_k[k] * nu_hat_k[k] * w_hat_kdd[k]) )
事前分布のときと同様に計算します。ただし、超パラメータが$K$個になったので、多次元ガウス分布も$K$個になります。$K$回分の計算結果を2次元配列に格納していきます。
クラスタ$k$の近似事後分布の平均は$\hat{\mathbf{m}}$で、精度行列として$\hat{\beta}_k \mathbb{E}[\boldsymbol{\Lambda}_k]$を使います。事前分布のときと同様に、$\mathbb{E}[\boldsymbol{\Lambda}_k] = \hat{\nu}_k \hat{\mathbf{W}}_k$です。
作成した配列は次のようになります。
# 確認 print(posterior_density_kg[:, :5])
[[2.26450129e-180 4.88467474e-179 1.03292054e-177 2.14124499e-176
4.35144993e-175]
[9.51465990e-177 1.90511954e-175 3.74355964e-174 7.21906315e-173
1.36618806e-171]
[5.43140939e-177 1.06410032e-175 2.04683448e-174 3.86556509e-173
7.16759358e-172]]
$\boldsymbol{\mu}$の近似事後分布を作図します。
# 初期値によるmuの近似事後分布を作図 plt.figure(figsize=(12, 9)) plt.scatter(x=mu_truth_kd[:, 0], y=mu_truth_kd[:, 1], label='true val', color='red', s=100, marker='x') # 真の平均 for k in range(K): plt.contour(mu_0_grid, mu_1_grid, posterior_density_kg[k].reshape(mu_dim)) # 近似事後分布 plt.suptitle('Gaussian Distribution', fontsize=20) plt.title('iter:' + str(0) + ', K=' + str(K), loc='left') plt.xlabel('$\mu_1$') plt.ylabel('$\mu_2$') plt.colorbar() plt.legend() plt.show()

事前分布のときと同様に作図できます。
m_hat_k, beta_hat_kとnu_hat_k, w_hat_ddkから求めた各パラメータの期待値を用いて、混合分布を計算します。
# 初期値による混合分布を計算 init_density = 0 for k in range(K): # クラスタkの分布の確率密度を計算 tmp_density = multivariate_normal.pdf( x=x_point, mean=m_hat_kd[k], cov=np.linalg.inv(nu_hat_k[k] * w_hat_kdd[k]) ) # K個の分布の加重平均を計算 init_density += alpha_hat_k[k] / np.sum(alpha_hat_k) * tmp_density
観測モデルのときと同様に、多次元ガウス混合分布の確率密度を計算します。ただし、パラメータ$\boldsymbol{\mu},\ \boldsymbol{\Lambda},\ \boldsymbol{\pi}$は未知なので、代わりに各パラメータの期待値$\mathbb{E}[\boldsymbol{\mu}],\ \mathbb{E}[\boldsymbol{\Lambda}],\ \mathbb{E}[\boldsymbol{\pi}]$を使うことにします。
クラスタ$k$における平均パラメータの期待値$\mathbb{E}[\boldsymbol{\mu}_k]$は、多次元ガウス分布の期待値(2.76)より
です。
また、混合比率パラメータの期待値は、ディリクレ分布の期待値(2.51)より
です。
超パラメータの初期値から求めた分布を作図します。
# 初期値による分布を作図 plt.figure(figsize=(12, 9)) plt.contour(x_1_grid, x_2_grid, true_model.reshape(x_dim), alpha=0.5, linestyles='dashed') # 真の分布 plt.contour(x_1_grid, x_2_grid, init_density.reshape(x_dim)) # 期待値による分布:(等高線) plt.suptitle('Gaussian Mixture Model', fontsize=20) plt.title('iter:' + str(0) + ', K=' + str(K), loc='left') plt.xlabel('$x_1$') plt.ylabel('$x_2$') plt.colorbar() plt.show()
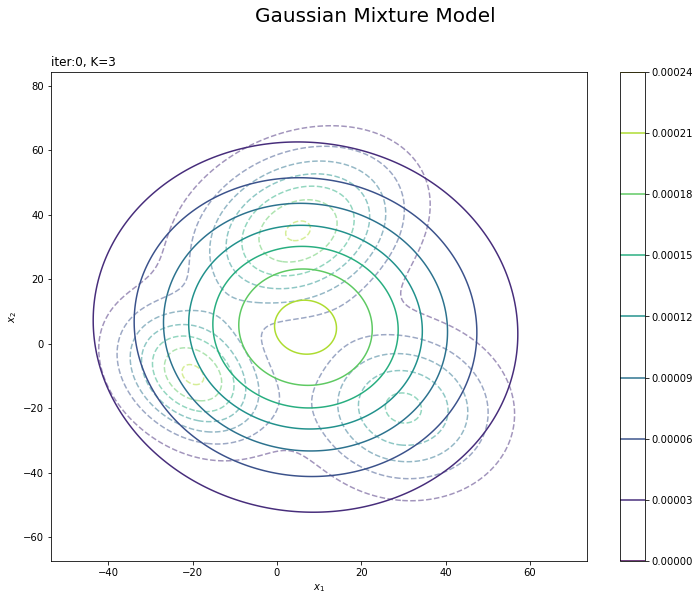
観測モデルのときと同様に作図します。更新を繰り返すことで真の分布に近付けていきます。
ここに、クラスタの初期値も重ねて確認してみましょう。$K$個のクラスタの内、確率が最大のクラスタをそのデータのクラスタとみなすことにします。
# 確率が最大のクラスタ番号を抽出 s_n = np.argmax(E_s_nk, axis=1) # 各データのクラスタとなる確率を抽出 prob_s_n = E_s_nk[np.arange(N), s_n] # 確認 print(s_n[:5]) print(prob_s_n[:5])
[1 2 0 0 0]
[0.63950703 0.41093467 0.40548386 0.60587686 0.61461574]
np.argmax()を使って、E_s_nkの行(データ)ごとに確率が一番高い列(クラスタ)番号を抽出してs_nとします。
また、抽出したクラスタとなる確率も取り出してprob_s_nとします。
クラスタの初期値の散布図を作成します。
# K個のカラーマップを指定 colormap_list = ['Blues', 'Oranges', 'Greens'] # クラスタの散布図を作成 plt.figure(figsize=(12, 9)) plt.contour(x_1_grid, x_2_grid, true_model.reshape(x_dim), alpha=0.5, linestyles='dashed') # 真の分布 plt.contourf(x_1_grid, x_2_grid, init_density.reshape(x_dim), alpha=0.5) # 期待値による分布:(塗りつぶし) for k in range(K): k_idx, = np.where(s_n == k) # クラスタkのデータのインデックス cm = plt.get_cmap(colormap_list[k]) # クラスタkのカラーマップを設定 plt.scatter(x=x_nd[k_idx, 0], y=x_nd[k_idx, 1], label='cluster:' + str(k + 1), c=[cm(p) for p in prob_s_n[k_idx]]) # 確率によるクラスタ plt.suptitle('Gaussian Mixture Model', fontsize=20) plt.title('iter:' + str(0)+ ', K=' + str(K), loc='left') plt.xlabel('$x_1$') plt.ylabel('$x_2$') plt.legend() plt.show()
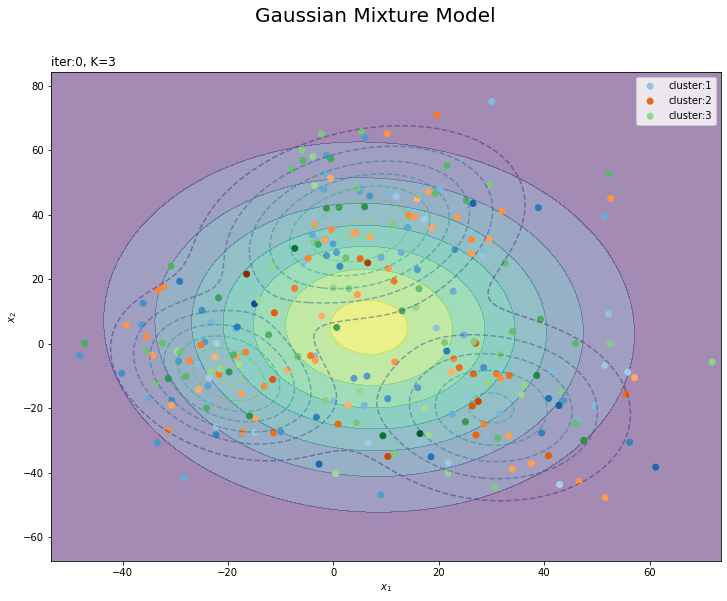
データの生成のときと同様に、各データに割り当てられたクラスタに従って色分けします。ただしここでは、そのクラスタとなる確率に従って濃淡を付けることにします。plt.get_cmap()によって確率値を色コードに変換したもの(よく分かってない…)を、plt.scatter()の色の引数cに指定します。
・変分推論
変分推論では、潜在変数$\mathbf{S}$の近似事後分布$q(\mathbf{S})$の期待値$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$の更新と、各パラメータ$\boldsymbol{\mu},\ \boldsymbol{\Lambda},\ \boldsymbol{\pi}$の近似事後分布$q(\boldsymbol{\mu} | \boldsymbol{\Lambda}),\ q(\boldsymbol{\Lambda}),\ q(\boldsymbol{\pi})$のパラメータ(超パラメータ)$\hat{\mathbf{m}},\ \hat{\boldsymbol{\beta}},\ \hat{\mathbf{W}},\ \hat{\boldsymbol{\nu}},\ \hat{\boldsymbol{\alpha}}$の更新を交互に行います。
まずは、超パラメータの初期値を用いて潜在変数の近似事後分布$q(\mathbf{S})$のパラメータを計算します。得られたパラメータが近似事後分布の期待値$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$になります。次に、求めた$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$を用いて超パラメータを更新します。ここまでが1回の試行です。
さらに次の試行では、前回更新した超パラメータを用いて$\mathbf{S}$の近似事後分布を更新となります。この処理を指定した回数繰り返します。
・コード全体
中間変数ln_eta_nkに関して、添字を使って代入するため予め変数を用意しておく必要があります。
また、後で各パラメータの更新値や分布の推移を確認するために、それぞれ試行ごとにtrace_***に値を保存していきます。関心のあるパラメータを記録してください。
# 試行回数を指定 MaxIter = 100 # 途中計算に用いる項の受け皿を作成 ln_eta_nk = np.zeros((N, K)) # 推移の確認用の受け皿 trace_E_s_ink = [E_s_nk.copy()] trace_beta_ik = [beta_hat_k.copy()] trace_m_ikd = [m_hat_kd.copy()] trace_w_ikdd = [w_hat_kdd.copy()] trace_nu_ik = [nu_hat_k.copy()] trace_alpha_ik = [alpha_hat_k.copy()] # 変分推論 for i in range(MaxIter): # 潜在変数の近似事後分布のパラメータを計算:式(4.109) for k in range(K): # クラスタkの中間変数を計算:式(4.119-4.122,4.62) E_lmd_dd = nu_hat_k[k] * w_hat_kdd[k] E_ln_det_lmd = np.sum(psi(0.5 * (nu_hat_k[k] - np.arange(D)))) E_ln_det_lmd += D * np.log(2) + np.log(np.linalg.det(w_hat_kdd[k])) E_lmd_mu_d1 = np.dot(E_lmd_dd, m_hat_kd[k].reshape((D, 1))) E_mu_lmd_mu = np.dot(m_hat_kd[k].reshape((1, D)), E_lmd_mu_d1).item() E_mu_lmd_mu += D / beta_hat_k[k] E_ln_pi = psi(alpha_hat_k[k]) - psi(np.sum(alpha_hat_k)) ln_eta_nk[:, k] = - 0.5 * np.diag(x_nd.dot(E_lmd_dd).dot(x_nd.T)) ln_eta_nk[:, k] += np.dot(x_nd, E_lmd_mu_d1).flatten() ln_eta_nk[:, k] += - 0.5 * E_mu_lmd_mu + 0.5 * E_ln_det_lmd + E_ln_pi tmp_eta_nk = np.exp(ln_eta_nk) eta_nk = (tmp_eta_nk + 1e-7) / np.sum(tmp_eta_nk + 1e-7, axis=1, keepdims=True) # 正規化 # 潜在変数の近似事後分布の期待値を計算:式(4.59) E_s_nk = eta_nk.copy() # muの近似事後分布のパラメータを計算:式(4.114) beta_hat_k = np.sum(E_s_nk, axis=0) + beta m_hat_kd = (np.dot(E_s_nk.T, x_nd) + beta * m_d) / beta_hat_k.reshape((K, 1)) # lambdaの近似事後分布のパラメータを計算:式(4.118) w_hat_kdd = np.zeros((K, D, D)) for k in range(K): inv_w_dd = np.dot(E_s_nk[:, k] * x_nd.T, x_nd) inv_w_dd += beta * np.dot(m_d.reshape((D, 1)), m_d.reshape((1, D))) inv_w_dd -= beta_hat_k[k] * np.dot(m_hat_kd[k].reshape((D, 1)), m_hat_kd[k].reshape((1, D))) inv_w_dd += np.linalg.inv(w_dd) w_hat_kdd[k] = np.linalg.inv(inv_w_dd) nu_hat_k = np.sum(E_s_nk, axis=0) + nu # piの近似事後分布のパラメータを計算:式(4.58) alpha_hat_k = np.sum(E_s_nk, axis=0) + alpha_k # i回目のパラメータを記録 trace_E_s_ink.append(E_s_nk.copy()) trace_beta_ik.append(beta_hat_k.copy()) trace_m_ikd.append(m_hat_kd.copy()) trace_w_ikdd.append(w_hat_kdd.copy()) trace_nu_ik.append(nu_hat_k.copy()) trace_alpha_ik.append(alpha_hat_k.copy()) # 動作確認 #print(str(i + 1) + ' (' + str(np.round((i + 1) / MaxIter * 100, 1)) + '%)')
・処理の解説
変分推論で行う処理を確認していきます。
・潜在変数のサンプリング
潜在変数$\mathbf{S}$の近似事後分布(のパラメータ)を計算して、新たな$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$を求めます。
$\mathbf{S}$の近似事後分布のパラメータを計算します。
# 潜在変数の近似事後分布のパラメータを計算:式(4.109) for k in range(K): # クラスタkの中間変数を計算:式(4.119-4.122,4.62) E_lmd_dd = nu_hat_k[k] * w_hat_kdd[k] E_ln_det_lmd = np.sum(psi(0.5 * (nu_hat_k[k] - np.arange(D)))) E_ln_det_lmd += D * np.log(2) + np.log(np.linalg.det(w_hat_kdd[k])) E_lmd_mu_d1 = np.dot(E_lmd_dd, m_hat_kd[k].reshape((D, 1))) E_mu_lmd_mu = np.dot(m_hat_kd[k].reshape((1, D)), E_lmd_mu_d1).item() E_mu_lmd_mu += D / beta_hat_k[k] E_ln_pi = psi(alpha_hat_k[k]) - psi(np.sum(alpha_hat_k)) ln_eta_nk[:, k] = - 0.5 * np.diag(x_nd.dot(E_lmd_dd).dot(x_nd.T)) ln_eta_nk[:, k] += np.dot(x_nd, E_lmd_mu_d1).flatten() ln_eta_nk[:, k] += - 0.5 * E_mu_lmd_mu + 0.5 * E_ln_det_lmd + E_ln_pi tmp_eta_nk = np.exp(ln_eta_nk) eta_nk = (tmp_eta_nk + 1e-7) / np.sum(tmp_eta_nk + 1e-7, axis=1, keepdims=True) # 正規化
$n$番目のデータの潜在変数$\mathbf{s}_n$の近似事後分布(カテゴリ分布)のパラメータ$\boldsymbol{\eta}_n = (\eta_{n,1}, \eta_{n,2}, \cdots, \eta_{n,K})$の各項を、次の式で計算します。
$\eta_{n,k}$は、$n$番目の観測データ$\mathbf{x}_n$にクラスタ$k$が割り当てられる($s_{n,k} = 1$となる)確率を表します。また、各項は
で計算できます。
ただし、$\mathbf{x}_n^{\top} \mathbb{E}_{q(\boldsymbol{\Lambda}_k)} [\boldsymbol{\Lambda}_k] \mathbf{x}_n$の計算において、$N$個全てのデータを一度で処理するために1から$N$の全ての組み合わせで行います(ln_eta_nk[:, k]の1つ目の計算時)。この計算結果は、$N \times N$の配列になります。これは例えば、1行$N$列目の要素は$\mathbf{x}_1^{\top} \mathbb{E}_{q(\boldsymbol{\Lambda}_k)} [\boldsymbol{\Lambda}_k] \mathbf{x}_N$の計算結果です。これは不要なので、np.diag()で対角成分(同じデータによる計算結果)のみを取り出します。
最後に、データごとの和が1となるように
で正規化します。ただし、0除算とならないように、微小な値1e-7($10^{-7} = 0.0000001$)を加えています。
# 確認 print(E_s_nk[:5]) print(np.sum(E_s_nk[:5], axis=1))
[[3.63790860e-01 6.33814363e-01 2.39477735e-03]
[3.13491641e-03 9.96589120e-01 2.75963249e-04]
[1.41781875e-02 9.85391010e-01 4.30802664e-04]
[1.27108362e-04 1.42034093e-04 9.99730858e-01]
[8.12386344e-02 9.10923970e-01 7.83739559e-03]]
[1. 1. 1. 1. 1.]
行(データ)ごとの和が1になるのを確認できます。
eta_nkが$\mathbf{S}$の近似事後分布の期待値です。
# 潜在変数の近似事後分布の期待値を計算:式(4.59)
E_s_nk = eta_nk.copy()
$\mathbf{S}$の近似事後分布の期待値$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$の各項は、カテゴリ分布の期待値(2.31)より
です。
これで$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$が得られました。次は、更新した$\mathbb{E}_{q(\mathbf{S})}[\mathbf{S}]$を用いて、超パラメータ$\hat{\mathbf{m}},\ \hat{\boldsymbol{\beta}},\ \hat{\mathbf{W}},\ \hat{\boldsymbol{\nu}},\ \hat{\boldsymbol{\alpha}}$を更新します。
「初期値の設定」のときと同様に計算できます。
以上が変分推論による近似推論で行うの個々の処理です。これを指定した回数繰り返し行うことで、各パラメータの値を徐々に真の値に近付けていきます。
・推論結果の確認
推論結果を確認していきます。
・最後のパラメータの確認
超パラメータm_hat_k, beta_hat_kとnu_hat_k, w_hat_ddkの最後の更新値を用いて、$\boldsymbol{\mu}$の近似事後分布を計算します。
# muの近似事後分布を計算 posterior_density_kg = np.empty((K, mu_point.shape[0])) for k in range(K): # クラスタkのmuの近似事後分布を計算 posterior_density_kg[k] = multivariate_normal.pdf( x=mu_point, mean=m_hat_kd[k], cov=np.linalg.inv(beta_hat_k[k] * nu_hat_k[k] * w_hat_kdd[k]) )
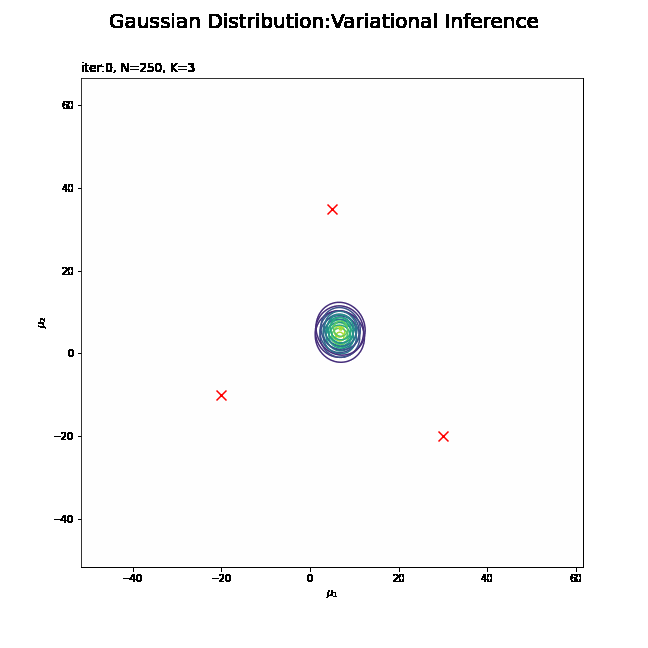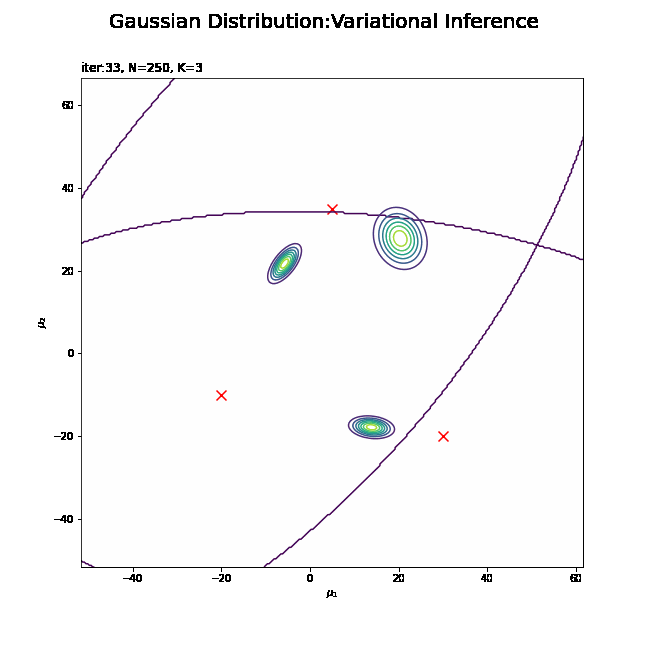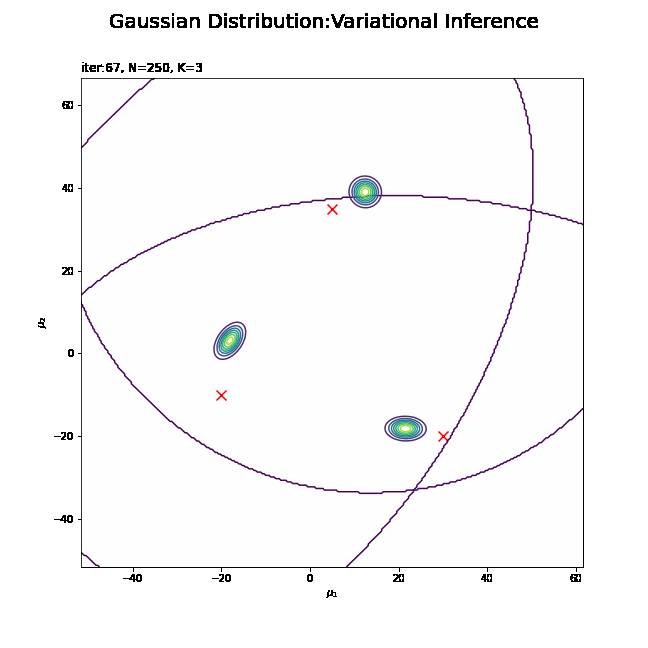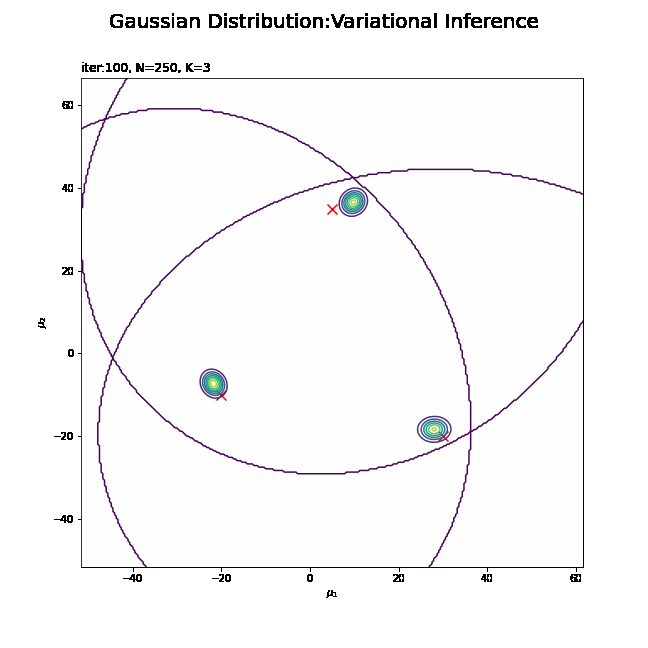
# muの近似事後分布を作図 plt.figure(figsize=(12, 9)) plt.scatter(x=mu_truth_kd[:, 0], y=mu_truth_kd[:, 1], label='true val', color='red', s=100, marker='x') # 真の平均 for k in range(K): plt.contour(mu_0_grid, mu_1_grid, posterior_density_kg[k].reshape(mu_dim)) # 事後分布 plt.suptitle('Gaussian Distribution', fontsize=20) plt.title('iter:' + str(MaxIter) + ', N=' + str(N) + ', K=' + str(K), loc='left') plt.xlabel('$\mu_1$') plt.ylabel('$\mu_2$') plt.colorbar() plt.legend() plt.show()
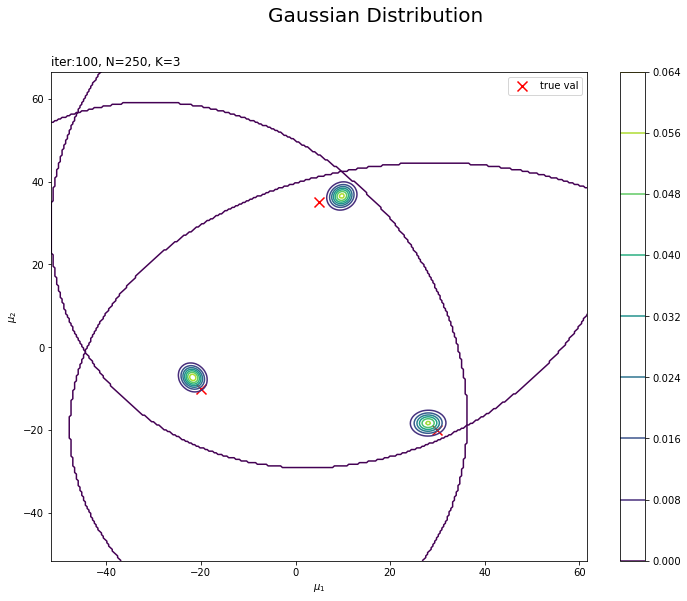
変数名やタイトル以外は「初期値の設定」のときと同じコードです。
$K$個のガウス分布がそれぞれ真の平均付近をピークとする分布を推定できています。
m_hat_k, beta_hat_kとnu_hat_k, w_hat_ddkから求めた各パラメータの期待値$\mathbb{E}[\boldsymbol{\mu}],\ \mathbb{E}[\boldsymbol{\Lambda}],\ \mathbb{E}[\boldsymbol{\pi}]$を用いて、混合分布を計算します。
# K個のカラーマップを指定 colormap_list = ['Blues', 'Oranges', 'Greens'] # 確率が最大のクラスタ番号を抽出 s_n = np.argmax(E_s_nk, axis=1) # 各データのクラスタとなる確率を抽出 prob_s_n = E_s_nk[np.arange(N), s_n] # 最後に更新したパラメータの期待値による混合分布を計算 res_density = 0 for k in range(K): # クラスタkの分布の確率密度を計算 tmp_density = multivariate_normal.pdf( x=x_point, mean=m_hat_kd[k], cov=np.linalg.inv(nu_hat_k[k] * w_hat_kdd[k]) ) # K個の分布の加重平均を計算 res_density += alpha_hat_k[k] / np.sum(alpha_hat_k) * tmp_density
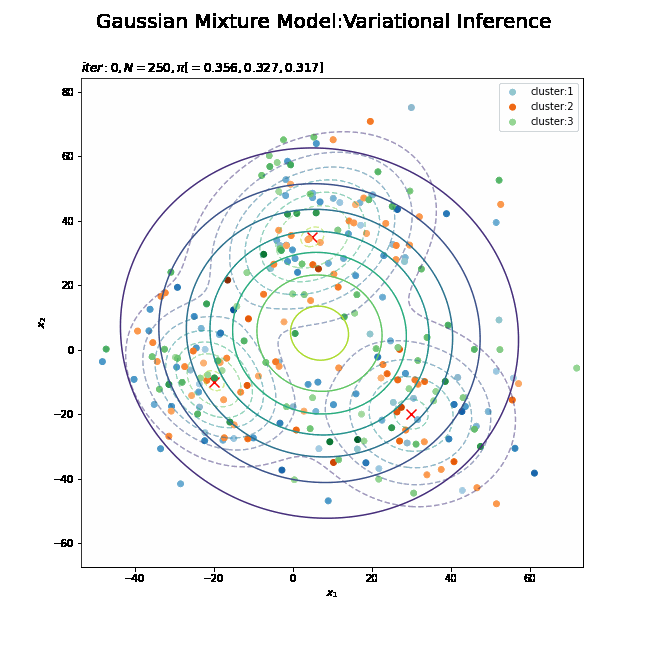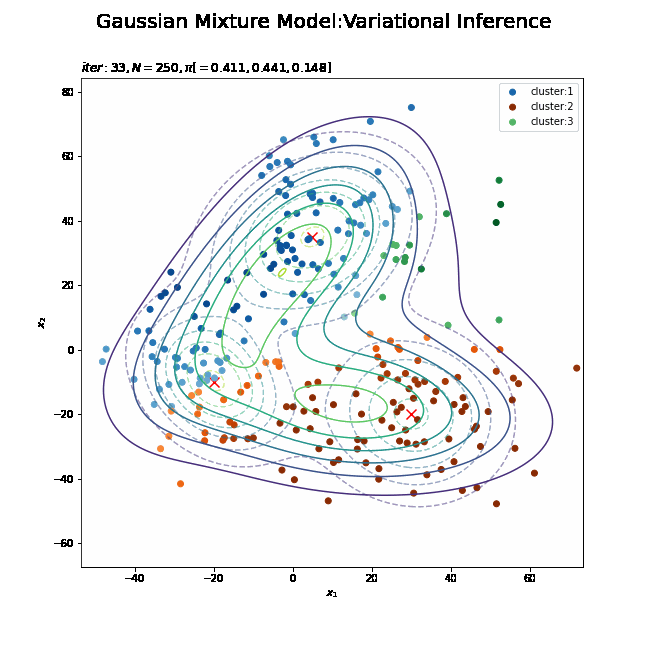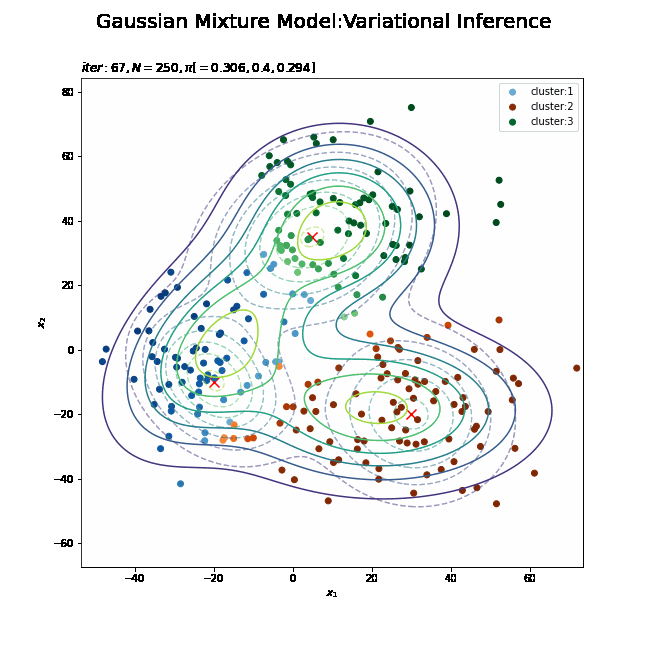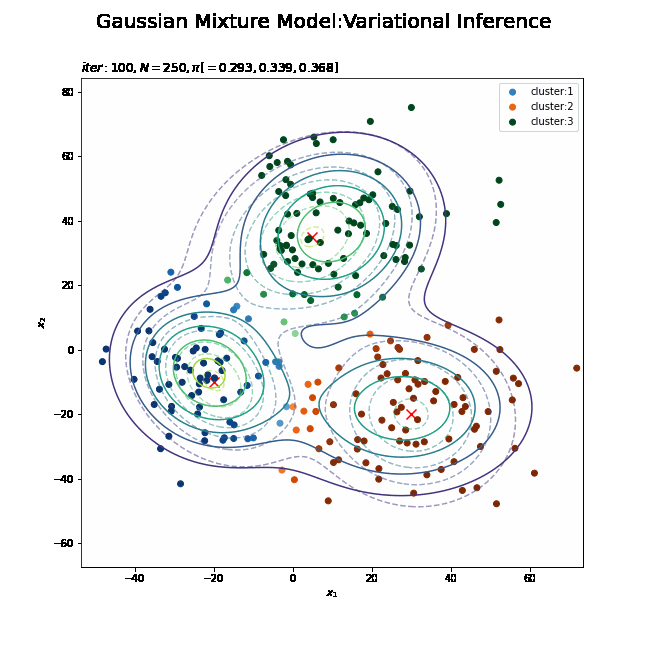
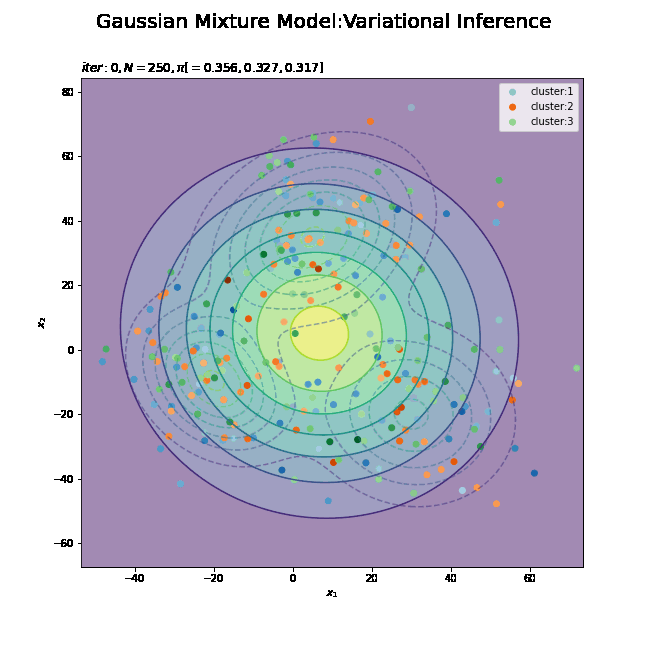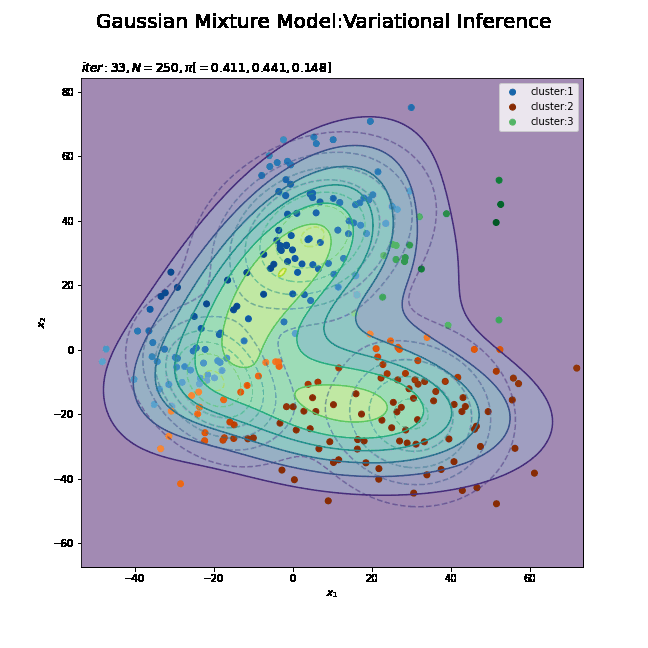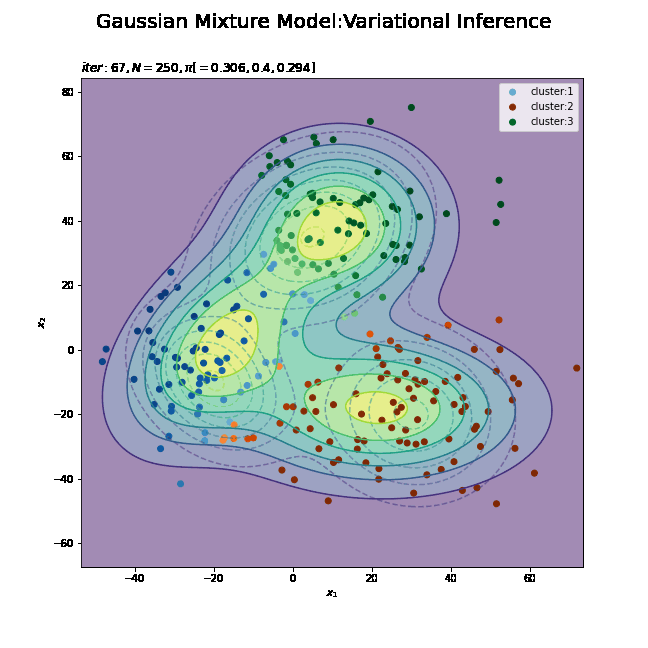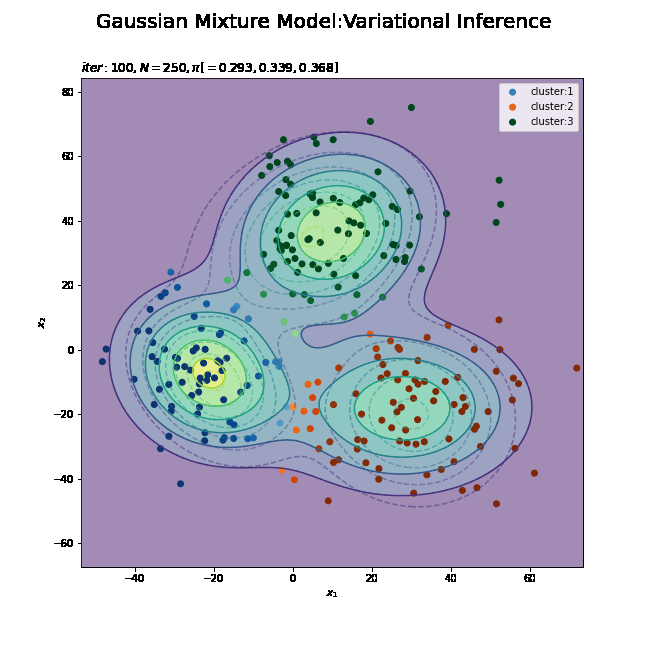
# 最後に更新したパラメータの期待値による分布を作図 plt.figure(figsize=(12, 9)) plt.contour(x_1_grid, x_2_grid, true_model.reshape(x_dim), alpha=0.5, linestyles='dashed') # 真の分布 plt.scatter(x=mu_truth_kd[:, 0], y=mu_truth_kd[:, 1], color='red', s=100, marker='x') # 真の平均 plt.contourf(x_1_grid, x_2_grid, res_density.reshape(x_dim), alpha=0.5) # 期待値による分布:(塗りつぶし) for k in range(K): k_idx, = np.where(s_n == k) # クラスタkのデータのインデックス cm = plt.get_cmap(colormap_list[k]) # クラスタkのカラーマップを設定 plt.scatter(x=x_nd[k_idx, 0], y=x_nd[k_idx, 1], label='cluster:' + str(k + 1), c=[cm(p) for p in prob_s_n[k_idx]]) # 確率によるクラスタ #plt.contour(x_1_grid, x_2_grid, res_density.reshape(x_dim)) # 期待値による分布:(等高線) #plt.colorbar() # 等高線の値:(等高線用) plt.suptitle('Gaussian Mixture Model:Variational Inference', fontsize=20) plt.title('$iter:' + str(MaxIter) + ', N=' + str(N) + ', \pi=[' + ', '.join([str(pi) for pi in np.round(alpha_hat_k / np.sum(alpha_hat_k), 3)]) + ']$', loc='left') plt.xlabel('$x_1$') plt.ylabel('$x_2$') plt.legend() plt.show()
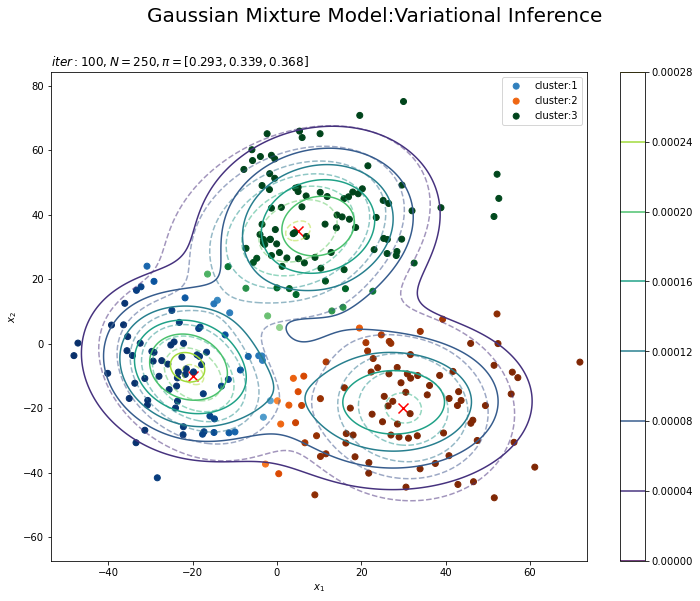
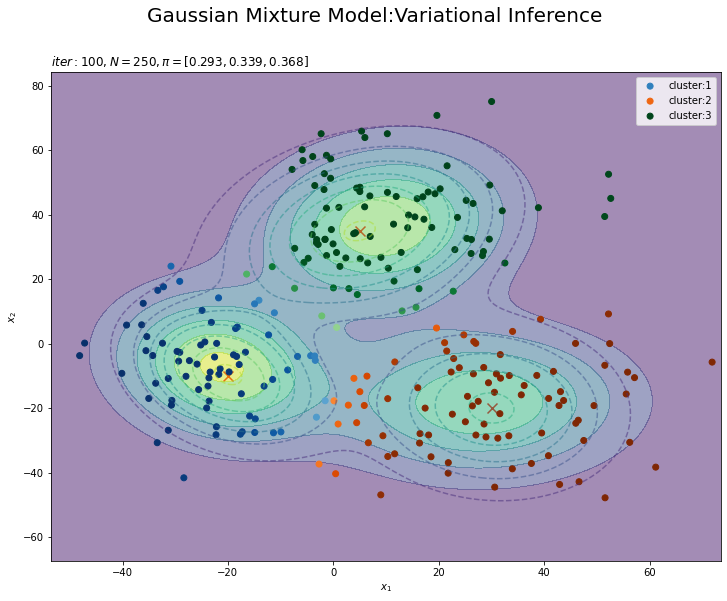
タイトル以外は「初期値の設定」のときと同じコードです。上はplt.contour()、下はplt.contourf()で作成したものです。
真の分布に近い分布になっています。
また、クラスタリングできていることが確認できます。クラスタの境界付近の色が薄く(確率が低く)なっています。ただし、クラスタの番号についてはランダムに決まるため真のクラスタの番号と一致しません。
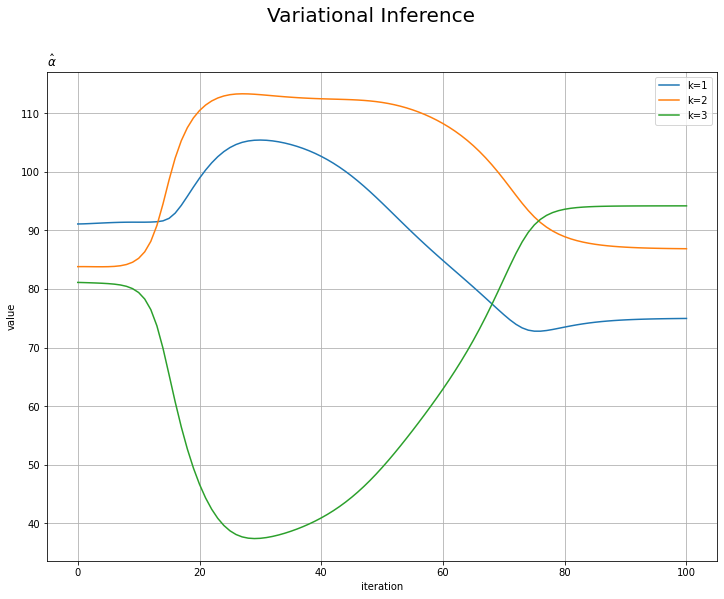
・超パラメータの推移の確認
超パラメータ$\hat{\mathbf{m}},\ \hat{\boldsymbol{\beta}},\ \hat{\boldsymbol{\nu}}, \hat{\mathbf{W}},\ \hat{\boldsymbol{\alpha}}$の更新値の推移を確認します。
・コード(クリックで展開)
学習ごとの値を格納した各パラメータのリストtrace_***をnp.arange()でNumPy配列に変換して作図します。
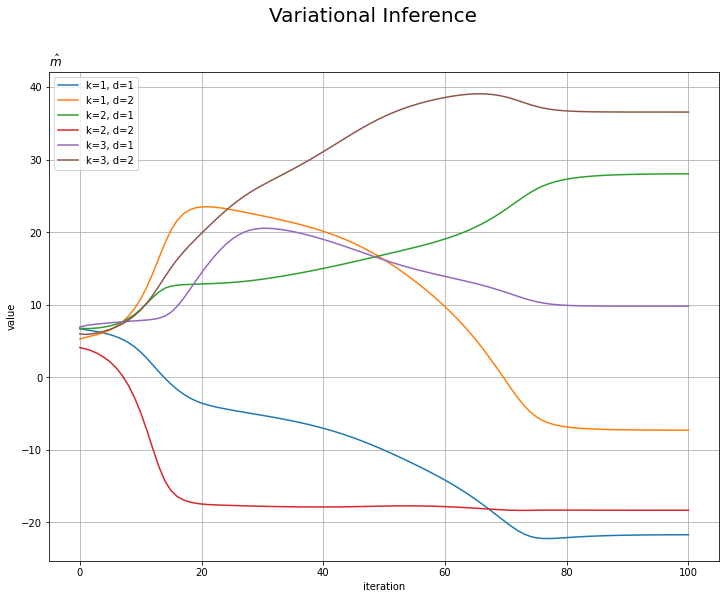
# mの推移を作図 plt.figure(figsize=(12, 9)) for k in range(K): for d in range(D): plt.plot(np.arange(MaxIter+1), np.array(trace_m_ikd)[:, k, d], label='k=' + str(k + 1) + ', d=' + str(d + 1)) plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('Variational Inference', fontsize=20) plt.title('$\hat{m}$', loc='left') plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()
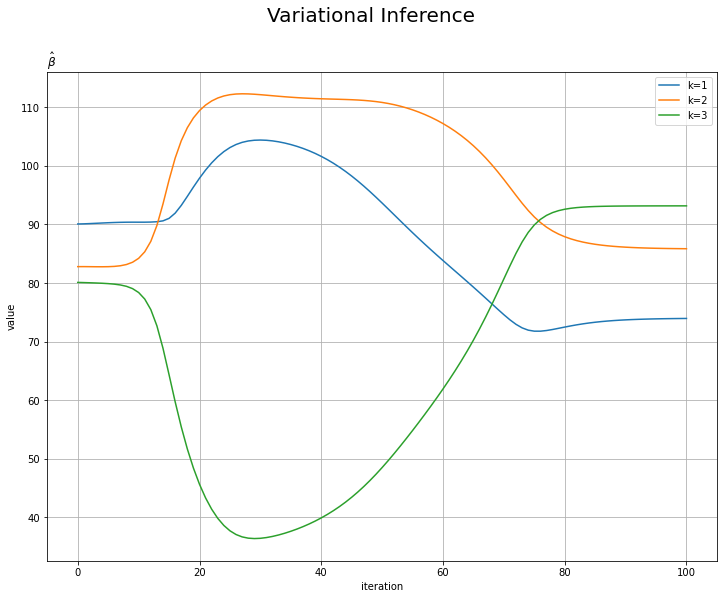
# betaの推移を作図 plt.figure(figsize=(12, 9)) for k in range(K): plt.plot(np.arange(MaxIter + 1), np.array(trace_beta_ik)[:, k], label='k=' + str(k + 1)) plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('Variational Inference', fontsize=20) plt.title('$\hat{\\beta}$', loc='left') plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()
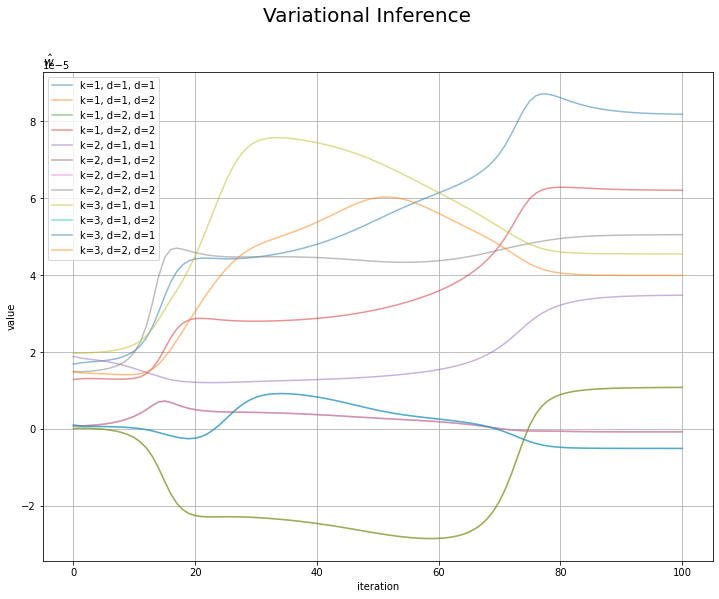
# wの推移を作図 plt.figure(figsize=(12, 9)) for k in range(K): for d1 in range(D): for d2 in range(D): plt.plot(np.arange(MaxIter + 1), np.array(trace_w_ikdd)[:, k, d1, d2], alpha=0.5, label='k=' + str(k + 1) + ', d=' + str(d1 + 1) + ', d''=' + str(d2 + 1)) plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('Variational Inference', fontsize=20) plt.title('$\hat{w}$', loc='left') plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()
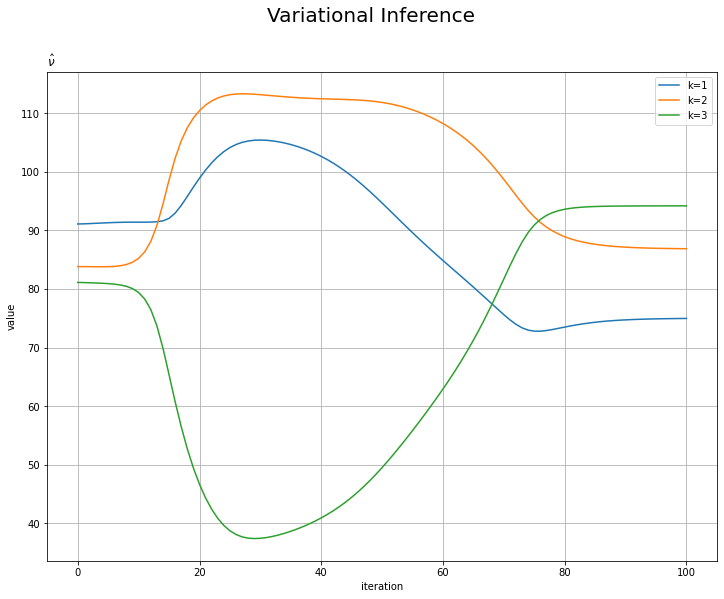
# nuの推移を作図 plt.figure(figsize=(12, 9)) for k in range(K): plt.plot(np.arange(MaxIter + 1), np.array(trace_nu_ik)[:, k], label='k=' + str(k + 1)) plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('Variational Inference', fontsize=20) plt.title('$\hat{\\nu}$', loc='left') plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()
# alphaの推移を作図 plt.figure(figsize=(12, 9)) for k in range(K): plt.plot(np.arange(MaxIter + 1), np.array(trace_alpha_ik)[:, k], label='k=' + str(k + 1)) plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('Variational Inference', fontsize=20) plt.title('$\hat{\\alpha}$', loc='left') plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()
・おまけ:アニメーションによる推移の確認
animationモジュールを利用して、各分布の推移のアニメーション(gif画像)を作成するためのコードです。
# 追加ライブラリ import matplotlib.animation as animation
・平均パラメータの近似事後分布の推移
・コード(クリックで展開)
# 画像サイズを指定 fig = plt.figure(figsize=(9, 9)) # 作図処理を関数として定義 def update_posterior(i): # i回目のmuの近似事後分布を計算 posterior_density_kg = np.empty((K, mu_point.shape[0])) for k in range(K): # クラスタkのmuの近似事後分布を計算 posterior_density_kg[k] = multivariate_normal.pdf( x=mu_point, mean=trace_m_ikd[i][k], cov=np.linalg.inv(trace_beta_ik[i][k] * trace_nu_ik[i][k] * trace_w_ikdd[i][k]) ) # 前フレームのグラフを初期化 plt.cla() # i回目のmuの近似事後分布を作図 plt.scatter(x=mu_truth_kd[:, 0], y=mu_truth_kd[:, 1], color='red', s=100, marker='x') # 真の平均 for k in range(K): plt.contour(mu_0_grid, mu_1_grid, posterior_density_kg[k].reshape(mu_dim)) # 近似事後分布 plt.suptitle('Gaussian Distribution:Variational Inference', fontsize=20) plt.title('iter:' + str(i) + ', N=' + str(N) + ', K=' + str(K), loc='left') plt.xlabel('$\mu_1$') plt.ylabel('$\mu_2$') # gif画像を作成 posterior_anime = animation.FuncAnimation(fig, update_posterior, frames=MaxIter + 1, interval=100) posterior_anime.save("ch4_4_3_Posterior.gif")
・パラメータの期待値による分布とクラスタの推移
・コード(クリックで展開)
# K個のカラーマップを指定 colormap_list = ['Blues', 'Oranges', 'Greens'] # 画像サイズを指定 fig = plt.figure(figsize=(9, 9)) # 作図処理を関数として定義 def update_model(i): # i回目の混合比率を計算 alpha_hat_k = trace_alpha_ik[i] / np.sum(trace_alpha_ik[i]) # i回目のサンプルによる混合分布を計算 res_density = 0 for k in range(K): # クラスタkの分布の確率密度を計算 tmp_density = multivariate_normal.pdf( x=x_point, mean=trace_m_ikd[i][k], cov=np.linalg.inv(trace_nu_ik[i][k] * trace_w_ikdd[i][k]) ) # K個の分布の加重平均を計算 res_density += alpha_hat_k[k] * tmp_density # 前フレームのグラフを初期化 plt.cla() # i回目の潜在変数の近似事後分布の期待値を取得 E_s_nk = trace_E_s_ink[i] # i回目のサンプルによる分布を作図 plt.contour(x_1_grid, x_2_grid, true_model.reshape(x_dim), alpha=0.5, linestyles='dashed') # 真の分布 #plt.contour(x_1_grid, x_2_grid, res_density.reshape(x_dim)) # 期待値による分布:(等高線) plt.contourf(x_1_grid, x_2_grid, res_density.reshape(x_dim), alpha=0.5) # 期待値による分布:(塗りつぶし) plt.scatter(x=mu_truth_kd[:, 0], y=mu_truth_kd[:, 1], color='red', s=100, marker='x') # 真の平均 for k in range(K): k_idx, = np.where(np.argmax(E_s_nk, axis=1) == k) cm = plt.get_cmap(colormap_list[k]) # クラスタkのカラーマップを設定 plt.scatter(x=x_nd[k_idx, 0], y=x_nd[k_idx, 1], label='cluster:' + str(k + 1), c=[cm(p) for p in E_s_nk[k_idx, k]]) # クラスタのサンプル plt.suptitle('Gaussian Mixture Model:Variational Inference', fontsize=20) plt.title('$iter:' + str(i) + ', N=' + str(N) + ', \pi[=' + ', '.join([str(pi) for pi in np.round(alpha_hat_k, 3)]) + ']$', loc='left') plt.xlabel('$x_1$') plt.ylabel('$x_2$') plt.legend() # gif画像を作成 model_anime = animation.FuncAnimation(fig, update_model, frames=MaxIter + 1, interval=100) model_anime.save("ch4_4_3_Model.gif")
(よく理解していないので、animationの解説は省略…とりあえずこれで動きます……)
参考文献
- 須山敦志『ベイズ推論による機械学習入門』(機械学習スタートアップシリーズ)杉山将監修,講談社,2017年.
おわりに
色々と言葉がごちゃごちゃしてくる。観測モデルのパラメータ$\boldsymbol{\mu},\ \boldsymbol{\Lambda},\ \boldsymbol{\pi}$を求めたい。そこでそれぞれ(近似)事後分布を求める(分布推定する)。パラメータの分布自体を描くのは省略して各分布の期待値(平均?)を求めて、それを用いて推定した観測モデル(?)を求めた(描画した)。この最後のグラフも近似事後分布と言っちゃったけど、本当は何と呼べばいいんだ?
Rの方ではやり方が分からなかった散布図を確率値でグラデーションにするのができて満足。でもクラスタ数に応じて色の設定を手打ちしなきゃいけないのがまだ不満。
次で4章ラストです!
【次節の内容】
- 2021/05/15:加筆修正しました。
事後分布が何なのか2週目をやっていてようやく理解した。でも、推定したパラメータを使う方の分布を何と呼べばいいのかはまだ分かってない。