はじめに
『スタンフォード ベクトル・行列からはじめる最適化数学』の学習ノートです。
「数式の行間埋め」や「Pythonを使っての再現」によって理解を目指します。本と一緒に読んでください。
この記事は7.1節「幾何変換」の内容です。
直線へのベクトルの射影の計算を確認して、グラフを作成します。
【前の内容】
【他の内容】
【今回の内容】
ベクトルの射影の可視化
行列計算によるベクトルの直線への射影(vector projection)を数式とグラフで確認します。
行列とベクトルの積については「【Python】行列のベクトル積の可視化【『スタンフォード線形代数入門』のノート】 - からっぽのしょこ」、射影については「【Python】5.3:正射影ベクトルの可視化【『スタンフォード線形代数入門』のノート】 - からっぽのしょこ」を参照してください。
利用するライブラリを読み込みます。
# 利用ライブラリ import numpy as np import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation
ベクトルの射影の計算式
まずは、ベクトルの射影を数式で確認します。
行列
を用いて、2次元ベクトル を変換します。
も2次元ベクトルになります。
ベクトルの射影の作図
次は、ベクトルの射影をグラフで確認します。
角度を指定して、射影用の行列を作成します。
# 角度(ラジアン)を指定 theta = 1.0/6.0 * np.pi print(theta) # 弧度法の角度 print(theta * 180.0/np.pi) # 度数法の角度 # 射影行列を作成 A = np.array( [[1.0 + np.cos(2.0 * theta), np.sin(2.0 * theta)], [np.sin(2.0 * theta), 1.0 - np.cos(2.0 * theta)]] ) A *= 0.5 print(A) print(A.shape)
0.5235987755982988
29.999999999999996
[[0.75 0.4330127]
[0.4330127 0.25 ]]
(2, 2)
水平線(x軸線の正の部分)からの角度(ラジアン) をスカラ
theta として値を指定します。
射影行列 を2次元配列
A として計算します。
ベクトルを指定して、行列との積により変換します。
# ベクトルを指定 x = np.array([-3.0, 2.0]) print(x) print(x.shape) # ベクトルを変換 y = np.dot(A, x) print(y) print(y.shape)
[-3. 2.]
(2,)
[-1.3839746 -0.79903811]
(2,)
入力ベクトル を1次元配列
x として値を指定します。
射影ベクトル(出力ベクトル) を計算して
y とします。
傾いた直線を描画するための座標を作成します。
# グラフサイズ用の値を設定 x1_min = np.floor(np.min([0.0, x[0], y[0]])) - 2 x1_max = np.ceil(np.max([0.0, x[0], y[0]])) + 2 x2_min = np.floor(np.min([0.0, x[1], y[1]])) - 1 x2_max = np.ceil(np.max([0.0, x[1], y[1]])) + 1 # 傾いた直線の座標を計算 x_vals = np.linspace(start=x1_min, stop=x1_max, num=101) line_arr = np.array( [x_vals, np.sin(theta)/np.cos(theta) * x_vals] ) print(line_arr[:, :5])
[[-5. -4.93 -4.86 -4.79 -4.72 ]
[-2.88675135 -2.84633683 -2.80592231 -2.76550779 -2.72509327]]
原点を通り水平から 傾いた直線の傾きは
で求まります。x軸の値
x_vals を作成して、y軸の値 を計算します。
射影ベクトルと平行な直線になります。
・装飾用の作図コード(クリックで展開)
直角マークを描画するための座標を作成します。
# 垂線ベクトルを計算 z = x - y print(z) # ベクトルを正規化 e_y = y / np.linalg.norm(y) e_z = z / np.linalg.norm(z) print(e_z) # 直角マークの座標を計算 r = 0.2 rightangle_mark_arr = np.array( [[y[0]+r*e_z[0], y[0]+r*(e_z[0]-e_y[0]), y[0]-r*e_y[0]], [y[1]+r*e_z[1], y[1]+r*(e_z[1]-e_y[1]), y[1]-r*e_y[1]]] ) print(rightangle_mark_arr)
[-1.6160254 2.79903811]
[-0.5 0.8660254]
[[-1.4839746 -1.31076952 -1.21076952]
[-0.62583302 -0.52583302 -0.69903811]]
点 の座標から、射影ベクトル
と垂線ベクトル
の方向にそれぞれ少しずつ移動した点の座標を配列に格納します。
傾きを示す角度マークと角度ラベルを描画するための座標を作成します。
# 角度マーク用のラジアンを作成 slope_rad_vals = np.linspace(start=0.0, stop=theta, num=100) # 角度マークの座標を計算 r = 0.3 slope_mark_arr = np.array( [r * np.cos(slope_rad_vals), r * np.sin(slope_rad_vals)] ) print(slope_mark_arr[:, :5]) # 角度ラベルの座標を計算 r = 0.45 slope_mark_vec = np.array( [r * np.cos(0.5 * theta), r * np.sin(0.5 * theta)] ) print(slope_mark_vec)
[[0.3 0.2999958 0.29998322 0.29996224 0.29993287]
[0. 0.00158666 0.00317327 0.00475979 0.00634618]]
[0.43466662 0.11646857]
x軸線の正の部分(原点と点 を結ぶ線分)から、中心角が
の円弧の座標を計算します。円弧の中点にラベルを配置します。
詳しくは「【Python】円周上の点とx軸を結ぶ円弧を作図したい - からっぽのしょこ」を参照してください。
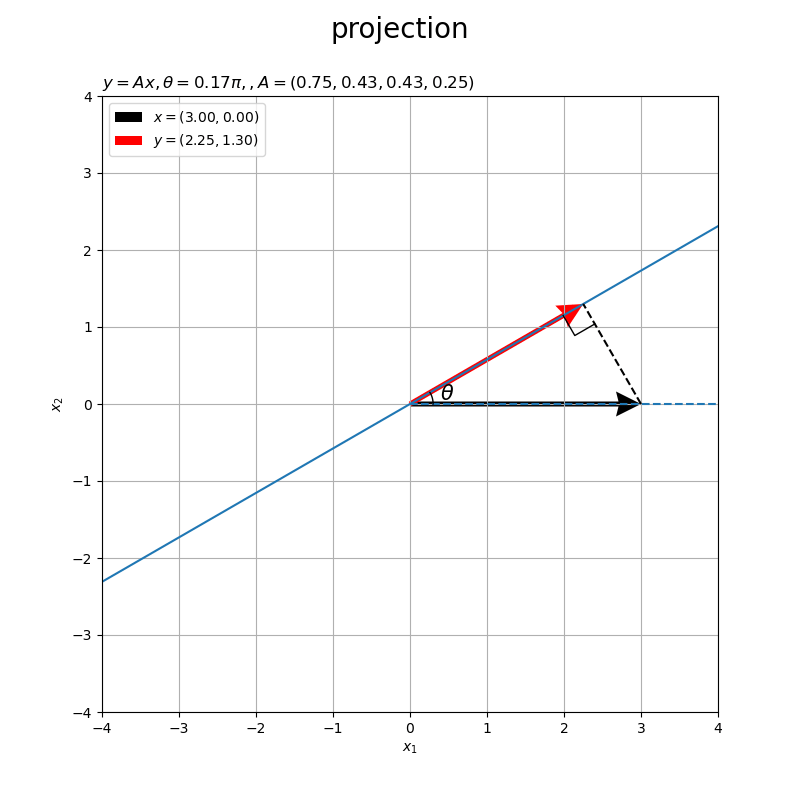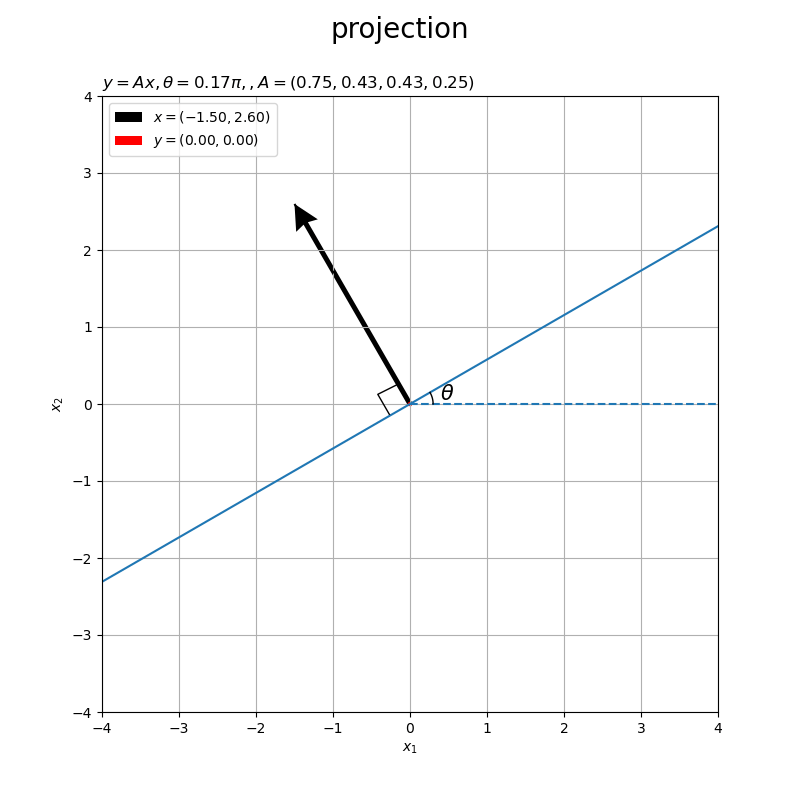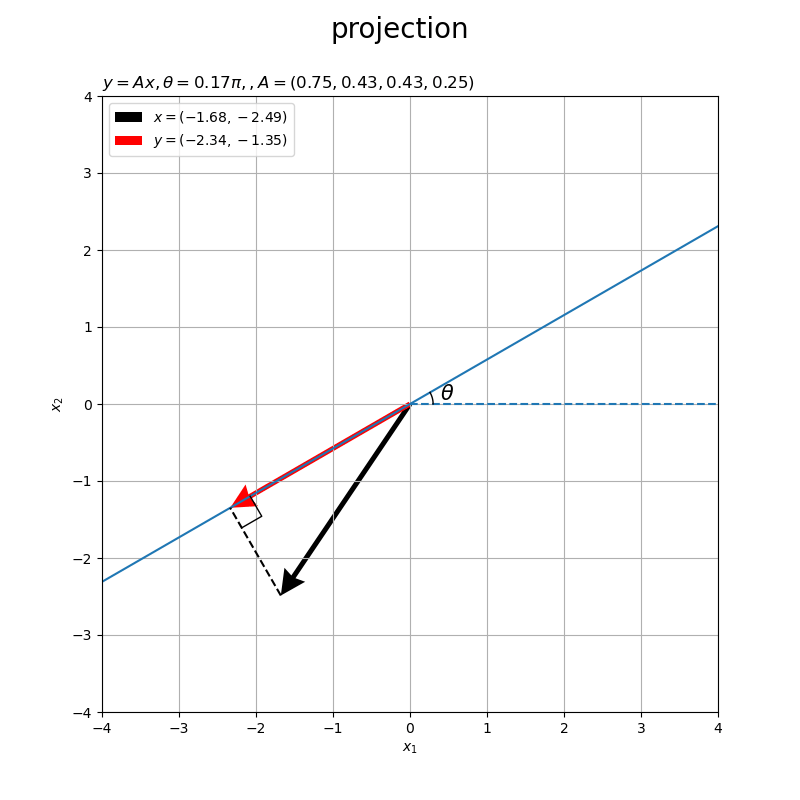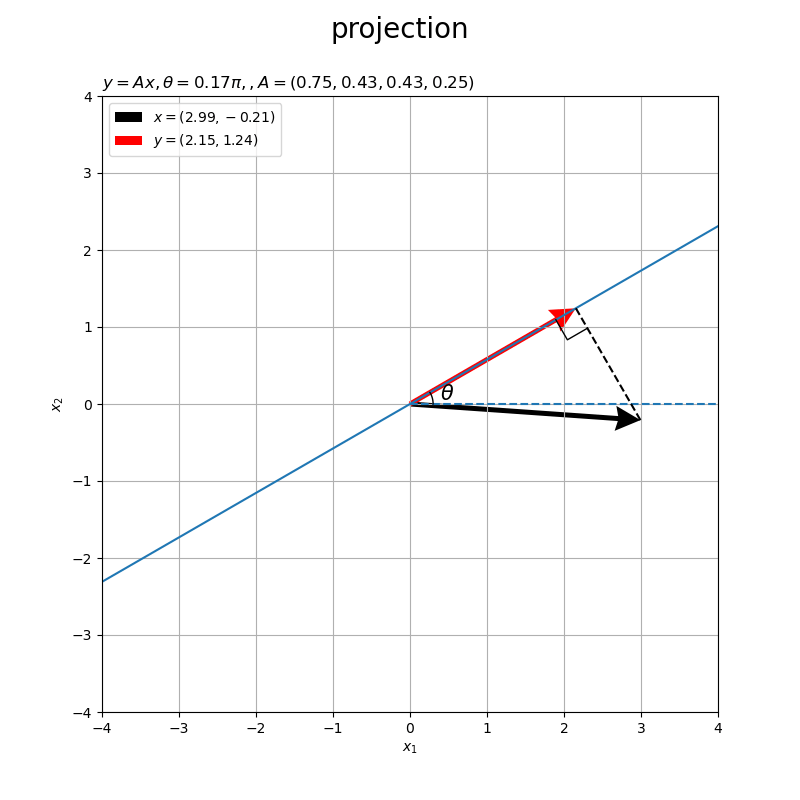
ベクトル のグラフを作成します。
# 2D射影ベクトルを作図 fig, ax = plt.subplots(figsize=(8, 6), facecolor='white') ax.quiver(0, 0, *x, color='black', units='dots', width=5, headwidth=5, angles='xy', scale_units='xy', scale=1, label='$x=({}, {})'.format(*x)+'$') # 入力ベクトル ax.quiver(0, 0, *y, color='red', units='dots', width=5, headwidth=5, angles='xy', scale_units='xy', scale=1, label='$y=({:.2f}, {:.2f})'.format(*y)+'$') # 出力ベクトル ax.plot(*line_arr) # 傾いた直線 ax.hlines(y=0.0, xmin=0.0, xmax=x1_max, linestyle='--') # 水平線 ax.plot([x[0], y[0]], [x[1], y[1]], color='black', linestyle='--') # 垂線 ax.plot(*rightangle_mark_arr, color='black', linewidth=1) # 直角マーク ax.plot(*slope_mark_arr, color='black', linewidth=1) # 傾き角度マーク ax.text(*slope_mark_vec, s='$\\theta$', size=15, ha='center', va='center') # 傾き角度ラベル ax.set_xticks(ticks=np.arange(x1_min, x1_max+1)) ax.set_yticks(ticks=np.arange(x2_min, x2_max+1)) ax.set_xlim(left=x1_min, right=x1_max) ax.set_ylim(bottom=x2_min, top=x2_max) ax.set_xlabel('$x_1$') ax.set_ylabel('$x_2$') ax.set_title('$y = A x, ' + '\\theta = {:.2f} \pi'.format(theta/np.pi)+', ' + 'A = ('+', '.join(['{:.2f}'.format(a) for a in A.flatten()])+')$', loc='left') ax.grid() fig.suptitle('projection', fontsize=20) ax.legend() ax.set_aspect('equal') plt.show()
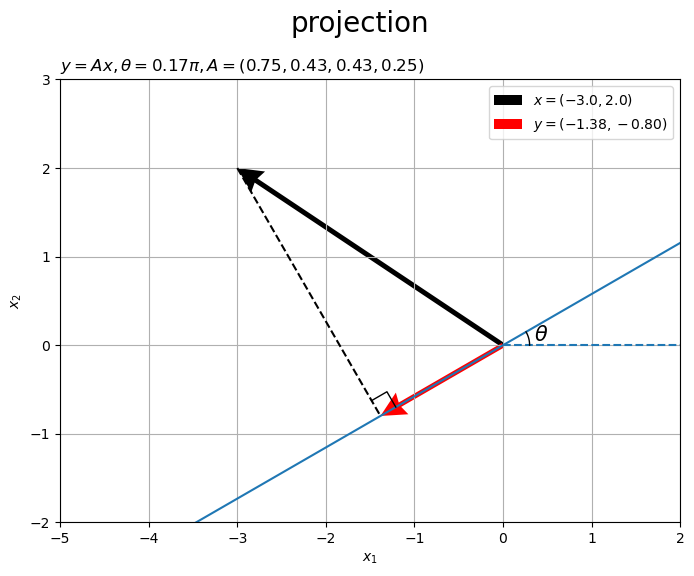
水平(水色の破線)から反時計回りに 傾いた直線(水色の実線)を直線
と呼ぶことにします。入力ベクトル
を黒色の矢印、出力ベクトルを
を赤色の矢印で示します。
行列 によって変換したベクトル
が、直線
と平行なのが分かります。
点 を通る直線(黒色の破線)が、直線
と垂直に交わります。よって、ベクトル
が、直線
に対するベクトル
の正射影ベクトルなのが分かります。また、点
が、直線
上における点
からの最短の点なのが分かります。
角度(直線の傾き)または入力ベクトルを変化させたアニメーションで確認します。
・作図コード(クリックで展開)
フレーム数を指定して、変化する角度と固定する入力ベクトルを作成します。
# フレーム数を指定 frame_num = 180 # 角度(ラジアン)の範囲を指定 theta_n = np.linspace(start=-2.0*np.pi, stop=2.0*np.pi, num=frame_num+1)[:frame_num] print(theta_n[:5]) # ベクトルを指定 x = np.array([-3.0, 2.0])
[-6.28318531 -6.21337214 -6.14355897 -6.0737458 -6.00393263]
フレーム数を frame_num として整数を指定します。
ラジアンの範囲を指定して、frame_num 個のラジアン theta_n を作成します。入力ベクトル x は先ほどと同様に指定します。
範囲を にして
frame_num + 1 個の等間隔の値を作成して最後の値を除くと、最後のフレームと最初のフレームがスムーズに繋がります。
または、固定する角度と変化する入力ベクトルを作成します。
# フレーム数を指定 #frame_num = 90 # 角度(ラジアン)を指定 theta = 1.0/6.0 * np.pi # ベクトルとして用いる値を指定 r = 3.0 rad_n = np.linspace(start=0.0, stop=2.0*np.pi, num=frame_num+1)[:frame_num] x_n = np.array( [r * np.cos(rad_n), r * np.sin(rad_n)] ).T print(x_n[:5])
[[3. 0. ]
[2.99269215 0.20926942]
[2.97080421 0.4175193 ]
[2.9344428 0.62373507]
[2.88378509 0.82691207]]
frame_num 個の入力ベクトル x_nを作成します。ラジアン theta は先ほどと同様に指定します。
この例では、入力ベクトル(の先端)が原点からの半径が r の円周上を移動するように設定しています。
角度と入力ベクトルの両方を変化させることもできます。
アニメーションを作成します。
# グラフサイズ用の値を設定 axis_size = np.ceil(abs(x).max()) + 1 #axis_size = np.ceil(abs(x_n).max()) + 1 # グラフオブジェクトを初期化 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white') fig.suptitle('projection', fontsize=20) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i番目の値を取得 theta = theta_n[i] #x = x_n[i] # 射影行列を作成 A = np.array( [[1.0 + np.cos(2.0*theta), np.sin(2.0*theta)], [np.sin(2.0*theta), 1.0 - np.cos(2.0*theta)]] ) * 0.5 # ベクトルを変換 y = np.dot(A, x) # 傾いた直線の座標を計算 x_vals = np.linspace(start=-axis_size, stop=axis_size, num=101) line_arr = np.array( [x_vals, np.sin(theta)/np.cos(theta) * x_vals] ) # 直角マークの座標を計算 r = 0.3 e_y = y / np.linalg.norm(y) # 単位正射影ベクトル e_z = (x - y) / np.linalg.norm(x - y) # 単位垂線ベクトル rightangle_mark_arr = np.array( [[y[0]+r*e_z[0], y[0]+r*(e_z[0]-e_y[0]), y[0]-r*e_y[0]], [y[1]+r*e_z[1], y[1]+r*(e_z[1]-e_y[1]), y[1]-r*e_y[1]]] ) # 角度マークの座標を計算 r = 0.3 slope_rad_vals = np.linspace(start=0.0, stop=theta, num=100) slope_mark_arr = np.array( [r * np.cos(slope_rad_vals), r * np.sin(slope_rad_vals)] ) # 角度ラベルの座標を計算 r = 0.5 slope_label_vec = np.array( [r * np.cos(0.5 * theta), r * np.sin(0.5 * theta)] ) # 2D射影ベクトルを作図 ax.quiver(0, 0, *x, color='black', units='dots', width=5, headwidth=5, angles='xy', scale_units='xy', scale=1, label='$x=({: .2f}, {: .2f})'.format(*x)+'$') # 入力ベクトル ax.quiver(0, 0, *y, color='red', units='dots', width=5, headwidth=5, angles='xy', scale_units='xy', scale=1, label='$y=({: .2f}, {: .2f})'.format(*y)+'$') # 出力ベクトル ax.plot(*line_arr) # 傾いた直線 ax.hlines(y=0.0, xmin=0.0, xmax=axis_size, linestyle='--') # 水平線 ax.plot([x[0], y[0]], [x[1], y[1]], color='black', linestyle='--') # 垂線 ax.plot(*rightangle_mark_arr, color='black', linewidth=1) # 直角マーク ax.plot(*slope_mark_arr, color='black', linewidth=1) # 傾き角度マーク ax.text(*slope_label_vec, s='$\\theta$', size=15, ha='center', va='center') # 傾き角度ラベル ax.set_xticks(ticks=np.arange(-axis_size, axis_size+1)) ax.set_yticks(ticks=np.arange(-axis_size, axis_size+1)) ax.set_xlim(left=-axis_size, right=axis_size) ax.set_ylim(bottom=-axis_size, top=axis_size) ax.set_xlabel('$x_1$') ax.set_ylabel('$x_2$') ax.set_title('$y = A x, ' + '\\theta = {: .2f} \pi, '.format(theta/np.pi)+', ' + 'A = ('+', '.join(['{: .2f}'.format(a) for a in A.flatten()])+')$', loc='left') ax.grid() ax.legend(loc='upper left') ax.set_aspect('equal') # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # gif画像を保存 ani.save('projection.gif')
作図処理をupdate()として定義して、FuncAnimation()でgif画像を作成します。
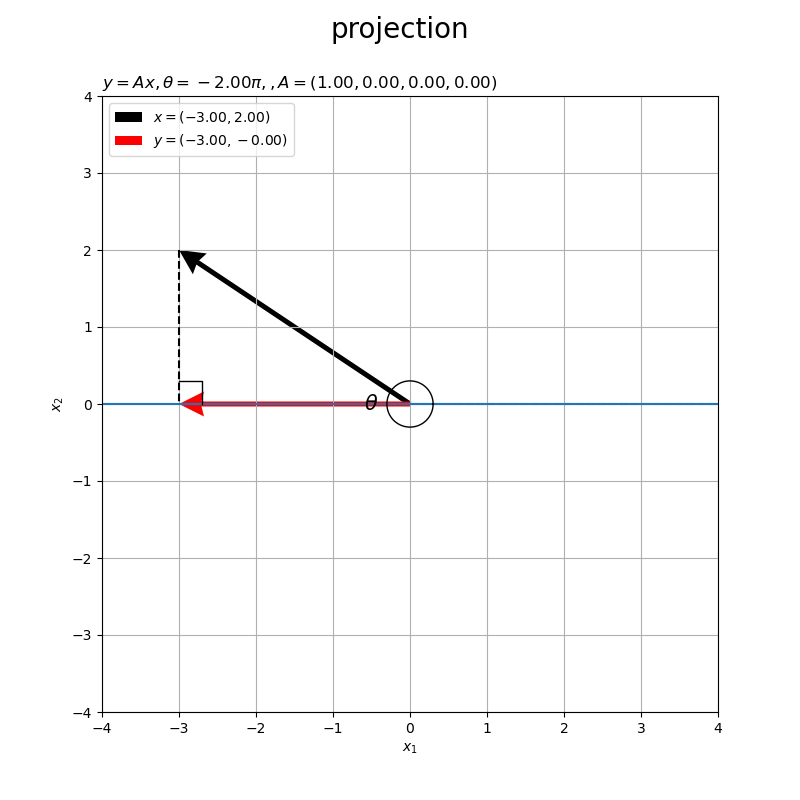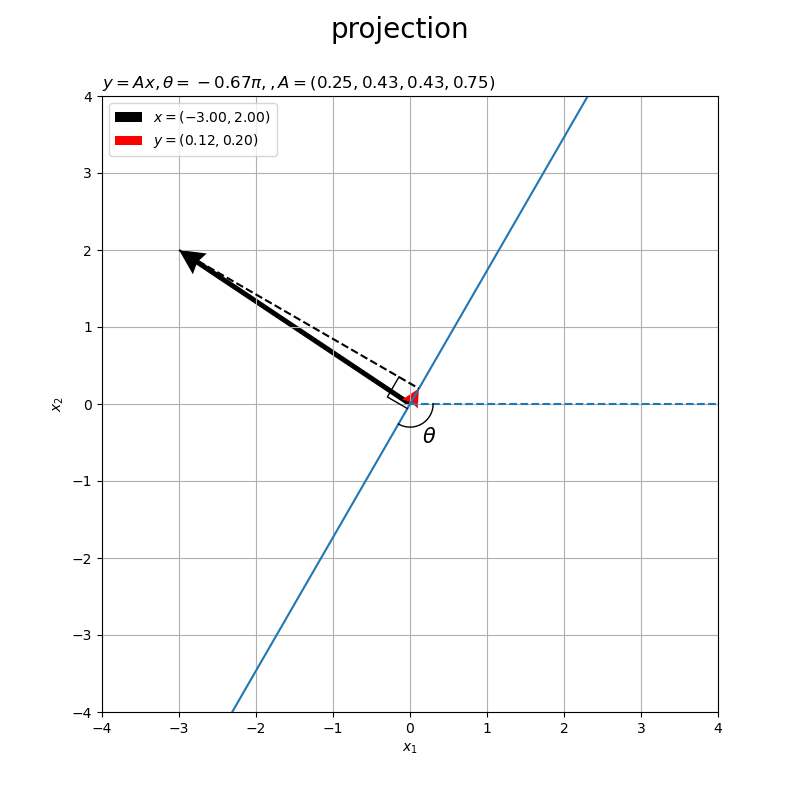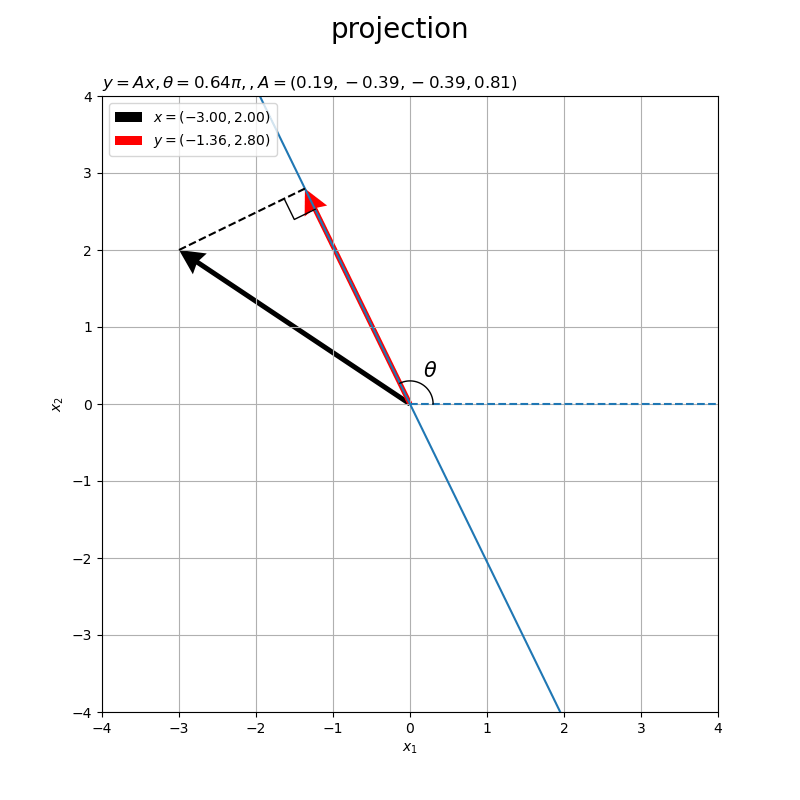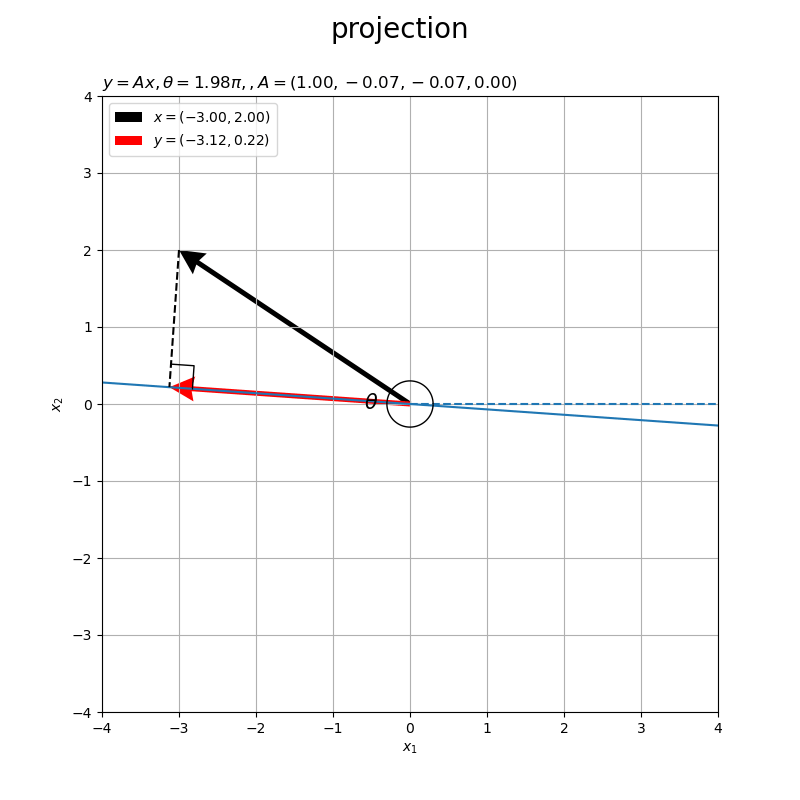
角度が負の値 だと右回りに傾きます。
この記事では、行列計算によるベクトルの射影を確認しました。次の記事では、ベクトルの鏡映を確認します。
参考書籍
- Stephen Boyd・Lieven Vandenberghe(著),玉木 徹(訳)『スタンフォード ベクトル・行列からはじめる最適化数学』講談社サイエンティク,2021年.
おわりに
これは5章でやった内容ですね。行列の計算を変形すると同じ計算式を導けるんだろうけど、寄り道してやってみますかね。それとも次の節に進みましょうかね。
【次の内容】