はじめに
『スタンフォード ベクトル・行列からはじめる最適化数学』の学習ノートです。
「数式の行間埋め」や「Pythonを使っての再現」によって理解を目指します。本と一緒に読んでください。
この記事は5.3節「正規直交ベクトル」の内容です。
2ベクトル間の正射影ベクトルと直交ベクトルのグラフを作成します。
【前の内容】
【他の内容】
【今回の内容】
正射影ベクトルの可視化
正射影ベクトル(orthographic projection of a vector・vector projection)をグラフで確認します。
なす角については「【Python】3.4:2つのベクトルのなす角の可視化【『スタンフォード線形代数入門』のノート】 - からっぽのしょこ」を参照してください。
利用するライブラリを読み込みます。
# 利用ライブラリ import numpy as np import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation
2次元の場合
まずは、2次元空間(平面)上で「ベクトルの正射影」と「正射影ベクトルの直交ベクトル」を可視化します。
2次元ベクトルを指定します。
# ベクトルを指定 a = np.array([4.0, 1.0]) b = np.array([2.0, 3.0])
2つのベクトルを
a, bとして値を指定します。Pythonでは0からインデックスが割り当てられるので、の値は
a[0]に対応します。
正射影ベクトルの計算の前に、正射影を図示するための補助線などを描画するための配列を用意します。正射影の計算自体には不要な処理です。
ベクトルのなす角を計算します。
# ベクトルa,bのなす角を計算 dot_ab = np.dot(a, b) norm_a = np.linalg.norm(a) norm_b = np.linalg.norm(b) cos_theta = dot_ab / norm_a / norm_b theta = np.arccos(cos_theta) print(theta) print(theta / np.pi)
0.7378150601204649
0.2348538278116319
のなす角
を計算します。
はラジアン(弧度法における角度)です。
コサイン関数の逆関数(逆コサイン関数)
は
np.arccos()、ユークリッドノルムは
np.linalg.norm()で計算できます。
なす角を示す角マークと角ラベルを描画するための座標を作成します。
# ベクトルaとx軸のなす角を計算 sgn_a = 1.0 if a[1] >= 0.0 else -1.0 theta_a = sgn_a * np.arccos(a[0] / norm_a) # ベクトルbとx軸のなす角を計算 sgn_b = 1.0 if b[1] >= 0.0 else -1.0 theta_b = sgn_b * np.arccos(b[0] / norm_b) # 差が180°を超える場合は、負の角度を優角に変換 if abs(theta_a - theta_b) > np.pi: theta_a = theta_a if a[1] >= 0.0 else theta_a + 2.0*np.pi theta_b = theta_b if b[1] >= 0.0 else theta_b + 2.0*np.pi # 角マーク用の値(ラジアン)を作成 rad_vals = np.linspace(start=theta_a, stop=theta_b, num=100) # 角マークの座標を計算 r = 0.3 angle_x_vals = r * np.cos(rad_vals) angle_y_vals = r * np.sin(rad_vals) print(angle_x_vals[:5]) print(angle_y_vals[:5]) print(np.linalg.norm(np.stack([angle_x_vals, angle_y_vals], axis=1), axis=1)[:5]) # ノルムがrになる # 角ラベルの座標を計算 r = 0.45 angle_x = r * np.cos(np.median(rad_vals)) angle_y = r * np.sin(np.median(rad_vals)) print(angle_x) print(angle_y) print(np.linalg.norm([angle_x, angle_y])) # ノルムがrになる
[0.29104275 0.29049241 0.28992594 0.28934336 0.28874471]
[0.07276069 0.07492769 0.07709054 0.0792491 0.08140327]
[0.3 0.3 0.3 0.3 0.3]
0.3678370022116635
0.2592217965448444
0.45000000000000007
詳しくは「円周上の2点を結ぶ弧を作図したい(数日後には書き上がってるはず)」を参照してください。
直角を示す角マークを描画するための座標を作成します。
# 正射影ベクトルを計算 p = dot_ab / norm_a**2 * a # ベクトルを正規化 e_a = a / norm_a e_bp = (b - p) / np.linalg.norm(b - p) # 直角マークの座標を計算 r = 0.2 rightangle_x = [p[0]+r*e_bp[0], p[0]+r*(e_bp[0]-e_a[0]), p[0]-r*e_a[0]] rightangle_y = [p[1]+r*e_bp[1], p[1]+r*(e_bp[1]-e_a[1]), p[1]-r*e_a[1]] print(rightangle_x) print(rightangle_y)
[2.5397281691103806, 2.345699669081314, 2.3942067940885807]
[0.8410873235584782, 0.7925801985512115, 0.5985516985221452]
点からベクトル
またはその延長線(原点と点
を通る直線)への垂線を描画します。その交点(垂線の足)
の座標から、垂線方向とベクトル
方向に少しずつ移動した点の座標をリスト(または配列)に格納します。
正射影ベクトルについては後ほど確認します。
ベクトルと平行な直線の座標を作成します。
# グラフサイズ用の値を設定 x_min = np.floor(np.min([0.0, a[0], b[0]])) - 1.0 x_max = np.ceil(np.max([0.0, a[0], b[0]])) + 1.0 y_min = np.floor(np.min([0.0, a[1], b[1]])) - 1.0 y_max = np.ceil(np.max([0.0, a[1], b[1]])) + 1.0 # ベクトルaと平行な直線の座標を計算 line_x_vals = np.linspace(start=x_min, stop=x_max, num=101) line_y_vals = a[1]/a[0] * line_x_vals print(line_x_vals[:5]) print(line_y_vals[:5])
[-1. -0.94 -0.88 -0.82 -0.76]
[-0.25 -0.235 -0.22 -0.205 -0.19 ]
ベクトルの傾き
を用いて、直線の座標
を計算します。
ただし、a[0]()が
0だと0除算になるため計算できません。
2次元空間上に、ベクトルまたはその延長線上へのベクトル
の正射影のグラフを作成します。
# 2D正射影を作図 fig, ax = plt.subplots(figsize=(8, 6), facecolor='white') ax.quiver(0, 0, *a, color='red', headwidth=5, headlength=5, angles='xy', scale_units='xy', scale=1, label='$a=('+', '.join(map(str, a))+')$') # ベクトルa ax.quiver(0, 0, *b, color='blue', headwidth=5, headlength=5, angles='xy', scale_units='xy', scale=1, label='$b=('+', '.join(map(str, b))+')$') # ベクトルb ax.plot(line_x_vals, line_y_vals, color='red', linestyle='--') # ベクトルaの延長線 ax.plot([b[0], p[0]], [b[1], p[1]], color='black', linestyle='--') # 点bから直線aへの垂線 ax.plot(rightangle_x, rightangle_y, color='black', linewidth=1) # 直角マーク ax.plot(angle_x_vals, angle_y_vals, color='black', linewidth=1) # なす角マーク ax.text(angle_x, angle_y, s='$\\theta$', size=15, ha='center', va='center') # なす角ラベル ax.text(0, 0, s='O', size=15, ha='right', va='top') # 原点ラベル ax.text(*p, s='P', size=15, ha='center', va='top') # 垂線の足ラベル ax.text(*a, s='a', size=15, ha='left', va='top') # 点aラベル ax.text(*b, s='b', size=15, ha='left', va='bottom') # 点bラベル ax.set_xticks(ticks=np.arange(x_min, x_max+1)) ax.set_yticks(ticks=np.arange(y_min, y_max+1)) ax.grid() ax.set_xlabel('$x_1$') ax.set_ylabel('$x_2$') ax.set_title('$\\theta=' + str((theta / np.pi).round(2)) + '\pi$', loc='left') fig.suptitle('vector projection', fontsize=20) ax.legend() ax.set_aspect('equal') plt.show()
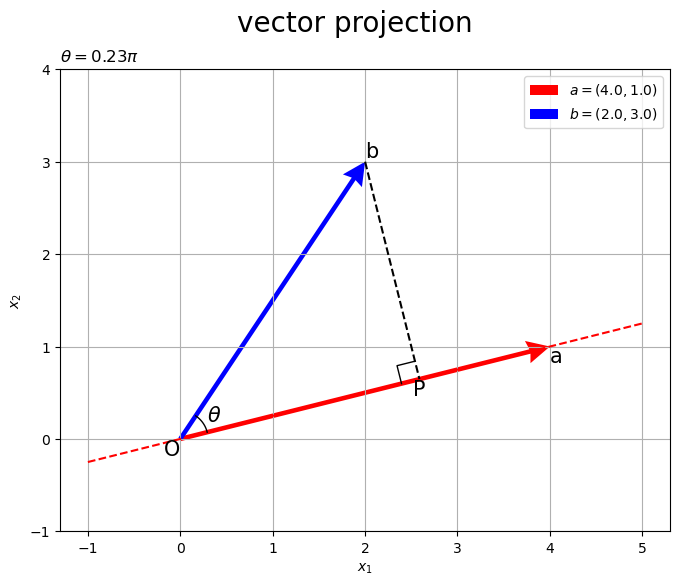
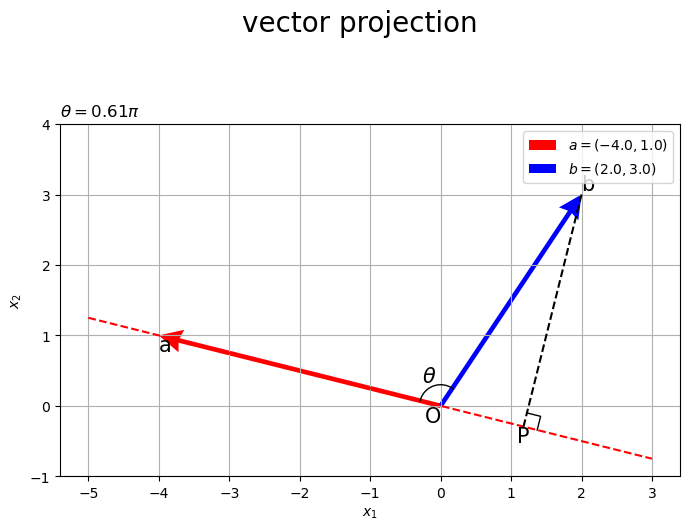
axes.quiver()でベクトルを描画します。第1・2引数に始点の座標、第3・4引数にベクトルのサイズ(移動量)を指定します。その他に、指定した値の通りに(調整せずに)矢印を描画するための設定をしています。
配列a, bの前に*を付けてアンパック(展開)して座標を指定しています。始点は原点です。
「点」から「ベクトル
と平行な直線」上におろした垂線の足を点
または
とします。
原点をとして、ベクトル
を正射影ベクトルと言います。以降は、正射影ベクトルを
で表します。
ベクトルは、ベクトル
と平行なベクトルです。よって、
で表わせます。
左図はなす角が90°()より小さい場合、右図は90°より大きい場合です。
正射影ベクトルを計算します。
# 正射影ベクトルを計算 beta = np.dot(a, b) / np.linalg.norm(a)**2 p = beta * a print(beta) print(p)
0.6470588235294118
[2.58823529 0.64705882]
正射影ベクトルは、次の式で計算できます。
内積もノルム
もスカラーになるので、
はスカラーです。つまり、ベクトル
のスカラー倍
の形です。
ベクトルを描画します。
# タイトル用の文字列を作成 coef_label = '\\frac{a^{\\top} b}{\|a\|^2}' # 2D正射影ベクトルを作図 fig, ax = plt.subplots(figsize=(8, 6), facecolor='white') ax.quiver(0, 0, *p, color='orange', headwidth=5, headlength=5, angles='xy', scale_units='xy', scale=1, label='$p=('+', '.join(map(str, p.round(2)))+')$') # 正射影ベクトル ax.quiver(0, 0, *a, fc='none', ec='red', ls='--', lw=1, width=0.001, headwidth=40, headlength=40, angles='xy', scale_units='xy', scale=1, label='$a=('+', '.join(map(str, a))+')$') # ベクトルa ax.quiver(0, 0, *b, color='blue', headwidth=5, headlength=5, angles='xy', scale_units='xy', scale=1, label='$b=('+', '.join(map(str, b))+')$') # ベクトルb ax.plot([b[0], p[0]], [b[1], p[1]], color='black', linestyle='--') # 点bから直線aへの垂線 ax.plot(rightangle_x, rightangle_y, color='black', linewidth=1) # 直角マーク ax.set_xticks(ticks=np.arange(x_min, x_max+1)) ax.set_yticks(ticks=np.arange(y_min, y_max+1)) ax.set_xlabel('$x_1$') ax.set_ylabel('$x_2$') ax.grid() ax.set_title('$' + coef_label + '=' + str(beta.round(2)) + '$', loc='left') fig.suptitle('$p=' + coef_label + 'a$', fontsize=20) ax.legend() ax.set_aspect('equal') plt.show()
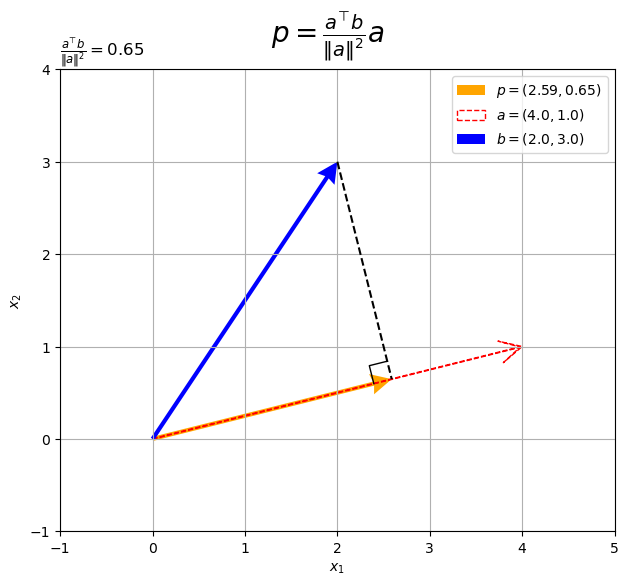
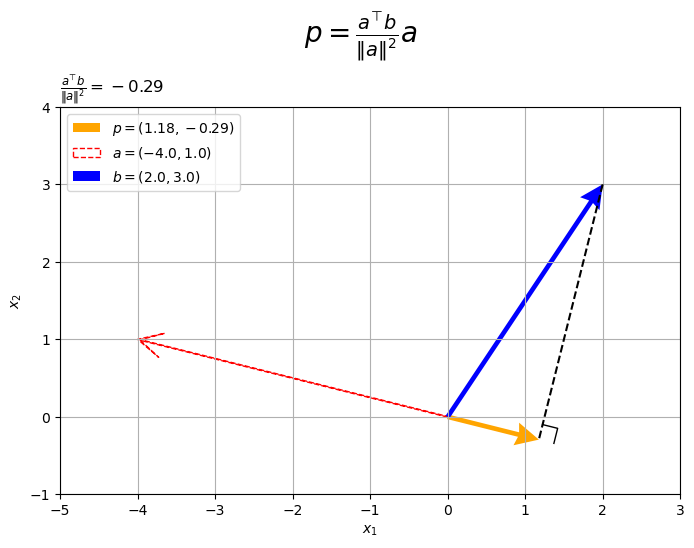
正射影ベクトルが、ベクトル
と平行で、原点から垂線の足への移動を表すのが分かります。
また、垂線はで表わせます。
# 2D垂線ベクトルを作図 fig, ax = plt.subplots(figsize=(8, 6), facecolor='white') ax.quiver(*p, *-p, color='orange', headwidth=5, headlength=5, angles='xy', scale_units='xy', scale=1, label='$-p=-('+', '.join(map(str, p.round(2)))+')$') # 正射影ベクトル ax.quiver(0, 0, *a, fc='none', ec='red', ls='--', lw=1, width=0.001, headwidth=40, headlength=40, angles='xy', scale_units='xy', scale=1, label='$a=('+', '.join(map(str, a))+')$') # ベクトルa ax.quiver(0, 0, *b, color='blue', headwidth=5, headlength=5, angles='xy', scale_units='xy', scale=1, label='$b=('+', '.join(map(str, b))+')$') # ベクトルb ax.quiver(*p, *b-p, color='chocolate', headwidth=5, headlength=5, angles='xy', scale_units='xy', scale=1, label='$b-p=('+', '.join(map(str, (b-p).round(2)))+')$') # ベクトルb-p ax.plot(rightangle_x, rightangle_y, color='black', linewidth=1) # 直角マーク ax.set_xticks(ticks=np.arange(x_min, x_max+1)) ax.set_yticks(ticks=np.arange(y_min, y_max+1)) ax.set_xlabel('$x_1$') ax.set_ylabel('$x_2$') ax.grid() ax.set_title('$p=' + str(beta.round(2)) + 'a, ' + 'p^{\\top} (b-p)=' + str(np.dot(p, b-p).round(2)) + '$', loc='left') fig.suptitle('$p \\bot (b-p)$', fontsize=20) ax.legend() ax.set_aspect('equal') plt.show()
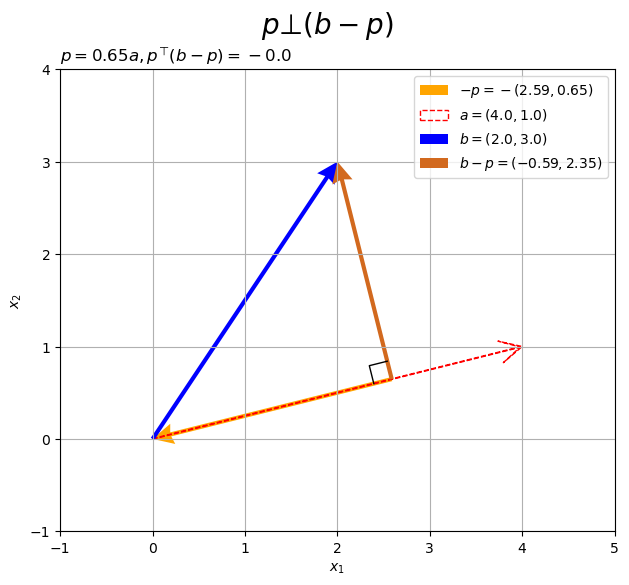
と
は直交するので、内積が0になります。
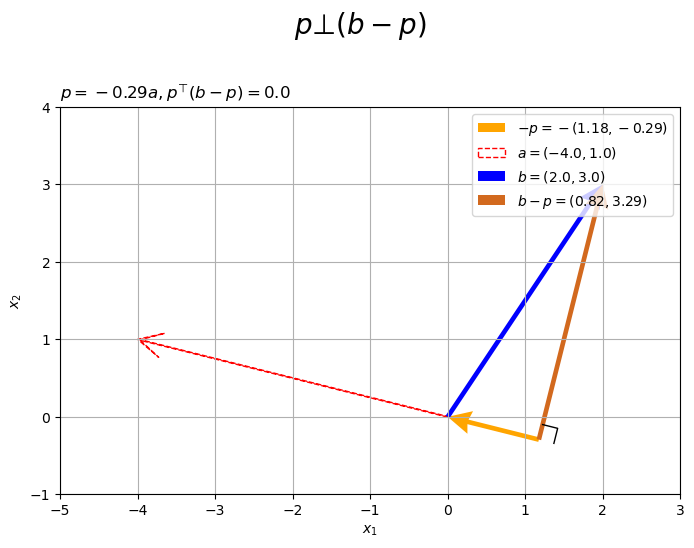
ベクトルの値を変化させたアニメーションを作成します。
・作図コード(クリックで展開)
# フレーム数を設定 frame_num = 60 # 固定するベクトルを指定 a = np.array([4.0, 1.0]) #b = np.array([2.0, 3.0]) # ベクトルのノルム(円形の軌道の半径)を指定 r = 3.0 # 変化するベクトルとして利用する値を指定 #rad_a_n = np.linspace(start=0.0, stop=2.0*np.pi, num=frame_num+1)[:frame_num] rad_a_n = np.linspace(start=-1.0/3.0*np.pi, stop=2.0/3.0*np.pi, num=frame_num+1)[:frame_num] a_n = np.array( [-r * np.cos(rad_a_n), r * np.sin(rad_a_n)] ).T rad_b_n = np.linspace(start=0.0, stop=2.0*np.pi, num=frame_num+1)[:frame_num] b_n = np.array( [r * np.cos(rad_b_n), r * np.sin(rad_b_n)] ).T # グラフサイズ用の値を設定 axis_size = r + 1.0 # グラフオブジェクトを初期化 fig, ax = plt.subplots(figsize=(8, 6), facecolor='white') fig.suptitle('vector projection', fontsize=20) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i番目のベクトルを取得 #a = a_n[i] b = b_n[i] # 正射影ベクトルを計算 dot_ab = np.dot(a, b) norm_a = np.linalg.norm(a) beta = dot_ab / norm_a**2 p = beta * a # ベクトルa,bのなす角を計算 norm_b = np.linalg.norm(b) theta = np.arccos(dot_ab / norm_a / norm_b) # ベクトルa,bとx軸のなす角を計算 sgn_a = 1.0 if a[1] >= 0.0 else -1.0 theta_a = sgn_a * np.arccos(a[0] / norm_a) sgn_b = 1.0 if b[1] >= 0.0 else -1.0 theta_b = sgn_b * np.arccos(b[0] / norm_b) if abs(theta_a - theta_b) > np.pi: theta_a = theta_a if a[1] >= 0.0 else theta_a + 2.0*np.pi theta_b = theta_b if b[1] >= 0.0 else theta_b + 2.0*np.pi # 角マーク用の値(ラジアン)を作成 rad_vals = np.linspace(start=theta_a, stop=theta_b, num=100) # 角マークの座標を計算 r = 0.3 angle_x_vals = r * np.cos(rad_vals) angle_y_vals = r * np.sin(rad_vals) # 角ラベルの座標を計算 r = 0.45 angle_x = r * np.cos(np.median(rad_vals)) angle_y = r * np.sin(np.median(rad_vals)) # 直角マークの座標を計算 r = 0.2 e_a = a / norm_a e_bp = (b - p) / np.linalg.norm(b - p) rightangle_x = [p[0]+r*e_bp[0], p[0]+r*(e_bp[0]-e_a[0]), p[0]-r*e_a[0]] rightangle_y = [p[1]+r*e_bp[1], p[1]+r*(e_bp[1]-e_a[1]), p[1]-r*e_a[1]] # ベクトルaと平行な直線の座標を計算 line_x_vals = np.linspace(start=-axis_size, stop=axis_size, num=101) line_y_vals = a[1]/a[0] * line_x_vals # 正射影ベクトルと垂線ベクトルを作図 ax.plot(line_x_vals, line_y_vals, color='red', linestyle=':', zorder=-100) # ベクトルaの延長線 ax.quiver(0, 0, *a, color='red', headwidth=5, headlength=5, #fc='none', ec='red', ls='--', lw=1, width=0.001, headwidth=40, headlength=40, angles='xy', scale_units='xy', scale=1, label='$a=('+', '.join(map(str, a.round(2)))+')$') # ベクトルa ax.quiver(0, 0, *b, color='blue', headwidth=5, headlength=5, angles='xy', scale_units='xy', scale=1, label='$b=('+', '.join(map(str, b.round(2)))+')$') # ベクトルb ax.quiver(0, 0, *p, color='orange', headwidth=5, headlength=5, angles='xy', scale_units='xy', scale=1, label='$p=('+', '.join(map(str, p.round(2)))+')$') # 正射影ベクトル ax.quiver(*p, *b-p, color='chocolate', headwidth=5, headlength=5, angles='xy', scale_units='xy', scale=1, label='$b-p=('+', '.join(map(str, (b-p).round(2)))+')$') # ベクトルb-p ax.plot(rightangle_x, rightangle_y, color='black', linewidth=1) # 直角マーク ax.plot(angle_x_vals, angle_y_vals, color='black', linewidth=1) # なす角マーク ax.text(angle_x, angle_y, s='$\\theta$', size=15, ha='center', va='center') # なす角ラベル ax.set_xticks(ticks=np.arange(-axis_size, axis_size+1)) ax.set_yticks(ticks=np.arange(-axis_size, axis_size+1)) ax.set_xlim(left=-axis_size, right=axis_size) ax.set_ylim(bottom=-axis_size, top=axis_size) ax.set_xlabel('$x_1$') ax.set_ylabel('$x_2$') ax.grid() ax.set_title('$\\theta=' + str((theta / np.pi).round(2)) + '\pi, ' + 'p=' + str(beta.round(2)) + 'a, ' + 'p^{\\top} (b-p)=' + str(np.dot(p, b-p).round(2)) + '$', loc='left') ax.legend(loc='upper left', prop={'size': 7}) ax.set_aspect('equal') # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # gif画像を保存 ani.save('projection_2d.gif')
作図処理をupdate()として定義して、FuncAnimation()でgif画像を作成します。
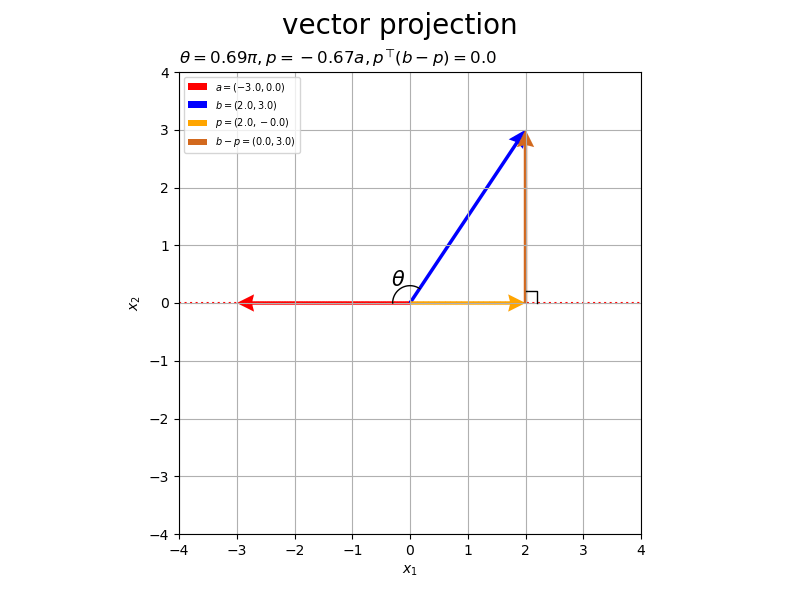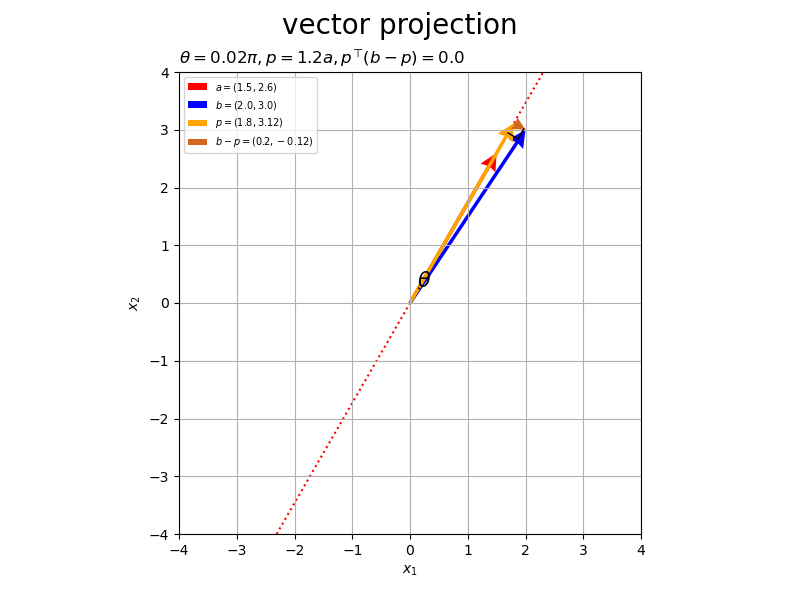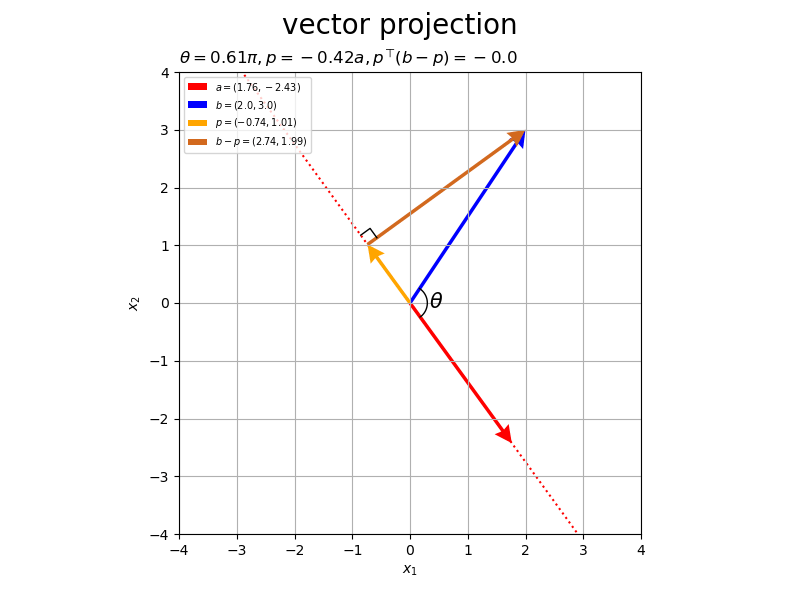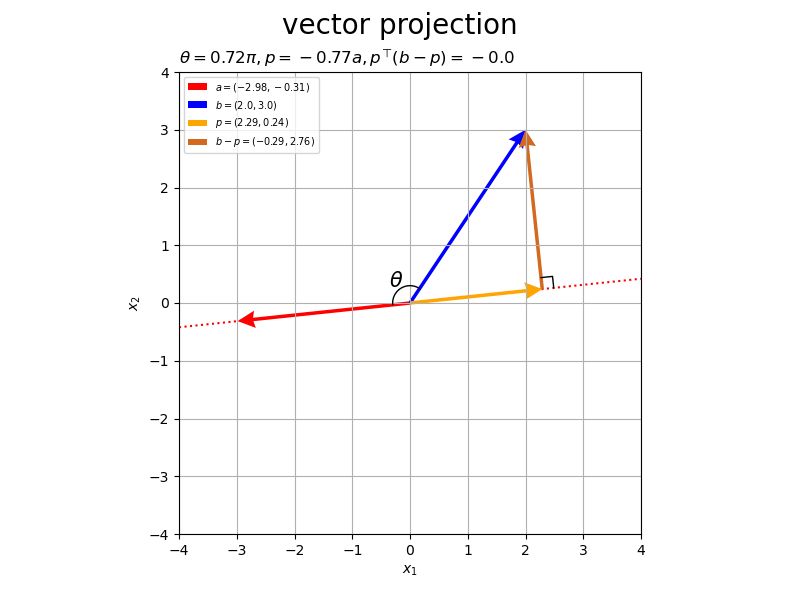
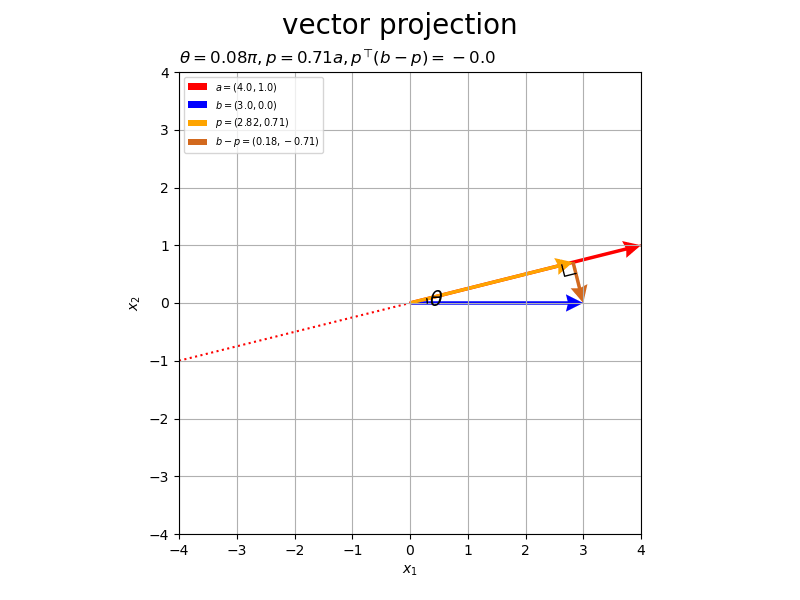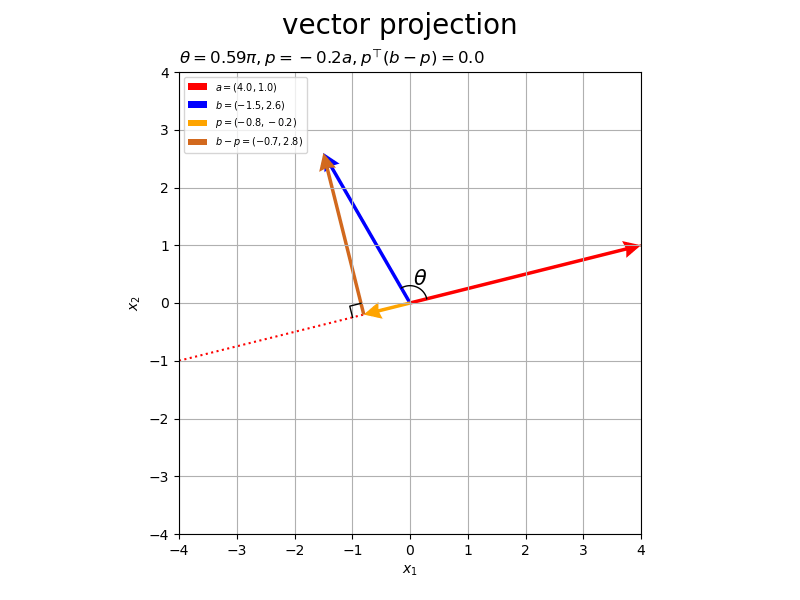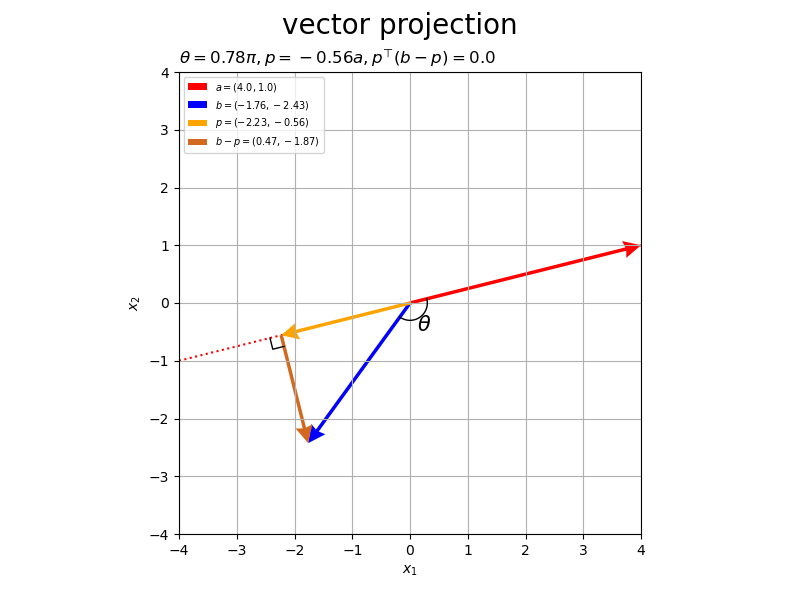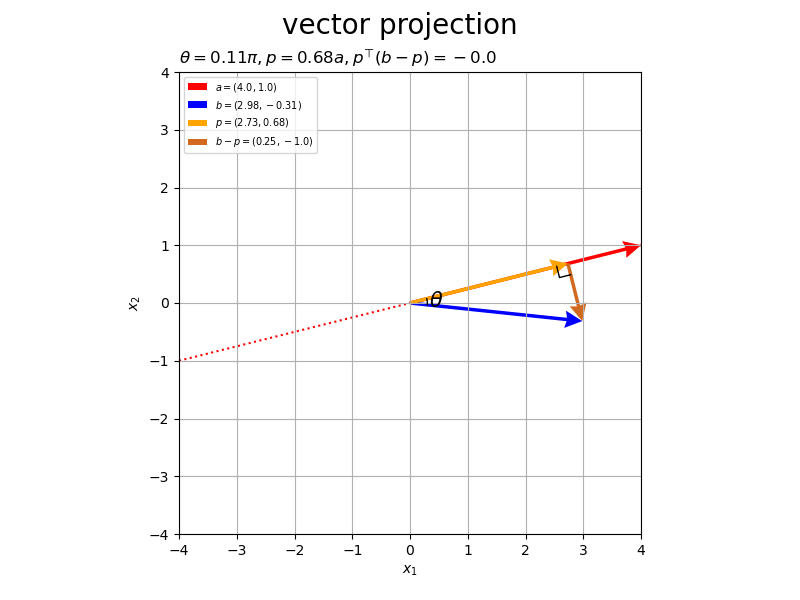
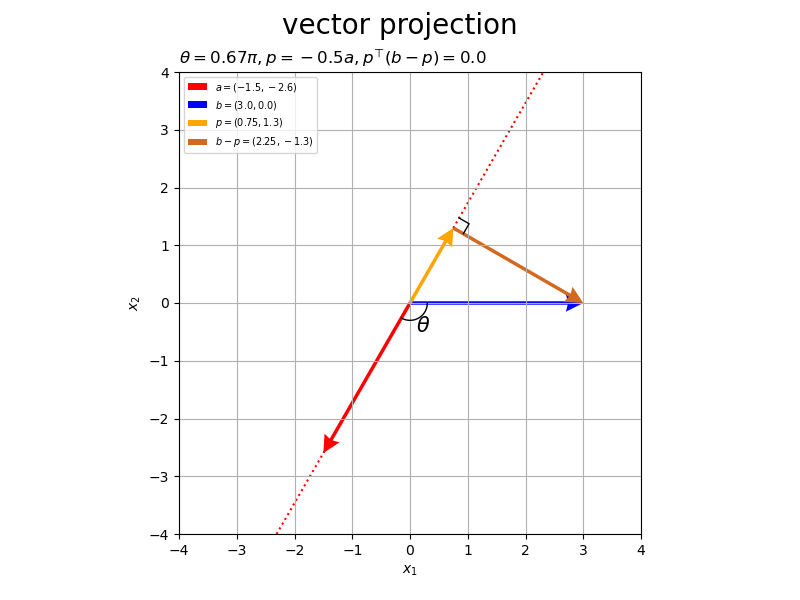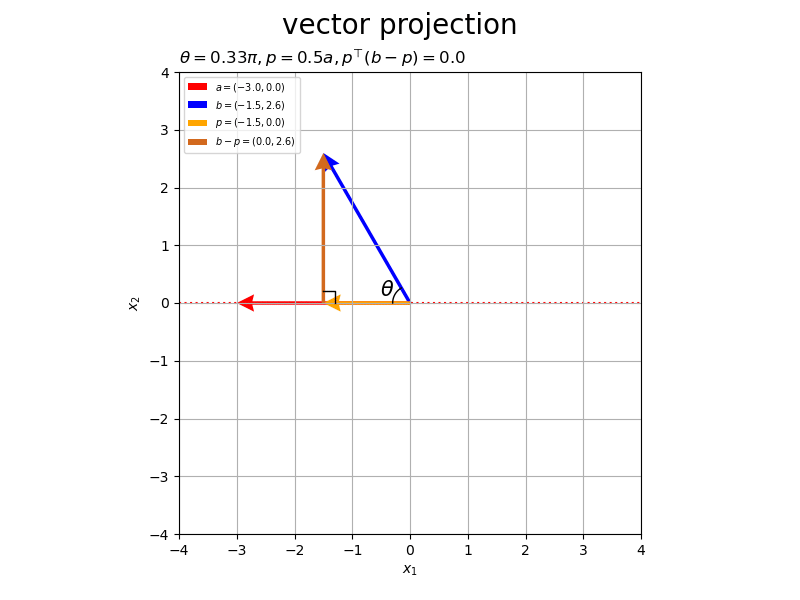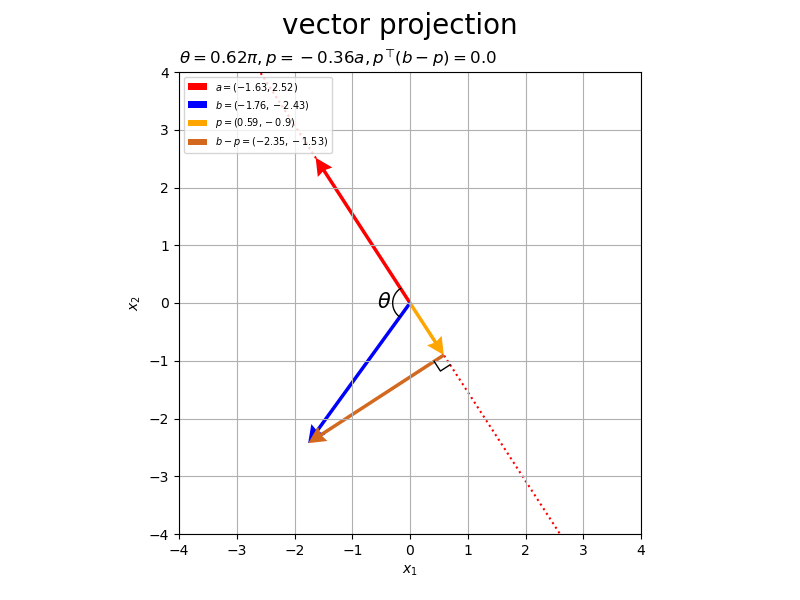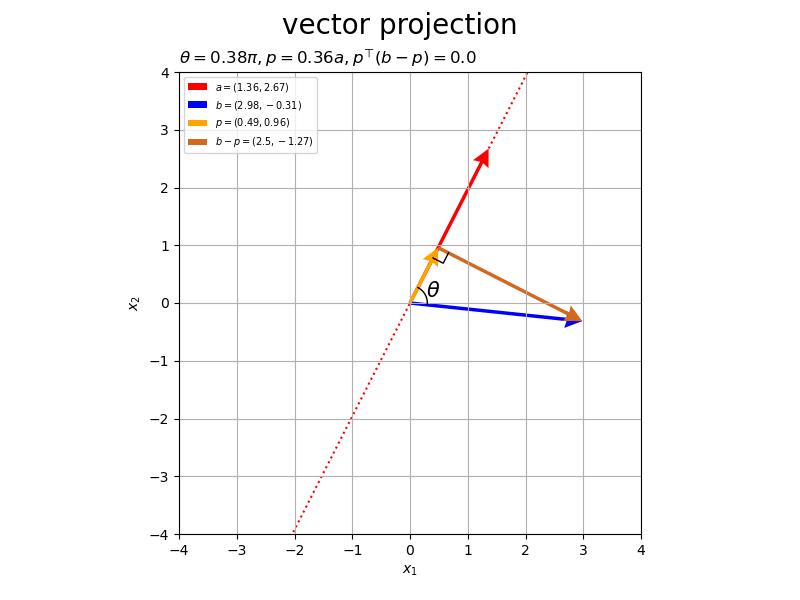
以上が、2次元における正射影ベクトルと垂線ベクトルの計算と可視化です。
3次元の場合
次は、3次元空間上で「ベクトルの正射影」と「正射影ベクトルの直交ベクトル」を可視化します。
3次元ベクトルを指定します。
# ベクトルを指定 a = np.array([4.0, 1.0, -1.0]) b = np.array([2.0, 3.0, 4.0])
2つのベクトルを
a, bとして値を指定します。
正射影ベクトルの計算の前に、正射影を図示するための補助線などを描画するための配列を用意します。正射影の計算自体には不要な処理です。
ベクトルのなす角を計算します。
# ベクトルa,bのなす角を計算 dot_ab = np.dot(a, b) norm_a = np.linalg.norm(a) norm_b = np.linalg.norm(b) cos_theta = dot_ab / norm_a / norm_b theta = np.arccos(cos_theta) print(theta) print(theta / np.pi)
1.2594067557276185
0.40088162107475533
「2次元の場合」のときのコードで計算できます。
なす角を示す角マークを描画するための座標を作成します。
# 角マーク用の値(ラジアン)を作成 rad_vals = np.linspace(start=0.0, stop=0.5*np.pi, num=100) # 混合率(線形結合の係数)を作成 beta1_vals = np.cos(rad_vals) beta2_vals = np.sin(rad_vals) # 角マーク用の曲線を計算(正規化したベクトルを線形結合) angle_x_vals = beta1_vals * a[0]/norm_a + beta2_vals * b[0]/norm_b angle_y_vals = beta1_vals * a[1]/norm_a + beta2_vals * b[1]/norm_b angle_z_vals = beta1_vals * a[2]/norm_a + beta2_vals * b[2]/norm_b # 点ごとにノルムを計算 xyz_arr = np.stack([angle_x_vals, angle_y_vals, angle_z_vals], axis=1) norm_xyz_vals = np.linalg.norm(xyz_arr, axis=1) # 角マークの座標を計算(曲線のサイズを調整) r = 0.5 angle_x_vals *= r / norm_xyz_vals angle_y_vals *= r / norm_xyz_vals angle_z_vals *= r / norm_xyz_vals print(angle_x_vals[:5]) print(angle_y_vals[:5]) print(angle_z_vals[:5]) print(np.linalg.norm(np.stack([angle_x_vals, angle_y_vals, angle_z_vals], axis=1), axis=1)[:5]) # rになる
[0.47140452 0.47200283 0.47249031 0.47286994 0.47314464]
[0.11785113 0.12166573 0.12541671 0.12910476 0.13273061]
[-0.11785113 -0.11140366 -0.10499314 -0.09862039 -0.09228614]
[0.5 0.5 0.5 0.5 0.5]
詳しくは「球面上の2点を結ぶ弧を作図したい(数日後には書き上がってるはず)」を参照してください。
なす角の角ラベルを描画するための座標を作成します。
# 角ラベル用の値(角マークの中点のラジアン)を作成 rad = 0.25 * np.pi # 混合率(線形結合の係数)を作成 beta1 = np.cos(rad) beta2 = np.sin(rad) # なす角の中点の座標を計算(正規化したベクトルを線形結合) angle_x = beta1 * a[0]/norm_a + beta2 * b[0]/norm_b angle_y = beta1 * a[1]/norm_a + beta2 * b[1]/norm_b angle_z = beta1 * a[2]/norm_a + beta2 * b[2]/norm_b # ノルムを計算 xyz = np.array([angle_x, angle_y, angle_z]) norm_xyz = np.linalg.norm(xyz) # 角ラベルの座標を計算(角ラベルのサイズを調整) r = 0.8 angle_x *= r / norm_xyz angle_y *= r / norm_xyz angle_z *= r / norm_xyz print(angle_x) print(angle_y) print(angle_z) print(np.linalg.norm([angle_x, angle_y, angle_z])) # rになる
0.650431129948327
0.39237124040791044
0.2509664417704098
0.8000000000000002
角マークの中点にラベルを配置することにします。詳しくは「球面上の2点を結ぶ弧を作図したい」を参照してください。
直角を示す角マークを描画するための座標を作成します。
# 正射影を計算 p = dot_ab / norm_a**2 * a # ベクトルを正規化 e_a = a / norm_a e_bp = (b - p) / np.linalg.norm(b - p) # 直角マーク用の座標を計算 r = 0.2 rightangle_x = [p[0]+r*e_bp[0], p[0]+r*(e_bp[0]-e_a[0]), p[0]-r*e_a[0]] rightangle_y = [p[1]+r*e_bp[1], p[1]+r*(e_bp[1]-e_a[1]), p[1]-r*e_a[1]] rightangle_z = [p[2]+r*e_bp[2], p[2]+r*(e_bp[2]-e_a[2]), p[2]-r*e_a[2]] print(rightangle_x) print(rightangle_y) print(rightangle_z)
[1.572895717922552, 1.3843339096061391, 1.3669937472391431]
[0.49076234279499126, 0.4436218907158881, 0.3417484368097858]
[-0.21765478551480208, -0.17051433343569888, -0.3417484368097858]
「2次元の場合」と同様に計算します。こちらは、z軸用のリスト(座標)も作成します。
ベクトルと平行な直線の座標を作成します。
# 作図用の値を設定 x_min = np.floor(np.min([0.0, a[0], b[0]])) - 1.0 x_max = np.ceil(np.max([0.0, a[0], b[0]])) + 1.0 y_min = np.floor(np.min([0.0, a[1], b[1]])) - 1.0 y_max = np.ceil(np.max([0.0, a[1], b[1]])) + 1.0 z_min = np.floor(np.min([0.0, a[2], b[2]])) - 1.0 z_max = np.ceil(np.max([0.0, a[2], b[2]])) + 1.0 # ベクトルaと平行な直線の座標を計算 line_x_vals = np.linspace(start=x_min, stop=x_max, num=101) line_y_vals = a[1]/a[0] * line_x_vals line_z_vals = a[2]/a[0] * line_x_vals # 描画範囲外の要素を除去 bool_idx = (line_y_vals < y_min) | (line_y_vals > y_max) | (line_z_vals < z_min) | (line_z_vals > z_max) bool_idx = [not bl for bl in bool_idx] line_x_vals = line_x_vals[bool_idx] line_y_vals = line_y_vals[bool_idx] line_z_vals = line_z_vals[bool_idx] print(line_x_vals[:5]) print(line_y_vals[:5]) print(line_z_vals[:5])
[-1. -0.94 -0.88 -0.82 -0.76]
[-0.25 -0.235 -0.22 -0.205 -0.19 ]
[0.25 0.235 0.22 0.205 0.19 ]
「2次元の場合」と同様に計算します。さらに、ベクトルのz軸方向の傾きは
なので、直線のz軸の値を
で計算します。
ただし、a[0]()が
0だと0除算になるため計算できません。
2次元プロットだとaxes.set_*lim()で設定した範囲外は描画されませんが、3次元プロットだと描画されてしまいます(なぜ?)。そこで、範囲外の要素を取り除きます(axes.plot()はマスクしても描画されるみたい?)。
y軸とz軸が*_min, *_maxの範囲外のインデックスを調べてbool_idxとします。範囲外の要素がTrueで範囲内の(描画する)要素がFalseになるので、notで反転させて各軸の値line_*_valsから範囲内の要素を抽出します。
3次元空間上に、ベクトルまたはその延長線上へのベクトル
の正射影のグラフを作成します。
# 矢のサイズを指定 l = 0.5 # 3D正射影を作図 fig, ax = plt.subplots(figsize=(8, 6), facecolor='white', subplot_kw={'projection': '3d'}) ax.quiver(0, 0, 0, *a, color='red', arrow_length_ratio=l/np.linalg.norm(a), label='$a=('+', '.join(map(str, a))+')$') # ベクトルa ax.quiver(0, 0, 0, *b, color='blue', arrow_length_ratio=l/np.linalg.norm(b), label='$b=('+', '.join(map(str, b))+')$') # ベクトルb ax.plot(line_x_vals, line_y_vals, line_z_vals, color='red', linestyle='--') # ベクトルaの延長線 ax.plot([b[0], p[0]], [b[1], p[1]], [b[2], p[2]], color='black', linestyle='--') # 点bから直線aへの垂線 ax.plot(rightangle_x, rightangle_y, rightangle_z, color='black', linewidth=1) # 直角マーク ax.plot(angle_x_vals, angle_y_vals, angle_z_vals, color='black', linewidth=1) # なす角マーク ax.text(angle_x, angle_y, angle_z, s='$\\theta$', size=15, ha='center', va='center', zorder=20) # なす角ラベル ax.text(0, 0, 0, s='O', size=15, ha='right', va='top', zorder=20) # 原点ラベル ax.text(*p, s='P', size=15, ha='right', va='top') # 垂線の足ラベル ax.text(*a, s='a', size=15, ha='right', va='top', zorder=20) # 点aラベル ax.text(*b, s='b', size=15, ha='left', va='bottom', zorder=20) # 点bラベル ax.quiver([0, a[0], b[0]], [0, a[1], b[1]], [0, a[2], b[2]], [0, 0, 0], [0, 0, 0], [z_min, z_min-a[2], z_min-b[2]], color=['gray', 'red', 'blue'], arrow_length_ratio=0, linestyle=':') # 座標用の補助線 ax.set_xticks(ticks=np.arange(x_min, x_max+1)) ax.set_yticks(ticks=np.arange(y_min, y_max+1)) ax.set_zticks(ticks=np.arange(z_min, z_max+1)) ax.set_zlim(bottom=z_min, top=z_max) ax.set_xlabel('$x_1$') ax.set_ylabel('$x_2$') ax.set_zlabel('$x_3$') ax.set_title('$\\theta=' + str((theta / np.pi).round(2)) + '\pi$', loc='left') fig.suptitle('vector projection', fontsize=20) ax.legend() ax.set_aspect('equal') #ax.view_init(elev=90, azim=270) plt.show()
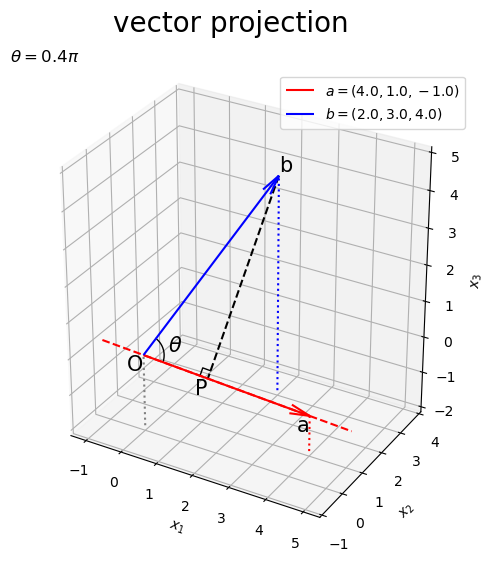
axes.quiver()でベクトルを描画します。第1・2・3引数に始点の座標、第4・5・6引数にベクトルのサイズ(移動量)を指定します。
配列a, bの前に*を付けてアンパック(展開)して座標を指定しています。始点は原点です。
2次元の場合と同じく、原点から垂線の足
への移動を表すベクトル
が、正射影ベクトル
です。
左図はなす角が90°()より小さい場合、右図は90°より大きい場合です。
正射影ベクトルを計算します。
# 正射影ベクトルを計算 beta = np.dot(a, b) / np.linalg.norm(a)**2 p = beta * a print(beta) print(p)
0.38888888888888895
[ 1.55555556 0.38888889 -0.38888889]
「2次元の場合」のときのコードで計算できます。
ベクトルを描画します。
# 3D正射影ベクトルを作図 fig, ax = plt.subplots(figsize=(8, 6), facecolor='white', subplot_kw={'projection': '3d'}) ax.quiver(0, 0, 0, *p, color='orange', arrow_length_ratio=l/np.linalg.norm(p), label='$p=('+', '.join(map(str, p.round(2)))+')$', zorder=-100) # 正射影ベクトル ax.quiver(0, 0, 0, *a, color='red', ls='--', lw=1, arrow_length_ratio=l/np.linalg.norm(a), label='$a=('+', '.join(map(str, a))+')$') # ベクトルa ax.quiver(0, 0, 0, *b, color='blue', arrow_length_ratio=l/np.linalg.norm(b), label='$b=('+', '.join(map(str, b))+')$') # ベクトルb ax.plot([b[0], p[0]], [b[1], p[1]], [b[2], p[2]], color='black', linestyle='--') # 点bから直線aへの垂線 ax.plot(rightangle_x, rightangle_y, rightangle_z, color='black', linewidth=1, zorder=100) # 直角マーク ax.quiver([0, a[0], b[0], p[0]], [0, a[1], b[1], p[1]], [0, a[2], b[2], p[2]], [0, 0, 0, 0], [0, 0, 0, 0], [z_min, z_min-a[2], z_min-b[2], z_min-p[2]], color=['gray', 'red', 'blue', 'orange'], arrow_length_ratio=0, linestyle=':') # 座標用の補助線 ax.set_xticks(ticks=np.arange(x_min, x_max+1)) ax.set_yticks(ticks=np.arange(y_min, y_max+1)) ax.set_zticks(ticks=np.arange(z_min, z_max+1)) ax.set_zlim(bottom=z_min, top=z_max) ax.set_xlabel('$x_1$') ax.set_ylabel('$x_2$') ax.set_zlabel('$x_3$') ax.set_title('$\\frac{a^{\\top} b}{\|a\|^2}=' + str(beta.round(2)) + '$', loc='left') fig.suptitle('$p = \\frac{a^{\\top} b}{\|a\|^2} a$', fontsize=20) ax.legend() ax.set_aspect('equal') plt.show()
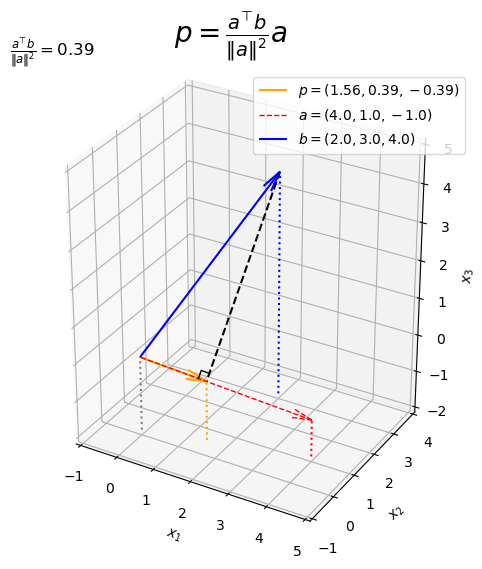
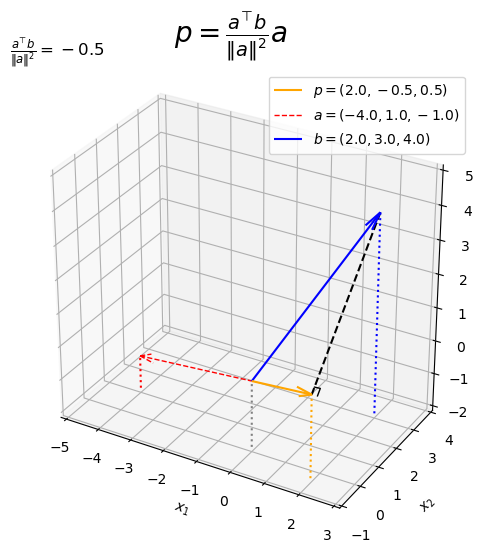
正射影ベクトルが、ベクトル
と平行で、原点から垂線の足への移動を表すのが分かります。
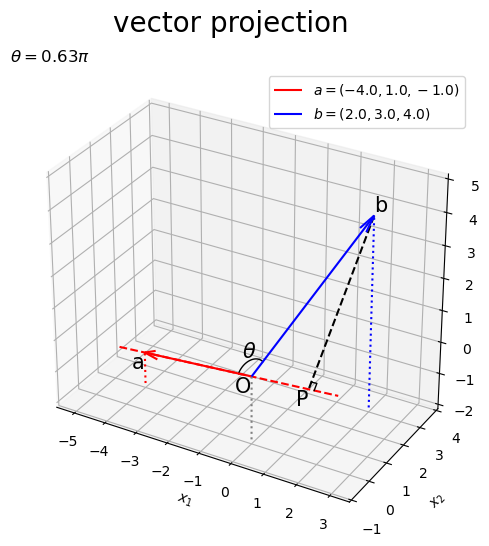
また、垂線はで表わせます。
# 3D垂線ベクトルを作図 fig, ax = plt.subplots(figsize=(8, 6), facecolor='white', subplot_kw={'projection': '3d'}) ax.quiver(*p, *-p, color='orange', arrow_length_ratio=l/np.linalg.norm(p), label='$-p=-('+', '.join(map(str, p.round(2)))+')$', zorder=-100) # 正射影ベクトル ax.quiver(0, 0, 0, *a, color='red', ls='--', lw=1, arrow_length_ratio=l/np.linalg.norm(a), label='$a=('+', '.join(map(str, a))+')$') # ベクトルa ax.quiver(0, 0, 0, *b, color='blue', arrow_length_ratio=l/np.linalg.norm(b), label='$b=('+', '.join(map(str, b))+')$') # ベクトルb ax.quiver(*p, *b-p, color='chocolate', arrow_length_ratio=l/np.linalg.norm(b-p), label='$b-p=-('+', '.join(map(str, (b-p).round(2)))+')$') # ベクトルb-p ax.plot(rightangle_x, rightangle_y, rightangle_z, color='black', linewidth=1, zorder=100) # 直角マーク ax.quiver([0, a[0], b[0], p[0]], [0, a[1], b[1], p[1]], [0, a[2], b[2], p[2]], [0, 0, 0, 0], [0, 0, 0, 0], [z_min, z_min-a[2], z_min-b[2], z_min-p[2]], color=['gray', 'red', 'blue', 'orange'], arrow_length_ratio=0, linestyle=':') # 座標用の補助線 ax.set_xticks(ticks=np.arange(x_min, x_max+1)) ax.set_yticks(ticks=np.arange(y_min, y_max+1)) ax.set_zticks(ticks=np.arange(z_min, z_max+1)) ax.set_zlim(bottom=z_min, top=z_max) ax.set_xlabel('$x_1$') ax.set_ylabel('$x_2$') ax.set_zlabel('$x_3$') ax.set_title('$p=' + str(beta.round(2)) + 'a, ' + 'p^{\\top} (b-p)=' + str(np.dot(p, b-p).round(2)) + '$', loc='left') fig.suptitle('$p \\bot (b-p)$', fontsize=20) ax.legend() ax.set_aspect('equal') plt.show()
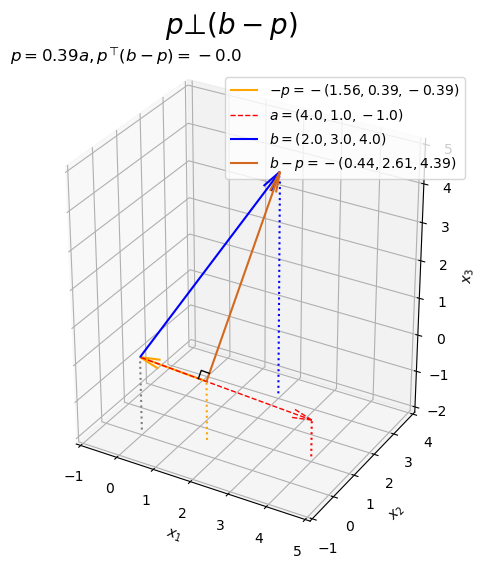
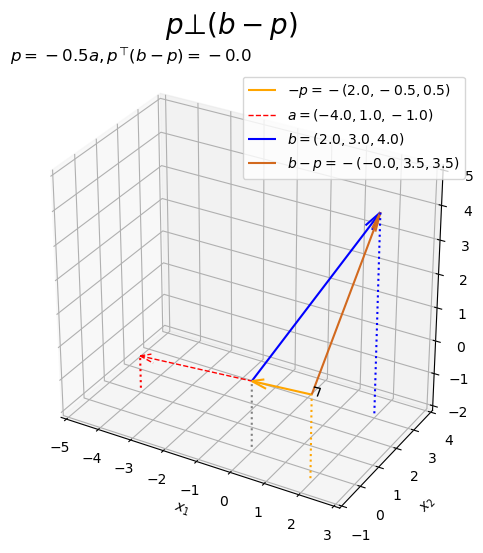
3次元の場合でも、内積が0になることからと
が直交するのが分かります。
ベクトルの値を変化させたアニメーションを作成します。
・作図コード(クリックで展開)
# フレーム数を設定 frame_num = 60 # 固定するベクトルを指定 #a = np.array([4.0, 1.0, 2.0]) b = np.array([2.0, 3.0, 4.0]) # ベクトルのノルム(球形の軌道の半径)を指定 r = 3.0 # 変化するベクトルとして利用する値を指定 psi_a_n = np.linspace(start=0.0, stop=2.0*np.pi, num=frame_num+1)[:frame_num] phi_a_n = np.linspace(start=1.0/3.0*np.pi, stop=1.0/3.0*np.pi, num=frame_num+1)[:frame_num] a_n = np.array( [r * np.sin(psi_a_n) * np.cos(phi_a_n), r * np.sin(psi_a_n) * np.sin(phi_a_n), r * np.cos(psi_a_n)] ).T psi_b_n = np.linspace(start=1.0/3.0*np.pi, stop=1.0/3.0*np.pi, num=frame_num+1)[:frame_num] phi_b_n = np.linspace(start=0.0, stop=2.0*np.pi, num=frame_num+1)[:frame_num] b_n = np.array( [r * np.sin(psi_b_n) * np.cos(phi_b_n), r * np.sin(psi_b_n) * np.sin(phi_b_n), r * np.cos(psi_b_n)] ).T # グラフサイズ用の値を設定 axis_size = r + 1.0 # 矢のサイズを指定 l = 0.5 # グラフオブジェクトを初期化 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white', subplot_kw={'projection': '3d'}) fig.suptitle('vector projection', fontsize=20) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i番目のベクトルを取得 #a = a_n[i] b = b_n[i] # 正射影ベクトルを計算 dot_ab = np.dot(a, b) norm_a = np.linalg.norm(a) beta = dot_ab / norm_a**2 p = beta * a # ベクトルa,bのなす角を計算 norm_b = np.linalg.norm(b) theta = np.arccos(dot_ab / norm_a / norm_b) #混合率(線形結合の係数)を作成 rad_vals = np.linspace(start=0.0, stop=0.5*np.pi, num=100) rad_arr = np.repeat(rad_vals[:, np.newaxis], repeats=3, axis=1) beta1_arr = np.cos(rad_arr) beta2_arr = np.sin(rad_arr) # 角マークの座標を計算 r = 0.3 angle_x_arr = beta1_arr * a/norm_a + beta2_arr * b/norm_b # 正規化ベクトルa,b間の曲線 angle_x_arr *= r / np.linalg.norm(angle_x_arr, axis=1, keepdims=True) # サイズ調整 #混合率(線形結合の係数)を作成 rad = 0.25 * np.pi beta1 = np.cos(rad) beta2 = np.sin(rad) # 角ラベルの座標を計算 r = 0.5 angle_x_vec = beta1 * a/norm_a + beta2 * b/norm_b # 正規化ベクトルa,b間の中点 angle_x_vec *= r / np.linalg.norm(angle_x_vec) # サイズ調整 # 直角マーク用の座標を計算 r = 0.2 e_a = a / norm_a e_bp = (b - p) / np.linalg.norm(b - p) rightangle_x = [p[0]+r*e_bp[0], p[0]+r*(e_bp[0]-e_a[0]), p[0]-r*e_a[0]] rightangle_y = [p[1]+r*e_bp[1], p[1]+r*(e_bp[1]-e_a[1]), p[1]-r*e_a[1]] rightangle_z = [p[2]+r*e_bp[2], p[2]+r*(e_bp[2]-e_a[2]), p[2]-r*e_a[2]] # ベクトルaと平行な直線の座標を計算 line_x_vals = np.linspace(start=-axis_size, stop=axis_size, num=201) line_y_vals = a[1]/a[0] * line_x_vals line_z_vals = a[2]/a[0] * line_x_vals bool_idx = (line_y_vals < -axis_size) | (line_y_vals > axis_size) | (line_z_vals < -axis_size) | (line_z_vals > axis_size) line_x_vals = line_x_vals[[not bl for bl in bool_idx]] line_y_vals = line_y_vals[[not bl for bl in bool_idx]] line_z_vals = line_z_vals[[not bl for bl in bool_idx]] # 正射影ベクトルと垂線ベクトルを作図 ax.plot(line_x_vals, line_y_vals, line_z_vals, color='red', linestyle='--', zorder=-100) # ベクトルaの延長線 ax.quiver(0, 0, 0, *a, color='red', arrow_length_ratio=l/np.linalg.norm(a), label='$a=('+', '.join(map(str, a.round(2)))+')$') # ベクトルa ax.quiver(0, 0, 0, *b, color='blue', arrow_length_ratio=l/np.linalg.norm(b), label='$b=('+', '.join(map(str, b.round(2)))+')$') # ベクトルb ax.quiver(0, 0, 0, *p, color='orange', arrow_length_ratio=l/np.linalg.norm(p), label='$p=('+', '.join(map(str, p.round(2)))+')$', zorder=100) # 正射影ベクトル ax.quiver(*p, *b-p, color='chocolate', arrow_length_ratio=l/np.linalg.norm(b-p), label='$b-p=-('+', '.join(map(str, (b-p).round(2)))+')$') # ベクトルb-p ax.plot(rightangle_x, rightangle_y, rightangle_z, color='black', linewidth=1, zorder=200) # 直角マーク ax.plot(*angle_x_arr.T, color='black', linewidth=1) # なす角マーク ax.text(*angle_x_vec, s='$\\theta$', size=15, ha='center', va='center', zorder=20) # なす角ラベル ax.quiver([0, a[0], b[0], p[0]], [0, a[1], b[1], p[1]], [0, a[2], b[2], p[2]], [0, 0, 0, 0], [0, 0, 0, 0], [-axis_size, -axis_size-a[2], -axis_size-b[2], -axis_size-p[2]], color=['gray', 'red', 'blue', 'orange'], arrow_length_ratio=0, linestyle=':') # 座標用の補助線 ax.set_xticks(ticks=np.arange(-axis_size, axis_size+1)) ax.set_yticks(ticks=np.arange(-axis_size, axis_size+1)) ax.set_zticks(ticks=np.arange(-axis_size, axis_size+1)) ax.set_xlim(left=-axis_size, right=axis_size) ax.set_ylim(bottom=-axis_size, top=axis_size) ax.set_zlim(bottom=-axis_size, top=axis_size) ax.set_xlabel('$x_1$') ax.set_ylabel('$x_2$') ax.set_zlabel('$x_3$') ax.grid() ax.set_title('$\\theta=' + str((theta / np.pi).round(2)) + '\pi, ' + 'p=' + str(beta.round(2)) + 'a, ' + 'p^{\\top} (b-p)=' + str(np.dot(p, b-p).round(2)) + '$', loc='left') ax.legend(loc='upper left', prop={'size': 7}) ax.set_aspect('equal') # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # gif画像を保存 ani.save('projection_3d_a.gif')
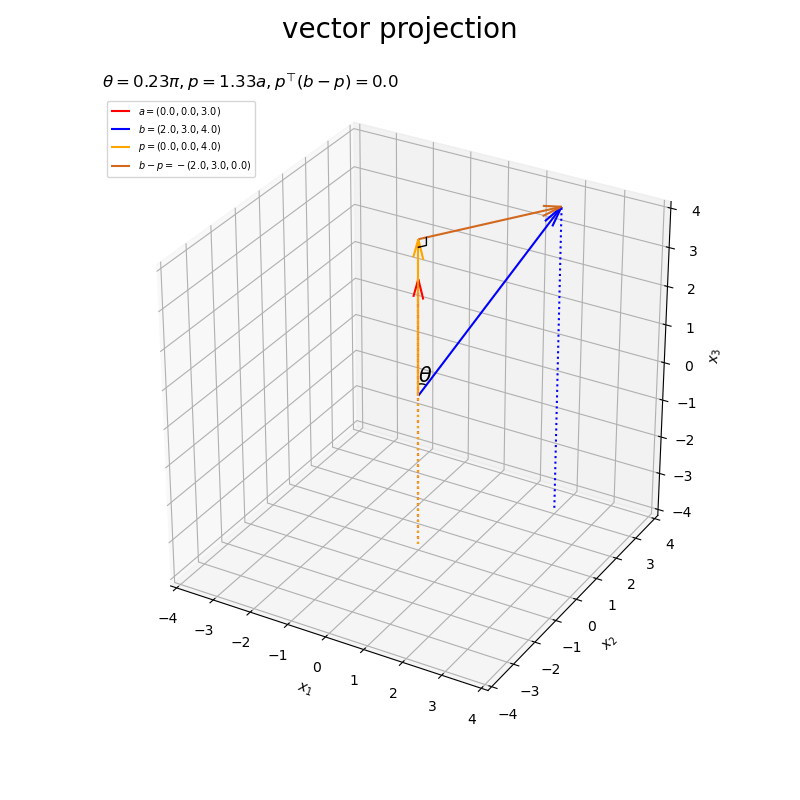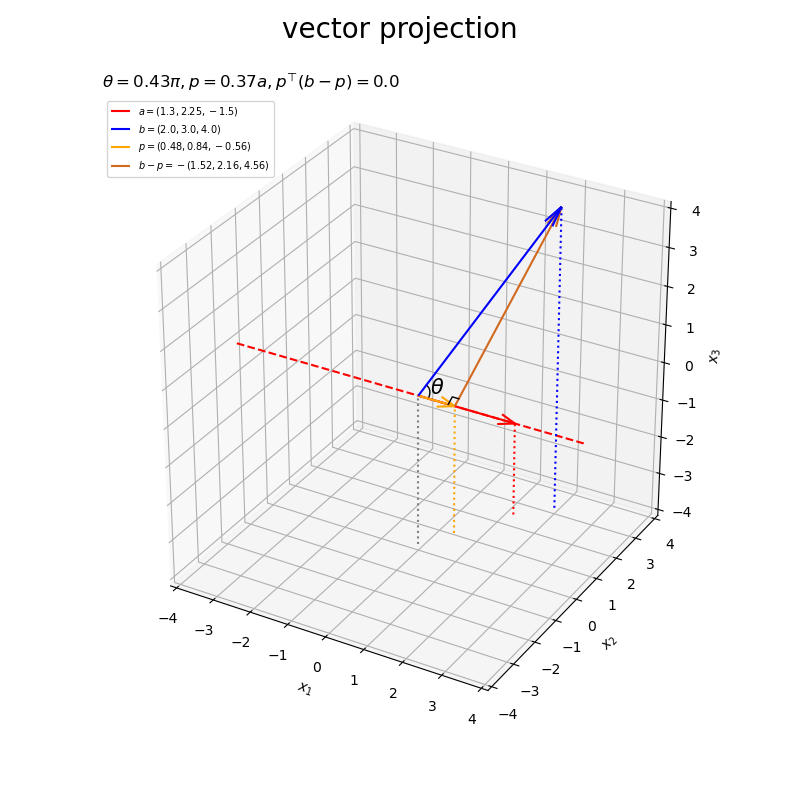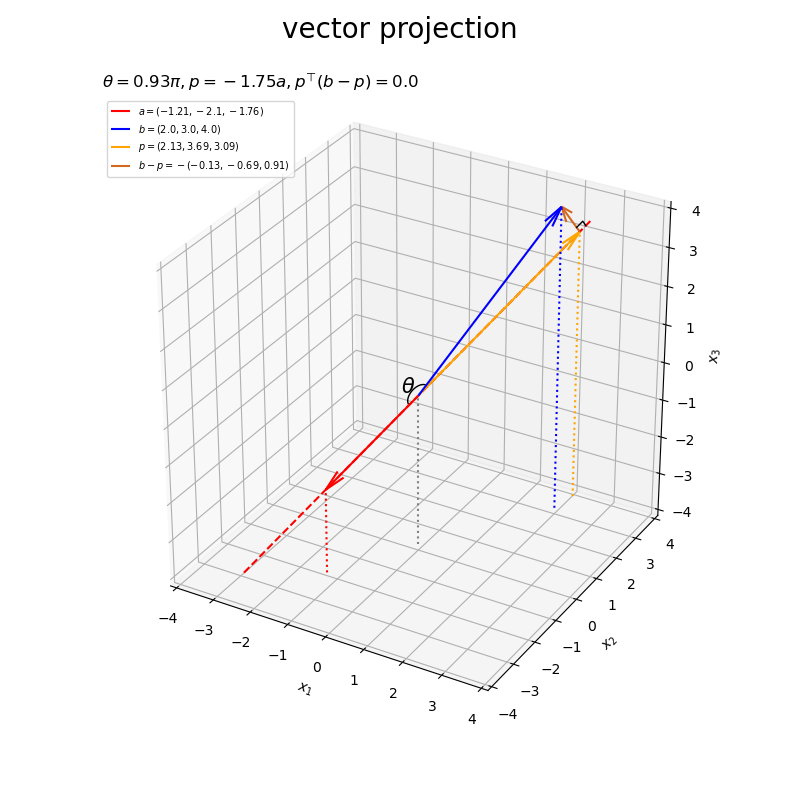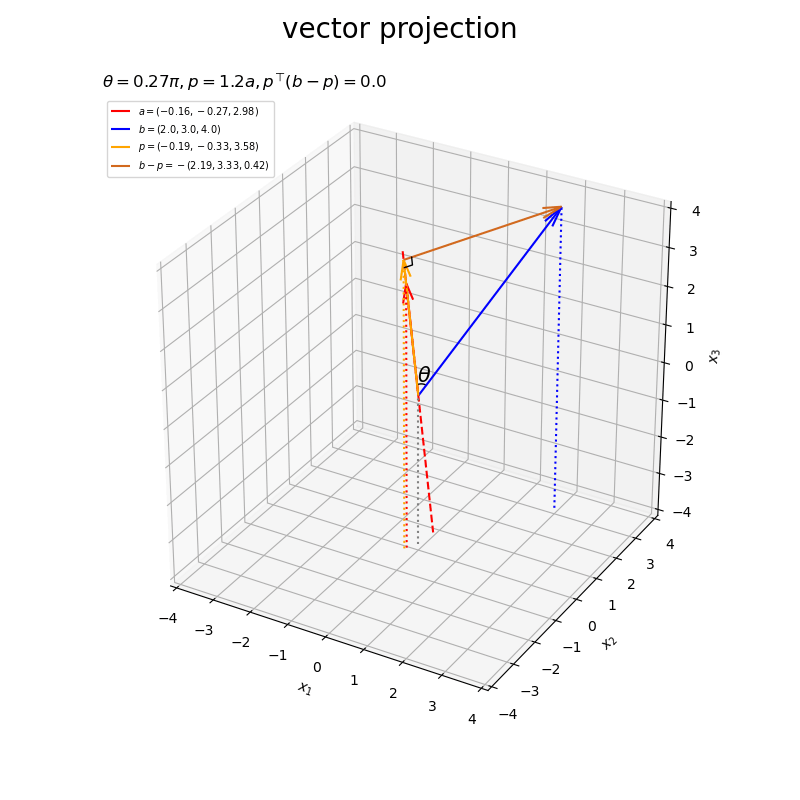
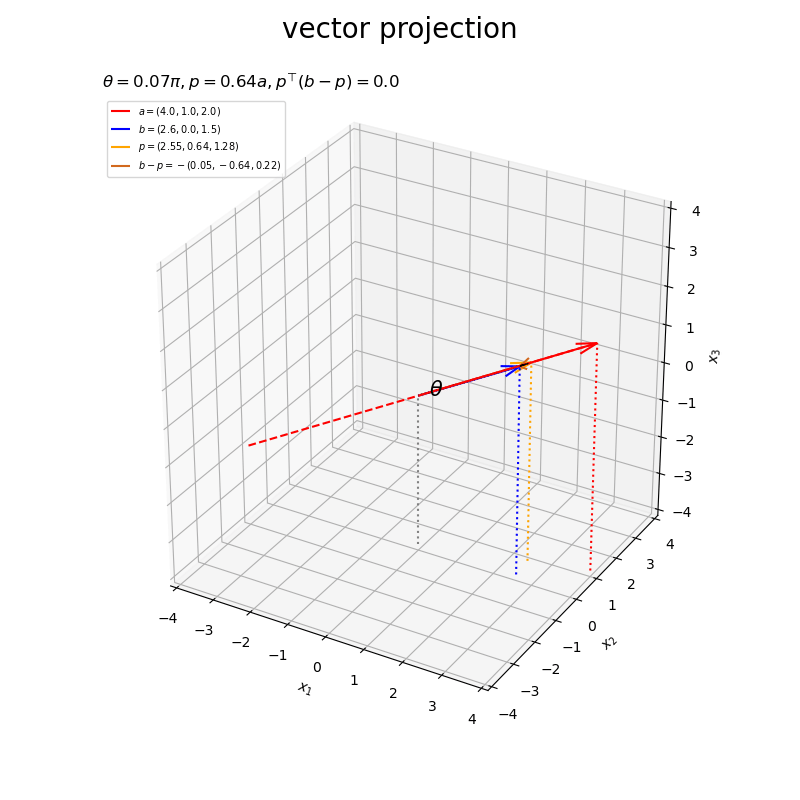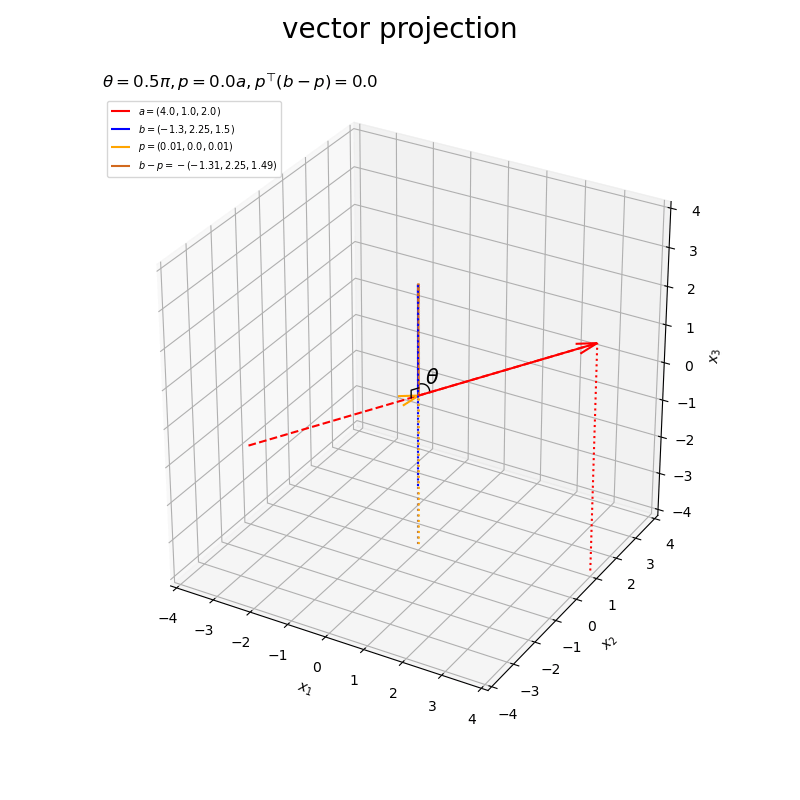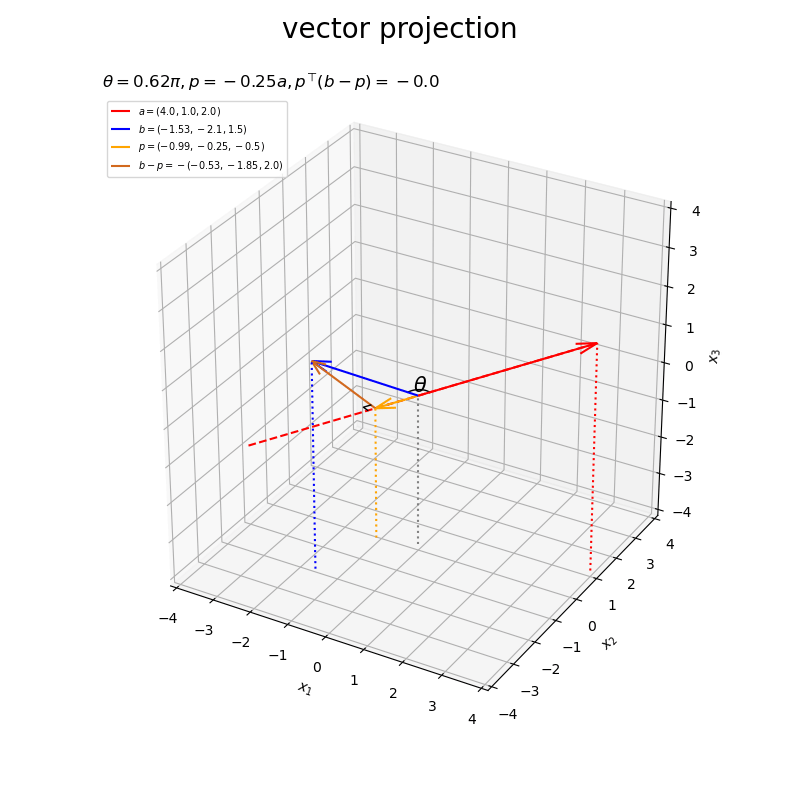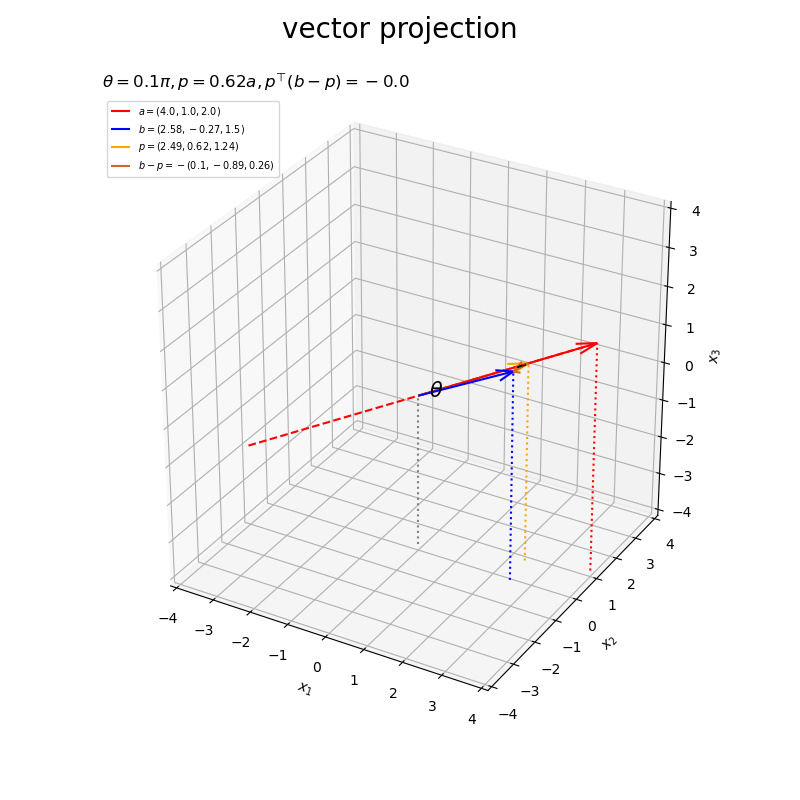
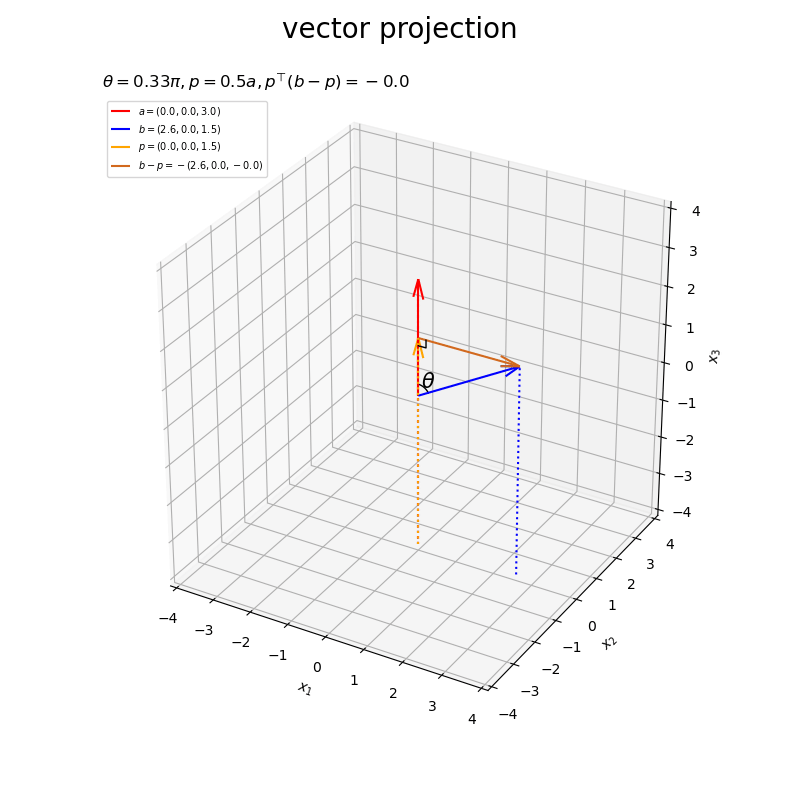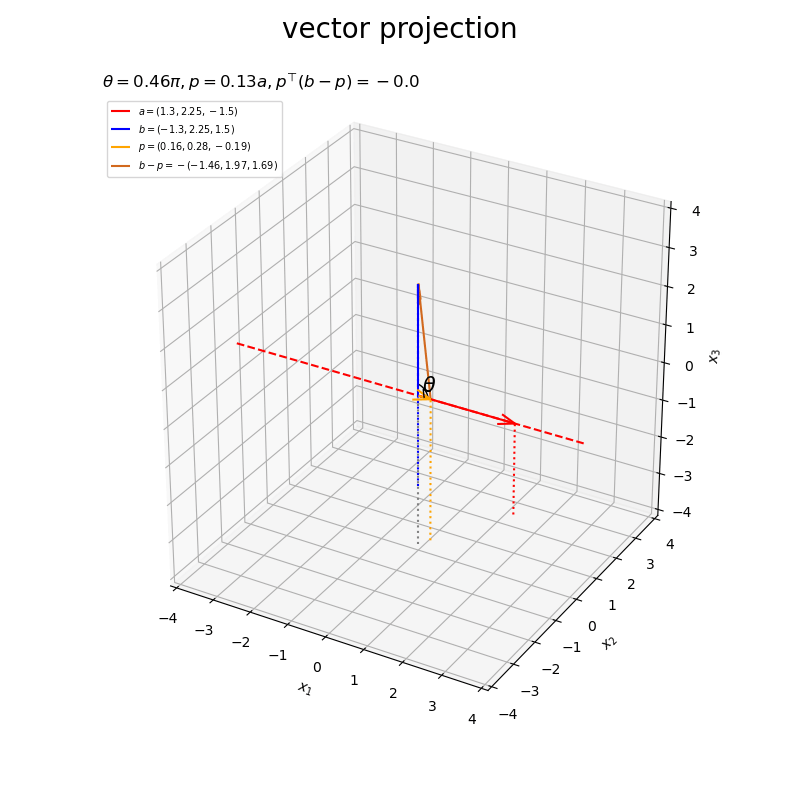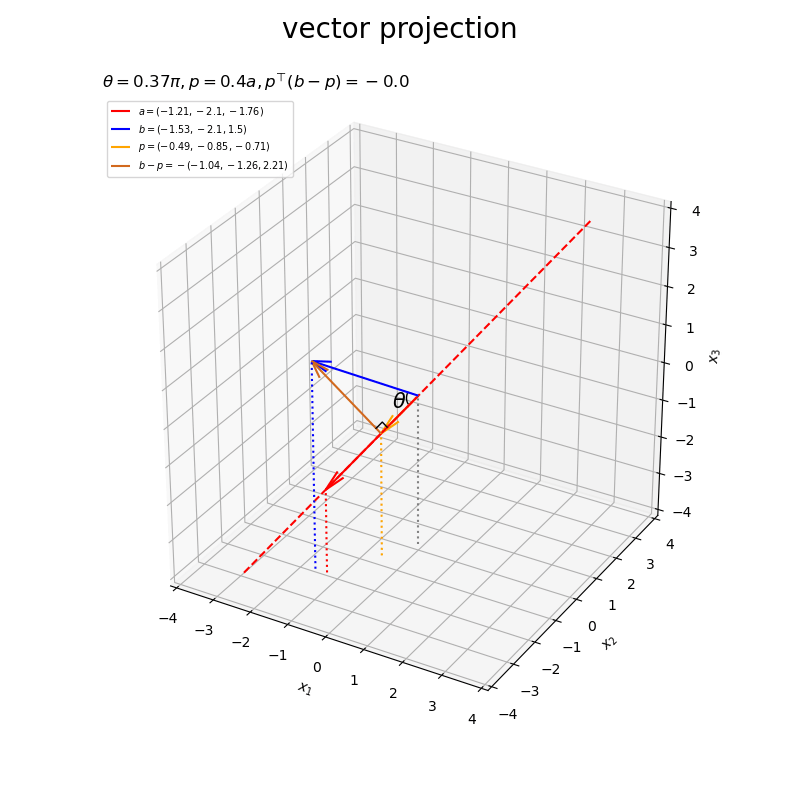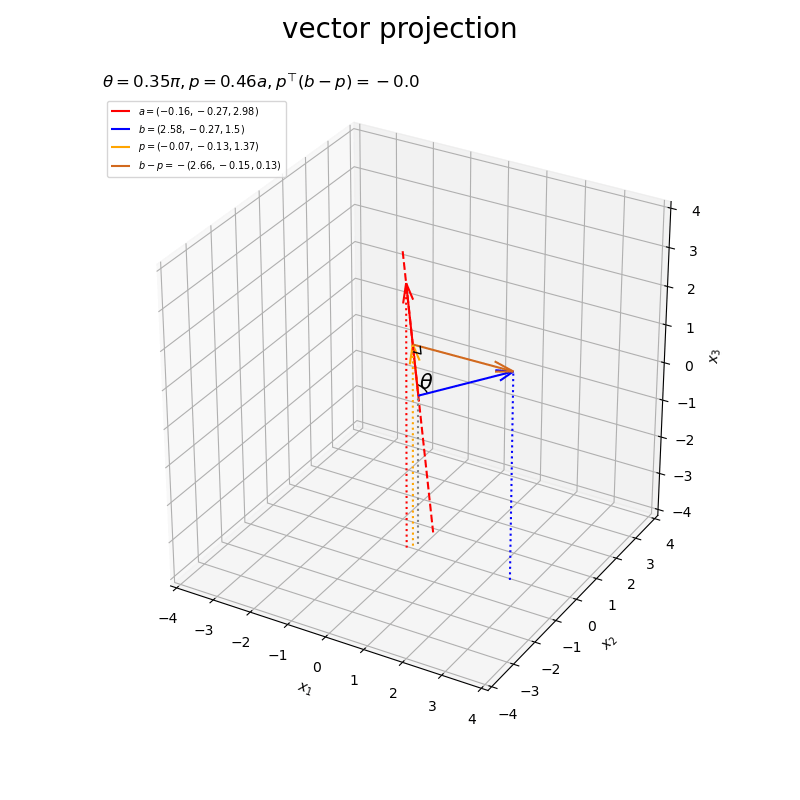
以上が、3次元における正射影ベクトルと垂線ベクトルの計算と可視化です。
この記事では、正射影を可視化しました。次の記事では、正射影を利用したグラム・シュミット法による直交化を可視化します。
参考書籍
- Stephen Boyd・Lieven Vandenberghe(著),玉木 徹(訳)『スタンフォード ベクトル・行列からはじめる最適化数学』講談社サイエンティク,2021年.
おわりに
グラム・シュミット法の直交化処理(計算)を理解するのに必要だったので、本に載ってないけど書きました。
2023年4月20日は、OCHA NORMAの石栗奏美さんの19歳のお誕生日です。
期待しかない新人メン(デビュー前も含めると活動歴は長いけど)で今後の活躍がとても楽しみ。
【次の内容】