はじめに
機械学習で登場する確率分布について色々な角度から理解したいシリーズです。
多項分布の計算とグラフの作成をR言語で行います。
【前の内容】
【他の記事一覧】
【目次】
多項分布
多項分布(Multinomial Distribution)の計算と作図を行います。
利用するパッケージを読み込みます。
# 利用するパッケージ library(tidyverse) library(barplot3d) library(gganimate)
分布の変化をアニメーション(gif画像)で確認するのにgganimateパッケージを利用します。不要であれば省略してください。
定義式の確認
まずは、多項分布の定義式を確認します。
多項分布は、次の式で定義されます。詳しくは「多項分布の定義式 - からっぽのしょこ」を参照してください。
ここで、$x_v$はクラス$v$が出現した回数、$M$は試行回数、$\phi_v$はクラス$v$の出現確率です。
確率変数の値$\mathbf{x} = (x_1, \cdots, x_V)$は、$x_v \in \{1, \cdots, V\}$、$\sum_{v=1}^V x_v = M$となります。パラメータ$\boldsymbol{\phi} = (\phi_1, \cdots, \phi_V)$は、$\phi_v \in (0, 1)$、$\sum_{v=1}^V \phi_v = 1$を満たす必要があります。
この式の対数をとると、次の式になります。
多項分布のクラス$v$における平均と分散は、次の式で計算できます。詳しくは「多項分布の平均と分散の導出 - からっぽのしょこ」を参照してください。
これらの計算を行いグラフを作成します。
確率の計算
多項分布に従う確率を計算する方法をいくつか確認します。
パラメータを設定します。
# パラメータを指定 phi_v <- c(0.3, 0.5, 0.2) # 確率変数の値を指定 x_v <- c(2, 3, 1) # データ数を計算 M <- sum(x_v)
多項分布のパラメータ$\boldsymbol{\phi} = (\phi_1, \cdots, \phi_V)$、$0 \leq \phi_v \leq 1$、$\sum_{v=1}^V \phi_v = 1$、試行回数$M$、確率変数がとり得る値$\mathbf{x} = (x_1, \cdots, x_V)$、$x_v \in \{0, 1, \cdots, M\}$、$\sum_{v=1}^V x_v = M$を指定します。設定した値に従う確率を計算します。
まずは、定義式から確率を計算します。
# 定義式により確率を計算 C <- gamma(M + 1) / prod(gamma(x_v + 1)) prob <- C * prod(phi_v^x_v) prob
## [1] 0.135
多項分布の定義式
で計算します。$C_{\mathrm{Mul}}$は、多項分布の正規化係数です。
階乗$x!$の計算は、ガンマ関数$\Gamma(x + 1) = x!$に置き換えて計算します。ガンマ関数は、gamma()で計算できます。
対数をとった定義式から計算します。
# 対数をとった定義式により確率を計算 log_C <- lgamma(M + 1) - sum(lgamma(x_v + 1)) log_prob <- log_C + sum(x_v * log(phi_v)) prob <- exp(log_prob) prob; log_prob
## [1] 0.135 ## [1] -2.002481
対数をとった定義式
を計算します。計算結果の指数をとると確率が得られます。
指数と対数の性質より$\exp(\log x) = x$です。
次は、関数を使って確率を計算します。
多項分布の確率関数dmultinom()を使って計算します。
# 多項分布の関数により確率を計算 prob <- dmultinom(x = x_v, size = M, prob = phi_v) prob
## [1] 0.135
出現頻度の引数xにx_v、試行回数の引数をsize = M、出現確率の引数probにphi_vを指定します。
log = TRUEを指定すると対数をとった確率を返します。
# 多項分布の対数をとった関数により確率を計算 log_prob <- dmultinom(x = x_v, size = M, prob = phi_v, log = TRUE) prob <- exp(log_prob) prob; log_prob
## [1] 0.135 ## [1] -2.002481
計算結果の指数をとると確率が得られます。
統計量の計算
多項分布の平均と分散を計算します。
クラスvの平均を計算します。
# クラス番号を指定 v <- 1 # クラスvの平均を計算 E_x <- M * phi_v[v] E_x
## [1] 1.8
多項分布の平均は、次の式で計算できます。
クラスvの分散を計算します。
# クラスvの分散を計算 V_x <- M * phi_v[v] * (1 - phi_v[v]) V_x
## [1] 1.26
多項分布の分散は、次の式で計算できます。
グラフの作成
多項分布のグラフを作成します。
多項分布の確率変数がとり得る値$\mathbf{x} = (x_1, x_2, x_3)$を作成します。ここでは3次元のグラフで描画するため$V = 3$とします。
# パラメータを指定 phi_v <- c(0.3, 0.5, 0.2) # 試行回数を指定 M <- 10 # 作図用のxの値を作成 x_vals <- 0:M # 作図用のxの点を作成 x_points <- tidyr::tibble( x_1 = rep(x = x_vals, times = M + 1), # 確率変数の成分1 x_2 = rep(x = x_vals, each = M + 1) # 確率変数の成分2 ) %>% dplyr::mutate( x_3 = dplyr::if_else(condition = x_1 + x_2 < M, true = M - (x_1 + x_2), false = 0) ) %>% # 確率変数の成分3 as.matrix() head(x_points)
## x_1 x_2 x_3 ## [1,] 0 0 10 ## [2,] 1 0 9 ## [3,] 2 0 8 ## [4,] 3 0 7 ## [5,] 4 0 6 ## [6,] 5 0 5
$\mathbf{x}$の各要素$x_v$がとり得る値0からMの整数をx_valsとします。
x_valsの全ての組み合わせを持つように$x_1, x_2$を作成します。そして、$x_1 + x_2 + x_3 = M$となるように$x_3$の値を決めます。ただし、$x_1 + x_2 > M$となる場合は、$x_3 = 0$とします。
$\mathbf{x}$の点ごとの確率を計算します。
# 確率変数の組み合わせごとに確率を計算 prob_df <- tidyr::tibble() for(i in 1:nrow(x_points)) { # 確率変数の値を取得 x_v <- x_points[i, ] # 多項分布の情報を格納 tmp_df <- tidyr::tibble( x_1 = x_v[1], # 確率変数の成分1 x_2 = x_v[2], # 確率変数の成分2 x_3 = x_v[3] # 確率変数の成分3 ) %>% dplyr::mutate( probability = dplyr::if_else( sum(x_v) == M, true = dmultinom(x = x_v, size = sum(x_v), prob = phi_v), false = 0 ) # (size = Mにすべきだけど何故かエラーになる) ) # 確率 # 結果を結合 prob_df <- rbind(prob_df, tmp_df) } head(prob_df)
## # A tibble: 6 x 4 ## x_1 x_2 x_3 probability ## <dbl> <dbl> <dbl> <dbl> ## 1 0 0 10 0.000000102 ## 2 1 0 9 0.00000154 ## 3 2 0 8 0.0000104 ## 4 3 0 7 0.0000415 ## 5 4 0 6 0.000109 ## 6 5 0 5 0.000196
x_pointsの各行を取り出し、確率を計算してデータフレームに格納します。ただし、x_pointsは$x_1 + x_2 > M$の値を含みます。$\mathbf{x}$がとり得ない値は計算できないため、dplyr::if_else()で0とします。
ggplot2による作図
ggplot2パッケージを利用して多項分布のグラフを作成します。
ヒートマップで可視化します。
# カテゴリ分布のグラフを作成 ggplot(data = prob_df, mapping = aes(x = x_1, y = x_2, fill = probability)) + # データ geom_tile() + # ヒートマップ scale_fill_gradientn(colors = c("blue", "green", "yellow", "red")) + # グラデーション scale_x_continuous(breaks = 0:M, labels = 0:M) + # x軸目盛 scale_y_continuous(breaks = 0:M, labels = 0:M) + # y軸目盛 coord_fixed(ratio = 1) + # アスペクト比 labs(title = "Multinomial Distribution", subtitle = paste0("phi=(", paste0(phi_v, collapse = ", "), "), M=", M), x = expression(x[1]), y = expression(x[2])) # ラベル
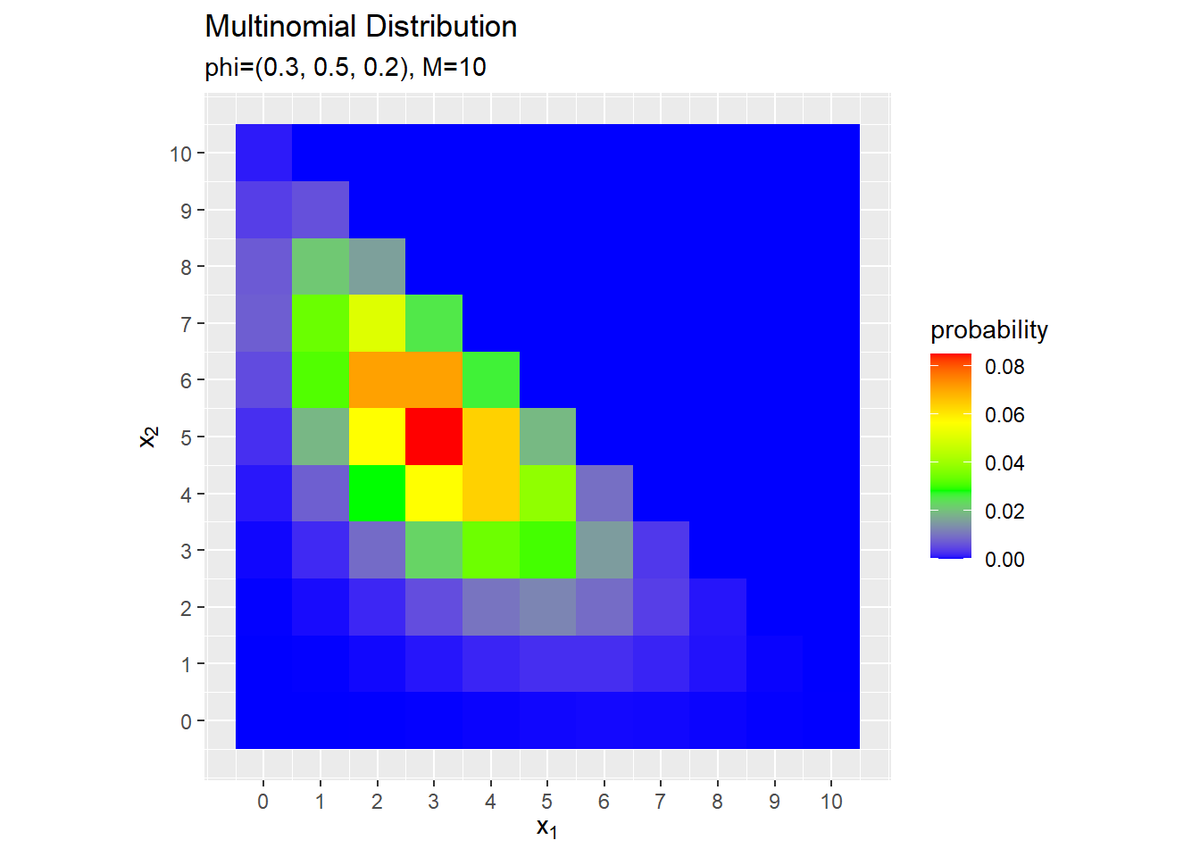
$x_1 + x_2 + x_3 = M$なので$x_3 = M - (x_1 + x_2)$、$\phi_1 + \phi_2 + \phi_3 = 1$なので$\phi_3 = 1 - (\phi_1 + \phi_2)$で表現できます(求まります)。つまり、$x_1, x_2$と$M$の値が分かれば分布の情報が得られます。
よって、$x_1$をx軸、$x_2$をy軸、各点の確率をヒートマップとして、$V = 3$の多項分布を表します。
平均と標準偏差の補助線を引きます。
# 補助線用の統計量を計算 E_x1 <- M * phi_v[1] V_x1 <- M * phi_v[1] * (1 - phi_v[1]) s_x1 <- sqrt(V_x1) E_x2 <- M * phi_v[2] V_x2 <- M * phi_v[2] * (1 - phi_v[2]) s_x2 <- sqrt(V_x2) # カテゴリ分布のグラフを作成 ggplot(data = prob_df, mapping = aes(x = x_1, y = x_2, fill = probability)) + # データ geom_tile() + # ヒートマップ geom_vline(xintercept = E_x1, color = "orange", size = 1, linetype = "dashed") + # 平均 geom_vline(xintercept = E_x1 - s_x1, color = "orange", size = 1, linetype = "dotted") + # 平均 - 標準偏差 geom_vline(xintercept = E_x1 + s_x1, color = "orange", size = 1, linetype = "dotted") + # 平均 + 標準偏差 geom_hline(yintercept = E_x2, color = "orange", size = 1, linetype = "dashed") + # 平均 geom_hline(yintercept = E_x2 - s_x2, color = "orange", size = 1, linetype = "dotted") + # 平均 - 標準偏差 geom_hline(yintercept = E_x2 + s_x2, color = "orange", size = 1, linetype = "dotted") + # 平均 + 標準偏差 scale_fill_gradientn(colors = c("blue", "green", "yellow", "red")) + # グラデーション scale_x_continuous(breaks = 0:M, labels = 0:M) + # x軸目盛 scale_y_continuous(breaks = 0:M, labels = 0:M) + # y軸目盛 coord_fixed(ratio = 1) + # アスペクト比 labs(title = "Multinomial Distribution", subtitle = paste0("phi=(", paste0(phi_v, collapse = ", "), "), M=", M), x = expression(x[1]), y = expression(x[2])) # ラベル
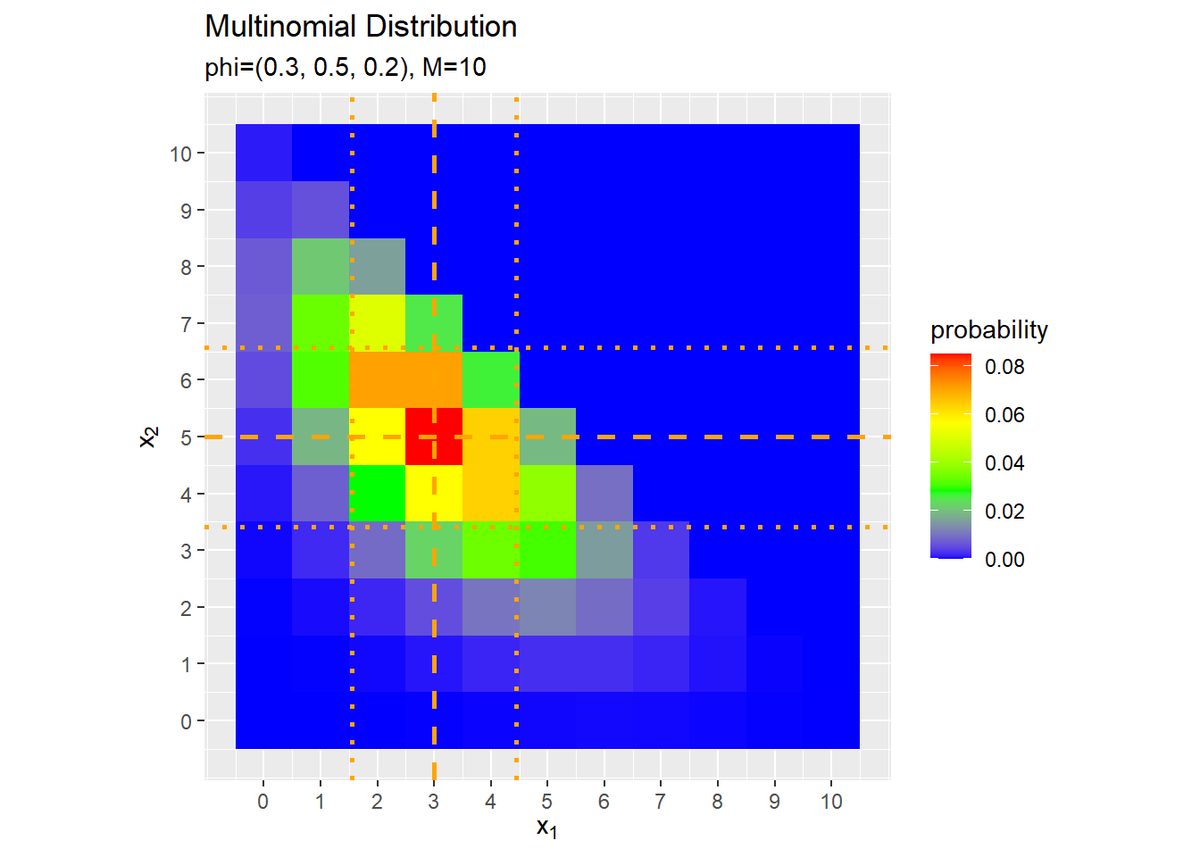
各軸$x_1, x_2$の平均(破線)が交差する点が確率の最大値であるのが分かります。
また、平均を中心に標準偏差の範囲(破線)で山が高く(赤に近い色に)なっているのが分かります。
barplot3dによる作図
barplot3dパッケージを利用して多項分布を3D棒グラフで可視化します。
y軸($x_2$)の値ごとに色付けした3D棒グラフを作成します。
# インデックスによる色付けを作成 rainbow_vec <- rep(rainbow(M + 1), each = M + 1) rainbow_vec[1:15]
## [1] "#FF0000" "#FF0000" "#FF0000" "#FF0000" "#FF0000" "#FF0000" "#FF0000" ## [8] "#FF0000" "#FF0000" "#FF0000" "#FF0000" "#FF8B00" "#FF8B00" "#FF8B00" ## [15] "#FF8B00"
この例では、$x_1$の値ごとに別の色にします。
rainbow()を使って、$x_2$の要素数$M + 1$個のカラーコードを作成します。作成した色ごとに$x_1$の要素数$M + 1$個ずつ複製します。
# カテゴリ分布のグラフを作成 barplot3d::barplot3d( rows = M + 1, cols = M + 1, z = prob_df[["probability"]], topcolors = rainbow_vec, sidecolors = rainbow_vec, alpha = 0.1, xlabels = as.character(0:M), ylabels = as.character(0:M), xsub = "x1", ysub = "x2", zsub = "probability", scalexy = 0.01, theta = 30, phi = 30 )
行数の引数rowsと列数の引数colsにM + 1を指定します。また、z軸の値(棒グラフの高さ)の引数zにデータフレームに格納した確率prob_df[["probability"]]を指定します。
上の面の色の引数topcolors、側面の色の引数sidecolors、辺の色の引数linecolorsにカラーコードを指定します。また、alphaで透過度を指定できます。
軸目盛の引数xlabels, ylabelsに0からMの整数を文字列で指定します。xsub, ysub, zsubは軸ラベルの引数です。
scalexyでグラフの幅、thetaで垂直方向のphiで水平方向の表示アングルを調整できます。
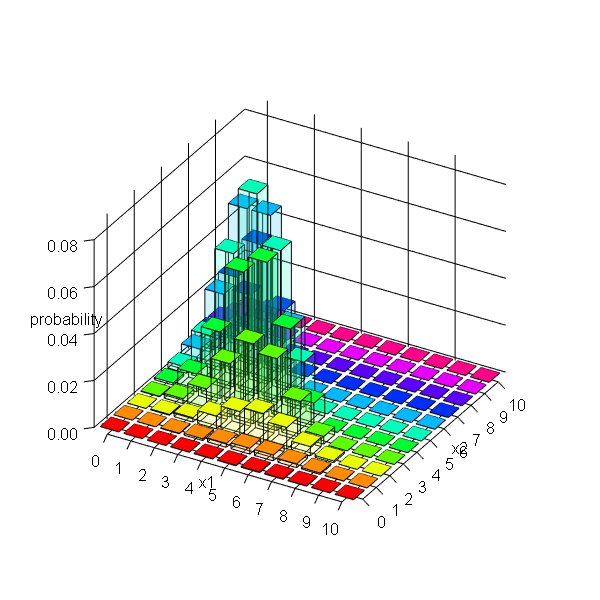
確率に応じて色付けした3D棒グラフを作成します。
# 確率による色付けを作成 p <- prob_df[["probability"]] heat_idx <- round((1 - p / max(p)) * 100) + 1 heat_vec <- heat.colors(101)[heat_idx] p[11:20]; heat_idx[11:20]; heat_vec[11:20]
## [1] 5.90490e-06 2.56000e-06 3.45600e-05 2.07360e-04 7.25760e-04 1.63296e-03 ## [7] 2.44944e-03 2.44944e-03 1.57464e-03 5.90490e-04 ## [1] 101 101 101 101 100 99 98 98 99 100 ## [1] "#FFFFFA" "#FFFFFA" "#FFFFFA" "#FFFFFA" "#FFFFF0" "#FFFFE6" "#FFFFDB" ## [8] "#FFFFDB" "#FFFFE6" "#FFFFF0"
heat.colors()は、赤・黄・白の順に変化するカラーコードを返します。確率が小さいほど白に近い色で、大きいほど赤に近い色となるように色付けします。
p / max(p)で、pの最大値が1となるように変換します。最小値は0です。1 - p / max(p)で、大小関係を入れ替えます。100を掛けてround()で小数点以下を丸めることで、0から100の整数にします。最後に、1を足すことで、確率pに従う1から101の整数になります。これをインデックスheat_idxとして使います。
heat.colors(101)で101個のカラーコードに作成します。heat_idx添字としてカラーコードを取り出すことで、確率に応じた色を取り出せます。
# カテゴリ分布のグラフを作成 barplot3d::barplot3d( rows = M + 1, cols = M + 1, z = prob_df[["probability"]], topcolors = heat_vec, sidecolors = heat_vec, alpha = 0.1, xlabels = as.character(0:M), ylabels = as.character(0:M), xsub = "x1", ysub = "x2", zsub = "probability", scalexy = 0.01, theta = 30, phi = 30 )<figure class="figure-image figure-image-fotolife" title="多項分布とパラメータの関係">[f:id:anemptyarchive:20220117072438g:plain]<figcaption>多項分布とパラメータの関係</figcaption></figure>
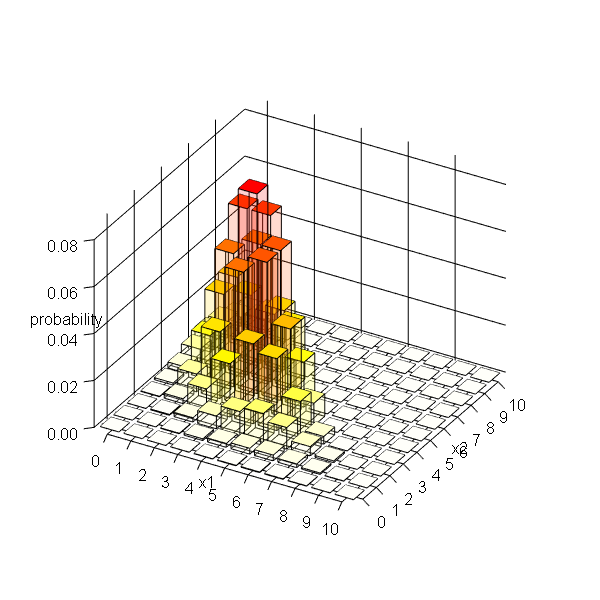
多項分布のグラフを描画できました。barplot3dの出力は別ウィンドウで表示され、マウスでアングルやサイズを操作できます。
図を保存する場合はrglパッケージを利用します。
# 利用するパッケージ library(rgl) # ウィンドウサイズを指定:(左, 上, 右, 下) rgl::par3d(windowRect=c(0, 100, 600, 700)) # ウィンドウのスクリーンショットを保存 rgl::rgl.snapshot("Multinomial_3dbar.png") # ウィンドウを閉じる rgl::rgl.close()
par3d()でウィンドウのサイズを変更し、rgl.snapshot()で図を保存します。rgl.close()でウィンドウを閉じます。
パラメータと分布の形状の関係
続いて、パラメータ$\phi_v$の値を少しずつ変更して、分布の変化をアニメーションで確認します。
・作図コード(クリックで展開)
# 作図用のphiの値を作成 phi_vals <- seq(from = 0, to = 1, by = 0.01) # phiの値ごとに分布を計算 anime_prob_df <- tidyr::tibble() for(phi in phi_vals) { # phi_1以外の割り当てを指定 phi_v <- c(phi, (1 - phi) * 0.6, (1 - phi) * 0.4) # 確率変数の組み合わせごとに確率を計算 tmp_prob_df <- tidyr::tibble() for(i in 1:nrow(x_points)) { # 確率変数の値を取得 x_v <- x_points[i, ] # 多項分布の情報を格納 tmp_df <- tidyr::tibble( x_1 = x_v[1], # 確率変数の成分1 x_2 = x_v[2], # 確率変数の成分2 x_3 = x_v[3] # 確率変数の成分3 ) %>% dplyr::mutate( probability = dplyr::if_else( sum(x_v) == M, true = dmultinom(x = x_v, size = sum(x_v), prob = phi_v), false = 0 ) # (size = Mにすべきだけど何故かエラーになる) ) # 確率 # 結果を結合 tmp_prob_df <- rbind(tmp_prob_df, tmp_df) } # フレーム切替用のラベルを付与 tmp_prob_df <- tmp_prob_df %>% dplyr::mutate( parameter = paste0("phi=(", paste0(round(phi_v, 2), collapse = ", "), "), M=", M) %>% as.factor() ) # 結果を結合 anime_prob_df <- rbind(anime_prob_df, tmp_prob_df) } head(anime_prob_df)
## # A tibble: 6 x 5 ## x_1 x_2 x_3 probability parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 0 0 10 0.000105 phi=(0, 0.6, 0.4), M=10 ## 2 1 0 9 0 phi=(0, 0.6, 0.4), M=10 ## 3 2 0 8 0 phi=(0, 0.6, 0.4), M=10 ## 4 3 0 7 0 phi=(0, 0.6, 0.4), M=10 ## 5 4 0 6 0 phi=(0, 0.6, 0.4), M=10 ## 6 5 0 5 0 phi=(0, 0.6, 0.4), M=10
$\phi_1$がとり得る値を作成してphi_valsとします。
for()ループを使ってphi_valsの値ごとにphi_vを更新して、anime_prob_dfに追加していきます。$\phi_1$以外の確率の和$1 - \phi_1$を他のクラスの確率として割り振ります。
gif画像を作成します。
# 最大値を指定 p_max <- 0.15 # アニメーション用の多項分布を作図 anime_prob_graph <- ggplot(data = anime_prob_df, mapping = aes(x = x_1, y = x_2, fill = probability)) + # データ geom_tile() + # ヒートマップ scale_fill_gradientn(colors = c("blue", "green", "yellow", "red"), limits = c(0, p_max)) + # グラデーション scale_x_continuous(breaks = 0:M, labels = 0:M) + # x軸目盛 scale_y_continuous(breaks = 0:M, labels = 0:M) + # y軸目盛 coord_fixed(ratio = 1) + # アスペクト比 gganimate::transition_manual(parameter) + # フレーム labs(title = "Multinomial Distribution", subtitle = "{current_frame}", x = expression(x[1]), y = expression(x[2])) # ラベル # gif画像を作成 gganimate::animate(anime_prob_graph, nframes = length(phi_vals), fps = 100)

$\phi_2$の値が大きいほど$x_2$が大きく、$\phi_1$が大きくなるほど$x_1$が大きい確率が高くなるのを確認できます。
続いて、$\boldsymbol{\phi}$を固定して$M$を変更してみます。
・作図コード(クリックで展開)
# パラメータを指定 phi_v <- c(0.3, 0.5, 0.2) # 試行回数の最大値を指定 M_max <- 25 # Mの値ごとに分布を計算 anime_prob_df <- tidyr::tibble() for(M in 1:M_max) { # 数値型に変換 M <- as.numeric(M) # 作図用のxの値を作成 x_vals <- 0:M # 作図用のxの点を作成 x_points <- tidyr::tibble( x_1 = rep(x = x_vals, times = M + 1), # 確率変数の成分1 x_2 = rep(x = x_vals, each = M + 1) # 確率変数の成分2 ) %>% dplyr::mutate( x_3 = dplyr::if_else(condition = x_1 + x_2 < M, true = M - (x_1 + x_2), false = 0) ) %>% # 確率変数の成分3 as.matrix() # 確率変数の組み合わせごとに確率を計算 tmp_prob_df <- tidyr::tibble() for(i in 1:nrow(x_points)) { # 確率変数の値を取得 x_v <- x_points[i, ] # 多項分布の情報を格納 tmp_df <- tidyr::tibble( x_1 = x_v[1], # 確率変数の成分1 x_2 = x_v[2], # 確率変数の成分2 x_3 = x_v[3] # 確率変数の成分3 ) %>% dplyr::mutate( probability = dplyr::if_else( sum(x_v) == M, true = dmultinom(x = x_v, size = sum(x_v), prob = phi_v), false = 0 ) # (xize = Mにすべきだけど何故かエラーになる) ) # 確率 # 結果を結合 tmp_prob_df <- rbind(tmp_prob_df, tmp_df) } # フレーム切替用のラベルを付与 tmp_prob_df <- tmp_prob_df %>% dplyr::mutate( parameter = paste0("phi=(", paste0(round(phi_v, 2), collapse = ", "), "), M=", M) %>% as.factor() ) # 結果を結合 anime_prob_df <- rbind(anime_prob_df, tmp_prob_df) # 途中経過を表示 print(paste0("M=", M, " (", round(M / M_max * 100, 2), "%)")) } head(anime_prob_df)
## # A tibble: 6 x 5 ## x_1 x_2 x_3 probability parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 0 0 1 0.2 phi=(0.3, 0.5, 0.2), M=1 ## 2 1 0 0 0.3 phi=(0.3, 0.5, 0.2), M=1 ## 3 0 1 0 0.5 phi=(0.3, 0.5, 0.2), M=1 ## 4 1 1 0 0 phi=(0.3, 0.5, 0.2), M=1 ## 5 0 0 2 0.04 phi=(0.3, 0.5, 0.2), M=2 ## 6 1 0 1 0.12 phi=(0.3, 0.5, 0.2), M=2
for()ループを使って1:M_maxの値ごとに確率を計算して、anime_prob_dfに追加していきます。
gif画像を作成します。
# 最大値を指定 p_max <- 0.15 # アニメーション用の多項分布を作図 anime_prob_graph <- ggplot(data = anime_prob_df, mapping = aes(x = x_1, y = x_2, fill = probability)) + # データ geom_tile() + # ヒートマップ scale_fill_gradientn(colors = c("blue", "green", "yellow", "red"), limits = c(0, p_max)) + # グラデーション coord_fixed(ratio = 1) + # アスペクト比 gganimate::transition_manual(parameter) + # フレーム labs(title = "Multinomial Distribution", subtitle = "{current_frame}", x = expression(x[1]), y = expression(x[2])) # ラベル # gif画像を作成 gganimate::animate(anime_prob_graph, nframes = M_max, fps = 100)
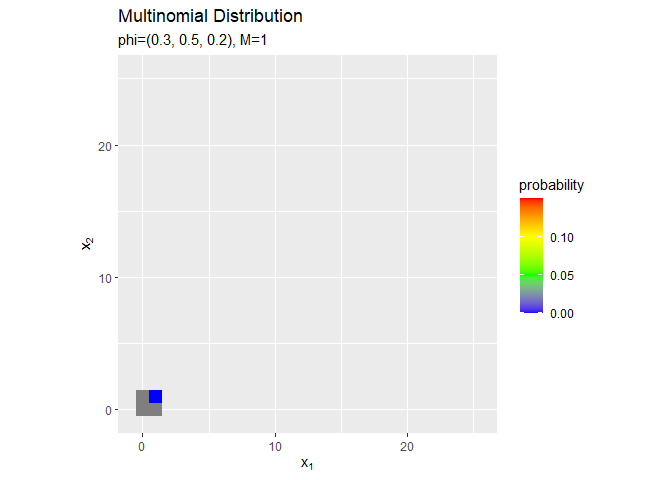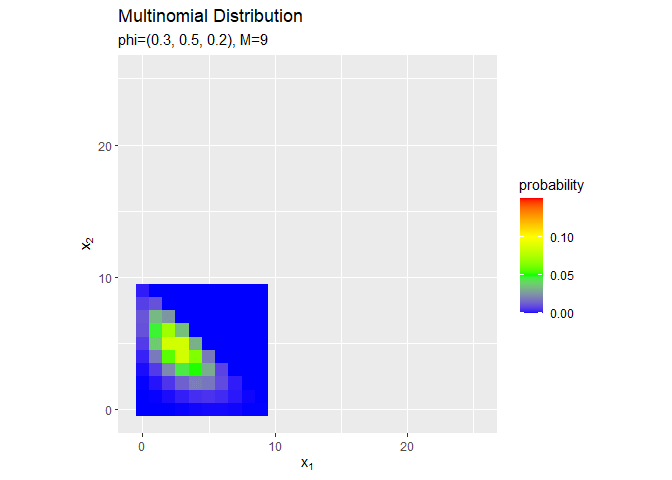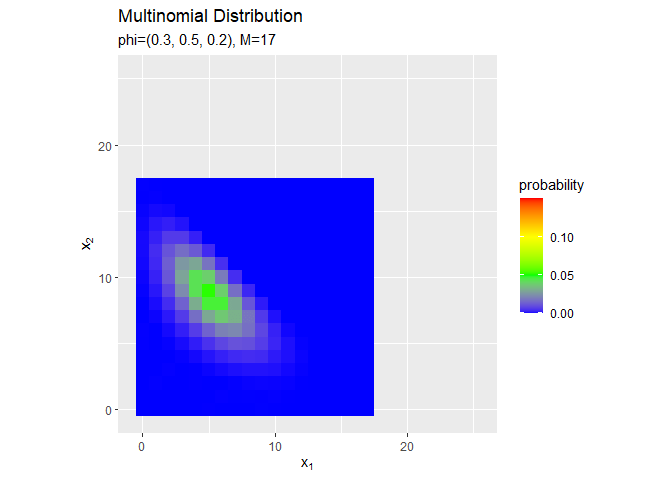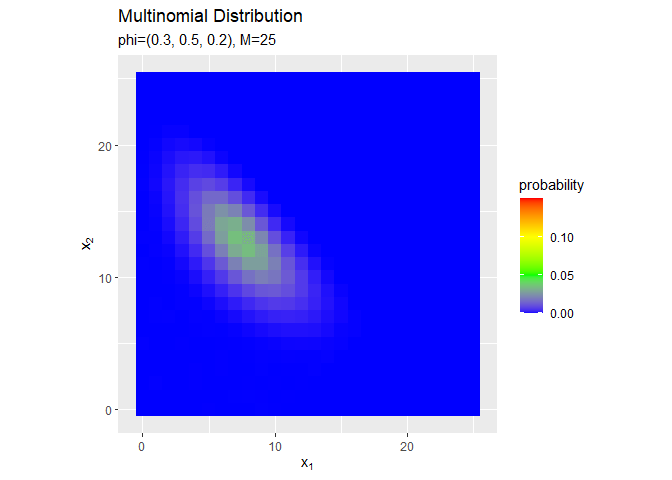
試行回数$M$が増えるのに従って、$x_1, x_2$が大きいほど確率が高くなる(山が右上に移動する)のを確認できます。ただし、$x_v$がとり得る値の範囲x_valsも広がっていくため、全体における相対的な山の位置は変わりません。
乱数の生成
多項分布の乱数を生成してヒストグラムを確認します。
パラメータを指定して、多項分布に従う乱数を生成します。
# パラメータを指定 phi_v <- c(0.3, 0.5, 0.2) # クラス数を取得 V <- length(phi_v) # 試行回数を指定 M <- 10 # データ数を指定 N <- 10000 # 多項分布に従う乱数を生成 x_nv <- rmultinom(n = N, size = M, prob = phi_v) %>% t() x_nv[1:5, ]
## [,1] [,2] [,3] ## [1,] 5 4 1 ## [2,] 1 6 3 ## [3,] 2 6 2 ## [4,] 2 7 1 ## [5,] 5 3 2
多項分布の乱数生成関数rmultinom()のデータ数(サンプルサイズ)の引数nにN、試行回数の引数sizeにM、出現確率の引数probにphi_vを指定します。
サンプルの値を集計します。
# 作図用のxの値を作成 x_vals <- 0:M # 作図用のxの点を作成 x_df <- tidyr::tibble( x_1 = rep(x = x_vals, times = M + 1), # 確率変数の成分1 x_2 = rep(x = x_vals, each = M + 1) # 確率変数の成分2 ) %>% dplyr::mutate( x_3 = dplyr::if_else(condition = x_1 + x_2 < M, true = M - (x_1 + x_2), false = 0) ) # 確率変数の成分3 # 乱数を集計して格納 freq_df <- tidyr::tibble( x_1 = x_nv[, 1], # 確率変数の成分1 x_2 = x_nv[, 2] # 確率変数の成分2 ) %>% # 乱数を格納 dplyr::count(x_1, x_2, name = "frequency") %>% # 乱数を集計 dplyr::right_join(x_df, by = c("x_1", "x_2")) %>% # 確率変数の全ての組み合わせを結合 dplyr::select(x_1, x_2, x_3, frequency) %>% # 頻度を測定 dplyr::mutate(frequency = tidyr::replace_na(frequency, 0)) %>% # サンプルにない場合のNAを0に置換 dplyr::mutate(proportion = frequency / N) %>% # 構成比を計算 dplyr::arrange(x_2, x_1) # 昇順に並び替え:(barplot3d用) head(freq_df)
## # A tibble: 6 x 5 ## x_1 x_2 x_3 frequency proportion ## <int> <int> <dbl> <dbl> <dbl> ## 1 0 0 10 0 0 ## 2 1 0 9 0 0 ## 3 2 0 8 0 0 ## 4 3 0 7 0 0 ## 5 4 0 6 1 0.0001 ## 6 5 0 5 1 0.0001
サンプリングした値x_nvの1列目と2列目をデータフレームに格納します。
count()で重複する値をカウントします。
サンプルx_nvにない値はデータフレームに保存されないため、0からMの全ての組み合わせを持つデータフレームx_dfを作成し、right_join()で結合します。
サンプルにない場合は頻度列frequencyが欠損値NAになるので、replace_na()で0に置換します。
得られた頻度frequencyをデータ数Nで割り、各値の構成比を計算してproportion列とします。
barplot3dではx軸とy軸の値が順番に並んでいる必要があるため、arrange()でx_1, x_2列を昇順に並び替えます。「グラフの作成」で作成したy軸の値ごとに色付けした棒グラフを見ると分かるように、$x_2 = 0$の$x_1 = 0$から$x_1 = M$の順に描画され、次に$x_2 = 1$の$x_1 = 0, \cdots, M$と描画され、$x_1 = M, x_2 = M$が最後の点になります。これに対応するように並び替えるにはarrange(x_2, x_1)と指定する必要があります。
ggplot2による作図
出現頻度をヒートマップで可視化します。
# サンプルのヒストグラムを作成 ggplot(data = freq_df, mapping = aes(x = x_1, y = x_2, fill = frequency)) + # データ geom_tile() + # ヒストグラム scale_fill_gradientn(colors = c("blue", "green", "yellow", "red")) + # グラデーション scale_x_continuous(breaks = 0:M, labels = 0:M) + # x軸目盛 scale_y_continuous(breaks = 0:M, labels = 0:M) + # y軸目盛 coord_fixed(ratio = 1) + # アスペクト比 labs(title = "Multinomial Distribution", subtitle = paste0("phi=(", paste0(phi_v, collapse = ", "), "), M=", M, ", N=", N), x = expression(x[1]), y = expression(x[2])) # ラベル
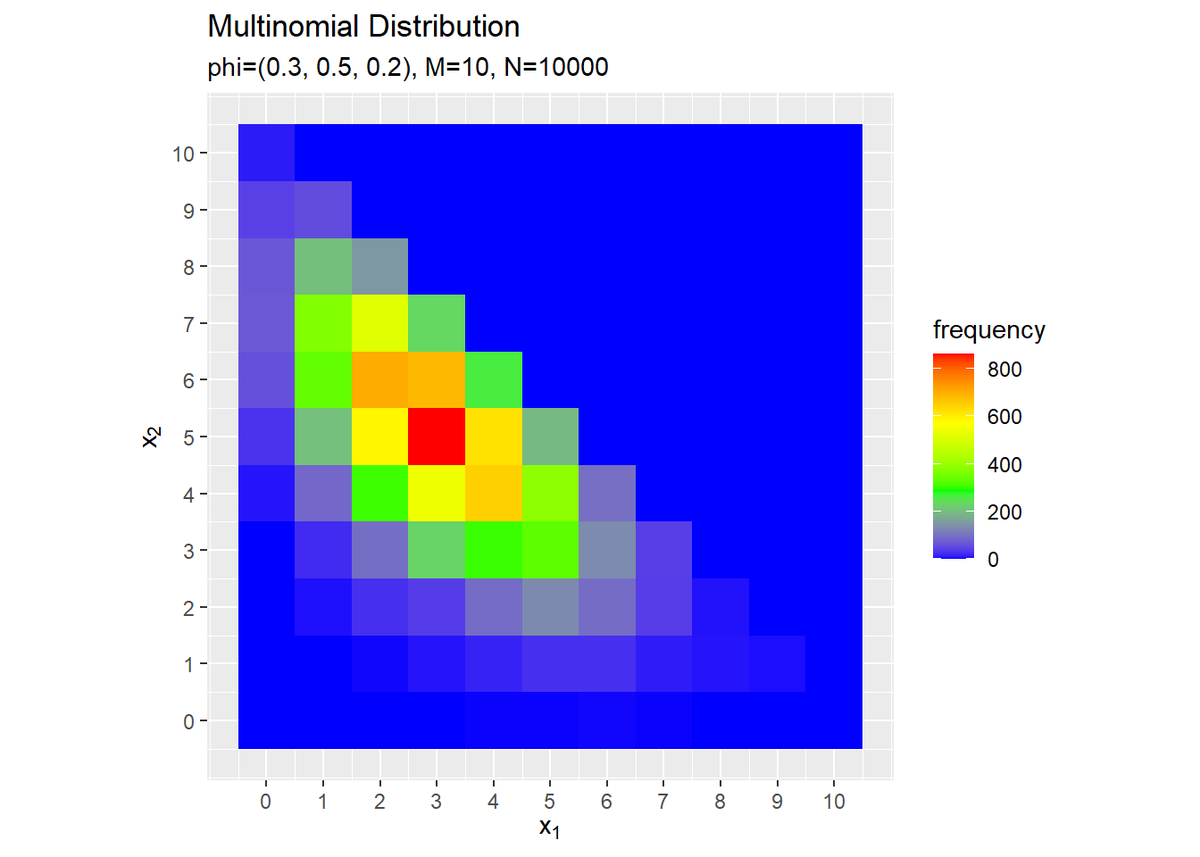
構成比を分布と重ねて描画します。
# 構成比と確率の最大値を取得 p_max <- max(freq_df[["proportion"]], prob_df[["probability"]]) # サンプルの構成比を作図 ggplot() + geom_tile(data = freq_df, mapping = aes(x = x_1, y = x_2, fill = proportion), alpha = 0.9) + # 構成比 geom_tile(data = prob_df, mapping = aes(x = x_1, y = x_2, color = probability), alpha = 0, size = 1, linetype = "dashed") + # 真の分布 scale_fill_gradientn(colors = c("blue", "green", "yellow", "red"), limits = c(0, p_max)) + # タイルのグラデーション scale_color_gradientn(colors = c("blue", "green", "yellow", "red"), limits = c(0, p_max)) + # 枠線のグラデーション scale_x_continuous(breaks = 0:M, labels = 0:M) + # x軸目盛 scale_y_continuous(breaks = 0:M, labels = 0:M) + # y軸目盛 coord_fixed(ratio = 1) + # アスペクト比 guides(color = FALSE) + # 凡例 labs(title = "Multinomial Distribution", subtitle = paste0("phi=(", paste0(phi_v, collapse = ", "), "), M=", M, ", N=", N), x = expression(x[1]), y = expression(x[2])) # ラベル
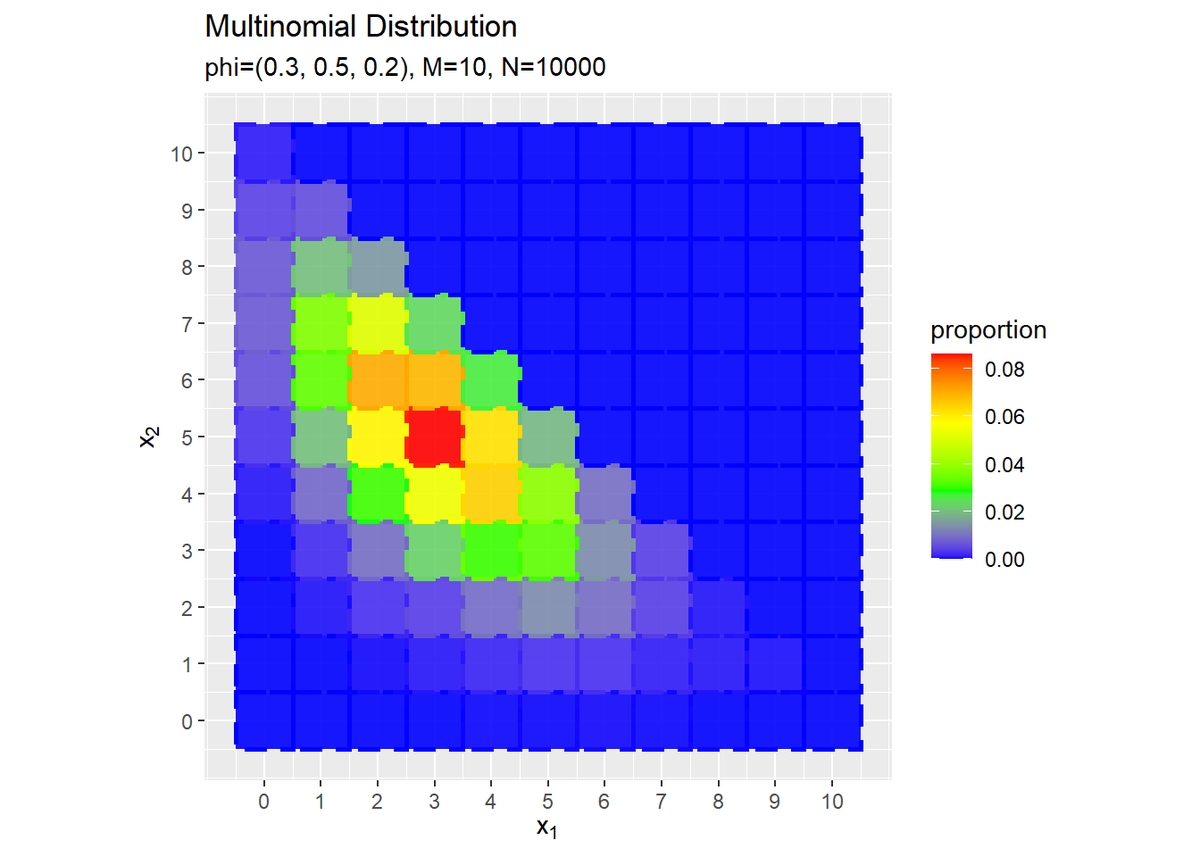
真の分布を破線で表示します。データ数が十分に増えると分布のグラフに形が近づきます。
barplot3dによる作図
サンプルの頻度と分布のそれぞれの値に応じたカラーコードを作成します。
# サンプルの構成比による色付けを作成 p <- freq_df[["proportion"]] heat_idx <- round((1 - p / max(p)) * 100) + 1 heat_prop <- heat.colors(101)[heat_idx] # 分布の確率による色付けを作成 p <- prob_df[["probability"]] heat_idx <- round((1 - p / max(p)) * 100) + 1 heat_prob <- heat.colors(101)[heat_idx]
出現頻度を3D棒グラフで可視化します。
# サンプルのヒストグラムを作成 barplot3d::barplot3d( rows = M + 1, cols = M + 1, z = freq_df[["frequency"]], topcolors = heat_prop, sidecolors = heat_prop, alpha = 0.1, xlabels = as.character(0:M), ylabels = as.character(0:M), xsub = "x1", ysub = "x2", zsub = "frequency", scalexy = 100, theta = 30, phi = 30 )
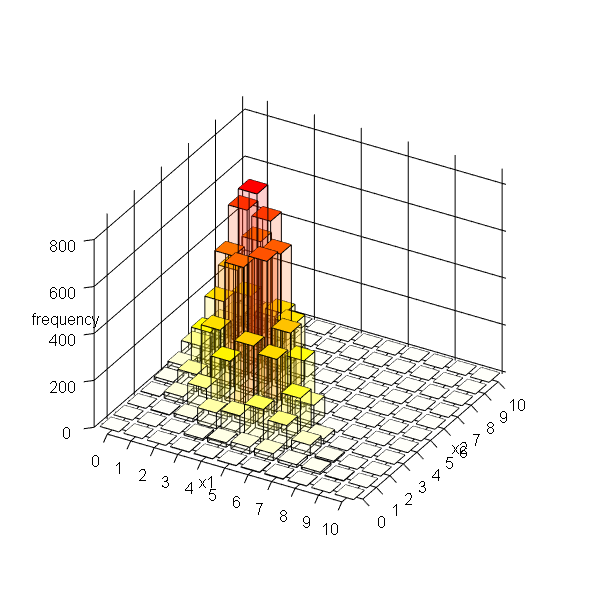
構成比を描画します。
# サンプルの構成比を作図 barplot3d::barplot3d( rows = M + 1, cols = M + 1, z = freq_df[["proportion"]], topcolors = heat_prop, sidecolors = heat_prop, linecolors = heat_prob, alpha = 0.1, xlabels = as.character(0:M), ylabels = as.character(0:M), xsub = "x1", ysub = "x2", zsub = "proportion", scalexy = 0.01, theta = 30, phi = 30 )
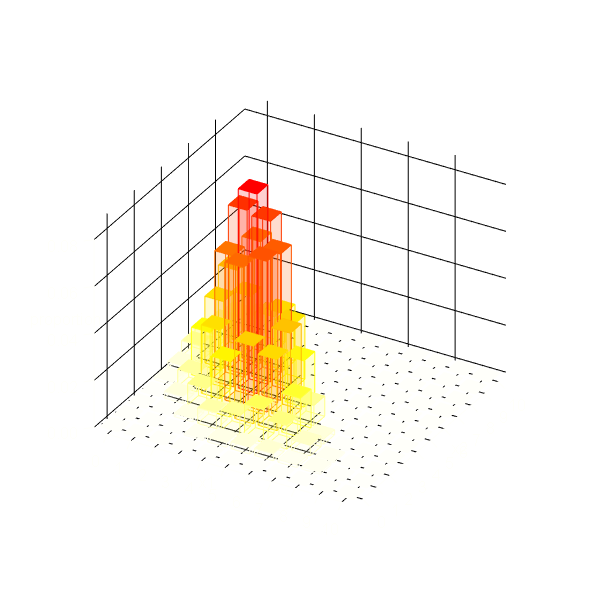
辺の色は元の分布の確率によって色付けしています。元の分布において確率が0に近いと辺の色が白になるので、右上などの棒(の上の面)が見えなくなっています。目盛やラベルが消えるのは謎の仕様(?)です。
資料作りの都合上、ggplot2による図とは別のデータです。
アニメーションによる可視化
サンプルサイズとヒストグラムの変化をアニメーションで確認します。
・作図コード(クリックで展開)
# データ数を指定 N <- 300 # z軸の最大値を指定 p_max <- 0.1 # 乱数を1つずつ生成 x_nv <- matrix(NA, nrow = N, ncol = V) anime_freq_df <- tidyr::tibble() anime_data_df <- tidyr::tibble() anime_prob_df <- tidyr::tibble() for(n in 1:N) { # 多項分布に従う乱数を生成 x_nv[n, ] <- rmultinom(n = 1, size = M, prob = phi_v) # n個の乱数を集計して格納 tmp_freq_df <- tidyr::tibble( x_1 = x_nv[, 1], # 確率変数の成分1 x_2 = x_nv[, 2] # 確率変数の成分2 ) %>% # 乱数を格納 dplyr::count(x_1, x_2, name = "frequency") %>% # 乱数を集計 dplyr::right_join(prob_df, by = c("x_1", "x_2")) %>% # 確率変数の全ての組み合わせを結合 dplyr::select(x_1, x_2, frequency) %>% # 頻度を測定 dplyr::mutate(frequency = tidyr::replace_na(frequency, 0)) %>% # サンプルにない場合のNAを0に置換 dplyr::mutate(proportion = frequency / n) # 構成比を計算 # ラベル用のテキストを作成 label_text <- paste0("phi=(", paste0(phi_v, collapse = ", "), "), M=", M, ", N=", n) # フレーム切替用のラベルを付与 tmp_freq_df <- tmp_freq_df %>% dplyr::mutate(parameter = as.factor(label_text)) # n番目の乱数を格納 tmp_data_df <- tidyr::tibble( x_1 = x_nv[n, 1], # サンプルの成分1 x_2 = x_nv[n, 2], # サンプルの成分2 parameter = as.factor(label_text) # フレーム切替用のラベル ) # n回目のラベルを付与 tmp_prob_df <- prob_df %>% dplyr::mutate(parameter = as.factor(label_text)) # 結果を結合 anime_freq_df <- rbind(anime_freq_df, tmp_freq_df) anime_data_df <- rbind(anime_data_df, tmp_data_df) anime_prob_df <- rbind(anime_prob_df, tmp_prob_df) } head(anime_freq_df)
## # A tibble: 6 x 5 ## x_1 x_2 frequency proportion parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 3 4 1 1 phi=(0.3, 0.5, 0.2), M=10, N=1 ## 2 0 0 0 0 phi=(0.3, 0.5, 0.2), M=10, N=1 ## 3 1 0 0 0 phi=(0.3, 0.5, 0.2), M=10, N=1 ## 4 2 0 0 0 phi=(0.3, 0.5, 0.2), M=10, N=1 ## 5 3 0 0 0 phi=(0.3, 0.5, 0.2), M=10, N=1 ## 6 4 0 0 0 phi=(0.3, 0.5, 0.2), M=10, N=1
乱数を1つず生成して、結果をanime_***_dfに追加していきます。
ヒストグラムのアニメーションを作成します。
# アニメーション用のサンプルのヒストグラムを作成 anime_freq_graph <- ggplot() + # データ geom_tile(data = anime_freq_df, mapping = aes(x = x_1, y = x_2, fill = frequency)) + # ヒストグラム geom_point(data = anime_data_df, mapping = aes(x = x_1, y = x_2), color = "orange", size = 5) + scale_fill_gradientn(colors = c("blue", "green", "yellow", "red")) + # グラデーション scale_x_continuous(breaks = 0:M, labels = 0:M) + # x軸目盛 scale_y_continuous(breaks = 0:M, labels = 0:M) + # y軸目盛 coord_fixed(ratio = 1) + # アスペクト比 gganimate::transition_manual(parameter) + # フレーム labs(title = "Multinomial Distribution", subtitle = "{current_frame}", x = expression(x[1]), y = expression(x[2])) # ラベル # gif画像を作成 gganimate::animate(anime_freq_graph, nframes = N, fps = 100)
構成比のアニメーションを作成します。
# アニメーション用のサンプルの構成比を作成 anime_prop_graph <- ggplot() + # データ geom_tile(data = anime_freq_df, mapping = aes(x = x_1, y = x_2, fill = proportion), alpha = 0.9) + # 構成比 geom_tile(data = anime_prob_df, mapping = aes(x = x_1, y = x_2, color = probability), alpha = 0, size = 0.7, linetype = "dashed") + # 真の分布 geom_point(data = anime_data_df, mapping = aes(x = x_1, y = x_2), color = "orange", size = 5) + # 真の分布 scale_fill_gradientn(colors = c("blue", "green", "yellow", "red"), limits = c(0, p_max)) + # タイルのグラデーション scale_color_gradientn(colors = c("blue", "green", "yellow", "red"), limits =c(0, p_max)) + # 枠線のグラデーション scale_x_continuous(breaks = 0:M, labels = 0:M) + # x軸目盛 scale_y_continuous(breaks = 0:M, labels = 0:M) + # y軸目盛 coord_fixed(ratio = 1) + # アスペクト比 guides(color = FALSE) + # 凡例 gganimate::transition_manual(parameter) + # フレーム labs(title = "Multinomial Distribution", subtitle = "{current_frame}", x = expression(x[1]), y = expression(x[2])) # ラベル # gif画像を作成 gganimate::animate(anime_prop_graph, nframes = N, fps = 100)
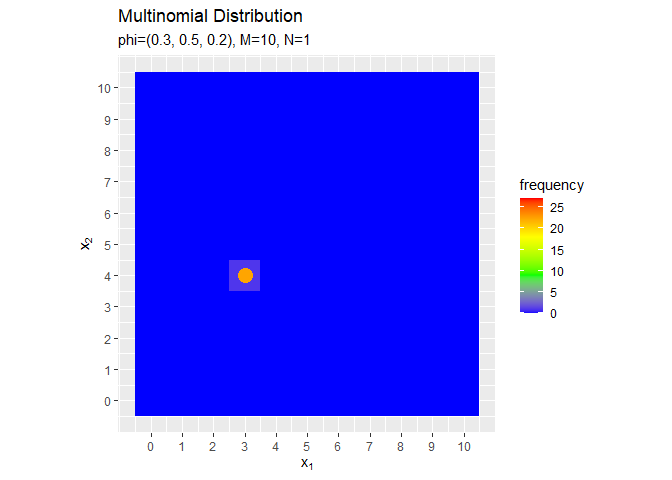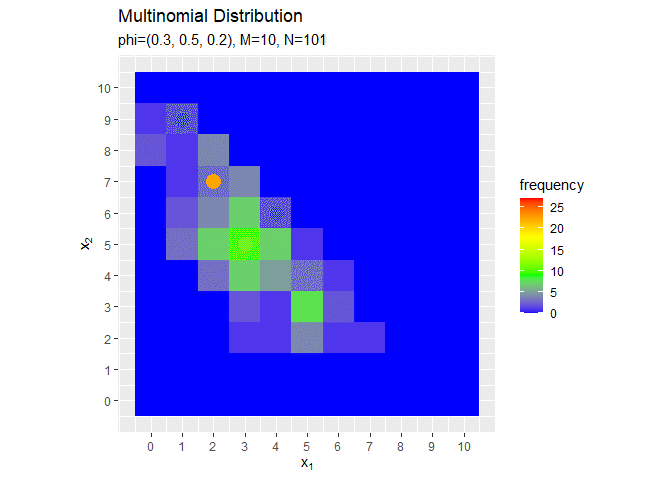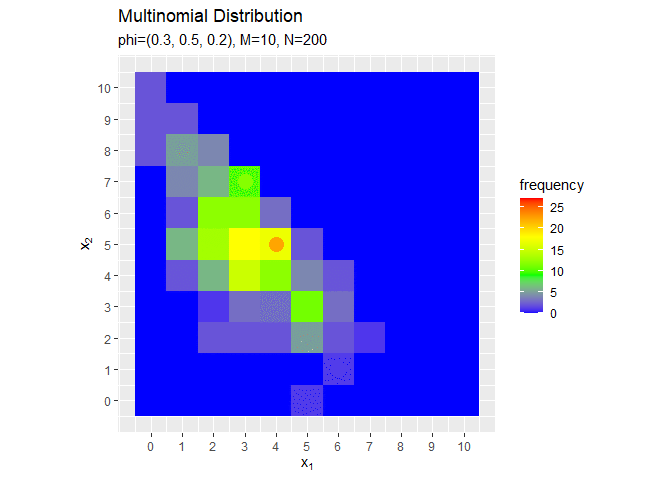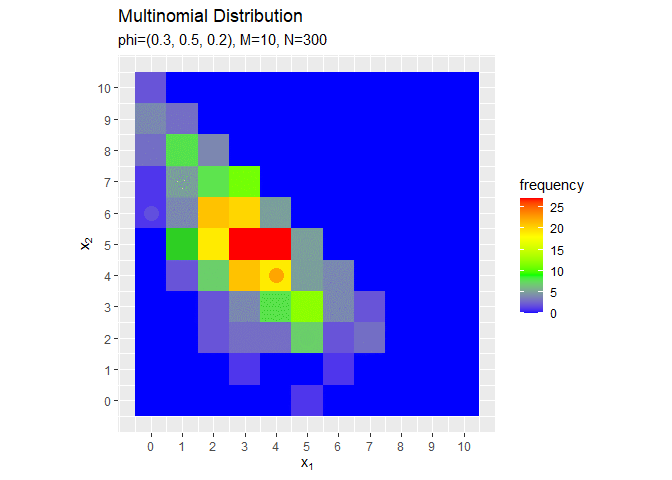

サンプルが増えるに従って、真の分布に近付いていくのを確認できます(?)。(最大値p_maxを越えたらグレーになるのをなんとかしたい。)
以上で、多項分布を確認できました。
参考文献
- 岩田具治『トピックモデル』(機械学習プロフェッショナルシリーズ)講談社,2015年.
おわりに
加筆修正の際に青トピシリーズから独立させました。
ggplot2で3Dのグラフを作りたい。よく分からなかったという人はPython版も見てください、、
【次の内容】
つづく