【R】ベータ関数の作図

はじめに

　機械学習で登場する確率分布について色々な角度から理解したいシリーズです。

　ベータ関数のグラフをR言語で作成します。

【前の内容】

www.anarchive-beta.com

【他の記事一覧】

www.anarchive-beta.com

【この記事の内容】

ベータ関数の作図

　ベータ関数(Beta Function)の計算を確認して、グラフを作成します。

　利用するパッケージを読み込みます。

# 利用するパッケージ
library(tidyverse)

定義式の確認

　まずは、ベータ関数の定義式を確認します。

　ベータ関数は、次の式で定義されます。

$$ B(\alpha,\beta) = \int_0^1 x^{\alpha-1} (1 - x)^{\beta-1} dx = \frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha + \beta)} $$

　ここで、$\Gamma(x)$はガンマ関数です。ガンマ関数については「ガンマ関数の性質の導出 - からっぽのしょこ」を参照してください。

ベータ関数の計算

　続いて、ベータ関数の計算方法を確認します。

　ガンマ関数gamma()を使って計算します。

# 変数の値を指定
a <- 2.1
b <- 3.2

# ガンマ関数によりベータ関数の計算
z <- gamma(a) * gamma(b) / gamma(a + b)
z

## [1] 0.06661713

　ガンマ関数の定義式

$$ B(\alpha,\beta) = \frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha + \beta)} $$

を計算します。

　対数ガンマ関数lgamma()を使って計算します。

# ガンマ関数によりベータ関数の計算
log_z <- lgamma(a) + lgamma(b) - lgamma(a + b)
z <- exp(log_z)
z

## [1] 0.06661713

　対数をとった定義式

$$ \log B(\alpha,\beta) = \log \Gamma(\alpha) + \log \Gamma(\beta) - \log \Gamma(\alpha + \beta) $$

を計算します。
　計算結果の指数をとります。

$$ B(\alpha,\beta) = \exp \Bigr( \log B(\alpha,\beta) \Bigr) $$

　指数と対数の性質より$\exp(\log x) = x$です。

　ベータ関数beta()を使って計算します。

# ベータ関数の計算
z <- beta(a, b)
z

## [1] 0.06661713

　対数ベータ関数lbeta()を使って計算します。

# 対数ベータ関数の計算
log_z <- lbeta(a, b)
z <- exp(log_z)
z

## [1] 0.06661713

　$x$が0または負の整数の場合は計算できません。

# ベータ関数の計算:(計算できない)
beta(2.5, 0); beta(-3.5, 2.5)

## [1] Inf
## [1] NaN

　負の値の計算ができないのは実装上の理由で、定義・数式的には計算できます。

　ベータ関数の計算を確認できました。次は、ベータ関数を可視化します。

グラフの作成

　ggplot2パッケージを利用して、ベータ関数のグラフを作成します。

非負の値の場合

　まずは、0より大きい実数$\alpha, \beta$を範囲として、ベータ関数を計算します。

# x軸とy軸の値を指定:(a > 0, b > 0)
a_vals <- seq(from = 0.01, to = 3, by = 0.01)
b_vals <- seq(from = 0.01, to = 3, by = 0.01)
a_vals[1:5]; b_vals[1:5]

## [1] 0.01 0.02 0.03 0.04 0.05
## [1] 0.01 0.02 0.03 0.04 0.05

　x軸($\alpha$)の値を作成してa_vals、y軸($\beta$)の値を作成してb_valsとします。

　格子点に変換します。

# 格子状の点を作成
points_df  <- expand.grid(alpha = a_vals, beta = b_vals)
a_grid <- points_df[["alpha"]]
b_grid <- points_df[["beta"]]
head(points_df)

##   alpha beta
## 1  0.01 0.01
## 2  0.02 0.01
## 3  0.03 0.01
## 4  0.04 0.01
## 5  0.05 0.01
## 6  0.06 0.01

　expand.grid()でa_vals, b_valsの全ての組み合わせを持つデータフレームを作成して、各列を取り出してa_grid, b_gridとします。引数名に指定した文字列が列名になります。

　ベータ関数を計算します。

# ベータ関数の計算
z_grid <- beta(a_grid, b_grid)

# 値を格納
beta_df <- tidyr::tibble(
  alpha = a_grid, 
  beta = b_grid, 
  z = z_grid
)
head(beta_df)

## # A tibble: 6 x 3
##   alpha  beta     z
##   <dbl> <dbl> <dbl>
## 1  0.01  0.01  200.
## 2  0.02  0.01  150.
## 3  0.03  0.01  133.
## 4  0.04  0.01  125.
## 5  0.05  0.01  120.
## 6  0.06  0.01  117.

　作成したa_grid, b_gridを用いて、beta()でベータ関数の計算をします。
　作図用に、a_grid, b_gridと各要素に対応する計算結果をデータフレームに格納します。

　ベータ関数のグラフを作成します。

# ベータ関数を作図
ggplot(data = beta_df, mapping = aes(x = alpha, y = beta, z = z, color = ..level..)) + 
  geom_contour() + # 等高線図
  scale_color_distiller(palette = "Spectral") + # 等高線の色
  coord_fixed(ratio = 1) + # アスペクト比
  labs(title = "Beta Function", 
       x = expression(alpha), y = expression(beta), color = expression(Beta(alpha, beta))) # ラベル

# ベータ関数を作図
ggplot(data = beta_df, mapping = aes(x = alpha, y = beta, z = z, fill = ..level..)) + 
  geom_contour_filled() + # 塗りつぶし等高線図
  scale_fill_brewer(palette = "Spectral", direction = -1) + # 塗りつぶしの色
  coord_fixed(ratio = 1) + # アスペクト比
  labs(title = "Beta Function", 
       x = expression(alpha), y = expression(beta), fill = expression(Beta(alpha, beta))) # ラベル

ベータ関数のグラフ

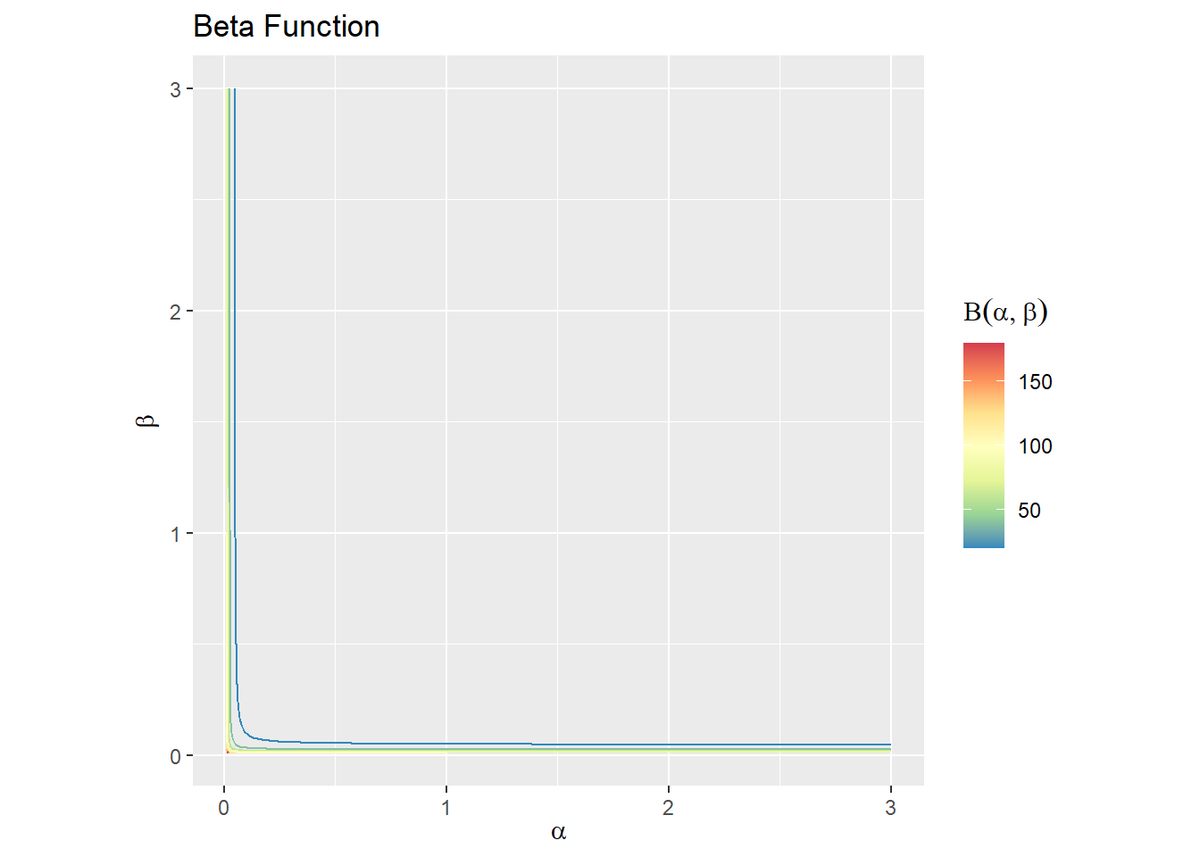
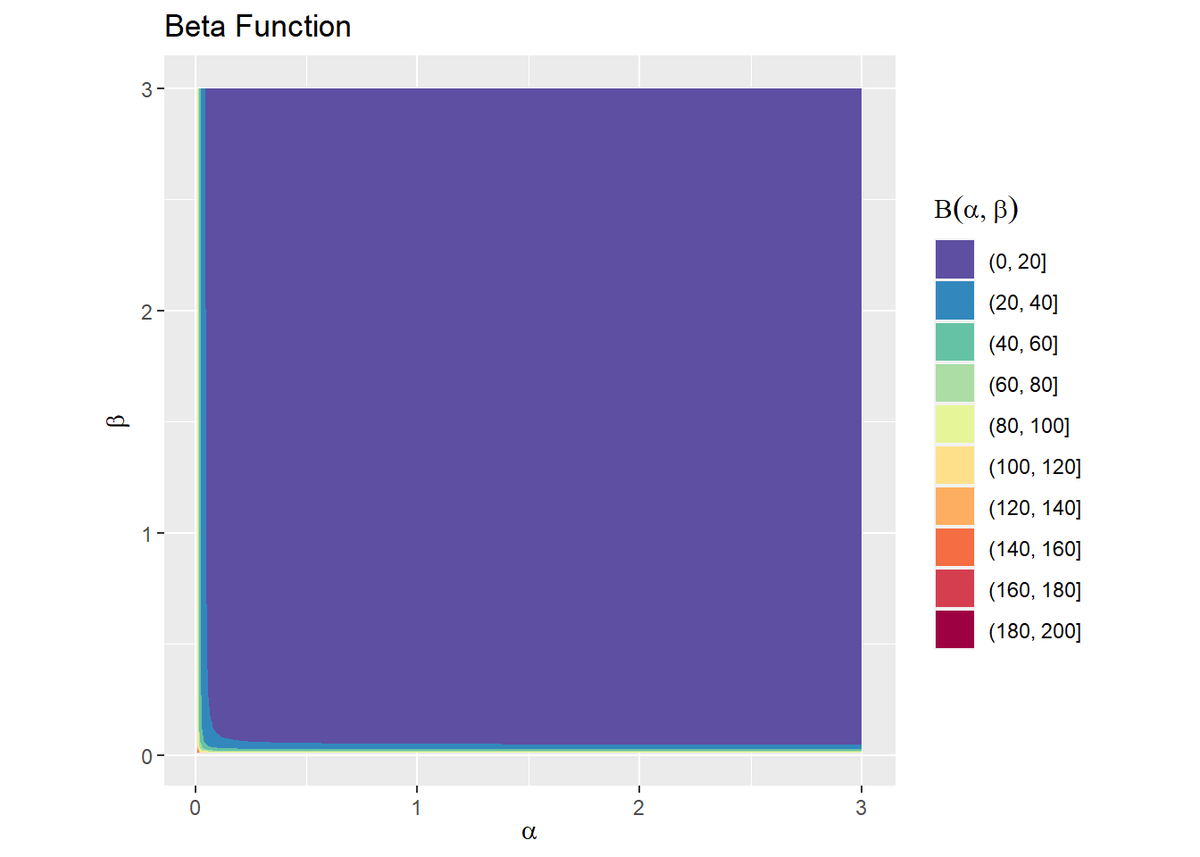
　$\alpha = 0$と$\beta = 0$の垂線に漸近しているのを分かってほしい。

負の値を含む場合

　続いて、負の実数も含めて、ベータ関数を計算します。

# x軸とy軸の値を指定:(0と負の整数は計算できない)
a_vals <- seq(from = -2, to = 2, by = 0.01)
b_vals <- seq(from = -2, to = 2, by = 0.01)

# 格子状の点を作成
points_df  <- expand.grid(alpha = a_vals, beta = b_vals)
a_grid <- points_df[["alpha"]]
b_grid <- points_df[["beta"]]

# ベータ関数の計算
z_grid <- gamma(a_grid) * gamma(b_grid) / gamma(a_grid + b_grid)

# 値を格納
beta_df <- tidyr::tibble(
  alpha = a_grid, 
  beta = b_grid, 
  z = z_grid
)
head(beta_df)

## # A tibble: 6 x 3
##   alpha  beta     z
##   <dbl> <dbl> <dbl>
## 1 -2       -2   NaN
## 2 -1.99    -2   NaN
## 3 -1.98    -2   NaN
## 4 -1.97    -2   NaN
## 5 -1.96    -2   NaN
## 6 -1.95    -2   NaN

　ベータ関数beta()では負の値を計算できないので、ガンマ関数gamma()で計算します。値が大きい場合は対数ガンマ関数lgamma()を使ってください。
　0のとき計算結果がInf、負の整数のとき計算結果がNaNになります。

　ベータ関数のグラフを作成します。

# 閾値を指定
threshold <- 10

# ベータ関数を作図
ggplot(data = beta_df, mapping = aes(x = alpha, y = beta, z = z, color = ..level..)) + 
  geom_contour() + # 等高線図:(デフォルト)
  #geom_contour(breaks = seq(from = -threshold, to = threshold, length.out = 10)) + # 等高線図:(線の位置を指定)
  scale_color_distiller(palette = "Spectral") + # 等高線の色
  coord_fixed(ratio = 1) + # アスペクト比
  labs(title = "Beta Function", 
       x = expression(alpha), y = expression(beta), color = expression(Beta(alpha, beta))) # ラベル

# ベータ関数を作図
ggplot(data = beta_df, mapping = aes(x = alpha, y = beta, z = z, fill = ..level..)) + 
  geom_contour_filled() + # 塗りつぶし等高線図:(デフォルト)
  #geom_contour_filled(breaks = seq(from = -threshold, to = threshold, length.out = 10)) + # 塗りつぶし等高線図:(線の位置を指定)
  scale_fill_brewer(palette = "Spectral", direction = -1) + # 塗りつぶしの色
  coord_fixed(ratio = 1) + # アスペクト比
  labs(title = "Beta Function", 
       x = expression(alpha), y = expression(beta), fill = expression(Beta(alpha, beta))) # ラベル

　等高線を引くz軸の値をbreaks引数に指定します。この例では、-thresholdからthresholdまでの値を等間隔に区切ります。

ベータ関数のグラフ

ベータ関数のグラフ

ベータ関数のグラフ

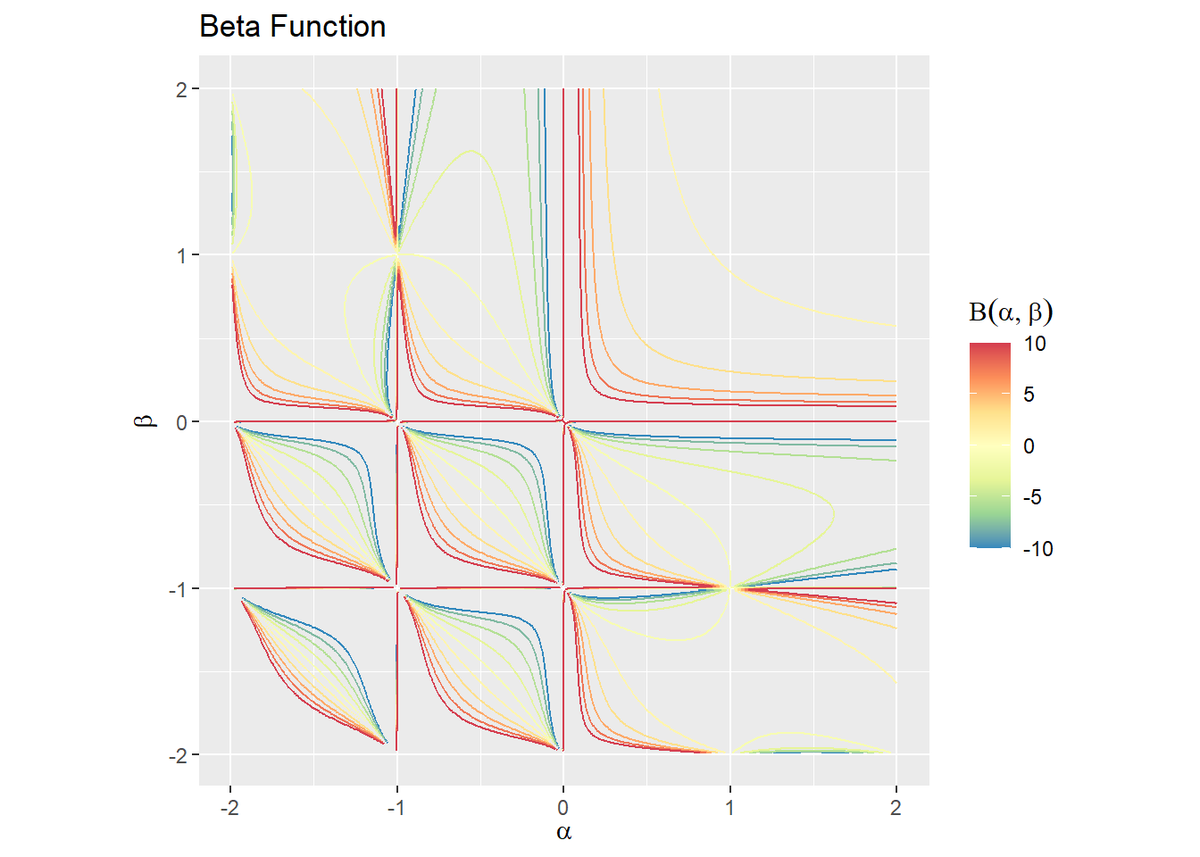
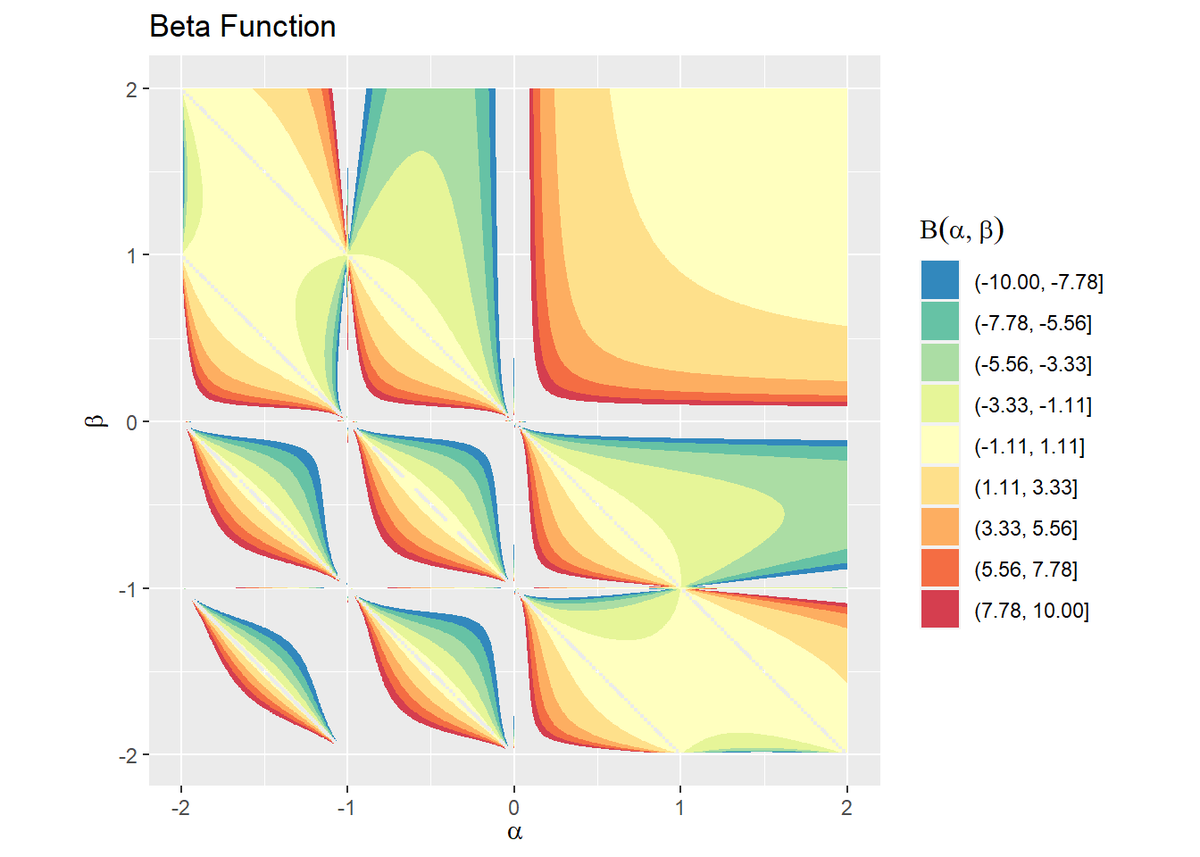
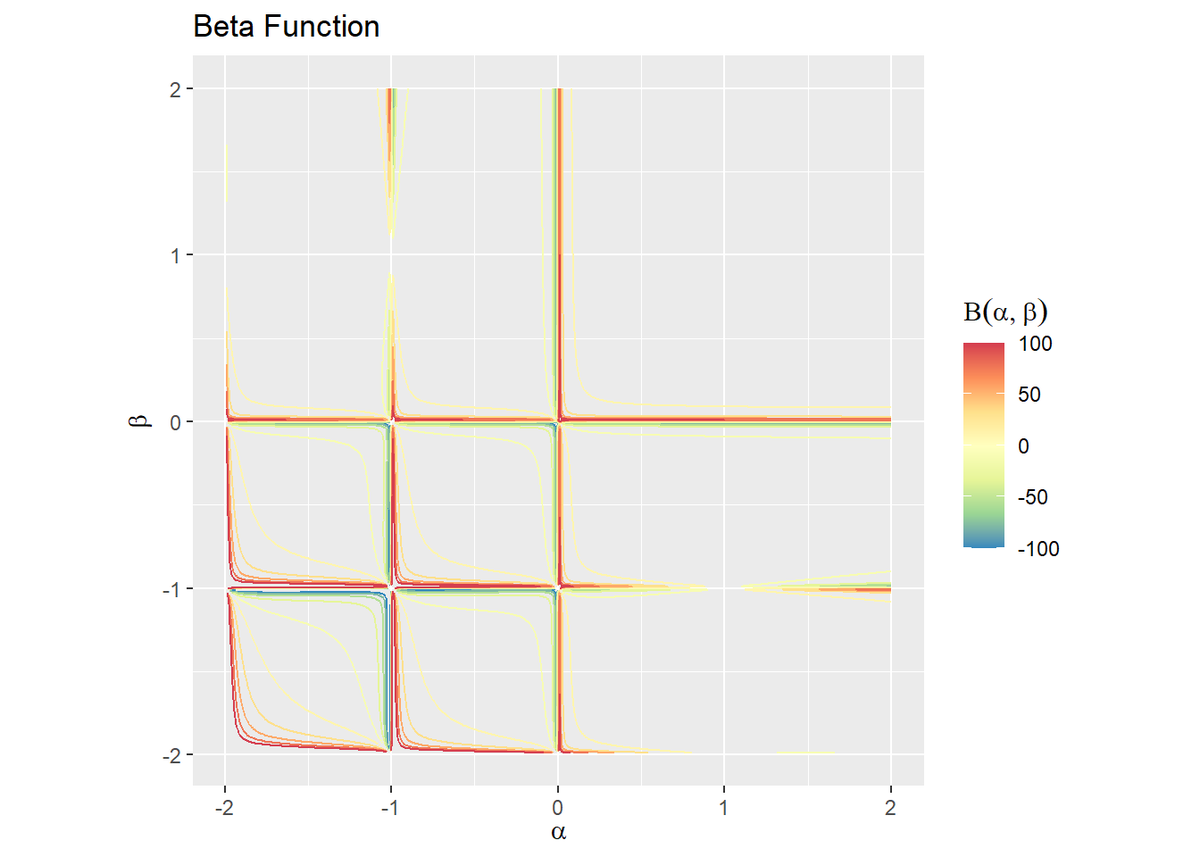
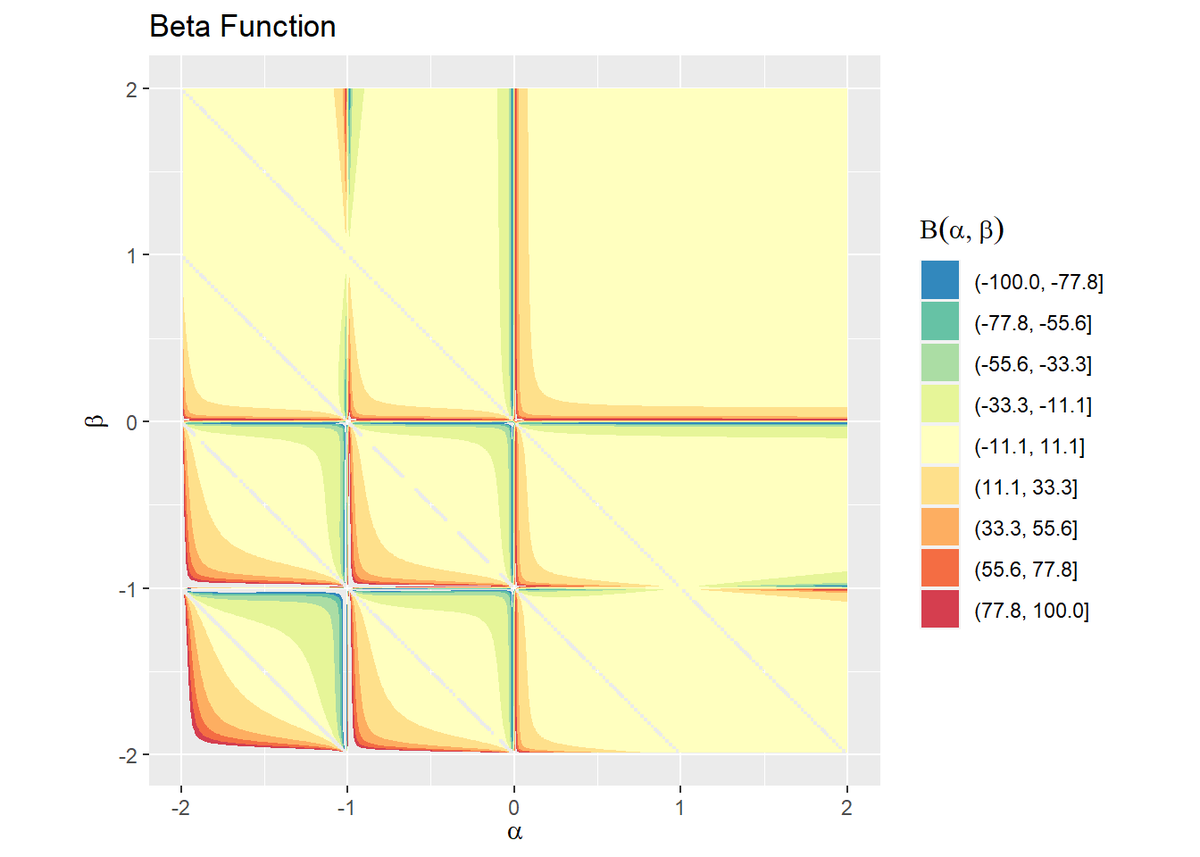
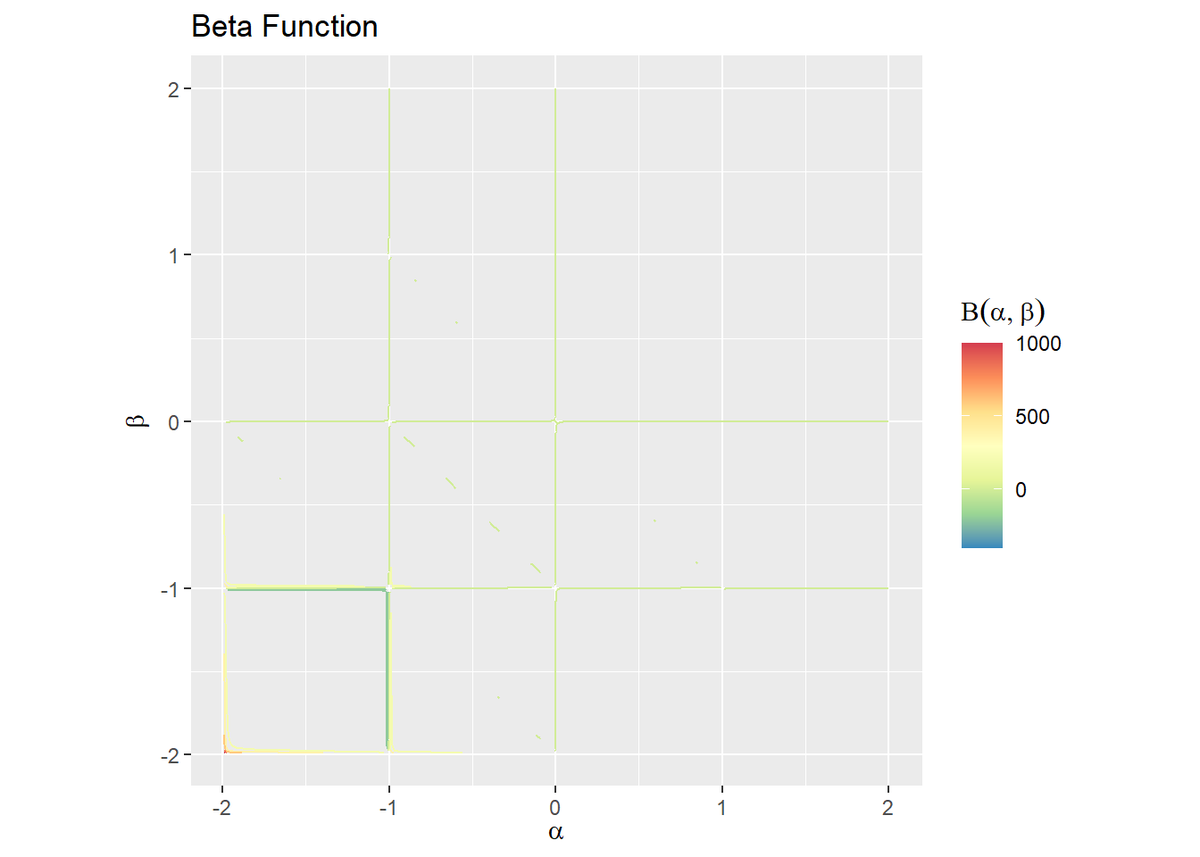
　各軸の値が負の整数と0の点において、不連続なグラフになっているのが分かります。

参考文献

• 岩田具治『トピックモデル』(機械学習プロフェッショナルシリーズ)講談社,2015年.

おわりに

　ggplot2で3次元グラフを描きたい(n度目)。

【次の内容】

つづく