はじめに
『ゼロから作るDeep Learning 4 ――強化学習編』の独学時のまとめノートです。初学者の補助となるようにゼロつくシリーズの4巻の内容に解説を加えていきます。本と一緒に読んでください。
この記事は、5.4.3項から5.4.5項の内容です。モンテカルロ法による方策制御(行動価値関数と方策の推定)と方策反復法を実装します。
【前節の内容】
【他の記事一覧】
【この記事の内容】
5.4 モンテカルロ法による方策反復法
前項までで、モンテカルロ法による方策制御の基本的な処理を実装しました。この項からは、推定方法を改善します。
利用するライブラリを読み込みます。
# ライブラリを読み込み import numpy as np from collections import defaultdict # 追加ライブラリ import matplotlib.pyplot as plt from matplotlib.colors import LinearSegmentedColormap from matplotlib.animation import FuncAnimation
推移をアニメーションで確認するのにanimationモジュールを利用します。不要であれば省略してください。
また、3×4マスのグリッドワールドのクラスGridWorldを読み込みます。
# 実装済みのクラスと関数を読み込み import sys sys.path.append('../deep-learning-from-scratch-4-master') from common.gridworld import GridWorld
実装済みクラスの読み込みについては「3.6.1:MNISTデータセットの読み込み【ゼロつく1のノート(Python)】 - からっぽのしょこ」、GridWorldクラスについては「4.2.1:GridWorldクラスの実装:評価と改善に関するメソッド【ゼロつく4のノート】 - からっぽのしょこ」「4.2.1:GridWorldクラスの実装:可視化に関するメソッド【ゼロつく4のノート】 - からっぽのしょこ」を参照してください。
5.4.3 ε-greedy法(1つ目の修正)
5.4.2項で実装したgreedy法では、少ないサンプルに依存してしまい上手く推定できませんでした。そこで、ε-greedy法により方策を改善することにします。低い確率でランダムな行動を取ることで、行動価値関数を推定するためのサンプルを得ます。
・処理の確認
改善版のgreedy_probs()の内部で行う処理を確認します。
例として、ダミーの行動価値関数のディクショナリを作成しておきます。
# 状態を指定 state = (1, 2) # 行動の種類数を設定 action_size = 4 # (仮の)行動価値関数を作成 Q = {(state, action): np.random.rand() for action in range(action_size)} print(list(Q.keys())) # 指定した状態における行動番号 print(np.round(list(Q.values()), 3)) # 指定した状態における行動確率
[((1, 2), 0), ((1, 2), 1), ((1, 2), 2), ((1, 2), 3)]
[0.413 0.771 0.326 0.955]
状態を指定して、上下左右の4つの行動に対する値を格納します。
行動価値を取り出してリストに格納します。
# 行動ごとの行動価値を抽出 qs = [Q[(state, action)] for action in range(action_size)] print(np.round(qs, 3))
[0.413 0.771 0.326 0.955]
リスト内包表記を使って、順番にキーを指定して値を取り出します。
行動価値が最大の行動を抽出します。
# 行動価値が最大の行動番号を抽出 max_action = np.argmax(qs) print(max_action)
3
要素のインデックスが行動番号に対応しています。
確率$\epsilon$でランダムに行動し、$1 - \epsilon$で行動価値が最大となる行動を取る確率論的方策を作成します。
# ランダムに行動する確率を指定 epsilon = 0.1 # 確率εでランダムに行動するための各行動確率を計算 base_prob = epsilon / action_size # 方策の受け皿を作成 action_probs = {action: base_prob for action in range(action_size)} print(action_probs) # 行動価値が最大の行動の確率を1-εに設定 action_probs[max_action] += (1.0 - epsilon) print(action_probs) print(np.sum(list(action_probs.values())))
{0: 0.025, 1: 0.025, 2: 0.025, 3: 0.025}
{0: 0.025, 1: 0.025, 2: 0.025, 3: 0.925}
1.0
ランダムに行動する確率を$\epsilon$、行動の種類数を$S$とすると、ランダムに各行動を取る確率は$\frac{\epsilon}{S}$です。確率分布を満たすには総和が1となる必要があるので、行動価値が最大となる行動を取る確率は$1 - \epsilon + \frac{\epsilon}{S}$となります。
ランダムに行動する確率epsilonを行動の種類数action_sizeで割った値をbase_probとします。全ての値がbase_probとなるようにディクショナリを作成して、max_actionの値に1.0 - epsilon加えます。
ε-greedy化した方策(確率分布)を試してみましょう。
# 行動番号・行動確率を取得 actions = list(action_probs.keys()) probs = list(action_probs.values()) # 記録用のリストを初期化 action_lt = [] # 行動を生成 for _ in range(1000): # 行動を出力 action = np.random.choice(a=actions, p=probs) # 行動を記録 action_lt.append(action) # 結果を確認 print(np.sum(action_lt == max_action)) # greedyな行動 print(np.sum(action_lt != max_action)) # 探索による行動
934
66
(確率$\epsilon$でランダムな行動を取ると表現していますが、ランダムに決まった行動がmax_actionの行動(greedyな行動)になることもあります。)
以上がε-greedy法の処理です。
・実装
処理の確認ができたので、ε-greedy化する処理を関数として実装します。
# ε-greedy化の実装 def greedy_probs(Q, state, epsilon=0, action_size=4): # 各状態における行動価値のリストを作成 qs = [Q[(state, action)] for action in range(action_size)] # 行動価値が最大の行動番号を抽出 max_action = np.argmax(qs) # 確率εでランダムに行動する疑似的な決定論的方策を作成 base_prob = epsilon / action_size # ランダムに各行動を取る確率 action_probs = {action: base_prob for action in range(action_size)} action_probs[max_action] += (1.0 - epsilon) return action_probs
実装した関数を試してみましょう。
# 方策のgreedy化 action_probs = greedy_probs(Q, state) print(action_probs)
{0: 0.0, 1: 0.0, 2: 0.0, 3: 1.0}
処理の確認時と同じ結果が得られました。
この項では、ε-greedy法による方策の改善を実装しました。次項では、行動価値関数の推定方法を考えます。
5.4.4 固定値α方式へ(2つ目の修正)
4.4.2項では、収益のサンプルの標本平均により行動価値関数を求めました。この項では、指数移動平均によって求めます。指数移動平均については「1.5.1:非定常問題のエージェントの実装【ゼロつく4のノート】 - からっぽのしょこ」を参照してください。
・数式の確認
まずは、行動価値関数の計算を数式で確認します。
5.4.2項では、行動価値関数の推定値として収益のサンプルの標本平均を用いました。
改善版では、収益のサンプルの指数移動平均を用います。
ここで、$\alpha$は重みで、0から1の値$0 < \alpha < 1$を指定します。指数移動平均では、新しいサンプル($n$が大きい)ほど影響が大きくなります。
標本平均の重み$\frac{1}{n}$はサンプルサイズ$n$の影響を受けますが、指数移動平均の重み$\alpha$はサンプルサイズに関わらず一定です。
・処理の確認
次は、McAgentクラスのupdateメソッドの内部で行う処理を確認します。他のメソッドについては「5.4.1-2:モンテカルロ法による方策制御【ゼロつく4のノート】 - からっぽのしょこ」を参照してください。
重み$\alpha$を指定します。また例として、ダミーの収益のサンプルを作成します。
# 割引率を指定 alpha = 0.1 # サンプルサイズを指定 N = 10 # (仮の)収益のサンプルを作成 gs = np.random.rand(N) * 10.0 print(np.round(gs, 2))
[9.32 8.87 6.95 3.04 1.6 6.32 7.15 5.97 1.82 0.63]
N個のサンプルを1度の処理(1つ目の式)で計算します。
# 行動価値関数を計算 Q = np.sum(alpha * (1.0 - alpha)**np.arange(N) * gs[::-1]) print(Q)
2.977136299749727
0乗は1なので、1つ目の項を$\alpha G^{(n)} = \alpha (1 - \alpha)^0 G^{(n)}$として、各項を計算し総和を取ります。gs[::-1]で要素を逆順に並べ替えています。
続いて、インクリメンタルな処理(3つ目の式)でN回の繰り返し計算します。
# 行動価値関数を計算 Q = 0.0 for n in range(N): Q += alpha * (gs[n] - Q) print(Q)
2.977136299749727
Qの初期値を0.0にしておき、for文で各項の計算結果を加えていきます。
以上が、行動価値関数の計算処理です。
・実装
処理の確認ができたので、マルコフ法におけるエージェントの処理をクラスとして実装します。
# マルコフ法におけるエージェントの実装 class McAgent: # 初期化メソッドの定義 def __init__(self): # 値の設定 self.gamma = 0.9 # 収益の計算用の割引率 self.epsilon = 0.1 # ランダムに行動する確率 self.alpha = 0.1 # 行動価値の計算用の割引率 self.action_size = 4 # 行動の種類数 # オブジェクトの初期化 random_actions = {0: 0.25, 1: 0.25, 2: 0.25, 3: 0.25} # 確率論的方策用の確率分布 self.pi = defaultdict(lambda: random_actions) # 確率論的方策 self.Q = defaultdict(lambda: 0) # 行動価値関数 self.memory = [] # サンプルデータ # 行動メソッドの定義 def get_action(self, state): # 現在の状態における方策の確率分布を取得 action_probs = self.pi[state] actions = list(action_probs.keys()) # 行動番号 probs = list(action_probs.values()) # 行動確率 # 確率論的方策による行動を出力 return np.random.choice(actions, p=probs) # 記録メソッドの定義 def add(self, state, action, reward): # 現在の時刻におけるサンプルデータをタプルに格納 data = (state, action, reward) # サンプルを格納 self.memory.append(data) # サンプルデータの初期化メソッドの定義 def reset(self): # 記録用のリストを初期化 self.memory.clear() # 方策の計算メソッドの定義 def update(self): # 行動価値関数を計算して、ε-greedy化した方策を作成 G = 0 for data in reversed(self.memory): # 各時刻におけるサンプルデータを取得 state, action, reward = data # 収益を計算:式(3.3) G = self.gamma * G + reward # 行動価値関数を計算:図(5.16) key = (state, action) self.Q[key] += (G - self.Q[key]) * self.alpha # 方策をε-greedy化:図(5.18) self.pi[state] = greedy_probs(self.Q, state, self.epsilon)
実装したクラスを試してみましょう。
環境(グリッドワールド)とエージェントのインスタンスを作成します。
# 環境とエージェントのインスタンスを作成 env = GridWorld() agent = McAgent() # 最初の状態を取得 state = env.start_state print(state) # 1エピソードのシミュレーション while True: # 確率論的方策に従い行動を決定 action = agent.get_action(state) # サンプルデータを取得 next_state, reward, done = env.step(action) # サンプルデータを格納 agent.add(state, action, reward) # ゴールに着いた場合 if done: # ループを終了 break # 状態を更新 state = next_state print(next_state)
(2, 0)
(0, 3)
agentのget_action()で方策に従い行動して、envのstep()で状態を遷移し報酬を出力します。現在の状態・行動・報酬をagentのadd()で記録します。
ゴールマスに着くとdoneがTrueになるので、breakでループ処理を終了します。
サンプルデータがmemoryに格納されているのを確認します。
# サンプルデータを確認 print(agent.memory[:5]) print(len(agent.memory))
[((2, 0), 0, 0), ((1, 0), 3, 0), ((1, 0), 2, 0), ((1, 0), 0, 0), ((0, 0), 2, 0)]
104
update()メソッドで行動価値関数と方策を計算します。
# (確認用に)状態を指定 state = (0, 2) # 行動価値関数と方策を確認 print(agent.Q.values()) print(agent.pi[state].values()) # 行動価値関数と方策を計算 agent.update() # 行動価値関数と方策を確認 print(np.round([agent.Q[(state, action)] for action in range(agent.action_size)], 4)) print(agent.pi[state].values())
dict_values([])
dict_values([0.25, 0.25, 0.25, 0.25])
[ 0.0623 -0.0026 -0.0024 0.1 ]
dict_values([0.025, 0.025, 0.025, 0.925])
サンプルとして得られなかった状態はagent.Qに含まれません。
reset()でサンプルデータを削除します。
# サンプルデータを削除 agent.reset() print(agent.memory)
[]
この項では、指数移動平均により行動価値関数を計算するエージェントを実装しました。次項では、改善版のエージェントを用いて行動価値関数と方策を推定します。
5.4.5 [修正版]モンテカルロ法を使った方策反復法の実装
5.4.2項の実装では、上手く推定できませんでした。この項では、3×4マスのグリッドワールド(図4-8)に対してモンテカルロ法により行動価値関数とε-greedy化した方策を求めます。
・推定
マルコフ法により行動価値関数を推定してε-greedyにより方策を求めます(方策を制御します)。
# インスタンスを作成 env = GridWorld() agent = McAgent() # エピソード数を指定 episodes = 1000 # 推移の可視化用のリストを初期化 trace_Q = [{(state, action): agent.Q[(state, action)] for state in env.states() for action in env.action_space}] # 初期値を記録 # 繰り返しシミュレーション for episode in range(episodes): # 状態を初期化(エージェントの位置をスタートマスに設定) state = env.reset() # サンプルデータを初期化 agent.reset() # 試行回数(時刻)を初期化 t = 0 # 1エピソードのシミュレーション while True: # 試行回数をカウント t += 1 # ε-greedy法により行動を決定 action = agent.get_action(state) # サンプルデータを取得 next_state, reward, done = env.step(action) # サンプルデータを格納 agent.add(state, action, reward) # ゴールに着いた場合 if done: # 行動価値関数を計算 agent.update() # 更新値を記録 trace_Q.append(agent.Q.copy()) # 試行回数を表示 print('episode '+str(episode+1) + ': T='+str(t)) # ループを終了して次のエピソード break # 状態を更新 state = next_state
episode 1: T=15
episode 2: T=45
episode 3: T=5
episode 4: T=5
episode 5: T=5
episode 6: T=19
episode 7: T=266
episode 8: T=8
episode 9: T=5
episode 10: T=5
(省略)
episode 991: T=8
episode 992: T=6
episode 993: T=5
episode 994: T=7
episode 995: T=6
episode 996: T=5
episode 997: T=5
episode 998: T=5
episode 999: T=5
episode 1000: T=6
スタートマスからゴールマスに着くまでを1エピソードとします。エピソードごとに、GridWorldクラスのreset()メソッドで状態を初期化し(エージェントをスタートマスに戻し)、McAgentクラスのreset()メソッドでサンプルデータを初期化(過去のデータを削除)します。
episodesに指定した回数のシミュレーションを行い、繰り返し行動価値関数と方策を更新します。
推移の確認用に、行動価値関数の更新値をtrace_Qに格納していきます。
推定した行動価値関数をヒートマップで、greedy化した方策を矢印のラベルで確認します。
# 行動価値関数のヒートマップを作図
env.render_q(agent.Q)
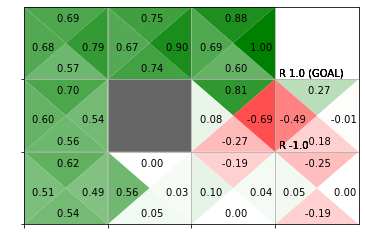
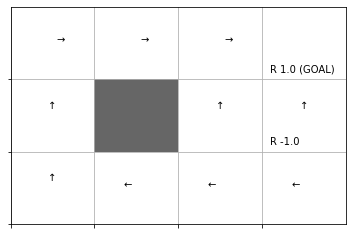
結果の解釈については本を参照してください。
・更新推移の可視化
ここまでで、繰り返しの更新処理を確認しました。続いて、途中経過をアニメーションで確認します。
行動価値関数のヒートマップのアニメーションを作成します。
・作図コード(クリックで展開)
# グリッドマップのサイズを取得 xs = env.width ys = env.height # 状態価値の最大値・最小値を取得 qmax = max([max(trace_Q[i].values()) for i in range(len(trace_Q))]) qmin = min([min(trace_Q[i].values()) for i in range(len(trace_Q))]) # 色付け用に最大値・最小値を再設定 qmax = max(qmax, abs(qmin)) qmin = -1 * qmax qmax = 1 if qmax < 1 else qmax qmin = -1 if qmin > -1 else qmin # カラーマップを設定 color_list = ['red', 'white', 'green'] cmap = LinearSegmentedColormap.from_list('colormap_name', color_list) # 図を初期化 fig = plt.figure(figsize=(12, 9), facecolor='white') # 図の設定 plt.suptitle('Monte Carlo Method', fontsize=20) # 全体のタイトル # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i回目の更新値を取得 Q = trace_Q[i] # マス(状態)ごとに処理 for state in env.states(): # 行動ごとに処理 for action in env.action_space: # インデックスを取得 y, x = state # 報酬を抽出 r = env.reward_map[y, x] # 報酬がある場合 if r != 0 and r is not None: # 報酬ラベル用の文字列を作成 txt = 'R ' + str(r) # ゴールの場合 if state == env.goal_state: # 報酬ラベルにゴールを追加 txt = txt + ' (GOAL)' # 報酬ラベルを描画 plt.text(x=x+0.1, y=ys-y-0.9, s=txt, ha='left', va='bottom', fontsize=15) # ゴールの場合 if state == env.goal_state: # 描画せず次の状態へ continue # 作図用のx軸・y軸の値を設定 tx, ty = x, ys-y-1 # 行動ごとの三角形の頂点を設定 action_map = { 0: ((0.5+tx, 0.5+ty), (1.0+tx, 1.0+ty), (tx, 1.0+ty)), # 上 1: ((tx, ty), (1.0+tx, ty), (0.5+tx, 0.5+ty)), # 下 2: ((tx, ty), (0.5+tx, 0.5+ty), (tx, 1.0+ty)), # 左 3: ((0.5+tx, 0.5+ty), (1.0+tx, ty), (1.0+tx, 1.0+ty)) # 右 } # 行動ごとの価値ラベルのプロット位置を設定 offset_map = { 0: (0.5, 0.75), # 上 1: (0.5, 0.25), # 下 2: (0.25, 0.5), # 左 3: (0.75, 0.5) # 右 } # 壁の場合 if state == env.wall_state: # 壁を描画 rect = plt.Rectangle(xy=(tx, ty), width=1, height=1, fc=(0.4, 0.4, 0.4, 1.0)) # 長方形を作成 plt.gca().add_patch(rect) # 重ねて描画 # (よく分からない) elif state in env.goal_state: plt.gca().add_patch(plt.Rectangle(xy=(tx, ty), width=1, height=1, fc=(0.0, 1.0, 0.0, 1.0))) # 壁以外の場合 else: # 行動価値を抽出 tq = Q[(state, action)] # 行動価値を0から1に正規化 color_scale = 0.5 + (tq / qmax) / 2 # 三角形を描画 poly = plt.Polygon(action_map[action],fc=cmap(color_scale)) # 三角形を作成 plt.gca().add_patch(poly) # 重ねて描画 # プロット位置の調整値を取得 offset = offset_map[action] # 行動価値ラベルを描画 plt.text(x=tx+offset[0], y=ty+offset[1], s=str(np.round(tq, 2)), ha='center', va='center', size=15) # 行動価値ラベル # グラフの設定 plt.xticks(ticks=np.arange(xs)) # x軸の目盛位置 plt.yticks(ticks=np.arange(ys), labels=ys-np.arange(ys)-1) # y軸の目盛位置 plt.xlim(xmin=0, xmax=xs) # x軸の範囲 plt.ylim(ymin=0, ymax=ys) # y軸の範囲 plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False) # 軸ラベル plt.grid() # グリッド線 plt.title('iter:'+str(i), loc='left') # タイトル # gif画像を作成 anime = FuncAnimation(fig=fig, func=update, frames=len(trace_Q), interval=50) # gif画像を保存 anime.save('../figure/ch05/ch5_4_5.gif')
各エピソードで更新した行動価値をtrace_Qから取り出してヒートマップを描画する処理を関数update()として定義して、FuncAnimation()でアニメーション(gif画像)を作成します。
行動価値関数の更新値の推移を折れ線グラフで確認します。
・作図コード(クリックで展開)
# 行動ラベルを指定 action_lt = ['Up', 'Down', 'Left', 'Right'] # 状態価値関数の推移を作図 plt.figure(figsize=(15, 10), facecolor='white') for state in env.states(): for action in range(agent.action_size): # 更新値を抽出 q_vals = [trace_Q[i][(state, action)] for i in range(episodes+1)] # 各状態の価値の推移を描画 plt.plot(np.arange(episodes+1), q_vals, label='$Q_i(L_{'+str(state[0])+','+str(state[1])+'},'+action_lt[action]+')$') plt.xlabel('episode') plt.ylabel('action-value') plt.suptitle('Monte Carlo Method', fontsize=20) plt.title('$\gamma='+str(agent.gamma) + ', \\alpha='+str(agent.alpha)+'$', loc='left') plt.grid() plt.legend(loc='upper left', bbox_to_anchor=(1, 1), ncol=2) plt.show()
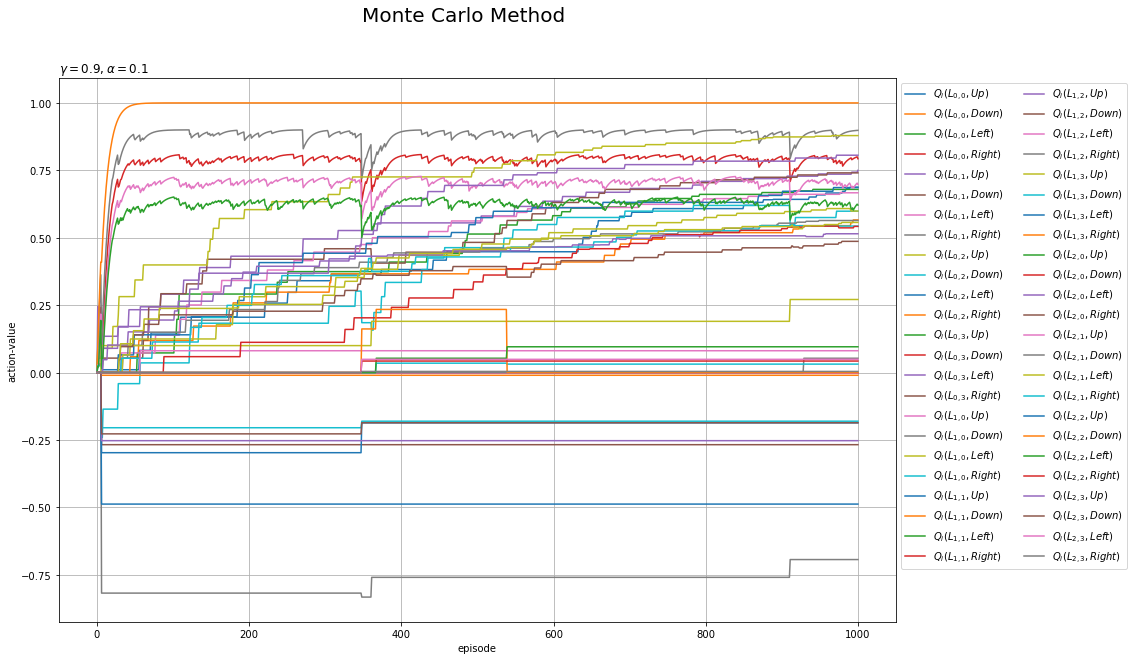
行番号を$h$、列番号を$w$として各マスを$L_{h,w}$で表します。また、$i$回目の状態(マス)$L_{h,w}$で行動$A$を取る価値を$Q_i(L_{h,w}, A)$で表します。マスのインデックスについては図4-9を参照してください。
各曲線の縦軸の値が、ヒートマップの色に対応します。
ここまでの節では、方策オン型のモンテカルロ法による方策制御を実装しました。しかし、ε-greedy法により方策を求めたことで、最適でない行動に対しても小さい確率を割り当てました。次節からは、greedy法により方策を求めるために、方策オフ型のモンテカルロ法による方策制御を考えます。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning 4 ――強化学習編』オライリー・ジャパン,2022年.
- サポートページ:GitHub - oreilly-japan/deep-learning-from-scratch-4
おわりに
ここまでで一区切りですね、順調に進められました。
【次節の内容】