はじめに
『ゼロから作るDeep Learning 4 ――強化学習編』の独学時のまとめノートです。初学者の補助となるようにゼロつくシリーズの4巻の内容に解説を加えていきます。本と一緒に読んでください。
この記事は、4.2.1節の内容です。3×4マスのグリッドワールドのクラスについて確認します。
【前節の内容】
【他の記事一覧】
【この記事の内容】
4.2.1 GridWorldクラスの実装
3×4マスのグリッドワールドのクラスGridWorldの内部で行われる処理と使い方を確認します。前回は、評価と改善に使うメソッドの処理を確認しました。今回は、可視化に使うメソッドの処理を確認します。
利用するライブラリを読み込みます。
# 利用するライブラリ import numpy as np import matplotlib.pyplot as plt from matplotlib.colors import LinearSegmentedColormap
実装済みのGridWorldクラスは、次のようにして読み込めます。
# 読み込み用のライブラリ import sys # フォルダパスを指定 sys.path.append('../deep-learning-from-scratch-4-master') # 実装済みクラスを読み込み from common.gridworld import GridWorld
実装済みクラスの読み込みについては「3.6.1:MNISTデータセットの読み込み【ゼロつく1のノート(Python)】 - からっぽのしょこ」を参照してください。
GridWorldクラスのインスタンスを作成しておきます。
# インスタンスを作成
env = GridWorld()
・render_vメソッド
状態価値関数のヒートマップを作成する「状態価値関数の可視化メソッド」の処理を確認します。ただし、作図コードがとても複雑なので、ここでは基本的な処理のみ確認します。
アルゴリズム自体とは直接関係しないので、飛ばしていいと思います。詳しくは「common」フォルダの「gridworld_render.py」ファイルを参照してください(見ない方がいいよ)。
グリッドワールドのマスの作図、ヒートマップによる状態価値関数の可視化、矢印による方策の可視化の3つの段階に分けて解説します。
・グリッドワールド
まずは、グリッドワールドの座標を作成します。
実装済みのメソッドを使って完成形を確認しましょう。
# グリッドワールドを作図
env.render_v()
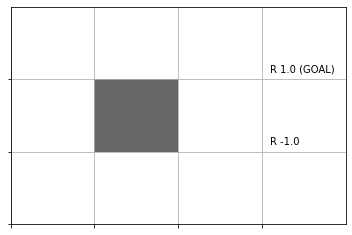
グリッド線を引いてマスを描画し、報酬のラベルを付けて、壁のマスを黒塗りで表現します。
グリッドワールドの縦・横のサイズ(マスの数)を取得します。
# 縦軸のサイズを取得 ys = len(env.reward_map) print(ys) # 横軸のサイズを取得 xs = len(env.reward_map[0]) print(xs)
3
4
各状態(マス)の報酬reward_mapの行数が縦のサイズys、各行の要素数が横のサイズxsに対応します。
3×4のマスを作図します。
# グラフの設定 plt.figure(figsize=(8, 6), facecolor='white') # 図の設定 plt.xticks(ticks=np.arange(xs)) # x軸の目盛位置 plt.yticks(ticks=np.arange(ys)) # y軸の目盛位置 plt.xlim(xmin=0, xmax=xs) # x軸の範囲 plt.ylim(ymin=0, ymax=ys) # y軸の範囲 plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False) # 軸ラベル plt.grid() # グリッド線 plt.title('grid lines', fontsize=20) # タイトル plt.show()
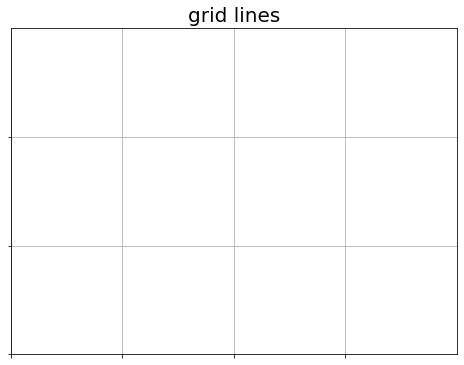
グリッド線を引く位置をplt.xticks()とplt.yticks()に指定します。また、描画範囲をplt.xlim()とplt.ylim()に指定します。グリッド線は、plt.grid()で表示されます。
plt.tick_params()の各引数をFalseにして、軸目盛ラベルなどを非表示にします。
マスの装飾をするために、各マスのy軸・x軸の値を確認しておきます。
# グラフの設定 plt.figure(figsize=(8, 6), facecolor='white') # 図の設定 plt.title('coordinate (y, x)', fontsize=20) # タイトル plt.xticks(ticks=np.arange(xs)) # x軸の目盛位置 plt.yticks(ticks=np.arange(ys)) # y軸の目盛位置 plt.xlim(xmin=0, xmax=xs) # x軸の範囲 plt.ylim(ymin=0, ymax=ys) # y軸の範囲 #plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False) # 軸ラベル plt.grid() # グリッド線 # マスごとに処理 for y in range(ys): for x in range(xs): # 装飾するマス(状態)を設定 state = (y, x) # 座標ラベルをそのまま描画 plt.text(x=x+0.5, y=y+0.5, s=str(state), ha='center', va='center', fontsize=20) plt.xlabel('x (width)') # x軸ラベル plt.ylabel('y') # y軸ラベル plt.show()
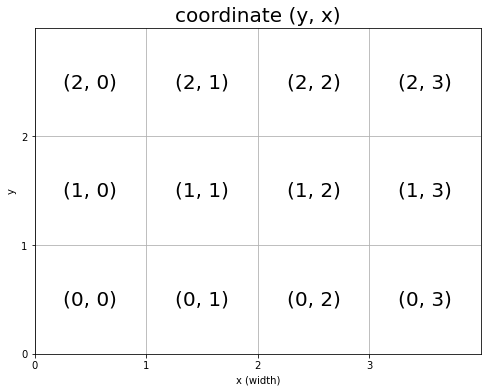
plt.text()で図の中に文字列を描画できます。x, y引数にプロット位置、s引数に描画する文字列を指定します。
マスの中心に描画するために、x, y引数にはそれぞれ0.5を加えた値を指定します。
ここで注意が必要なのが、通常のグラフでは、横軸は右に行くほど値が大きく、縦軸は上に行くほど値が大きくなります。しかし、図4-9のように下に行くほど値が大きくなるようにしたいです。
そこで、y軸に関しては、縦のサイズysから各マスの値y+1を引いた値(あるいはys-1からy引いた値)を使います。
# グラフの設定 plt.figure(figsize=(8, 6), facecolor='white') # 図の設定 plt.title('index (h, w)', fontsize=20) # タイトル plt.xticks(ticks=np.arange(xs)) # x軸の目盛位置 plt.yticks(ticks=np.arange(ys), labels=ys-np.arange(ys)-1) # y軸の目盛位置 plt.xlim(xmin=0, xmax=xs) # x軸の範囲 plt.ylim(ymin=0, ymax=ys) # y軸の範囲 #plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False) # 軸ラベル plt.grid() # グリッド線 # マスごとに処理 for y in range(ys): for x in range(xs): # 装飾するマス(状態) state = (y, x) # 座標ラベルをマスに対応させて描画 plt.text(x=x+0.5, y=ys-y-0.5, s=str(state), ha='center', va='center', fontsize=20) plt.xlabel('x (width)') # x軸ラベル plt.ylabel('y (height)') # y軸ラベル plt.show()
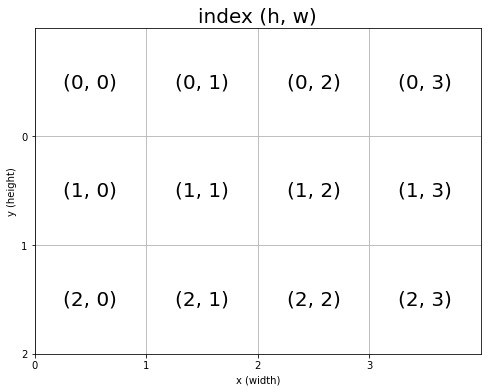
各マスの中心は、ys-y-1+0.5なので、ys-y-0.5になります。
各マスのインデックスと座標の関係を確認できました。
では、マスごとに報酬の値を描画します。
# グラフの設定 plt.figure(figsize=(8, 6), facecolor='white') # 図の設定 plt.title('reward', fontsize=20) # タイトル plt.xticks(ticks=np.arange(xs)) # x軸の目盛位置 plt.yticks(ticks=np.arange(ys), labels=ys-np.arange(ys)-1) # y軸の目盛位置 plt.xlim(xmin=0, xmax=xs) # x軸の範囲 plt.ylim(ymin=0, ymax=ys) # y軸の範囲 plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False) # 軸ラベル plt.grid() # グリッド線 # マスごとに処理 for y in range(ys): for x in range(xs): # 報酬を抽出 r = env.reward_map[y, x] # 報酬ラベルを描画 plt.text(x=x+0.5, y=ys-y-0.5, s=str(r), ha='center', va='center', fontsize=20) plt.show()
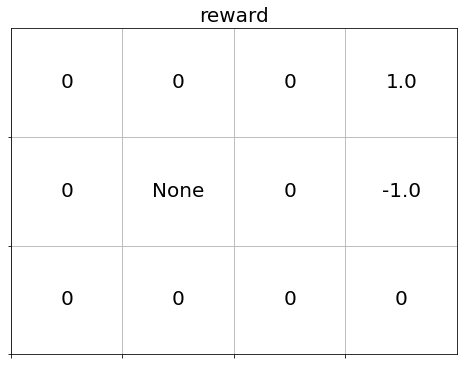
reward_mapから各マス(状態)の報酬を取り出して描画します。
reward_mapに設定した報酬と一致しています。
# 報酬を確認 print(env.reward_map)
[[0 0 0 1.0]
[0 None 0 -1.0]
[0 0 0 0]]
報酬の無い0, Noneは省略して、ゴールの位置も描画します。
# グラフの設定 plt.figure(figsize=(8, 6), facecolor='white') # 図の設定 plt.title('reward and goal', fontsize=20) # タイトル plt.xticks(ticks=np.arange(xs)) # x軸の目盛位置 plt.yticks(ticks=np.arange(ys), labels=ys-np.arange(ys)-1) # y軸の目盛位置 plt.xlim(xmin=0, xmax=xs) # x軸の範囲 plt.ylim(ymin=0, ymax=ys) # y軸の範囲 plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False) # 軸ラベル plt.grid() # グリッド線 # マスごとに処理 for y in range(ys): for x in range(xs): # 装飾するマス(状態)を設定 state = (y, x) # 報酬を抽出 r = env.reward_map[y, x] # 報酬がある場合 if r != 0 and r is not None: # 報酬ラベル用の文字列を作成 txt = 'R ' + str(r) # ゴールの場合 if state == env.goal_state: # 報酬ラベルにゴールを追加 txt = txt + ' (GOAL)' # 報酬ラベルを描画 plt.text(x=x+0.1, y=ys-y-0.9, s=txt, ha='left', va='bottom', fontsize=12) plt.show()
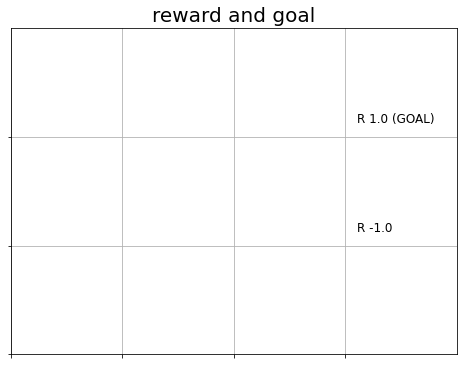
報酬rが0でもNoneでもない場合に、報酬ラベルを描画します。
また、ゴールのマスの場合には、ゴールを示す文字列を追加します。+演算子で、文字列を結合できます。
表示位置を中心から調整しました。
続いて、壁のマスを黒く塗りつぶします。
# グラフの設定 plt.figure(figsize=(8, 6), facecolor='white') # 図の設定 plt.title('wall', fontsize=20) # タイトル plt.xticks(ticks=np.arange(xs)) # x軸の目盛位置 plt.yticks(ticks=np.arange(ys), labels=ys-np.arange(ys)-1) # y軸の目盛位置 plt.xlim(xmin=0, xmax=xs) # x軸の範囲 plt.ylim(ymin=0, ymax=ys) # y軸の範囲 plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False) # 軸ラベル plt.grid() # グリッド線 # マスごとに処理 for y in range(ys): for x in range(xs): # 装飾するマス(状態)を設定 state = (y, x) # 報酬を抽出 r = env.reward_map[y, x] # 報酬がある場合 if r != 0 and r is not None: # 報酬ラベル用の文字列を作成 txt = 'R ' + str(r) # ゴールの場合 if state == env.goal_state: # 報酬ラベルにゴールを追加 txt = txt + ' (GOAL)' # 報酬ラベルを描画 plt.text(x=x+0.1, y=ys-y-0.9, s=txt, ha='left', va='bottom', fontsize=12) # 壁のマスの場合 if state == env.wall_state: # 壁を描画 rect = plt.Rectangle(xy=(x, ys-y-1), width=1, height=1, fc=(0.4, 0.4, 0.4, 1.0)) # 長方形を作成 plt.gca().add_patch(rect) # 重ねて描画 plt.show()
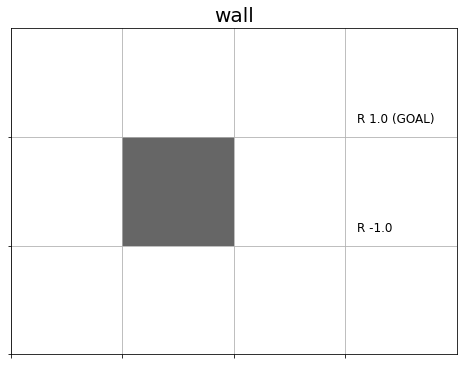
plt.Rectangle()で長方形を描画できます。xy引数に長方形の左下の頂点の位置、width引数に横幅、height引数に高さ、fc引数に色を指定します。この例では、濃いグレーになるように値を指定しています。
作成した長方形を、add_patch()でグリッドワールドに重ねて描画します。
以上で、基本となるグリッドワールドを作図できました。
・状態価値のヒートマップ
次に、状態価値関数のヒートマップを作成します。
例として、ダミーの状態価値関数のディクショナリを作成しておきます。
# (仮の)状態価値のディクショナリを作成 V = {state: np.random.randn() for state in env.states()} print(list(V.keys())[:5]) print(np.round(list(V.values())[:5], 2))
[(0, 0), (0, 1), (0, 2), (0, 3), (1, 0)]
[-0.41 -0.54 -0.8 0.86 -1.8 ]
状態(マスのインデックス)をキー、状態価値を値とします。(リスト内包表記を使っていますが、処理の内容は101ページと同じです。)
完成形を確認しましょう。
# 状態価値関数のヒートマップを作図
env.render_v(v=V)
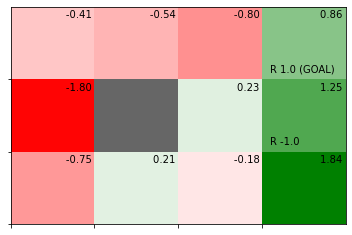
状態価値関数の値が、負の値なら赤色、0なら白色、正の値なら緑色になります。また、値が小さいほど濃い赤色、大きいほど濃い緑色になります。
さらに、状態価値のラベルを表示します。
状態価値関数のディクショナリをNumPy配列に変換します。
# 状態価値の受け皿(配列)を作成 v = np.zeros(env.reward_map.shape) # 要素ごとに処理 for state, value in V.items(): # 状態をインデックスとして値を格納 v[state] = value print(np.round(v, 2))
[[-0.41 -0.54 -0.8 0.86]
[-1.8 -0.25 0.23 1.25]
[-0.75 0.21 -0.18 1.84]]
状態(マスの位置)を示すタプル型のキーを、配列のインデックスとして利用して、対応する要素に値を格納します。
状態価値の最小値と最大値を作成します。また、カラーマップを作成します。
# 最小値・最大値を取得 vmin = v.min() vmax = v.max() print(vmin) print(vmax) # カラーマップを設定 color_list = ['red', 'white', 'green'] cmap = LinearSegmentedColormap.from_list('colormap_name', color_list)
-1.8027212035973819
1.8434332056884268
最小値と最大値は、色の濃淡を付けるのに利用します。
赤・白・緑に変化するカラーマップを設定します。
ヒートマップを作成して、状態価値のラベルを付けます。
# グラフの設定 plt.figure(figsize=(8, 6), facecolor='white') # 図の設定 plt.title('heatmap', fontsize=20) # タイトル plt.xticks(ticks=np.arange(xs)) # x軸の目盛位置 plt.yticks(ticks=np.arange(ys), labels=ys-np.arange(ys)-1) # y軸の目盛位置 plt.xlim(xmin=0, xmax=xs) # x軸の範囲 plt.ylim(ymin=0, ymax=ys) # y軸の範囲 plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False) # 軸ラベル # 状態価値のヒートマップを描画 plt.pcolormesh(np.flipud(v), cmap=cmap, vmin=vmin, vmax=vmax) # ヒートマップ # マスごとに処理 for y in range(ys): for x in range(xs): # 装飾するマス(状態)を設定 state = (y, x) # 報酬を抽出 r = env.reward_map[y, x] # 報酬がある場合 if r != 0 and r is not None: # 報酬ラベル用の文字列を作成 txt = 'R ' + str(r) # ゴールの場合 if state == env.goal_state: # 報酬ラベルにゴールを追加 txt = txt + ' (GOAL)' # 報酬ラベルを描画 plt.text(x=x+0.1, y=ys-y-0.9, s=txt, ha='left', va='bottom', fontsize=12) # 壁以外の場合 if state != env.wall_state: # 状態価値ラベルを描画 plt.text(x=x+0.9, y=ys-y-0.1, s=str(np.round(v[y, x], 2)), ha='right', va='top', fontsize=12) # 壁の場合 if state == env.wall_state: # 壁を描画 rect = plt.Rectangle(xy=(x, ys-y-1), width=1, height=1, fc=(0.4, 0.4, 0.4, 1.0)) # 長方形を作成 plt.gca().add_patch(rect) # 重ねて描画 plt.show()
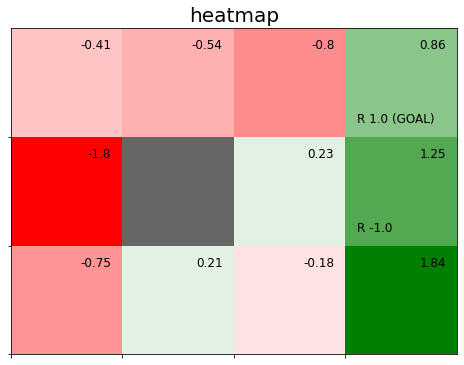
pcolormesh()でヒートマップを描画できます。第1引数に値、cmapにカラーマップ、vmin, vmax引数に最小値・最大値を指定します。(plt.pcolormesh()とplt.grid()を同時に使うのは非推奨になったようです。)
最小値・最大値によって各マス(値)の濃淡が決まります。
ただし、配列の位置(インデックス)とグラフ上の位置(座標)には、ズレがあるのでした。そこで、配列の要素をnp.flipud()で縦方向に反転させます。
# 配列を確認 print(np.round(v, 2)) # 縦方向に反転 print(np.round(np.flipud(v), 2))
[[-0.41 -0.54 -0.8 0.86]
[-1.8 -0.25 0.23 1.25]
[-0.75 0.21 -0.18 1.84]]
[[-0.75 0.21 -0.18 1.84]
[-1.8 -0.25 0.23 1.25]
[-0.41 -0.54 -0.8 0.86]]
ラベルの表示上は元の配列と一致しますが、描画には反転させた配列を利用します。
赤・白・緑の色付けは、最小値と最大値により自動で決まります。負の値なら赤色、0なら白色、正の値なら緑色になるように、最小値と最大値を調整します。
# 最小値・最大値の絶対値に応じて再設定 vmax = max(vmax, abs(vmin)) vmin = -1 * vmax print(vmin) print(vmax) # 最大値が1より小さい場合は1に再設定 if vmax < 1: vmax = 1 # 最小値が-1より大きい場合は-1に再設定 if vmin > -1: vmin = -1 print(vmin) print(vmax)
-1.8434332056884268
1.8434332056884268
-1.8434332056884268
1.8434332056884268
最小値の絶対値と最大値を比較して、大きい方の値を最大値として利用します。また、その最大値をマイナスにした値を最小値とします。
例えば、状態価値が-2から3の範囲であれば、ヒートマップの設定範囲を-3から3にします。これにより、中央値の0が白色になり、また赤色と緑色の境界になります。
さらに、最大値が1未満のときは1に、最小値が-1より大きい場合は-1にします。
先ほどの作図コード(タイトルは変えました)を使って、再設定した範囲でヒートマップを作成します。
# グラフの設定 plt.figure(figsize=(12, 9), facecolor='white') # 図の設定 plt.title('State-Value Function', fontsize=20) # タイトル plt.xticks(ticks=np.arange(xs)) # x軸の目盛位置 plt.yticks(ticks=np.arange(ys), labels=ys-np.arange(ys)-1) # y軸の目盛位置 plt.xlim(xmin=0, xmax=xs) # x軸の範囲 plt.ylim(ymin=0, ymax=ys) # y軸の範囲 plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False) # 軸ラベル # 状態価値のヒートマップを描画 plt.pcolormesh(np.flipud(v), cmap=cmap, vmin=vmin, vmax=vmax) # ヒートマップ # マスごとに処理 for y in range(ys): for x in range(xs): # 装飾するマス(状態)を設定 state = (y, x) # 報酬を抽出 r = env.reward_map[y, x] # 報酬がある場合 if r != 0 and r is not None: # 報酬ラベル用の文字列を作成 txt = 'R ' + str(r) # ゴールの場合 if state == env.goal_state: # 報酬ラベルにゴールを追加 txt = txt + ' (GOAL)' # 報酬ラベルを描画 plt.text(x=x+0.1, y=ys-y-0.9, s=txt, ha='left', va='bottom', fontsize=15) # 壁以外の場合 if state != env.wall_state: # 状態価値ラベルを描画 plt.text(x=x+0.9, y=ys-y-0.1, s=str(np.round(v[y, x], 2)), ha='right', va='top', fontsize=15) # 壁の場合 if state == env.wall_state: # 壁を描画 rect = plt.Rectangle(xy=(x, ys-y-1), width=1, height=1, fc=(0.4, 0.4, 0.4, 1.0)) # 長方形を作成 plt.gca().add_patch(rect) # 重ねて描画 plt.show()

以上で、状態価値関数のヒートマップを作図できました。
・方策ラベル
最後に、方策を矢印で可視化します。
例として、ダミーの方策のディクショナリを作成しておきます。
# 仮の方策を作成 pi = {state: {0: 0.4, 1: 0.15, 2: 0.4, 3: 0.05} for state in env.states()}
状態(マスのインデックス)をキー、確率論的方策のディクショナリを値とします。ディクショナリの値として、ディクショナリを格納します。
完成形を確認しましょう。
# 方策を重ねた状態価値関数のヒートマップを作図
env.render_v(v=V, policy=pi)

マスごとに、確率が最大の行動を矢印で表現します。最大値が複数ある場合は、複数の行動を描画します。ただし、エージェントがゴールに辿り着くとエピソードが終了するという問題設定なので、ゴールのマスでは描画されません。
ここでは簡単な例として全ての状態(マス)で同じ方策にしていますが、実際には状態ごとに確率分布が異なります。
確率が最大の行動を抽出する処理を確認します。
# 状態を指定 state = (0, 0) # 確率論的方策を抽出 actions = pi[state] print(actions) # 確率が最大の行動を抽出 max_actions = [key for key, value in actions.items() if value == max(actions.values())] print(max_actions)
{0: 0.4, 1: 0.15, 2: 0.4, 3: 0.05}
[0, 2]
全ての方策piから、指定した状態の確率論的方策actionsを抽出します。
actionsから、キー(行動番号)keyと値(確率)valueを順番に取り出して、値が最大値であればキーをリストに格納します。
この処理を各状態で行います。
行動に対応した矢印を描画するのに利用するリストを作成します。
# 矢印の描画用のリストを作成 arrows = ['↑', '↓', '←', '→'] offsets = [(0, 0.1), (0, -0.1), (-0.1, 0), (0.1, 0)]
ラベルの表示位置を調整するときと、エージェントの移動のときと同じ要領で、行動(矢印)ごとに表示位置を矢印と同じ方向に0.1ズラします。そのためのx軸とy軸の値をリストに格納します。
確率が最大の行動を矢印で表示します。
# グラフの設定 plt.figure(figsize=(12, 9), facecolor='white') # 図の設定 plt.title('State-Value Function & Policy', fontsize=20) # タイトル plt.xticks(ticks=np.arange(xs)) # x軸の目盛位置 plt.yticks(ticks=np.arange(ys), labels=ys-np.arange(ys)-1) # y軸の目盛位置 plt.xlim(xmin=0, xmax=xs) # x軸の範囲 plt.ylim(ymin=0, ymax=ys) # y軸の範囲 plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False) # 軸ラベル # 状態価値のヒートマップを描画 plt.pcolormesh(np.flipud(v), cmap=cmap, vmin=vmin, vmax=vmax) # ヒートマップ # マスごとに処理 for y in range(ys): for x in range(xs): # 装飾するマス(状態)を設定 state = (y, x) # 報酬を抽出 r = env.reward_map[y, x] # 報酬がある場合 if r != 0 and r is not None: # 報酬ラベル用の文字列を作成 txt = 'R ' + str(r) # ゴールの場合 if state == env.goal_state: # 報酬ラベルにゴールを追加 txt = txt + ' (GOAL)' # 報酬ラベルを描画 plt.text(x=x+0.1, y=ys-y-0.9, s=txt, ha='left', va='bottom', fontsize=12) # 壁以外の場合 if state != env.wall_state: # 状態価値ラベルを描画 plt.text(x=x+0.9, y=ys-y-0.1, s=str(np.round(v[y, x], 2)), ha='right', va='top', fontsize=15) # 確率論的方策を抽出 actions = pi[state] # 確率が最大の行動を抽出 max_actions = [k for k, v in actions.items() if v == max(actions.values())] # 行動ごとに処理 for action in max_actions: # 矢印の描画用の値を抽出 arrow = arrows[action] offset = offsets[action] # ゴールの場合 if state == env.goal_state: # 描画せず次の状態へ continue # 方策ラベル(矢印)を描画 plt.text(x=x+0.5+offset[0], y=ys-y-0.5+offset[1], s=arrow, ha='center', va='center', size=20) # 壁の場合 if state == env.wall_state: # 壁を描画 rect = plt.Rectangle(xy=(x, ys-y-1), width=1, height=1, fc=(0.4, 0.4, 0.4, 1.0)) # 長方形を作成 plt.gca().add_patch(rect) # 重ねて描画 plt.show()
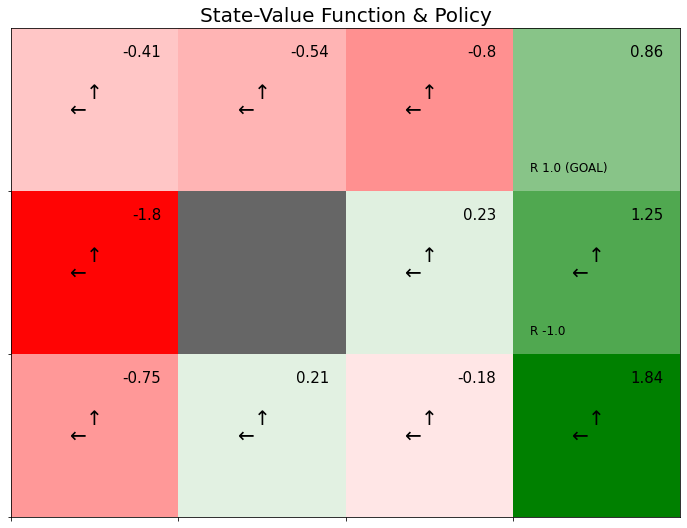
以上で、方策のラベルを描画できました。
以上が、状態価値関数の可視化メソッドの処理です。実際の実装では、状態価値関数や方策が指定されていないときの場合分けや、状態価値ラベルの有無を設定するprint_value引数、サイズによってグラフを調整するなどの処理が含まれています。また、グラフをインスタンス変数として扱うため、オブジェクト指向で作図しています。
・render_qメソッド
続いて、行動価値関数のヒートマップを作成する「行動価値関数の可視化メソッド」の処理を確認します。こちらも作図コードがとても複雑なので、基本的な処理のみ確認します。
このメソッドは5章以降で利用します(必要になってから読みましょう。そもそも読まなくても問題ないです)。
1マスの処理、3×4マスの処理の2段階に分けて解説します。
実装済みのメソッドを使って完成形を確認しましょう。
ダミーの行動価値関数のディクショナリを作成しておきます。
# (仮の)行動価値関数を作成 Q = {(state, action): np.random.randn() for action in env.action_space for state in env.states()} # (仮の)行動価値関数を作成 Q = {} for state in env.states(): # 各状態 for action in env.action_space: # 各行動 # ランダムに値を設定 Q[(state, action)] = np.random.randn() print(list(Q.keys())[:5]) print(np.round(list(Q.values())[:5], 2))
[((0, 0), 0), ((0, 0), 1), ((0, 0), 2), ((0, 0), 3), ((0, 1), 0)]
[-0.68 1.39 1.31 -0.26 1.46]
「状態(マスのインデックスのタプル)」と「行動番号」を格納したタプルをキー、行動価値を値とします。
「行動価値関数のヒートマップ」と「行動価値関数をgreedy化した方策」を作成します。
# 行動価値関数を作図 env.render_q(q=Q, print_value=True)
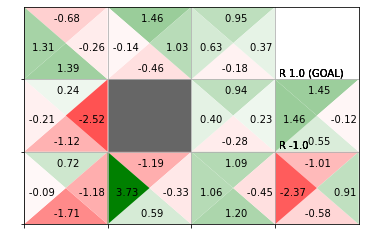
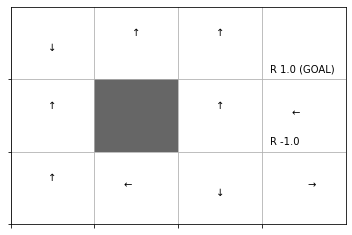
行動価値関数は、状態(マス)ごとに全ての行動(この例だと上下左右)に対応した値を持ちます。そのため、1つのマスを4つの三角形に区切ったヒートマップにより可視化します。行動価値関数の値が、負の値なら赤色、0なら白色、正の値なら緑色になります。また、値が小さいほど濃い赤色、大きいほど濃い緑色になります。
さらに、デフォルトだと(print_value=Trueを指定すると)行動価値関数が最大の行動(greedy化した方策)ラベルのグラフも出力します。
・1マス
まずは、1マスの場合を考えます。
1マスの枠線を描画して、マスの4つの頂点と中心の点を確認します。
# 頂点となるx軸・y軸の値を設定 vertex_x = np.array([0.0, 0.0, 0.5, 1.0, 1.0]) vertex_y = np.array([0.0, 1.0, 0.5, 0.0, 1.0]) # グラフの設定 plt.figure(figsize=(8, 6), facecolor='white') plt.title('vertex', fontsize=20) plt.xticks(ticks=[0, 1]) plt.yticks(ticks=[0, 1]) plt.grid() plt.axis('equal') # 確認用の頂点を描画 plt.scatter(x=vertex_x, y=vertex_y, s=100) # 頂点 for i in range(len(vertex_x)): plt.text(x=vertex_x[i], y=vertex_y[i], s=str((vertex_y[i], vertex_x[i])), ha='center', va='top', size=15) # 座標ラベル plt.show()

確認用に、5つの点のx軸の値をvertex_x、y軸の値をvertex_yとして、三角形の頂点の位置を点と座標ラベルで描画します。
「グリッドワールド」で確認したように、マスの縦軸のインデックス(状態)は下に行くほど値が大きくなるのでした(図4-9)。今は作図時の値を確認したいので、上に行くほどy軸の値が大きくなります。
「中心の点」と「各辺の両端の頂点」を結ぶ三角形を描画します。
# 三角形の頂点を設定 vertex = ((0.5, 0.5), (1.0, 1.0), (0.0, 1.0)) # 上 #vertex = ((0.0, 0.0), (1.0, 0.0), (0.5, 0.5)) # 下 #vertex = ((0.0, 0.0), (0.5, 0.5), (0.0, 1.0)) # 左 #vertex = ((0.5, 0.5), (1.0, 0.0), (1.0, 1.0)) # 右 # グラフの設定 plt.figure(figsize=(8, 6), facecolor='white') plt.title('$L_{00}$ action', fontsize=20) plt.xticks(ticks=[0, 1]) plt.yticks(ticks=[0, 1]) plt.grid() plt.axis('equal') # 行動を描画 poly = plt.Polygon(xy=vertex, alpha=0.5)# 三角形を作成 plt.gca().add_patch(poly) # 重ねて描画 # 確認用の頂点を描画 plt.scatter(x=vertex_x, y=vertex_y, s=100) # 頂点 for i in range(len(vertex_x)): plt.text(x=vertex_x[i], y=vertex_y[i], s=str((vertex_y[i], vertex_x[i])), ha='center', va='top', size=15) # 座標ラベル plt.show()
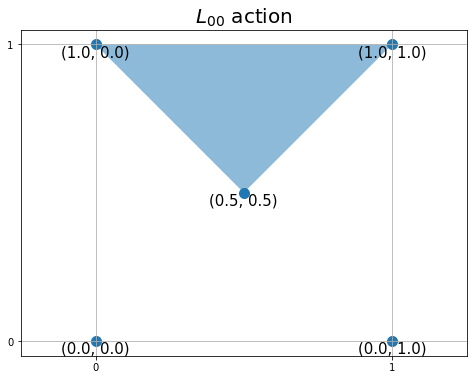
壁の塗りつぶしのときと同様にして、plt.Polygon()で多角形を描画できます。xy引数に多角形を構成する頂点のx軸・y軸の値をまとめて指定します。ここでは、三角形を描画するので3つの点(タプル)をタプルやリストに格納して指定します。
行動ごとに三角形の頂点が変わります。それぞれに対応した頂点の値を用意する必要があります。
作成した三角形を、add_patch()でグリッドワールドに重ねて描画します。
ここまでは、$L{0,0}$マス(縦軸・横軸が0から1の範囲)でした。次は、$L{h,w}$マスの場合を考えます。
状態を指定して、1つの三角形を描画します。
# 状態を指定 state = (1, 2) # x軸・y軸の値を設定 ty, tx = state # 三角形の頂点を設定 #vertex = ((0.5+tx, 0.5+ty), (1.0+tx, 1.0+ty), (tx, 1.0+ty)) # 上 vertex = ((tx, ty), (1.0+tx, ty), (0.5+tx, 0.5+ty)) # 下 #vertex = ((tx, ty), (0.5+tx, 0.5+ty), (tx, 1.0+ty)) # 左 #vertex = ((0.5+tx, 0.5+ty), (1.0+tx, ty), (1.0+tx, 1.0+ty)) # 右 # グラフの設定 plt.figure(figsize=(8, 6), facecolor='white') plt.title('$L_{'+str(y)+str(x)+'}$ action', fontsize=20) plt.xticks(ticks=[tx, 1+tx]) plt.yticks(ticks=[ty, 1+ty]) plt.grid() plt.axis('equal') # 行動を描画 poly = plt.Polygon(xy=vertex, alpha=0.5)# 三角形を作成 plt.gca().add_patch(poly) # 重ねて描画 # 確認用の頂点を描画 plt.scatter(x=vertex_x+tx, y=vertex_y+ty, s=100) # 頂点 for i in range(len(vertex_x)): plt.text(x=vertex_x[i]+tx, y=vertex_y[i]+ty, s=str((vertex_y[i]+ty, vertex_x[i]+tx)), ha='center', va='top', size=15) # 座標ラベル plt.show()
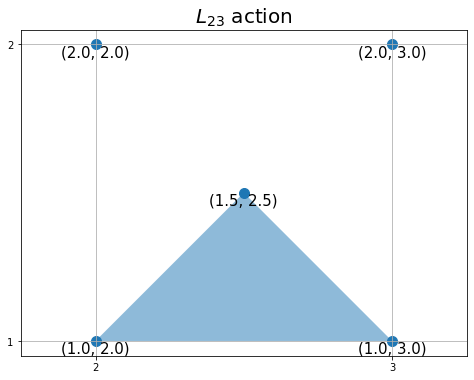
状態の0番目の要素をy軸の値ty、1番目の要素をx軸の値txとして使います。
頂点や軸の値などそれぞれx軸方向にtx、y軸方向にtyを加えます。
行動価値の値に応じて三角形の色を付け、行動価値ラベルを描画します。
# 行動価値ラベルのプロット位置を設定 #offset = (0.5, 0.75) # 上 offset = (0.5, 0.25) # 下 #offset = (0.25, 0.5) # 左 #offset = (0.75, 0.5) # 右 # カラーマップを設定 color_list = ['red', 'white', 'green'] cmap = LinearSegmentedColormap.from_list('colormap_name', color_list) # (仮の)正規化した行動価値を生成 tq = np.random.rand(1)[0] color_scale = tq # グラフの設定 plt.figure(figsize=(8, 6), facecolor='white') plt.title('$L_{'+str(y)+str(x)+'}$ Action-Value', fontsize=20) plt.xticks(ticks=[tx, 1+tx]) plt.yticks(ticks=[ty, 1+ty]) plt.grid() plt.axis('equal') # 行動価値を描画 poly = plt.Polygon(xy=vertex, fc=cmap(color_scale))# 三角形を作成 plt.gca().add_patch(poly) # 重ねて描画 # 行動価値ラベルを描画 plt.text(x=tx+offset[0], y=ty+offset[1], s=str(np.round(tq, 2)), ha='center', va='center', size=12) # 確認用の頂点を描画 plt.scatter(x=vertex_x+tx, y=vertex_y+ty, s=100) # 頂点 for i in range(len(vertex_x)): plt.text(x=vertex_x[i]+tx, y=vertex_y[i]+ty, s=str((vertex_y[i]+ty, vertex_x[i]+tx)), ha='center', va='top', size=15) # 座標ラベル plt.show()
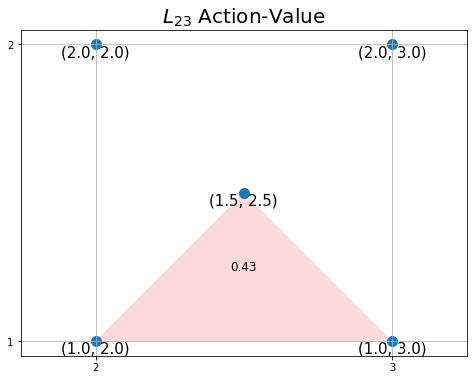
赤・白・緑に変化するカラーマップを設定して、plt.Polygon()のfc引数に指定します。
行動価値ラベルの表示位置も行動(三角形)に応じて用意する必要があります。
同様の処理を繰り返して、4つの行動(4つの三角形)を描画します。
# 全ての行動 action_space = [0, 1, 2, 3] # (仮の)行動価値関数を設定 q = {(state, action): np.random.randn(1)[0] for action in action_space} # 行動価値の最大値を取得 qmax = max(q.values()) # 行動ごとの三角形の頂点を設定 action_map = { 0: ((0.5+tx, 0.5+ty), (1.0+tx, 1.0+ty), (tx, 1.0+ty)), # 上 1: ((tx, ty), (1.0+tx, ty), (0.5+tx, 0.5+ty)), # 下 2: ((tx, ty), (0.5+tx, 0.5+ty), (tx, 1.0+ty)), # 左 3: ((0.5+tx, 0.5+ty), (1.0+tx, ty), (1.0+tx, 1.0+ty)) # 右 } # 行動ごとの価値ラベルのプロット位置を設定 offset_map = { 0: (0.5, 0.75), # 上 1: (0.5, 0.25), # 下 2: (0.25, 0.5), # 左 3: (0.75, 0.5) # 右 } # グラフの設定 plt.figure(figsize=(8, 6), facecolor='white') plt.title('$L_{'+str(y)+str(x)+'}$ Action-Values', fontsize=20) plt.xticks(ticks=[tx, 1+tx]) plt.yticks(ticks=[ty, 1+ty]) plt.grid() plt.axis('equal') # 行動ごとに処理 for action in action_space: # 行動価値を抽出 tq = q[(state, action)] # 行動価値を正規化 color_scale = 0.5 + (tq / qmax) / 2 # 行動価値を描画 poly = plt.Polygon(action_map[action], fc=cmap(color_scale)) # 三角形を作成 plt.gca().add_patch(poly) # 重ねて描画 # プロット位置の調整値を取得 offset = offset_map[action] # 行動価値ラベルを描画 plt.text(x=tx+offset[0], y=ty+offset[1], s=str(np.round(tq, 2)), ha='center', va='center', size=12) # 行動価値ラベル # 確認用の頂点を描画 plt.scatter(x=vertex_x+tx, y=vertex_y+ty, s=100) # 頂点 for i in range(len(vertex_x)): plt.text(x=vertex_x[i]+tx, y=vertex_y[i]+ty, s=str((vertex_y[i]+ty, vertex_x[i]+tx)), ha='center', va='top', size=15) # 座標ラベル plt.show()
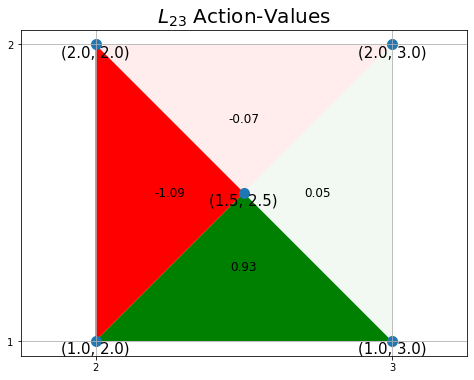
行動番号actionを使って対応する値を取り出せるように、三角形の頂点とラベルの表示位置をディクショナリに格納します。
for文を使って、行動ごとにこれまでの作図処理を繰り返して、4つの三角形を描画します。
行動価値の正規化については次で確認します。
ここまでがグリッドワールドの1マスで行う処理です。
・3×4マス
各マス(各状態)の処理を確認できたので、次は3×4マス(全ての状態)のグリッドワールドの場合を考えます。
グリッド線用の値を設定します。
# 縦軸・横軸のサイズを取得 ys = len(env.reward_map) xs = len(env.reward_map[0]) print(ys) print(xs)
3
4
各状態(マス)の報酬reward_mapの行数が縦のサイズys、各行の要素数が横のサイズxsに対応します。
全ての行動番号を設定します。また、カラーマップを作成します。
# 行動番号を取得 action_space = env.action_space print(action_space) # カラーマップを設定 color_list = ['red', 'white', 'green'] cmap = LinearSegmentedColormap.from_list('colormap_name', color_list)
[0, 1, 2, 3]
負の値なら赤色、0なら白色、正の値なら緑色になるように、グラデーション用の最小値と最大値を設定します。
# 行動価値の最小値・最大値を取得 qmax = max(Q.values()) qmin = min(Q.values()) print(qmin) print(qmax) # 最小値・最大値の絶対値に応じて再設定 qmax = max(qmax, abs(qmin)) qmin = -1 * qmax print(qmin) print(qmax) # 絶対値が1より小さい場合は1に再設定 qmax = 1 if qmax < 1 else qmax qmin = -1 if qmin > -1 else qmin print(qmin) print(qmax)
-2.5156937312073944
3.7310016055319273
-3.7310016055319273
3.7310016055319273
-3.7310016055319273
3.7310016055319273
「状態価値の可視化」のときと同様に、行動価値関数の最小値・最大値の絶対値を使って、グラデーションの最小値・最大値を設定します。
ヒートマップの色付け時の正規化の計算を確認します。
# 行動価値がとり得る値を作成 tq = np.linspace(qmin, qmax, num=5) # 行動価値を-1から1に正規化 scaled_tq = tq / qmax print(scaled_tq) # 行動価値を-0.5から0.5に正規化 scaled_tq = (tq / qmax) / 2 print(scaled_tq) # 行動価値を0から1に正規化 color_scale = 0.5 + (tq / qmax) / 2 print(color_scale)
[-1. -0.5 0. 0.5 1. ]
[-0.5 -0.25 0. 0.25 0.5 ]
[0. 0.25 0.5 0.75 1. ]
qminからqmaxの範囲の値tqを作成して、正規化の計算をします。
tqを最大値で割ることで-1から1の値になります。その値を、2で割ると-0.5から0.5の値になります。さらに、0.5を加えると0から1の値になります。
カラーマップcmapには0から1の値を渡す必要があります。
全てのマスで、行動価値のヒートマップとラベルを描画します。
# グラフの設定 plt.figure(figsize=(12, 9), facecolor='white') # 図の設定 plt.title('heatmap', fontsize=20) # タイトル plt.xticks(ticks=np.arange(xs)) # x軸の目盛位置 plt.yticks(ticks=np.arange(ys), labels=ys-np.arange(ys)-1) # y軸の目盛位置 plt.xlim(xmin=0, xmax=xs) # x軸の範囲 plt.ylim(ymin=0, ymax=ys) # y軸の範囲 plt.grid() # グリッド線 # マスごとに処理 for y in range(ys): for x in range(xs): # 行動ごとに処理 for action in action_space: # 装飾するマス(状態)を設定 state = (y, x) # ゴールの場合 if state == env.goal_state: # 描画せず次の状態へ continue # 作図用のx軸・y軸の値を設定 tx, ty = x, ys-y-1 # 行動ごとの三角形の頂点を設定 action_map = { 0: ((0.5+tx, 0.5+ty), (1.0+tx, 1.0+ty), (tx, 1.0+ty)), # 上 1: ((tx, ty), (1.0+tx, ty), (0.5+tx, 0.5+ty)), # 下 2: ((tx, ty), (0.5+tx, 0.5+ty), (tx, 1.0+ty)), # 左 3: ((0.5+tx, 0.5+ty), (1.0+tx, ty), (1.0+tx, 1.0+ty)) # 右 } # 行動ごとの価値ラベルのプロット位置を設定 offset_map = { 0: (0.5, 0.75), # 上 1: (0.5, 0.25), # 下 2: (0.25, 0.5), # 左 3: (0.75, 0.5) # 右 } # 壁の場合 if state == env.wall_state: # 壁を描画 rect = plt.Rectangle(xy=(tx, ty), width=1, height=1, fc=(0.4, 0.4, 0.4, 1.0)) # 長方形を作成 plt.gca().add_patch(rect) # 重ねて描画 # (よく分からない) elif state in env.goal_state: plt.gca().add_patch(plt.Rectangle(xy=(tx, ty), width=1, height=1, fc=(0.0, 1.0, 0.0, 1.0))) # 壁以外の場合 else: # 行動価値を抽出 tq = Q[(state, action)] # 行動価値を0から1に正規化 color_scale = 0.5 + (tq / qmax) / 2 # 三角形を描画 poly = plt.Polygon(action_map[action],fc=cmap(color_scale)) # 三角形を作成 plt.gca().add_patch(poly) # 重ねて描画 # プロット位置の調整値を取得 offset = offset_map[action] # 行動価値ラベルを描画 plt.text(x=tx+offset[0], y=ty+offset[1], s=str(np.round(tq, 2)), ha='center', va='center', size=12) # 行動価値ラベル plt.xlabel('x (width)') # x軸ラベル plt.ylabel('y (height)') # y軸ラベル plt.show()
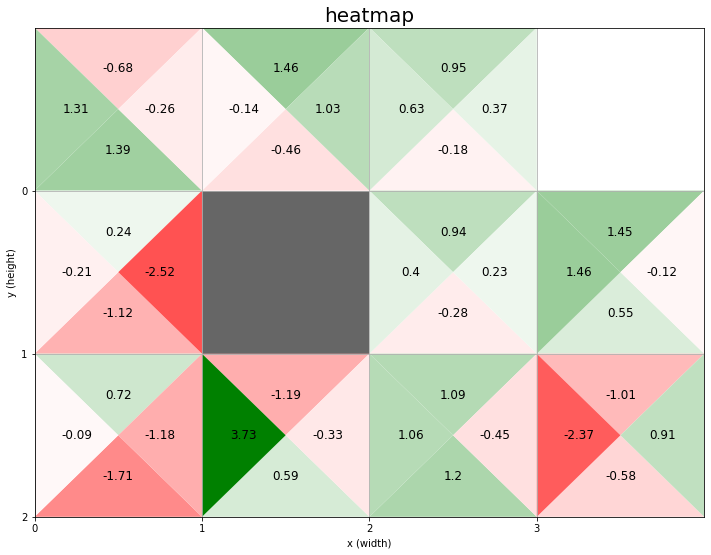
for文を使ってマス(状態)ごとに4つの三角形を描画する処理を繰り返します。ただし、壁のマスでは黒塗りの処理を行い、ゴールのマスでは処理しません(elifの処理って実行されなくないですか?)。
下のマスほどy軸の値が大きくなるのでした。そこで、ys-y-1をy軸の値として使います。
「状態価値関数の可視化」と同様に、報酬ラベルを表示します。
# グラフの設定 plt.figure(figsize=(12, 9), facecolor='white') # 図の設定 plt.title('Action-Value Function', fontsize=20) # タイトル plt.xticks(ticks=np.arange(xs)) # x軸の目盛位置 plt.yticks(ticks=np.arange(ys), labels=ys-np.arange(ys)-1) # y軸の目盛位置 plt.xlim(xmin=0, xmax=xs) # x軸の範囲 plt.ylim(ymin=0, ymax=ys) # y軸の範囲 plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False) # 軸ラベル plt.grid() # グリッド線 # マスごとに処理 for y in range(ys): for x in range(xs): # 行動ごとに処理 for action in action_space: # 装飾するマス(状態)を設定 state = (y, x) # 報酬を抽出 r = env.reward_map[y, x] # 報酬がある場合 if r != 0 and r is not None: # 報酬ラベル用の文字列を作成 txt = 'R ' + str(r) # ゴールの場合 if state == env.goal_state: # 報酬ラベルにゴールを追加 txt = txt + ' (GOAL)' # 報酬ラベルを描画 plt.text(x=x+0.1, y=ys-y-0.9, s=txt, ha='left', va='bottom', fontsize=15) # ゴールの場合 if state == env.goal_state: # 描画せず次の状態へ continue # 作図用のx軸・y軸の値を設定 tx, ty = x, ys-y-1 # 行動ごとの三角形の頂点を設定 action_map = { 0: ((0.5+tx, 0.5+ty), (1.0+tx, 1.0+ty), (tx, 1.0+ty)), # 上 1: ((tx, ty), (1.0+tx, ty), (0.5+tx, 0.5+ty)), # 下 2: ((tx, ty), (0.5+tx, 0.5+ty), (tx, 1.0+ty)), # 左 3: ((0.5+tx, 0.5+ty), (1.0+tx, ty), (1.0+tx, 1.0+ty)) # 右 } # 行動ごとの価値ラベルのプロット位置を設定 offset_map = { 0: (0.5, 0.75), # 上 1: (0.5, 0.25), # 下 2: (0.25, 0.5), # 左 3: (0.75, 0.5) # 右 } # 壁の場合 if state == env.wall_state: # 壁を描画 rect = plt.Rectangle(xy=(tx, ty), width=1, height=1, fc=(0.4, 0.4, 0.4, 1.0)) # 長方形を作成 plt.gca().add_patch(rect) # 重ねて描画 # (よく分からない) elif state in env.goal_state: plt.gca().add_patch(plt.Rectangle(xy=(tx, ty), width=1, height=1, fc=(0.0, 1.0, 0.0, 1.0))) # 壁以外の場合 else: # 行動価値を抽出 tq = Q[(state, action)] # 行動価値を0から1に正規化 color_scale = 0.5 + (tq / qmax) / 2 # 三角形を描画 poly = plt.Polygon(action_map[action],fc=cmap(color_scale)) # 三角形を作成 plt.gca().add_patch(poly) # 重ねて描画 # プロット位置の調整値を取得 offset = offset_map[action] # 行動価値ラベルを描画 plt.text(x=tx+offset[0], y=ty+offset[1], s=str(np.round(tq, 2)), ha='center', va='center', size=15) # 行動価値ラベル plt.show()
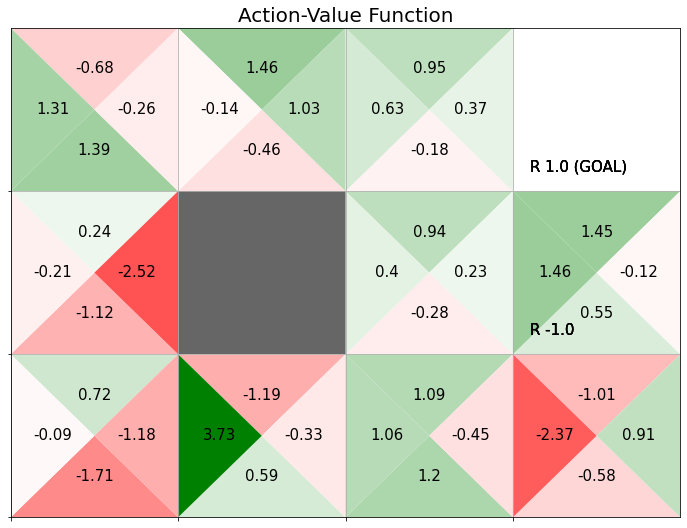
以上で、行動価値関数のヒートマップを作図できました。
・greedy化した方策ラベル
最後に、行動価値関数に従いgreedy化した方策を作成して、方策ラベルを描画します。
# 方策を初期化 pi = {} # マスごとに処理 for y in range(ys): for x in range(xs): # 装飾するマス(状態)を設定 state = (y, x) # 行動価値を抽出 qs = [Q[state, action] for action in action_space] # action_size # 行動価値が最大の行動番号を取得 max_action = np.argmax(qs) # 確率論的方策(疑似の決定論的方策)を作成 probs = {0: 0.0, 1: 0.0, 2: 0.0, 3: 0.0} # 初期化 probs[max_action] = 1.0 # 価値が最大となる行動の確率を1に設定 pi[state] = probs # ディクショナリを格納 # 方策を作図 env.render_v(v=None, policy=pi)
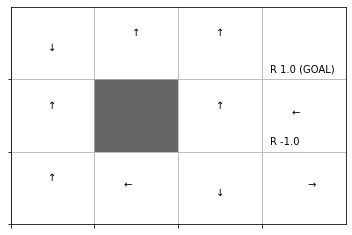
方策ラベルを描画できました。
以上が、行動価値関数の可視化メソッドの処理です。こちらも実際の実装では、方策ラベルのグラフを出力するかの設定などの処理が含まれます。また、オブジェクト指向で作図します。
この項では、GridWorldクラスを確認しました。以降の節で利用します。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning 4 ――強化学習編』オライリー・ジャパン,2022年.
- サポートページ:GitHub - oreilly-japan/deep-learning-from-scratch-4
おわりに
5章が進んだので行動価値関数の可視化について取り組みました。
「render_qメソッド」について追加する際に「render_vメソッド」の内容を修正して「評価と改善に関するメソッド」から記事を分割しました。
4章の内容の記事については修正前の作図コードを使っています。
先日公開された新曲をどうぞ♪
This is Hello!Project.
【次節の内容】