はじめに
『ゼロから作るDeep Learning 4 ――強化学習編』の独学時のまとめノートです。初学者の補助となるようにゼロつくシリーズの4巻の内容に解説を加えていきます。本と一緒に読んでください。
この記事は、5.4.1項と5.4.2項の内容です。モンテカルロ法による方策制御(行動価値関数と方策の推定)の基本的な処理を実装します。
【前節の内容】
【他の記事一覧】
【この記事の内容】
5.4 モンテカルロ法による方策制御
モンテカルロ法により行動価値関数を求めて、行動価値が最大となる行動を抽出(方策を制御)するエージェントを実装します。
利用するライブラリを読み込みます。
# ライブラリを読み込み import numpy as np from collections import defaultdict
また、3×4マスのグリッドワールドのクラスGridWorldを読み込みます。
# 実装済みのクラスと関数を読み込み import sys sys.path.append('../deep-learning-from-scratch-4-master') from common.gridworld import GridWorld
実装済みクラスの読み込みについては「3.6.1:MNISTデータセットの読み込み【ゼロつく1のノート(Python)】 - からっぽのしょこ」、GridWorldクラスについては「4.2.1:GridWorldクラスの実装:評価と改善に関するメソッド【ゼロつく4のノート】 - からっぽのしょこ」「4.2.1:GridWorldクラスの実装:可視化に関するメソッド【ゼロつく4のノート】 - からっぽのしょこ」を参照してください。
5.4.1 評価と改善
まずは、行動価値関数と方策のgreedy化の計算を数式で確認します。
・数式の確認
時刻$t$の収益は、割引率$0 \leq \gamma \leq 1$を用いて、次の式で計算するのでした(2.3.2項・3.1.2項)。
行動価値関数は、現在の状態$s$で行動$a$を行った後の収益$G$の期待値で定義されました(3.3.1項)。
真の行動価値関数$q_{\pi}(s, a)$を求めるには、方策$\pi$や報酬関数$r(s, a, s')$が既知である必要があります。
そこで、方策が未知の場合は、サンプリングした収益$G^{(i)}$の標本平均を行動価値関数の推定値$Q_{\pi}(s, a)$とします。
ここで、$i$回目のエピソードで得られた収益を$G^{(i)}$で表します。
標本平均をインクリメンタルに求める場合は、次の式を繰り返し計算します(1.3.2項)。
$n$回更新した行動価値関数の推定値($n$個の収益の標本平均)を$Q_n(s)$で表します。
行動価値関数が最大となる行動$a$を選びます(3.5.2項・4.4.1項)。
greedy化した方策では1つの行動を取るので、確率分布(確率論的方策)$\pi(a | s)$ではなく、関数(決定論的方策)$\mu(s)$で表します。
5.4.2 モンテカルロ法を使った方策制御の実装
次は、モンテカルロ法により行動価値関数の計算とgreedy化した方策の作成(方策の制御)を行うエージェントを実装します。
・処理の確認:greedy化
まずは、greedy_probs()の内部で行う処理を確認します。状態ごとに、行動価値が最大となる行動を選び(方策をgreedy化し)ます。
例として、ダミーの行動価値関数のディクショナリを作成しておきます。
# 状態を指定 state = (1, 2) # 行動の種類数を設定 action_size = 4 # (仮の)行動価値関数を作成 Q = {(state, action): np.random.rand() for action in range(action_size)} print(list(Q.keys())) print(np.round(list(Q.values()), 3))
[((1, 2), 0), ((1, 2), 1), ((1, 2), 2), ((1, 2), 3)]
[0.641 0.129 0.468 0.567]
状態を指定して、上下左右の4つの行動に対する値を格納します。
行動価値を取り出してリストに格納します。
# 行動ごとの行動価値を抽出 qs = [Q[(state, action)] for action in range(action_size)] print(np.round(qs, 3))
[0.641 0.129 0.468 0.567]
リスト内包表記を使って、順番にキーを指定して値を取り出します。
行動価値が最大の行動を抽出します。
# 行動価値の最大値のインデックスを抽出 max_action = np.argmax(qs) print(max_action)
0
要素のインデックスが行動番号に対応しているので、np.argmax()で最大値のインデックスを抽出します。
ちなみに、最大値が複数ある場合はインデックスが小さい方が出力されます。
# 値が同じ場合 print(np.argmax([0, 1, 2, 0, 1, 2]))
2
決定論的に行動が決まるように確率論的方策を作成します。
# 全ての値を0に設定 action_probs = {action: 0.0 for action in range(action_size)} print(action_probs) # 行動価値が最大の行動の確率を1に設定 action_probs[max_action] = 1.0 print(action_probs)
{0: 0.0, 1: 0.0, 2: 0.0, 3: 0.0}
{0: 1.0, 1: 0.0, 2: 0.0, 3: 0.0}
全ての値が0.0となるようにディクショナリを作成して、max_actionの値を1.0に置き換えます。
max_actionの行動確率を1にすることで、常にmax_actionの行動を取ります。
# 行動番号・行動確率を取得 actions = list(action_probs.keys()) probs = list(action_probs.values()) # 行動を生成 for _ in range(5): action = np.random.choice(a=actions, p=probs) print(action)
0
0
0
0
0
max_actionのみが出力されました。
以上がgreedy化の処理です。
・実装:greedy化
処理の確認ができたので、greedy化する処理を関数として実装します。
# greedy化の実装 def greedy_probs(Q, state, action_size=4): # 各状態における行動価値のリストを作成 qs = [Q[(state, action)] for action in range(action_size)] # 行動価値が最大の行動番号を抽出 max_action = np.argmax(qs) # 疑似的な決定論的方策を作成 action_probs = {action: 0.0 for action in range(action_size)} action_probs[max_action] = 1.0 return action_probs
実装した関数を試してみましょう。
# greedy化した方策を作成 action_probs = greedy_probs(Q, state) print(action_probs)
{0: 1.0, 1: 0.0, 2: 0.0, 3: 0.0}
処理の確認時と同じ結果が得られました。
・処理の確認:エージェント
次は、McAgentクラスの内部で行う処理を確認します。基本的な処理はRandomAgentと同じなので、「5.3:モンテカルロ法による方策評価の実装【ゼロつく4のノート】 - からっぽのしょこ」も参照してください。
全ての方策を格納するディクショナリを作成します。
# 確率論的方策用の確率分布を指定 random_actions = {0: 0.25, 1: 0.25, 2: 0.25, 3: 0.25} # 確率論的方策を初期化 pi = defaultdict(lambda: random_actions) print(pi.items())
dict_items([])
各状態の確率論的方策の初期値をrandom_actionsとして、全ての状態の確率論的方策を格納するpiを作成します。
サンプリングの際に、遷移した状態の確率論的方策が格納されるのでした。
# 状態を指定 state = (1, 2) # 指定した状態の方策を取得 action_probs = pi[state] print(action_probs)
{0: 0.25, 1: 0.25, 2: 0.25, 3: 0.25}
1エピソードのサンプリングが終了すると、行動価値関数を計算します。状態価値関数のときと同様なのでここでは簡単に、ランダムな値を設定しておきます。
# 行動の種類数を設定 action_size = 4 # (仮の)行動価値関数を作成 Q = {(state, action): np.random.rand() for action in range(action_size)} print(list(Q.keys())) print(np.round(list(Q.values()), 3))
[((1, 2), 0), ((1, 2), 1), ((1, 2), 2), ((1, 2), 3)]
[0.217 0.425 0.622 0.963]
状態価値関数Vでは状態stateをキーにしました。行動価値関数Qでは状態stateと行動actionをキーにします。これは、それぞれ状態または状態と行動によって値が一意に定まり、また関数の引数$V(s), Q(s, a)$に対応しています。
行動価値関数に応じてgreedy化した方策に更新します。
# greedy化した方策を作成 pi[state] = action_probs = greedy_probs(Q, state) print(pi.items())
dict_items([((1, 2), {0: 0.0, 1: 0.0, 2: 0.0, 3: 1.0})])
greedy_probs()で行動価値が最大の行動を取る方策を作成して、piの値を置き換えます。
以上が、モンテカルロ法による方策制御を行うエージェントの処理です。
・実装:エージェント
処理の確認ができたので、マルコフ法におけるエージェントの処理をクラスとして実装します。
# マルコフ法におけるエージェントの実装 class McAgent: # 初期化メソッドの定義 def __init__(self): # 値の設定 self.gamma = 0.9 # 割引率 self.action_size = 4 # 行動の種類数 # オブジェクトの初期化 random_actions = {0: 0.25, 1: 0.25, 2: 0.25, 3: 0.25} # 確率論的方策用の確率分布 self.pi = defaultdict(lambda: random_actions) # 確率論的方策 self.Q = defaultdict(lambda: 0) # 行動価値関数 self.cnts = defaultdict(lambda: 0) # 遷移回数 self.memory = [] # サンプルデータ # 行動メソッドの定義 def get_action(self, state): # 現在の状態における方策の確率分布を取得 action_probs = self.pi[state] actions = list(action_probs.keys()) # 行動番号 probs = list(action_probs.values()) # 行動確率 # 確率論的方策による行動を出力 return np.random.choice(actions, p=probs) # 記録メソッドの定義 def add(self, state, action, reward): # 現在の時刻におけるサンプルデータをタプルに格納 data = (state, action, reward) # サンプルを格納 self.memory.append(data) # 記録の初期化メソッドの定義 def reset(self): # 記録用のリストを初期化 self.memory.clear() # 方策の計算メソッドの定義 def update(self): # 行動価値関数を計算して、greedy化した方策を作成 G = 0 for data in reversed(self.memory): # 各時刻におけるサンプルデータを取得 state, action, reward = data # 収益を計算:式(3.3) G = self.gamma * G + reward # キーを作成 key = (state, action) # 遷移回数をカウント self.cnts[key] += 1 # 行動価値関数を計算:式(5.5) self.Q[key] += (G - self.Q[key]) / self.cnts[key] # 方策をgreedy化:式(5.3) self.pi[state] = greedy_probs(self.Q, state)
実装したクラスを試してみましょう。
環境(グリッドワールド)とエージェントのインスタンスを作成します。
# 環境とエージェントのインスタンスを作成 env = GridWorld() agent = McAgent() # 最初の状態を取得 state = env.start_state print(state) # 1エピソードのシミュレーション while True: # 確率論的方策に従い行動を決定 action = agent.get_action(state) # サンプルデータを取得 next_state, reward, done = env.step(action) # サンプルデータを格納 agent.add(state, action, reward) # ゴールに着いた場合 if done: # ループを終了 break # 状態を更新 state = next_state print(next_state)
(2, 0)
(0, 3)
agentのget_action()で方策に従い行動して、envのstep()で状態を遷移し報酬を出力します。現在の状態・行動・報酬をagentのadd()で記録します。
ゴールマスに着くとdoneがTrueになるので、breakでループ処理を終了します。
サンプルデータがmemoryに格納されているのを確認します。
# サンプルデータを確認 print(agent.memory[:5]) print(len(agent.memory))
[((2, 0), 2, 0), ((2, 0), 3, 0), ((2, 1), 0, 0), ((2, 1), 3, 0), ((2, 2), 3, 0)]
11
update()メソッドで行動価値関数と方策を計算します。
# (確認用に)状態を指定 state = (0, 2) # 行動価値関数と方策を確認 print(agent.Q.values()) print(agent.pi[state].values()) # 行動価値関数と方策を計算 agent.update() # 行動価値関数と方策を確認 print(np.round([agent.Q[(state, action)] for action in range(agent.action_size)], 4)) print(agent.pi[state].values())
dict_values([])
dict_values([0.25, 0.25, 0.25, 0.25])
[0 0 0 0]
dict_values([0.25, 0.25, 0.25, 0.25])
サンプルとして得られなかった状態はagent.Qに含まれません。
reset()でサンプルデータを削除します。
# サンプルデータを削除 agent.reset() print(agent.memory)
[]
この項では、エージェントを実装しました。次項では、行動価値関数と方策を推定します。
・モンテカルロ法を動かす
3×4マスのグリッドワールド(図4-8)に対してモンテカルロ法により行動価値関数とgreedy化した方策を求めます。処理の内容については5.4.5項を参照してください。
・推定
マルコフ法により行動価値関数を推定してgreedyな方策を求めます(方策を制御します)。
# インスタンスを作成 env = GridWorld() agent = McAgent() # エピソード数を指定 episodes = 100 # 推移の可視化用のリストを初期化 trace_Q = [{(state, action): agent.Q[state] for action in env.action_space for state in env.states()}] # 初期値を記録 # 無限ループ回避用のフラグを設定 flag = False # 繰り返しシミュレーション for episode in range(episodes): # 状態を初期化(エージェントの位置をスタートマスに設定) state = env.reset() # サンプルデータを初期化 agent.reset() # 無限ループの場合 if flag: # シミュレーションを終了 print('episode ' + str(episode) + ': stop') break # 試行回数(時刻)を初期化 t = 0 # 1エピソードのシミュレーション while True: # 試行回数をカウント t += 1 # ε-greedy法により行動を決定 action = agent.get_action(state) # サンプルデータを取得 next_state, reward, done = env.step(action) # サンプルデータを格納 agent.add(state, action, reward) # ゴールに着いた場合 if done: # 行動価値関数を計算 agent.update() # 更新値を記録 trace_Q.append(agent.Q.copy()) # 試行回数を表示 print('episode '+str(episode+1) + ': T='+str(t)) # ループを終了して次のエピソード break # ゴールに着かない場合 elif t > 200: # フラグを設定してループを終了 flag = True break # 状態を更新 state = next_state
episode 1: T=18
episode 2: stop
スタートマスからゴールマスに着くまでを1エピソードとします。エピソードごとに、GridWorldクラスのreset()メソッドで状態を初期化し(エージェントをスタートマスに戻し)、McAgentクラスのreset()メソッドでサンプルデータを初期化(過去のデータを削除)します。
episodesに指定した回数のシミュレーションを行い、繰り返し行動価値関数と方策を更新します。
ただし、現在の実装では上手く推定できず、無限ループが生じることがあります。そこで、サンプリング回数tが一定以上になるとシミュレーションを終了するようにしています。
推定した行動価値関数をヒートマップで、greedy化した方策を矢印のラベルで確認します。
# 行動価値関数のヒートマップを作成
env.render_q(q=agent.Q)
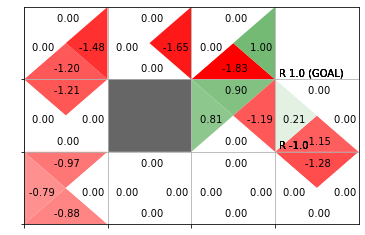

greedy化した方策では決定論的に行動します。そのため、矢印の方向にだけ遷移するとゴールに辿り着けないのが分かります。これは少ないサンプルに依存して方策を推定したためです。
この節では、モンテカルロ法により方策制御を行うエージェントを実装しました。ただし、行動価値関数とgreedy化した方策を求める際に問題が生じました。次節では、サンプリングと行動価値の計算に関して改善を行います。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning 4 ――強化学習編』オライリー・ジャパン,2022年.
- サポートページ:GitHub - oreilly-japan/deep-learning-from-scratch-4
おわりに
あまり上手くいかないと書いてあるので実際にやってみました。無限ループになったので焦りました。
【次節の内容】