8.1：OpenAI Gym：Classic Control【ゼロつく4のノート】

はじめに

　『ゼロから作るDeep Learning 4 ――強化学習編』の独学時のまとめノートです。初学者の補助となるようにゼロつくシリーズの4巻の内容に解説を加えていきます。本と一緒に読んでください。

　この記事は、8.1節の内容です。OpenAI GymのClassic Controlのゲームを確認します。

【前節の内容】

www.anarchive-beta.com

【他の記事一覧】

www.anarchive-beta.com

【この記事の内容】

8.1 OpenAI Gym

　OpenAI GymのClassic Controlのゲームについて確認します。

　利用するライブラリを読み込みます。

# ライブラリを読み込み
import gym
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

　gymライブラリは依存関係が膨大なため、pip install gymを行っても全てをインストールしません。そのため、renderメソッドを使うと次のメッセージが出ます。

DependencyNotInstalled: pygame is not installed, run `pip install gym[classic_control]`

　メッセージの通り、pip install gym[classic_control]を実行すると、描画に利用するpygameライブラリがインストールされます。

8.1.1-2 OpenAI Gymの基礎知識

　Classic Controlの4つのゲームに関して、それぞれ状態・行動・報酬などを確認します。
　ライブラリのドキュメント等では観測(observation)という表現を使いますが、他の記事との兼ね合い等から状態(state)と表現します。

Cart Pole

　カートポールは、ポールが倒れないようにカートを制御するゲームです。

状態と報酬

　カートポールのインスタンスを作成します。

# 環境のインスタンスを作成
env = gym.make('CartPole-v1', render_mode='rgb_array')

# 状態を初期化
state, info = env.reset()
print(state)
print(info)

[ 0.00119186 -0.04395894  0.0015907  -0.00124087]
{}

　カートポールの状態は、「カートの位置・カートの速度・ポールの角度(ラジアン)・ポールの角速度」の4つの値で表されます。それぞれ初期値は、-0.05から0.05のランダムな値が設定されます。

　作図用の配列を出力します。

# 画像データを作成
rgb_data = env.render()
print(rgb_data.shape)
print(rgb_data[250:300, 300:350, 0])

(400, 600, 3)
[[202 202 202 ... 255 255 255]
 [202 202 202 ... 255 255 255]
 [202 202 202 ... 255 255 255]
 ...
 [129 136 158 ... 255 255 255]
 [  0   0   0 ... 255 255 255]
 [  0   0   0 ...   0   0   0]]

　インスタンス作成時の引数にrender_mode='rgb_array'を指定しておくと、render()で状態の描画用の配列を作成できます。
　カートポールの画像データは、縦400・横600の要素(ピクセル)がそれぞれ赤・緑・青の3色分で構成されます。各要素は、0から255の256段階の離散値です。最大値の255で割ると0から1の値に正規化できます。

　最初の状態のカートポールを作図します。

# 状態ラベルを作成
state_text = f'cart position={state[0]:5.2f}, '
state_text += f'cart velocity={state[1]:6.3f}\n'
state_text += f'pole angle   ={state[2]:5.2f}, '
state_text += f'pole velocity={state[3]:6.3f}'

# カートポールを描画
plt.figure(figsize=(9, 7), facecolor='white')
plt.suptitle('Cart Pole', fontsize=20)
plt.imshow(rgb_data)
plt.xticks(ticks=[])
plt.yticks(ticks=[])
plt.title(state_text, loc='left')
plt.show()

カートポールの初期状態

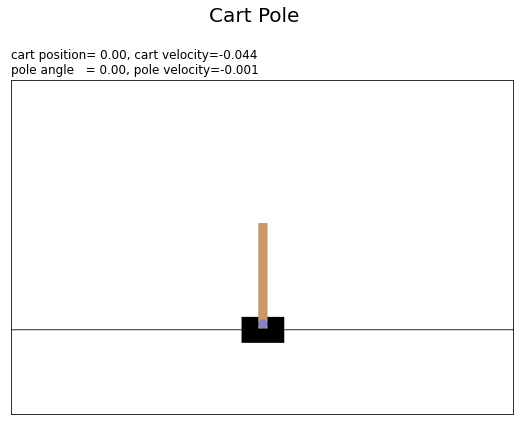
　plt.imshow()でRGBデータを描画します。

　カートの位置とポールの角度について、アニメーションで確認します。

・作図コード(クリックで展開)

# 状態として利用する値を指定
position_vals = np.arange(-2.4, 2.41, step=0.1).round(1) # カートの位置
angle_vals = np.arange(-3.1, 3.11, step=0.1).round(1) # ポールの角度

# フレーム数を設定
frame_num = len(position_vals)
#frame_num = len(angle_vals)
print(frame_num)

# 図を初期化
fig = plt.figure(figsize=(9, 7), facecolor='white')
fig.suptitle('Cart Pole', fontsize=20)

# 作図処理を関数として定義
def update(i):
    # i番目の値を取得
    x = position_vals[i]
    #theta = angle_vals[i]
    
    # 固定する値を指定
    #x = 0.0
    x_dot = 0.0
    theta = 0.0
    theta_dot = 0.0
    
    # インスタンスを初期化
    env = gym.make('CartPole-v1', render_mode='rgb_array')
    _, _ = env.reset()
    
    # 状態を設定
    state = np.array([x, x_dot, theta, theta_dot])
    env.env.env.env.__dict__['state'] = state
    
    # 画像データを作成
    rgb_data = env.render()
    
    # 状態ラベルを作成
    state_text = f'cart position={x:5.2f}, '
    state_text += 'cart velocity=' + str(x_dot) + '\n'
    state_text += f'pole angle   ={theta:5.2f}, '
    state_text += 'pole velocity=' + str(theta_dot)
    
    # カートポールを描画
    plt.imshow(rgb_data)
    plt.xticks(ticks=[])
    plt.yticks(ticks=[])
    plt.title(state_text, loc='left')

# gif画像を作成
anime = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100)

# gif画像を保存
anime.save('CartPole_state.gif')

　作図処理を関数update()として定義して、FuncAnimation()でアニメーション(gif画像)を作成します。各フレームの図はimshow()で描画します。
　(おそらく作図処理軽減のため)インスタンス内の状態stateを書き換えてもrender()に反映されないので、フレームごとにインスタンスを初期化します。

　フレームごとに、カートの位置xまたはポールの角度thetaの値を変更して描画します。(x, x_dot, theta, theta_dotは、クラス内部での変数名です。)

カートポールの状態

　カートの位置state[0]が-2.4より大きく2.4より小さい範囲、またポールの角度state[2]が-0.209より大きく0.209より小さい(正確には$\pm 12 \frac{\pi}{180}$の)範囲のとき、報酬1が得られます。範囲外になると、以降の報酬が0になります。

行動

　カートポールは、2種類の行動を取ります。

# 行動の種類数を確認
print(env.action_space)

Discrete(3)

　0はカートを左に押し、1は右に押します。

　行動を生成してみます。

# 行動をサンプリング
for _ in range(5):
    # ランダムに行動を決定
    action = env.action_space.sample()
    print(action)

1
1
0
1
0

　ランダムな行動を繰り返します。

# 環境のインスタンスを作成
env = gym.make('CartPole-v1', render_mode='rgb_array')

# 総時刻(行動回数)を指定
T = 100

# 最初の状態を取得
state, info = env.reset()

# 状態の記録用リストを初期化
state_data = []
render_data = [env.render()] # 最初の状態

# 1エピソードのシミュレーション
for t in range(T):
    # ランダムに行動を決定
    action = env.action_space.sample()
    
    # 状態を遷移
    next_state, reward, terminated, truncated, info = env.step(action)
    
    # 状態を保存
    state_data.append((state, action, reward, terminated)) # 現在
    render_data.append(env.render()) # 次
    
    # サンプルを表示
    print(
        't=' + str(t) + 
        ', state(position)=' + str(state[0].round(3)) + 
        ', action=' + str(action) + 
        ', reward=' + str(reward) + 
        ', terminated:' + str(terminated) + 
        ', truncated:' + str(truncated)
    )
    
    # 状態を更新
    state = next_state

# 最後の状態を保存
state_data.append((state, None, None, None))

t=0, state(position)=0.035, action=1, reward=1.0, terminated:False, truncated:False
t=1, state(position)=0.034, action=0, reward=1.0, terminated:False, truncated:False
t=2, state(position)=0.037, action=0, reward=1.0, terminated:False, truncated:False
t=3, state(position)=0.036, action=0, reward=1.0, terminated:False, truncated:False
t=4, state(position)=0.031, action=0, reward=1.0, terminated:False, truncated:False
(省略)
t=95, state(position)=-0.428, action=1, reward=0.0, terminated:True, truncated:False
t=96, state(position)=-0.439, action=1, reward=0.0, terminated:True, truncated:False
t=97, state(position)=-0.447, action=0, reward=0.0, terminated:True, truncated:False
t=98, state(position)=-0.45, action=0, reward=0.0, terminated:True, truncated:False
t=99, state(position)=-0.458, action=0, reward=0.0, terminated:True, truncated:False

　カートの位置またはポールの角度が閾値を超えると、終了フラグterminatedがFalse(エピソードが終了)になります。また、総時刻(行動回数)が500になると、打ち切りフラグtruncatedがTrue(エピソードが打ち切り)になります。
　(terminatedがTrueなのにstep()を続けるな的な警告文が出ました。)

　カートポールのアニメーションを作成します。

・作図コード(クリックで展開)

# 図を初期化
fig = plt.figure(figsize=(9, 7), facecolor='white')
fig.suptitle('Cart Pole', fontsize=20)

# 作図処理を関数として定義
def update(t):
    # 時刻tの状態を取得
    state, action, reward, terminated = state_data[t]
    rgb_data = render_data[t]
    
    # 状態ラベルを作成
    state_text = 't=' + str(t) + '\n'
    state_text += f'cart position={state[0]:5.2f}, '
    state_text += f'cart velocity={state[1]:6.3f}\n'
    state_text += f'pole angle   ={state[2]:5.2f}, '
    state_text += f'pole velocity={state[3]:6.3f}\n'
    state_text += 'action=' + str(action) + ', '
    state_text += 'reward=' + str(reward) + ', '
    state_text += 'terminated:' + str(terminated)
    
    # カートポールを描画
    plt.imshow(rgb_data)
    plt.xticks(ticks=[])
    plt.yticks(ticks=[])
    plt.title(state_text, loc='left')

# gif画像を作成
anime = FuncAnimation(fig=fig, func=update, frames=T+1, interval=50)

# gif画像を保存
anime.save('CartPole_random.gif')

カートポールの行動と状態遷移

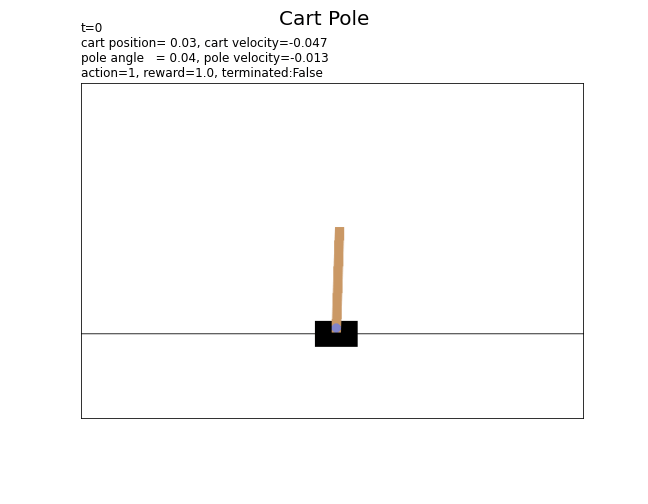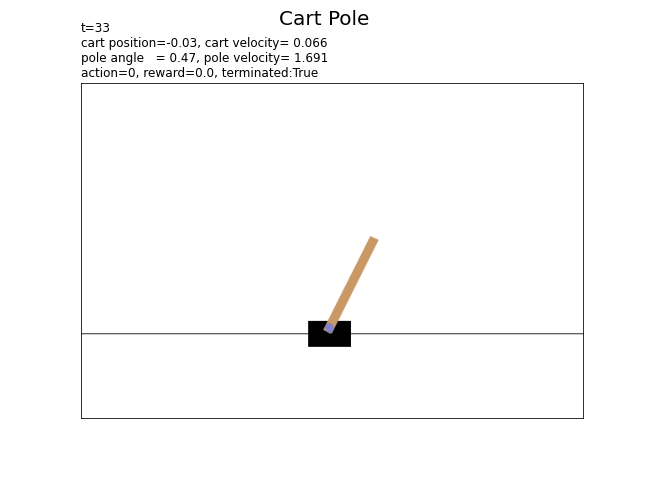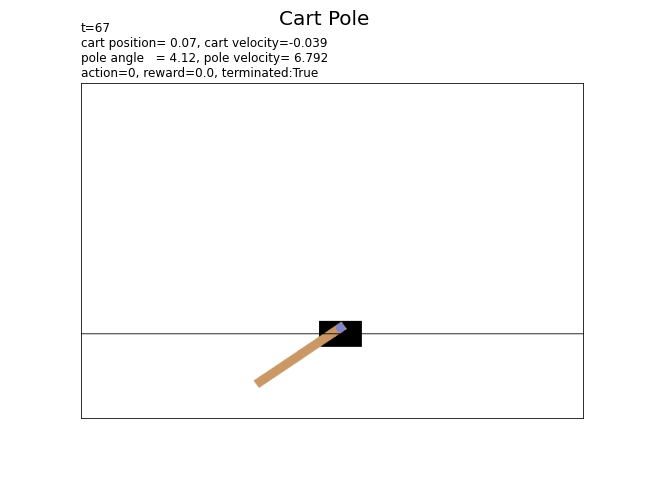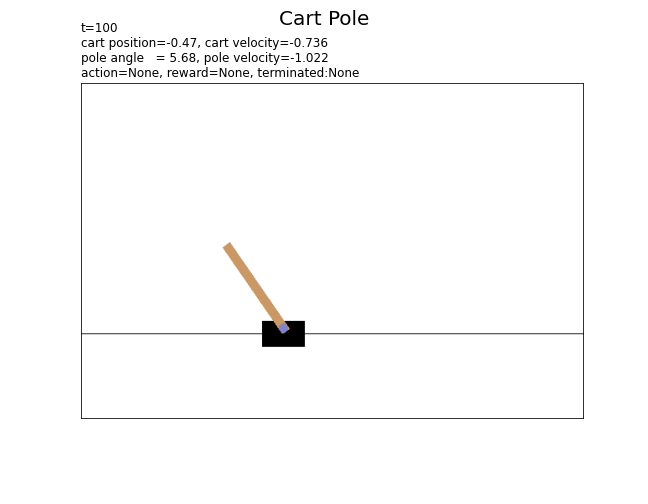
　以上が、カートポールの基本的な設定です。

Mountain Car

　マウンテンカーは、車を制御して右の山の頂上にあるゴールを目指すゲームです。

状態と報酬

　マウンテンカーのインスタンスを作成します。

# 環境のインスタンスを作成
env = gym.make('MountainCar-v0', render_mode='rgb_array')

# 状態を初期化
state, info = env.reset()
print(state)
print(_)

[-0.44273546  0.        ]
{}

　マウンテンカーの状態は、「車の位置・車の速度」の2つの値で表されます。車の位置の初期値は-0.6から-0.4のランダムな値、速度の初期値は0が設定されます。

　作図用の配列を出力します。

# 画像データを作成
rgb_data = env.render()
print(rgb_data.shape)

(400, 600, 3)

　マウンテンカーの画像データは、縦400×横600×3色の値で構成されます。

　最初の状態のマウンテンカーを作図します。

# 状態ラベルを作成
state_text = f'position={state[0]:.2f}, '
state_text += f'velocity={state[1]:.3f}'

# カートポールを描画
plt.figure(figsize=(9, 7), facecolor='white')
plt.suptitle('Mountain Car', fontsize=20)
plt.imshow(rgb_data)
plt.xticks(ticks=[])
plt.yticks(ticks=[])
plt.title(state_text, loc='left')
plt.show()

マウンテンカーの初期状態

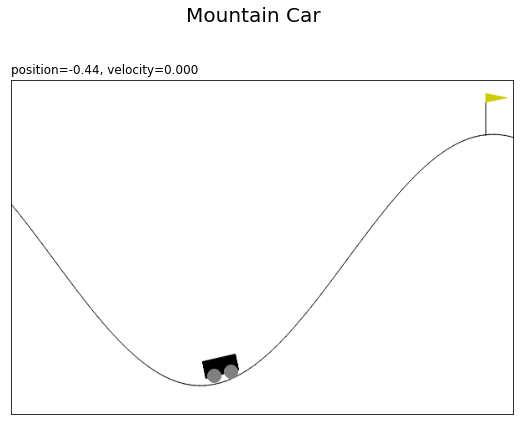
　車の位置について、アニメーションで確認します。

・作図コード(クリックで展開)

# 状態として利用する値を指定
position_vals = np.arange(-1.2, 0.61, step=0.05).round(2) # 車の位置

# フレーム数を設定
frame_num = len(position_vals)
print(frame_num)

# 図を初期化
fig = plt.figure(figsize=(9, 7), facecolor='white')
fig.suptitle('Mountain Car', fontsize=20)

# 作図処理を関数として定義
def update(i):
    # i番目の値を取得
    position = position_vals[i]
    
    # 固定する値を指定
    velocity = 0.0
    
    # インスタンスを初期化
    env = gym.make('MountainCar-v0', render_mode='rgb_array')
    _, _ = env.reset()
    
    # 状態を設定
    state = np.array([position, velocity])
    env.env.env.env.__dict__['state'] = state
    
    # 画像データを作成
    rgb_data = env.render()
    
    # 状態ラベルを作成
    state_text = f'position={position:5.2f}, '
    state_text += 'velocity=' + str(velocity)

    # マウンテンカーを描画
    plt.imshow(rgb_data)
    plt.xticks(ticks=[])
    plt.yticks(ticks=[])
    plt.title(state_text, loc='left')

# gif画像を作成
anime = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100)

# gif画像を保存
anime.save('MountainCar_state.gif')

　フレームごとに、車の位置positionの値を変更して描画します。

マウンテンカーの状態

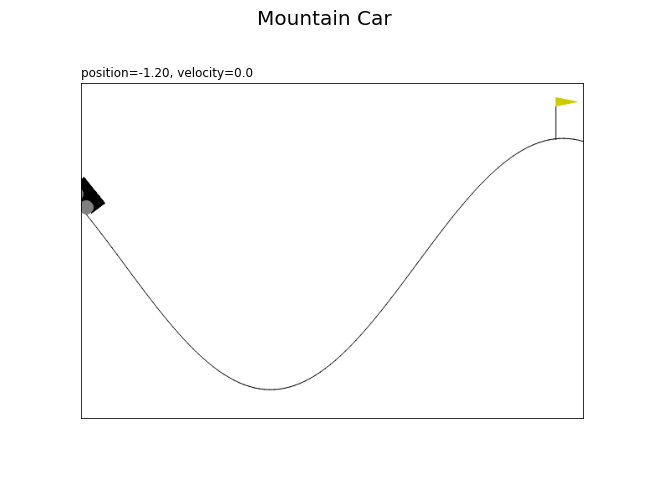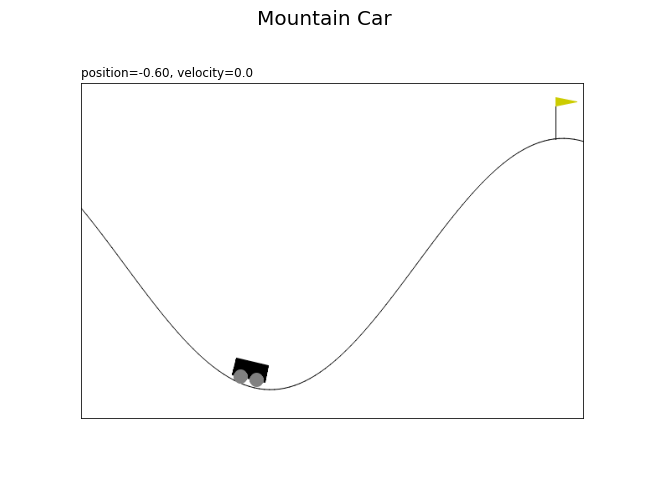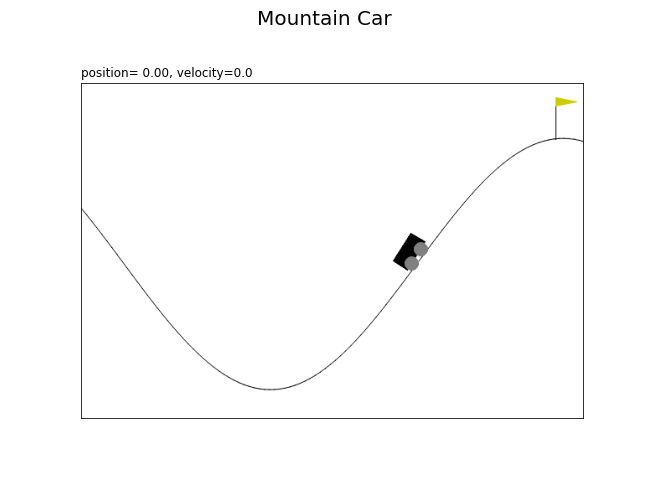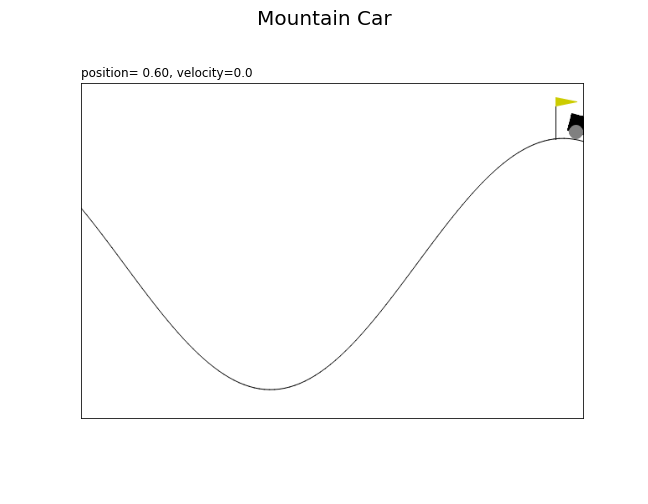
　車の位置がゴールの位置に着く、つまりstate[0]が0.5以上になることを目指します。

行動

　マウンテンカーは、3種類の行動を取ります。

# 行動の種類数を確認
print(env.action_space)

Discrete(3)

　0は車を左に押し、1は押さない、2は右に押します。

　行動を生成してみます。

# 行動をサンプリング
for _ in range(5):
    # ランダムに行動を決定
    action = env.action_space.sample()
    print(action)

0
0
2
1
2

　ランダムな行動を繰り返します。

# 環境のインスタンスを作成
env = gym.make('MountainCar-v0', render_mode='rgb_array')

# 総時刻(行動回数)を指定
T = 100

# 最初の状態を取得
state, info = env.reset()

# 状態の記録用リストを初期化
state_data = []
render_data = [env.render()] # 最初の状態

# 1エピソードのシミュレーション
for t in range(T):
    # ランダムに行動を決定
    action = env.action_space.sample()
    
    # 状態を遷移
    next_state, reward, terminated, truncated, info = env.step(action)
    
    # 状態を保存
    state_data.append((state, action, reward, terminated)) # 現在
    render_data.append(env.render()) # 次
    
    # サンプルを表示
    print(
        't=' + str(t) + 
        ', state(position)=' + str(state[0].round(3)) + 
        ', action=' + str(action) + 
        ', reward=' + str(reward) + 
        ', terminated:' + str(terminated) + 
        ', truncated:' + str(truncated)
    )
    
    # 状態を更新
    state = next_state

# 最後の状態を保存
state_data.append((state, None, None, None))

t=0, state(position)=-0.493, action=0, reward=-1.0, terminated:False, truncated:False
t=1, state(position)=-0.494, action=2, reward=-1.0, terminated:False, truncated:False
t=2, state(position)=-0.495, action=0, reward=-1.0, terminated:False, truncated:False
t=3, state(position)=-0.496, action=0, reward=-1.0, terminated:False, truncated:False
t=4, state(position)=-0.499, action=0, reward=-1.0, terminated:False, truncated:False
(省略)
t=95, state(position)=-0.56, action=1, reward=-1.0, terminated:False, truncated:False
t=96, state(position)=-0.566, action=1, reward=-1.0, terminated:False, truncated:False
t=97, state(position)=-0.572, action=0, reward=-1.0, terminated:False, truncated:False
t=98, state(position)=-0.579, action=2, reward=-1.0, terminated:False, truncated:False
t=99, state(position)=-0.584, action=1, reward=-1.0, terminated:False, truncated:False

　車の位置state[0]がゴールの位置0.5に辿り着くと、終了フラグterminatedがFalse(エピソードが終了)になります。また、総時刻(行動回数)が200になると、打ち切りフラグtruncatedがTrue(エピソードが打ち切り)になります。
　時刻(行動)ごとに報酬-1が与えられます。ゴールに着いても報酬は変化しません。

　マウンテンカーのアニメーションを作成します。

・作図コード(クリックで展開)

# 図を初期化
fig = plt.figure(figsize=(9, 7), facecolor='white')
fig.suptitle('Mountain Car', fontsize=20)

# 作図処理を関数として定義
def update(t):
    # 時刻tの状態を取得
    state, action, reward, terminated = state_data[t]
    rgb_data = render_data[t]
    
    # 状態ラベルを作成
    state_text = 't=' + str(t) + '\n'
    state_text += f'position={state[0]:5.2f}, '
    state_text += f'velocity={state[1]:6.3f}\n'
    state_text += 'action=' + str(action) + ', '
    state_text += 'reward=' + str(reward) + ', '
    state_text += 'terminated:' + str(terminated)
    
    # マウンテンカーを描画
    plt.imshow(rgb_data)
    plt.xticks(ticks=[])
    plt.yticks(ticks=[])
    plt.title(state_text, loc='left')

# gif画像を作成
anime = FuncAnimation(fig=fig, func=update, frames=T+1, interval=50)

# gif画像を保存
anime.save('MountainCar_random.gif')

マウンテンカーの行動と状態遷移

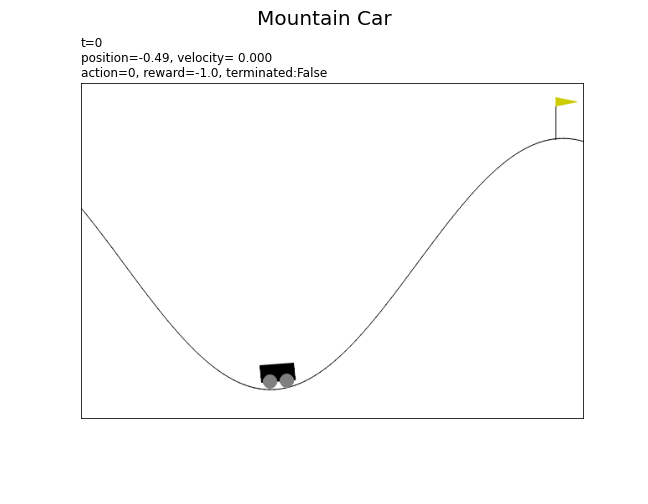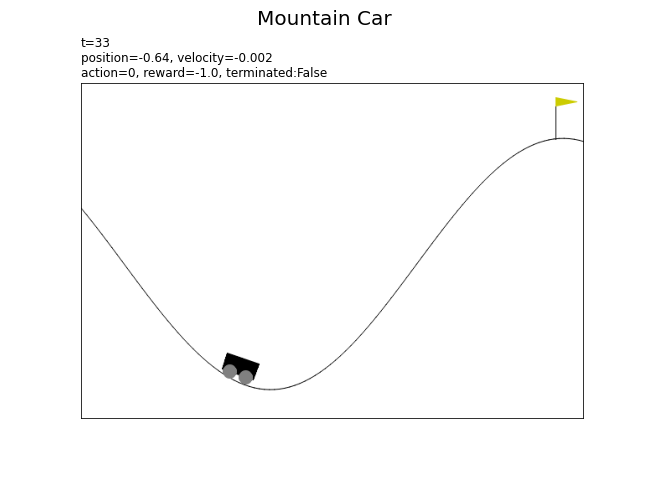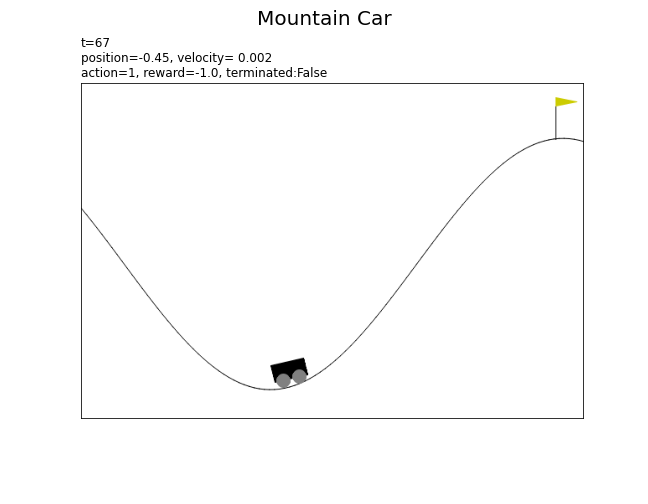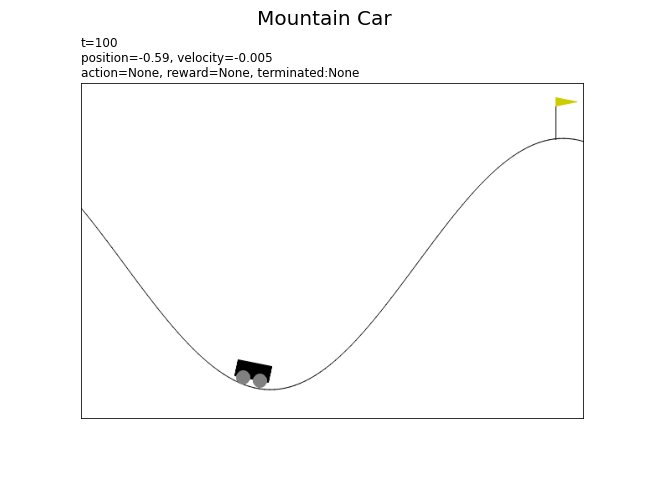
　以上が、マウンテンカーの基本的な設定です。

Pendulum

　ペンデュラムは、振り子を制御して直立させるゲームです。

状態

　ペンデュラムのインスタンスを作成します。

# 環境のインスタンスを作成
env = gym.make('Pendulum-v1', render_mode='rgb_array')

# 状態を初期化
state, info = env.reset()
print(state)
print(_)

[-0.26849654  0.9632807  -0.1207489 ]
{}

　ペンデュラムの状態は、「振り子の角度(ラジアン)を$\theta$として$\cos(\theta)$・$\sin(\theta)$・振り子の角速度」の3つの値で表されます。角度の初期値は$-\pi$から$\pi$、角速度の初期値は-1から1のランダムな値が設定されます。

　ただし、インスタンス内では、状態として「振り子の角度・振り子の角速度」の2つの値が保存されています。

# インスタンス内の状態を確認
print(env.state)

[ 1.84262824 -0.1207489 ]

　角度$\theta$から状態$\cos(\theta), \sin(\theta)$が計算されます。

# 振り子の角度を取得
theta = env.state[0]

# 振り子の状態を計算
print(np.cos(theta), np.sin(theta))

-0.26849653758121517 0.9632806492953645

　state[:2]と一致しているのが分かります。

　作図用の配列を出力します。

# 画像データを作成
rgb_data = env.render()
print(rgb_data.shape)

(500, 500, 3)

　ペンデュラムの画像データは、縦500×横500×3色の値で構成されます。

　最初の状態のペンデュラムを作図します。

# 状態ラベルを作成
state_text = f'$\\theta$={env.state[0]:.2f}, '
state_text += f'$\cos(\\theta)$={state[0]:.2f}, '
state_text += f'$\\sin(\\theta)$={state[1]:.2f}, '
state_text += f'velocity={state[2]:.3f}'

# ペンデュラムを描画
plt.figure(figsize=(7, 7), facecolor='white')
plt.suptitle('Pendulum', fontsize=20)
plt.imshow(rgb_data)
plt.xticks(ticks=[])
plt.yticks(ticks=[])
plt.title(state_text, loc='left')
plt.show()

ペンデュラムの初期状態

　振り子の角度について、アニメーションで確認します。

・作図コード(クリックで展開)

# 状態として利用する値を指定
theta_vals = np.arange(-3.1, 3.11, step=0.1).round(1) # 振り子の角度

# フレーム数を設定
frame_num = len(theta_vals)
print(frame_num)

# 図を初期化
fig = plt.figure(figsize=(7, 7), facecolor='white')
fig.suptitle('Pendulum', fontsize=20)

# 作図処理を関数として定義
def update(i):
    # i番目の値を取得
    theta = theta_vals[i]
    
    # 固定する値を指定
    theta_dot = 0.0
    
    # インスタンスを初期化
    env = gym.make('Pendulum-v1', render_mode='rgb_array')
    _, _ = env.reset()
    
    # 状態を設定
    state = np.array([theta, theta_dot])
    env.env.env.env.__dict__['state'] = state
    
    # 画像データを作成
    rgb_data = env.render()
    
    # 状態ラベルを作成
    state_text = f'$\\theta$={theta:5.2f}, '
    state_text += f'$\cos(\\theta)$={np.cos(theta):5.2f}, '
    state_text += f'$\\sin(\\theta)$={np.sin(theta):5.2f}\n'
    state_text += 'velocity=' + str(theta_dot)
    
    # ペンデュラムを描画
    plt.imshow(rgb_data)
    plt.xticks(ticks=[])
    plt.yticks(ticks=[])
    plt.title(state_text, loc='left')

# gif画像を作成
anime = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100)

# gif画像を保存
anime.save('Pendulum_state.gif')

　フレームごとに、振り子の角度thetaの値を変更して描画します。(theta, theta_dot(またはth, thdot)は、クラス内部での変数名です。)

ペンデュラムの状態

行動と報酬

　ペンデュラムは、-2から2の連続値の行動を取ります。

# 行動の範囲を確認
print(env.action_space)

Box(-2.0, 2.0, (1,), float32)

　負の値だと時計回り、正の値だと反時計回りに、絶対値が大きいほど強い力が働きます。

　行動を生成してみます。

# 行動をサンプリング
for _ in range(5):
    # ランダムに行動を決定
    action = env.action_space.sample()
    print(action)

[1.5870019]
[-1.7179161]
[-0.36254844]
[-0.32057714]
[1.5297734]

　行動を$\tau$、角速度を$v$として、報酬$r$は次の式で計算されます。$v$の計算式については省略します。

$$ r = - \left( \theta^2 + \frac{1}{10} v^2 + \frac{1}{1000} \tau^2 \right) $$

　よって、報酬の最小値・最大値は次のときになります。

# 最小値となる設定
theta, theta_dot, action = np.pi, 8.0, 2.0

# 最大値となる設定
#theta, theta_dot, action = 0.0, 0.0, 0.0

# 報酬を計算
reward = -(theta**2 + 0.1 * theta_dot**2 + 0.001 * action**2)
print(reward)

-16.27360440108936

　報酬は0から-16.27の値です。(負の値にしかならないのでクラス内部的にはcostsでした。)

　最小値・最大値のときの振り子を確認します。

・作図コード(クリックで展開)

# 最小値となる設定
theta, theta_dot = np.pi, 8.0

# 最大値となる設定
#theta, theta_dot = 0.0, 0.0

# インスタンスを初期化
env = gym.make('Pendulum-v1', render_mode='rgb_array')
_, _ = env.reset()

# 状態を設定
env.env.env.env.__dict__['state'] = np.array([theta, theta_dot])
state = env.state

# 画像データを作成
rgb_data = env.render()

# 状態ラベルを作成
state_text = f'$\\theta$={env.state[0]:.2f}, '
state_text += f'$\cos(\\theta)$={np.cos(env.state[0]):.2f}, '
state_text += f'$\\sin(\\theta)$={np.sin(env.state[0]):.2f}'

# ペンデュラムを描画
plt.figure(figsize=(7, 7), facecolor='white')
plt.suptitle('Pendulum', fontsize=20)
plt.imshow(rgb_data)
plt.xticks(ticks=[])
plt.yticks(ticks=[])
plt.title(state_text, loc='left')
plt.show()

ペンデュラムの報酬が最小値・最大値となる状態

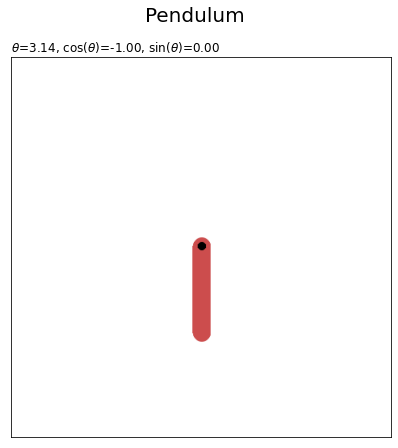
　(state[0]がx軸の値、state[1]がy軸の値っぽく書かれています？が、振り子の先端のx軸の値は$-\sin(\theta)$、y軸の値は$\cos(\theta)$ですよね。)

　ランダムな行動を繰り返します。

# 環境のインスタンスを作成
env = gym.make('Pendulum-v1', render_mode='rgb_array') # ポールカート

# 総時刻(行動回数)を指定
T = 100

# 最初の状態を取得
state, info = env.reset()

# 状態の記録用リストを初期化
state_data = []
render_data = [env.render()] # 最初の状態

# 1エピソードのシミュレーション
for t in range(T):
    # 記録用に現在の角度を複製
    theta = env.state[0].copy()
    
    # ランダムに行動を決定
    action = env.action_space.sample()
    
    # 状態を遷移
    next_state, reward, terminated, truncated, info = env.step(action)
    
    # 状態を保存
    state_data.append((theta, state, action.item(), reward, terminated)) # 現在
    render_data.append(env.render()) # 次
    
    # サンプルを表示
    print(
        't=' + str(t) + 
        ', state(angle)=' + str(theta.round(3)) + 
        ', action=' + str(action[0].round(2)) + 
        ', reward=' + str(reward.round(2)) + 
        ', terminated:' + str(terminated) + 
        ', truncated:' + str(truncated)
    )
    
    # 状態を更新
    state = next_state

# 最後の状態を保存
state_data.append((env.state[0], state, None, None, None))

t=0, state(angle)=3.027, action=0.08, reward=-9.21, terminated:False, truncated:False
t=1, state(angle)=2.998, action=-1.94, reward=-9.03, terminated:False, truncated:False
t=2, state(angle)=2.96, action=-1.11, reward=-8.82, terminated:False, truncated:False
t=3, state(angle)=2.921, action=1.89, reward=-8.6, terminated:False, truncated:False
t=4, state(angle)=2.903, action=-1.21, reward=-8.44, terminated:False, truncated:False
(省略)
t=95, state(angle)=3.341, action=-1.47, reward=-8.66, terminated:False, truncated:False
t=96, state(angle)=3.312, action=-0.26, reward=-8.86, terminated:False, truncated:False
t=97, state(angle)=3.275, action=0.42, reward=-9.1, terminated:False, truncated:False
t=98, state(angle)=3.236, action=-0.1, reward=-9.34, terminated:False, truncated:False
t=99, state(angle)=3.193, action=1.03, reward=-9.63, terminated:False, truncated:False

　エピソードの終了条件はなく、総時刻(行動回数)が200を超えると、打ち切りフラグtruncatedがTrue(エピソードが打ち切り)になります。

　ペンデュラムのアニメーションを作成します。

・作図コード(クリックで展開)

# 図を初期化
fig = plt.figure(figsize=(7, 7.5), facecolor='white')
fig.suptitle('Pendulum', fontsize=20)

# 作図処理を関数として定義
def update(t):
    # 時刻tの状態を取得
    theta, state, action, reward, terminated = state_data[t]
    rgb_data = render_data[t]
    
    # 状態ラベルを作成
    state_text = 't=' + str(t) + '\n'
    state_text += f'$\\theta$={theta:5.2f}, '
    state_text += f'$\cos(\\theta)$={state[0]:5.2f}, '
    state_text += f'$\\sin(\\theta)$={state[1]:5.2f}\n'
    state_text += f'velocity={state[2]:6.3f}\n'
    if t < T:
        state_text += f'action={action:5.2f}, '
        state_text += f'reward={reward:5.2f}, '
    else:
        state_text += 'action=' + str(action) + ', '
        state_text += 'reward=' + str(reward) + ', '
    state_text += 'terminated:' + str(terminated)
    
    # ペンデュラムを描画
    plt.imshow(rgb_data)
    plt.xticks(ticks=[])
    plt.yticks(ticks=[])
    plt.title(state_text, loc='left')

# gif画像を作成
anime = FuncAnimation(fig=fig, func=update, frames=T+1, interval=100)

# gif画像を保存
anime.save('Pendulum_random.gif')

ペンデュラムの行動と状態遷移

　以上が、ペンデュラムの基本的な設定です。

Acrobot

　アクロボットは、連結された振り子のジョイントを制御して先端を一定の高さまで持ち上げるゲームです。

状態と報酬

　アクロボットのインスタンスを作成します。

# 環境のインスタンスを作成
env = gym.make('Acrobot-v1', render_mode='rgb_array')

# 状態を初期化
state, info = env.reset()
print(state)
print(_)

[ 0.9960905  -0.08833884  0.9986852  -0.05126289 -0.02907794  0.08922382]
{}

　アクロボットの状態は、「1つ目のジョイントの角度(ラジアン)を$\theta_1$として$\cos(\theta_1)$・$\sin(\theta_1)$・2つ目のジョイントの角度を$\theta_2$として$\cos(\theta_2)$・$\sin(\theta_2)$・1つ目の角速度・2つ目の角速度」の6つの値で状態が表されます。角度と角速度の初期値は、それぞれ-0.1から0.1のランダムな値が設定されます。

　ただし、インスタンス内では、状態として「1つ目の角度・2つ目の角度・1つ目の角速度・2つ目の角速度」の4つの値が保存されています。

# インスタンス内の状態を確認
print(env.state)

[-0.08845413 -0.05128537 -0.02907794  0.08922382]

　角度$\theta_1$・$\theta_2$からそれぞれのジョイントの状態$\cos(\theta_1), \sin(\theta_1)$・$\cos(\theta_2), \sin(\theta_2)$が計算されます。

# ジョイントの角度を取得
theta1 = env.state[
0]
theta2 = env.state[1]

# 各ジョイントの状態を計算
print(np.cos(theta1), np.sin(theta1))
print(np.cos(theta2), np.sin(theta2))

0.9960905 -0.08833884
0.9986852 -0.05126289

　state[:5]と一致しているのが分かります。

　作図用の配列を出力します。

# 画像データを作成
rgb_data = env.render()
print(rgb_data.shape)

(500, 500, 3)

　アクロボットの画像データは、縦500×横500×3色の値で構成されます。

　最初の状態のアクロボットを作図します。

# 状態ラベルを作成
state_text = f'$\\theta_1$={theta1:5.2f}, '
state_text += f'$\cos(\\theta_1)$={np.cos(theta1):5.2f}, '
state_text += f'$\\sin(\\theta_1)$={np.sin(theta1):5.2f}\n'
state_text += f'$\\theta_2$={theta2:5.2f}, '
state_text += f'$\cos(\\theta_2)$={np.cos(theta2):5.2f}, '
state_text += f'$\\sin(\\theta_2)$={np.sin(theta2):5.2f}\n'
state_text += f'velocity1={state[4]:.3f}'
state_text += f', velocity2={state[5]:.3f}'

# アクロボットを描画
plt.figure(figsize=(7, 8), facecolor='white')
plt.suptitle('Acrobot', fontsize=20)
plt.imshow(rgb_data)
plt.xticks(ticks=[])
plt.yticks(ticks=[])
plt.title(state_text, loc='left')
plt.show()

アクロボットの初期状態

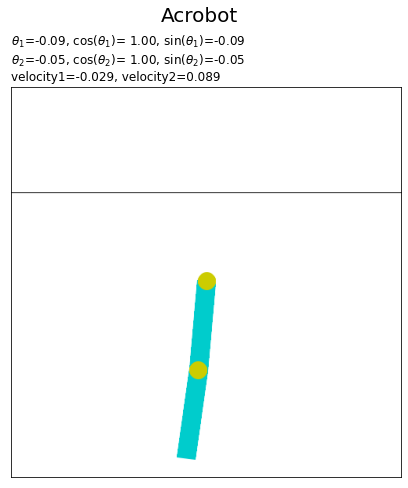
　各ジョイントの角度について、アニメーションで確認します。

・作図コード(クリックで展開)

# 状態として利用する値を指定
theta_vals = np.arange(-3.1, 3.1, step=0.1).round(1) # ジョイントの角度

# フレーム数を設定
frame_num = len(theta_vals)
print(frame_num)

# 図を初期化
fig = plt.figure(figsize=(7, 8), facecolor='white')
fig.suptitle('Acrobot', fontsize=20)

# 作図処理を関数として定義
def update(i):
    # i番目の値を取得
    theta1 = theta_vals[i]
    #theta2 = theta_vals[i]
    
    # 固定する値を指定
    #theta1 = 0.0
    theta2 = 0.0
    dtheta1 = 0.0
    dtheta2 = 0.0
    
    # インスタンスを初期化
    env = gym.make('Acrobot-v1', render_mode='rgb_array')
    _, _ = env.reset()
    
    # 状態を設定
    state = np.array([theta1, theta2, dtheta1, dtheta2])
    env.env.env.env.__dict__['state'] = state
    
    # 画像データを作成
    rgb_data = env.render()
    
    # 状態ラベルを作成
    state_text = f'$\\theta_1$={theta1:5.2f}, '
    state_text += f'$\cos(\\theta_1)$={np.cos(theta1):5.2f}, '
    state_text += f'$\\sin(\\theta_1)$={np.sin(theta1):5.2f}\n'
    state_text += f'$\\theta_2$={theta2:5.2f}, '
    state_text += f'$\cos(\\theta_2)$={np.cos(theta2):5.2f}, '
    state_text += f'$\\sin(\\theta_2)$={np.sin(theta2):5.2f}\n'
    state_text += 'velocity1=' + str(dtheta1) + ', '
    state_text += 'velocity2=' + str(dtheta2)

    # アクロボットを描画
    plt.imshow(rgb_data)
    plt.xticks(ticks=[])
    plt.yticks(ticks=[])
    plt.title(state_text, loc='left')

# gif画像を作成
anime = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100)

# gif画像を保存
anime.save('Acrobot_theta.gif')

　フレームごとに、ジョイントの角度theta1またはtheta2の値を変更して描画します。(theta1, theta2, dtheta1, dtheta2はクラス内部での変数名です。)

アクロボットの状態

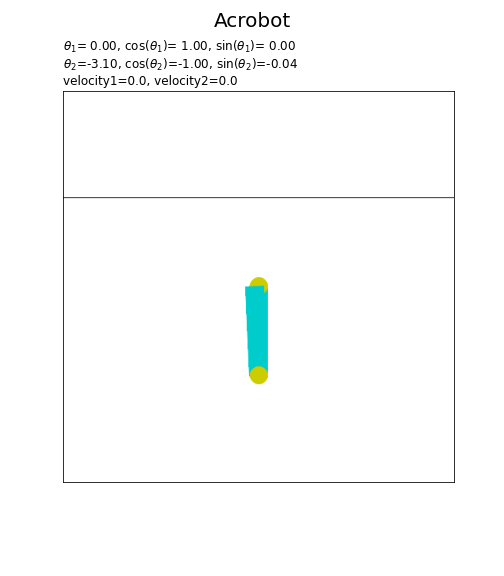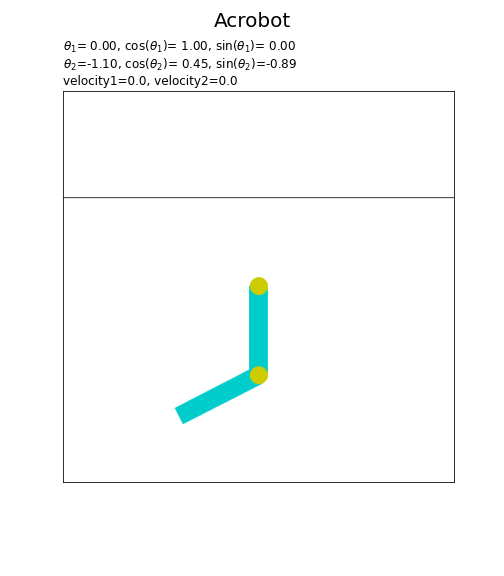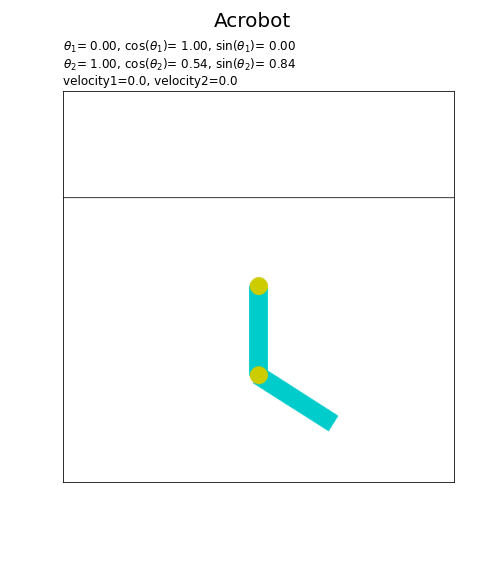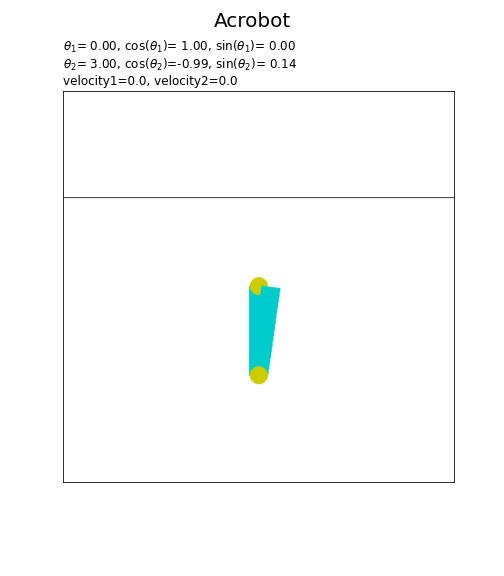
　2つ目のジョイントの角度$\theta_2$は、1つ目のジョイントに対しての角度を表します。
　先端が閾値を超えている間(正確には$-\cos(\theta_1) - \cos(\theta_2 + \theta_1) > 1.0$のとき)報酬0になり、閾値以下の時刻(行動)では-1が与えられます。

行動

　アクロボットは、3種類の行動を取ります。

# 行動の種類数を確認
print(env.action_space)

Discrete(3)

　0は時計回り、2は反時計回りに力が働きます。1は力が働きません(が、ずっと1でも止まることはなさそう？慣性？)。

　行動を生成してみます。

# 行動をサンプリング
for _ in range(5):
    # ランダムに行動を決定
    action = env.action_space.sample()
    print(action)

1
0
0
2
0

　ランダムな行動を繰り返します。

# 環境のインスタンスを作成
env = gym.make('Acrobot-v1', render_mode='rgb_array')

# 総時刻(行動回数)を指定
T = 100

# 最初の状態を取得
state, info = env.reset()

# 状態の記録用リストを初期化
state_data = []
render_data = [env.render()] # 最初の状態

# 1エピソードのシミュレーション
for t in range(T):
    # 記録用に現在の角度を複製
    theta = env.state[:2].copy()
    
    # ランダムに行動を決定
    action = env.action_space.sample()
    
    # 状態を遷移
    next_state, reward, terminated, truncated, info = env.step(action)
    
    # 状態を保存
    state_data.append((theta, state, action, reward, terminated)) # 現在
    render_data.append(env.render()) # 次
    
    # サンプルを表示
    print(
        't=' + str(t) + 
        ', state(angle)=' + str(theta.round(3)) + 
        ', action=' + str(action) + 
        ', reward=' + str(reward) + 
        ', terminated:' + str(terminated) + 
        ', truncated:' + str(truncated)
    )
    
    # 状態を更新
    state = next_state

# 最後の状態を保存
state_data.append((env.state[:2], state, None, None, None))

t=0, state(angle)=[-0.025  0.064], action=0, reward=-1.0, terminated:False, truncated:False
t=1, state(angle)=[0.   0.01], action=0, reward=-1.0, terminated:False, truncated:False
t=2, state(angle)=[ 0.051 -0.115], action=0, reward=-1.0, terminated:False, truncated:False
t=3, state(angle)=[ 0.112 -0.274], action=1, reward=-1.0, terminated:False, truncated:False
t=4, state(angle)=[ 0.149 -0.391], action=1, reward=-1.0, terminated:False, truncated:False
(省略)
t=95, state(angle)=[ 0.584 -1.083], action=2, reward=-1.0, terminated:False, truncated:False
t=96, state(angle)=[ 0.408 -0.82 ], action=0, reward=-1.0, terminated:False, truncated:False
t=97, state(angle)=[ 0.113 -0.328], action=2, reward=-1.0, terminated:False, truncated:False
t=98, state(angle)=[-0.226  0.267], action=1, reward=-1.0, terminated:False, truncated:False
t=99, state(angle)=[-0.511  0.788], action=0, reward=-1.0, terminated:False, truncated:False

　先端が閾値を超えている間は終了フラグterminatedがTrue(エピソードが終了)になります。閾値を下回るとFalseに戻ります。また、総時刻(行動回数)が500を超えると、打ち切りフラグtruncatedがTrue(エピソードが打ち切り)になります。

　アクロボットのアニメーションを作成します。

・作図コード(クリックで展開)

# 図を初期化
fig = plt.figure(figsize=(7, 8.5), facecolor='white')
fig.suptitle('Acrobot', fontsize=20)

# 作図処理を関数として定義
def update(t):
    # 時刻tの状態を取得
    theta, state, action, reward, terminated = state_data[t]
    rgb_data = render_data[t]
    
    # 状態ラベルを作成
    state_text = 't=' + str(t) + '\n'
    state_text += f'$\\theta_1$={theta[0]:5.2f}, '
    state_text += f'$\cos(\\theta_1)$={state[0]:5.2f}, '
    state_text += f'$\\sin(\\theta_1)$={state[1]:5.2f}\n'
    state_text += f'$\\theta_2$={theta[1]:5.2f}, '
    state_text += f'$\cos(\\theta_2)$={state[2]:5.2f}, '
    state_text += f'$\\sin(\\theta_2)$={state[3]:5.2f}\n'
    state_text += f'velocity1={state[4]:6.3f}, '
    state_text += f'velocity2={state[5]:6.3f}\n'
    state_text += 'action=' + str(action) + ', '
    state_text += 'reward=' + str(reward) + ', '
    state_text += 'terminated:' + str(terminated)
    
    # アクロボットを描画
    plt.imshow(rgb_data)
    plt.xticks(ticks=[])
    plt.yticks(ticks=[])
    plt.title(state_text, loc='left')

# gif画像を作成
anime = FuncAnimation(fig=fig, func=update, frames=T+1, interval=50)

# gif画像を保存
anime.save('Acrobot_random.gif')

アクロボットの行動と状態遷移

　以上が、アクロボットの基本的な設定です。

　この節では、gymライブラリを確認しました。次節では、DQNを実装してカートポールを学習します。

参考文献

• 斎藤康毅『ゼロから作るDeep Learning 4 ――強化学習編』オライリー・ジャパン,2022年.
• サポートページ：GitHub - oreilly-japan/deep-learning-from-scratch-4

• ドキュメントページ：Classic Control - Gym Documentation
• GitHubページ：GitHub - openai/gym: A toolkit for developing and comparing reinforcement learning algorithms.
• Wikiページ：Home · openai/gym Wiki · GitHub

おわりに

　ちょっと確認するだけでこんな記事を書くつもりは全くなかったのですが、なんか本の通り動かないし、ちょっとズルなやりたいこと(状態の書き換え)もできないしで、解説記事を探してドキュメントを読んでソースコードまで見るはめになりました。思いの外苦労したので記事にしておきます。
　4月に出版されてから半年の間にライブラリが更新されたようです。本を書くってホント大変ですね。
　次は、カートポールをDQNで学習するわけですが、そのままでは他のゲームは上手くいかないっぽいです？

【次節の内容】

www.anarchive-beta.com