はじめに
『ゼロから作るDeep Learning 4 ――強化学習編』の独学時のまとめノートです。初学者の補助となるようにゼロつくシリーズの4巻の内容に解説を加えていきます。本と一緒に読んでください。
この記事は、4.5.2節の内容です。価値反復法を実装して最適状態価値関数と最適方策を求めます。
【前節の内容】
【他の記事一覧】
【この記事の内容】
4.5.2 価値反復法の実装
3×4マスのグリッドワールド(図4-8)に対して、価値反復法により最適状態価値関数と最適方策を求めます。価値反復法のアルゴリズムについては「4.5.1:価値反復法の導出【ゼロつく4のノート】 - からっぽのしょこ」を参照してください。
利用するライブラリを読み込みます。
# 利用するライブラリを読み込み import numpy as np from collections import defaultdict # 追加ライブラリ import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation from matplotlib.colors import LinearSegmentedColormap
MatplotlibライブラリのanimationモジュールからFuncAnimationを使って、推移の確認用のアニメーションを作成します。その際に、colorsモジュールからLinearSegmentedColormapも使います。不要であれば省略してください。
また、3×4マスのグリッドワールドのクラスGridWorldを読み込みます。
# 実装済みのクラスを読み込み import sys sys.path.append('../deep-learning-from-scratch-4-master') from common.gridworld import GridWorld from ch04.policy_iter import greedy_policy
GridWorldクラスについては「4.2.1:GridWorldクラスの実装:評価と改善に関するメソッド【ゼロつく4のノート】 - からっぽのしょこ」、greedy_policy関数については「4.4:方策反復法の実装【ゼロつく4のノート】 - からっぽのしょこ」を参照してください。
・value_iter_onestep関数の実装
まずは、価値反復法により状態価値関数を1回更新する処理を関数value_iter_onestep()として実装します。
・計算式の確認
関数内で行う計算について数式で確認します。
価値反復法による状態価値関数の更新式は、次の式でした(4.5.1項)。
図4-8の問題設定では、決定論的に状態が遷移するので、次の式になります。
・処理の確認
value_iter_onestep()の内部で行われる処理を確認します。
引数に指定する(関数内で利用する)オブジェクトを作成します。
# グリッドワールドのインスタンスを作成 env = GridWorld() # 全ての状態価値関数を初期化 V = defaultdict(lambda: 0) # 割引率を指定 gamma = 0.9
GridWorldクラスのインスタンスenvを作成します。
全てのマスの状態価値関数の初期値を0として格納したディクショナリVを作成します。
割引率gammaを指定します。
初期値による状態価値関数のヒートマップを確認しましょう。
# 状態価値関数のヒートマップを作図
env.render_v(v=V)
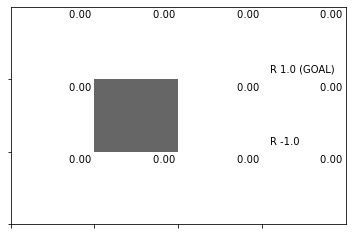
全ての状態(マス)で初期値が0なので、全て白色になっています。
価値反復法により状態価値関数を1回更新します。
# 状態ごとに処理 for state in env.states(): # ゴールの場合 if state == env.goal_state: # 状態価値は常に0 V[state] = 0 continue # 以降は処理せず次の状態へ # 行動価値関数を初期化 action_values = [] # 行動ごとに処理 for action in env.actions(): # 次の状態を取得 next_state = env.next_state(state, action) # 報酬を取得 r = env.reward(state, action, next_state) # 行動価値関数を計算:式(4.13)の波括弧 value = r + gamma * V[next_state] # 行動価値を格納 action_values.append(value) # 状態価値関数を更新:式(4.13) V[state] = max(action_values) # 結果を確認 print(list(V.keys())) # 状態 print(np.round(list(V.values()), 2)) # 状態価値
[(0, 0), (1, 0), (0, 1), (0, 2), (1, 2), (0, 3), (2, 0), (2, 1), (1, 1), (2, 2), (1, 3), (2, 3)]
[0. 0. 0. 1. 0.9 0. 0. 0. 0. 0.81 1. 0.73]
for文とstate()メソッドを使って、状態ごとに処理します。
この例の問題設定では、ゴールに辿り着くとエピソード終了なので、ゴールのマスの状態価値は常に0になります。そのため、0を代入して、その後の処理はcontinueで飛ばして次の状態に移ります。
さらに、for文とactions()メソッドを使って、行動ごとに処理します。
next_state()メソッドで次の状態、reward()メソッドで報酬を取得して、行動価値関数(状態価値関数の更新式(4.13)の波括弧部分)を計算して、valueとします。
全ての行動の価値をaction_valueに格納して、価値の最大値をmax()で抽出して状態価値関数を更新します。この処理が更新式(4.13)の計算です。
全ての状態(マス)を1回更新した状態価値関数をgreedy化して方策を改善して、ヒートマップを作成します。
# 方策を改善(状態価値関数をgreedy化して方策を計算):式(4.8) pi = greedy_policy(V, env, gamma) # 状態価値関数のヒートマップを作図 env.render_v(v=V, policy=pi)
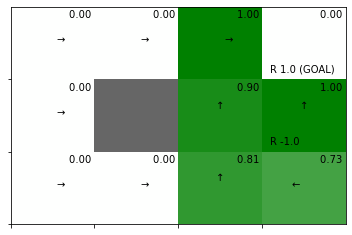
このプログラムでは、状態価値関数の初期値を0として、左上のマスから図4.12の順番に状態価値関数を計算(更新)します。またこの例では、報酬のあるマスが右端にあります。そのため、1回目の更新では、左側のマスの状態価値関数の計算に報酬が反映されません。よって、左側のマスは状態価値が0(白色)になっています。
以上が、価値反復法における1回の更新処理です。
・実装
処理の確認ができたので、価値反復法の1回の更新処理を関数として実装します。value_iter_onestep関数の定義については、次のページを参照してください。
実装した関数を試してみましょう。
# グリッドワールドのインスタンスを作成 env = GridWorld() # 全ての状態価値関数を初期化 V = defaultdict(lambda: 0) # 割引率を指定 gamma = 0.9 # 状態価値関数を更新:式(4.13) V = value_iter_onestep(V, env, gamma) # 方策を改善(状態価値関数をgreedy化して方策を計算):式(4.8) pi = greedy_policy(V, env, gamma) # 状態価値関数のヒートマップを作図 env.render_v(v=V, policy=pi)
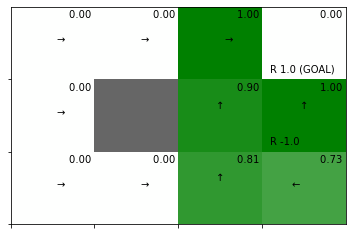
処理の確認時と同じ結果が得られました。
以上で、1回の更新処理を実装できました。次は、収束するまで更新を繰り返す関数を実装します。
・value_iter関数の実装
次は、価値反復法により状態価値関数を収束するまで更新する関数をvalue_iter()として実装します。
・処理の確認
value_iter()の内部で行われる処理を確認します。
先ほどと同様に、引数に指定する(関数内で利用する)オブジェクトを作成します。
# グリッドワールドのインスタンスを作成 env = GridWorld() # 全ての状態価値関数を初期化 V = defaultdict(lambda: 0) # 割引率を指定 gamma = 0.9 # 閾値を指定 threshold =0.001
先ほどに加えて、閾値thresholdを指定します。
価値反復法によって、状態価値関数を更新幅が閾値を下回るまで更新を繰り返します。
# 記録用のリストを初期化 trace_V = [{state: 0 for state in env.states()}] # 初期値を記録 # 試行回数のカウントを初期化 cnt = 0 # 繰り返し処理 while True: # 現在の状態を複製 old_V = V.copy() # 状態価値関数を更新:式(4.13) V = value_iter_onestep(V, env, gamma) # 更新幅の最大値を初期化 delta = 0 # 更新幅の最大値を記録 for state in V.keys(): # 更新量の絶対値を計算 t = abs(V[state] - old_V[state]) # 最大値を更新したら記録 if delta < t: delta = t # 試行回数をカウント cnt += 1 # 途中経過を表示 print('iter', cnt, ': delta', delta) # 状態価値関数の更新値を記録 trace_V.append(V.copy()) # 更新幅が閾値未満になると終了 if delta < threshold: break
iter 1 : delta 1.0
iter 2 : delta 0.9
iter 3 : delta 0.81
iter 4 : delta 0
更新量を計算するため、現在の状態価値をold_Vとして保存しておきます。
value_iter_onestep()で状態価値関数を1回更新します。
更新後の値Vと更新前の値old_Vの差の絶対値を各状態で計算し、最大値をdeltaとします。
deltaがthresholdを下回ると、while文による繰り返し処理をbreakで終了します。
途中経過の出力を見ると、4回目の時点では更新量が0なので、3回更新されたのが分かります。
収束した状態価値関数(最適状態価値関数)とそれをgreedy化した方策(最適方策)のヒートマップを作成します。
# 方策を改善(状態価値関数をgreedy化して方策を計算):式(4.8) pi = greedy_policy(V, env, gamma) # 状態価値関数のヒートマップを作図 env.render_v(v=V, policy=pi)

最適状態価値関数を基にしたgreedyな方策が得られました。方策反復法による結果(4.4節)と一致しています。
・更新推移の可視化
ここまでで、繰り返しの更新処理を確認できました。続いて、途中経過をアニメーションで確認します。
状態価値関数のヒートマップのアニメーションを作成します。
・作図コード(クリックで展開)
# グリッドマップのサイズを取得 xs = env.width ys = env.height # 最後の状態価値の最小値・最大値を取得 vmin = min(trace_V[-1].values()) vmax = max(trace_V[-1].values()) # 色付け用に最小値・最大値を再設定 vmax = max(vmax, abs(vmin)) vmin = -1 * vmax if vmax < 1: vmax = 1 if vmin > -1: vmin = -1 # カラーマップを設定 color_list = ['red', 'white', 'green'] cmap = LinearSegmentedColormap.from_list('colormap_name', color_list) # 図を初期化 fig = plt.figure(figsize=(9, 6)) # 図の設定 plt.suptitle('Value Iteration', fontsize=20) # 全体のタイトル # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i回目の更新値を取得 V = trace_V[i] # 方策を改善(状態価値関数をgreedy化して方策を計算):式(4.8) pi = greedy_policy(V, env, gamma) # ディクショナリを配列に変換 v = np.zeros((env.shape)) for state, value in V.items(): v[state] = value # 状態価値のヒートマップを描画 plt.pcolormesh(np.flipud(v), cmap=cmap, vmin=vmin, vmax=vmax) # ヒートマップ # マス(状態)ごとに処理 for state in env.states(): # インデックスを取得 y, x = state # 報酬を抽出 r = env.reward_map[state] # 報酬がある場合 if r != 0 and r is not None: # 報酬ラベル用の文字列を作成 txt = 'R ' + str(r) # ゴールの場合 if state == env.goal_state: # 報酬ラベルにゴールを追加 txt = txt + ' (GOAL)' # 報酬ラベルを描画 plt.text(x=x+0.1, y=ys-y-0.9, s=txt) # 壁以外の場合 if state != env.wall_state: # 状態価値ラベルを描画 plt.text(x=x+0.4, y=ys-y-0.15, s='{:12.2f}'.format(v[y, x])) # 確率が最大の行動を抽出 actions = pi[state] max_actions = [k for k, v in actions.items() if v == max(actions.values())] # 矢印の描画用のリストを作成 arrows = ['↑', '↓', '←', '→'] offsets = [(0, 0.1), (0, -0.1), (-0.1, 0), (0.1, 0)] # 行動ごとに処理 for action in max_actions: # 矢印の描画用の値を抽出 arrow = arrows[action] offset = offsets[action] # ゴールの場合 if state == env.goal_state: # 描画せず次の状態へ continue # 方策ラベル(矢印)を描画 plt.text(x=x+0.45+offset[0], y=ys-y-0.5+offset[1], s=arrow, fontsize=20) # 壁の場合 if state == env.wall_state: # 壁を描画 plt.gca().add_patch(plt.Rectangle(xy=(x, ys-y-1), width=1, height=1, fc=(0.4, 0.4, 0.4, 1.0))) # 長方形を重ねる # マスを描画 plt.xticks(ticks=np.arange(xs)) # x軸の目盛位置 plt.yticks(ticks=np.arange(ys)) # y軸の目盛位置 plt.xlim(xmin=0, xmax=xs) # x軸の範囲 plt.ylim(ymin=0, ymax=ys) # y軸の範囲 plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False) # 軸ラベル plt.grid() # グリッド線 plt.title('iter:'+str(i), loc='left') # タイトル # gif画像を作成 anime = FuncAnimation(fig, update, frames=len(trace_V), interval=500) # gif画像を保存 anime.save('value_iter.gif')
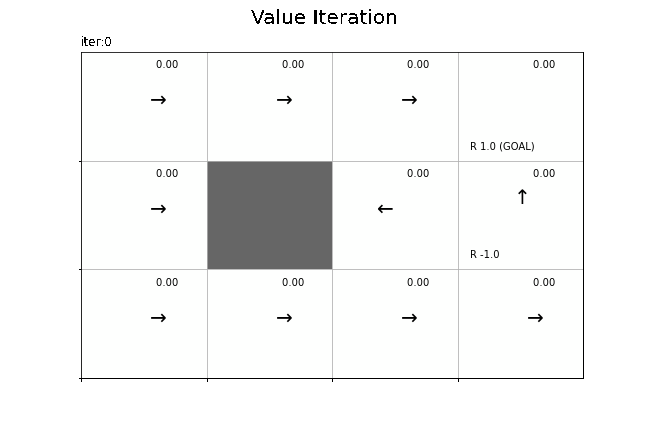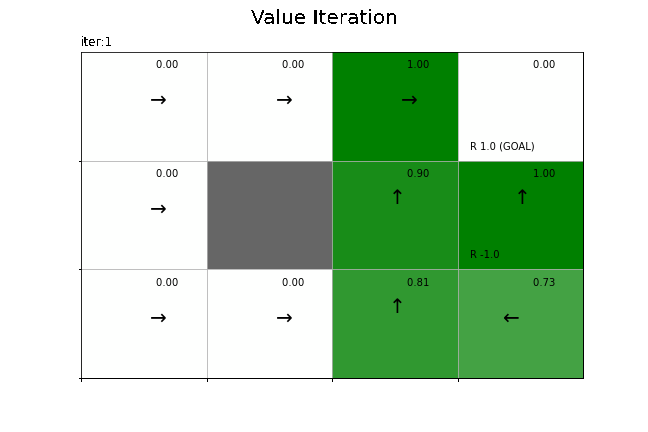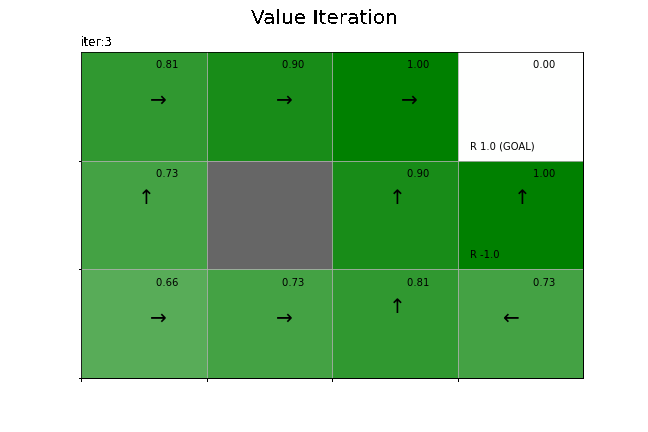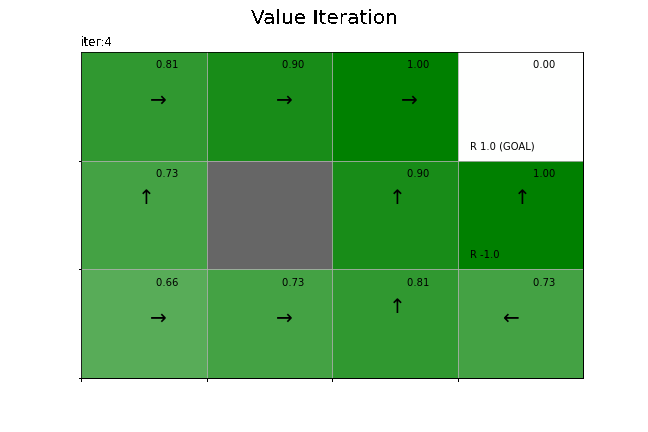
状態価値関数の更新値の推移をグラフで確認します。
・作図コード(クリックで展開)
# 更新回数を取得 max_iter = len(trace_V) # 状態数を取得 state_size = env.reward_map.size # 作図用の配列を作成 trace_V_arr = np.zeros((max_iter, state_size)) for i in range(max_iter): # i回目の更新値を抽出 V = trace_V[i] # 配列に格納 trace_V_arr[i] = list(V.values()) # 状態価値関数の推移を作図 plt.figure(figsize=(8, 6)) for s in range(env.reward_map.size): plt.plot(np.arange(max_iter), trace_V_arr[:, s]) plt.xlabel('iteration') plt.ylabel('state-value') plt.suptitle('Value Iteration', fontsize=20) plt.title('$\gamma='+str(gamma)+'$', loc='left') plt.grid() plt.show()
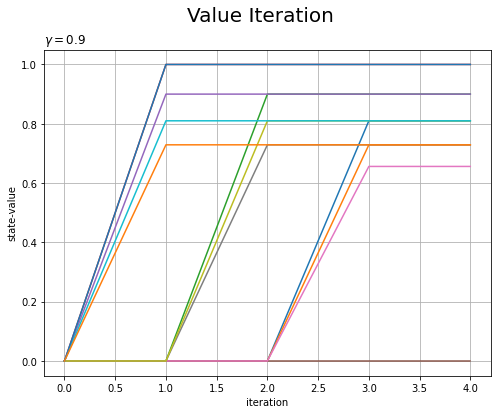
アニメーションでは、状態価値を色の濃淡で表しました。こちらは、y軸で表しています。
・実装
処理の確認ができたので、価値反復法を関数として実装します。value_iter関数の定義については、value_iter_onestep関数のときと同じページを参照してください。
実装した関数を試してみましょう。
# グリッドワールドのインスタンスを作成 env = GridWorld() # 全ての状態価値関数を初期化 V = defaultdict(lambda: 0) # 割引率を指定 gamma = 0.9 # 閾値を指定 threshold =0.001 # 状態価値関数を更新:式(4.13) V = value_iter(V, env, gamma, threshold, is_render=True)
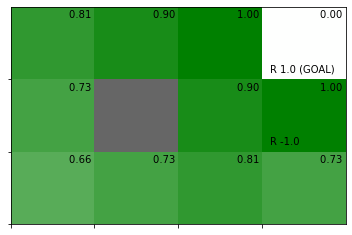
処理の確認時と同じ結果が得られました。
最適状態価値関数をgreedy化して最適方策を得ます。
# 方策を改善(状態価値関数をgreedy化して方策を計算):式(4.8) pi = greedy_policy(V, env, gamma) # 状態価値関数と方策のヒートマップを作図 env.render_v(v=V, policy=pi)
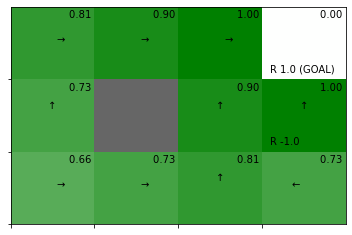
処理の確認時と同じ結果が得られました。
この節では、価値反復法を実装しました。これにより、状態価値関数の更新を繰り返して最適状態価値関数を得て、さらにそれをgreedy化することで最適方策を得られました。また4章では、動的計画法(方策の評価と改善)を学びました。次節では、モンテカルロ法を学びます。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning 4 ――強化学習編』オライリー・ジャパン,2022年.
- サポートページ:GitHub - oreilly-japan/deep-learning-from-scratch-4
おわりに
4章終了です!ここまでが強化学習の基礎とのことです。
やっぱり、数式を眺めてるだけでなくプログラミングして実際に動かすと楽しいですね。
【次節の内容】