はじめに
素直なやり方ではできなかったのでむりくりなんとかする黒魔術シリーズです。もっといい方法があれば教えてください。
この記事では、、Pythonで三角図の等高線図とヒートマップを作成します。
【前の内容】
【目次】
Matplotlibで三角グラフの等高線を作図したい
前回は、三角図や三角ダイアグラム(ternary diagram)などと呼ばれるグラフをMatplotlibライブラリのPyplotモジュールを利用して作成した。今回は、三角図上に等高線図(contour map)を描画したい。しかし、Pyplotで等高線を作図するには格子状の点(直交する点)を使う必要があり、三角座標に変換すると格子点にならない。そこで、三角座標を含めた2次元座標上の格子点を作成して、元の3次元座標に戻して目的の計算をすることで、三角図上に等高線を描画する。
三角図の座標の作図については前回の記事を参照のこと。
利用するライブラリを読み込む。
# 利用ライブラリ import numpy as np import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation from scipy.stats import dirichlet
三角座標からの再変換式の確認
まずは、三角座標上の点$\mathbf{y}$から3次元座標上の点$\mathbf{x}$に変換する計算式を確認する。式の導出については「ggplot2で三角グラフの等高線を作図したい - からっぽのしょこ」を参照のこと。
総和が1の3次元の変数(点)
に対して、次の式で2次元の変数(点)$\mathbf{y}$に変換する。
$\mathbf{y}$は、正三角形の座標上の点になるのであった。
次の式で、$\mathbf{y}$から$\mathbf{x}$に再変換できる。
格子点$\mathbf{y}$を用意して、$\mathbf{x}$に変換した上で目的の計算を行うことで等高線を作図できる。Pythonのインデックスに合わせて添字を0から付けることにする。
三角座標の準備
三角座標の描画に次の配列を利用する。詳しくは「Matplotlibで三角グラフを作図したい - からっぽのしょこ」を参照のこと。
# 軸目盛の位置を指定 axis_vals = np.arange(start=0.0, stop=1.1, step=0.1) # 軸線用の値を作成 axis_x = np.array([0.5, 0.0, 1.0]) axis_y = np.array([0.5*np.sqrt(3.0), 0.0, 0.0]) axis_u = np.array([-0.5, 1.0, -0.5]) axis_v = np.array([-0.5*np.sqrt(3.0), 0.0, 0.5*np.sqrt(3.0)]) # グリッド線用の値を作成 grid_x = np.hstack([ 0.5 * axis_vals, axis_vals, 0.5 * axis_vals + 0.5 ]) grid_y = np.hstack([ 0.5 * axis_vals * np.sqrt(3.0), np.zeros_like(axis_vals), 0.5 * (1.0 - axis_vals) * np.sqrt(3.0) ]) grid_u = np.hstack([ 0.5 * axis_vals, 0.5 * (1.0 - axis_vals), -axis_vals ]) grid_v = np.hstack([ -0.5 * axis_vals * np.sqrt(3.0), 0.5 * (1.0 - axis_vals) * np.sqrt(3.0), np.zeros_like(axis_vals) ])
等高線図
三角座標上の等高線図を作成する。例として、ディリクレ分布の確率密度の等高線図を作成する。
$y_0$と$y_1$の値を作成する。
# 2次元座標の値を作成 y_0_vals = np.linspace(start=0.0, stop=1.0, num=201) y_1_vals = np.linspace(start=0.0, stop=0.5*np.sqrt(3.0), num=200) print(y_0_vals[:5]) print(np.round(y_1_vals[:5], 3))
[0. 0.005 0.01 0.015 0.02 ]
[0. 0.004 0.009 0.013 0.017]
$0 \leq y_0 \leq 1$の値をy_1_vals、$0 \leq y_1 \leq \frac{\sqrt{3}}{2}$の値をy_2_valsとして作成する。グラフが粗い場合や処理が重い場合は、y_*_valsの間隔(np.arange()のstep(第3)引数)や要素数(np.linspace()のnum(第3)引数)を調整する。
$\mathbf{y}$の値を作成する。
# 2次元座標の格子点を作成 y_0_grid, y_1_grid = np.meshgrid(y_0_vals, y_1_vals) print(y_0_grid[:5, :5]) print(np.round(y_1_grid[:5, :5], 3)) # 格子点の形状を保存 y_shape = y_0_grid.shape print(y_shape)
[[0. 0.005 0.01 0.015 0.02 ]
[0. 0.005 0.01 0.015 0.02 ]
[0. 0.005 0.01 0.015 0.02 ]
[0. 0.005 0.01 0.015 0.02 ]
[0. 0.005 0.01 0.015 0.02 ]]
[[0. 0. 0. 0. 0. ]
[0.004 0.004 0.004 0.004 0.004]
[0.009 0.009 0.009 0.009 0.009]
[0.013 0.013 0.013 0.013 0.013]
[0.017 0.017 0.017 0.017 0.017]]
(200, 201)
y_0_valsとy_1_valsの要素の全ての組み合わせ(格子状の点)をnp.meshgrid()で作成する。y_0_grid, y_1_gridはグラフ描画用の値で、同じインデックスの各要素が$\mathbf{y} = (y_0, y_1)$に対応する。
$\mathbf{x}$の値を作成する。
# 3次元座標の値に変換 x_1_vals = y_0_grid.flatten() - y_1_grid.flatten() / np.sqrt(3.0) x_2_vals = 2.0 * y_1_grid.flatten() / np.sqrt(3.0) # 範囲外の点を欠損値に置換 x_1_vals = np.where( (x_1_vals >= 0.0) & (x_1_vals <= 1.0), x_1_vals, np.nan ) x_2_vals = np.where( (x_2_vals >= 0.0) & (x_2_vals <= 1.0), x_2_vals, np.nan ) # 3次元座標の値に変換 x_0_vals = 1.0 - x_1_vals - x_2_vals # 範囲外の点を欠損値に置換 x_0_vals = np.where( (x_0_vals >= 0.0) & (x_0_vals <= 1.0), x_0_vals, np.nan ) # 計算用の3次元座標の点を作成 x_points = np.stack([x_0_vals, x_1_vals, x_2_vals], axis=1) print(x_points)
[[1. 0. 0. ]
[0.995 0.005 0. ]
[0.99 0.01 0. ]
...
[ nan 0.49 1. ]
[ nan 0.495 1. ]
[ nan 0.5 1. ]]
$\mathbf{y}$の値y_0_grid, y_1_gridから$\mathbf{x}$の値x_pointsに変換する。ただし、y_0_grid, y_1_gridは三角座標外の値を含み、その値を変換式で計算すると総和が1でない点になる。範囲外の値(点)を取り除くのではなく、欠損値np.nanに置換する。
x_pointsの各行が$\mathbf{x} = (x_0, x_1, x_2)$に対応するように配列に格納する。
ディリクレ分布のパラメータを設定して、確率密度を計算する。
# ディリクレ分布のパラメータを指定 alpha_k = np.array([2.5, 3.5, 4.5]) # ディリクレ分布の確率密度を計算 dens_vals = np.array( [dirichlet.pdf(x=x_k, alpha=alpha_k) if all(x_k != np.nan) else np.nan for x_k in x_points] ) print(dens_vals)
[ 0. 0. 0. ... nan nan nan]
ディリクレ分布の確率密度は、SciPyライブラリのディリクレ分布のモジュールdirichletのpdf()メソッドで計算できる。確率変数の引数xにx_pointsの各行、パラメータの引数alphaに設定したパラメータalpha_kを指定する。
リスト内包表記を使って、x_pointsの行ごとに確率密度を計算する。ただし、np.nanを含む行の場合は計算を行わず、np.nanを格納する。
三角図上に確率密度の等高線を描画する。
# パラメータラベル用の文字列を作成 param_text = '$' + '\\alpha=('+', '.join([str(val) for val in alpha_k])+')' + ', x=(x_0, x_1, x_2)' + '$' # 三角座標上の等高線図を作成 plt.figure(figsize=(12, 10), facecolor='white') # 図の設定 plt.quiver(grid_x, grid_y, grid_u, grid_v, scale_units='xy', scale=1, units='dots', width=0.1, headwidth=0.1, fc='none', ec='gray', linewidth=1.5, linestyle=':') # 三角座標のグリッド線 plt.quiver(axis_x, axis_y, axis_u, axis_v, scale_units='xy', scale=1, units='dots', width=1.5, headwidth=1.5, fc='black', linestyle='-') # 三角座標の枠線 for val in axis_vals: plt.text(x=0.5*val, y=0.5*val*np.sqrt(3.0), s=str(np.round(1.0-val, 1))+' '*2, ha='right', va='bottom', rotation=-60) # 三角座標のx軸目盛 plt.text(x=val, y=0.0, s=str(np.round(val, 1))+' '*10, ha='center', va='center', rotation=60) # 三角座標のy軸目盛 plt.text(x=0.5*val+0.5, y=0.5*(1.0-val)*np.sqrt(3.0), s=' '*3+str(np.round(1.0-val, 1)), ha='left', va='center') # 三角座標のz軸目盛 plt.text(x=0.25, y=0.25*np.sqrt(3.0), s='$x_0$'+' '*5, ha='right', va='center', size=25) # 三角座標のx軸ラベル plt.text(x=0.5, y=0.0, s='\n'+'$x_1$', ha='center', va='top', size=25) # 三角座標のy軸ラベル plt.text(x=0.75, y=0.25*np.sqrt(3.0), s=' '*4+'$x_2$', ha='left', va='center', size=25) # 三角図のz軸ラベル cnf = plt.contourf(y_0_grid, y_1_grid, dens_vals.reshape(y_shape), alpha = 0.8) # 確率密度の等高線 plt.xticks(ticks=[0.0, 0.5, 1.0], labels='') # 2次元座標のx軸目盛 plt.yticks(ticks=[0.0, 0.25*np.sqrt(3.0), 0.5*np.sqrt(3.0)], labels='') # 2次元座標のy軸目盛 plt.grid() # 2次元座標のグリッド線 plt.axis('equal') # アスペクト比 plt.colorbar(cnf, label='density') # カラーバー plt.suptitle(t='Ternary Contour Plot', fontsize=20) # タイトル plt.title(label=param_text, loc='left') # パラメータラベル plt.show() # 描画
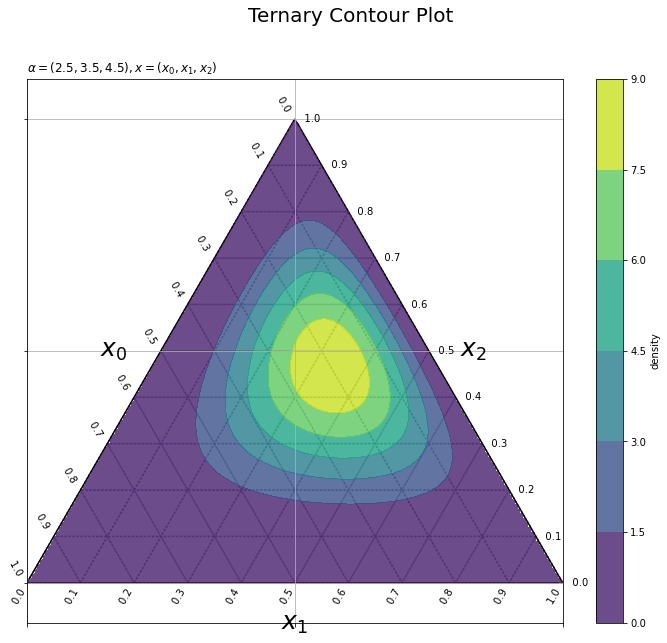
plt.contour()またはplt.contourf()で等高線図を描画する。三角図外の点は欠損値np.nanなので描画されない(つまりデータの半分を捨てる非効率設計である)。
以上で、私が欲しいグラフが得られた。
ヒートマップ
ついでに、ヒートマップを作成する。
# 三角座標上の等高線図を作成 plt.figure(figsize=(12, 10), facecolor='white') # 図の設定 plt.quiver(grid_x, grid_y, grid_u, grid_v, scale_units='xy', scale=1, units='dots', width=0.1, headwidth=0.1, fc='none', ec='gray', linewidth=1.5, linestyle=':') # 三角座標のグリッド線 plt.quiver(axis_x, axis_y, axis_u, axis_v, scale_units='xy', scale=1, units='dots', width=1.5, headwidth=1.5, fc='black', linestyle='-') # 三角座標の枠線 for val in axis_vals: plt.text(x=0.5*val, y=0.5*val*np.sqrt(3.0), s=str(np.round(1.0-val, 1))+' '*2, ha='right', va='bottom', rotation=-60) # 三角座標のx軸目盛 plt.text(x=val, y=0.0, s=str(np.round(val, 1))+' '*10, ha='center', va='center', rotation=60) # 三角座標のy軸目盛 plt.text(x=0.5*val+0.5, y=0.5*(1.0-val)*np.sqrt(3.0), s=' '*3+str(np.round(1.0-val, 1)), ha='left', va='center') # 三角座標のz軸目盛 plt.text(x=0.25, y=0.25*np.sqrt(3.0), s='$x_0$'+' '*5, ha='right', va='center', size=25) # 三角座標のx軸ラベル plt.text(x=0.5, y=0.0, s='\n'+'$x_1$', ha='center', va='top', size=25) # 三角座標のy軸ラベル plt.text(x=0.75, y=0.25*np.sqrt(3.0), s=' '*4+'$x_2$', ha='left', va='center', size=25) # 三角図のz軸ラベル pcl = plt.pcolor(y_0_grid, y_1_grid, dens_vals.reshape(y_shape), alpha = 0.8) # 確率密度の等高線 plt.xticks(ticks=[0.0, 0.5, 1.0], labels='') # 2次元座標のx軸目盛 plt.yticks(ticks=[0.0, 0.25*np.sqrt(3.0), 0.5*np.sqrt(3.0)], labels='') # 2次元座標のy軸目盛 plt.grid() # 2次元座標のグリッド線 plt.axis('equal') # アスペクト比 plt.colorbar(pcl, label='density') # カラーバー plt.suptitle(t='Ternary Heatmap', fontsize=20) # タイトル plt.title(label=param_text, loc='left') # パラメータラベル plt.show() # 描画
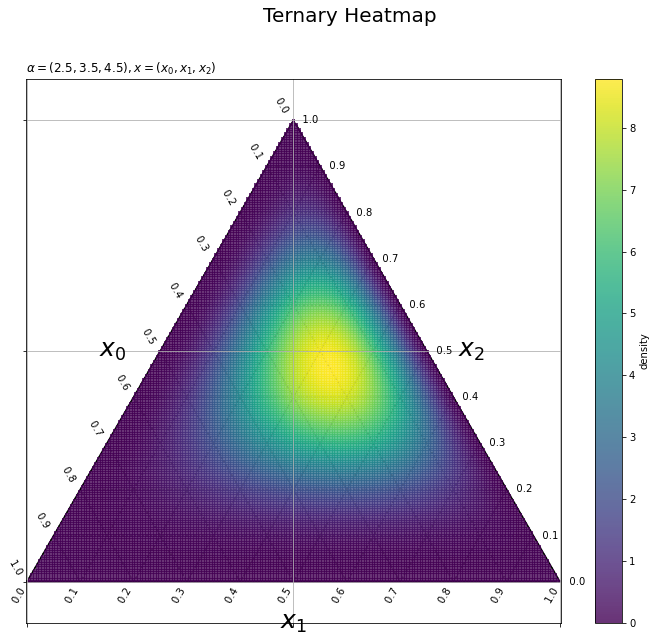
plt.pcolor()でヒートマップを描画する。
同様に、散布図を使ってヒートマップを描画する。
# 三角座標上の等高線図を作成 plt.figure(figsize=(12, 10), facecolor='white') # 図の設定 sct = plt.scatter(x=y_0_grid.flatten(), y=y_1_grid.flatten(), c=dens_vals, alpha = 0.5) # 確率密度の等高線 plt.quiver(grid_x, grid_y, grid_u, grid_v, scale_units='xy', scale=1, units='dots', width=0.1, headwidth=0.1, fc='none', ec='gray', linewidth=1.5, linestyle=':') # 三角座標のグリッド線 plt.quiver(axis_x, axis_y, axis_u, axis_v, scale_units='xy', scale=1, units='dots', width=1.5, headwidth=1.5, fc='black', linestyle='-') # 三角座標の枠線 for val in axis_vals: plt.text(x=0.5*val, y=0.5*val*np.sqrt(3.0), s=str(np.round(1.0-val, 1))+' '*2, ha='right', va='bottom', rotation=-60) # 三角座標のx軸目盛 plt.text(x=val, y=0.0, s=str(np.round(val, 1))+' '*10, ha='center', va='center', rotation=60) # 三角座標のy軸目盛 plt.text(x=0.5*val+0.5, y=0.5*(1.0-val)*np.sqrt(3.0), s=' '*3+str(np.round(1.0-val, 1)), ha='left', va='center') # 三角座標のz軸目盛 plt.text(x=0.25, y=0.25*np.sqrt(3.0), s='$x_0$'+' '*5, ha='right', va='center', size=25) # 三角座標のx軸ラベル plt.text(x=0.5, y=0.0, s='\n'+'$x_1$', ha='center', va='top', size=25) # 三角座標のy軸ラベル plt.text(x=0.75, y=0.25*np.sqrt(3.0), s=' '*4+'$x_2$', ha='left', va='center', size=25) # 三角図のz軸ラベル plt.xticks(ticks=[0.0, 0.5, 1.0], labels='') # 2次元座標のx軸目盛 plt.yticks(ticks=[0.0, 0.25*np.sqrt(3.0), 0.5*np.sqrt(3.0)], labels='') # 2次元座標のy軸目盛 plt.grid() # 2次元座標のグリッド線 plt.axis('equal') # アスペクト比 plt.colorbar(sct, label='density') # カラーバー plt.suptitle(t='Ternary Heatmap', fontsize=20) # タイトル plt.title(label=param_text, loc='left') # パラメータラベル plt.show() # 描画
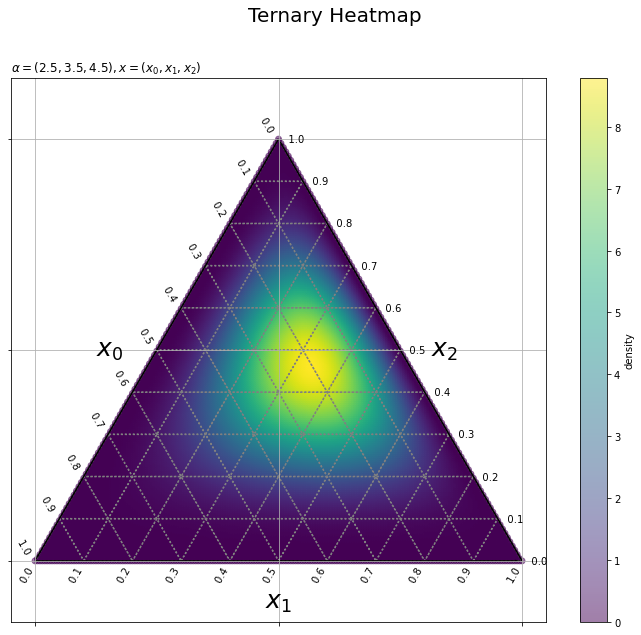
(グリッド線がうまく透けなかったので上から表示した。点の数を減らせば透けると思う。また、点が重なることでカラーバーよりも色が濃くなっている。)
等高線図のアニメーション
最後に、等高線図のアニメーション(gif画像)を作成する。
ディリクレ分布のパラメータとして利用する値を指定する。
# ディリクレ分布のパラメータとして利用する値を指定 alpha_0_vals = np.arange(start=1.0, stop=10.1, step=0.1).round(decimals=1) alpha_1_vals = np.arange(start=2.0, stop=11.1, step=0.1).round(decimals=1) alpha_2_vals = np.arange(start=3.0, stop=12.1, step=0.1).round(decimals=1) # フレーム数を設定 frame_num = len(alpha_0_vals)
$\alpha_0, \alpha_1, \alpha_2$ごとに要素数が同じになるように配列に値を作成する。
等高線図のアニメーションを作成する。
# 図を初期化 fig = plt.figure(figsize=(10, 10), facecolor='white') # 図の設定 fig.suptitle(t='Ternary Contour Plot', fontsize=20) # タイトル # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i番目のパラメータを取得 alpha_k = np.array([alpha_0_vals[i], alpha_1_vals[i], alpha_2_vals[i]]) # ディリクレ分布の確率密度を計算 dens_vals = np.array( [dirichlet.pdf(x=x_k, alpha=alpha_k) if all(x_k != np.nan) else np.nan for x_k in x_points] ) # パラメータラベル用の文字列を作成 param_text = '$' + '\\alpha=('+', '.join([str(val) for val in alpha_k])+')' + ', x=(x_0, x_1, x_2)' + '$' # 三角座標上の等高線図を作成 plt.quiver(grid_x, grid_y, grid_u, grid_v, scale_units='xy', scale=1, units='dots', width=0.1, headwidth=0.1, fc='none', ec='gray', linewidth=1.5, linestyle=':') # 三角座標のグリッド線 plt.quiver(axis_x, axis_y, axis_u, axis_v, scale_units='xy', scale=1, units='dots', width=1.5, headwidth=1.5, fc='black', linestyle='-') # 三角座標の枠線 for val in axis_vals: plt.text(x=0.5*val, y=0.5*val*np.sqrt(3.0), s=str(np.round(1.0-val, 1))+' '*2, ha='right', va='bottom', rotation=-60) # 三角座標のx軸目盛 plt.text(x=val, y=0.0, s=str(np.round(val, 1))+' '*10, ha='center', va='center', rotation=60) # 三角座標のy軸目盛 plt.text(x=0.5*val+0.5, y=0.5*(1.0-val)*np.sqrt(3.0), s=' '*3+str(np.round(1.0-val, 1)), ha='left', va='center') # 三角座標のz軸目盛 plt.text(x=0.25, y=0.25*np.sqrt(3.0), s='$x_0$'+' '*5, ha='right', va='center', size=25) # 三角座標のx軸ラベル plt.text(x=0.5, y=0.0, s='\n'+'$x_1$', ha='center', va='top', size=25) # 三角座標のy軸ラベル plt.text(x=0.75, y=0.25*np.sqrt(3.0), s=' '*4+'$x_2$', ha='left', va='center', size=25) # 三角図のz軸ラベル plt.contourf(y_0_grid, y_1_grid, dens_vals.reshape(y_shape), alpha = 0.8) # 確率密度の等高線 plt.xticks(ticks=[0.0, 0.5, 1.0], labels='') # 2次元座標のx軸目盛 plt.yticks(ticks=[0.0, 0.25*np.sqrt(3.0), 0.5*np.sqrt(3.0)], labels='') # 2次元座標のy軸目盛 plt.grid() # 2次元座標のグリッド線 plt.axis('equal') # アスペクト比 plt.title(label=param_text, loc='left') # パラメータラベル # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # gif画像を保存 ani.save('../figure/ternary_contour_0.gif')
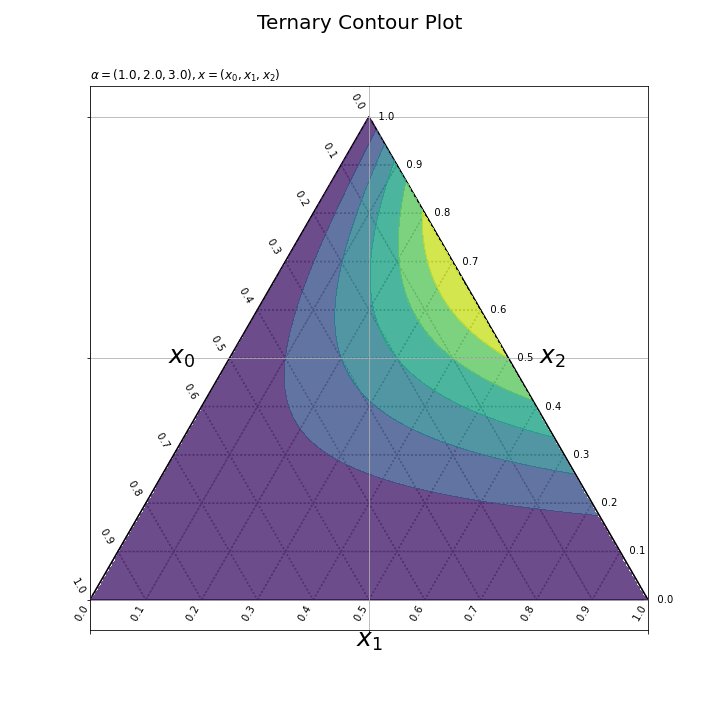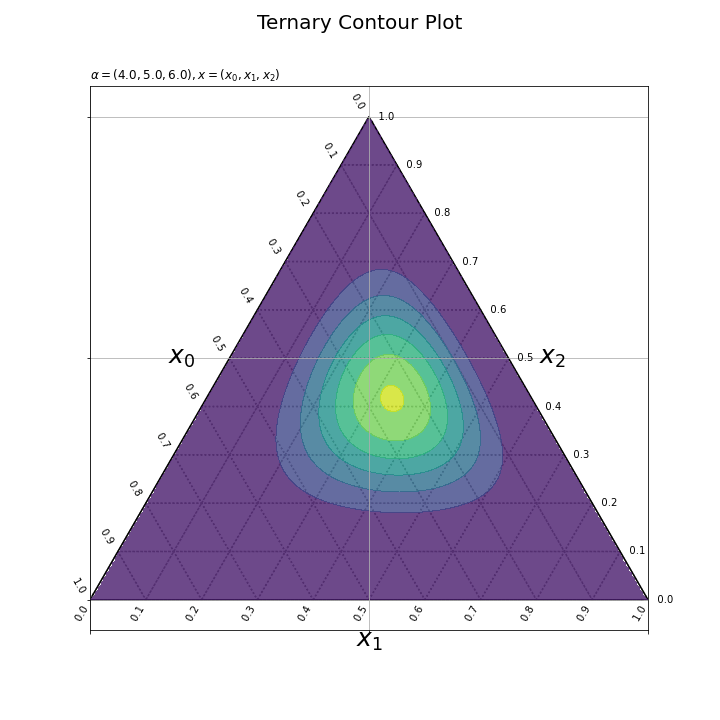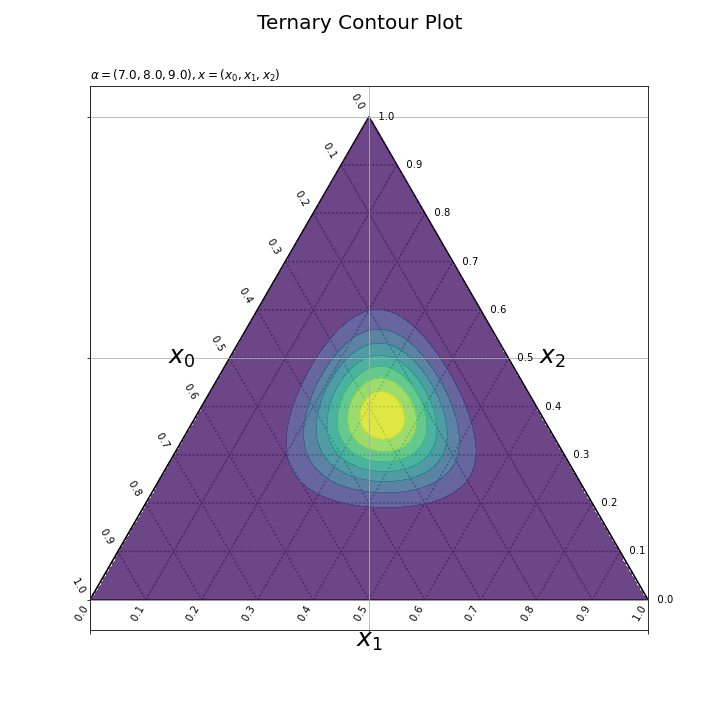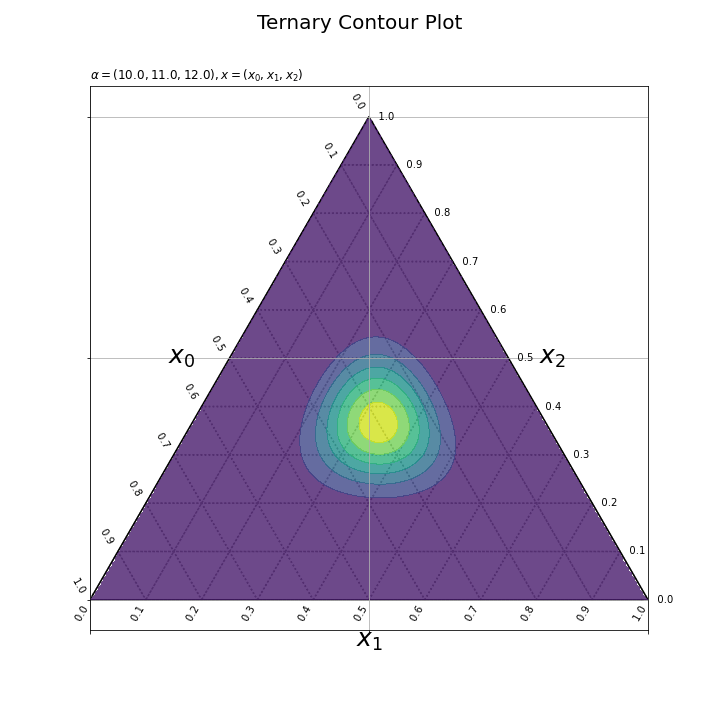
各フレームの確率密度の計算と作図処理を関数として定義して、FuncAnimation()を使ってアニメーション(gif画像)を作成する。
パラメータごとに確率密度の等高線を描画できた。ただし、フレームごとに等高線を引く値が変わっている。
そこで、z軸の値の最小値・最大値と等高線を引く値を指定する。
# z軸の最小値と最大値を設定 dens_min = 0.0 dens_max = 27.0 alpha_max_k = np.array([alpha_0_vals.max(), alpha_1_vals.max(), alpha_2_vals.max()]) dens_max = np.ceil( dirichlet.pdf(x=(alpha_max_k-1.0)/(np.sum(alpha_max_k)-3.0), alpha=alpha_max_k) ) # 等高線を引く値を設定 dens_levels = np.linspace(dens_min, dens_max, num=10) print(dens_levels)
[ 0. 3. 6. 9. 12. 15. 18. 21. 24. 27.]
最大値については、直接指定するか、上手いこと最頻値の確率密度を求める。
等高線に関する指定を行って、等高線図のアニメーションを作成する。
# 図を初期化 fig = plt.figure(figsize=(10, 10), facecolor='white') # 図の設定 fig.suptitle(t='Ternary Contour Plot', fontsize=20) # タイトル # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i番目のパラメータを取得 alpha_k = np.array([alpha_0_vals[i], alpha_1_vals[i], alpha_2_vals[i]]) # ディリクレ分布の確率密度を計算 dens_vals = np.array( [dirichlet.pdf(x=x_k, alpha=alpha_k) if all(x_k != np.nan) else np.nan for x_k in x_points] ) # パラメータラベル用の文字列を作成 param_text = '$' + '\\alpha=('+', '.join([str(val) for val in alpha_k])+')' + ', x=(x_0, x_1, x_2)' + '$' # 三角座標上の等高線図を作成 plt.quiver(grid_x, grid_y, grid_u, grid_v, scale_units='xy', scale=1, units='dots', width=0.1, headwidth=0.1, fc='none', ec='gray', linewidth=1.5, linestyle=':') # 三角座標のグリッド線 plt.quiver(axis_x, axis_y, axis_u, axis_v, scale_units='xy', scale=1, units='dots', width=1.5, headwidth=1.5, fc='black', linestyle='-') # 三角座標の枠線 for val in axis_vals: plt.text(x=0.5*val, y=0.5*val*np.sqrt(3.0), s=str(np.round(1.0-val, 1))+' '*2, ha='right', va='bottom', rotation=-60) # 三角座標のx軸目盛 plt.text(x=val, y=0.0, s=str(np.round(val, 1))+' '*10, ha='center', va='center', rotation=60) # 三角座標のy軸目盛 plt.text(x=0.5*val+0.5, y=0.5*(1.0-val)*np.sqrt(3.0), s=' '*3+str(np.round(1.0-val, 1)), ha='left', va='center') # 三角座標のz軸目盛 plt.text(x=0.25, y=0.25*np.sqrt(3.0), s='$x_0$'+' '*5, ha='right', va='center', size=25) # 三角座標のx軸ラベル plt.text(x=0.5, y=0.0, s='\n'+'$x_1$', ha='center', va='top', size=25) # 三角座標のy軸ラベル plt.text(x=0.75, y=0.25*np.sqrt(3.0), s=' '*4+'$x_2$', ha='left', va='center', size=25) # 三角図のz軸ラベル plt.contourf(y_0_grid, y_1_grid, dens_vals.reshape(y_shape), vmin=dens_min, vmax=dens_max, levels=dens_levels, alpha = 0.8) # 確率密度の等高線 plt.xticks(ticks=[0.0, 0.5, 1.0], labels='') # 2次元座標のx軸目盛 plt.yticks(ticks=[0.0, 0.25*np.sqrt(3.0), 0.5*np.sqrt(3.0)], labels='') # 2次元座標のy軸目盛 plt.grid() # 2次元座標のグリッド線 plt.axis('equal') # アスペクト比 plt.title(label=param_text, loc='left') # パラメータラベル # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # gif画像を保存 ani.save('../figure/ternary_contour_1.gif')
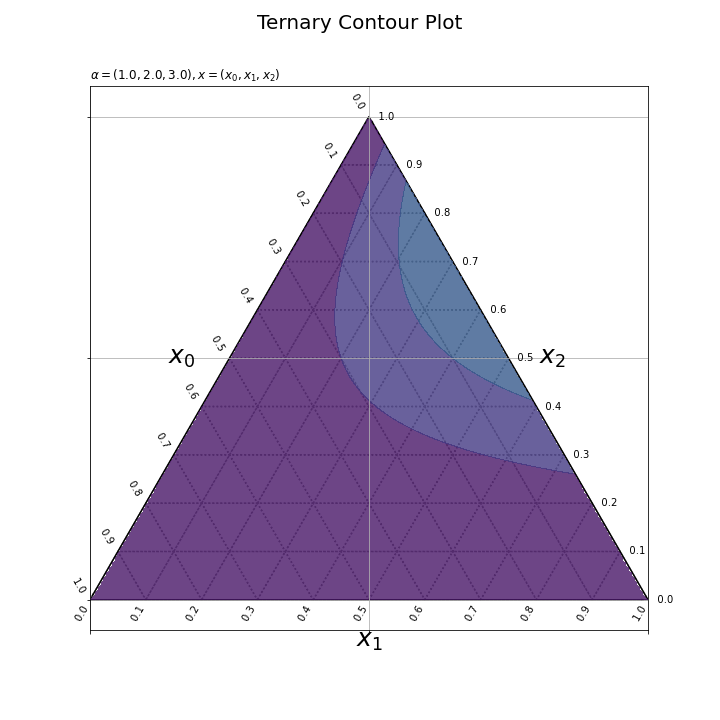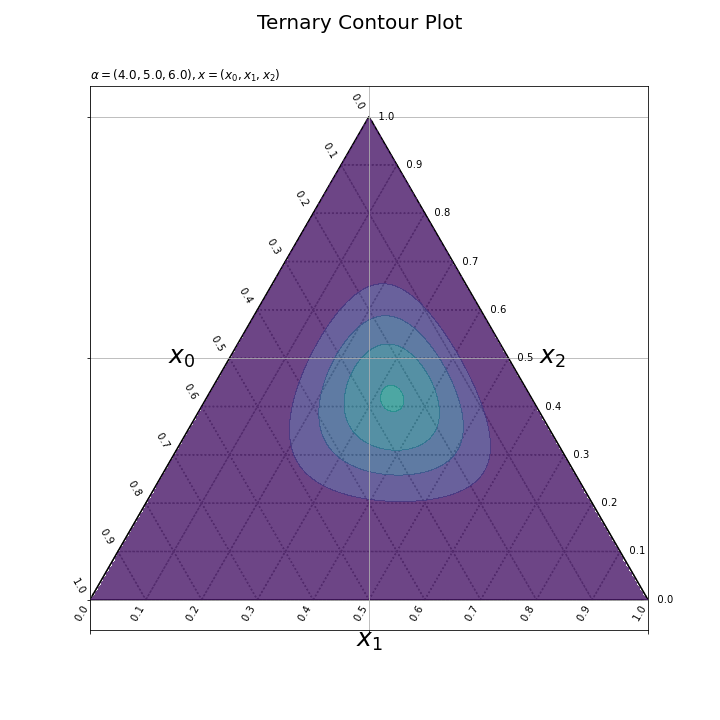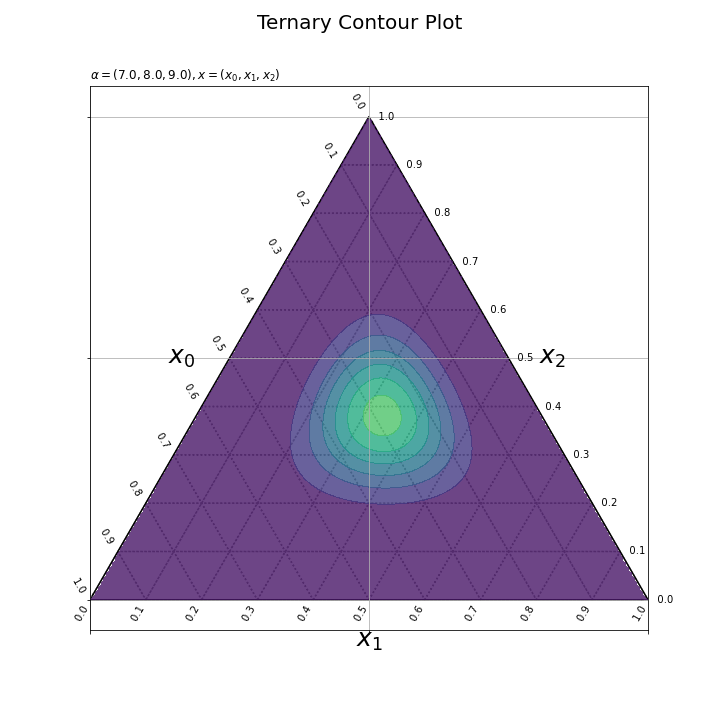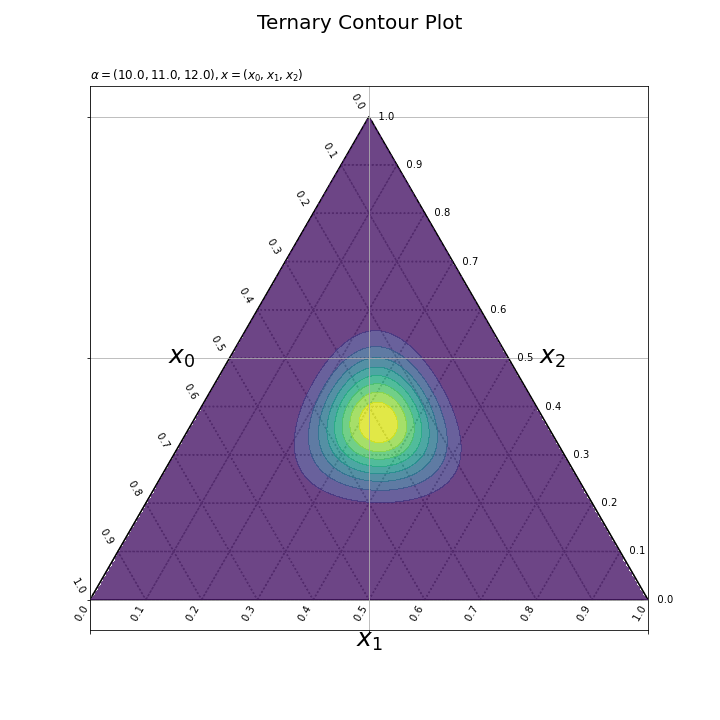
z軸の最小値をdens_min、最大値をdens_maxとして指定する。dens_minからdens_maxの範囲で、等高線を引く値を設定する(数をnum引数に指定する)。
plt.contourf()の最小値の引数vminにdens_min、最大値の引数vmaxにdens_max、等高線を引く値の引数levelsにdens_levelsを指定しすると、全てのフレームで共通の設定にできる。
さらに、カラーバーを表示する。
# 図を初期化 fig = plt.figure(figsize=(12, 10), facecolor='white') # 図の設定 fig.suptitle(t='Ternary Contour Plot', fontsize=20) # タイトル tmp = plt.contourf(y_0_grid, y_1_grid, np.zeros(y_shape), vmin=dens_min, vmax=dens_max, levels=dens_levels, alpha = 0.8) # カラーバー用のダミー fig.colorbar(tmp, label='density') # カラーバー # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i番目のパラメータを取得 alpha_k = np.array([alpha_0_vals[i], alpha_1_vals[i], alpha_2_vals[i]]) # ディリクレ分布の確率密度を計算 dens_vals = np.array( [dirichlet.pdf(x=x_k, alpha=alpha_k) if all(x_k != np.nan) else np.nan for x_k in x_points] ) # パラメータラベル用の文字列を作成 param_text = '$' + '\\alpha=('+', '.join([str(val) for val in alpha_k])+')' + ', x=(x_0, x_1, x_2)' + '$' # 三角座標上の等高線図を作成 plt.quiver(grid_x, grid_y, grid_u, grid_v, scale_units='xy', scale=1, units='dots', width=0.1, headwidth=0.1, fc='none', ec='gray', linewidth=1.5, linestyle=':') # 三角座標のグリッド線 plt.quiver(axis_x, axis_y, axis_u, axis_v, scale_units='xy', scale=1, units='dots', width=1.5, headwidth=1.5, fc='black', linestyle='-') # 三角座標の枠線 for val in axis_vals: plt.text(x=0.5*val, y=0.5*val*np.sqrt(3.0), s=str(np.round(1.0-val, 1))+' '*2, ha='right', va='bottom', rotation=-60) # 三角座標のx軸目盛 plt.text(x=val, y=0.0, s=str(np.round(val, 1))+' '*10, ha='center', va='center', rotation=60) # 三角座標のy軸目盛 plt.text(x=0.5*val+0.5, y=0.5*(1.0-val)*np.sqrt(3.0), s=' '*3+str(np.round(1.0-val, 1)), ha='left', va='center') # 三角座標のz軸目盛 plt.text(x=0.25, y=0.25*np.sqrt(3.0), s='$x_0$'+' '*5, ha='right', va='center', size=25) # 三角座標のx軸ラベル plt.text(x=0.5, y=0.0, s='\n'+'$x_1$', ha='center', va='top', size=25) # 三角座標のy軸ラベル plt.text(x=0.75, y=0.25*np.sqrt(3.0), s=' '*4+'$x_2$', ha='left', va='center', size=25) # 三角図のz軸ラベル plt.contourf(y_0_grid, y_1_grid, dens_vals.reshape(y_shape), vmin=dens_min, vmax=dens_max, levels=dens_levels, alpha = 0.8) # 確率密度の等高線 plt.xticks(ticks=[0.0, 0.5, 1.0], labels='') # 2次元座標のx軸目盛 plt.yticks(ticks=[0.0, 0.25*np.sqrt(3.0), 0.5*np.sqrt(3.0)], labels='') # 2次元座標のy軸目盛 plt.grid() # 2次元座標のグリッド線 plt.axis('equal') # アスペクト比 plt.title(label=param_text, loc='left') # パラメータラベル # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # gif画像を保存 ani.save('../figure/ternary_contour_2.gif')
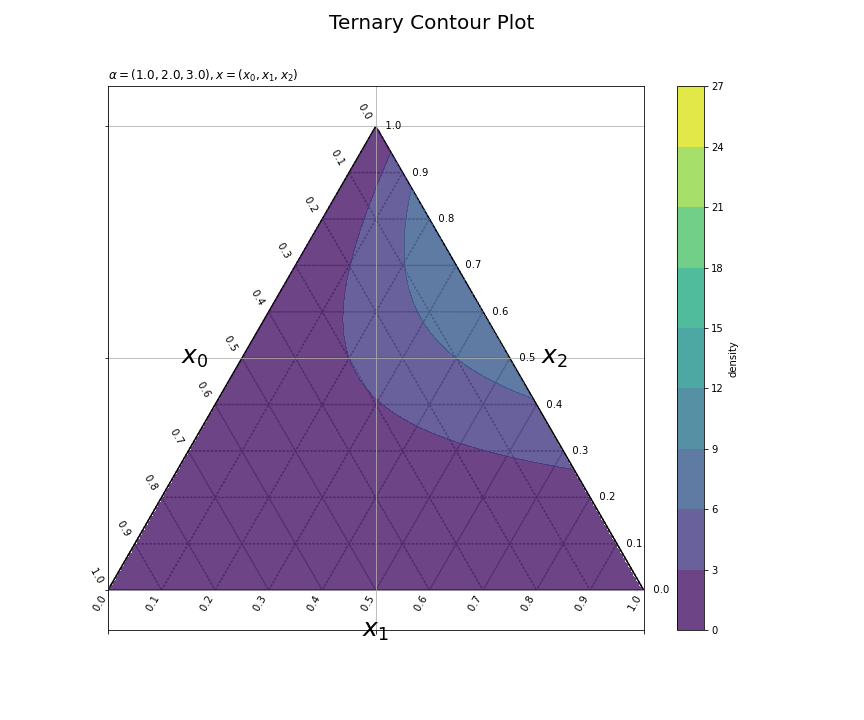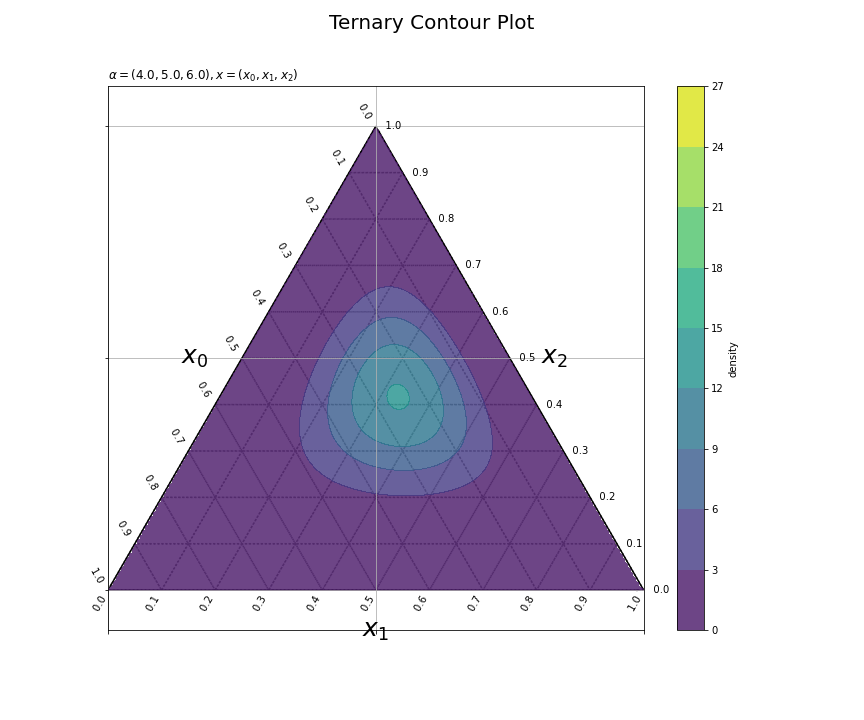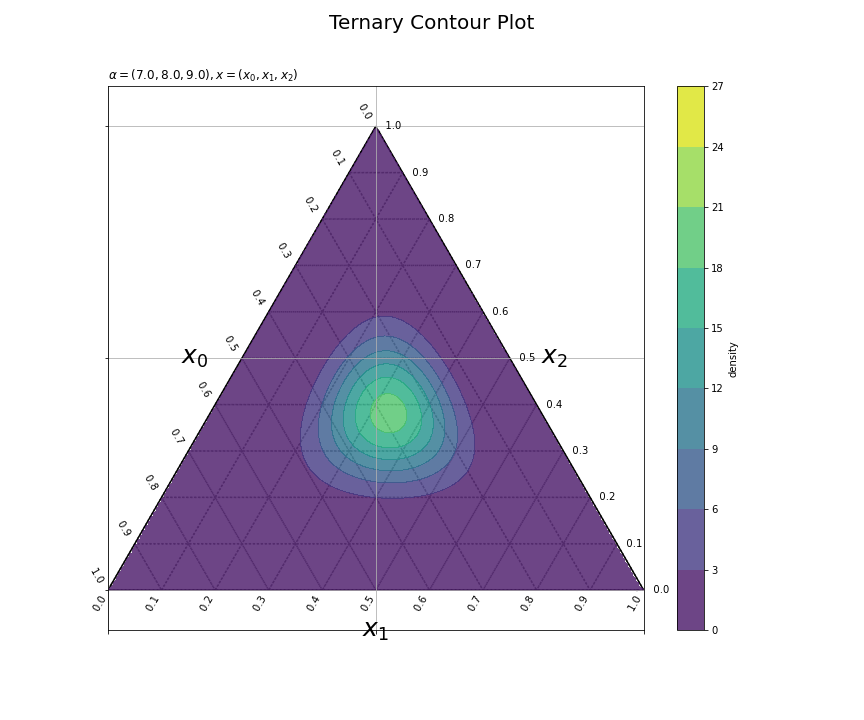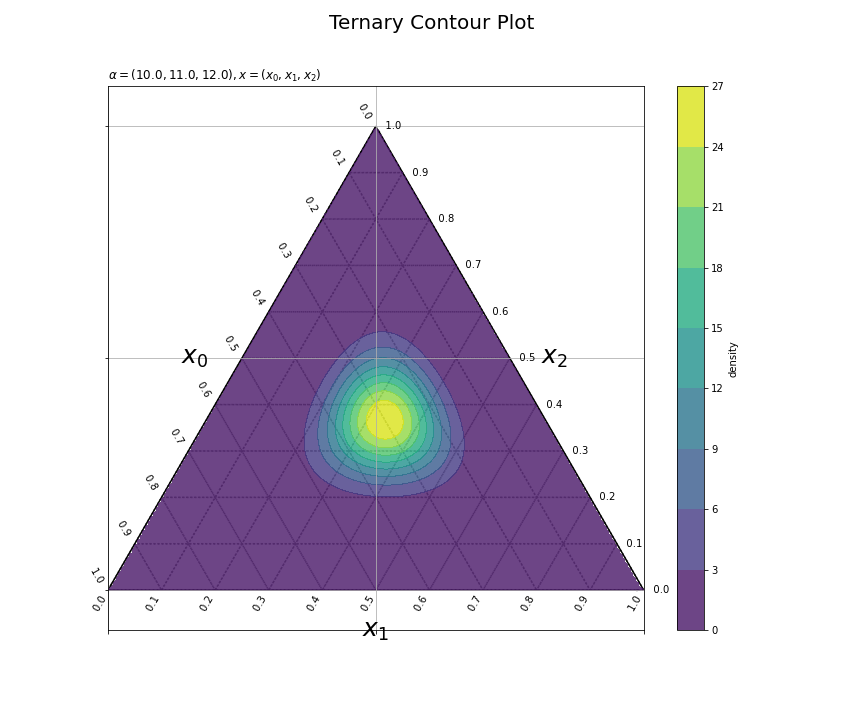
update()の中でplt.colorbar()を行うと、フレームごとにカラーバーが追加され、フレーム数分のカラーバーが表示される。そこで、ダミーのヒートマップtmpを使って、fig.colorbar()でカラーバーを1つ表示する。
以上で、2次元の三角図を作成できた。次は3次元の作図を考える。
おわりに
もう1つ続きます。
2022年10月18日はつばきファクトリーの福田真琳さんの18歳のお誕生日です!
もうずっと癒されてます。
【次の内容】