はじめに
機械学習で登場する確率分布について色々な角度から理解したいシリーズです。
この記事では、R言語でウィシャート分布の乱数を用いたマハラノビス距離の等高線とその軸により可視化します。
【前の内容】
【他の記事一覧】
【この記事の内容】
ウィシャート分布の可視化
ウィシャート分布(Wishart Distribution)の確率密度をグラフで表現するのは難しいので、期待値と乱数を用いたマハラノビス距離(Mahalanobis Distance)のグラフにより可視化します。ウィシャート分布については「ウィシャート分布の定義式 - からっぽのしょこ」、マハラノビス距離については「分散共分散行列とユークリッド距離・マハラノビス距離の関係の導出 - からっぽのしょこ」、固有ベクトルについては「2.3.0:分散共分散行列と固有値・固有ベクトルの関係の導出【PRMLのノート】 - からっぽのしょこ」、楕円の軸については「【R】2次元ガウス分布の作図 - からっぽのしょこ」を参照してください。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(gganimate)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているため、ggplot2は読み込む必要があります。
magrittrパッケージのパイプ演算子%>%ではなく、ベースパイプ(ネイティブパイプ)演算子|>を使っています。%>%に置き換えても処理できます。
分布の変化をアニメーション(gif画像)で確認するのにgganimateパッケージを利用します。不要であれば省略してください。
期待値による距離と軸の計算
まずは、ウィシャート分布のパラメータを設定して、分散共分散行列(確率変数の逆行列)の期待値によるマハラノビス距離の楕円と軸を計算します。
ウィシャート分布のパラメータ$\nu, \mathbf{W}$とサンプルサイズ$N$を設定します。この例では、2次元のグラフで描画するため、次元数を$D = 2$とします。
# 次元数を指定 D <- 2 # 自由度を指定 nu <- D + 8 # 逆スケール行列を指定 w_dd <- matrix(c(5, 0.6, 0.6, 12), nrow = D, ncol = D) # パラメータの数(サンプルサイズ)を指定 N <- 100
自由度$\nu$と逆スケール行列$\mathbf{W}$、サンプルサイズ$N$を指定します。
自由度は$\nu > D - 1$、逆スケール行列は$D \times D$の正定値行列を満たす必要があります。
分散共分散行列の期待値$\mathbb{E}[\boldsymbol{\Sigma}]$を計算します。
# 分散共分散行列の期待値を計算 E_sigma_dd <- solve(nu * w_dd) E_sigma_dd
## [,1] [,2] ## [1,] 0.020120724 -0.001006036 ## [2,] -0.001006036 0.008383635
ウィシャート分布の期待値(精度行列$\boldsymbol{\Lambda}$の期待値)$\mathbb{E}[\boldsymbol{\Lambda}] = \nu \mathbf{W}$の逆行列をとり、分散共分散行列の期待値$\mathbb{E}[\boldsymbol{\Sigma}] = (\nu \mathbf{W})^{-1}$を求めます。
分散共分散行列に対応する変数の値$\mathbf{x}$を作成します。
# xの値を作成 x_1_vals <- seq( from = - sqrt(E_sigma_dd[1, 1]) * 3, to = sqrt(E_sigma_dd[1, 1]) * 3, length.out = 100 ) x_2_vals <- seq( from = - sqrt(E_sigma_dd[2, 2]) * 3, to = sqrt(E_sigma_dd[2, 2]) * 3, length.out = 100 ) # xの点を作成 x_mat <- tidyr::expand_grid( x_1 = x_1_vals, x_2 = x_2_vals ) |> # 格子点を作成 as.matrix() # マトリクスに変換 head(x_mat)
## x_1 x_2 ## [1,] -0.4255426 -0.2746866 ## [2,] -0.4255426 -0.2691374 ## [3,] -0.4255426 -0.2635881 ## [4,] -0.4255426 -0.2580389 ## [5,] -0.4255426 -0.2524897 ## [6,] -0.4255426 -0.2469405
$x_1$(x軸)の値をx_1_vals、$x_2$(y軸)の値をx_2_valsとします。この例では、それぞれ平均を中心に標準偏差の期待値の3倍を範囲とします。
x_1_valsとx_2_valsの要素の全ての組み合わせ(格子状の点)をexpand_grid()で作成します。データフレームが出力されるので、as.matrix()でマトリクスに変換してx_matとします。x_matの各行が点$\mathbf{x} = (x_1, x_2)$に対応します。
分散共分散行列の期待値$\mathbb{E}[\boldsymbol{\Sigma}]$によるマハラノビス距離を計算します。
# 期待値によるマハラノビス距離(楕円)を計算 E_delta_df <- tibble::tibble( x_1 = x_mat[, 1], # x軸の値 x_2 = x_mat[, 2], # y軸の値 delta = mahalanobis(x = x_mat, center = 0, cov = E_sigma_dd) |> sqrt() # マハラノビス距離 ) E_delta_df
## # A tibble: 10,000 × 3 ## x_1 x_2 delta ## <dbl> <dbl> <dbl> ## 1 -0.426 -0.275 4.42 ## 2 -0.426 -0.269 4.37 ## 3 -0.426 -0.264 4.33 ## 4 -0.426 -0.258 4.29 ## 5 -0.426 -0.252 4.24 ## 6 -0.426 -0.247 4.20 ## 7 -0.426 -0.241 4.16 ## 8 -0.426 -0.236 4.12 ## 9 -0.426 -0.230 4.07 ## 10 -0.426 -0.225 4.03 ## # … with 9,990 more rows
マハラノビス距離は、mahalanobis()で計算できます。変数の引数Xにx_mat、平均ベクトルの引数centerに0(またはc(0, 0))、分散共分散行列の引数covにE_sigma_ddを指定します。
分散共分散行列の期待値$\mathbb{E}[\boldsymbol{\Sigma}]$の固有値と固有ベクトルを計算します。
# 期待値の固有値・固有ベクトルを計算 res_eigen <- eigen(E_sigma_dd) E_lambda_d <- res_eigen[["values"]] E_u_dd <- res_eigen[["vectors"]] |> t() E_lambda_d; E_u_dd
## [1] 0.020206332 0.008298028 ## [,1] [,2] ## [1,] -0.99639908 0.08478722 ## [2,] -0.08478722 -0.99639908
固有値$\lambda_1, \lambda_2$と固有ベクトル$\mathbf{u}_1 = (u_{1,1}, u_{1,2}), \mathbf{u}_2 = (u_{2,1}, u_{2,2})$をeigen()で計算します。リストが出力されるので、"values"で固有値(をまとめたベクトル)、"vectors"で固有ベクトル(をまとめたマトリクス)を取り出します。数式での成分と合わせるために転置しておきます。
固有値と固有ベクトルを用いて、楕円の軸を計算します。
# 期待値による楕円の長軸を計算 E_axis_df <- tibble::tibble( xend = E_u_dd[1, 1] * sqrt(E_lambda_d[1]), yend = E_u_dd[1, 2] * sqrt(E_lambda_d[1]) ) E_axis_df
## # A tibble: 1 × 2 ## xend yend ## <dbl> <dbl> ## 1 -0.142 0.0121
軸番号を$i$、次元を$j$として、軸の先端の点を$u_{j,i} \sqrt{\lambda_j}$で計算します。ここでは、長い方の軸($i = 1$)のデータフレームに格納します。
ここまでは、ウィシャート分布の期待値に用いて計算しました。続いて、ウィシャート分布のサンプルに用いて計算します。
マハラノビス距離(楕円)の作図
次は、ウィシャート分布から精度行列をサンプリングして、サンプルごとにマハラノビス距離の楕円と軸を計算します。乱数生成については「【R】ウィシャート分布から確率分布の生成 - からっぽのしょこ」を参照してください。
ウィシャート分布に従う乱数を生成します。
# 分散共分散行列を生成 lambda_ddn <- rWishart(n = N, df = nu, Sigma = w_dd) lambda_ddn[, , 1:3]
## , , 1 ## ## [,1] [,2] ## [1,] 35.01167 -23.27527 ## [2,] -23.27527 64.35598 ## ## , , 2 ## ## [,1] [,2] ## [1,] 66.733981 7.994431 ## [2,] 7.994431 115.121494 ## ## , , 3 ## ## [,1] [,2] ## [1,] 81.253923 6.525797 ## [2,] 6.525797 232.926304
ウィシャート分布の乱数は、rWishart()で生成できます。データ数の引数nにN、自由度の引数dfにnu、逆スケール行列の引数Sigmaにw_ddを指定します。
生成した値をガウス分布の精度行列$\boldsymbol{\Lambda}_n = (\lambda_{1,1,n}, \cdots, \lambda_{D,D, n})$のN個のサンプルlambda_ddnとします。(記号が被っていますが、$\lambda_{i,j,n}$はウィシャート分布の乱数(精度行列)の各成分です。)
精度行列のサンプル$\boldsymbol{\Lambda}_n$ごとにマハラノビス距離を計算します。
# サンプルごとにマハラノビス距離(楕円)を計算 res_delta_df <- tidyr::expand_grid( n = 1:N, # データ番号 x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(n) |> # 距離の計算用にグループ化 dplyr::mutate( delta = mahalanobis(x = x_mat, center = 0, cov = lambda_ddn[, , unique(n)], inverted = TRUE) |> sqrt() # マハラノビス距離 ) |> dplyr::ungroup() # グループ化を解除 res_delta_df
## # A tibble: 1,000,000 × 4 ## n x_1 x_2 delta ## <int> <dbl> <dbl> <dbl> ## 1 1 -0.426 -0.275 2.40 ## 2 1 -0.426 -0.269 2.38 ## 3 1 -0.426 -0.264 2.36 ## 4 1 -0.426 -0.258 2.35 ## 5 1 -0.426 -0.252 2.33 ## 6 1 -0.426 -0.247 2.32 ## 7 1 -0.426 -0.241 2.30 ## 8 1 -0.426 -0.236 2.29 ## 9 1 -0.426 -0.230 2.28 ## 10 1 -0.426 -0.225 2.27 ## # … with 999,990 more rows
パラメータ番号(1からNの整数)と変数x_1_vals, x_2_valsの要素の全ての組み合わせをexpand_grid()を作成します。これにより、サンプルごとにx_matを複製できます。
パラメータ列nでグループ化することで、x_matごとにマハラノビス距離を計算できます。
mahalanobis()のx引数にx_mat、center引数に0、cov引数にlambda_ddnのn番目の値(マトリクス)を指定します。cov引数に精度行列を指定する場合は、inverted引数にTRUEを指定します。
精度行列のサンプル$\boldsymbol{\Lambda}_n$ごとのマハラノビス距離の等高線図を作成します。
# 等高線を引く距離を指定 delta <- 1 # サンプルごとにマハラノビス距離(楕円)を作図 ggplot() + geom_contour(data = E_delta_df, mapping = aes(x = x_1, y = x_2, z = delta), breaks = delta, color ="red", size = 1, linetype = "dashed") + # 期待値による分布 geom_contour(data = res_delta_df, mapping = aes(x = x_1, y = x_2, z = delta, color = factor(n)), breaks = delta, alpha = 0.5, show.legend = FALSE) + # サンプルによる分布 coord_fixed(ratio = 1, xlim = c(min(x_1_vals), max(x_1_vals)), ylim = c(min(x_2_vals), max(x_2_vals))) + # アスペクト比 labs(title = "Mahalabobis Distance", subtitle = parse(text = paste0("list(nu==", nu, ", W==(list(", paste0(round(w_dd, 2), collapse = ", "), ")), N==", N, ")")), x = expression(x[1]), y = expression(x[2]))
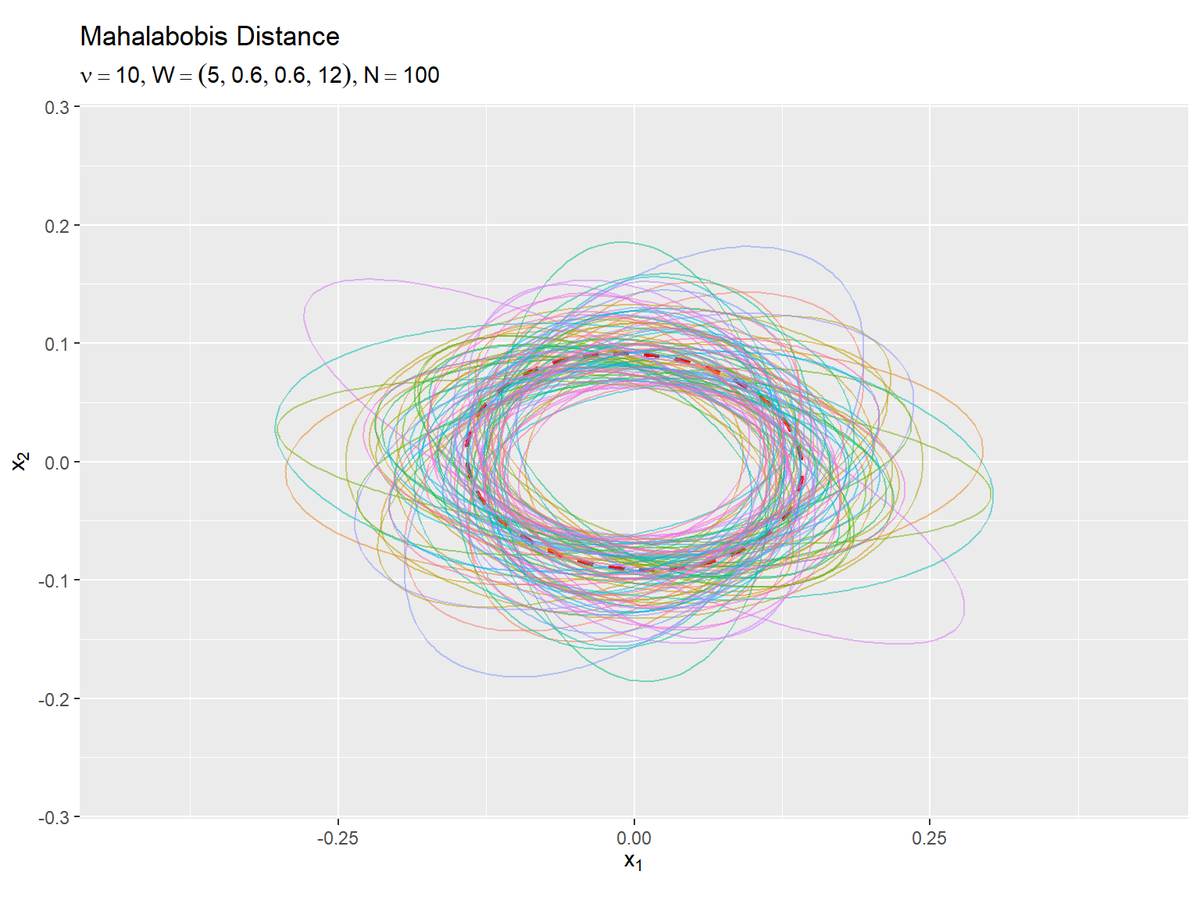
geom_contour()のbreaks引数に値を指定すると、その値で等高線を引きます。
期待値による楕円を赤色の破線で示します。
それぞれ楕円形になります。
精度行列のサンプル$\boldsymbol{\Lambda}_n$ごとに固有値と固有ベクトルを計算して、楕円の軸を計算します。
# サンプルごとに楕円の長軸を計算 res_axis_df <- tibble::tibble( n = 1:N # データ番号 ) |> dplyr::group_by(n) |> # 軸の計算用にグループ化 dplyr::mutate( lambda_1 = lambda_ddn[, , n] |> solve() |> eigen() |> (\(.){.[["values"]][1]})(), # 固有値 u_11 = lambda_ddn[, , n] |> solve() |> eigen() |> (\(.){t(.[["vectors"]])[1, 1]})(), # 固有ベクトルの成分 u_12 = lambda_ddn[, , n] |> solve() |> eigen() |> (\(.){t(.[["vectors"]])[1, 2]})(), # 固有ベクトルの成分 xend = u_11 * sqrt(lambda_1), # 終点のx軸の値 yend = u_12 * sqrt(lambda_1) # 終点のy軸の値 ) |> dplyr::ungroup() # グループ化を解除 res_axis_df
## # A tibble: 100 × 6 ## n lambda_1 u_11 u_12 xend yend ## <int> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 1 0.0451 -0.876 -0.483 -0.186 -0.103 ## 2 2 0.0153 -0.987 0.159 -0.122 0.0196 ## 3 3 0.0123 -0.999 0.0429 -0.111 0.00477 ## 4 4 0.0292 0.621 0.784 0.106 0.134 ## 5 5 0.0211 -0.938 0.345 -0.136 0.0501 ## 6 6 0.0161 -0.989 -0.146 -0.125 -0.0185 ## 7 7 0.0868 -0.999 -0.0374 -0.294 -0.0110 ## 8 8 0.0255 -0.793 0.609 -0.127 0.0973 ## 9 9 0.0318 -0.975 0.223 -0.174 0.0397 ## 10 10 0.0190 -1.00 -0.00472 -0.138 -0.000650 ## # … with 90 more rows
上手いことして(もっといいやり方があれば教えてください)、固有値と固有ベクトルの値の列を作成して、軸の先端の点を$u_{j,i}^{(n)} \sqrt{\lambda_j^{(n)}}$で計算します。($\lambda_j^{(n)}$はウィシャート分布の$n$番目の乱数$\boldsymbol{\Lambda}_n$の逆行列$\boldsymbol{\Sigma}_n$の固有値です。)
精度行列のサンプル$\boldsymbol{\Lambda}_n$ごとの楕円の軸を描画します。
# サンプルごとに楕円の長軸を作図 ggplot() + geom_contour(data = E_delta_df, mapping = aes(x = x_1, y = x_2, z = delta), breaks = delta, color ="red", size = 1, linetype = "dashed") + # 期待値による分布 geom_segment(data = E_axis_df, mapping = aes(x = 0, y = 0, xend = xend, yend = yend), color = "red", size = 1, linetype = "dashed", arrow = arrow(length = unit(10, "pt"))) + # 期待値による分布の長軸 geom_segment(data = res_axis_df, mapping = aes(x = 0, y = 0, xend = xend, yend = yend), color = "orange", alpha = 0.5, arrow = arrow(length = unit(5, "pt"))) + # サンプルによる分布の長軸 coord_fixed(ratio = 1, xlim = c(min(x_1_vals), max(x_1_vals)), ylim = c(min(x_2_vals), max(x_2_vals))) + # アスペクト比 labs(title = "Mahalanobis Distance", subtitle = parse(text = paste0("list(nu==", nu, ", W==(list(", paste0(round(w_dd, 2), collapse = ", "), ")), N==", N, ")")), x = expression(x[1]), y = expression(x[2]))
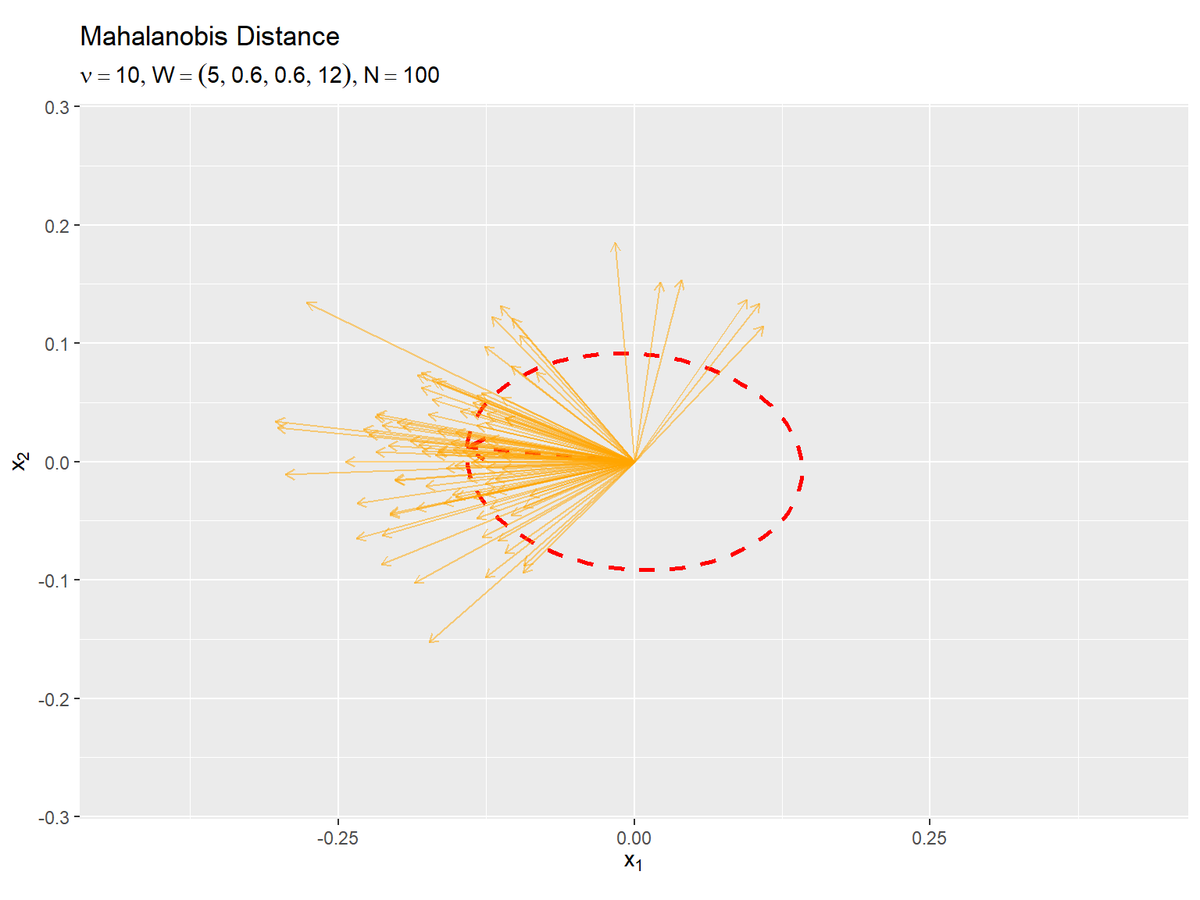
geom_segment()で楕円の軸を描画します。軸の始点の引数x, yに原点0、終点の引数xend, yendにaxis_dfのxstart, ystart列を指定すると、長さが$\sqrt{\lambda_j^{(n)}}$のベクトルを描画できます。
サンプルの軸(オレンジ色の矢印)が期待値による軸(赤色の矢印)に近い方向を向いているのを確認できます。
アニメーションによる可視化
次は、パラメータの値を少しずつ変化させて、期待値とサンプルによるマハラノビス距離の楕円と軸の変化をアニメーションで確認します。
自由度の影響
まずは、自由度$\nu$の値を変化させ、$\mathbf{W}$を固定します。
・作図コード(クリックで展開)
# 次元数を指定 D <- 2 # 自由度として利用する値を指定 nu_vals <- seq(from = D, to = 50, by = 1) # 逆スケール行列を指定 w_dd <- matrix(c(6, -0.6, -0.6, 10), nrow = D, ncol = D) # フレーム数を設定 frame_num <- length(nu_vals) frame_num
## [1] 49
値の間隔が一定になるように$\nu$の値をnu_valsとして作成します。パラメータごとにフレームを切り替えるので、nu_valsの要素数がアニメーションのフレーム数になります。
設定したパラメータに応じて、変数の値$\mathbf{x}$を作成します。
# 作図用の共分散行列を作成 E_sigma_dd <- solve(max(nu_vals) * w_dd) # xの値を作成 x_1_vals <- seq( from = - sqrt(E_sigma_dd[1, 1]) * 3, to = sqrt(E_sigma_dd[1, 1]) * 3, length.out = 100 ) x_2_vals <- seq( from = - sqrt(E_sigma_dd[2, 2]) * 3, to = sqrt(E_sigma_dd[2, 2]) * 3, length.out = 100 ) # xの点を作成 x_mat <- tidyr::expand_grid( x_1 = x_1_vals, x_2 = x_2_vals ) |> # 格子点を作成 as.matrix() # マトリクスに変換 head(x_mat)
## x_1 x_2 ## [1,] -0.173727 -0.1345684 ## [2,] -0.173727 -0.1318498 ## [3,] -0.173727 -0.1291313 ## [4,] -0.173727 -0.1264127 ## [5,] -0.173727 -0.1236942 ## [6,] -0.173727 -0.1209756
ここで計算するE_sigma_ddは、描画範囲を一定にするための仮の値です。
パラメータごとに分散共分散行列の期待値$\mathbb{E}[\boldsymbol{\Sigma}]$を計算して、マハラノビス距離を計算します。
# パラメータごとに共分散行列の期待値によるマハラノビス距離(楕円)を計算 anime_E_delta_df <- tidyr::expand_grid( nu = nu_vals, # パラメータ x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(nu) |> # 距離の計算用にグループ化 dplyr::mutate( delta = mahalanobis( x = x_mat, center = 0, cov = unique(nu) * w_dd, # 精度行列の期待値を指定 inverted = TRUE ), # 確率密度 parameter = paste0("nu=", unique(nu), ", W=(", paste0(w_dd, collapse = ", "), ")") |> factor(levels = paste0("nu=", nu_vals, ", W=(", paste0(w_dd, collapse = ", "), ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_E_delta_df
## # A tibble: 490,000 × 5 ## nu x_1 x_2 delta parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 2 -0.174 -0.135 0.668 nu=2, W=(6, -0.6, -0.6, 10) ## 2 2 -0.174 -0.132 0.655 nu=2, W=(6, -0.6, -0.6, 10) ## 3 2 -0.174 -0.129 0.642 nu=2, W=(6, -0.6, -0.6, 10) ## 4 2 -0.174 -0.126 0.629 nu=2, W=(6, -0.6, -0.6, 10) ## 5 2 -0.174 -0.124 0.617 nu=2, W=(6, -0.6, -0.6, 10) ## 6 2 -0.174 -0.121 0.604 nu=2, W=(6, -0.6, -0.6, 10) ## 7 2 -0.174 -0.118 0.593 nu=2, W=(6, -0.6, -0.6, 10) ## 8 2 -0.174 -0.116 0.581 nu=2, W=(6, -0.6, -0.6, 10) ## 9 2 -0.174 -0.113 0.570 nu=2, W=(6, -0.6, -0.6, 10) ## 10 2 -0.174 -0.110 0.559 nu=2, W=(6, -0.6, -0.6, 10) ## # … with 489,990 more rows
パラメータnu_valsと確率変数x_1_vals, x_2_valsの要素の全ての組み合わせをexpand_grid()を作成します。これにより、パラメータごとにx_matを複製できます。
パラメータ列nuでグループ化することで、x_matごとに距離を計算できます。
パラメータごとにフレーム切替用のラベルを作成します。文字列型だと文字列の基準で順序が決まるので、因子型にしてパラメータに応じたレベル(順序)を設定します。
パラメータごとに分散共分散行列の期待値$\mathbb{E}[\boldsymbol{\Sigma}]$の固有値・固有ベクトルを計算して、楕円の軸を計算します。
# パラメータごとに共分散行列の期待値による楕円の軸を計算 anime_E_axis_df <- tidyr::expand_grid( nu = nu_vals, # パラメータ name = paste0(rep(c("x", "y"), each = 2, times = 2), rep(c("start", "end"), each = 4)) # 列名 ) |> # パラメータごとに受け皿を複製 dplyr::group_by(nu) |> # 軸の計算用にグループ化 dplyr::mutate( axis = rep(c("y_1", "y_2"), times = 4), # pivot_wider用の列 sign = rep(c(-1, 1), each = 4), # 始点・終点の計算用の符号 lambda = solve(unique(nu) * w_dd) |> # 共分散行列の期待値を計算 (\(.){eigen(.)[["values"]]})() |> (\(.){rep(sqrt(.), times = 4)})(), # 固有値 u = solve(unique(nu) * w_dd) |> # 共分散行列の期待値を計算 (\(.){t(eigen(.)[["vectors"]])})() |> (\(.){rep(as.vector(.), times = 2)})(), # 固有ベクトル value = sign * u * lambda, # 軸の始点・終点を計算 parameter = paste0("nu=", nu, ", W=(", paste0(w_dd, collapse = ", "), ")") |> factor(levels = paste0("nu=", nu_vals, ", W=(", paste0(w_dd, collapse = ", "), ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() |> # グループ化を解除 dplyr::select(axis, name, value, parameter) |> # 利用する列を選択 tidyr::pivot_wider( id_cols = c(axis, parameter), names_from = name, values_from = value ) # 軸の視点・終点の列を分割 anime_E_axis_df
## # A tibble: 98 × 6 ## axis parameter xstart ystart xend yend ## <chr> <fct> <dbl> <dbl> <dbl> <dbl> ## 1 y_1 nu=2, W=(6, -0.6, -0.6, 10) 0.288 0.0422 -0.288 -0.0422 ## 2 y_2 nu=2, W=(6, -0.6, -0.6, 10) -0.0323 0.220 0.0323 -0.220 ## 3 y_1 nu=3, W=(6, -0.6, -0.6, 10) 0.235 0.0345 -0.235 -0.0345 ## 4 y_2 nu=3, W=(6, -0.6, -0.6, 10) -0.0264 0.180 0.0264 -0.180 ## 5 y_1 nu=4, W=(6, -0.6, -0.6, 10) 0.203 0.0299 -0.203 -0.0299 ## 6 y_2 nu=4, W=(6, -0.6, -0.6, 10) -0.0229 0.156 0.0229 -0.156 ## 7 y_1 nu=5, W=(6, -0.6, -0.6, 10) 0.182 0.0267 -0.182 -0.0267 ## 8 y_2 nu=5, W=(6, -0.6, -0.6, 10) -0.0204 0.139 0.0204 -0.139 ## 9 y_1 nu=6, W=(6, -0.6, -0.6, 10) 0.166 0.0244 -0.166 -0.0244 ## 10 y_2 nu=6, W=(6, -0.6, -0.6, 10) -0.0187 0.127 0.0187 -0.127 ## # … with 88 more rows
パラメータごとに2つの軸の始点と終点の8つの値を計算します。
パラメータsigma2_1_valsと8つの値に対応する列名の全ての組み合わせをexpand_grid()で作成します。これにより、パラメータごとに列名を複製できます。
eigen()で固有値と固有ベクトルをそれぞれ計算し、上手いことして軸の始点と終点を計算します(誰かもっと上手く処理してください…)。
求めた値をpivot_wider()で列名と対応付けて分割します。
パラメータごとにウィシャート分布の乱数(精度行列$\boldsymbol{\Lambda}_n$)を生成して、サンプルごとに距離を計算します。
# 楕円の数(サンプルサイズ)を指定 N <- 30 # パラメータごとに楕円のサンプルを計算 anime_sample_delta_df <- tidyr::expand_grid( nu = nu_vals, # パラメータ n = 1:N, # サンプル番号 x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータとサンプルごとに格子点を複製 dplyr::group_by(nu, n) |> # 距離の計算用にグループ化 dplyr::mutate( delta = mahalanobis( x = x_mat, center = 0, cov = rWishart(n = 1, df = nu, Sigma = w_dd)[, , 1], # 精度行列を生成 inverted = TRUE ), parameter = paste0("nu=", nu, ", W=(", paste0(w_dd, collapse = ", "), ")") |> factor(levels = paste0("nu=", nu_vals, ", W=(", paste0(w_dd, collapse = ", "), ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_sample_delta_df
## # A tibble: 14,700,000 × 6 ## nu n x_1 x_2 delta parameter ## <dbl> <int> <dbl> <dbl> <dbl> <fct> ## 1 2 1 -0.174 -0.135 0.189 nu=2, W=(6, -0.6, -0.6, 10) ## 2 2 1 -0.174 -0.132 0.188 nu=2, W=(6, -0.6, -0.6, 10) ## 3 2 1 -0.174 -0.129 0.188 nu=2, W=(6, -0.6, -0.6, 10) ## 4 2 1 -0.174 -0.126 0.187 nu=2, W=(6, -0.6, -0.6, 10) ## 5 2 1 -0.174 -0.124 0.186 nu=2, W=(6, -0.6, -0.6, 10) ## 6 2 1 -0.174 -0.121 0.186 nu=2, W=(6, -0.6, -0.6, 10) ## 7 2 1 -0.174 -0.118 0.185 nu=2, W=(6, -0.6, -0.6, 10) ## 8 2 1 -0.174 -0.116 0.185 nu=2, W=(6, -0.6, -0.6, 10) ## 9 2 1 -0.174 -0.113 0.184 nu=2, W=(6, -0.6, -0.6, 10) ## 10 2 1 -0.174 -0.110 0.184 nu=2, W=(6, -0.6, -0.6, 10) ## # … with 14,699,990 more rows
パラメータnu_vals・サンプル番号(1からNの整数)・確率変数x_1_vals, x_2_valsの要素の全ての組み合わせを作成します。これにより、パラメータとサンプルの組み合わせごとにx_matを複製します。
x_matごとにサンプルを生成してマハラノビス距離を計算します。
パラメータごとにウィシャート分布の乱数(精度行列$\boldsymbol{\Lambda}_n$)を生成して、サンプルごとに軸を計算します。
# 軸の数(サンプルサイズ)を指定 N <- 100 # パラメータごとに楕円の長軸のサンプルを計算 anime_sample_axis_df <- tidyr::expand_grid( nu = nu_vals, # パラメータ n = 1:N # サンプル番号 ) |> # パラメータごとに受け皿を複製 dplyr::group_by(nu, n) |> # 軸の計算用にグループ化 dplyr::mutate( eigen_lt = rWishart(n = 1, df = nu, Sigma = w_dd)[, , 1] |> # 精度行列を生成 solve() |> # 分散共分散行列に変換 eigen() |> # 固有値・固有ベクトルを計算 list(), # リストに格納 lambda_1 = eigen_lt[[1]][["values"]][1], # 固有値 u_11 = eigen_lt[[1]][["vectors"]][1, 1], # 固有ベクトルの成分 u_12 = eigen_lt[[1]][["vectors"]][2, 1], # 固有ベクトルの成分 xend = u_11 * sqrt(lambda_1), # 終点のx軸の値 yend = u_12 * sqrt(lambda_1), # 終点のy軸の値 parameter = paste0("nu=", nu, ", W=(", paste0(w_dd, collapse = ", "), ")") |> factor(levels = paste0("nu=", nu_vals, ", W=(", paste0(w_dd, collapse = ", "), ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_sample_axis_df
## # A tibble: 4,900 × 9 ## nu n eigen_lt lambda_1 u_11 u_12 xend yend parameter ## <dbl> <int> <list> <dbl> <dbl> <dbl> <dbl> <dbl> <fct> ## 1 2 1 <eigen> 0.479 -0.993 0.115 -0.687 0.0794 nu=2, W=(6, -0.6,… ## 2 2 2 <eigen> 0.336 -0.945 -0.326 -0.548 -0.189 nu=2, W=(6, -0.6,… ## 3 2 3 <eigen> 3.90 -0.151 0.989 -0.297 1.95 nu=2, W=(6, -0.6,… ## 4 2 4 <eigen> 0.149 -0.809 -0.588 -0.312 -0.227 nu=2, W=(6, -0.6,… ## 5 2 5 <eigen> 0.326 -0.860 -0.510 -0.491 -0.291 nu=2, W=(6, -0.6,… ## 6 2 6 <eigen> 0.0527 -0.786 0.618 -0.180 0.142 nu=2, W=(6, -0.6,… ## 7 2 7 <eigen> 6.43 0.661 0.751 1.68 1.90 nu=2, W=(6, -0.6,… ## 8 2 8 <eigen> 0.450 -0.567 0.824 -0.381 0.553 nu=2, W=(6, -0.6,… ## 9 2 9 <eigen> 4.06 -0.837 0.547 -1.69 1.10 nu=2, W=(6, -0.6,… ## 10 2 10 <eigen> 0.0929 -0.714 0.700 -0.218 0.213 nu=2, W=(6, -0.6,… ## # … with 4,890 more rows
パラメータnu_valsとサンプル番号(1からNの整数)の要素の全ての組み合わせを作成します。これにより、パラメータとごとにN個のサンプルを格納するための行を複製します。
パラメータとサンプル番号の組み合わせごとにサンプルを生成して、固有値と固有ベクトルを計算し、楕円の軸の先端の値を計算します。
パラメータごとに分散共分散行列の期待値$\mathbb{E}[\boldsymbol{\Sigma}]$を計算して、ラベルを作成します。
# パラメータごとに精度行列の期待値のラベルを作成 anime_label_df <- tibble::tibble( nu = nu_vals # パラメータ ) |> dplyr::group_by(nu) |> # 期待値の計算用にグループ化 dplyr::mutate( label = paste0("E[Lambda]=(", paste0(round(unique(nu) * w_dd, 2), collapse = ", "), ")"), # 精度行列ラベル parameter = paste0("nu=", nu, ", W=(", paste0(w_dd, collapse = ", "), ")") |> factor(levels = paste0("nu=", nu_vals, ", W=(", paste0(w_dd, collapse = ", "), ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_label_df
## # A tibble: 49 × 3 ## nu label parameter ## <dbl> <chr> <fct> ## 1 2 E[Lambda]=(12, -1.2, -1.2, 20) nu=2, W=(6, -0.6, -0.6, 10) ## 2 3 E[Lambda]=(18, -1.8, -1.8, 30) nu=3, W=(6, -0.6, -0.6, 10) ## 3 4 E[Lambda]=(24, -2.4, -2.4, 40) nu=4, W=(6, -0.6, -0.6, 10) ## 4 5 E[Lambda]=(30, -3, -3, 50) nu=5, W=(6, -0.6, -0.6, 10) ## 5 6 E[Lambda]=(36, -3.6, -3.6, 60) nu=6, W=(6, -0.6, -0.6, 10) ## 6 7 E[Lambda]=(42, -4.2, -4.2, 70) nu=7, W=(6, -0.6, -0.6, 10) ## 7 8 E[Lambda]=(48, -4.8, -4.8, 80) nu=8, W=(6, -0.6, -0.6, 10) ## 8 9 E[Lambda]=(54, -5.4, -5.4, 90) nu=9, W=(6, -0.6, -0.6, 10) ## 9 10 E[Lambda]=(60, -6, -6, 100) nu=10, W=(6, -0.6, -0.6, 10) ## 10 11 E[Lambda]=(66, -6.6, -6.6, 110) nu=11, W=(6, -0.6, -0.6, 10) ## # … with 39 more rows
パラメータごとにラベル用の文字列を作成します。
等高線図のアニメーション(gif画像)を作成します。
# 等高線を引く距離を指定 delta <- 1 # マハラノビス距離(楕円)のアニメーションを作図 anime_delta_graph <- ggplot() + geom_contour(data = anime_E_delta_df, mapping = aes(x = x_1, y = x_2, z = delta), breaks = delta, color ="red", size = 1, linetype = "dashed") + # 期待値による分布 geom_contour(data = anime_sample_delta_df, mapping = aes(x = x_1, y = x_2, z = delta, color = factor(n)), breaks = delta, alpha = 0.5, show.legend = FALSE) + # サンプルによる分布 geom_label(data = anime_label_df, mapping = aes(x = min(x_1_vals), y = max(x_2_vals), label = label), hjust = 0, vjust = 0, alpha = 0.5) + # 分散共分散行列の期待値ラベル gganimate::transition_manual(parameter) + # フレーム coord_fixed(ratio = 1, xlim = c(min(x_1_vals), max(x_1_vals)), ylim = c(min(x_2_vals), max(x_2_vals))) + # アスペクト比 labs(title = "Mahalanobis Distance", subtitle = "{current_frame}", x = expression(x[1]), y = expression(x[2])) # gif画像を作成 gganimate::animate(anime_delta_graph, nframes = frame_num, fps = 10, width = 800, height = 600)
transition_manual()にフレームの順序を表す列を指定します。この例では、因子型のラベルのレベルの順に描画されます。
animate()のフレーム数の引数nframesにパラメータ数、フレームレートの引数fpsに1秒当たりのフレーム数を指定します。fps引数の値が大きいほどフレームが早く切り替わります。ただし、値が大きいと意図通りに動作しません。
同様に、マハラノビス距離(楕円)の軸のアニメーションを作成します。
# 楕円の軸のアニメーションを作図 anime_axis_graph <- ggplot() + geom_contour_filled(data = anime_E_delta_df, mapping = aes(x = x_1, y = x_2, z = delta, fill = ..level..), alpha = 0.8) + # 期待値による分布 geom_contour(data = anime_E_delta_df, mapping = aes(x = x_1, y = x_2, z = delta), breaks = 1, color = "red", size = 1, linetype = "dotted") + # 期待値による分布の断面 geom_segment(data = anime_E_axis_df, mapping = aes(x = xstart, y = ystart, xend = xend, yend = yend), color = "red", size = 1, linetype = "dashed", arrow = arrow(length = unit(10, "pt"))) + # 期待値による断面の軸 geom_segment(data = anime_sample_axis_df, mapping = aes(x = 0, y = 0, xend = xend, yend = yend), color = "orange", alpha = 0.5, size = 1, arrow = arrow(length = unit(5, "pt"))) + # サンプルによる分布の長軸 geom_label(data = anime_label_df, mapping = aes(x = min(x_1_vals), y = max(x_2_vals), label = label), hjust = 0, vjust = 0, alpha = 0.5) + # 分散共分散行列の期待値ラベル gganimate::transition_manual(parameter) + # フレーム coord_fixed(ratio = 1, xlim = c(min(x_1_vals), max(x_1_vals)), ylim = c(min(x_2_vals), max(x_2_vals))) + # アスペクト比 labs(title ="Mahalanobis Distance", subtitle = "{current_frame}", fill = "distance", x = expression(x[1]), y = expression(x[2])) # gif画像を作成 gganimate::animate(anime_axis_graph, nframes = frame_num, fps = 10, width = 800, height = 600)

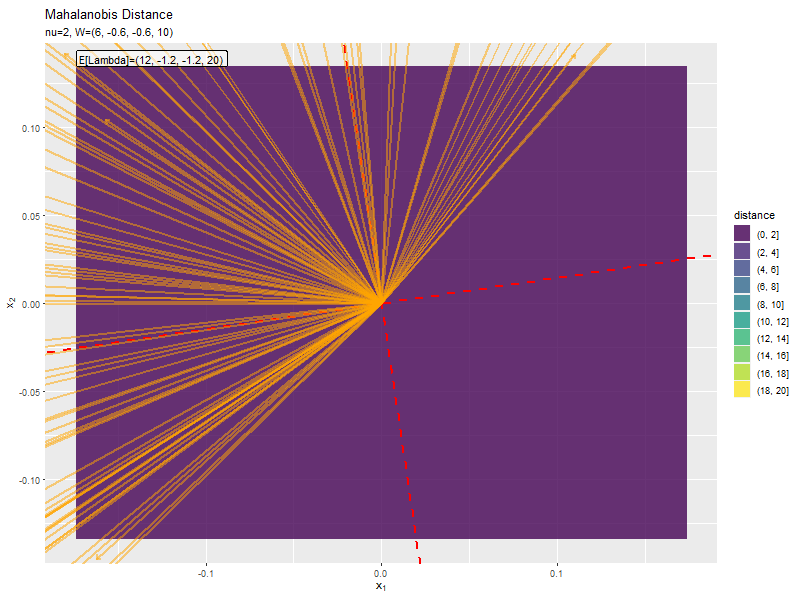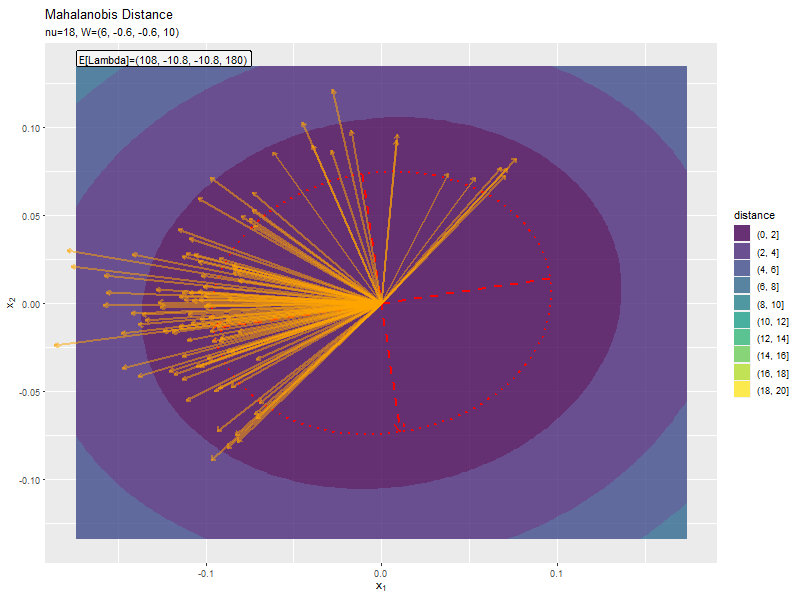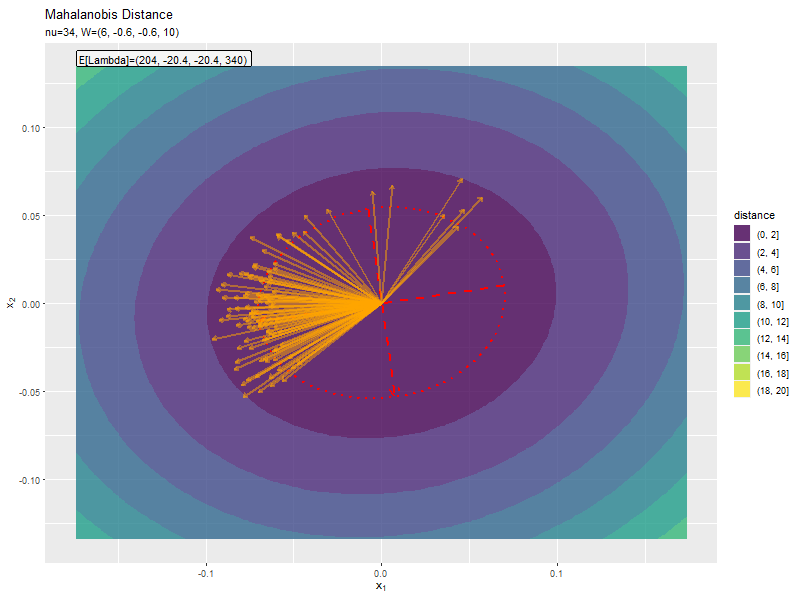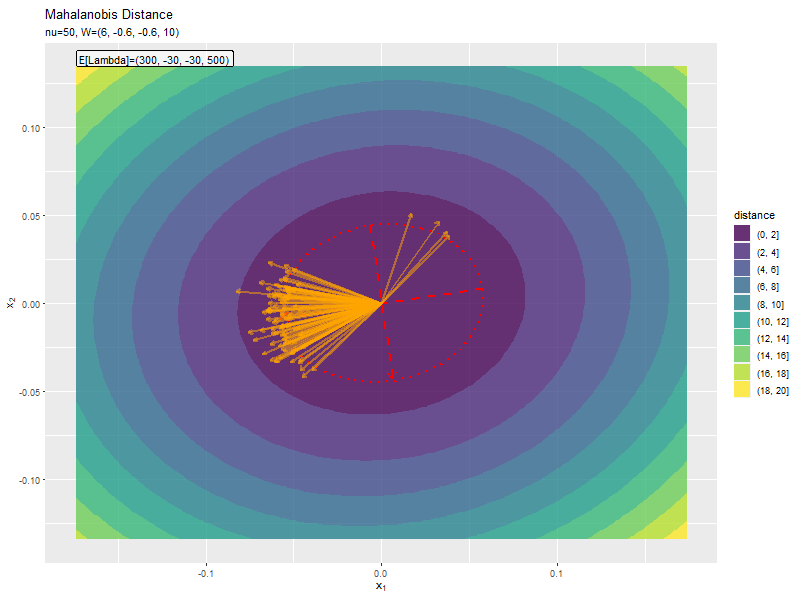
$\nu$が大きくなるほど、サンプルによる楕円と軸が期待値による楕円と軸に近付いています(なぜ?)。
スケール行列(1,1成分)の影響
続いて、$\mathbf{W}$の$1,1$成分$w_{1,1}$の値を変化させ、$\nu, w_{1,2}, w_{2,2}$を固定します。
・作図コード(クリックで展開)
# 次元数を指定 D <- 2 # 自由度を指定 nu <- D + 18 # 逆スケール行列を指定 w_11_vals <- seq(from = 1, to = 10, by = 0.1) |> round(digits = 2) w_12 <- 0.6 w_22 <- 5 # フレーム数を設定 frame_num <- length(w_11_vals) frame_num
## [1] 91
値の間隔が一定になるように$w_{1,1}$の値をw_11_valsとして作成します。また、$w_{1,2} = w_{2,1}$をw_12、$w_{2,2}$の値をw_22として値を指定します。
設定したパラメータに応じて、変数の値$\mathbf{x}$を作成します。
# 作図用の共分散行列を作成 E_sigma_dd <- solve(nu * matrix(c(min(w_11_vals), w_12, w_12, w_22), nrow = D, ncol = D)) # xの値を作成 x_1_vals <- seq( from = - sqrt(E_sigma_dd[1, 1]) * 1.5, to = sqrt(E_sigma_dd[1, 1]) * 1.5, length.out = 100 ) x_2_vals <- seq( from = - sqrt(E_sigma_dd[2, 2]) * 3, to = sqrt(E_sigma_dd[2, 2]) * 3, length.out = 100 ) # xの点を作成 x_mat <- tidyr::expand_grid( x_1 = x_1_vals, x_2 = x_2_vals ) |> # 格子点を作成 as.matrix() # マトリクスに変換 head(x_mat)
## x_1 x_2 ## [1,] -0.3481788 -0.3114205 ## [2,] -0.3481788 -0.3051292 ## [3,] -0.3481788 -0.2988379 ## [4,] -0.3481788 -0.2925466 ## [5,] -0.3481788 -0.2862553 ## [6,] -0.3481788 -0.2799639
パラメータごとに期待値による距離を計算します。
# パラメータごとに共分散行列の期待値によるマハラノビス距離(楕円)を計算 anime_E_delta_df <- tidyr::expand_grid( w_11 = w_11_vals, # パラメータ x_1 = x_1_vals, x_2 = x_2_vals ) |> # サンプルごとに格子点を複製 dplyr::group_by(w_11) |> # 距離の計算用にグループ化 dplyr::mutate( delta = mahalanobis( x = x_mat, center = 0, cov = nu * matrix(c(unique(w_11), w_12, w_12, w_22), nrow = D, ncol = D), # 精度行列の期待値を指定 inverted = TRUE ), # 確率密度 parameter = paste0("nu=", nu, ", W=(", unique(w_11), ", ", w_12, ", ", w_12, ", ", w_22, ")") |> factor(levels = paste0("nu=", nu, ", W=(", w_11_vals, ", ", w_12, ", ", w_12, ", ", w_22, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_E_delta_df
## # A tibble: 910,000 × 5 ## w_11 x_1 x_2 delta parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 1 -0.348 -0.311 14.7 nu=20, W=(1, 0.6, 0.6, 5) ## 2 1 -0.348 -0.305 14.3 nu=20, W=(1, 0.6, 0.6, 5) ## 3 1 -0.348 -0.299 13.9 nu=20, W=(1, 0.6, 0.6, 5) ## 4 1 -0.348 -0.293 13.4 nu=20, W=(1, 0.6, 0.6, 5) ## 5 1 -0.348 -0.286 13.0 nu=20, W=(1, 0.6, 0.6, 5) ## 6 1 -0.348 -0.280 12.6 nu=20, W=(1, 0.6, 0.6, 5) ## 7 1 -0.348 -0.274 12.2 nu=20, W=(1, 0.6, 0.6, 5) ## 8 1 -0.348 -0.267 11.8 nu=20, W=(1, 0.6, 0.6, 5) ## 9 1 -0.348 -0.261 11.4 nu=20, W=(1, 0.6, 0.6, 5) ## 10 1 -0.348 -0.255 11.0 nu=20, W=(1, 0.6, 0.6, 5) ## # … with 909,990 more rows
「自由度の影響」のnu, nu_valsとw_11, w_11_valsを置き換えるように処理します。
パラメータごとに期待値による軸を計算します。
# パラメータごとに共分散行列の期待値による楕円の軸を計算 anime_E_axis_df <- tidyr::expand_grid( w_11 = w_11_vals, # パラメータごとに name = paste0(rep(c("x", "y"), each = 2, times = 2), rep(c("start", "end"), each = 4)) # 列名 ) |> # パラメータごとに受け皿を複製 dplyr::group_by(w_11) |> # 軸の計算用にグループ化 dplyr::mutate( axis = rep(c("y_1", "y_2"), times = 4), # pivot_wider用の列 sign = rep(c(-1, 1), each = 4), # 始点・終点の計算用の符号 lambda = solve(nu * matrix(c(unique(w_11), w_12, w_12, w_22), nrow = D, ncol = D)) |> # 共分散行列の期待値を計算 (\(.){eigen(.)[["values"]]})() |> (\(.){rep(sqrt(.), times = 4)})(), # 固有値 u = solve(nu * matrix(c(unique(w_11), w_12, w_12, w_22), nrow = D, ncol = D)) |> # 共分散行列の期待値を計算 (\(.){t(eigen(.)[["vectors"]])})() |> (\(.){rep(as.vector(.), times = 2)})(), # 固有ベクトル value = sign * u * lambda, # 軸の始点・終点を計算 parameter = paste0("nu=", nu, ", W=(", unique(w_11), ", ", w_12, ", ", w_12, ", ", w_22, ")") |> factor(levels = paste0("nu=", nu, ", W=(", w_11_vals, ", ", w_12, ", ", w_12, ", ", w_22, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() |> # グループ化を解除 dplyr::select(axis, name, value, parameter) |> # 利用する列を選択 tidyr::pivot_wider( id_cols = c(axis, parameter), names_from = name, values_from = value ) # 軸の視点・終点の列を分割 anime_E_axis_df
## # A tibble: 182 × 6 ## axis parameter xstart ystart xend yend ## <chr> <fct> <dbl> <dbl> <dbl> <dbl> ## 1 y_1 nu=20, W=(1, 0.6, 0.6, 5) 0.232 -0.0340 -0.232 0.0340 ## 2 y_2 nu=20, W=(1, 0.6, 0.6, 5) 0.0144 0.0981 -0.0144 -0.0981 ## 3 y_1 nu=20, W=(1.1, 0.6, 0.6, 5) 0.220 -0.0331 -0.220 0.0331 ## 4 y_2 nu=20, W=(1.1, 0.6, 0.6, 5) 0.0147 0.0980 -0.0147 -0.0980 ## 5 y_1 nu=20, W=(1.2, 0.6, 0.6, 5) 0.210 -0.0324 -0.210 0.0324 ## 6 y_2 nu=20, W=(1.2, 0.6, 0.6, 5) 0.0151 0.0979 -0.0151 -0.0979 ## 7 y_1 nu=20, W=(1.3, 0.6, 0.6, 5) 0.201 -0.0318 -0.201 0.0318 ## 8 y_2 nu=20, W=(1.3, 0.6, 0.6, 5) 0.0155 0.0978 -0.0155 -0.0978 ## 9 y_1 nu=20, W=(1.4, 0.6, 0.6, 5) 0.193 -0.0314 -0.193 0.0314 ## 10 y_2 nu=20, W=(1.4, 0.6, 0.6, 5) 0.0159 0.0978 -0.0159 -0.0978 ## # … with 172 more rows
パラメータごとにサンプリングして距離を計算します。
# 楕円の数(サンプルサイズ)を指定 N <- 30 # パラメータごとに楕円のサンプルを計算 anime_sample_delta_df <- tidyr::expand_grid( w_11 = w_11_vals, # パラメータ n = 1:N, # サンプル番号 x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータとサンプルごとに格子点を複製 dplyr::group_by(w_11, n) |> # 距離の計算用にグループ化 dplyr::mutate( delta = mahalanobis( x = x_mat, center = 0, cov = rWishart( n = 1, df = nu, Sigma = matrix(c(unique(w_11), w_12, w_12, w_22), nrow = D, ncol = D) )[, , 1], # 精度行列を生成 inverted = TRUE ), parameter = paste0("nu=", nu, ", W=(", unique(w_11), ", ", w_12, ", ", w_12, ", ", w_22, ")") |> factor(levels = paste0("nu=", nu, ", W=(", w_11_vals, ", ", w_12, ", ", w_12, ", ", w_22, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_sample_delta_df
## # A tibble: 27,300,000 × 6 ## w_11 n x_1 x_2 delta parameter ## <dbl> <int> <dbl> <dbl> <dbl> <fct> ## 1 1 1 -0.348 -0.311 24.3 nu=20, W=(1, 0.6, 0.6, 5) ## 2 1 1 -0.348 -0.305 23.6 nu=20, W=(1, 0.6, 0.6, 5) ## 3 1 1 -0.348 -0.299 22.8 nu=20, W=(1, 0.6, 0.6, 5) ## 4 1 1 -0.348 -0.293 22.1 nu=20, W=(1, 0.6, 0.6, 5) ## 5 1 1 -0.348 -0.286 21.4 nu=20, W=(1, 0.6, 0.6, 5) ## 6 1 1 -0.348 -0.280 20.7 nu=20, W=(1, 0.6, 0.6, 5) ## 7 1 1 -0.348 -0.274 20.1 nu=20, W=(1, 0.6, 0.6, 5) ## 8 1 1 -0.348 -0.267 19.4 nu=20, W=(1, 0.6, 0.6, 5) ## 9 1 1 -0.348 -0.261 18.7 nu=20, W=(1, 0.6, 0.6, 5) ## 10 1 1 -0.348 -0.255 18.1 nu=20, W=(1, 0.6, 0.6, 5) ## # … with 27,299,990 more rows
パラメータごとにサンプリングして軸を計算します。
# 軸の数(サンプルサイズ)を指定 N <- 100 # パラメータごとに楕円の長軸のサンプルを計算 anime_sample_axis_df <- tidyr::expand_grid( w_11 = w_11_vals, # パラメータ n = 1:N # サンプル番号 ) |> # パラメータごとに受け皿を複製 dplyr::group_by(w_11, n) |> # 軸の計算用にグループ化 dplyr::mutate( eigen_lt = rWishart( n = 1, df = nu, Sigma = matrix(c(unique(w_11), w_12, w_12, w_22), nrow = D, ncol = D) )[, , 1] |> # 精度行列を生成 solve() |> # 分散共分散行列に変換 eigen() |> # 固有値・固有ベクトルを計算 list(), # リストに格納 lambda_1 = eigen_lt[[1]][["values"]][1], # 固有値 u_11 = eigen_lt[[1]][["vectors"]][1, 1], # 固有ベクトルの成分 u_12 = eigen_lt[[1]][["vectors"]][2, 1], # 固有ベクトルの成分 xend = u_11 * sqrt(lambda_1), # 終点のx軸の値 yend = u_12 * sqrt(lambda_1), # 終点のy軸の値 parameter = paste0("nu=", nu, ", W=(", unique(w_11), ", ", w_12, ", ", w_12, ", ", w_22, ")") |> factor(levels = paste0("nu=", nu, ", W=(", w_11_vals, ", ", w_12, ", ", w_12, ", ", w_22, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_sample_axis_df
## # A tibble: 9,100 × 9 ## w_11 n eigen_lt lambda_1 u_11 u_12 xend yend parameter ## <dbl> <int> <list> <dbl> <dbl> <dbl> <dbl> <dbl> <fct> ## 1 1 1 <eigen> 0.0470 -0.994 0.112 -0.215 0.0242 nu=20, W=(1, 0.6,… ## 2 1 2 <eigen> 0.0556 -0.977 0.213 -0.230 0.0502 nu=20, W=(1, 0.6,… ## 3 1 3 <eigen> 0.0510 -0.984 0.178 -0.222 0.0402 nu=20, W=(1, 0.6,… ## 4 1 4 <eigen> 0.0839 -0.991 0.136 -0.287 0.0394 nu=20, W=(1, 0.6,… ## 5 1 5 <eigen> 0.0460 -0.999 0.0435 -0.214 0.00933 nu=20, W=(1, 0.6,… ## 6 1 6 <eigen> 0.0835 -0.972 0.235 -0.281 0.0678 nu=20, W=(1, 0.6,… ## 7 1 7 <eigen> 0.124 -0.992 0.129 -0.350 0.0455 nu=20, W=(1, 0.6,… ## 8 1 8 <eigen> 0.0525 -0.997 0.0759 -0.228 0.0174 nu=20, W=(1, 0.6,… ## 9 1 9 <eigen> 0.0658 -0.974 0.227 -0.250 0.0582 nu=20, W=(1, 0.6,… ## 10 1 10 <eigen> 0.0492 -0.997 0.0827 -0.221 0.0183 nu=20, W=(1, 0.6,… ## # … with 9,090 more rows
パラメータごとに期待値のラベルを作成します。
# パラメータごとに共分散行列の期待値のラベルを作成 anime_label_df <- tibble::tibble( w_11 = w_11_vals # パラメータ ) |> dplyr::group_by(w_11) |> # 期待値の計算用にグループ化 dplyr::mutate( label = paste0("E[Lambda]=(", paste0(round(unique(nu) * matrix(c(unique(w_11), w_12, w_12, w_22), nrow = D, ncol = D), 2), collapse = ", "), ")"), # 分散共分散行列ラベル parameter = paste0("nu=", nu, ", W=(", unique(w_11), ", ", w_12, ", ", w_12, ", ", w_22, ")") |> factor(levels = paste0("nu=", nu, ", W=(", w_11_vals, ", ", w_12, ", ", w_12, ", ", w_22, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_label_df
## # A tibble: 91 × 3 ## w_11 label parameter ## <dbl> <chr> <fct> ## 1 1 E[Lambda]=(20, 12, 12, 100) nu=20, W=(1, 0.6, 0.6, 5) ## 2 1.1 E[Lambda]=(22, 12, 12, 100) nu=20, W=(1.1, 0.6, 0.6, 5) ## 3 1.2 E[Lambda]=(24, 12, 12, 100) nu=20, W=(1.2, 0.6, 0.6, 5) ## 4 1.3 E[Lambda]=(26, 12, 12, 100) nu=20, W=(1.3, 0.6, 0.6, 5) ## 5 1.4 E[Lambda]=(28, 12, 12, 100) nu=20, W=(1.4, 0.6, 0.6, 5) ## 6 1.5 E[Lambda]=(30, 12, 12, 100) nu=20, W=(1.5, 0.6, 0.6, 5) ## 7 1.6 E[Lambda]=(32, 12, 12, 100) nu=20, W=(1.6, 0.6, 0.6, 5) ## 8 1.7 E[Lambda]=(34, 12, 12, 100) nu=20, W=(1.7, 0.6, 0.6, 5) ## 9 1.8 E[Lambda]=(36, 12, 12, 100) nu=20, W=(1.8, 0.6, 0.6, 5) ## 10 1.9 E[Lambda]=(38, 12, 12, 100) nu=20, W=(1.9, 0.6, 0.6, 5) ## # … with 81 more rows
「自由度の影響」のコードで作図できます。
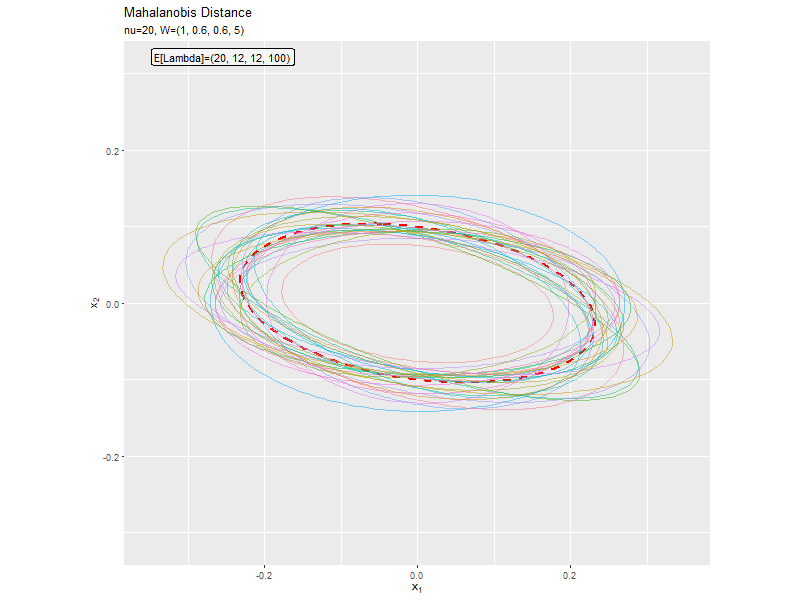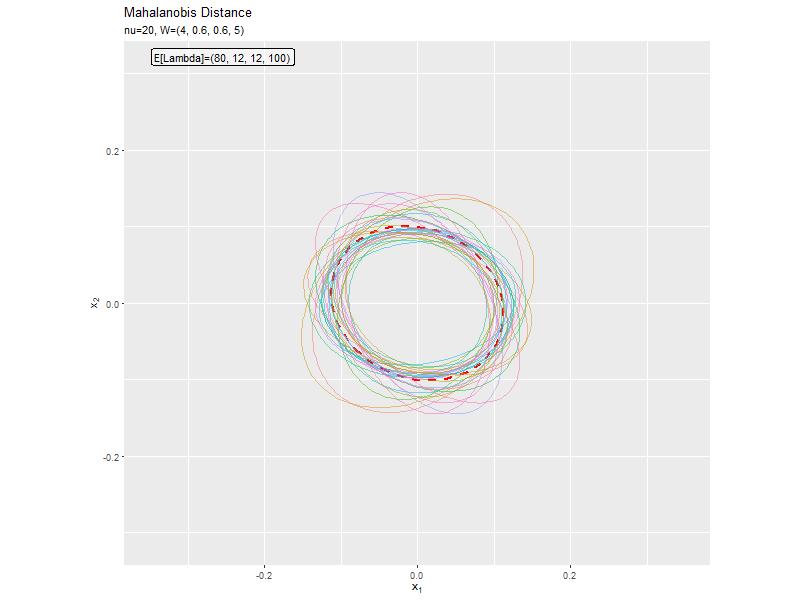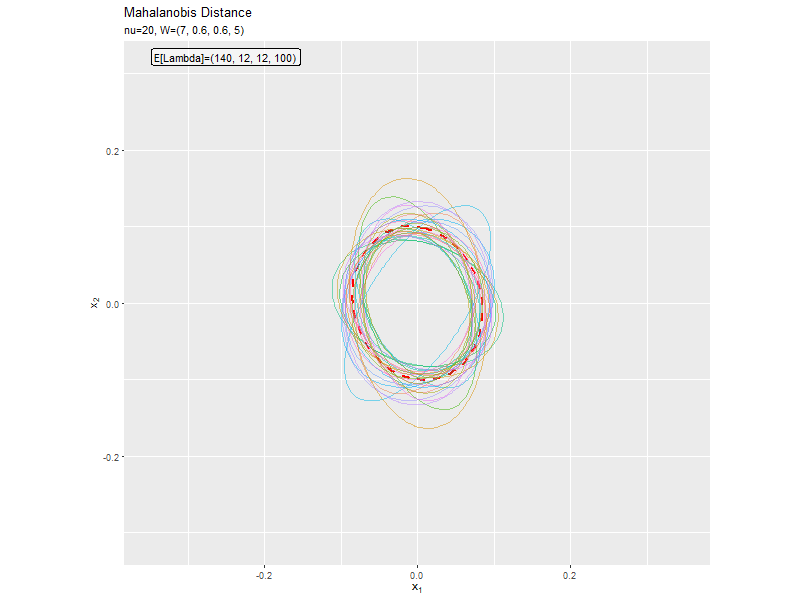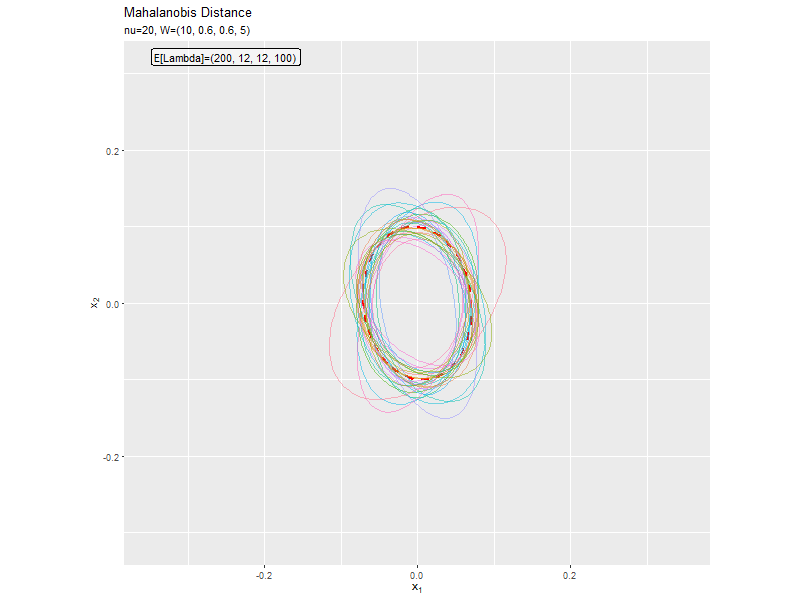
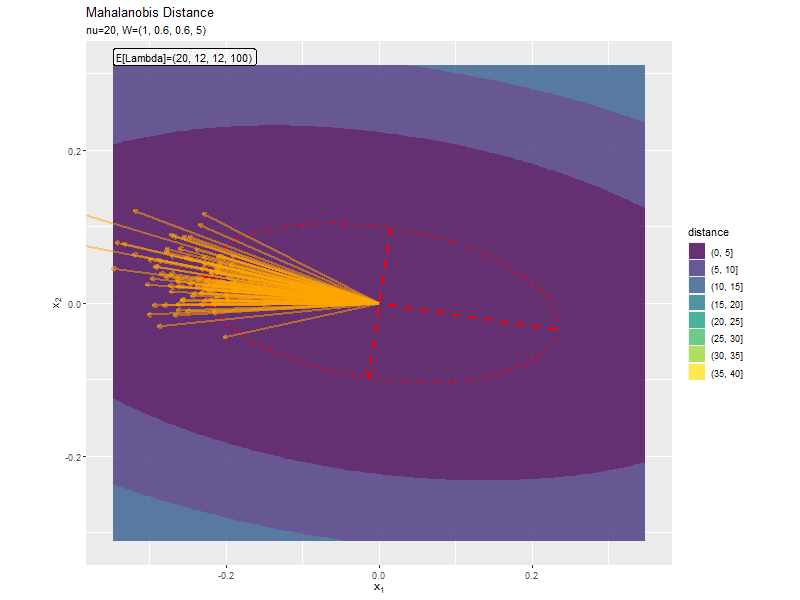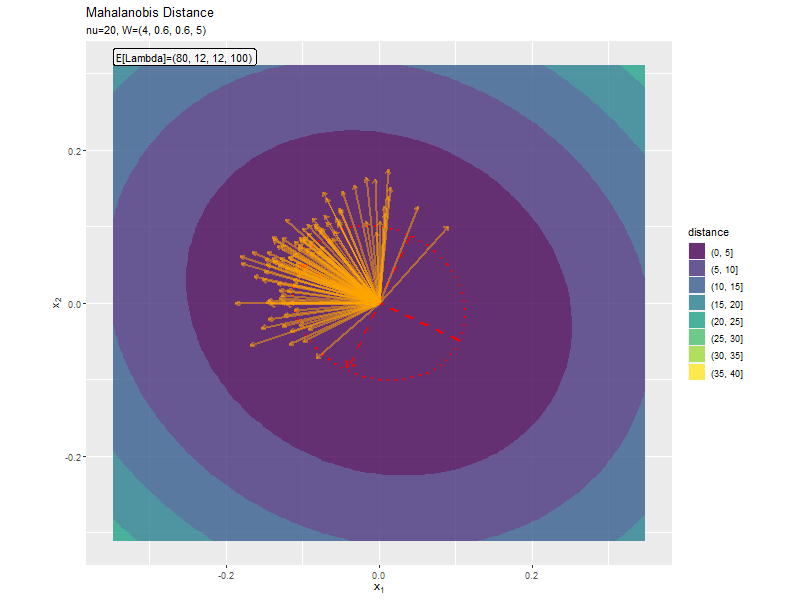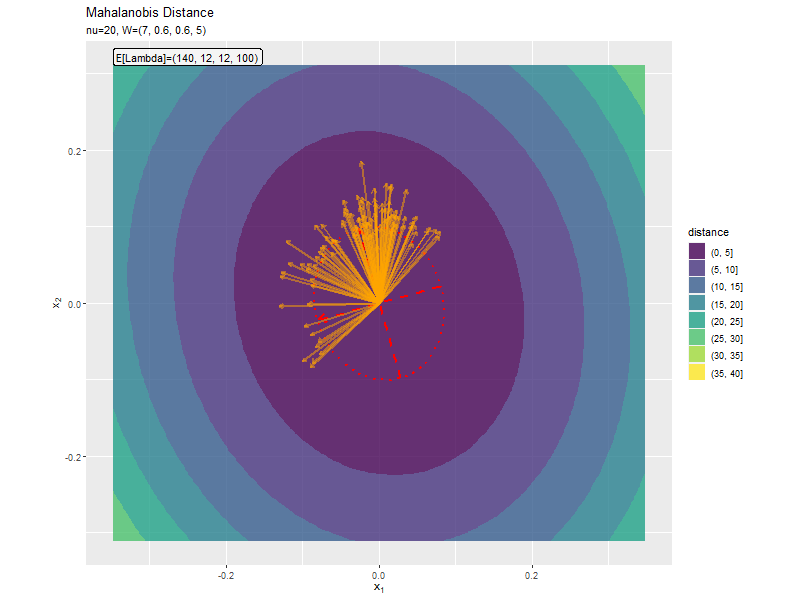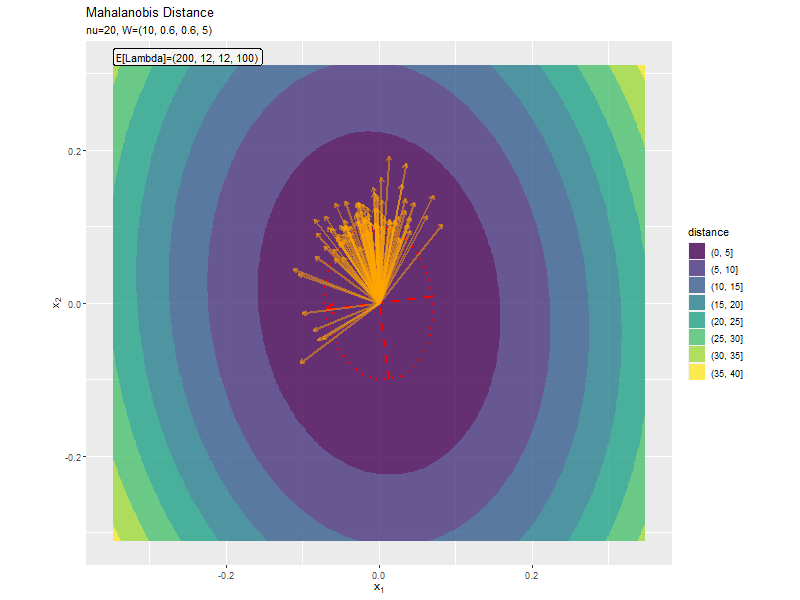
$w_{1,1} < w_{2,2}$なほど楕円の軸の傾きが小さく、$w_{1,1} < w_{2,2}$なほど楕円の軸の傾きが大きくなっています。また、$w_{1,1}, w_{2,2}$の差が小さいと、サンプルによる楕円・軸と期待値による楕円・軸のばらつきが大きくなっています。
スケール行列(1,2成分)の影響
$w_{1,2} = w_{2,1}$の値を変化させ、$\nu, w_{1,1}, w_{2,2}$を固定します。
・作図コード(クリックで展開)
# 次元数を指定 D <- 2 # 自由度を指定 nu <- D + 18 # 逆スケール行列を指定 w_11 <- 6 w_12_vals <- seq(from = -4, to = 4, by = 0.1) |> round(digits = 2) w_22 <- 5 # フレーム数を設定 frame_num <- length(w_12_vals) frame_num
## [1] 81
値の間隔が一定になるように$w_{1,2} = w_{2,1}$の値をw_12_valsとして作成します。また、$w_{1,1}$をw_11、$w_{2,2}$の値をw_22として値を指定します。
設定したパラメータに応じて、変数の値$\mathbf{x}$を作成します。
# 作図用の共分散行列を作成 E_sigma_dd <- solve(nu * matrix(c(w_11, median(w_12_vals), median(w_12_vals), w_22), nrow = D, ncol = D)) # xの値を作成 x_1_vals <- seq( from = - sqrt(E_sigma_dd[1, 1]) * 3, to = sqrt(E_sigma_dd[1, 1]) * 3, length.out = 100 ) x_2_vals <- seq( from = - sqrt(E_sigma_dd[2, 2]) * 3, to = sqrt(E_sigma_dd[2, 2]) * 3, length.out = 100 ) # xの点を作成 x_mat <- tidyr::expand_grid( x_1 = x_1_vals, x_2 = x_2_vals ) |> # 格子点を作成 as.matrix() # マトリクスに変換 head(x_mat)
## x_1 x_2 ## [1,] -0.2738613 -0.3000000 ## [2,] -0.2738613 -0.2939394 ## [3,] -0.2738613 -0.2878788 ## [4,] -0.2738613 -0.2818182 ## [5,] -0.2738613 -0.2757576 ## [6,] -0.2738613 -0.2696970
パラメータごとに期待値による距離を計算します。
# パラメータごとに共分散行列の期待値によるマハラノビス距離(楕円)を計算 anime_E_delta_df <- tidyr::expand_grid( w_12 = w_12_vals, # パラメータ x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(w_12) |> # 距離の計算用にグループ化 dplyr::mutate( delta = mahalanobis( x = x_mat, center = 0, cov = nu * matrix(c(w_11, unique(w_12), unique(w_12), w_22), nrow = D, ncol = D), # 精度行列の期待値を計算 inverted = TRUE ), # 確率密度 parameter = paste0("nu=", nu, ", W=(", w_11, ", ", unique(w_12), ", ", unique(w_12), ", ", w_22, ")") |> factor(levels = paste0("nu=", nu, ", W=(", w_11, ", ", w_12_vals, ", ", w_12_vals, ", ", w_22, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_E_delta_df
## # A tibble: 810,000 × 5 ## w_12 x_1 x_2 delta parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 -4 -0.274 -0.3 4.85 nu=20, W=(6, -4, -4, 5) ## 2 -4 -0.274 -0.294 4.76 nu=20, W=(6, -4, -4, 5) ## 3 -4 -0.274 -0.288 4.67 nu=20, W=(6, -4, -4, 5) ## 4 -4 -0.274 -0.282 4.59 nu=20, W=(6, -4, -4, 5) ## 5 -4 -0.274 -0.276 4.52 nu=20, W=(6, -4, -4, 5) ## 6 -4 -0.274 -0.270 4.46 nu=20, W=(6, -4, -4, 5) ## 7 -4 -0.274 -0.264 4.40 nu=20, W=(6, -4, -4, 5) ## 8 -4 -0.274 -0.258 4.35 nu=20, W=(6, -4, -4, 5) ## 9 -4 -0.274 -0.252 4.31 nu=20, W=(6, -4, -4, 5) ## 10 -4 -0.274 -0.245 4.27 nu=20, W=(6, -4, -4, 5) ## # … with 809,990 more rows
「自由度の影響」のnu, nu_valsとw_12, w_12_valsを置き換えるように処理します。
パラメータごとに期待値による軸を計算します。
# パラメータごとに共分散行列の期待値による楕円の軸を計算 anime_E_axis_df <- tidyr::expand_grid( w_12 = w_12_vals, # パラメータ name = paste0(rep(c("x", "y"), each = 2, times = 2), rep(c("start", "end"), each = 4)) # 列名 ) |> # パラメータごとに受け皿を複製 dplyr::group_by(w_12) |> # 軸の計算用にグループ化 dplyr::mutate( axis = rep(c("y_1", "y_2"), times = 4), # pivot_wider用の列 sign = rep(c(-1, 1), each = 4), # 始点・終点の計算用の符号 lambda = solve(nu * matrix(c(w_11, unique(w_12), unique(w_12), w_22), nrow = D, ncol = D)) |> # 共分散行列の期待値を計算 (\(.){eigen(.)[["values"]]})() |> (\(.){rep(sqrt(.), times = 4)})(), # 固有値 u = solve(nu * matrix(c(w_11, unique(w_12), unique(w_12), w_22), nrow = D, ncol = D)) |> # 共分散行列の期待値を計算 (\(.){t(eigen(.)[["vectors"]])})() |> (\(.){rep(as.vector(.), times = 2)})(), # 固有ベクトル value = sign * u * lambda, # 軸の始点・終点を計算 parameter = paste0("nu=", nu, ", W=(", w_11, ", ", unique(w_12), ", ", unique(w_12), ", ", w_22, ")") |> factor(levels = paste0("nu=", nu, ", W=(", w_11, ", ", w_12_vals, ", ", w_12_vals, ", ", w_22, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() |> # グループ化を解除 dplyr::select(axis, name, value, parameter) |> # 利用する列を選択 tidyr::pivot_wider( id_cols = c(axis, parameter), names_from = name, values_from = value ) # 軸の視点・終点の列を分割 anime_E_axis_df
## # A tibble: 162 × 6 ## axis parameter xstart ystart xend yend ## <chr> <fct> <dbl> <dbl> <dbl> <dbl> ## 1 y_1 nu=20, W=(6, -4, -4, 5) -0.122 -0.138 0.122 0.138 ## 2 y_2 nu=20, W=(6, -4, -4, 5) 0.0543 -0.0479 -0.0543 0.0479 ## 3 y_1 nu=20, W=(6, -3.9, -3.9, 5) -0.118 -0.134 0.118 0.134 ## 4 y_2 nu=20, W=(6, -3.9, -3.9, 5) 0.0547 -0.0481 -0.0547 0.0481 ## 5 y_1 nu=20, W=(6, -3.8, -3.8, 5) -0.114 -0.130 0.114 0.130 ## 6 y_2 nu=20, W=(6, -3.8, -3.8, 5) 0.0550 -0.0483 -0.0550 0.0483 ## 7 y_1 nu=20, W=(6, -3.7, -3.7, 5) -0.111 -0.127 0.111 0.127 ## 8 y_2 nu=20, W=(6, -3.7, -3.7, 5) 0.0554 -0.0484 -0.0554 0.0484 ## 9 y_1 nu=20, W=(6, -3.6, -3.6, 5) -0.108 -0.123 0.108 0.123 ## 10 y_2 nu=20, W=(6, -3.6, -3.6, 5) 0.0558 -0.0486 -0.0558 0.0486 ## # … with 152 more rows
パラメータごとにサンプリングして距離を計算します。
# 楕円の数(サンプルサイズ)を指定 N <- 30 # パラメータごとに楕円のサンプルを計算 anime_sample_delta_df <- tidyr::expand_grid( w_12 = w_12_vals, # パラメータ n = 1:N, # サンプル番号 x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータとサンプルごとに格子点を複製 dplyr::group_by(w_12, n) |> # 距離の計算用にグループ化 dplyr::mutate( delta = mahalanobis( x = x_mat, center = 0, cov = rWishart( n = 1, df = nu, Sigma = matrix(c(w_11, unique(w_12), unique(w_12), w_22), nrow = D, ncol = D) )[, , 1], # 精度行列を生成 inverted = TRUE ), parameter = paste0("nu=", nu, ", W=(", w_11, ", ", unique(w_12), ", ", unique(w_12), ", ", w_22, ")") |> factor(levels = paste0("nu=", nu, ", W=(", w_11, ", ", w_12_vals, ", ", w_12_vals, ", ", w_22, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_sample_delta_df
## # A tibble: 24,300,000 × 6 ## w_12 n x_1 x_2 delta parameter ## <dbl> <int> <dbl> <dbl> <dbl> <fct> ## 1 -4 1 -0.274 -0.3 1.88 nu=20, W=(6, -4, -4, 5) ## 2 -4 1 -0.274 -0.294 1.84 nu=20, W=(6, -4, -4, 5) ## 3 -4 1 -0.274 -0.288 1.80 nu=20, W=(6, -4, -4, 5) ## 4 -4 1 -0.274 -0.282 1.77 nu=20, W=(6, -4, -4, 5) ## 5 -4 1 -0.274 -0.276 1.75 nu=20, W=(6, -4, -4, 5) ## 6 -4 1 -0.274 -0.270 1.73 nu=20, W=(6, -4, -4, 5) ## 7 -4 1 -0.274 -0.264 1.71 nu=20, W=(6, -4, -4, 5) ## 8 -4 1 -0.274 -0.258 1.70 nu=20, W=(6, -4, -4, 5) ## 9 -4 1 -0.274 -0.252 1.69 nu=20, W=(6, -4, -4, 5) ## 10 -4 1 -0.274 -0.245 1.69 nu=20, W=(6, -4, -4, 5) ## # … with 24,299,990 more rows
パラメータごとにサンプリングして軸を計算します。
# 軸の数(サンプルサイズ)を指定 N <- 100 # パラメータごとに楕円の長軸のサンプルを計算 anime_sample_axis_df <- tidyr::expand_grid( w_12 = w_12_vals, # パラメータ n = 1:N # サンプル番号 ) |> dplyr::group_by(w_12, n) |> # 軸の計算用にグループ化 dplyr::mutate( eigen_lt = rWishart( n = 1, df = nu, Sigma = matrix(c(w_11, unique(w_12), unique(w_12), w_22), nrow = D, ncol = D) )[, , 1] |> # 精度行列を生成 solve() |> # 分散共分散行列に変換 eigen() |> # 固有値・固有ベクトルを計算 list(), # リストに格納 lambda_1 = eigen_lt[[1]][["values"]][1], # 固有値 u_11 = eigen_lt[[1]][["vectors"]][1, 1], # 固有ベクトルの成分 u_12 = eigen_lt[[1]][["vectors"]][2, 1], # 固有ベクトルの成分 xend = u_11 * sqrt(lambda_1), # 終点のx軸の値 yend = u_12 * sqrt(lambda_1), # 終点のy軸の値 parameter = paste0("nu=", nu, ", W=(", w_11, ", ", unique(w_12), ", ", unique(w_12), ", ", w_22, ")") |> factor(levels = paste0("nu=", nu, ", W=(", w_11, ", ", w_12_vals, ", ", w_12_vals, ", ", w_22, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_sample_axis_df
## # A tibble: 8,100 × 9 ## w_12 n eigen_lt lambda_1 u_11 u_12 xend yend parameter ## <dbl> <int> <list> <dbl> <dbl> <dbl> <dbl> <dbl> <fct> ## 1 -4 1 <eigen> 0.0408 -0.825 -0.565 -0.167 -0.114 nu=20, W=(6, -4, … ## 2 -4 2 <eigen> 0.0418 0.652 0.758 0.133 0.155 nu=20, W=(6, -4, … ## 3 -4 3 <eigen> 0.0713 -0.835 -0.551 -0.223 -0.147 nu=20, W=(6, -4, … ## 4 -4 4 <eigen> 0.0999 -0.725 -0.689 -0.229 -0.218 nu=20, W=(6, -4, … ## 5 -4 5 <eigen> 0.0342 -0.711 -0.704 -0.131 -0.130 nu=20, W=(6, -4, … ## 6 -4 6 <eigen> 0.0394 0.666 0.746 0.132 0.148 nu=20, W=(6, -4, … ## 7 -4 7 <eigen> 0.0214 -0.725 -0.689 -0.106 -0.101 nu=20, W=(6, -4, … ## 8 -4 8 <eigen> 0.0251 -0.790 -0.613 -0.125 -0.0971 nu=20, W=(6, -4, … ## 9 -4 9 <eigen> 0.0416 0.612 0.791 0.125 0.161 nu=20, W=(6, -4, … ## 10 -4 10 <eigen> 0.0598 0.445 0.896 0.109 0.219 nu=20, W=(6, -4, … ## # … with 8,090 more rows
パラメータごとに期待値のラベルを作成します。
# パラメータごとに精度行列の期待値のラベルを作成 anime_label_df <- tibble::tibble( w_12 = w_12_vals # パラメータ ) |> dplyr::group_by(w_12) |> # 期待値の計算用にグループ化 dplyr::mutate( label = paste0("E[Lambda]=(", paste0(round(nu * matrix(c(w_11, unique(w_12), unique(w_12), w_22), nrow = D, ncol = D), 2), collapse = ", "), ")"), # 分散共分散行列ラベル parameter = paste0("nu=", nu, ", W=(", w_11, ", ", unique(w_12), ", ", unique(w_12), ", ", w_22, ")") |> factor(levels = paste0("nu=", nu, ", W=(", w_11, ", ", w_12_vals, ", ", w_12_vals, ", ", w_22, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_label_df
## # A tibble: 81 × 3 ## w_12 label parameter ## <dbl> <chr> <fct> ## 1 -4 E[Lambda]=(120, -80, -80, 100) nu=20, W=(6, -4, -4, 5) ## 2 -3.9 E[Lambda]=(120, -78, -78, 100) nu=20, W=(6, -3.9, -3.9, 5) ## 3 -3.8 E[Lambda]=(120, -76, -76, 100) nu=20, W=(6, -3.8, -3.8, 5) ## 4 -3.7 E[Lambda]=(120, -74, -74, 100) nu=20, W=(6, -3.7, -3.7, 5) ## 5 -3.6 E[Lambda]=(120, -72, -72, 100) nu=20, W=(6, -3.6, -3.6, 5) ## 6 -3.5 E[Lambda]=(120, -70, -70, 100) nu=20, W=(6, -3.5, -3.5, 5) ## 7 -3.4 E[Lambda]=(120, -68, -68, 100) nu=20, W=(6, -3.4, -3.4, 5) ## 8 -3.3 E[Lambda]=(120, -66, -66, 100) nu=20, W=(6, -3.3, -3.3, 5) ## 9 -3.2 E[Lambda]=(120, -64, -64, 100) nu=20, W=(6, -3.2, -3.2, 5) ## 10 -3.1 E[Lambda]=(120, -62, -62, 100) nu=20, W=(6, -3.1, -3.1, 5) ## # … with 71 more rows
「自由度の影響」のコードで作図できます。
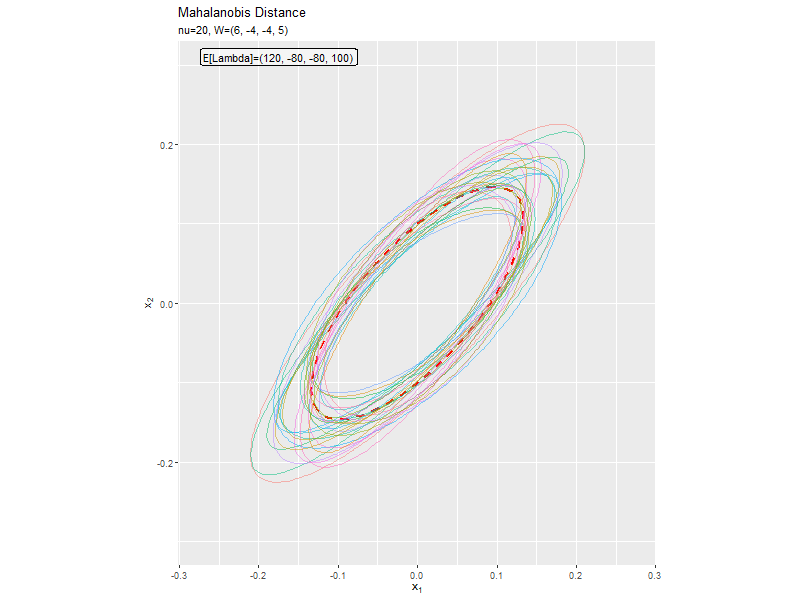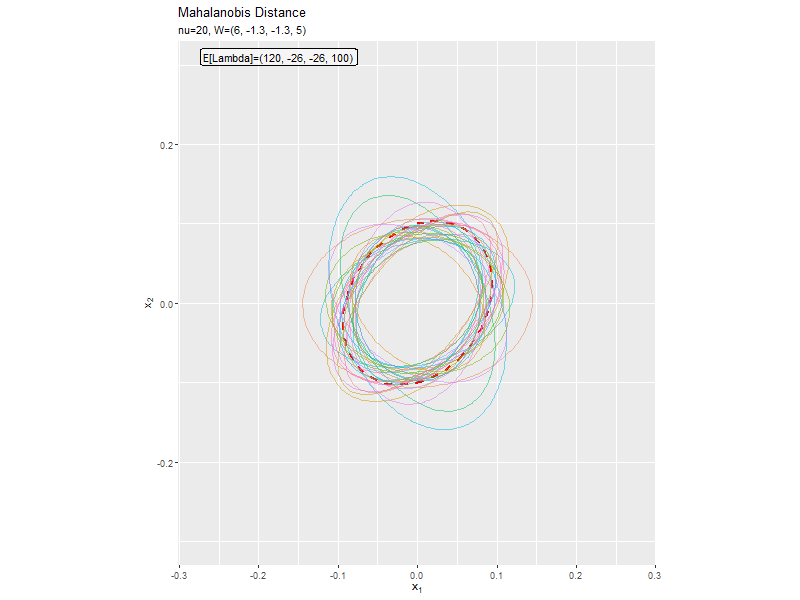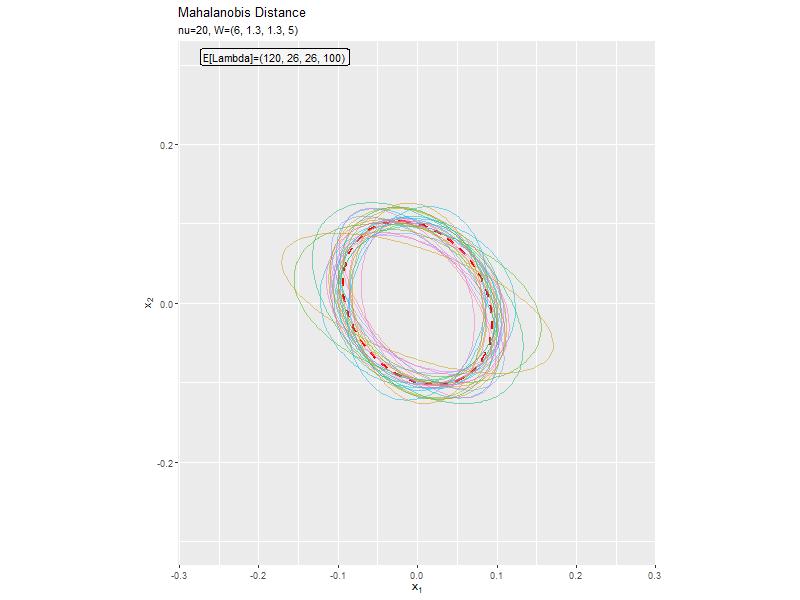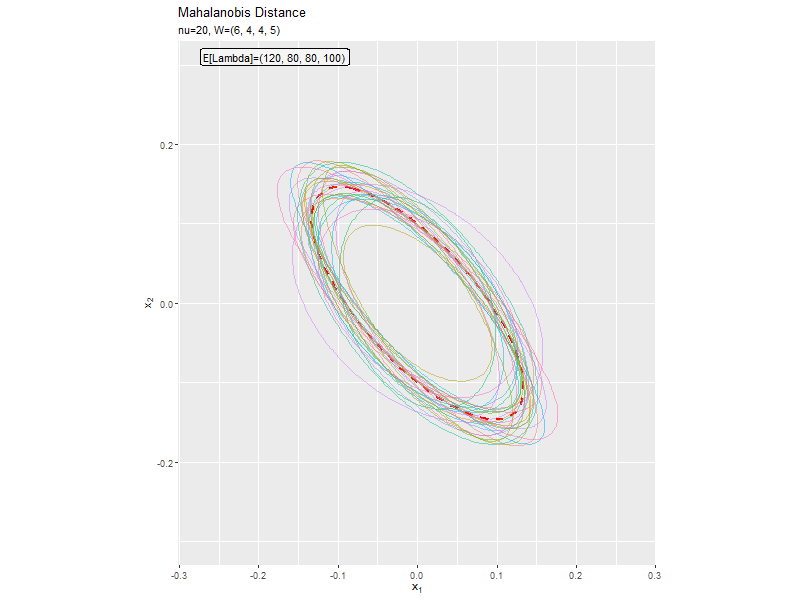
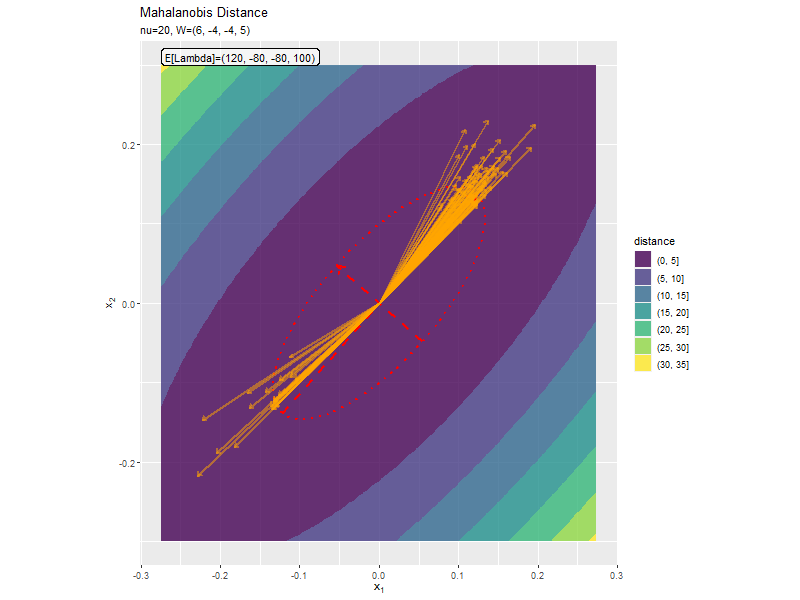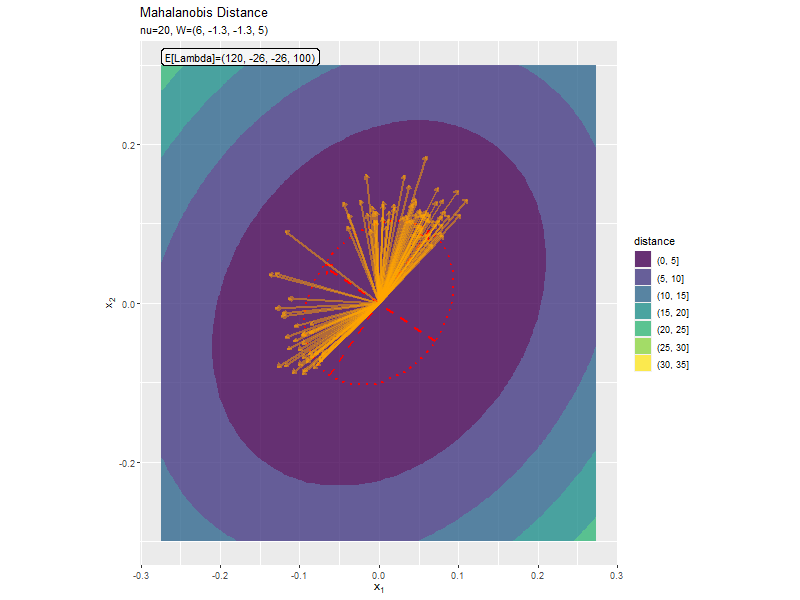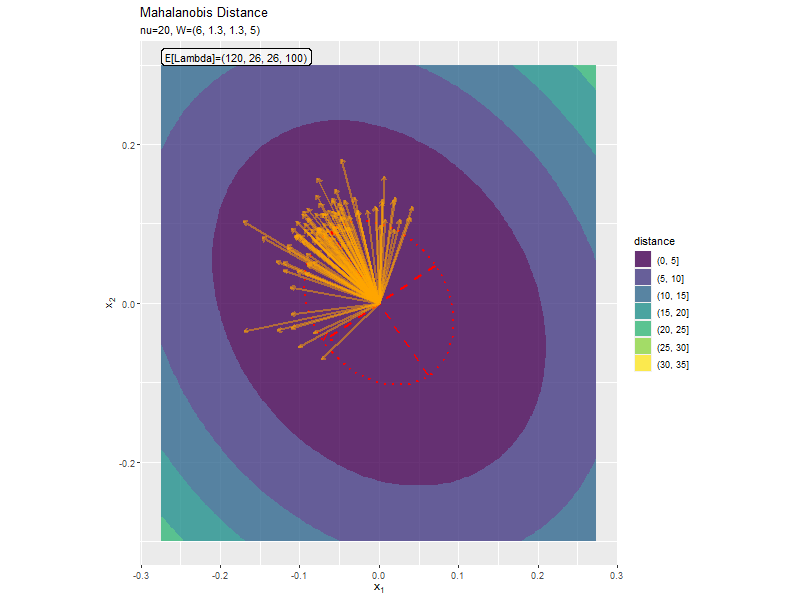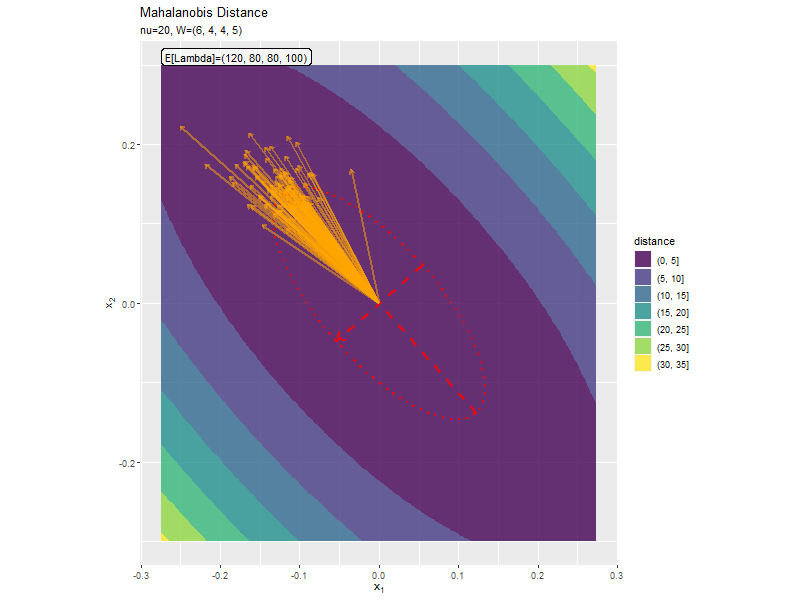
$w_{1,2} < 0$なほど軸の傾きが大きく、$w_{1,2} > 0$なほど軸の傾きが小さくなっています。
スケール行列(2,2成分)の影響
$w_{2,2}$の値を変化させ、$\nu, w_{1,1}, w_{1,2}$を固定します。
・作図コード(クリックで展開)
# 次元数を指定 D <- 2 # 自由度を指定 nu <- D + 18 # 逆スケール行列を指定 w_11 <- 5 w_12 <- 0.6 w_22_vals <- seq(from = 1, to = 10, by = 0.1) |> round(digits = 2) # フレーム数を設定 frame_num <- length(w_22_vals) frame_num
## [1] 91
値の間隔が一定になるように$w_{2,2}$の値をw_22_valsとして作成します。また、$w_{1,1}, w_{2,2}$をw_11, w_22として値を指定します。
設定したパラメータに応じて、変数の値$\mathbf{x}$を作成します。
# 作図用の共分散行列を作成 E_sigma_dd <- solve(nu * matrix(c(w_11, w_12, w_12, min(w_22_vals)), nrow = D, ncol = D)) # xの値を作成 x_1_vals <- seq( from = - sqrt(E_sigma_dd[1, 1]) * 3, to = sqrt(E_sigma_dd[1, 1]) * 3, length.out = 100 ) x_2_vals <- seq( from = - sqrt(E_sigma_dd[2, 2]) * 1.5, to = sqrt(E_sigma_dd[2, 2]) * 1.5, length.out = 100 ) # xの点を作成 x_mat <- tidyr::expand_grid( x_1 = x_1_vals, x_2 = x_2_vals ) |> # 格子点を作成 as.matrix() # マトリクスに変換 head(x_mat)
## x_1 x_2 ## [1,] -0.3114205 -0.3481788 ## [2,] -0.3114205 -0.3411448 ## [3,] -0.3114205 -0.3341109 ## [4,] -0.3114205 -0.3270770 ## [5,] -0.3114205 -0.3200431 ## [6,] -0.3114205 -0.3130092
「自由度の影響」のnu, nu_valsとw_22, w_22_valsを置き換えるように処理します。
パラメータごとに期待値による距離を計算します。
# パラメータごとに共分散行列の期待値によるマハラノビス距離(楕円)を計算 anime_E_delta_df <- tidyr::expand_grid( w_22 = w_22_vals, # パラメータ x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(w_22) |> # 距離の計算用にグループ化 dplyr::mutate( delta = mahalanobis( x = x_mat, center = 0, cov = nu * matrix(c(w_11, w_12, w_12, unique(w_22)), nrow = D, ncol = D), # 精度行列の期待値を指定 inverted = TRUE ), # 確率密度 parameter = paste0("nu=", nu, ", W=(", w_11, ", ", w_12, ", ", w_12, ", ", unique(w_22), ")") |> factor(levels = paste0("nu=", nu, ", W=(", w_11, ", ", w_12, ", ", w_12, ", ", w_22_vals, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_E_delta_df
## # A tibble: 910,000 × 5 ## w_22 x_1 x_2 delta parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 1 -0.311 -0.348 14.7 nu=20, W=(5, 0.6, 0.6, 1) ## 2 1 -0.311 -0.341 14.6 nu=20, W=(5, 0.6, 0.6, 1) ## 3 1 -0.311 -0.334 14.4 nu=20, W=(5, 0.6, 0.6, 1) ## 4 1 -0.311 -0.327 14.3 nu=20, W=(5, 0.6, 0.6, 1) ## 5 1 -0.311 -0.320 14.1 nu=20, W=(5, 0.6, 0.6, 1) ## 6 1 -0.311 -0.313 14.0 nu=20, W=(5, 0.6, 0.6, 1) ## 7 1 -0.311 -0.306 13.9 nu=20, W=(5, 0.6, 0.6, 1) ## 8 1 -0.311 -0.299 13.7 nu=20, W=(5, 0.6, 0.6, 1) ## 9 1 -0.311 -0.292 13.6 nu=20, W=(5, 0.6, 0.6, 1) ## 10 1 -0.311 -0.285 13.5 nu=20, W=(5, 0.6, 0.6, 1) ## # … with 909,990 more rows
パラメータごとに期待値による軸を計算します。
# パラメータごとに共分散行列の期待値による楕円の軸を計算 anime_E_axis_df <- tidyr::expand_grid( w_22 = w_22_vals, # パラメータごとに name = paste0(rep(c("x", "y"), each = 2, times = 2), rep(c("start", "end"), each = 4)) # 列名 ) |> # パラメータごとに受け皿を複製 dplyr::group_by(w_22) |> # 軸の計算用にグループ化 dplyr::mutate( axis = rep(c("y_1", "y_2"), times = 4), # pivot_wider用の列 sign = rep(c(-1, 1), each = 4), # 始点・終点の計算用の符号 lambda = solve(nu * matrix(c(w_11, w_12, w_12, unique(w_22)), nrow = D, ncol = D)) |> # 共分散行列の期待値を計算 (\(.){eigen(.)[["values"]]})() |> (\(.){rep(sqrt(.), times = 4)})(), # 固有値 u = solve(nu * matrix(c(w_11, w_12, w_12, unique(w_22)), nrow = D, ncol = D)) |> # 共分散行列の期待値を計算 (\(.){t(eigen(.)[["vectors"]])})() |> (\(.){rep(as.vector(.), times = 2)})(), # 固有ベクトル value = sign * u * lambda, # 軸の始点・終点を計算 parameter = paste0("nu=", nu, ", W=(", w_11, ", ", w_12, ", ", w_12, ", ", unique(w_22), ")") |> factor(levels = paste0("nu=", nu, ", W=(", w_11, ", ", w_12, ", ", w_12, ", ", w_22_vals, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() |> # グループ化を解除 dplyr::select(axis, name, value, parameter) |> # 利用する列を選択 tidyr::pivot_wider( id_cols = c(axis, parameter), names_from = name, values_from = value ) # 軸の視点・終点の列を分割 anime_E_axis_df
## # A tibble: 182 × 6 ## axis parameter xstart ystart xend yend ## <chr> <fct> <dbl> <dbl> <dbl> <dbl> ## 1 y_1 nu=20, W=(5, 0.6, 0.6, 1) 0.0340 -0.232 -0.0340 0.232 ## 2 y_2 nu=20, W=(5, 0.6, 0.6, 1) 0.0981 0.0144 -0.0981 -0.0144 ## 3 y_1 nu=20, W=(5, 0.6, 0.6, 1.1) 0.0331 -0.220 -0.0331 0.220 ## 4 y_2 nu=20, W=(5, 0.6, 0.6, 1.1) 0.0980 0.0147 -0.0980 -0.0147 ## 5 y_1 nu=20, W=(5, 0.6, 0.6, 1.2) 0.0324 -0.210 -0.0324 0.210 ## 6 y_2 nu=20, W=(5, 0.6, 0.6, 1.2) 0.0979 0.0151 -0.0979 -0.0151 ## 7 y_1 nu=20, W=(5, 0.6, 0.6, 1.3) 0.0318 -0.201 -0.0318 0.201 ## 8 y_2 nu=20, W=(5, 0.6, 0.6, 1.3) 0.0978 0.0155 -0.0978 -0.0155 ## 9 y_1 nu=20, W=(5, 0.6, 0.6, 1.4) 0.0314 -0.193 -0.0314 0.193 ## 10 y_2 nu=20, W=(5, 0.6, 0.6, 1.4) 0.0978 0.0159 -0.0978 -0.0159 ## # … with 172 more rows
パラメータごとにサンプリングして距離を計算します。
# 楕円の数(サンプルサイズ)を指定 N <- 30 # パラメータごとに楕円のサンプルを計算 anime_sample_delta_df <- tidyr::expand_grid( w_22 = w_22_vals, # パラメータ n = 1:N, # サンプル番号 x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータとサンプルごとに格子点を複製 dplyr::group_by(w_22, n) |> # 距離の計算用にグループ化 dplyr::mutate( delta = mahalanobis( x = x_mat, center = 0, cov = rWishart( n = 1, df = nu, Sigma = matrix(c(w_11, w_12, w_12, unique(w_22)), nrow = D, ncol = D) )[, , 1], # 精度行列を生成 inverted = TRUE ), parameter = paste0("nu=", nu, ", W=(", w_11, ", ", w_12, ", ", w_12, ", ", unique(w_22), ")") |> factor(levels = paste0("nu=", nu, ", W=(", w_11, ", ", w_12, ", ", w_12, ", ", w_22_vals, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_sample_delta_df
## # A tibble: 27,300,000 × 6 ## w_22 n x_1 x_2 delta parameter ## <dbl> <int> <dbl> <dbl> <dbl> <fct> ## 1 1 1 -0.311 -0.348 14.0 nu=20, W=(5, 0.6, 0.6, 1) ## 2 1 1 -0.311 -0.341 13.9 nu=20, W=(5, 0.6, 0.6, 1) ## 3 1 1 -0.311 -0.334 13.7 nu=20, W=(5, 0.6, 0.6, 1) ## 4 1 1 -0.311 -0.327 13.6 nu=20, W=(5, 0.6, 0.6, 1) ## 5 1 1 -0.311 -0.320 13.5 nu=20, W=(5, 0.6, 0.6, 1) ## 6 1 1 -0.311 -0.313 13.3 nu=20, W=(5, 0.6, 0.6, 1) ## 7 1 1 -0.311 -0.306 13.2 nu=20, W=(5, 0.6, 0.6, 1) ## 8 1 1 -0.311 -0.299 13.1 nu=20, W=(5, 0.6, 0.6, 1) ## 9 1 1 -0.311 -0.292 12.9 nu=20, W=(5, 0.6, 0.6, 1) ## 10 1 1 -0.311 -0.285 12.8 nu=20, W=(5, 0.6, 0.6, 1) ## # … with 27,299,990 more rows
パラメータごとにサンプリングして軸を計算します。
# 軸の数(サンプルサイズ)を指定 N <- 100 # パラメータごとに楕円の長軸のサンプルを計算 anime_sample_axis_df <- tidyr::expand_grid( w_22 = w_22_vals, # パラメータ n = 1:N # サンプル番号 ) |> dplyr::group_by(w_22, n) |> # 軸の計算用にグループ化 dplyr::mutate( eigen_lt = rWishart( n = 1, df = nu, Sigma = matrix(c(w_11, w_12, w_12, unique(w_22)), nrow = D, ncol = D) )[, , 1] |> # 精度行列を生成 solve() |> # 分散共分散行列に変換 eigen() |> # 固有値・固有ベクトルを計算 list(), # リストに格納 lambda_1 = eigen_lt[[1]][["values"]][1], # 固有値 u_11 = eigen_lt[[1]][["vectors"]][1, 1], # 固有ベクトルの成分 u_12 = eigen_lt[[1]][["vectors"]][2, 1], # 固有ベクトルの成分 xend = u_11 * sqrt(lambda_1), # 終点のx軸の値 yend = u_12 * sqrt(lambda_1), # 終点のy軸の値 parameter = paste0("nu=", nu, ", W=(", w_11, ", ", w_12, ", ", w_12, ", ", unique(w_22), ")") |> factor(levels = paste0("nu=", nu, ", W=(", w_11, ", ", w_12, ", ", w_12, ", ", w_22_vals, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_sample_axis_df
## # A tibble: 9,100 × 9 ## w_22 n eigen_lt lambda_1 u_11 u_12 xend yend parameter ## <dbl> <int> <list> <dbl> <dbl> <dbl> <dbl> <dbl> <fct> ## 1 1 1 <eigen> 0.0420 -0.231 0.973 -0.0474 0.199 nu=20, W=(5, 0.6, … ## 2 1 2 <eigen> 0.0622 -0.243 0.970 -0.0607 0.242 nu=20, W=(5, 0.6, … ## 3 1 3 <eigen> 0.0727 0.0629 0.998 0.0170 0.269 nu=20, W=(5, 0.6, … ## 4 1 4 <eigen> 0.0719 -0.171 0.985 -0.0459 0.264 nu=20, W=(5, 0.6, … ## 5 1 5 <eigen> 0.0258 -0.334 0.942 -0.0537 0.151 nu=20, W=(5, 0.6, … ## 6 1 6 <eigen> 0.0803 -0.293 0.956 -0.0830 0.271 nu=20, W=(5, 0.6, … ## 7 1 7 <eigen> 0.0627 -0.110 0.994 -0.0275 0.249 nu=20, W=(5, 0.6, … ## 8 1 8 <eigen> 0.0688 -0.254 0.967 -0.0666 0.254 nu=20, W=(5, 0.6, … ## 9 1 9 <eigen> 0.0760 -0.187 0.982 -0.0515 0.271 nu=20, W=(5, 0.6, … ## 10 1 10 <eigen> 0.0520 -0.129 0.992 -0.0294 0.226 nu=20, W=(5, 0.6, … ## # … with 9,090 more rows
パラメータごとに期待値のラベルを作成します。
# パラメータごとに分散共分散行列の期待値のラベルを作成 anime_label_df <- tibble::tibble( w_22 = w_22_vals # パラメータ ) |> dplyr::group_by(w_22) |> # 期待値の計算用にグループ化 dplyr::mutate( label = paste0("E[Lambda]=(", paste0(round(nu * matrix(c(w_11, w_12, w_12, unique(w_22)), nrow = D, ncol = D), 2), collapse = ", "), ")"), # 分散共分散行列ラベル parameter = paste0("nu=", nu, ", W=(", w_11, ", ", w_12, ", ", w_12, ", ", unique(w_22), ")") |> factor(levels = paste0("nu=", nu, ", W=(", w_11, ", ", w_12, ", ", w_12, ", ", w_22_vals, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_label_df
## # A tibble: 91 × 3 ## w_22 label parameter ## <dbl> <chr> <fct> ## 1 1 E[Lambda]=(100, 12, 12, 20) nu=20, W=(5, 0.6, 0.6, 1) ## 2 1.1 E[Lambda]=(100, 12, 12, 22) nu=20, W=(5, 0.6, 0.6, 1.1) ## 3 1.2 E[Lambda]=(100, 12, 12, 24) nu=20, W=(5, 0.6, 0.6, 1.2) ## 4 1.3 E[Lambda]=(100, 12, 12, 26) nu=20, W=(5, 0.6, 0.6, 1.3) ## 5 1.4 E[Lambda]=(100, 12, 12, 28) nu=20, W=(5, 0.6, 0.6, 1.4) ## 6 1.5 E[Lambda]=(100, 12, 12, 30) nu=20, W=(5, 0.6, 0.6, 1.5) ## 7 1.6 E[Lambda]=(100, 12, 12, 32) nu=20, W=(5, 0.6, 0.6, 1.6) ## 8 1.7 E[Lambda]=(100, 12, 12, 34) nu=20, W=(5, 0.6, 0.6, 1.7) ## 9 1.8 E[Lambda]=(100, 12, 12, 36) nu=20, W=(5, 0.6, 0.6, 1.8) ## 10 1.9 E[Lambda]=(100, 12, 12, 38) nu=20, W=(5, 0.6, 0.6, 1.9) ## # … with 81 more rows
「自由度の影響」のコードで作図できます。

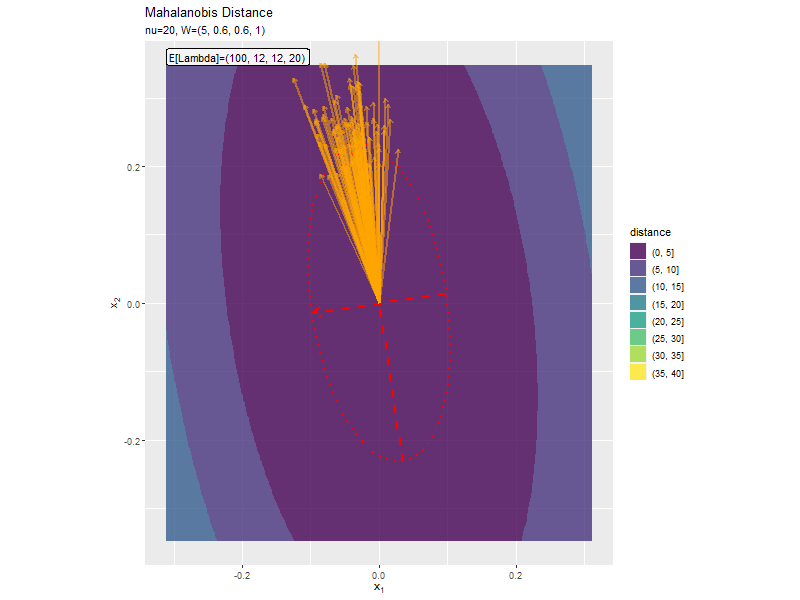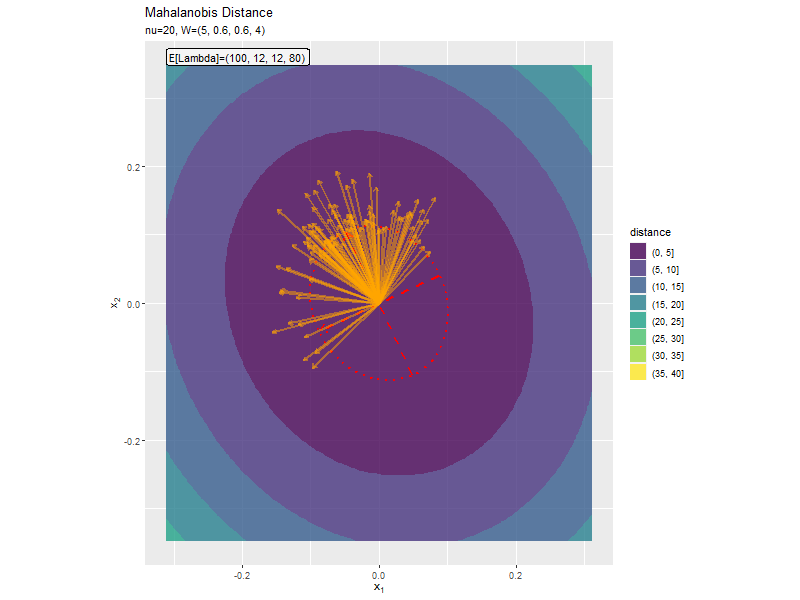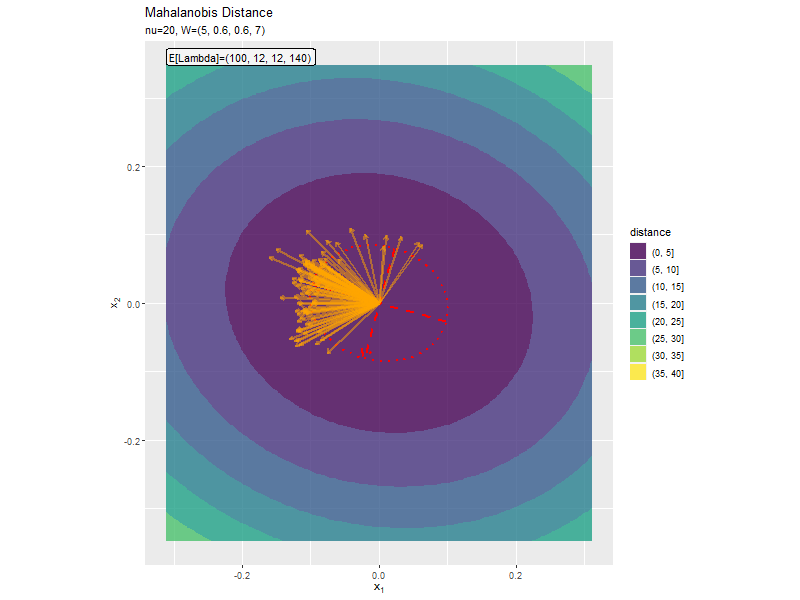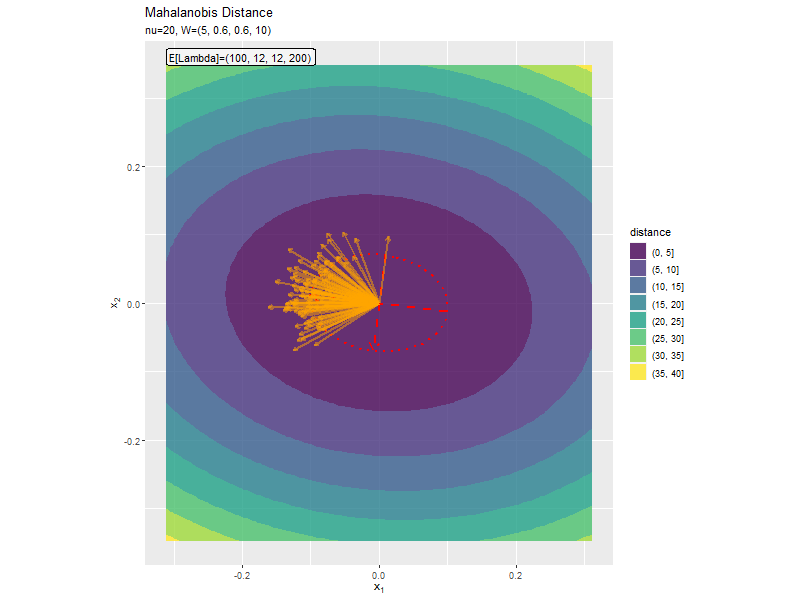
「1,1成分の影響」と同様に、$w_{1,1}, w_{2,2}$の大小関係によって軸の向きが変化しています。
この記事では、ウィシャート分布をマハラノビス距離とその軸を用いて可視化しました。
参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上』,丸善出版,2012年.
おわりに
やってることは前回の記事と被ってるのですが、目的が違うので別記事にしました。
色々面倒ながら頑張ったのですが、分かりやすいとは言えませんね。もう少し勉強して、他の記事との対応関係を整理しつつ構成し直したいです、来年くらいには。
さて、この分布で終わりと思ってたのですが、まだガウス・ウィシャート分布がありました。忘れてました。というわけでまだ続きます。
2022年9月11日は、Juice=Juiceのメジャーデビュー9周年記念日です!!!!!!
気付けば私がハマってからの期間の方が長くなってました。これからも末永く聴いていたい。
【次の内容】