はじめに
素直なやり方ではできなかったのでむりくりなんとかする黒魔術シリーズです。もっといい方法があれば教えてください。
この記事では、任意の値で変化する等高線図のアニメーションを作成します。
【目次】
任意の値で等高線を動かしたい
geom_contour()を使って等高線図のアニメーションを作成する際に、フレームごとに等高線を引く値を変更したい。しかし、breaks引数はaes()の中で設定できないのでデータフレームの列を使うなどの方法をとれず、全てのフレームで共通の値になる。
そこで、スマートではない方法(黒魔術)を使ってなんとかする(スマートな方法があればぜひ教えてください)。
この記事では、2次元ガウス分布を例とする。作図処理についての詳細は「【R】2次元ガウス分布の作図 - からっぽのしょこ」を参照のこと。
次のパッケージを利用する。
# 利用パッケージ library(tidyverse) library(mvnfast)
基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はない。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているので、ggplot2を読み込む必要がある。
また、magrittrパッケージのパイプ演算子%>%ではなく、ネイティブパイプ演算子|>を使っている。%>%に置き換えても処理できるが、その場合はmagrittrを読み込む必要がある。
等高線図の作成
まずは、静止画の等高線図の作成方法を確認しておく。
2次元ガウス分布の確率変数の点を作成する。
# x軸とy軸の値を作成 x_vals <- seq(from = -3, to = 3, length.out = 301) |> round(digits = 2) # 格子点を作成 x_mat <- tidyr::expand_grid( x1 = x_vals, x2 = x_vals ) |> # 全ての組み合わせを作成 as.matrix() # マトリクスに変換 head(x_mat)
## x1 x2 ## [1,] -3 -3.00 ## [2,] -3 -2.98 ## [3,] -3 -2.96 ## [4,] -3 -2.94 ## [5,] -3 -2.92 ## [6,] -3 -2.90
簡単な例として、x軸とy軸で同じ値x_valsを使う。グラフが粗い場合や処理が重い場合は、x_valsの間隔(by引数)や要素数(length.out引数)を調整する。
格子状の点(x_vecの要素の全ての組み合わせ)をexpand_grid()で作成する。geom_contour()を使う場合は、格子点(x軸とy軸の値が直交する点)を用意する必要がある。
2次元ガウス分布のパラメータを設定する。
# 次元数を設定:(固定) D <- 2 # 平均ベクトルを指定 mu_d <- rep(0, times = D) # 分散共分散行列を指定 sigma_dd <- diag(D) # 単位行列
要素数2のベクトルmu_dと、2行2列のマトリクスsigma_ddに値を指定する。
2次元ガウス分布の確率密度を計算する。
# ガウス分布を計算 dens_df <- tibble::tibble( x1 = x_mat[, 1], # x軸の値 x2 = x_mat[, 2], # y軸の値 dens = mvnfast::dmvn(X = x_mat, mu = mu_d, sigma = sigma_dd) # 確率密度 ) dens_df
## # A tibble: 90,601 × 3 ## x1 x2 dens ## <dbl> <dbl> <dbl> ## 1 -3 -3 0.0000196 ## 2 -3 -2.98 0.0000209 ## 3 -3 -2.96 0.0000221 ## 4 -3 -2.94 0.0000235 ## 5 -3 -2.92 0.0000249 ## 6 -3 -2.9 0.0000264 ## 7 -3 -2.88 0.0000280 ## 8 -3 -2.86 0.0000296 ## 9 -3 -2.84 0.0000313 ## 10 -3 -2.82 0.0000332 ## # … with 90,591 more rows
mvnfastパッケージのdmvn()を使って、x_matの行ごとに確率密度を計算する。
2次元ガウス分布の等高線図を作成する。
# 等高線図を作成 ggplot() + geom_contour(data = dens_df, mapping = aes(x = x1, y = x2, z = dens, color = ..level..)) + # 等高線 coord_fixed(ratio = 1, xlim = c(min(x_vals), max(x_vals)), ylim = c(min(x_vals), max(x_vals))) + # アスペクト比 labs(x = expression(x[1]), y = expression(x[2]))

geom_contour()で等高線図を描画できる。
等高線図の基本形を作成できた。続いて、等高線を引く位置を指定する。
geom_contour()のbreaks引数に、等高線を引く値を指定できる。
# 等高線を引く値を指定 breaks_vals <- seq(from = 0, to = 0.1, by = 0.01) # 値を指定して等高線図を作成 ggplot() + # 等高線 geom_contour(data = dens_df, mapping = aes(x = x1, y = x2, z = dens, color = ..level..), breaks = breaks_vals) + # 等高線 coord_fixed(ratio = 1, xlim = c(min(x_vals), max(x_vals)), ylim = c(min(x_vals), max(x_vals))) + # アスペクト比 labs(x = expression(x[1]), y = expression(x[2]))

一定の間隔の確率密度で等高線を引いた
同様に、確率密度の最大値の0.5倍の値で線を引く。
# 倍率を指定 rate <- 0.5 # 確率密度の最大値を計算 max_dens <- mvnfast::dmvn(X = mu_d, mu = mu_d, sigma = sigma_dd) # 値を指定して等高線図を作成 ggplot() + geom_contour(data = dens_df, mapping = aes(x = x1, y = x2, z = dens, color = ..level..), breaks = max_dens*rate) + # 等高線 coord_fixed(ratio = 1, xlim = c(min(x_vals), max(x_vals)), ylim = c(min(x_vals), max(x_vals))) + # アスペクト比 labs(x = expression(x[1]), y = expression(x[2]))

確率密度が次の値の点を結んだ等高線が引かれた。
# 値を確認 max_dens * rate
## [1] 0.07957747
次からは、この線を動かすことを考える。
等高線図のアニメーションを作成
では、等高線図のアニメーションの作成方法を確認する。例として、共分散(分散共分散行列の対角要素(分散)以外の要素)が変化したときの、2次元ガウス分布のアニメーションを作成する。
分散共分散行列の各要素の値を設定する。
# x軸の分散を指定 sigma2_1 <- 1 # y軸の分散を指定 sigma2_2 <- 1 # 共分散として利用する値を指定 sigma_12_vals <- seq(from = -0.8, to = 0.8, by = 0.1) |> round(digits = 1)
分散をsigma2_1, sigma2_2として値を指定する。共分散をsigma_12_valsとして一定の間隔の値を指定する。
共分散の値ごとに、2次元ガウス分布の確率密度を計算する。
# 共分散の値ごとにガウス分布を計算 anime_dens_df <- tidyr::expand_grid( sigma_12 = sigma_12_vals, # 共分散 x1 = x_vals, # x軸の値 x2 = x_vals # y軸の値 ) |> # 格子点を複製 dplyr::group_by(sigma_12) |> # 分布の計算用にグループ化 dplyr::mutate( dens = mvnfast::dmvn( X = x_mat, mu = mu_d, sigma = matrix(c(sigma2_1, unique(sigma_12), unique(sigma_12), sigma2_2), nrow = D, ncol = D) ) # 確率密度 ) |> dplyr::ungroup() # グループ化を解除 anime_dens_df
## # A tibble: 1,540,217 × 4 ## sigma_12 x1 x2 dens ## <dbl> <dbl> <dbl> <dbl> ## 1 -0.8 -3 -3 7.59e-21 ## 2 -0.8 -3 -2.98 1.02e-20 ## 3 -0.8 -3 -2.96 1.38e-20 ## 4 -0.8 -3 -2.94 1.86e-20 ## 5 -0.8 -3 -2.92 2.50e-20 ## 6 -0.8 -3 -2.9 3.36e-20 ## 7 -0.8 -3 -2.88 4.50e-20 ## 8 -0.8 -3 -2.86 6.03e-20 ## 9 -0.8 -3 -2.84 8.08e-20 ## 10 -0.8 -3 -2.82 1.08e-19 ## # … with 1,540,207 more rows
詳しくは冒頭にリンクした記事を参照のこと。
共分散の値ごとに、2次元ガウス分布のグラフを描画するアニメーション(gif画像)を作成する。
# 等高線図のアニメーションを作成 anime_graph <- ggplot() + geom_contour(data = anime_dens_df, mapping = aes(x = x1, y = x2, z = dens, color = ..level..)) + # 等高線 gganimate::transition_manual(sigma_12) + # フレーム coord_fixed(ratio = 1, xlim = c(min(x_vals), max(x_vals)), ylim = c(min(x_vals), max(x_vals))) + # アスペクト比 labs(title = paste0("covariance = ", "{current_frame}"), x = expression(x[1]), y = expression(x[2])) # gif画像を作成 gganimate::animate( plot = anime_graph, nframes = length(sigma_12_vals), fps = 10, width = 800, height = 800 )
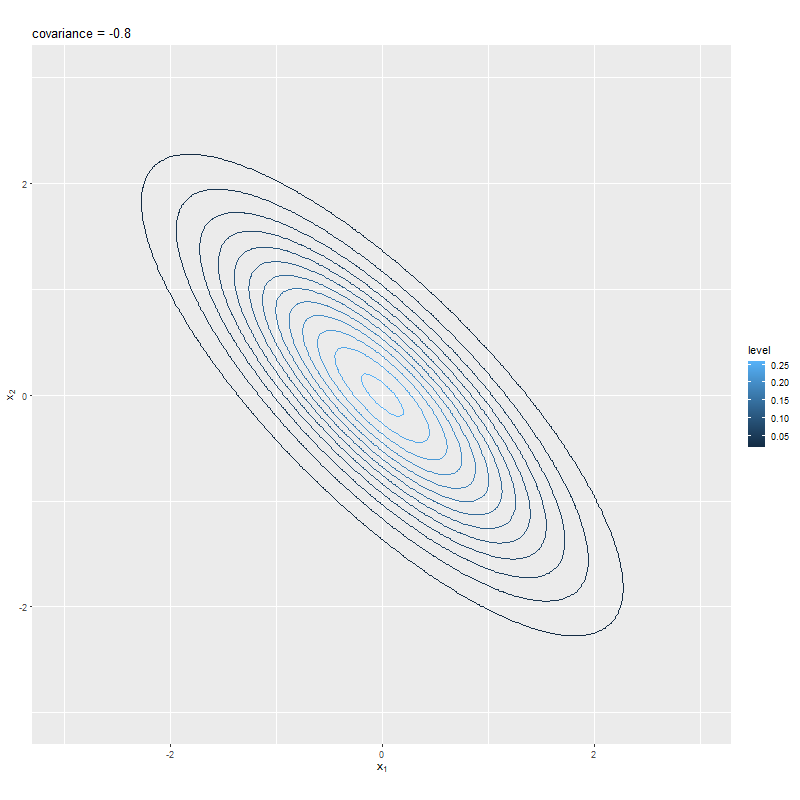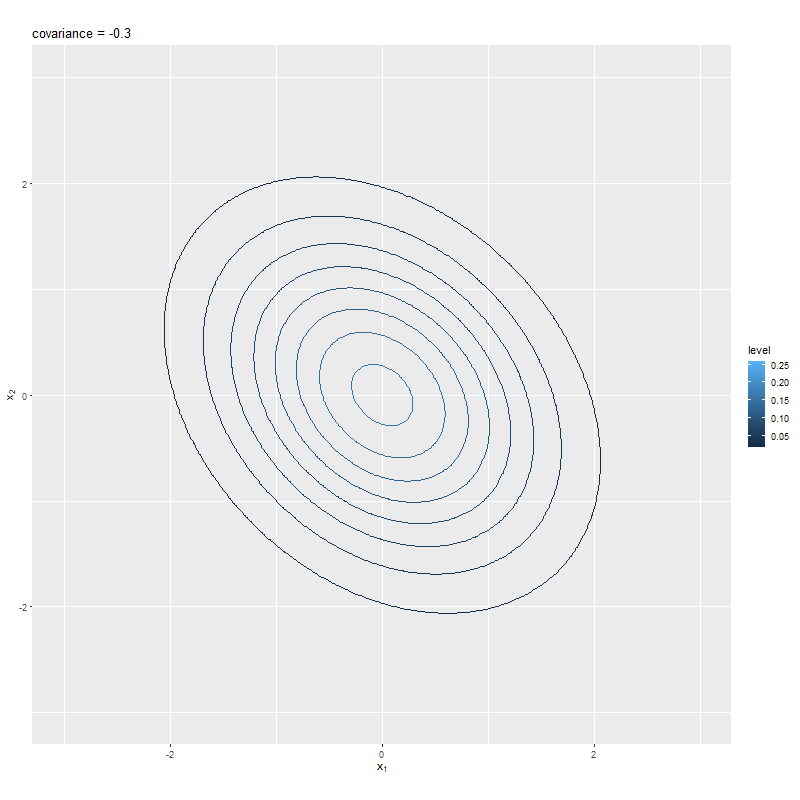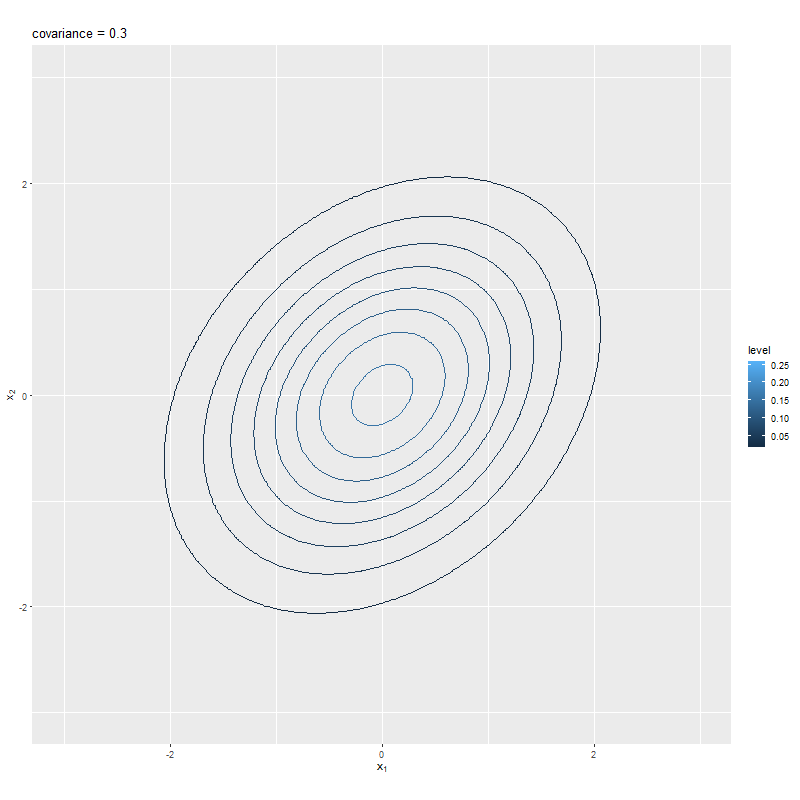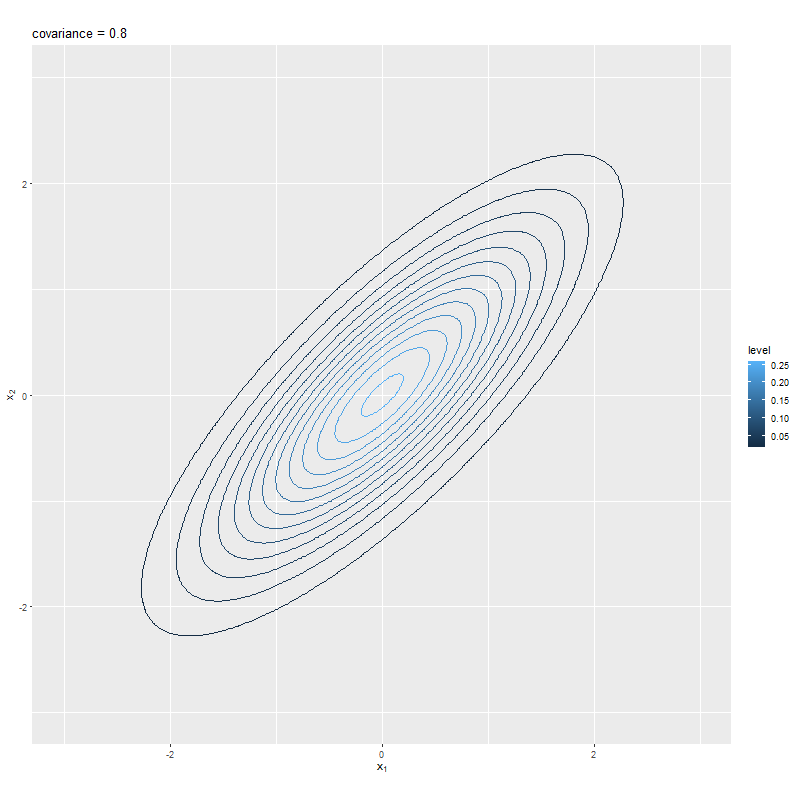
gganimateパッケージのtransition_manual()にフレームを制御する列を指定して、animate()でgif画像に変換する。この例では、sigma_12_valsの値ごとにフレーム(グラフ)を切り替えるので、フレーム数はsigma_12_valsの要素数になる。
等高線図のアニメーションの基本形を作成できた。続いて、等高線を引く位置を指定する。
geom_contour()のbreaks引数に、「全ての共分散(フレーム)において最大の確率密度」の0.5倍の値で線を引いてみる。
# 倍率を指定 rate <- 0.5 # 確率密度の最大値を計算 max_dens <- mvnfast::dmvn( X = mu_d, mu = mu_d, sigma = matrix(c(sigma2_1, max(sigma_12_vals), max(sigma_12_vals), sigma2_2), nrow = D, ncol = D) ) # 値を指定して等高線図のアニメーションを作成 anime_graph <- ggplot() + geom_contour(data = anime_dens_df, mapping = aes(x = x1, y = x2, z = dens, color = ..level..), breaks = max_dens*rate) + # 等高線 gganimate::transition_manual(sigma_12) + # フレーム coord_fixed(ratio = 1, xlim = c(min(x_vals), max(x_vals)), ylim = c(min(x_vals), max(x_vals))) + # アスペクト比 labs(title = "covariance = {current_frame}", x = expression(x[1]), y = expression(x[2])) # gif画像を作成 gganimate::animate( plot = anime_graph, nframes = length(sigma_12_vals), fps = 10, width = 800, height = 800 )

今回の設定だと、sigma_12_valsの最小値または最大値のとき確率密度が最大になる。各分布(フレーム)で共通して、次の値で等高線を引いた。
# 値を確認 max_dens * rate
## [1] 0.1326291
sigma_12_valsごとに確率密度の最大値が変化するので、各分布の最大値に対して、指定した倍率の値で等高線を引くことを考える。
指定した倍率を超える確率密度を指定した倍率の値に変更することで、分布の断面のデータフレームを作成する。
# 倍率を指定 rate <- 0.5 # ガウス分布の断面を計算 anime_ellipse_df <- anime_dens_df |> dplyr::group_by(sigma_12) |> # 断面の計算用にグループ化 dplyr::mutate( max_dens = mvnfast::dmvn( X = mu_d, mu = mu_d, sigma = matrix(c(sigma2_1, unique(sigma_12), unique(sigma_12), sigma2_2), nrow = D, ncol = D) ), # 確率密度の最大値 dens = dplyr::if_else( dens >= max_dens * rate, true = max_dens * rate, false = 0 # (true引数の値から離れた値を設定) ) # 断面を作成 ) |> dplyr::ungroup() # グループ化を解除 anime_ellipse_df
## # A tibble: 1,540,217 × 5 ## sigma_12 x1 x2 dens max_dens ## <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 -0.8 -3 -3 0 0.265 ## 2 -0.8 -3 -2.98 0 0.265 ## 3 -0.8 -3 -2.96 0 0.265 ## 4 -0.8 -3 -2.94 0 0.265 ## 5 -0.8 -3 -2.92 0 0.265 ## 6 -0.8 -3 -2.9 0 0.265 ## 7 -0.8 -3 -2.88 0 0.265 ## 8 -0.8 -3 -2.86 0 0.265 ## 9 -0.8 -3 -2.84 0 0.265 ## 10 -0.8 -3 -2.82 0 0.265 ## # … with 1,540,207 more rows
共分散(sigma_12_vals)の値ごとに、確率密度の最大値を計算してmax_dens列とする。
if_elseを使って、各点の確率密度(dens列)がmax_dens * rate以下であれば、値をmax_dens * rateに変更する。
共分散の値ごとに、「各分布(フレーム)の確率密度の最大値」の0.5倍の等高線のアニメーションを作成する。
# 値を指定して等高線図のアニメーションを作成 anime_graph <- ggplot() + geom_contour(data = anime_ellipse_df, mapping = aes(x = x1, y = x2, z = dens, color = ..level..), bins = 2) + # 等高線 gganimate::transition_manual(sigma_12) + # フレーム coord_fixed(ratio = 1, xlim = c(min(x_vals), max(x_vals)), ylim = c(min(x_vals), max(x_vals))) + # アスペクト比 labs(title = "covariance = {current_frame}", x = expression(x[1]), y = expression(x[2])) # gif画像を作成 gganimate::animate( plot = anime_graph, nframes = length(sigma_12_vals), fps = 10, width = 800, height = 800 )
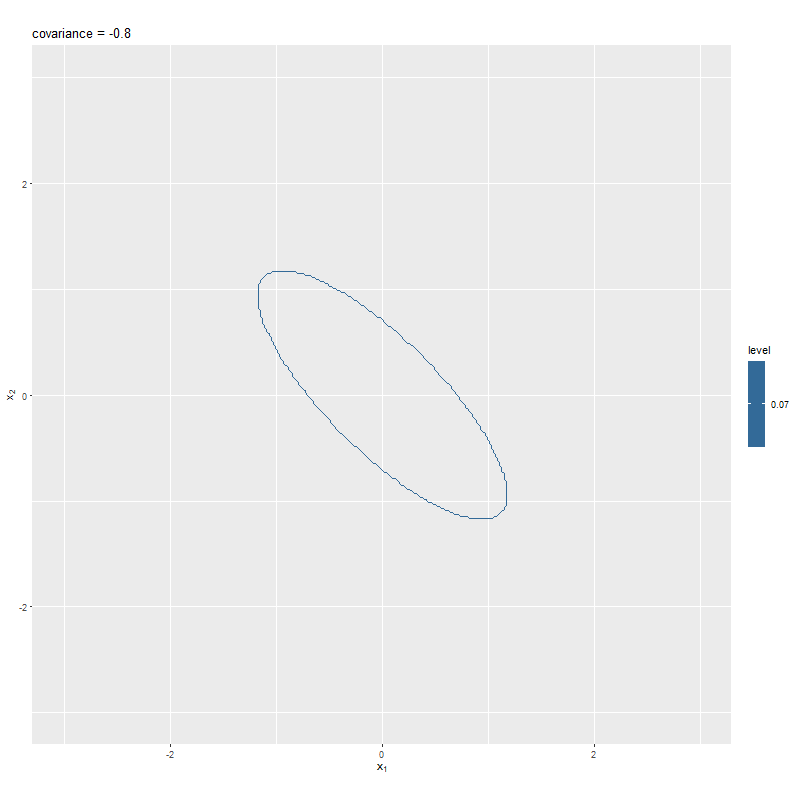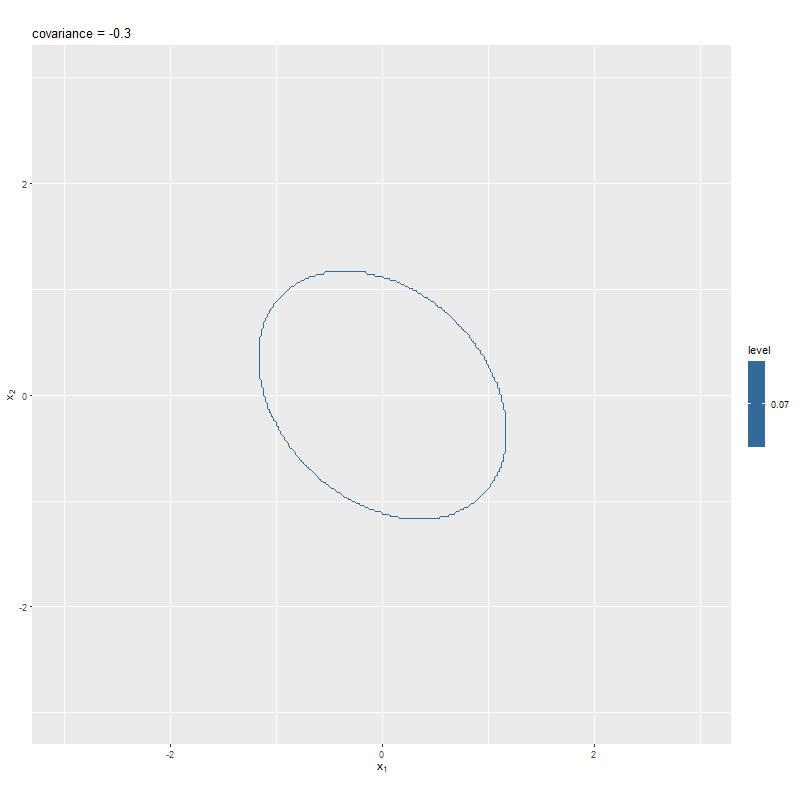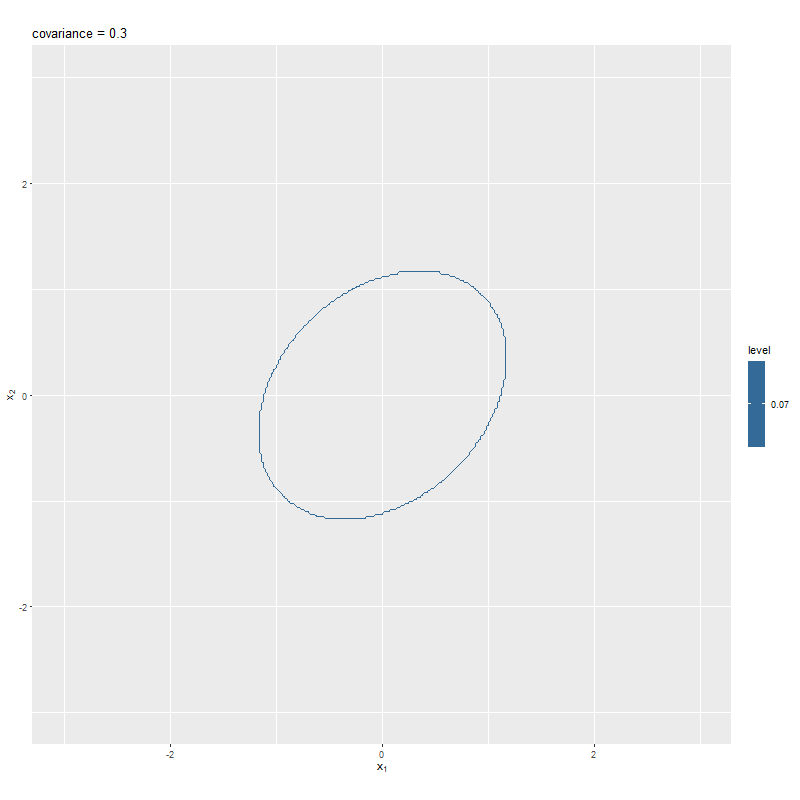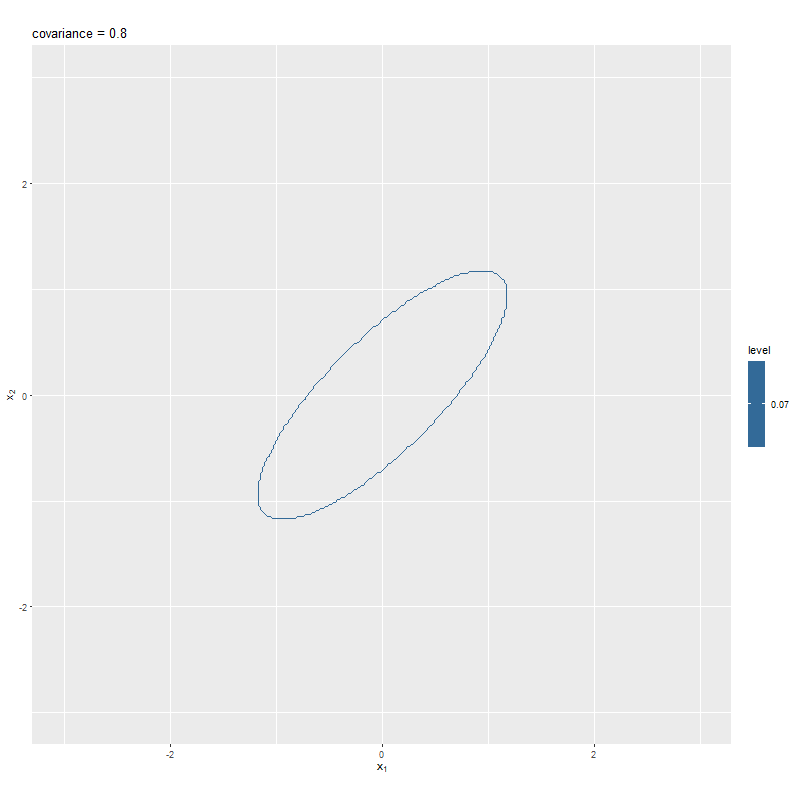
目的の等高線図が得られた。(線がガタガタしているのは見逃す。)
上のやり方だと、線と無関係な点の情報(行)を持ち、メモリ効率が割る過ぎるので、散布図で代用してみる。
等高線として描画する点を抽出する。
# 閾値を指定 threshold <- 0.001 # 等高線の点を抽出 anime_point_df <- anime_dens_df |> dplyr::group_by(sigma_12) |> # 点の抽出用にグループ化 dplyr::mutate( max_dens = mvnfast::dmvn( X = mu_d, mu = mu_d, sigma = matrix(c(sigma2_1, unique(sigma_12), unique(sigma_12), sigma2_2), nrow = D, ncol = D) ) # 確率密度の最大値 ) |> dplyr::ungroup() |> # グループ化を解除 dplyr::filter(abs(dens - max_dens*rate) <= threshold) # 等高線の点を抽出 anime_point_df
## # A tibble: 5,056 × 5 ## sigma_12 x1 x2 dens max_dens ## <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 -0.8 -1.18 0.9 0.132 0.265 ## 2 -0.8 -1.18 0.92 0.132 0.265 ## 3 -0.8 -1.18 0.94 0.132 0.265 ## 4 -0.8 -1.18 0.96 0.132 0.265 ## 5 -0.8 -1.18 0.98 0.132 0.265 ## 6 -0.8 -1.18 1 0.132 0.265 ## 7 -0.8 -1.16 0.8 0.132 0.265 ## 8 -0.8 -1.16 0.82 0.133 0.265 ## 9 -0.8 -1.16 1.04 0.133 0.265 ## 10 -0.8 -1.16 1.06 0.132 0.265 ## # … with 5,046 more rows
共分散(sigma_12_vals)の値ごとに、各点の確率密度(dens列)とmax_dens * rateの差が閾値threshold以下の点(行)を抽出する。
散布図によって等高線を描画する。
# 散布図による等高線のアニメーションを作成 anime_graph <- ggplot() + geom_point(data = anime_point_df, mapping = aes(x = x1, y = x2, color = dens), size = 2) + # 散布図 gganimate::transition_manual(sigma_12) + # フレーム coord_fixed(ratio = 1, xlim = c(min(x_vals), max(x_vals)), ylim = c(min(x_vals), max(x_vals))) + # アスペクト比 labs(title = "covariance = {current_frame}", color = "density", x = expression(x[1]), y = expression(x[2])) # gif画像を作成 gganimate::animate( plot = anime_graph, nframes = length(sigma_12_vals), fps = 10, width = 800, height = 800 )
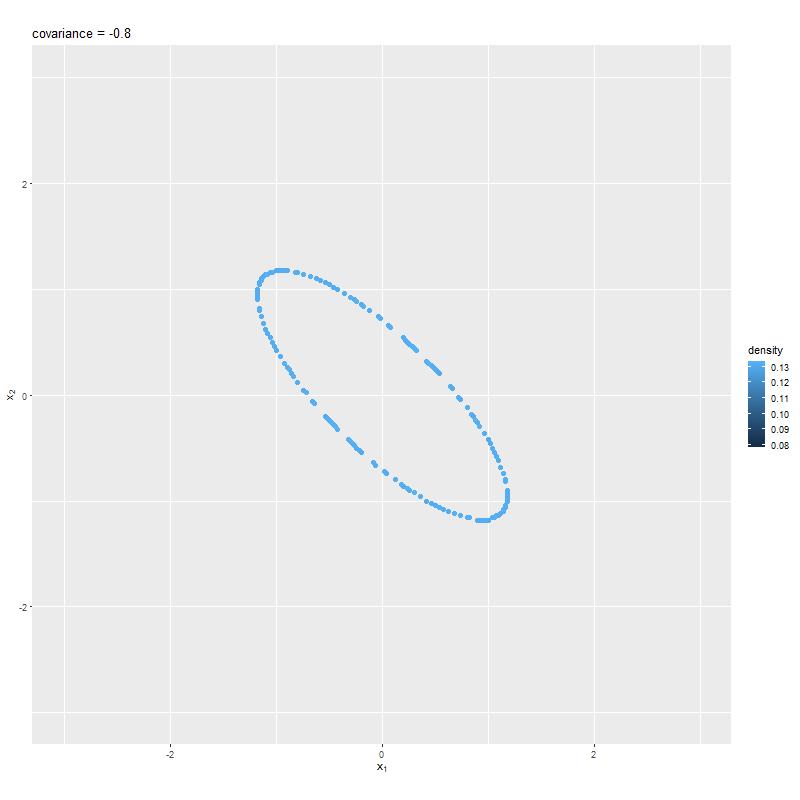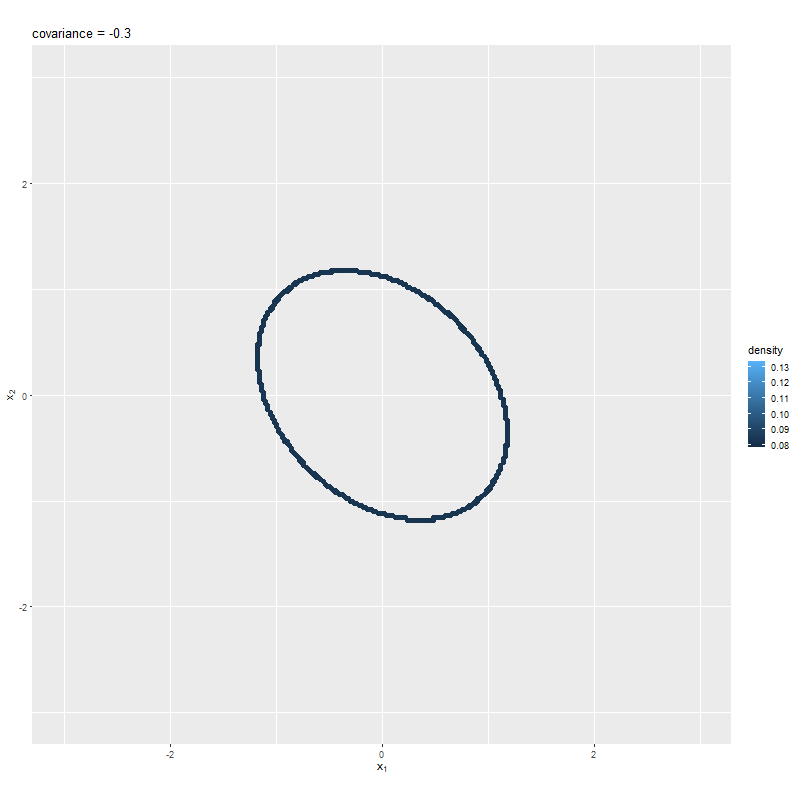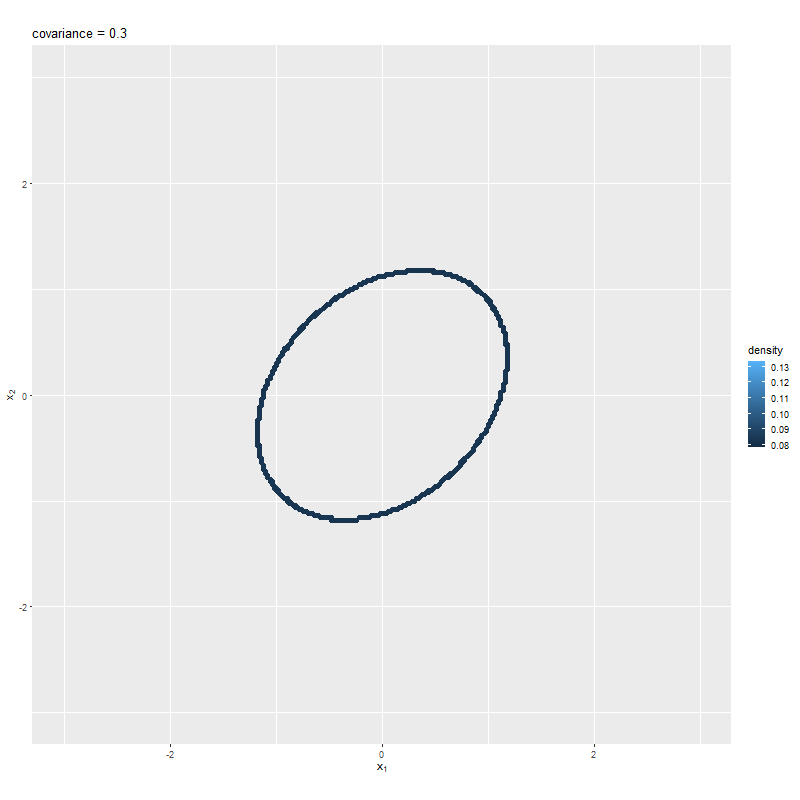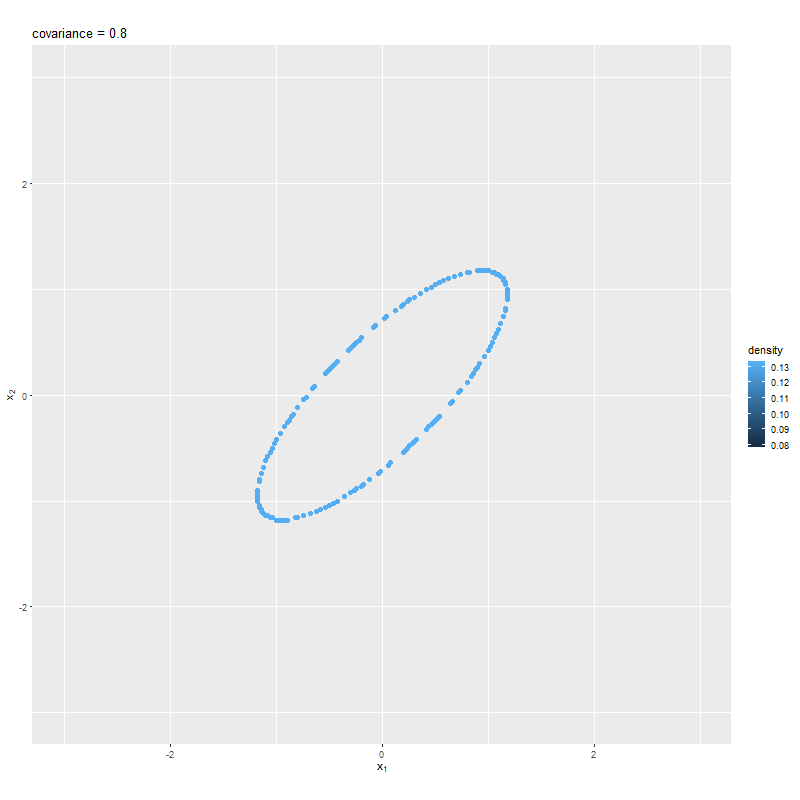
綺麗な線にならない場合は、x_valsの間隔やthresholdの値を調整するか、geom_point()のsizeやshapeで調整する。
完成例
最後に、それっぽいアニメーションを作成する。
等高線を引く値を表示する用の文字列を作成する。
# 等高線の値のラベルを作成 anime_label_df <- anime_ellipse_df |> dplyr::distinct(sigma_12, max_dens) |> # 各共分散と確率密度の最大値を抽出 dplyr::mutate( dens_label = paste0( "max density : ", round(max_dens, digits = 5), "\n", "drawn density : ", round(max_dens * rate, digits = 5) ) ) # ラベルを作成 anime_label_df
## # A tibble: 17 × 3 ## sigma_12 max_dens dens_label ## <dbl> <dbl> <chr> ## 1 -0.8 0.265 "max density : 0.26526\ndrawn density : 0.13263" ## 2 -0.7 0.223 "max density : 0.22286\ndrawn density : 0.11143" ## 3 -0.6 0.199 "max density : 0.19894\ndrawn density : 0.09947" ## 4 -0.5 0.184 "max density : 0.18378\ndrawn density : 0.09189" ## 5 -0.4 0.174 "max density : 0.17365\ndrawn density : 0.08683" ## 6 -0.3 0.167 "max density : 0.16684\ndrawn density : 0.08342" ## 7 -0.2 0.162 "max density : 0.16244\ndrawn density : 0.08122" ## 8 -0.1 0.160 "max density : 0.15996\ndrawn density : 0.07998" ## 9 0 0.159 "max density : 0.15915\ndrawn density : 0.07958" ## 10 0.1 0.160 "max density : 0.15996\ndrawn density : 0.07998" ## 11 0.2 0.162 "max density : 0.16244\ndrawn density : 0.08122" ## 12 0.3 0.167 "max density : 0.16684\ndrawn density : 0.08342" ## 13 0.4 0.174 "max density : 0.17365\ndrawn density : 0.08683" ## 14 0.5 0.184 "max density : 0.18378\ndrawn density : 0.09189" ## 15 0.6 0.199 "max density : 0.19894\ndrawn density : 0.09947" ## 16 0.7 0.223 "max density : 0.22286\ndrawn density : 0.11143" ## 17 0.8 0.265 "max density : 0.26526\ndrawn density : 0.13263"
anime_ellipse_dfは全ての点の情報(x_matに対応する行)を持つので、distinct()で重複を削除して、sigma_12_valsの値ごとに確率密度の最大値(max_dens列)と等高線を引く値(max_dens * rate)を文字列結合する。
分布全体の塗りつぶし等高線図に、指定した倍率の等高線を重ねて描画する。
# 2次元ガウス分布の等高線図のアニメーションを作成 anime_graph <- ggplot() + geom_contour_filled(data = anime_dens_df, mapping = aes(x = x1, y = x2, z = dens, fill = ..level..), alpha = 0.8) + # 塗りつぶし等高線 geom_contour(data = anime_ellipse_df, mapping = aes(x = x1, y = x2, z = dens, color = ..level..), bins = 2, color = "red", size = 1, linetype = "dashed") + # 等高線 geom_label(data = anime_label_df, mapping = aes(x = min(x_vals), y = max(x_vals), label = dens_label), hjust = "inward", vjust = "inward", color = "red") + # 等高線ラベル gganimate::transition_manual(sigma_12) + # フレーム coord_fixed(ratio = 1) + # アスペクト比 labs(title = "Bivariate Normal Distribution", subtitle = "covariance = {current_frame}", fill = "density", x = expression(x[1]), y = expression(x[2])) # gif画像を作成 gganimate::animate( plot = anime_graph, nframes = length(sigma_12_vals), fps = 10, width = 800, height = 800 )

山の半分の高さっぽいところで線を引けているのが分かる。
以上で、私が欲しかった図が得られた。
おわりに
無駄の多い処理なので恥ずかしいのですが、このブログで度々登場するのでまとめておきます。同じことをしたい誰かの役に立てば嬉しいし、まともなやり方を教えてもらえればありがたいです。ぜひぜひ教えてください、お願いします。
他にもいくつか怪しい処理をしたことがあるので、それも記事にして誰かに修正してもらいたい。そんなシリーズの1つ目の記事です(続きたくない)。
2022年9月14日は、モーニング娘。の結成25周年記念日です!!!!!
25年って凄すぎですね。私がハマったのは2017年の7月末でした。楽しい日々をありがとうございます。これからもよろしくお願いします。