はじめに
機械学習で登場する確率分布について色々な角度から理解したいシリーズです。
この記事では、R言語で2次元ガウス分布(二変量正規分布)のグラフを作成します。
【前の内容】
【他の記事一覧】
【この記事の内容】
2次元ガウス分布の作図
2次元ガウス分布(Two-dimensional Gaussian Distribution)・二変量正規分布(Bivariate Normal Distribution)のグラフを作成します。ガウス分布については「多次元ガウス分布の定義式 - からっぽのしょこ」を参照してください。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(mvnfast) library(gganimate)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているため、ggplot2は読み込む必要があります。
magrittrパッケージのパイプ演算子%>%ではなく、ベースパイプ(ネイティブパイプ)演算子|>を使っています。%>%に置き換えても処理できます。
分布の変化をアニメーション(gif画像)で確認するのにgganimateパッケージを利用します。不要であれば省略してください。
定義式の確認
まずは、多次元ガウス分布の定義式を確認します。
ガウス分布は、次の式で定義されます。
ここで、$\boldsymbol{\mu}$は平均ベクトル、$\boldsymbol{\Sigma}$は分散共分散行列、$\pi$は円周率です。また、$\mathbf{A}^{\top}$は転置行列、$\mathbf{A}^{-1}$は逆行列、$|\mathbf{A}|$は行列式、ネイピア数$e$による指数関数$e^x = \exp(x)$、平方根$\sqrt{a} = a^{\frac{1}{2}}$です。
$\mathbf{x}, \boldsymbol{\mu}$は$D$次元ベクトル、$\boldsymbol{\Sigma}$は$D \times D$の行列です。
$\sigma_d$は$x_d$の標準偏差、$\sigma_d^2 = \sigma_{d,d}$は$x_d$の分散、$\sigma_{i,j} = \sigma_{j,i}$は$x_i, x_j$の共分散です。
$x_d$は実数をとり、$\mu_d$は実数、$\sigma, \sigma_d^2$は正の実数、$\sigma_{i,j}\ (i \neq j)$は実数、また$\boldsymbol{\Sigma}$は正定値行列を満たす必要があります。
グラフの作成
ggplot2パッケージを利用して、ガウス分布のグラフを作成します。ガウス分布の確率密度の計算については「【R】多次元ガウス分布の計算 - からっぽのしょこ」を参照してください。
ガウス分布のパラメータ$\boldsymbol{\mu}, \boldsymbol{\Sigma}$を設定します。この例では、2次元のグラフで描画するため、次元数を$D = 2$とします。
# 平均ベクトルを指定 mu_d <- c(6, 10) # 分散共分散行列を指定 sigma_dd <- diag(2) # 単位行列 sigma_dd <- c(1, 0.6, 0.6, 4) |> # 値を指定 matrix(nrow = 2, ncol = 2) # マトリクスに変換
平均ベクトル$\boldsymbol{\mu} = (\mu_1, \mu_2)$、分散共分散行列$\boldsymbol{\Sigma} = (\sigma_1^2, \sigma_{2,1}, \sigma_{1,2}, \sigma_2^2)$を指定します。
平均$\mu_d$は実数、分散$\sigma_d^2$は正の実数、共分散$\sigma_{i,j} = \sigma_{j,i}$は実数、また$\boldsymbol{\Sigma}$は正定値行列を満たす必要があります。
設定したパラメータに応じて、ガウス分布の確率変数がとり得る値$\mathbf{x}$の成分$x_1, x_2$の値を作成します。
# xの値を作成 x_1_vals <- seq( from = mu_d[1] - sqrt(sigma_dd[1, 1]) * 3, to = mu_d[1] + sqrt(sigma_dd[1, 1]) * 3, length.out = 101 ) x_2_vals <- seq( from = mu_d[2] - sqrt(sigma_dd[2, 2]) * 3, to = mu_d[2] + sqrt(sigma_dd[2, 2]) * 3, length.out = 101 ) head(x_1_vals); head(x_2_vals)
## [1] 3.00 3.06 3.12 3.18 3.24 3.30 ## [1] 4.00 4.12 4.24 4.36 4.48 4.60
$x_1$(x軸)の値をx_1_vals、$x_2$(y軸)の値をx_2_valsとします。この例では、それぞれ平均を中心に標準偏差の3倍を範囲とします。
$\mathbf{x}$を作成します。
# xの点を作成 x_mat <- tidyr::expand_grid( x_1 = x_1_vals, x_2 = x_2_vals ) |> # 格子点を作成 as.matrix() # マトリクスに変換 head(x_mat)
## x_1 x_2 ## [1,] 3 4.00 ## [2,] 3 4.12 ## [3,] 3 4.24 ## [4,] 3 4.36 ## [5,] 3 4.48 ## [6,] 3 4.60
x_1_valsとx_2_valsの要素の全ての組み合わせ(格子状の点)をexpand_grid()で作成します。データフレームが出力されるので、as.matrix()でマトリクスに変換してx_matとします。x_matの各行が点$\mathbf{x} = (x_1, x_2)$に対応します。
$\mathbf{x}$の点ごとの確率密度を計算します。
# 多次元ガウス分布を計算 dens_df <- tibble::tibble( x_1 = x_mat[, 1], # x軸の値 x_2 = x_mat[, 2], # y軸の値 density = mvnfast::dmvn(X = x_mat, mu = mu_d, sigma = sigma_dd) # 確率密度 ) dens_df
## # A tibble: 10,201 × 3 ## x_1 x_2 density ## <dbl> <dbl> <dbl> ## 1 3 4 0.0000822 ## 2 3 4.12 0.0000942 ## 3 3 4.24 0.000108 ## 4 3 4.36 0.000122 ## 5 3 4.48 0.000138 ## 6 3 4.6 0.000156 ## 7 3 4.72 0.000176 ## 8 3 4.84 0.000197 ## 9 3 4.96 0.000219 ## 10 3 5.08 0.000243 ## # … with 10,191 more rows
多次元ガウス分布の確率密度は、mvnfastパッケージのdmvn()で計算できます。確率変数の引数Xにx_mat、平均の引数muにmu_d、共分散の引数sigmaにsigma_ddを指定します。
パラメータの値を数式で表示するための文字列を作成します。
# パラメータラベルを作成:(数式表示用) formula_text <- paste0( "list(", "mu==group('(', list(", paste0(mu_d, collapse = ", "), "), ')')", ", Sigma==group('(', list(", paste0(sigma_dd, collapse = ", "), "), ')')", ")" ) formula_text
## [1] "list(mu==group('(', list(6, 10), ')'), Sigma==group('(', list(1, 0.6, 0.6, 4), ')'))"
ギリシャ文字などの記号を使った数式を表示する場合は、expression()の記法を使います。等号は"=="、複数の(数式上の)変数を並べるには"list(変数1, 変数2)"とします。(プログラム上の)変数の値を使う場合は、parse()のtext引数に指定します。
ガウス分布の等高線図を作成します。
# 2次元ガウス分布のグラフを作成:等高線図 ggplot() + geom_contour(data = dens_df, mapping = aes(x = x_1, y = x_2, z = density, color = ..level..)) + # 等高線 #geom_contour_filled(data = dens_df, mapping = aes(x = x_1, y = x_2, z = density, fill = ..level..), alpha = 0.8) + # 塗りつぶし等高線 labs( title ="Maltivariate Gaussian Distribution", subtitle = paste0("mu=(", paste0(mu_d, collapse = ', '), "), Sigma=(", paste0(sigma_dd, collapse = ', '), ")"), # (文字列表記用) #subtitle = parse(text = formula_text), # (数式表示用) color = "density", # (等高線用) fill = "density", # (塗りつぶし等高線用) x = expression(x[1]), y = expression(x[2]) )

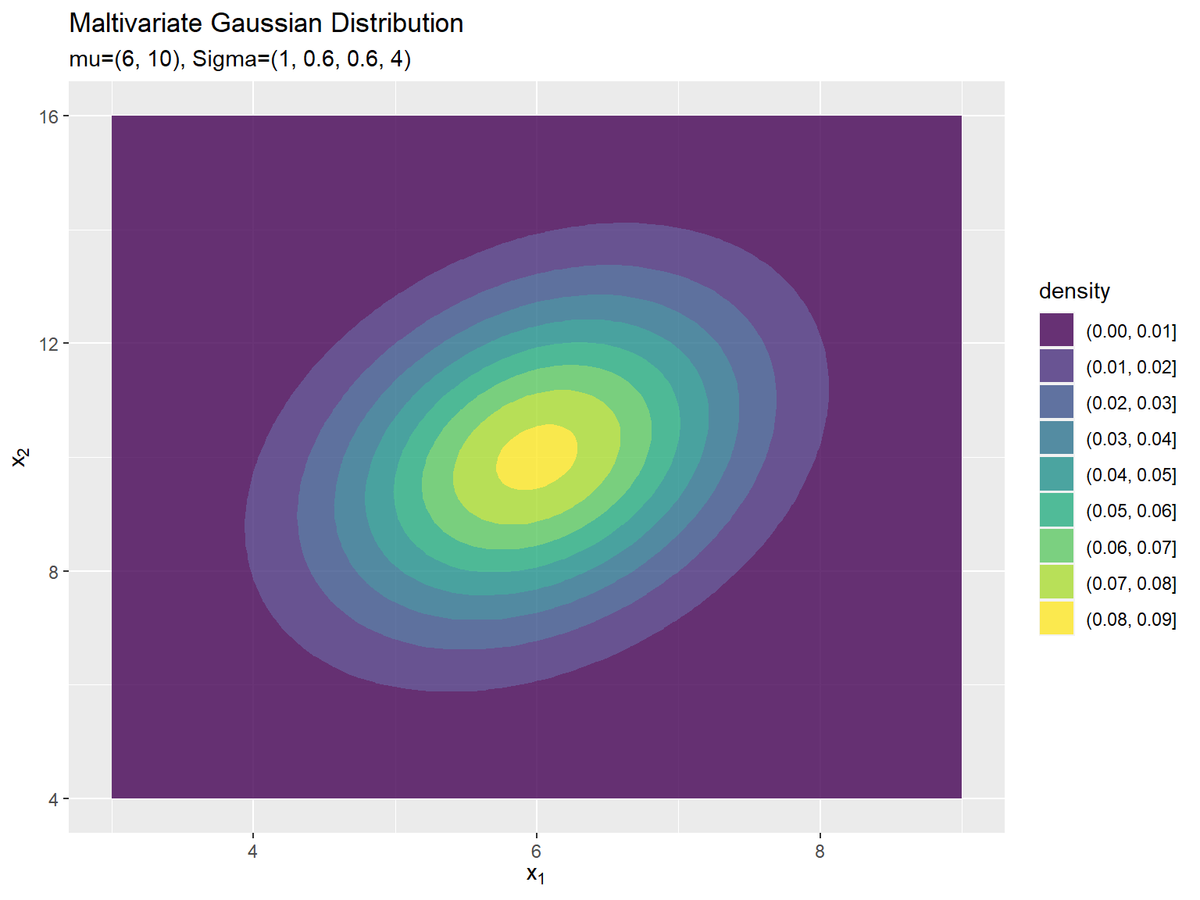
等高線はgeom_contour()、塗りつぶし等高線はgeom_contour_filled()で描画できます。z軸の値の引数zにdensityを指定して、等高線の色の引数colorまたは塗りつぶしの色の引数fillに..level..を指定すると、確率密度に応じてグラデーションが付けられます。
確率密度の変化を細かく見るには、ヒートマップで可視化します。
# 2次元ガウス分布のグラフを作成:ヒートマップ ggplot() + geom_tile(data = dens_df, mapping = aes(x = x_1, y = x_2, fill = density, color = density), alpha = 0.8) + # ヒートマップ scale_color_viridis_c(option = "D") + # タイルの色 scale_fill_viridis_c(option = "D") + # 枠線の色 #scale_fill_gradientn(colors = c("blue", "green", "yellow", "red")) + # タイルの色 #scale_color_gradientn(colors = c("blue", "green", "yellow", "red")) + # 枠線の色 labs( title ="Maltivariate Gaussian Distribution", #subtitle = paste0("mu=(", paste0(mu_d, collapse = ', '), "), Sigma=(", paste0(sigma_dd, collapse = ', '), ")"), # (文字列表記用) subtitle = parse(text = formula_text), # (数式表記用) fill = "density", color = "density", x = expression(x[1]), y = expression(x[2]) )


ヒートマップはgeom_tile()で描画できます。
グラデーションはscale_***_viridis_c()やscale_***_gradientn()で設定できます。
ガウス分布のグラフを描画できました。以降は、ここまでの作図処理を用いて、パラメータの影響を確認していきます。
軸の可視化
分散共分散行列の固有値と固有ベクトルを用いて、ガウス分布の断面図の軸を作図します。詳しくは「2.3.0:分散共分散行列と固有値・固有ベクトルの関係の導出【PRMLのノート】 - からっぽのしょこ」を参照してください。
分散共分散行列の固有値と固有ベクトルを計算します。
# 固有値と固有ベクトルを計算 res_eigen <- eigen(sigma_dd) # 固有値を取得 lambda_d <- res_eigen[["values"]] # 固有ベクトルを取得 u_dd <- res_eigen[["vectors"]] |> t() lambda_d; u_dd
## [1] 4.1155494 0.8844506 ## [,1] [,2] ## [1,] 0.1891075 0.9819564 ## [2,] -0.9819564 0.1891075
固有値$\lambda_1, \lambda_2$と固有ベクトル$\mathbf{u}_1 = (u_{1,1}, u_{1,2}), \mathbf{u}_2 = (u_{2,1}, u_{2,2})$をeigen()で計算します。リストが出力されるので、"values"で固有値(をまとめたベクトル)、"vectors"で固有ベクトル(をまとめたマトリクス)を取り出します。数式での成分と合わせるために転置しておきます。
軸の前に、固有ベクトルをグラフで確認するために、固有ベクトルをデータフレームに格納します。
# 固有ベクトル eigen_df <- tibble::tibble( xstart = 0, ystart = 0, xend = u_dd[, 1], yend = u_dd[, 2] ) eigen_df
## # A tibble: 2 × 4 ## xstart ystart xend yend ## <dbl> <dbl> <dbl> <dbl> ## 1 0 0 0.189 0.982 ## 2 0 0 -0.982 0.189
作図時の引数に対応するように列を作成します。
固有ベクトルのグラフを作成します。
# 固有ベクトル(軸の方向)のグラフを作成 ggplot() + geom_segment(data = eigen_df, mapping = aes(x = xstart, y = ystart, xend = xend, yend = yend), size = 1, arrow = arrow()) + # 軸の方向 coord_fixed(ratio = 1) + # アスペクト比 labs(title = "Eigenvector", subtitle = parse(text = paste0("U==(list(", paste0(round(u_dd, 2), collapse = ", "), "))")), x = expression(x[1]), y = expression(x[2]))

線分はgeom_segment()で描画できます。x引数に始点のx軸の値、y引数に始点のy軸の値、xend引数に終点のx軸の値、yend引数に終点のy軸の値を指定します。arrow引数にarrow()を指定すると矢印になります。
固有ベクトルが直交ベクトルである(線分が直角に交わる)のを確認するには、アスペクト比を1にします。アスペクト比はcoord_fixed()で指定できます。
同様に、軸の始点と終点を計算して、作図用のデータフレームを作成します。
# 断面図の軸を計算 axis_df <- tibble::tibble( xstart = mu_d[1] - u_dd[, 1] * sqrt(lambda_d), ystart = mu_d[2] - u_dd[, 2] * sqrt(lambda_d), xend = mu_d[1] + u_dd[, 1] * sqrt(lambda_d), yend = mu_d[2] + u_dd[, 2] * sqrt(lambda_d) ) axis_df
## # A tibble: 2 × 4 ## xstart ystart xend yend ## <dbl> <dbl> <dbl> <dbl> ## 1 5.62 8.01 6.38 12.0 ## 2 6.92 9.82 5.08 10.2
先ほどは、原点から伸びる長さが1のベクトル(線分)を描画しました。今度は、平均値の点で交差する長さが$\sqrt{\lambda_d}$のベクトル(線分)を描画します。
軸番号を$i$、次元を$j$として、始点は$\mu_i - u_{j,i} \sqrt{\lambda_j}$、終点は$\mu_i + u_{j,i} \sqrt{\lambda_j}$で計算できます。
固有値と固有ベクトルの値を数式で表示するための文字列を作成します。
# 固有値・固有ベクトルラベルを作成:(数式表示用) eigen_text <- paste0( "list(", "lambda==group('(', list(", paste0(round(lambda_d, 2), collapse = ", "), "), ')')", ", U==group('(', list(", paste0(round(u_dd, 2), collapse = ", "), "), ')')", ")" ) eigen_text
## [1] "list(lambda==group('(', list(4.12, 0.88), ')'), U==group('(', list(0.19, -0.98, 0.98, 0.19), ')'))"
パラメータラベルと同様に指定します。
分布の断面の作図用に、確率密度の最大値を計算します。
# 確率密度の最大値を計算 max_dens <- mvnfast::dmvn(X = mu_d, mu = mu_d, sigma = sigma_dd) max_dens
## [1] 0.08341986
$\mathbf{x} = \boldsymbol{\mu}$のとき学率密度が最大になります。
ガウス分布の等高線に軸を重ねたグラフを作成します。
# 固有ベクトルを重ねた2次元ガウス分布のグラフを作成 ggplot() + geom_contour(data = dens_df, mapping = aes(x = x_1, y = x_2, z = density, color = ..level..)) + # ヒートマップ #geom_contour_filled(data = dens_df, mapping = aes(x = x_1, y = x_2, z = density, fill = ..level..), # alpha = 0.8) + # 塗りつぶし等高線 geom_contour(data = dens_df, mapping = aes(x = x_1, y = x_2, z = density), breaks = max_dens*exp(-0.5), color = "red", size = 1, linetype = "dashed") + # 分布の断面図 geom_segment(data = axis_df, mapping = aes(x = mu_d[1], y = mu_d[2], xend = xend, yend = yend), color = "blue", size = 1, arrow = arrow(length = unit(10, "pt"))) + # 断面図の軸:サイズが固有値の固有ベクトル #geom_segment(data = axis_df, mapping = aes(x = xstart, y = ystart, xend = xend, yend = yend), # color = "blue", size = 1, arrow = arrow(length = unit(10, "pt"))) + # 断面図の軸:サイズが固有値の倍の固有ベクトル geom_label(mapping = aes(x = mu_d[1], y = mu_d[2]+sqrt(sigma_dd[2, 2])*2, label = eigen_text), parse = TRUE, hjust = 0.5, vjust = 0) + # 固有値・固有ベクトルラベル:(等高線用) #geom_label(mapping = aes(x = min(x_1_vals), y = max(x_2_vals), label = eigen_text), # parse = TRUE, hjust = 0, vjust = 0) + # 固有値・固有ベクトルラベル:(塗りつぶし等高線用) coord_fixed(ratio = 1) + # アスペクト比 labs(title ="Maltivariate Gaussian Distribution", subtitle = parse(text = formula_text), color = "density", fill = "density", x = expression(x[1]), y = expression(x[2]))
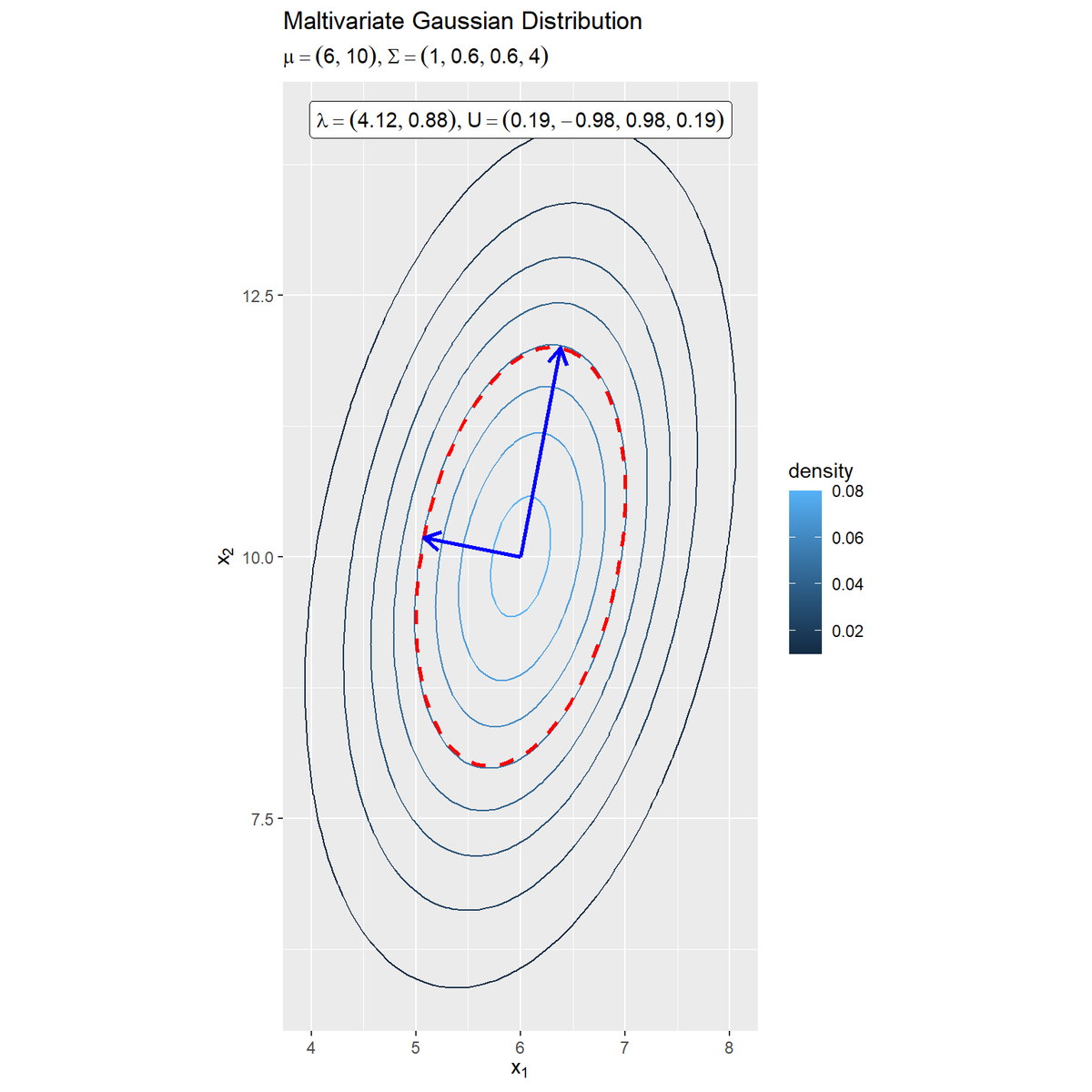
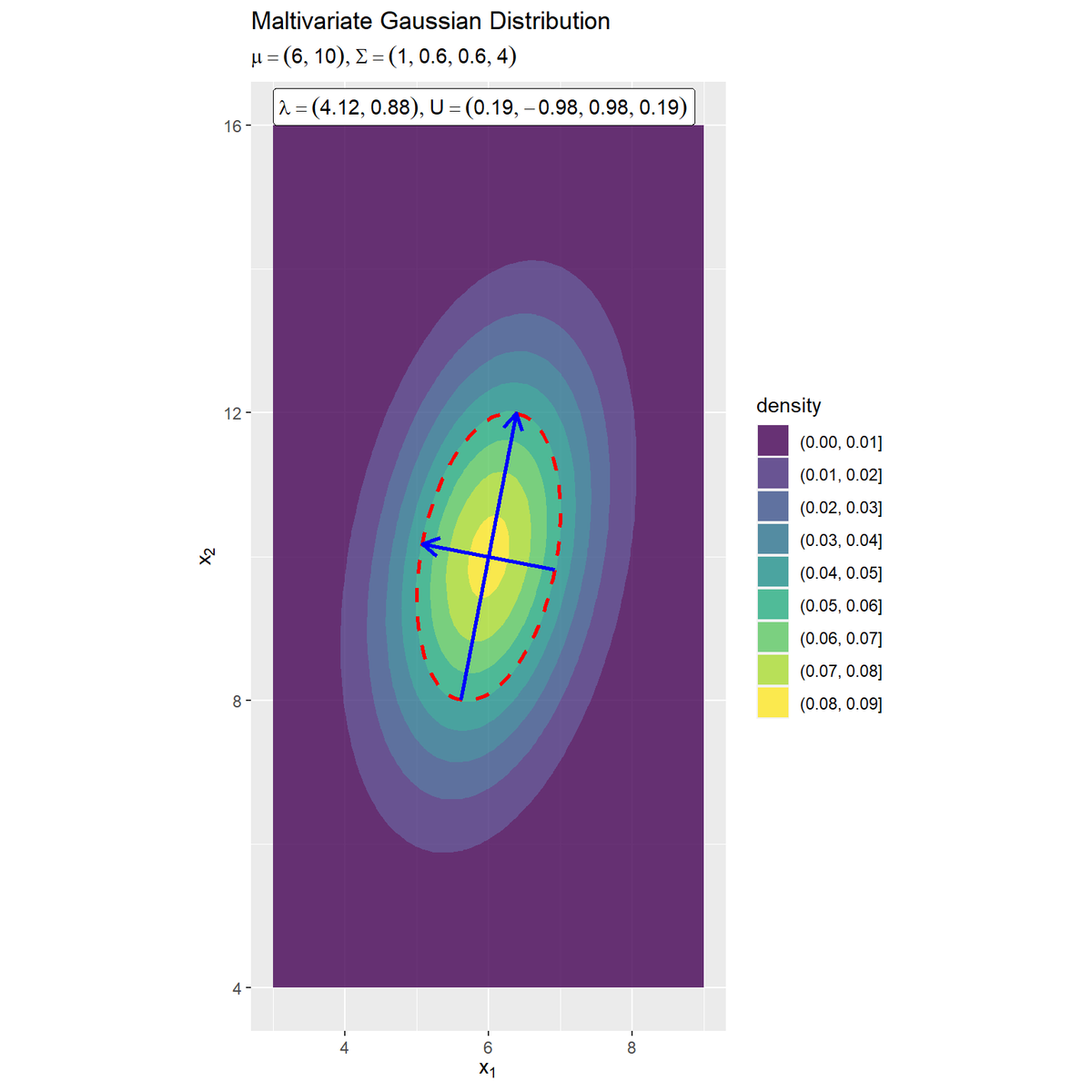
geom_contour()のbreaks引数に値を指定すると、その値で等高線を引きます。この例では、確率密度の最大値の$\exp(-\frac{1}{2})$倍を指定します。z軸(確率密度)がこの値の面で切断すると断面図(等高線)が軸の先端になります。
geom_segment()で断面図の軸を描画します。軸の始点x, y引数に平均値mu_dを指定すると、平均値から伸びる長さ$\sqrt{\lambda_d}$の固有ベクトル、axis_dfのxstart, ystart列を指定すると断面図全体を通る軸を描画します。
パラメータと分布の形状の関係
次は、パラメータの値を少しずつ変化させて、分布の形状の変化をアニメーションで確認します。
平均(1軸)の影響
まずは、x軸方向の平均$\mu_1$の値を変化させ、$\mu_2, \boldsymbol{\Sigma}$を固定します。
・作図コード(クリックで展開)
# x軸の平均として利用する値を指定 mu_1_vals <- seq(from = -2, to = 2, by = 0.04) |> round(digits = 2) # y軸の平均を指定 mu_2 <- 10 # 分散共分散行列を指定 sigma_dd <- matrix(c(1, 0.6, 0.6, 4), nrow = 2, ncol = 2) # フレーム数を設定 frame_num <- length(mu_1_vals) frame_num
## [1] 101
値の間隔が一定になるように$\mu_1$の値をmu_1_valsとして作成します。パラメータごとにフレームを切り替えるので、mu_1_valsの要素数がアニメーションのフレーム数になります。
また、y軸方向の平均$\mu_2$をmu_2として値を指定します。
設定したパラメータに応じて、確率変数の値$\mathbf{x}$の成分$x_1, x_2$の値を作成して、パラメータごとに確率密度を計算します。
# xの値を作成 x_1_vals <- seq( from = min(mu_1_vals) - sqrt(sigma_dd[1, 1]) * 2, to = max(mu_1_vals) + sqrt(sigma_dd[1, 1]) * 2, length.out = 101 ) x_2_vals <- seq( from = mu_2 - sqrt(sigma_dd[2, 2]) * 3, to = mu_2 + sqrt(sigma_dd[2, 2]) * 3, length.out = 101 ) # パラメータごとに多次元ガウス分布を計算 anime_dens_df <- tidyr::expand_grid( mu_1 = mu_1_vals, # パラメータ x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(mu_1) |> # 分布の計算用にグループ化 dplyr::mutate( density = mvnfast::dmvn( X = as.matrix(cbind(x_1, x_2)), mu = unique(cbind(mu_1, mu_2)), sigma = sigma_dd ), # 確率密度 parameter = paste0("mu=(", mu_1, ", ", mu_2, "), Sigma=(", paste0(sigma_dd, collapse = ", "), ")") |> factor(levels = paste0("mu=(", mu_1_vals, ", ", mu_2, "), Sigma=(", paste0(sigma_dd, collapse = ", "), ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_dens_df
## # A tibble: 1,030,301 × 5 ## mu_1 x_1 x_2 density parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 -2 -4 4 0.000477 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4) ## 2 -2 -4 4.12 0.000557 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4) ## 3 -2 -4 4.24 0.000649 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4) ## 4 -2 -4 4.36 0.000753 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4) ## 5 -2 -4 4.48 0.000870 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4) ## 6 -2 -4 4.6 0.00100 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4) ## 7 -2 -4 4.72 0.00115 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4) ## 8 -2 -4 4.84 0.00131 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4) ## 9 -2 -4 4.96 0.00149 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4) ## 10 -2 -4 5.08 0.00169 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4) ## # … with 1,030,291 more rows
パラメータmu_1_valsと確率変数x_1_vals, x_2_valsの要素の全ての組み合わせをexpand_grid()を作成します。これにより、パラメータごとにx_matを複製できます。
パラメータ列mu_1でグループ化することで、x_matごとに確率密度を計算できます。
パラメータごとにフレーム切替用のラベルを作成します。文字列型だと文字列の基準で順序が決まるので、因子型にしてパラメータに応じたレベル(順序)を設定します。
等高線図のアニメーション(gif画像)を作成します。
# 2次元ガウス分布のアニメーションを作図 anime_dens_graph <- ggplot() + #geom_contour(data = anime_dens_df, mapping = aes(x = x_1, y = x_2, z = density, color = ..level..)) + # 等高線 geom_contour_filled(data = anime_dens_df, mapping = aes(x = x_1, y = x_2, z = density, fill = ..level..), alpha = 0.8) + # 塗りつぶし等高線 gganimate::transition_manual(parameter) + # フレーム labs(title ="Maltivariate Gaussian Distribution", subtitle = "{current_frame}", color = "density", fill = "density", x = expression(x[1]), y = expression(x[2])) # gif画像を作成 gganimate::animate(anime_dens_graph, nframes = frame_num, fps = 10, width = 800, height = 600)
transition_manual()にフレームの順序を表す列を指定します。この例では、因子型のラベルのレベルの順に描画されます。
animate()のフレーム数の引数nframesにパラメータ数、フレームレートの引数fpsに1秒当たりのフレーム数を指定します。fps引数の値が大きいほどフレームが早く切り替わります。ただし、値が大きいと意図通りに動作しません。
同様に、ヒートマップのアニメーションを作成します。
# 2次元ガウス分布のアニメーションを作図 anime_dens_graph <- ggplot() + geom_tile(data = anime_dens_df, mapping = aes(x = x_1, y = x_2, fill = density), alpha = 0.8) + # ヒートマップ gganimate::transition_manual(parameter) + # フレーム scale_fill_viridis_c(option = "D") + # 等高線の色 labs(title ="Maltivariate Gaussian Distribution", subtitle = "{current_frame}", fill = "density", x = expression(x[1]), y = expression(x[2])) # gif画像を作成 gganimate::animate(anime_dens_graph, nframes = frame_num, fps = 10, width = 800, height = 600)


$\mu_1$の値に応じて、x軸方向に移動するのが分かります。
平均(2軸)の影響
続いて、y軸方向の平均$\mu_2$の値を変化させ、$\mu_1, \boldsymbol{\Sigma}$を固定します。
・作図コード(クリックで展開)
# x軸の平均を指定 mu_1 <- 6 # y軸の平均として利用する値を指定 mu_2_vals <- seq(from = -2, to = 2, by = 0.04) |> round(digits = 2) # 分散共分散行列を指定 sigma_dd <- matrix(c(1, 0.6, 0.6, 4), nrow = 2, ncol = 2) # フレーム数を設定 frame_num <- length(mu_2_vals) frame_num
## [1] 101
値の間隔が一定になるように$\mu_2$の値をmu_2_valsとして作成し、x軸方向の平均$\mu_1$をmu_1として値を指定します。
パラメータごとに分布を計算します。
# xの値を作成 x_1_vals <- seq( from = mu_1 - sqrt(sigma_dd[1, 1]) * 3, to = mu_1 + sqrt(sigma_dd[1, 1]) * 3, length.out = 101 ) x_2_vals <- seq( from = min(mu_2_vals) - sqrt(sigma_dd[2, 2]) * 2, to = max(mu_2_vals) + sqrt(sigma_dd[2, 2]) * 2, length.out = 101 ) # パラメータごとに多次元ガウス分布を計算 anime_dens_df <- tidyr::expand_grid( mu_2 = mu_2_vals, # パラメータ x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(mu_2) |> # 分布の計算用にグループ化 dplyr::mutate( density = mvnfast::dmvn( X = as.matrix(cbind(x_1, x_2)), mu = unique(cbind(mu_1, mu_2)), sigma = sigma_dd ), # 確率密度 parameter = paste0("mu=(", mu_1, ", ", mu_2, "), Sigma=(", paste0(sigma_dd, collapse = ", "), ")") |> factor(levels = paste0("mu=(", mu_1, ", ", mu_2_vals, "), Sigma=(", paste0(sigma_dd, collapse = ", "), ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_dens_df
## # A tibble: 1,030,301 × 5 ## mu_2 x_1 x_2 density parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 -2 3 -6 0.000477 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4) ## 2 -2 3 -5.88 0.000512 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4) ## 3 -2 3 -5.76 0.000547 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4) ## 4 -2 3 -5.64 0.000582 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4) ## 5 -2 3 -5.52 0.000617 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4) ## 6 -2 3 -5.4 0.000652 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4) ## 7 -2 3 -5.28 0.000686 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4) ## 8 -2 3 -5.16 0.000719 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4) ## 9 -2 3 -5.04 0.000750 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4) ## 10 -2 3 -4.92 0.000780 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4) ## # … with 1,030,291 more rows
「平均(1軸)の影響」のmu_1, mu_1_valsとmu_2, mu_2_valsを入れ換えるように処理します。
「平均(1軸)の影響」のコードで作図できます。


$\mu_2$の値に応じて、y軸方向に移動するのが分かります。
平均(1,2軸)の影響
$\boldsymbol{\mu}$の値を変化させ、$\boldsymbol{\Sigma}$を固定します。
・作図コード(クリックで展開)
# 平均ベクトルとして利用する値を指定 mu_1_vals <- seq(from = -3, to = 1, by = 0.04) |> round(digits = 2) mu_2_vals <- seq(from = -4, to = 4, by = 0.08) |> round(digits = 2) # 分散共分散行列を指定 sigma_dd <- matrix(c(1, 0.6, 0.6, 4), nrow = 2, ncol = 2) # フレーム数を設定 frame_num <- length(mu_1_vals) frame_num
## [1] 101
mu_1_valsとmu_2_valsの要素数が同じになるように作成します。
パラメータごとに分布を計算します。
# xの値を作成 x_1_vals <- seq( from = min(mu_1_vals) - sqrt(sigma_dd[1, 1]) * 2, to = max(mu_1_vals) + sqrt(sigma_dd[1, 1]) * 2, length.out = 101 ) x_2_vals <- seq( from = min(mu_2_vals) - sqrt(sigma_dd[2, 2]) * 2, to = max(mu_2_vals) + sqrt(sigma_dd[2, 2]) * 2, length.out = 101 ) # パラメータごとに多次元ガウス分布を計算 anime_dens_df <- tidyr::expand_grid( idx = seq_along(mu_1_vals), # パラメータ番号 x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(idx) |> # 分布の計算用にグループ化 dplyr::mutate( mu_1 = mu_1_vals[idx], mu_2 = mu_2_vals[idx], density = mvnfast::dmvn( X = as.matrix(cbind(x_1, x_2)), mu = unique(cbind(mu_1, mu_2)), sigma = sigma_dd ), # 確率密度 parameter = paste0("mu=(", mu_1, ", ", mu_2, "), Sigma=(", paste0(sigma_dd, collapse = ", "), ")") |> factor(levels = paste0("mu=(", mu_1_vals, ", ", mu_2_vals, "), Sigma=(", paste0(sigma_dd, collapse = ", "), ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_dens_df
## # A tibble: 1,030,301 × 7 ## idx x_1 x_2 mu_1 mu_2 density parameter ## <int> <dbl> <dbl> <dbl> <dbl> <dbl> <fct> ## 1 1 -5 -8 -3 -4 0.00385 mu=(-3, -4), Sigma=(1, 0.6, 0.6, 4) ## 2 1 -5 -7.84 -3 -4 0.00433 mu=(-3, -4), Sigma=(1, 0.6, 0.6, 4) ## 3 1 -5 -7.68 -3 -4 0.00485 mu=(-3, -4), Sigma=(1, 0.6, 0.6, 4) ## 4 1 -5 -7.52 -3 -4 0.00539 mu=(-3, -4), Sigma=(1, 0.6, 0.6, 4) ## 5 1 -5 -7.36 -3 -4 0.00595 mu=(-3, -4), Sigma=(1, 0.6, 0.6, 4) ## 6 1 -5 -7.2 -3 -4 0.00652 mu=(-3, -4), Sigma=(1, 0.6, 0.6, 4) ## 7 1 -5 -7.04 -3 -4 0.00709 mu=(-3, -4), Sigma=(1, 0.6, 0.6, 4) ## 8 1 -5 -6.88 -3 -4 0.00766 mu=(-3, -4), Sigma=(1, 0.6, 0.6, 4) ## 9 1 -5 -6.72 -3 -4 0.00822 mu=(-3, -4), Sigma=(1, 0.6, 0.6, 4) ## 10 1 -5 -6.56 -3 -4 0.00876 mu=(-3, -4), Sigma=(1, 0.6, 0.6, 4) ## # … with 1,030,291 more rows
パラメータ番号として1からパラメータの要素数までの整数をseq_along()で作成し、確率変数x_1_vals, x_2_valsの要素との全ての組み合わせをexpand_grid()を作成します。これにより、パラメータごとにx_matを複製できます。
パラメータ列idxでグループ化し、またidx列の値を使ってmu_1_vals, mu_2_valsから値を取り出して、x_matごとに確率密度を計算します。
「平均(1軸)の影響」のコードで作図できます。


$\boldsymbol{\mu}$の値に応じて、x軸とy軸の両方向に移動するのが分かります。
分散(1軸)の影響
$\sigma_1^2$の値を変化させ、$\boldsymbol{\mu}, \sigma_{1,2}, \sigma_{2,1}, \sigma_2^2$を固定します。
・作図コード(クリックで展開)
# 平均ベクトルを指定 mu_d <- c(6, 10) # x軸の分散として利用する値を指定 sigma2_1_vals <- seq(from = 0.5, to = 6, by = 0.1) |> round(digits = 2) # y軸の分散を指定 sigma2_2 <- 4 # 共分散を指定 sigma_12 <- 0.6 # フレーム数を設定 frame_num <- length(sigma2_1_vals) frame_num
## [1] 56
値の間隔が一定になるように$\sigma_1^2$の値をsigma2_1_valsとして作成し、共分散$\sigma_{1,2} = \sigma_{2,1}$をsigma_12、y軸方向の分散$\sigma_2^2$をsigma2_2として値を指定します。
パラメータごとに分布を計算します。
# x軸とy軸の値を作成 x_1_vals <- seq( from = mu_d[1] - sqrt(max(sigma2_1_vals)) * 2, to = mu_d[1] + sqrt(max(sigma2_1_vals)) * 2, length.out = 101 ) x_2_vals <- seq( from = mu_d[2] - sqrt(sigma2_2) * 3, to = mu_d[2] + sqrt(sigma2_2) * 3, length.out = 101 ) # パラメータごとに多次元ガウス分布を計算 anime_dens_df <- tidyr::expand_grid( sigma2_1 = sigma2_1_vals, # パラメータ x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(sigma2_1) |> # 分布の計算用にグループ化 dplyr::mutate( density = mvnfast::dmvn( X = as.matrix(cbind(x_1, x_2)), mu = mu_d, sigma = matrix(c(unique(sigma2_1), sigma_12, sigma_12, sigma2_2), nrow = 2, ncol = 2) ), # 確率密度 parameter = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2, ")") |> factor(levels = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1_vals, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_dens_df
## # A tibble: 571,256 × 5 ## sigma2_1 x_1 x_2 density parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 0.5 1.10 4 4.68e-12 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) ## 2 0.5 1.10 4.12 4.69e-12 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) ## 3 0.5 1.10 4.24 4.68e-12 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) ## 4 0.5 1.10 4.36 4.65e-12 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) ## 5 0.5 1.10 4.48 4.60e-12 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) ## 6 0.5 1.10 4.6 4.53e-12 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) ## 7 0.5 1.10 4.72 4.44e-12 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) ## 8 0.5 1.10 4.84 4.34e-12 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) ## 9 0.5 1.10 4.96 4.21e-12 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) ## 10 0.5 1.10 5.08 4.08e-12 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) ## # … with 571,246 more rows
「平均(1軸)の影響」のmu_1, mu_1_valsとsigma2_1, sigma2_1_valsを入れ換えるように処理します。
「平均(1軸)の影響」のコードで作図できます。


$\sigma_1^2$の値に応じて、x軸方向に広がり全体の確率密度が小さくなるが分かります。
分散(2軸)の影響
$\sigma_2^2$の値を変化させ、$\boldsymbol{\mu}, \sigma_1^2, \sigma_{1,2}, \sigma_{2,1}$を固定します。
・作図コード(クリックで展開)
# 平均ベクトルを指定 mu_d <- c(6, 10) # x軸の分散を指定 sigma2_1 <- 1 # y軸の分散として利用する値を指定 sigma2_2_vals <- seq(from = 0.5, to = 5, by = 0.1) |> round(digits = 2) # 共分散を指定 sigma_12 <- 0.6 # フレーム数を設定 frame_num <- length(sigma2_2_vals) frame_num
## [1] 46
値の間隔が一定になるように$\sigma_2^2$の値をsigma2_2_valsとして作成し、x軸方向の分散$\sigma_1^2$をsigma2_1、共分散$\sigma_{1,2} = \sigma_{2,1}$をsigma_12として値を指定します。
パラメータごとに分布を計算します。
# xの値を作成 x_1_vals <- seq( from = mu_d[1] - sqrt(sigma2_1) * 3, to = mu_d[1] + sqrt(sigma2_1) * 3, length.out = 101 ) x_2_vals <- seq( from = mu_d[2] - sqrt(max(sigma2_2_vals)) * 2, to = mu_d[2] + sqrt(max(sigma2_2_vals)) * 2, length.out = 101 ) # パラメータごとに多次元ガウス分布を計算 anime_dens_df <- tidyr::expand_grid( sigma2_2 = sigma2_2_vals, # パラメータ x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(sigma2_2) |> # 分布の計算用にグループ化 dplyr::mutate( density = mvnfast::dmvn( X = as.matrix(cbind(x_1, x_2)), mu = mu_d, sigma = matrix(c(sigma2_1, sigma_12, sigma_12, unique(sigma2_2)), nrow = 2, ncol = 2) ), # 確率密度 parameter = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2, ")") |> factor(levels = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2_vals, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_dens_df
## # A tibble: 469,246 × 5 ## sigma2_2 x_1 x_2 density parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 0.5 3 5.53 3.98e-14 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) ## 2 0.5 3 5.62 2.13e-13 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) ## 3 0.5 3 5.71 1.08e-12 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) ## 4 0.5 3 5.80 5.15e-12 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) ## 5 0.5 3 5.89 2.33e-11 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) ## 6 0.5 3 5.98 9.91e-11 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) ## 7 0.5 3 6.06 3.99e-10 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) ## 8 0.5 3 6.15 1.52e- 9 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) ## 9 0.5 3 6.24 5.45e- 9 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) ## 10 0.5 3 6.33 1.85e- 8 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) ## # … with 469,236 more rows
「平均(1軸)の影響」のmu_1, mu_1_valsとsigma2_2, sigma2_2_valsを入れ換えるように処理します。
「平均(1軸)の影響」のコードで作図できます。


$\sigma_2^2$の値に応じて、y軸方向に広がり全体の確率密度が小さくなるが分かります。
分散(1,2軸)の影響
$\sigma_2^2, \sigma_2^2$の値を変化させ、$\boldsymbol{\mu}, \sigma_{1,2}, \sigma_{2,1}$を固定します。
・作図コード(クリックで展開)
# 平均ベクトルを指定 mu_d <- c(6, 10) # 分散として利用する値を指定 sigma2_1_vals <- seq(from = 1, to = 4.5, by = 0.1) |> round(digits = 2) sigma2_2_vals <- seq(from = 1, to = 4.5, by = 0.1) |> round(digits = 2) # 共分散を指定 sigma_12 <- 0.6 # フレーム数を設定 frame_num <- length(sigma2_1_vals) frame_num
## [1] 36
sigma2_1_valsとsigma2_2_valsの要素数が同じになるように作成します。
パラメータごとに分布を計算します。
# xの値を作成 x_1_vals <- seq( from = mu_d[1] - sqrt(max(sigma2_1_vals)) * 2, to = mu_d[1] + sqrt(max(sigma2_1_vals)) * 2, length.out = 101 ) x_2_vals <- seq( from = mu_d[2] - sqrt(max(sigma2_2_vals)) * 2, to = mu_d[2] + sqrt(max(sigma2_2_vals)) * 2, length.out = 101 ) # パラメータごとに多次元ガウス分布を計算 anime_dens_df <- tidyr::expand_grid( idx = seq_along(sigma2_1_vals), # パラメータ番号 x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(idx) |> # 分布の計算用にグループ化 dplyr::mutate( sigma2_1 = sigma2_1_vals[idx], sigma2_2 = sigma2_2_vals[idx], density = mvnfast::dmvn( X = as.matrix(cbind(x_1, x_2)), mu = mu_d, sigma = matrix(c(unique(sigma2_1), sigma_12, sigma_12, unique(sigma2_2)), nrow = 2, ncol = 2) ), # 確率密度 parameter = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2, ")") |> factor(levels = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1_vals, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2_vals, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_dens_df
## # A tibble: 367,236 × 7 ## idx x_1 x_2 sigma2_1 sigma2_2 density parameter ## <int> <dbl> <dbl> <dbl> <dbl> <dbl> <fct> ## 1 1 1.76 5.76 1 1 0.00000259 mu=(6, 10), Sigma=(1, 0.6, 0.… ## 2 1 1.76 5.84 1 1 0.00000322 mu=(6, 10), Sigma=(1, 0.6, 0.… ## 3 1 1.76 5.93 1 1 0.00000397 mu=(6, 10), Sigma=(1, 0.6, 0.… ## 4 1 1.76 6.01 1 1 0.00000483 mu=(6, 10), Sigma=(1, 0.6, 0.… ## 5 1 1.76 6.10 1 1 0.00000582 mu=(6, 10), Sigma=(1, 0.6, 0.… ## 6 1 1.76 6.18 1 1 0.00000693 mu=(6, 10), Sigma=(1, 0.6, 0.… ## 7 1 1.76 6.27 1 1 0.00000815 mu=(6, 10), Sigma=(1, 0.6, 0.… ## 8 1 1.76 6.35 1 1 0.00000949 mu=(6, 10), Sigma=(1, 0.6, 0.… ## 9 1 1.76 6.44 1 1 0.0000109 mu=(6, 10), Sigma=(1, 0.6, 0.… ## 10 1 1.76 6.52 1 1 0.0000124 mu=(6, 10), Sigma=(1, 0.6, 0.… ## # … with 367,226 more rows
「平均(1,2軸)の影響」のmu_1_vals, mu_2_valsとsigma2_1_vals, sigma2_2_valsを入れ換えるように処理します。
「平均(1軸)の影響」のコードで作図できます。


$\sigma_1^2, \sigma_2^2$の値に応じて、x軸とy軸の両方向に広がり全体の確率密度が小さくなるが分かります。
共分散の影響
$\sigma_{1,2} = \sigma_{1,2}$の値を変化させ、$\boldsymbol{\mu}, \sigma_1^2, \sigma_2^2$を固定します。
・作図コード(クリックで展開)
# 平均ベクトルを指定 mu_d <- c(6, 10) # 分散を指定 sigma2_1 <- 1 sigma2_2 <- 1 # 共分散として利用する値を指定 sigma_12_vals <- seq(from = -0.8, to = 0.8, by = 0.02) |> round(digits = 2) # フレーム数を設定 frame_num <- length(sigma_12_vals) frame_num
## [1] 81
値の間隔が一定になるように$\sigma_{1,2} = \sigma_{2,1}$の値をsigma_12_valsとして作成し、分散$\sigma_1^2, \sigma_2^2$をsigma2_1, sigma2_2として値を指定します。
パラメータごとに分布を計算します。
# xの値を作成 x_1_vals <- seq( from = mu_d[1] - sqrt(sigma2_1) * 3, to = mu_d[1] + sqrt(sigma2_1) * 3, length.out = 101 ) x_2_vals <- seq( from = mu_d[2] - sqrt(sigma2_2) * 3, to = mu_d[2] + sqrt(sigma2_2) * 3, length.out = 101 ) # パラメータごとに多次元ガウス分布を計算 anime_dens_df <- tidyr::expand_grid( sigma_12 = sigma_12_vals, # パラメータ x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(sigma_12) |> # 分布の計算用にグループ化 dplyr::mutate( density = mvnfast::dmvn( X = as.matrix(cbind(x_1, x_2)), mu = mu_d, sigma = matrix(c(sigma2_1, unique(sigma_12), unique(sigma_12), sigma2_2), nrow = 2, ncol = 2) ), # 確率密度 parameter = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2, ")") |> factor(levels = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12_vals, ", ", sigma_12_vals, ", ", sigma2_2, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_dens_df
## # A tibble: 826,281 × 5 ## sigma_12 x_1 x_2 density parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 -0.8 3 7 7.59e-21 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) ## 2 -0.8 3 7.06 1.86e-20 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) ## 3 -0.8 3 7.12 4.50e-20 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) ## 4 -0.8 3 7.18 1.08e-19 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) ## 5 -0.8 3 7.24 2.57e-19 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) ## 6 -0.8 3 7.3 6.03e-19 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) ## 7 -0.8 3 7.36 1.40e-18 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) ## 8 -0.8 3 7.42 3.24e-18 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) ## 9 -0.8 3 7.48 7.39e-18 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) ## 10 -0.8 3 7.54 1.67e-17 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) ## # … with 826,271 more rows
「平均(1軸)の影響」のmu_1, mu_1_valsとsigma_12, sigma_12_valsを入れ換えるように処理します。
「平均(1軸)の影響」のコードで作図できます。


$\sigma_{1,2}$が0に近いほど全体への散らばり具合が大きくなり、値が小さいほど負の相関が強く、大きいほど正の相関が強くなるのが分かります。
パラメータと断面図の軸の関係
前節では、パラメータと分布の関係を確認しました。次は、分布の断面図とその軸を重ねたグラフをアニメーションで確認します。
分散(1軸)の影響
「分布の形状の関係」のコードで、$\sigma_1^2$の値を変化させ、$\boldsymbol{\mu}, \sigma_{1,2}, \sigma_{2,1}, \sigma_2^2$を固定して、anime_dens_dfを作成します。
・作図コード(クリックで展開)
分布の断面図を描画する用のデータフレームを作成します。
# パラメータごとに楕円を計算 anime_ellipse_df <- anime_dens_df |> dplyr::group_by(sigma2_1) |> # 分布の計算用にグループ化 dplyr::mutate( max_dens = mvnfast::dmvn( X = mu_d, mu = mu_d, sigma = matrix(c(unique(sigma2_1), sigma_12, sigma_12, sigma2_2), nrow = 2, ncol = 2) ), # 確率密度の最大値 density = dplyr::if_else( density >= max_dens * exp(-0.5), true = max_dens * exp(-0.5), false = -1 ) # 断面に変換 ) |> dplyr::ungroup() # グループ化を解除 anime_ellipse_df
## # A tibble: 571,256 × 6 ## sigma2_1 x_1 x_2 density parameter max_dens ## <dbl> <dbl> <dbl> <dbl> <fct> <dbl> ## 1 0.5 1.10 4 -1 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) 0.124 ## 2 0.5 1.10 4.12 -1 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) 0.124 ## 3 0.5 1.10 4.24 -1 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) 0.124 ## 4 0.5 1.10 4.36 -1 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) 0.124 ## 5 0.5 1.10 4.48 -1 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) 0.124 ## 6 0.5 1.10 4.6 -1 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) 0.124 ## 7 0.5 1.10 4.72 -1 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) 0.124 ## 8 0.5 1.10 4.84 -1 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) 0.124 ## 9 0.5 1.10 4.96 -1 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) 0.124 ## 10 0.5 1.10 5.08 -1 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) 0.124 ## # … with 571,246 more rows
anime_dens_dfの確率密度(density列)に対して、パラメータごとに最大値の$\exp(-\frac{1}{2})$倍以上であればこの値に、小さければ-1にします(小さい方は他の値でもいいのですが、断面の値に近いとうまく描画できないようです)。
断面の軸を計算します。
# パラメータごとに楕円の軸を計算 anime_axis_df <- tidyr::expand_grid( sigma2_1 = sigma2_1_vals, # パラメータごとに name = paste0(rep(c("x", "y"), each = 2, times = 2), rep(c("start", "end"), each = 4)) # 列名 ) |> # パラメータごとに受け皿を複製 dplyr::group_by(sigma2_1) |> # 軸の計算用にグループ化 dplyr::mutate( axis = rep(c("y_1", "y_2"), times = 4), # pivot_wider用の列 mu = rep(mu_d, each = 2, times = 2), # 平均値 sign = rep(c(-1, 1), each = 4), # 始点・終点の計算用の符号 u = matrix(c(unique(sigma2_1), sigma_12, sigma_12, sigma2_2), nrow = 2, ncol = 2) |> (\(.){eigen(.)[["vectors"]]})() |> t() |> (\(.){rep(as.vector(.), times = 2)})(), # 固有ベクトル lambda = matrix(c(unique(sigma2_1), sigma_12, sigma_12, sigma2_2), nrow = 2, ncol = 2) |> (\(.){eigen(.)[["values"]]})() |> (\(.){rep(sqrt(.), times = 4)})(), # 固有値 value = mu + sign * u * lambda, # 軸の始点・終点を計算 parameter = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2, ")") |> factor(levels = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1_vals, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() |> # グループ化を解除 dplyr::select(axis, name, value, parameter) |> tidyr::pivot_wider( id_cols = c(axis, parameter), names_from = name, values_from = value ) # 軸の視点・終点の列を分割 anime_axis_df
## # A tibble: 112 × 6 ## axis parameter xstart ystart xend yend ## <chr> <fct> <dbl> <dbl> <dbl> <dbl> ## 1 y_1 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) 5.67 8.00 6.33 12.0 ## 2 y_2 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4) 6.62 9.90 5.38 10.1 ## 3 y_1 mu=(6, 10), Sigma=(0.6, 0.6, 0.6, 4) 5.66 8.00 6.34 12.0 ## 4 y_2 mu=(6, 10), Sigma=(0.6, 0.6, 0.6, 4) 6.70 9.88 5.30 10.1 ## 5 y_1 mu=(6, 10), Sigma=(0.7, 0.6, 0.6, 4) 5.65 8.00 6.35 12.0 ## 6 y_2 mu=(6, 10), Sigma=(0.7, 0.6, 0.6, 4) 6.76 9.87 5.24 10.1 ## 7 y_1 mu=(6, 10), Sigma=(0.8, 0.6, 0.6, 4) 5.64 8.01 6.36 12.0 ## 8 y_2 mu=(6, 10), Sigma=(0.8, 0.6, 0.6, 4) 6.82 9.85 5.18 10.1 ## 9 y_1 mu=(6, 10), Sigma=(0.9, 0.6, 0.6, 4) 5.63 8.01 6.37 12.0 ## 10 y_2 mu=(6, 10), Sigma=(0.9, 0.6, 0.6, 4) 6.87 9.84 5.13 10.2 ## # … with 102 more rows
パラメータごとに2つの軸の始点と終点の8つの値を計算します。
パラメータsigma2_1_valsと8つの値に対応する列名の全ての組み合わせをexpand_grid()で作成します。これにより、パラメータごとに列名を複製できます。
eigen()で固有値と固有ベクトルをそれぞれ計算し、上手いことして軸の始点と終点を計算します(誰かもっと上手く処理してください…)。
求めた値をpivot_wider()で列名と対応付けて分割します。
断面図とその軸のアニメーション(gif画像)を作成します。
# 楕円の軸のアニメーションを作図 anime_eigen_graph <- ggplot() + geom_contour_filled(data = anime_dens_df, mapping = aes(x = x_1, y = x_2, z = density, fill = ..level..), alpha = 0.8) + # 2次元ガウス分布 geom_contour(data = anime_ellipse_df, mapping = aes(x = x_1, y = x_2, z = density), bins = 2, color = "red", size = 1, linetype = "dotted") + # 分布の断面 geom_segment(data = anime_axis_df, mapping = aes(x = mu_d[1], y = mu_d[2], xend = xend, yend = yend), color = "blue", size = 1, arrow = arrow()) + # 断面の軸:サイズが固有値の固有ベクトル #geom_segment(data = anime_axis_df, mapping = aes(x = xstart, y = ystart, xend = xend, yend = yend), # color = "blue", size = 1, arrow = arrow()) + # 断面の軸:サイズが固有値の倍の固有ベクトル gganimate::transition_manual(parameter) + # フレーム coord_fixed(ratio = 1) + # アスペクト比 labs(title ="Maltivariate Gaussian Distribution", subtitle = "{current_frame}", fill = "density", x = expression(x[1]), y = expression(x[2])) # gif画像を作成 gganimate::animate(anime_eigen_graph, nframes = frame_num, fps = 10, width = 800, height = 600)
geom_contour()のbreaks引数で任意の値の等高線を引けますが、フレームごとに変更できないので、等高線を引く(断面の)値とそれ以外の値の2値を格納したデータフレームを使います。bins引数に等高線の数を指定します。(1だとエラーになったので2にしています。)


分布の形状に応じて、断面図の軸も変化します。
分散(2軸)の影響
「分布の形状の関係」のコードで、$\sigma_2^2$の値を変化させ、$\boldsymbol{\mu}, \sigma_1^2, \sigma_{1,2}, \sigma_{2,1}$を固定して、anime_dens_dfを作成します。
・作図コード(クリックで展開)
分布の断面図を描画する用のデータフレームを作成します。
# パラメータごとに楕円を計算 anime_ellipse_df <- anime_dens_df |> dplyr::group_by(sigma2_2) |> # 分布の計算用にグループ化 dplyr::mutate( max_dens = mvnfast::dmvn( X = mu_d, mu = mu_d, sigma = matrix(c(sigma2_1, sigma_12, sigma_12, unique(sigma2_2)), nrow = 2, ncol = 2) ), # 確率密度の最大値 density = dplyr::if_else( density >= max_dens * exp(-0.5), true = max_dens * exp(-0.5), false = -1 ) # 断面に変換 ) |> dplyr::ungroup() # グループ化を解除 anime_ellipse_df
## # A tibble: 418,241 × 6 ## sigma2_2 x_1 x_2 density parameter max_dens ## <dbl> <dbl> <dbl> <dbl> <fct> <dbl> ## 1 0.5 3 5.76 -1 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) 0.425 ## 2 0.5 3 5.84 -1 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) 0.425 ## 3 0.5 3 5.93 -1 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) 0.425 ## 4 0.5 3 6.01 -1 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) 0.425 ## 5 0.5 3 6.10 -1 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) 0.425 ## 6 0.5 3 6.18 -1 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) 0.425 ## 7 0.5 3 6.27 -1 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) 0.425 ## 8 0.5 3 6.35 -1 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) 0.425 ## 9 0.5 3 6.44 -1 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) 0.425 ## 10 0.5 3 6.52 -1 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) 0.425 ## # … with 418,231 more rows
「分散(1軸)の影響」のsigma2_1列をsigma2_2列に置き換えるように処理します。
断面の軸を計算します。
# パラメータごとに楕円の軸を計算 anime_axis_df <- tidyr::expand_grid( sigma2_2 = sigma2_2_vals, # パラメータごとに name = paste0(rep(c("x", "y"), each = 2, times = 2), rep(c("start", "end"), each = 4)) # 列名 ) |> # パラメータごとに受け皿を複製 dplyr::group_by(sigma2_2) |> # 軸の計算用にグループ化 dplyr::mutate( axis = rep(c("y_1", "y_2"), times = 4), # pivot_wider用の列 mu = rep(mu_d, each = 2, times = 2), # 平均値 sign = rep(c(-1, 1), each = 4), # 始点・終点の計算用の符号 u = matrix(c(sigma2_1, sigma_12, sigma_12, unique(sigma2_2)), nrow = 2, ncol = 2) |> (\(.){eigen(.)[["vectors"]]})() |> t() |> (\(.){rep(as.vector(.), times = 2)})(), # 固有ベクトル lambda = matrix(c(sigma2_1, sigma_12, sigma_12, unique(sigma2_2)), nrow = 2, ncol = 2) |> (\(.){eigen(.)[["values"]]})() |> (\(.){rep(sqrt(.), times = 4)})(), # 固有値 value = mu + sign * u * lambda, # 軸の始点・終点を計算 parameter = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2, ")") |> factor(levels = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2_vals, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() |> # グループ化を解除 dplyr::select(axis, name, value, parameter) |> tidyr::pivot_wider( id_cols = c(axis, parameter), names_from = name, values_from = value ) # 軸の視点・終点の列を分割 anime_axis_df
## # A tibble: 82 × 6 ## axis parameter xstart ystart xend yend ## <chr> <fct> <dbl> <dbl> <dbl> <dbl> ## 1 y_1 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) 6.98 10.7 5.02 9.34 ## 2 y_2 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5) 5.82 10.3 6.18 9.74 ## 3 y_1 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.6) 6.97 10.7 5.03 9.30 ## 4 y_2 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.6) 5.76 10.3 6.24 9.67 ## 5 y_1 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.7) 6.96 10.7 5.04 9.25 ## 6 y_2 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.7) 5.70 10.4 6.30 9.62 ## 7 y_1 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.8) 6.94 10.8 5.06 9.21 ## 8 y_2 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.8) 5.65 10.4 6.35 9.59 ## 9 y_1 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.9) 6.92 10.8 5.08 9.16 ## 10 y_2 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.9) 5.60 10.4 6.40 9.57 ## # … with 72 more rows
「分散(1軸)の影響」のsigma2_1列をsigma2_2列に置き換えるように処理します。
「分散(1軸)の影響」のコードで作図できます。


分散(1,2軸)の影響
「分布の形状の関係」のコードで、$\sigma_2^2, \sigma_2^2$の値を変化させ、$\boldsymbol{\mu}, \sigma_{1,2}, \sigma_{2,1}$を固定して、anime_dens_dfを作成します。
・作図コード(クリックで展開)
分布の断面図を描画する用のデータフレームを作成します。
# パラメータごとに楕円を計算 anime_ellipse_df <- anime_dens_df |> dplyr::group_by(sigma2_1, sigma2_2) |> # 分布の計算用にグループ化 dplyr::mutate( max_dens = mvnfast::dmvn( X = mu_d, mu = mu_d, sigma = matrix(c(unique(sigma2_1), sigma_12, sigma_12, unique(sigma2_2)), nrow = 2, ncol = 2) ), # 確率密度の最大値 density = dplyr::if_else( density >= max_dens * exp(-0.5), true = max_dens * exp(-0.5), false = -1 ) # 断面に変換 ) |> dplyr::ungroup() # グループ化を解除 anime_ellipse_df
## # A tibble: 367,236 × 8 ## idx x_1 x_2 sigma2_1 sigma2_2 density parameter max_dens ## <int> <dbl> <dbl> <dbl> <dbl> <dbl> <fct> <dbl> ## 1 1 1.76 5.76 1 1 -1 mu=(6, 10), Sigma=(1, 0… 0.199 ## 2 1 1.76 5.84 1 1 -1 mu=(6, 10), Sigma=(1, 0… 0.199 ## 3 1 1.76 5.93 1 1 -1 mu=(6, 10), Sigma=(1, 0… 0.199 ## 4 1 1.76 6.01 1 1 -1 mu=(6, 10), Sigma=(1, 0… 0.199 ## 5 1 1.76 6.10 1 1 -1 mu=(6, 10), Sigma=(1, 0… 0.199 ## 6 1 1.76 6.18 1 1 -1 mu=(6, 10), Sigma=(1, 0… 0.199 ## 7 1 1.76 6.27 1 1 -1 mu=(6, 10), Sigma=(1, 0… 0.199 ## 8 1 1.76 6.35 1 1 -1 mu=(6, 10), Sigma=(1, 0… 0.199 ## 9 1 1.76 6.44 1 1 -1 mu=(6, 10), Sigma=(1, 0… 0.199 ## 10 1 1.76 6.52 1 1 -1 mu=(6, 10), Sigma=(1, 0… 0.199 ## # … with 367,226 more rows
「分散(1軸)の影響」のsigma2_1列にsigma2_2列を加えるように処理します。
断面の軸を計算します。
# パラメータごとに楕円の軸を計算 anime_axis_df <- tidyr::expand_grid( idx = seq_along(sigma2_1_vals), # パラメータ番号 name = paste0(rep(c("x", "y"), each = 2, times = 2), rep(c("start", "end"), each = 4)), # 列名 ) |> # パラメータごとに受け皿を複製 dplyr::group_by(idx) |> # 軸の計算用にグループ化 dplyr::mutate( sigma2_1 = sigma2_1_vals[idx], sigma2_2 = sigma2_2_vals[idx], axis = rep(c("y_1", "y_2"), times = 4), # pivot_wider用の列 mu = rep(mu_d, each = 2, times = 2), # 平均値 sign = rep(c(-1, 1), each = 4), # 始点・終点の計算用の符号 u = matrix(c(unique(sigma2_1), sigma_12, sigma_12, unique(sigma2_2)), nrow = 2, ncol = 2) |> (\(.){eigen(.)[["vectors"]]})() |> t() |> (\(.){rep(as.vector(.), times = 2)})(), # 固有ベクトル lambda = matrix(c(unique(sigma2_1), sigma_12, sigma_12, unique(sigma2_2)), nrow = 2, ncol = 2) |> (\(.){eigen(.)[["values"]]})() |> (\(.){rep(sqrt(.), times = 4)})(), # 固有値 value = mu + sign * u * lambda, # 軸の始点・終点を計算 parameter = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2, ")") |> factor(levels = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1_vals, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2_vals, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() |> # グループ化を解除 dplyr::select(axis, name, value, parameter) |> tidyr::pivot_wider( id_cols = c(axis, parameter), names_from = name, values_from = value ) # 軸の視点・終点の列を分割 anime_axis_df
## # A tibble: 72 × 6 ## axis parameter xstart ystart xend yend ## <chr> <fct> <dbl> <dbl> <dbl> <dbl> ## 1 y_1 mu=(6, 10), Sigma=(1, 0.6, 0.6, 1) 5.11 9.11 6.89 10.9 ## 2 y_2 mu=(6, 10), Sigma=(1, 0.6, 0.6, 1) 6.45 9.55 5.55 10.4 ## 3 y_1 mu=(6, 10), Sigma=(1.1, 0.6, 0.6, 1.1) 5.08 9.08 6.92 10.9 ## 4 y_2 mu=(6, 10), Sigma=(1.1, 0.6, 0.6, 1.1) 6.5 9.5 5.5 10.5 ## 5 y_1 mu=(6, 10), Sigma=(1.2, 0.6, 0.6, 1.2) 5.05 9.05 6.95 10.9 ## 6 y_2 mu=(6, 10), Sigma=(1.2, 0.6, 0.6, 1.2) 6.55 9.45 5.45 10.5 ## 7 y_1 mu=(6, 10), Sigma=(1.3, 0.6, 0.6, 1.3) 5.03 9.03 6.97 11.0 ## 8 y_2 mu=(6, 10), Sigma=(1.3, 0.6, 0.6, 1.3) 6.59 9.41 5.41 10.6 ## 9 y_1 mu=(6, 10), Sigma=(1.4, 0.6, 0.6, 1.4) 5 9 7 11 ## 10 y_2 mu=(6, 10), Sigma=(1.4, 0.6, 0.6, 1.4) 6.63 9.37 5.37 10.6 ## # … with 62 more rows
パラメータ番号として1からパラメータの要素数までの整数をseq_along()で作成し、始点と終点用の列名との全ての組み合わせをexpand_grid()を作成します。
idx列の値を使ってsigma_1_vals, sigma_2_valsから値を取り出して、軸の視点と終点を計算します。
「分散(1軸)の影響」のコードで作図できます。


共分散の影響
「分布の形状の関係」のコードで、$\sigma_{1,2} = \sigma_{1,2}$の値を変化させ、$\boldsymbol{\mu}, \sigma_1^2, \sigma_2^2$を固定して、anime_dens_dfを作成します。
・作図コード(クリックで展開)
分布の断面図を描画する用のデータフレームを作成します。
# パラメータごとに楕円を計算 anime_ellipse_df <- anime_dens_df |> dplyr::group_by(sigma_12) |> # 分布の計算用にグループ化 dplyr::mutate( max_dens = mvnfast::dmvn( X = mu_d, mu = mu_d, sigma = matrix(c(sigma2_1, unique(sigma_12), unique(sigma_12), sigma2_2), nrow = 2, ncol = 2) ), # 確率密度の最大値 density = dplyr::if_else( density >= max_dens * exp(-0.5), true = max_dens * exp(-0.5), false = -1 ) # 断面に変換 ) |> dplyr::ungroup() # グループ化を解除 anime_ellipse_df
## # A tibble: 826,281 × 6 ## sigma_12 x_1 x_2 density parameter max_dens ## <dbl> <dbl> <dbl> <dbl> <fct> <dbl> ## 1 -0.8 3 7 -1 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) 0.265 ## 2 -0.8 3 7.06 -1 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) 0.265 ## 3 -0.8 3 7.12 -1 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) 0.265 ## 4 -0.8 3 7.18 -1 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) 0.265 ## 5 -0.8 3 7.24 -1 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) 0.265 ## 6 -0.8 3 7.3 -1 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) 0.265 ## 7 -0.8 3 7.36 -1 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) 0.265 ## 8 -0.8 3 7.42 -1 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) 0.265 ## 9 -0.8 3 7.48 -1 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) 0.265 ## 10 -0.8 3 7.54 -1 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) 0.265 ## # … with 826,271 more rows
「分散(1軸)の影響」のsigma2_1列をsigma_12列に置き換えるように処理します。
断面の軸を計算します。
# パラメータごとに楕円の軸を計算 anime_axis_df <- tidyr::expand_grid( sigma_12 = sigma_12_vals, # パラメータごとに name = paste0(rep(c("x", "y"), each = 2, times = 2), rep(c("start", "end"), each = 4)) # 列名 ) |> # パラメータごとに受け皿を複製 dplyr::group_by(sigma_12) |> # 軸の計算用にグループ化 dplyr::mutate( axis = rep(c("y_1", "y_2"), times = 4), # pivot_wider用の列 mu = rep(mu_d, each = 2, times = 2), # 平均値 sign = rep(c(-1, 1), each = 4), # 始点・終点の計算用の符号 u = matrix(c(sigma2_1, unique(sigma_12), unique(sigma_12), sigma2_2), nrow = 2, ncol = 2) |> (\(.){eigen(.)[["vectors"]]})() |> t() |> (\(.){rep(as.vector(.), times = 2)})(), # 固有ベクトル lambda = matrix(c(sigma2_1, unique(sigma_12), unique(sigma_12), sigma2_2), nrow = 2, ncol = 2) |> (\(.){eigen(.)[["values"]]})() |> (\(.){rep(sqrt(.), times = 4)})(), # 固有値 value = mu + sign * u * lambda, # 軸の始点・終点を計算 parameter = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2, ")") |> factor(levels = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12_vals, ", ", sigma_12_vals, ", ", sigma2_2, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() |> # グループ化を解除 dplyr::select(axis, name, value, parameter) |> tidyr::pivot_wider( id_cols = c(axis, parameter), names_from = name, values_from = value ) # 軸の視点・終点の列を分割 anime_axis_df
## # A tibble: 162 × 6 ## axis parameter xstart ystart xend yend ## <chr> <fct> <dbl> <dbl> <dbl> <dbl> ## 1 y_1 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) 6.95 9.05 5.05 10.9 ## 2 y_2 mu=(6, 10), Sigma=(1, -0.8, -0.8, 1) 6.32 10.3 5.68 9.68 ## 3 y_1 mu=(6, 10), Sigma=(1, -0.78, -0.78, 1) 6.94 9.06 5.06 10.9 ## 4 y_2 mu=(6, 10), Sigma=(1, -0.78, -0.78, 1) 6.33 10.3 5.67 9.67 ## 5 y_1 mu=(6, 10), Sigma=(1, -0.76, -0.76, 1) 6.94 9.06 5.06 10.9 ## 6 y_2 mu=(6, 10), Sigma=(1, -0.76, -0.76, 1) 6.35 10.3 5.65 9.65 ## 7 y_1 mu=(6, 10), Sigma=(1, -0.74, -0.74, 1) 6.93 9.07 5.07 10.9 ## 8 y_2 mu=(6, 10), Sigma=(1, -0.74, -0.74, 1) 6.36 10.4 5.64 9.64 ## 9 y_1 mu=(6, 10), Sigma=(1, -0.72, -0.72, 1) 6.93 9.07 5.07 10.9 ## 10 y_2 mu=(6, 10), Sigma=(1, -0.72, -0.72, 1) 6.37 10.4 5.63 9.63 ## # … with 152 more rows
「分散(1軸)の影響」のsigma2_1列をsigma_12列に置き換えるように処理します。
「分散(1軸)の影響」のコードで作図できます。


参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上』,丸善出版,2012年.
おわりに
時計にしか見えないんだよなぁ。
これまでの通りの構成で気楽にあるいは作業的に書くつもりだったのですが、少し気になったことを調べてみるとあれこれ新しいことが登場して苦労しました。それぞれ調べて読んで試して理解してまとめては情報過多で別の記事として出力されていき、この記事が中々書き上がりませんでした。そうやって多次元ガウス分布シリーズのスピンオフで分散共分散行列シリーズができました。固有値とかなんとなく避けてたのについに勉強してしまった。
それと、mutate()の中で色々と怪しい処理をしているのですがアレって良いんですかね?まぁ動いたのでヨシ!
2022年9月1日はアンジュルムの松本わかなさんの15歳のお誕生日です。
見た目とのギャップが凄いんよほんと。
【次の内容】
つづく