はじめに
機械学習で登場する確率分布について色々な角度から理解したいシリーズです。
この記事では、R言語で多次元(多変量)スチューデントのt分布のグラフを作成します。
【前の内容】
【他の記事一覧】
【この記事の内容】
2次元スチューデントのt分布の作図
2次元スチューデントのt分布(Bivariate Student's t Distribution)のグラフを作成します。t分布については「多次元スチューデントのt分布の定義式 - からっぽのしょこ」を参照してください。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(mvnfast) library(gganimate)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているため、ggplot2は読み込む必要があります。
magrittrパッケージのパイプ演算子%>%ではなく、ベースパイプ(ネイティブパイプ)演算子|>を使っています。%>%に置き換えても処理できます。
分布の変化をアニメーション(gif画像)で確認するのにgganimateパッケージを利用します。不要であれば省略してください。
定義式の確認
まずは、多次元t分布の定義式を確認します。
t分布は、次の式で定義されます。
ここで、$\nu$は形状(自由度)パラメータ、$\boldsymbol{\mu}$は位置ベクトルパラメータ、$\boldsymbol{\Sigma}$はスケール行列パラメータ、$\boldsymbol{\Lambda}$は逆スケール行列パラメータです。また、$\mathbf{A}^{\top}$は行列$\mathbf{A}$の転置行列、$\mathbf{A}^{-1}$は逆行列、$|\mathbf{A}|$は行列式、2分の1乗は平方根$\sqrt{a} = a^{\frac{1}{2}}$です。
$\mathbf{x}, \boldsymbol{\mu}$は$D$次元ベクトル、$\boldsymbol{\Sigma}$は$D \times D$の正定値行列です。
$x_d$は実数をとり、$\nu$は正の実数、$\mu_d$は実数、$\sigma_{d,d}$は正の実数、$\sigma_{i,j} = \sigma_{j,i}\ (i \neq j)$は実数、また$\boldsymbol{\Sigma}$は正定値行列を満たす必要があります。
この計算を行いグラフを作成します。
グラフの作成
ggplot2パッケージを利用して、2次元t分布のグラフを作成します。t分布の確率密度の計算については「【R】多次元スチューデントのt分布の計算 - からっぽのしょこ」を参照してください。
t分布のパラメータ$\nu, \boldsymbol{\mu}, \boldsymbol{\Sigma}$を設定します。この例では、2次元のグラフで描画するため、次元数を$D = 2$とします。
# 次元数を設定 D <- 2 # 自由度を指定 nu <- 3 # 位置ベクトルを指定 mu_d <- c(6, 10) # スケール行列を指定 sigma_dd <- c(1, 0.6, 0.6, 4) |> # 値を指定 matrix(nrow = D, ncol = D) # マトリクスに変換
位置ベクトル$\boldsymbol{\mu} = (\mu_1, \mu_2)$、スケール行列$\boldsymbol{\Sigma} = (\sigma_{1,1}, \sigma_{2,1}, \sigma_{1,2}, \sigma_{2,2})$を指定します。
設定したパラメータに応じて、t分布の確率変数がとり得る値$\mathbf{x}$の成分$x_1, x_2$の値を作成します。
# xの値を作成 x_1_vals <- seq( from = mu_d[1] - sqrt(sigma_dd[1, 1]) * 3, to = mu_d[1] + sqrt(sigma_dd[1, 1]) * 3, length.out = 101 ) x_2_vals <- seq( from = mu_d[2] - sqrt(sigma_dd[2, 2]) * 3, to = mu_d[2] + sqrt(sigma_dd[2, 2]) * 3, length.out = 101 ) head(x_1_vals); head(x_2_vals)
## [1] 3.00 3.06 3.12 3.18 3.24 3.30 ## [1] 4.00 4.12 4.24 4.36 4.48 4.60
$x_1$(x軸)の値をx_1_vals、$x_2$(y軸)の値をx_2_valsとします。この例では、それぞれ$\mu_d$を中心に$\sqrt{\sigma_{d,d}}$の3倍を範囲とします。
$\mathbf{x}$を作成します。
# xの点を作成 x_mat <- tidyr::expand_grid( x_1 = x_1_vals, x_2 = x_2_vals ) |> # 格子点を作成 as.matrix() # マトリクスに変換 head(x_mat)
## x_1 x_2 ## [1,] 3 4.00 ## [2,] 3 4.12 ## [3,] 3 4.24 ## [4,] 3 4.36 ## [5,] 3 4.48 ## [6,] 3 4.60
x_1_valsとx_2_valsの要素の全ての組み合わせ(格子状の点)をexpand_grid()で作成します。データフレームが出力されるので、as.matrix()でマトリクスに変換してx_matとします。x_matの各行が点$\mathbf{x} = (x_1, x_2)$に対応します。
$\mathbf{x}$の点ごとの確率密度を計算します。
# 多次元t分布を計算 dens_df <- tibble::tibble( x_1 = x_mat[, 1], # x軸の値 x_2 = x_mat[, 2], # y軸の値 density = mvnfast::dmvt(X = x_mat, mu = mu_d, sigma = sigma_dd, df = nu) # 確率密度 ) dens_df
## # A tibble: 10,201 × 3 ## x_1 x_2 density ## <dbl> <dbl> <dbl> ## 1 3 4 0.00112 ## 2 3 4.12 0.00116 ## 3 3 4.24 0.00121 ## 4 3 4.36 0.00126 ## 5 3 4.48 0.00131 ## 6 3 4.6 0.00136 ## 7 3 4.72 0.00141 ## 8 3 4.84 0.00147 ## 9 3 4.96 0.00152 ## 10 3 5.08 0.00158 ## # … with 10,191 more rows
多次元t分布の確率密度は、mvnfastパッケージのdmvt()で計算できます。確率変数の引数Xにx_mat、位置ベクトルの引数muにmu_d、スケール行列の引数sigmaにsigma_dd、自由度の引数dfにnuを指定します。
パラメータの値を数式で表示するための文字列を作成します。
# パラメータラベルを作成:(数式表示用) param_text <- paste0( "list(", "mu==group('(', list(", paste0(mu_d, collapse = ", "), "), ')')", ", Sigma==group('(', list(", paste0(sigma_dd, collapse = ", "), "), ')')", ", nu==", nu, ")" )
## [1] "list(mu==group('(', list(6, 10), ')'), Sigma==group('(', list(1, 0.6, 0.6, 4), ')'), nu==3)"
ギリシャ文字などの記号を使った数式を表示する場合は、expression()の記法を使います。等号は"=="、複数の(数式上の)変数を並べるには"list(変数1, 変数2)"とします。(プログラム上の)変数の値を使う場合は、parse()のtext引数に指定します。
t分布の等高線図を作成します。
# 2次元t分布のグラフを作成:等高線図 ggplot() + geom_contour(data = dens_df, mapping = aes(x = x_1, y = x_2, z = density, color = ..level..)) + # 等高線 #geom_contour_filled(data = dens_df, mapping = aes(x = x_1, y = x_2, z = density, fill = ..level..), alpha = 0.8) + # 塗りつぶし等高線 labs( title ="Bivariate Student's t-Distribution", subtitle = paste0("mu=(", paste0(mu_d, collapse = ', '), "), Sigma=(", paste0(sigma_dd, collapse = ', '), "), nu=", nu), # (文字列表記用) #subtitle = parse(text = param_text), # (数式表示用) color = "density", # (等高線用) fill = "density", # (塗りつぶし等高線用) x = expression(x[1]), y = expression(x[2]) )
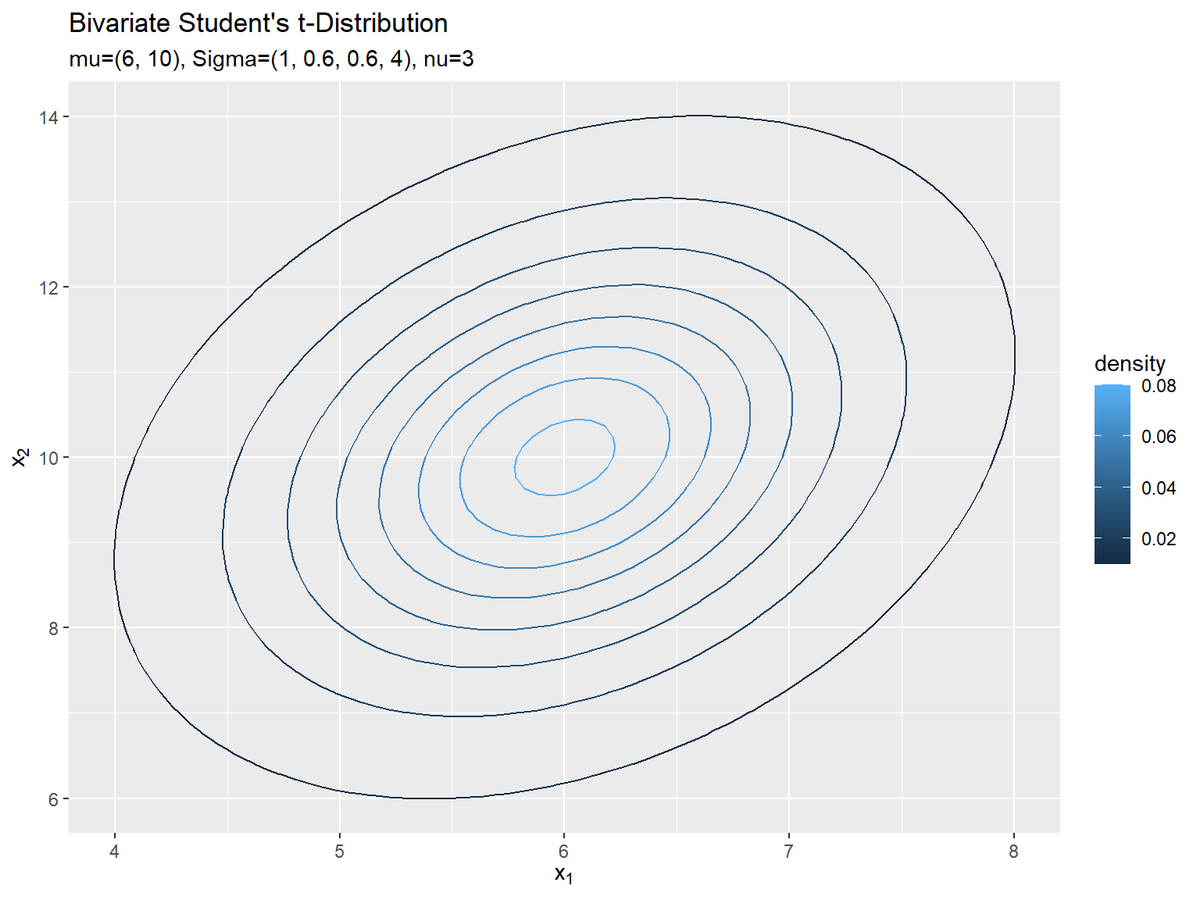
等高線はgeom_contour()、塗りつぶし等高線はgeom_contour_filled()で描画できます。z軸の値の引数zにdensityを指定して、等高線の色の引数colorまたは塗りつぶしの色の引数fillに..level..を指定すると、確率密度に応じてグラデーションが付けられます。
確率密度の変化を細かく見るには、ヒートマップで可視化します。
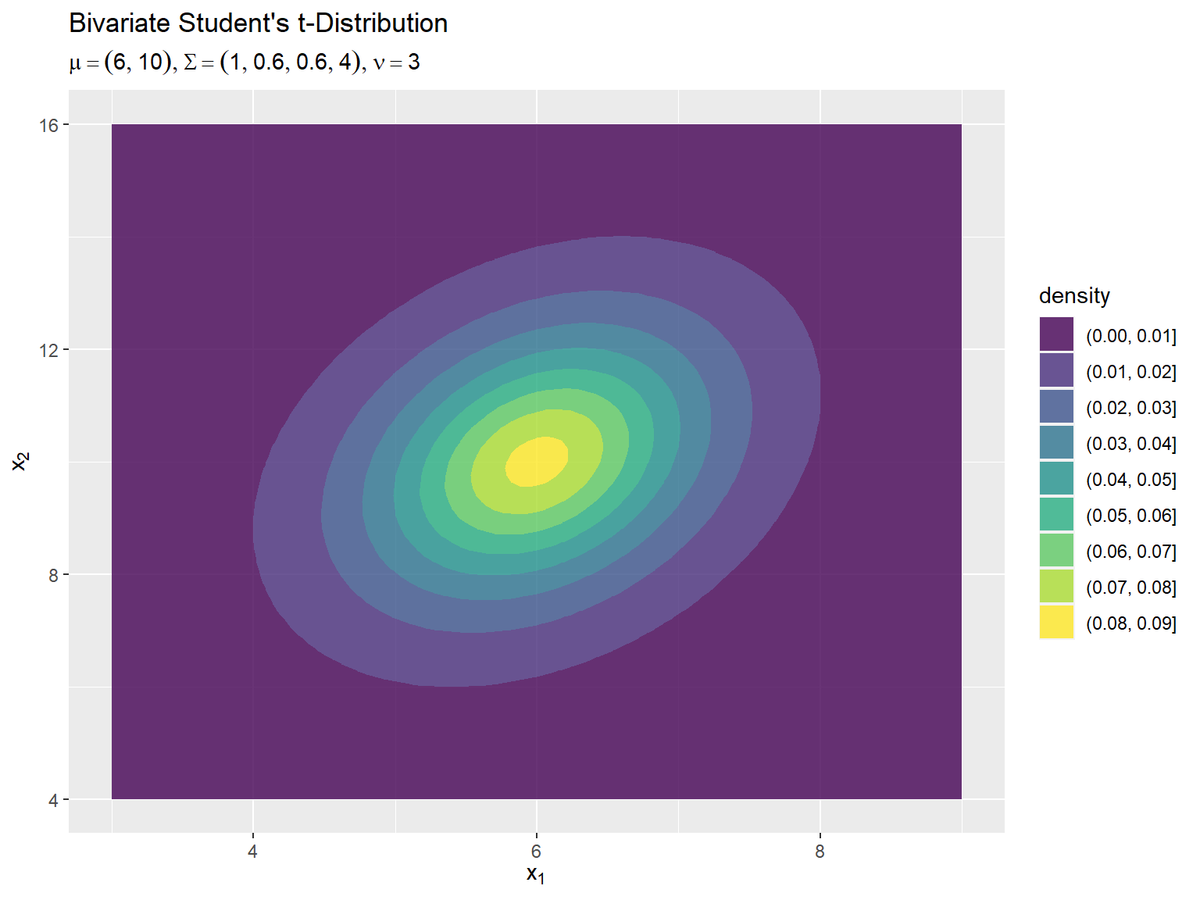
# 2次元t分布のグラフを作成:ヒートマップ ggplot() + geom_tile(data = dens_df, mapping = aes(x = x_1, y = x_2, fill = density, color = density), alpha = 0.8) + # ヒートマップ scale_color_viridis_c(option = "D") + # タイルの色 scale_fill_viridis_c(option = "D") + # 枠線の色 #scale_fill_gradientn(colors = c("blue", "green", "yellow", "red")) + # タイルの色 #scale_color_gradientn(colors = c("blue", "green", "yellow", "red")) + # 枠線の色 labs( title ="Bivariate Student's t-Distribution", #subtitle = paste0("mu=(", paste0(mu_d, collapse = ', '), "), Sigma=(", paste0(sigma_dd, collapse = ', '), "), nu=", nu), # (文字列表記用) subtitle = parse(text = param_text), # (数式表示用) fill = "density", color = "density", x = expression(x[1]), y = expression(x[2]) )
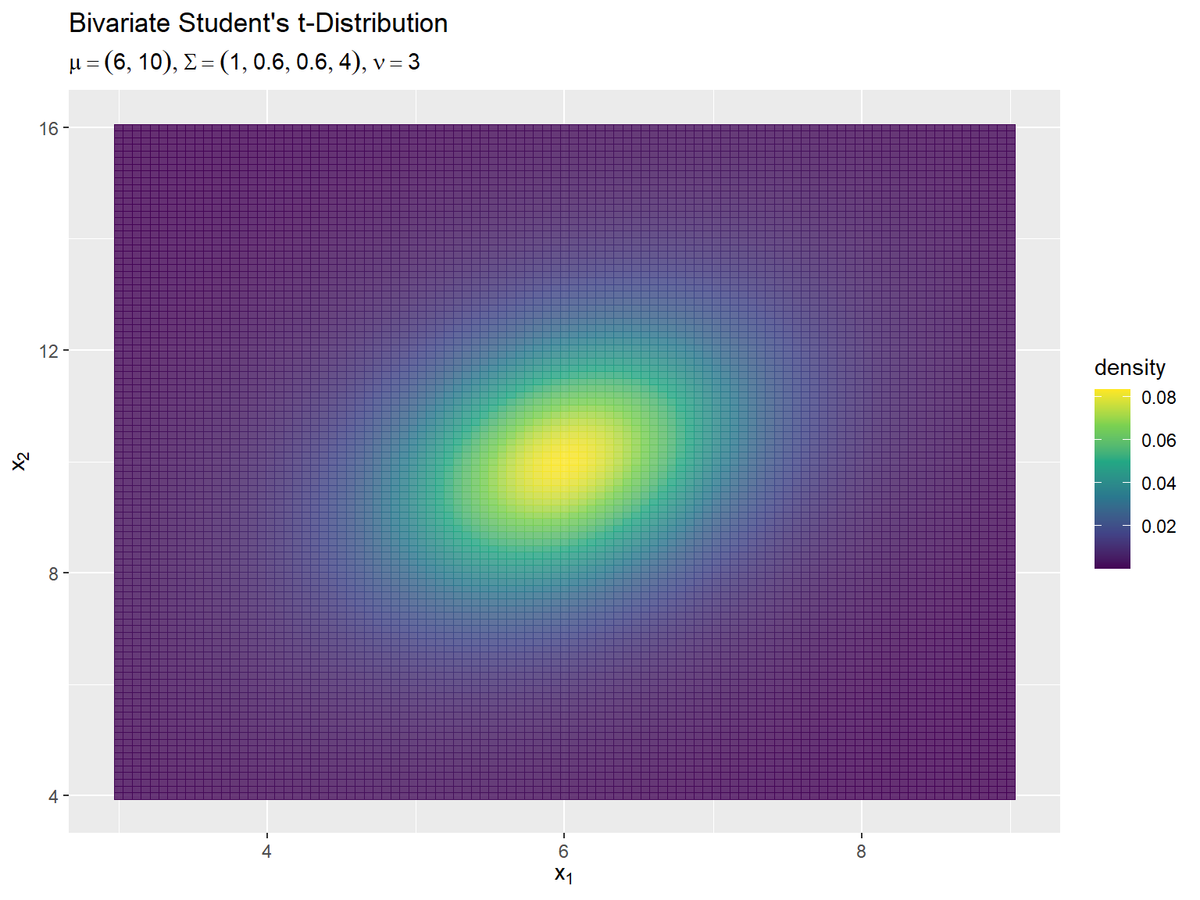
ヒートマップはgeom_tile()で描画できます。
グラデーションはscale_***_viridis_c()やscale_***_gradientn()で設定できます。
t分布のグラフを描画できました。以降は、ここまでの作図処理を用いて、パラメータの影響を確認していきます。
パラメータと分布の形状の関係
パラメータの値を少しずつ変化させて、分布の形状の変化をアニメーションで確認します。
自由度の影響
まずは、自由度$\nu$の値を変化させ、$\boldsymbol{\mu}, \boldsymbol{\Sigma}$を固定します。
・コード(クリックで展開)
# 次元数を設定 D <- 2 # 自由度パラメータとして利用する値を指定 nu_vals <- seq(from = 0.1, to = 15, by = 0.1) |> round(digits = 1) # 位置ベクトルを指定 mu_d <- c(6, 10) # スケール行列を指定 sigma_dd <- c(1, 0.6, 0.6, 4) |> # 値を指定 matrix(nrow = D, ncol = D) # マトリクスに変換 # フレーム数を設定 frame_num <- length(nu_vals) frame_num
## [1] 150
値の間隔が一定になるように$\nu$の値をnu_valsとして作成します。パラメータごとにフレームを切り替えるので、nu_valsの要素数がアニメーションのフレーム数になります。
設定したパラメータに応じて、確率変数の値$\mathbf{x}$の成分$x_1, x_2$の値を作成して、パラメータごとに確率密度を計算します。
# xの値を作成 x_1_vals <- seq( from = mu_d[1] - sqrt(sigma_dd[1, 1]) * 3, to = mu_d[1] + sqrt(sigma_dd[1, 1]) * 3, length.out = 101 ) x_2_vals <- seq( from = mu_d[2] - sqrt(sigma_dd[2, 2]) * 3, to = mu_d[2] + sqrt(sigma_dd[2, 2]) * 3, length.out = 101 ) # パラメータごとに多次元t分布を計算 anime_dens_df <- tidyr::expand_grid( nu = nu_vals, x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(nu) |> # 分布の計算用にグループ化 dplyr::mutate( density = mvnfast::dmvt( X = as.matrix(cbind(x_1, x_2)), mu = mu_d, sigma = sigma_dd, df = unique(nu) ), # 確率密度 parameter = paste0("mu=(", paste0(mu_d, collapse = ", "), "), Sigma=(", paste0(sigma_dd, collapse = ", "), "), nu=", nu) |> factor(levels = paste0("mu=(", paste0(mu_d, collapse = ", "), "), Sigma=(", paste0(sigma_dd, collapse = ", "), "), nu=", nu_vals)) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_dens_df
## # A tibble: 1,530,150 × 5 ## nu x_1 x_2 density parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 0.1 3 4 0.000467 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## 2 0.1 3 4.12 0.000477 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## 3 0.1 3 4.24 0.000487 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## 4 0.1 3 4.36 0.000497 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## 5 0.1 3 4.48 0.000507 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## 6 0.1 3 4.6 0.000517 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## 7 0.1 3 4.72 0.000527 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## 8 0.1 3 4.84 0.000538 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## 9 0.1 3 4.96 0.000548 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## 10 0.1 3 5.08 0.000558 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## # … with 1,530,140 more rows
パラメータmu_1_valsと確率変数x_1_vals, x_2_valsの要素の全ての組み合わせをexpand_grid()を作成します。これにより、パラメータごとにx_matを複製できます。
パラメータ列mu_1でグループ化することで、x_matごとに確率密度を計算できます。(as.matrix(cbind(x_1, x_2))の処理はx_matに置き換えられます。)
パラメータごとにフレーム切替用のラベルを作成します。文字列型だと文字列の基準で順序が決まるので、因子型にしてパラメータに応じたレベル(順序)を設定します。
等高線図のアニメーション(gif画像)を作成します。
# 2次元t分布のアニメーションを作図:等高線図 anime_dens_graph <- ggplot() + #geom_contour(data = anime_dens_df, mapping = aes(x = x_1, y = x_2, z = density, color = ..level..)) + # 等高線 geom_contour_filled(data = anime_dens_df, mapping = aes(x = x_1, y = x_2, z = density, fill = ..level..), alpha = 0.8) + # 塗りつぶし等高線 gganimate::transition_manual(parameter) + # フレーム labs(title ="Bivariate Student's t-Distribution", subtitle = "{current_frame}", color = "density", fill = "density", x = expression(x[1]), y = expression(x[2])) # gif画像を作成 gganimate::animate(anime_dens_graph, nframes = frame_num, fps = 10, width = 800, height = 600)
transition_manual()にフレームの順序を表す列を指定します。この例では、因子型のラベルのレベルの順に描画されます。
animate()のフレーム数の引数nframesにパラメータ数、フレームレートの引数fpsに1秒当たりのフレーム数を指定します。fps引数の値が大きいほどフレームが早く切り替わります。ただし、値が大きいと意図通りに動作しません。
同様に、ヒートマップのアニメーションを作成します。
# 2次元t分布のアニメーションを作図:ヒートマップ anime_dens_graph <- ggplot() + geom_tile(data = anime_dens_df, mapping = aes(x = x_1, y = x_2, fill = density), alpha = 0.8) + # ヒートマップ gganimate::transition_manual(parameter) + # フレーム scale_fill_viridis_c(option = "D") + # 等高線の色 labs(title ="Bivariate Student's t-Distribution", subtitle = "{current_frame}", fill = "density", x = expression(x[1]), y = expression(x[2])) # gif画像を作成 gganimate::animate(anime_dens_graph, nframes = frame_num, fps = 10, width = 800, height = 600)

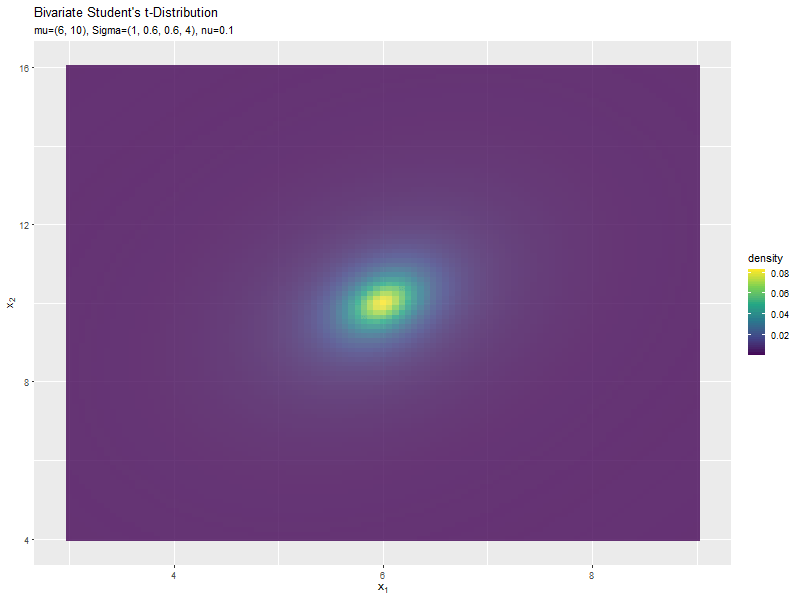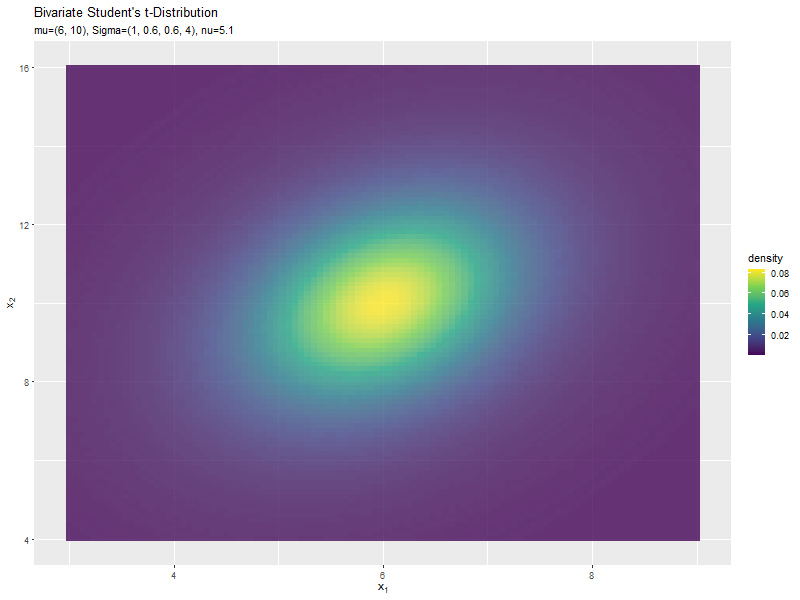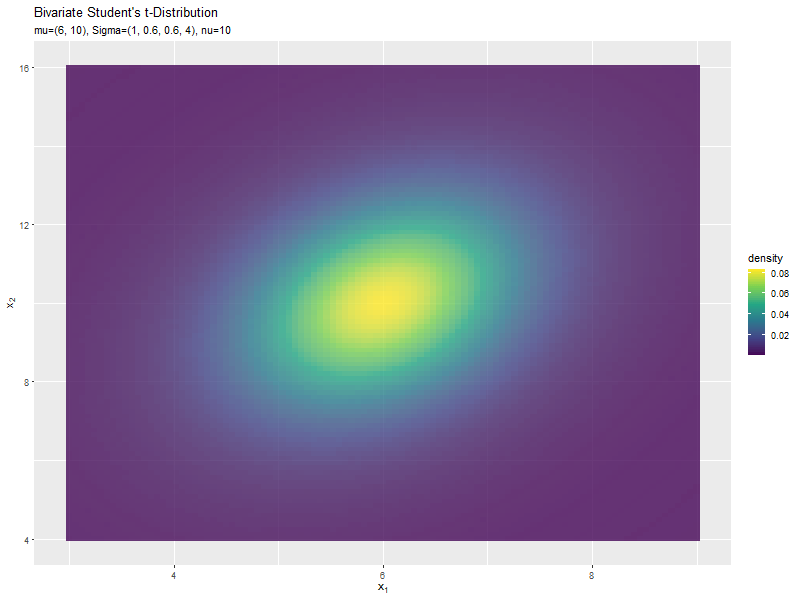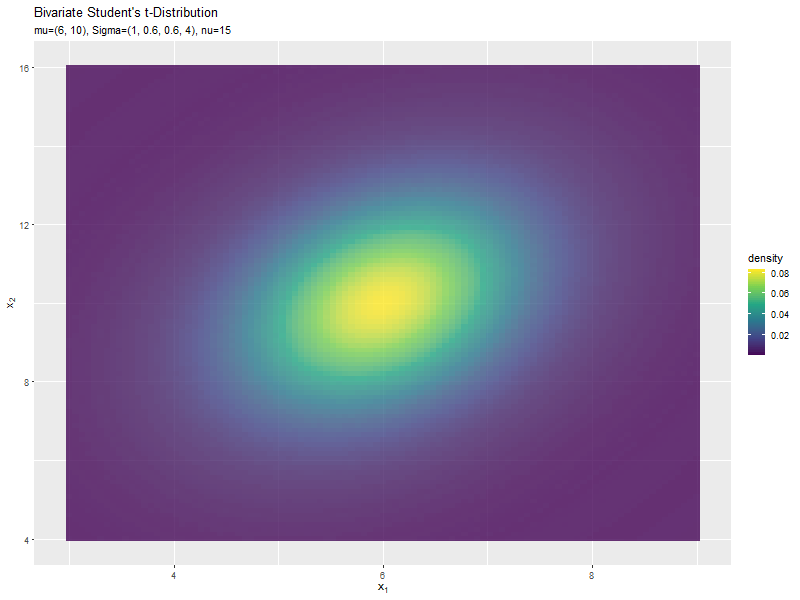
$\nu$の値に応じて、形状が変化するのが分かります。
位置ベクトル(1軸)の影響
次は、x軸方向の位置パラメータ$\mu_1$の値を変化させ、$\nu, \mu_2, \boldsymbol{\Sigma}$を固定します。
・コード(クリックで展開)
# 次元数を設定 D <- 2 # 自由度を指定 nu <- 3 # x軸の位置パラメータとして利用する値を指定 mu_1_vals <- seq(from = -2, to = 2, by = 0.04) |> round(digits = 2) # y軸の位置パラメータを指定 mu_2 <- 10 # スケール行列を指定 sigma_dd <- matrix(c(1, 0.6, 0.6, 4), nrow = D, ncol = D) # フレーム数を設定 frame_num <- length(mu_1_vals) frame_num
## [1] 101
値の間隔が一定になるように$\mu_1$の値をmu_1_valsとして作成します。また、$\mu_2$をmu_2として値を指定します。
パラメータごとに分布を計算します。
# xの値を作成 x_1_vals <- seq( from = min(mu_1_vals) - sqrt(sigma_dd[1, 1]) * 2, to = max(mu_1_vals) + sqrt(sigma_dd[1, 1]) * 2, length.out = 101 ) x_2_vals <- seq( from = mu_2 - sqrt(sigma_dd[2, 2]) * 3, to = mu_2 + sqrt(sigma_dd[2, 2]) * 3, length.out = 101 ) # パラメータごとに多次元t分布を計算 anime_dens_df <- tidyr::expand_grid( mu_1 = mu_1_vals, x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(mu_1) |> # 分布の計算用にグループ化 dplyr::mutate( density = mvnfast::dmvt( X = as.matrix(cbind(x_1, x_2)), mu = unique(cbind(mu_1, mu_2)), sigma = sigma_dd, df = nu ), # 確率密度 parameter = paste0("mu=(", mu_1, ", ", mu_2, "), Sigma=(", paste0(sigma_dd, collapse = ", "), "), nu=", nu) |> factor(levels = paste0("mu=(", mu_1_vals, ", ", mu_2, "), Sigma=(", paste0(sigma_dd, collapse = ", "), "), nu=", nu)) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_dens_df
## # A tibble: 1,030,301 × 5 ## mu_1 x_1 x_2 density parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 -2 -4 4 0.00200 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4), nu=3 ## 2 -2 -4 4.12 0.00213 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4), nu=3 ## 3 -2 -4 4.24 0.00226 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4), nu=3 ## 4 -2 -4 4.36 0.00239 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4), nu=3 ## 5 -2 -4 4.48 0.00254 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4), nu=3 ## 6 -2 -4 4.6 0.00269 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4), nu=3 ## 7 -2 -4 4.72 0.00285 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4), nu=3 ## 8 -2 -4 4.84 0.00302 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4), nu=3 ## 9 -2 -4 4.96 0.00320 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4), nu=3 ## 10 -2 -4 5.08 0.00339 mu=(-2, 10), Sigma=(1, 0.6, 0.6, 4), nu=3 ## # … with 1,030,291 more rows
「自由度の影響」のnu, nu_valsとmu_1, mu_1_valsを入れ換えるように処理します。
「自由度の影響」のコードで作図できます。
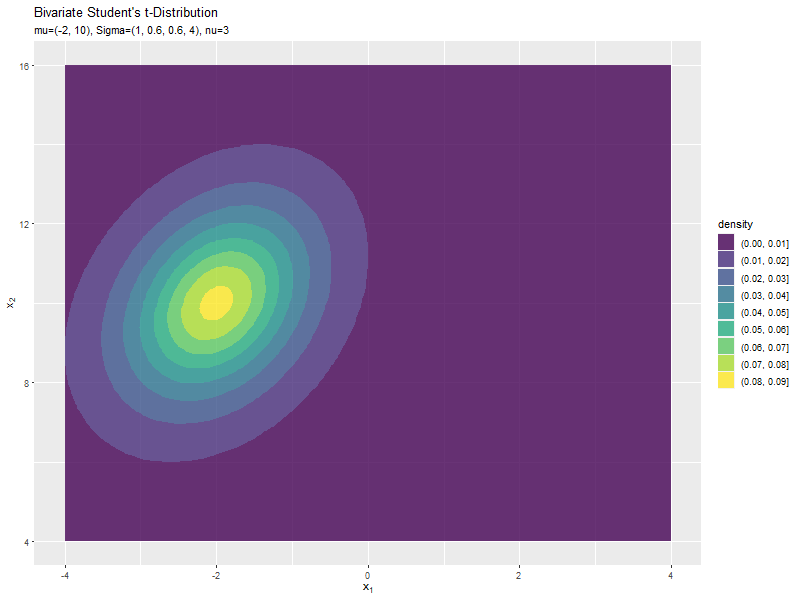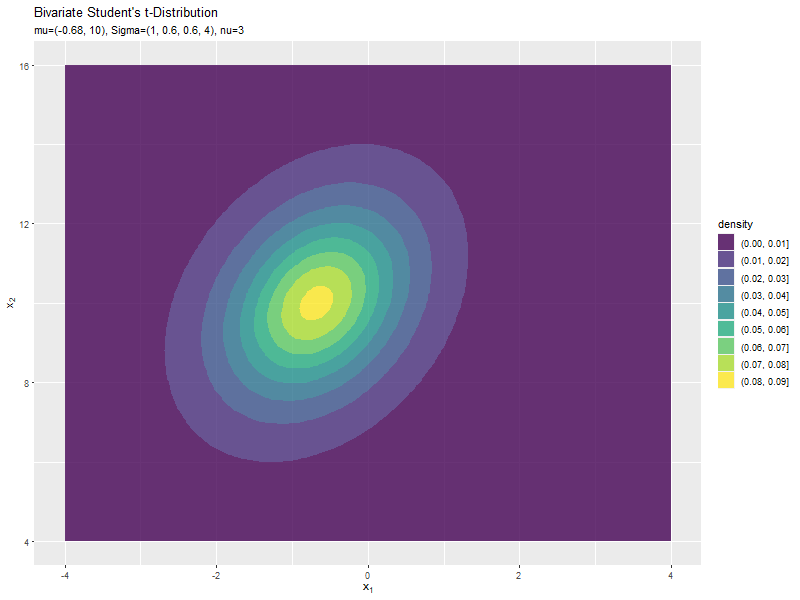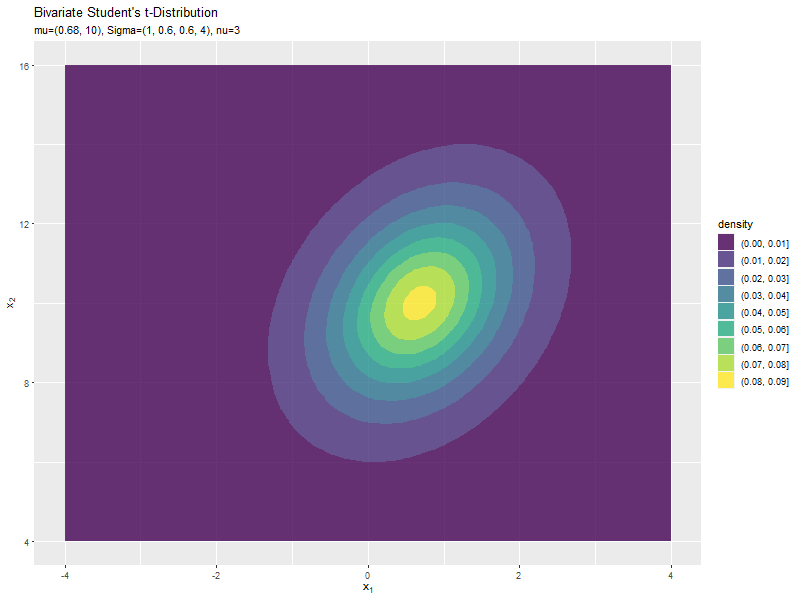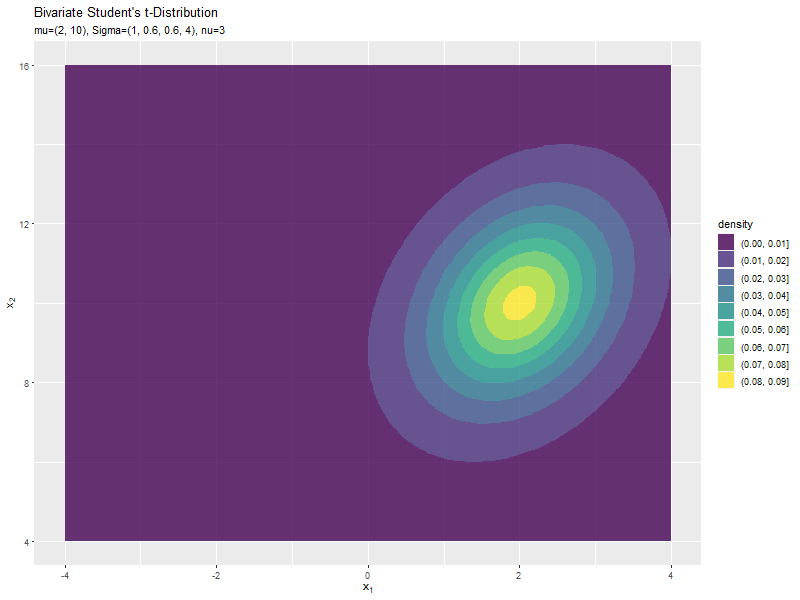
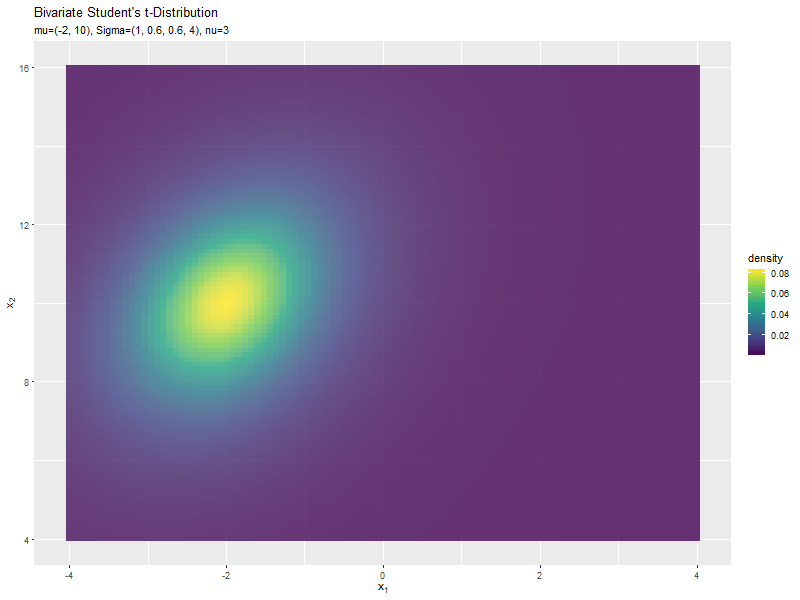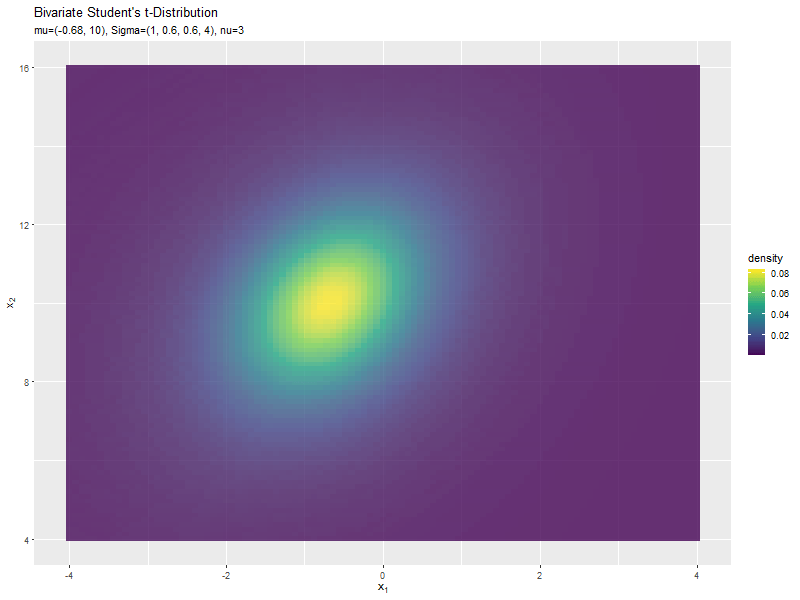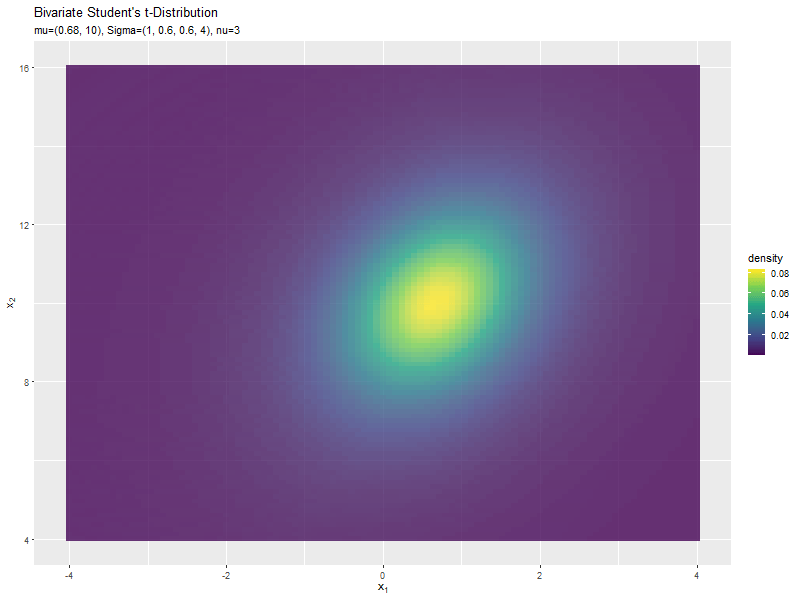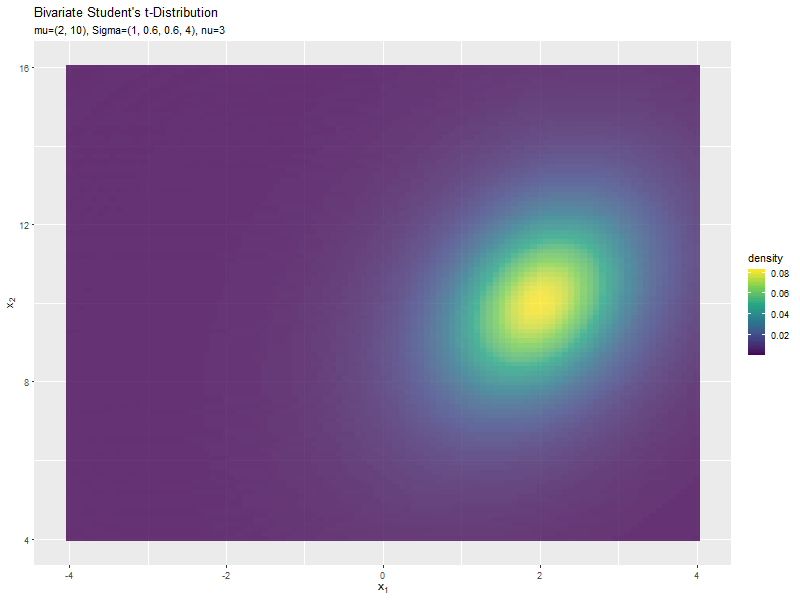
$\mu_1$の値に応じて、x軸方向に移動するのが分かります。
位置ベクトル(2軸)の影響
y軸方向の位置パラメータ$\mu_2$の値を変化させ、$\nu, \mu_1, \boldsymbol{\Sigma}$を固定します。
・コード(クリックで展開)
# 次元数を設定 D <- 2 # 自由度を指定 nu <- 3 # x軸の位置パラメータを指定 mu_1 <- 6 # y軸の位置パラメータとして利用する値を指定 mu_2_vals <- seq(from = -2, to = 2, by = 0.04) |> round(digits = 2) # スケール行列を指定 sigma_dd <- matrix(c(1, 0.6, 0.6, 4), nrow = D, ncol = D) # フレーム数を設定 frame_num <- length(mu_2_vals) frame_num
## [1] 101
値の間隔が一定になるように$\mu_2$の値をmu_2_valsとして作成します。また、$\mu_1$をmu_1として値を指定します。
パラメータごとに分布を計算します。
# xの値を作成 x_1_vals <- seq( from = mu_1 - sqrt(sigma_dd[1, 1]) * 3, to = mu_1 + sqrt(sigma_dd[1, 1]) * 3, length.out = 101 ) x_2_vals <- seq( from = min(mu_2_vals) - sqrt(sigma_dd[2, 2]) * 2, to = max(mu_2_vals) + sqrt(sigma_dd[2, 2]) * 2, length.out = 101 ) # パラメータごとに多次元t分布を計算 anime_dens_df <- tidyr::expand_grid( mu_2 = mu_2_vals, x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(mu_2) |> # 分布の計算用にグループ化 dplyr::mutate( density = mvnfast::dmvt( X = as.matrix(cbind(x_1, x_2)), mu = unique(cbind(mu_1, mu_2)), sigma = sigma_dd, df = nu ), # 確率密度 parameter = paste0("mu=(", mu_1, ", ", mu_2, "), Sigma=(", paste0(sigma_dd, collapse = ", "), "), nu=", nu) |> factor(levels = paste0("mu=(", mu_1, ", ", mu_2_vals, "), Sigma=(", paste0(sigma_dd, collapse = ", "), "), nu=", nu)) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_dens_df
## # A tibble: 1,030,301 × 5 ## mu_2 x_1 x_2 density parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 -2 3 -6 0.00200 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4), nu=3 ## 2 -2 3 -5.88 0.00206 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4), nu=3 ## 3 -2 3 -5.76 0.00211 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4), nu=3 ## 4 -2 3 -5.64 0.00216 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4), nu=3 ## 5 -2 3 -5.52 0.00221 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4), nu=3 ## 6 -2 3 -5.4 0.00226 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4), nu=3 ## 7 -2 3 -5.28 0.00231 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4), nu=3 ## 8 -2 3 -5.16 0.00235 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4), nu=3 ## 9 -2 3 -5.04 0.00239 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4), nu=3 ## 10 -2 3 -4.92 0.00243 mu=(6, -2), Sigma=(1, 0.6, 0.6, 4), nu=3 ## # … with 1,030,291 more rows
「自由度の影響」のnu, nu_valsとmu_2, mu_2_valsを入れ換えるように処理します。
「自由度の影響」のコードで作図できます。
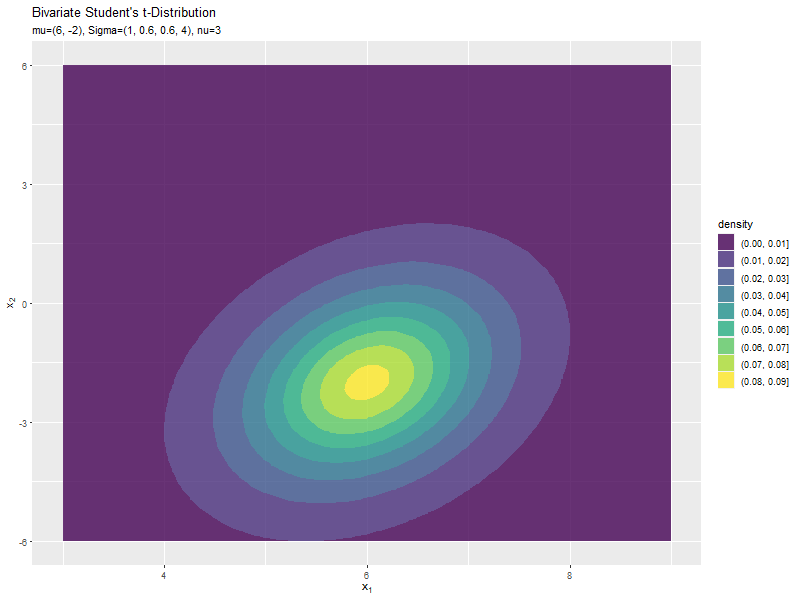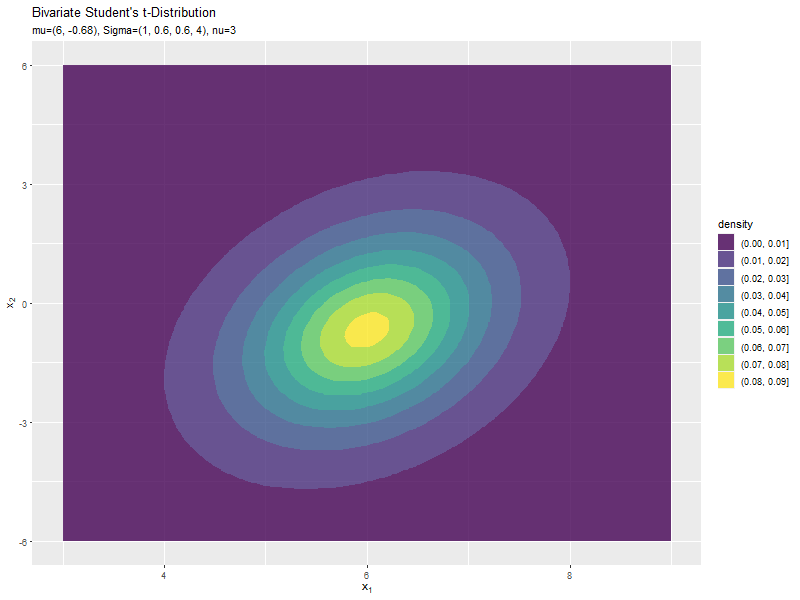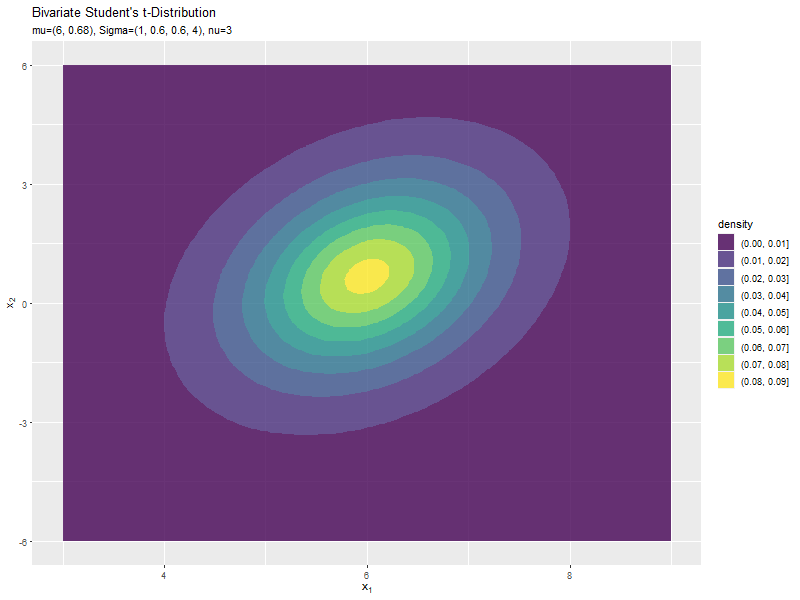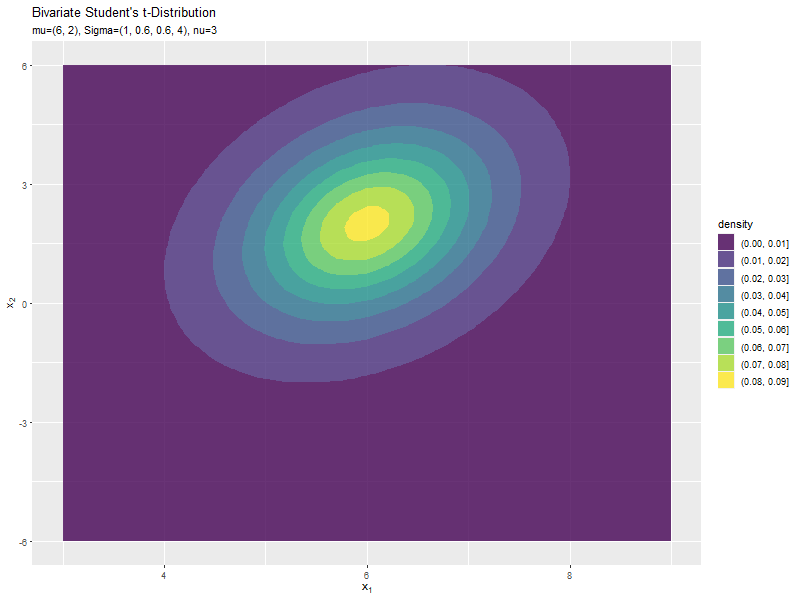
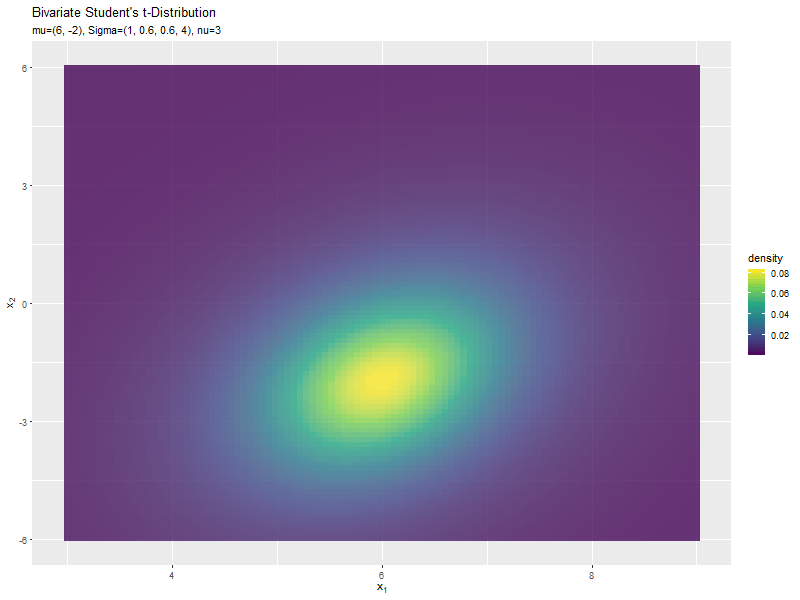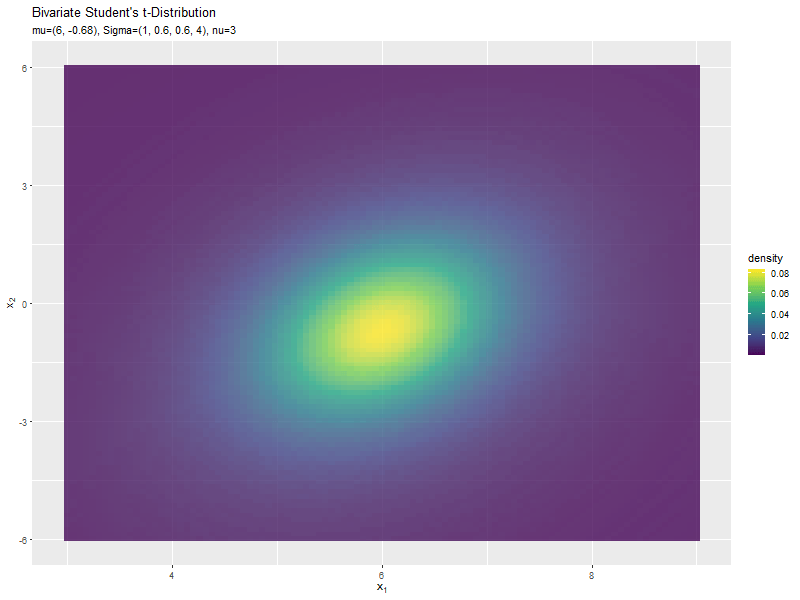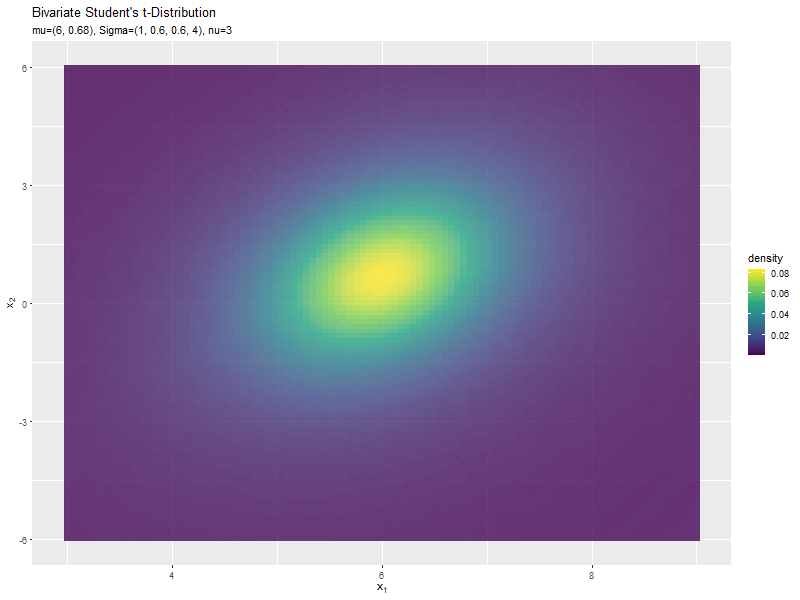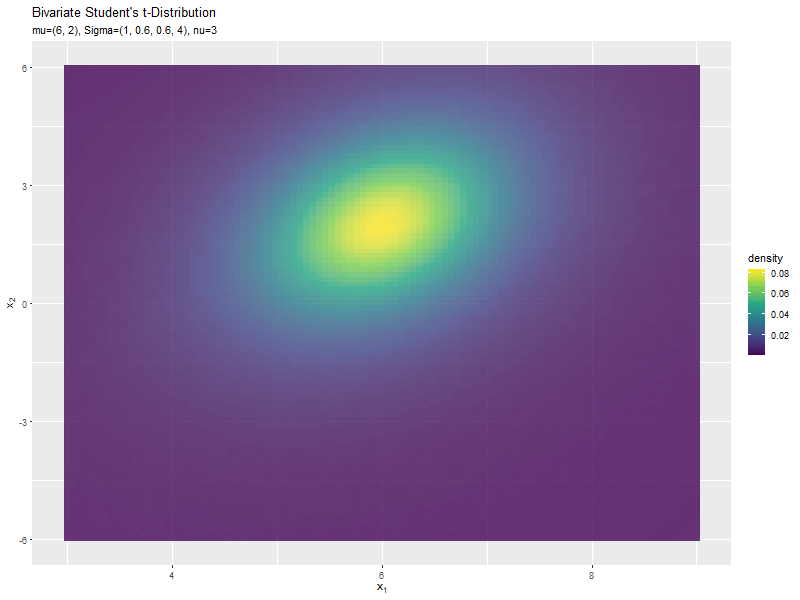
$\mu_2$の値に応じて、y軸方向に移動するのが分かります。
スケール行列(1,1成分)の影響
続いて、x軸方向のスケール$\sigma_{1,1}$の値を変化させ、$\nu, \boldsymbol{\mu}, \sigma_{1,2}, \sigma_{2,1}, \sigma_{2,2}$を固定します。
・コード(クリックで展開)
# 次元数を設定 D <- 2 # 自由度を指定 nu <- 3 # 位置ベクトルを指定 mu_d <- c(6, 10) # x軸のスケールパラメータとして利用する値を指定 sigma_11_vals <- seq(from = 0.5, to = 6, by = 0.1) |> round(digits = 1) # y軸のスケールパラメータを指定 sigma_22 <- 4 # x・y軸のスケールパラメータを指定 sigma_12 <- 0.6 # フレーム数を設定 frame_num <- length(sigma_11_vals) frame_num
## [1] 56
値の間隔が一定になるように$\sigma_{1,1}$の値をsigma_11_valsとして作成します。また、$\sigma_{1,2} = \sigma_{2,1}$をsigma_12、$\sigma_{2,2}$をsigma_22として値を指定します。
パラメータごとに分布を計算します。
# xの値を作成 x_1_vals <- seq( from = mu_d[1] - sqrt(max(sigma_11_vals)) * 2, to = mu_d[1] + sqrt(max(sigma_11_vals)) * 2, length.out = 101 ) x_2_vals <- seq( from = mu_d[2] - sqrt(sigma_22) * 3, to = mu_d[2] + sqrt(sigma_22) * 3, length.out = 101 ) # パラメータごとに多次元t分布を計算 anime_dens_df <- tidyr::expand_grid( sigma_11 = sigma_11_vals, # パラメータ x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(sigma_11) |> # 分布の計算用にグループ化 dplyr::mutate( density = mvnfast::dmvt( X = as.matrix(cbind(x_1, x_2)), mu = mu_d, sigma = matrix(c(unique(sigma_11), sigma_12, sigma_12, sigma_22), nrow = D, ncol = D), df = nu ), # 確率密度 parameter = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma_11, ", ", sigma_12, ", ", sigma_12, ", ", sigma_22, "), nu=", nu) |> factor(levels = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma_11_vals, ", ", sigma_12, ", ", sigma_12, ", ", sigma_22, "), nu=", nu)) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_dens_df
## # A tibble: 571,256 × 5 ## sigma_11 x_1 x_2 density parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 0.5 1.10 4 0.000104 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4), nu=3 ## 2 0.5 1.10 4.12 0.000104 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4), nu=3 ## 3 0.5 1.10 4.24 0.000104 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4), nu=3 ## 4 0.5 1.10 4.36 0.000104 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4), nu=3 ## 5 0.5 1.10 4.48 0.000104 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4), nu=3 ## 6 0.5 1.10 4.6 0.000104 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4), nu=3 ## 7 0.5 1.10 4.72 0.000104 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4), nu=3 ## 8 0.5 1.10 4.84 0.000103 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4), nu=3 ## 9 0.5 1.10 4.96 0.000103 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4), nu=3 ## 10 0.5 1.10 5.08 0.000103 mu=(6, 10), Sigma=(0.5, 0.6, 0.6, 4), nu=3 ## # … with 571,246 more rows
「自由度の影響」のnu, nu_valsとsigma_11, sigma_11_valsを入れ換えるように処理します。
「自由度の影響」のコードで作図できます。
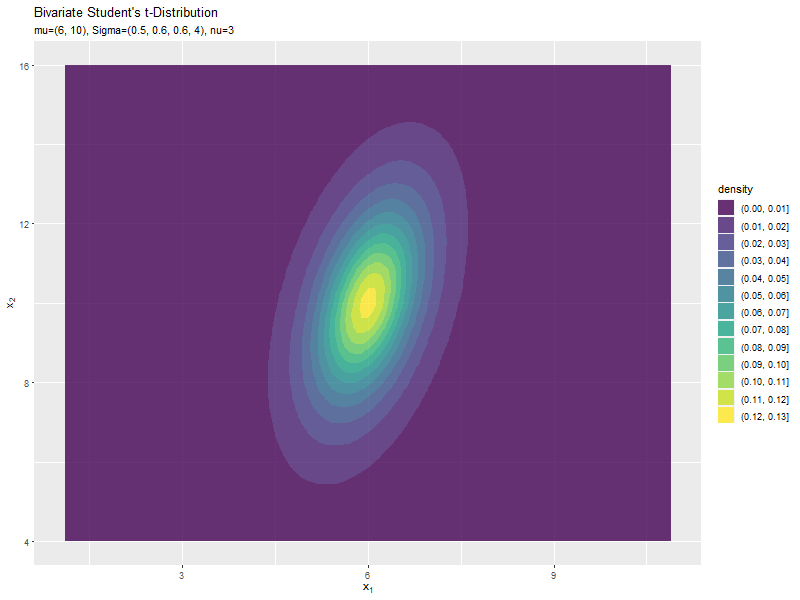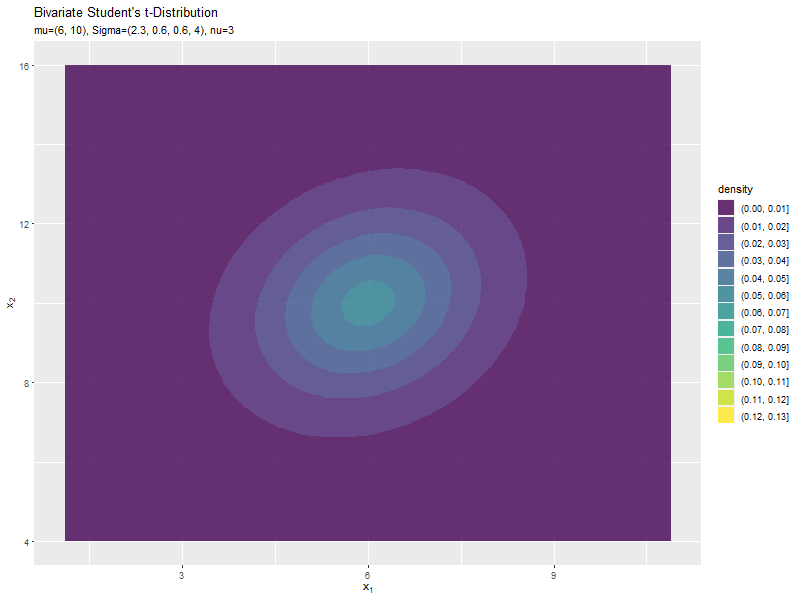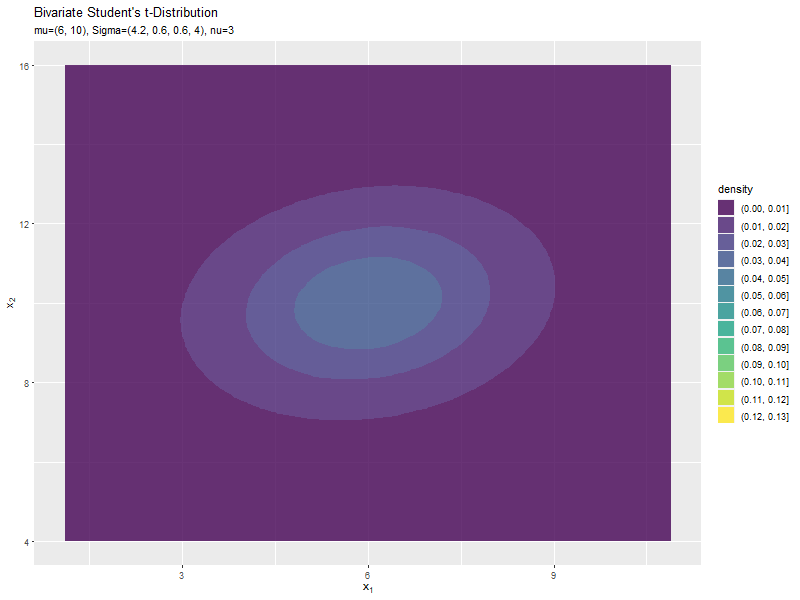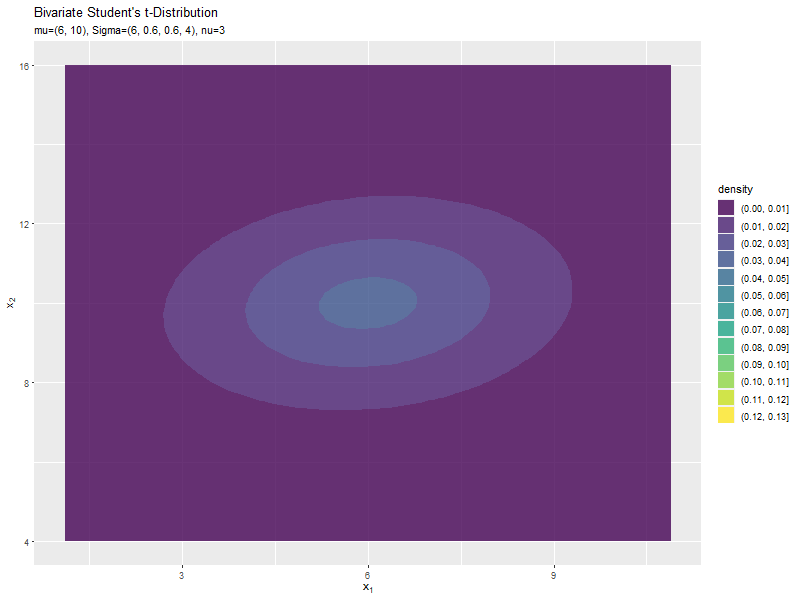
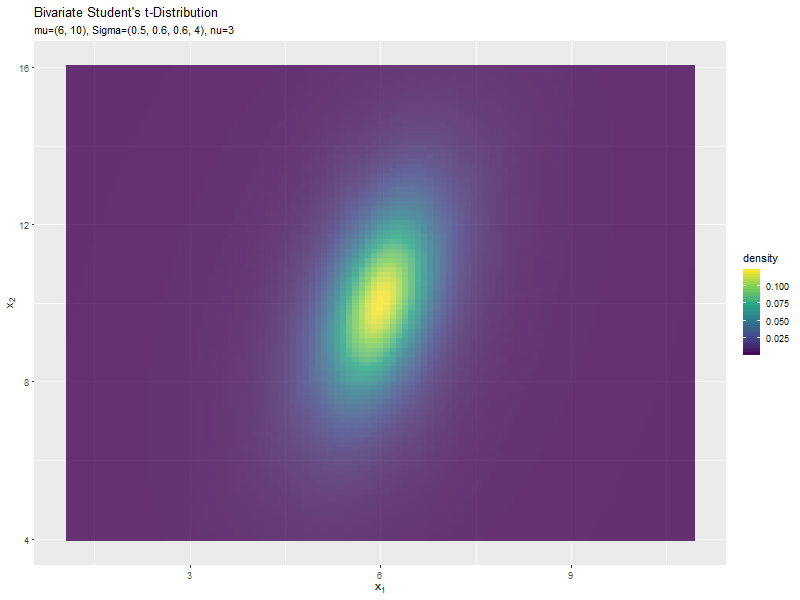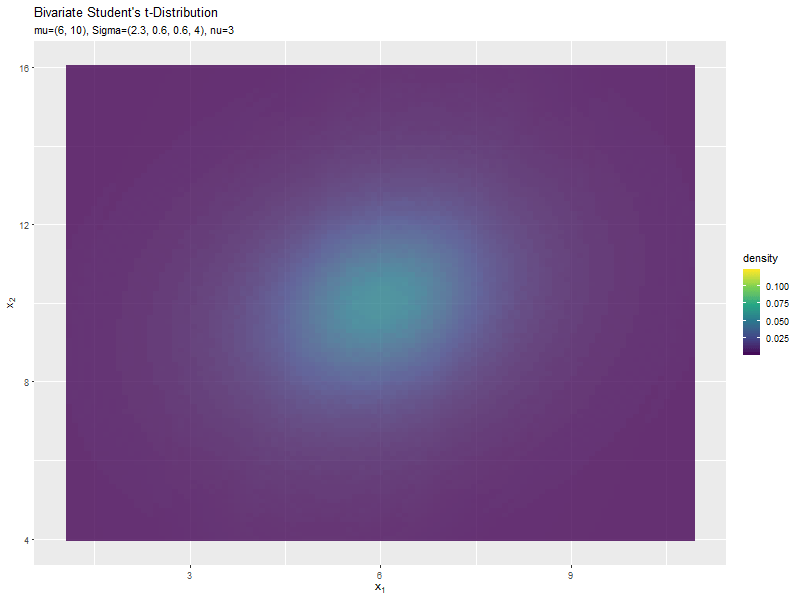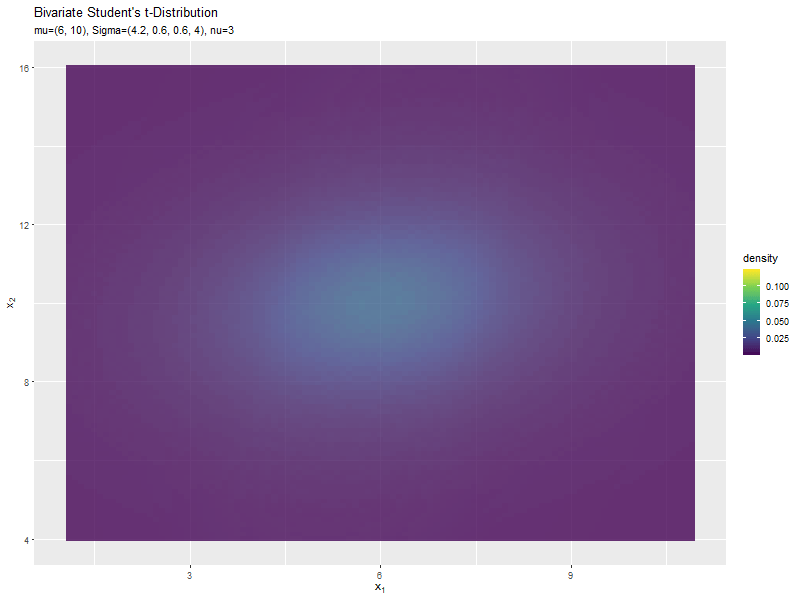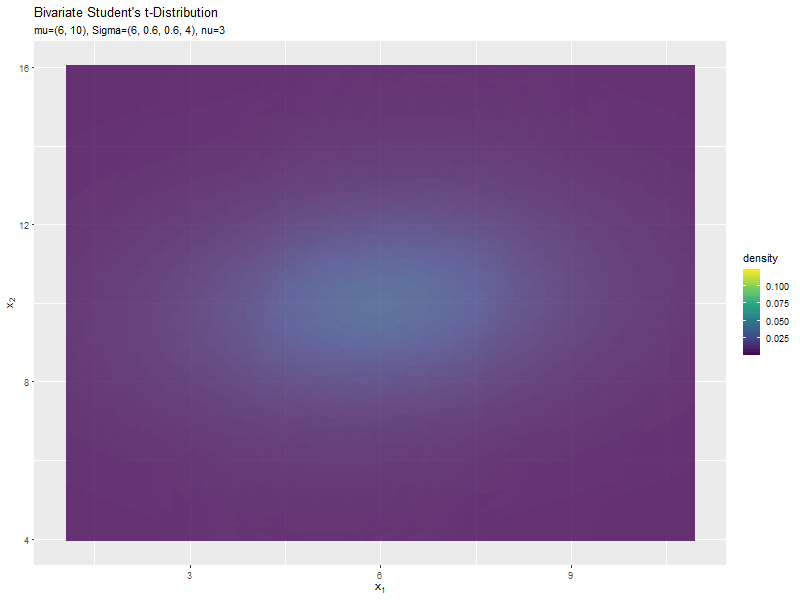
$\sigma_{1,1}$の値に応じて、x軸方向に広がるのが分かります。
スケール行列(2,2成分)の影響
y軸方向のスケール$\sigma_{2,2}$の値を変化させ、$\nu, \boldsymbol{\mu}, \sigma_{1,1}, \sigma_{1,2}, \sigma_{2,1}$を固定します。
・コード(クリックで展開)
# 次元数を設定 D <- 2 # 自由度を指定 nu <- 3 # 位置ベクトルを指定 mu_d <- c(6, 10) # x軸のスケールパラメータを指定 sigma_11 <- 1 # y軸のスケールパラメータとして利用する値を指定 sigma_22_vals <- seq(from = 0.5, to = 6, by = 0.1) |> round(digits = 1) # x・y軸のスケールパラメータを指定 sigma_12 <- 0.6 # フレーム数を設定 frame_num <- length(sigma_22_vals) frame_num
## [1] 56
値の間隔が一定になるように$\sigma_{2,2}$の値をsigma_22_valsとして作成します。また、$\sigma_{1,1}$をsigma_11、$\sigma_{1,2} = \sigma_{2,1}$をsigma_12として値を指定します。
パラメータごとに分布を計算します。
# xの値を作成 x_1_vals <- seq( from = mu_d[1] - sqrt(sigma_11) * 3, to = mu_d[1] + sqrt(sigma_11) * 3, length.out = 101 ) x_2_vals <- seq( from = mu_d[2] - sqrt(max(sigma_22_vals)) * 2, to = mu_d[2] + sqrt(max(sigma_22_vals)) * 2, length.out = 101 ) # パラメータごとに多次元t分布を計算 anime_dens_df <- tidyr::expand_grid( sigma_22 = sigma_22_vals, # パラメータ x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(sigma_22) |> # 分布の計算用にグループ化 dplyr::mutate( density = mvnfast::dmvt( X = as.matrix(cbind(x_1, x_2)), mu = mu_d, sigma = matrix(c(sigma_11, sigma_12, sigma_12, unique(sigma_22)), nrow = D, ncol = D), df = nu ), # 確率密度 parameter = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma_11, ", ", sigma_12, ", ", sigma_12, ", ", sigma_22, "), nu=", nu) |> factor(levels = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma_11, ", ", sigma_12, ", ", sigma_12, ", ", sigma_22_vals, "), nu=", nu)) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_dens_df
## # A tibble: 571,256 × 5 ## sigma_22 x_1 x_2 density parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 0.5 3 5.10 0.000114 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5), nu=3 ## 2 0.5 3 5.20 0.000130 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5), nu=3 ## 3 0.5 3 5.30 0.000150 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5), nu=3 ## 4 0.5 3 5.39 0.000173 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5), nu=3 ## 5 0.5 3 5.49 0.000200 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5), nu=3 ## 6 0.5 3 5.59 0.000232 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5), nu=3 ## 7 0.5 3 5.69 0.000270 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5), nu=3 ## 8 0.5 3 5.79 0.000315 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5), nu=3 ## 9 0.5 3 5.88 0.000370 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5), nu=3 ## 10 0.5 3 5.98 0.000435 mu=(6, 10), Sigma=(1, 0.6, 0.6, 0.5), nu=3 ## # … with 571,246 more rows
「自由度の影響」のnu, nu_valsとsigma_22, sigma_22_valsを入れ換えるように処理します。
「自由度の影響」のコードで作図できます。
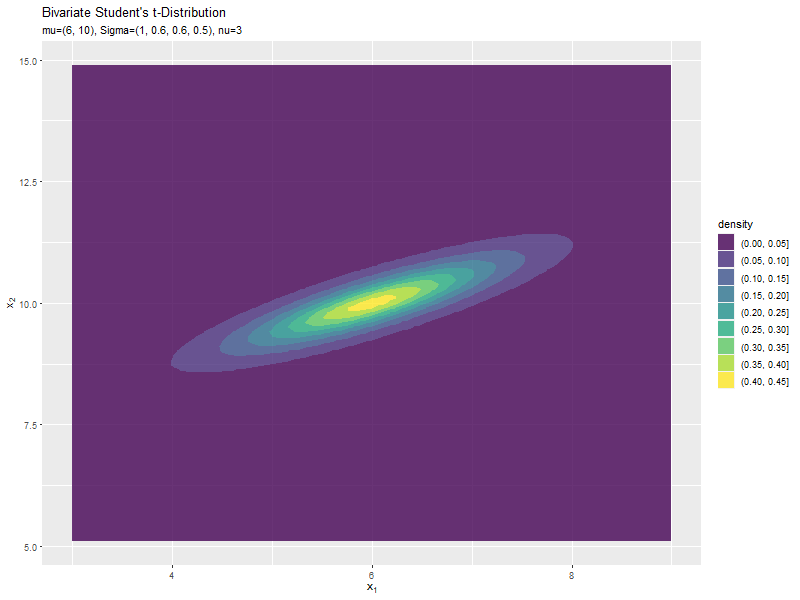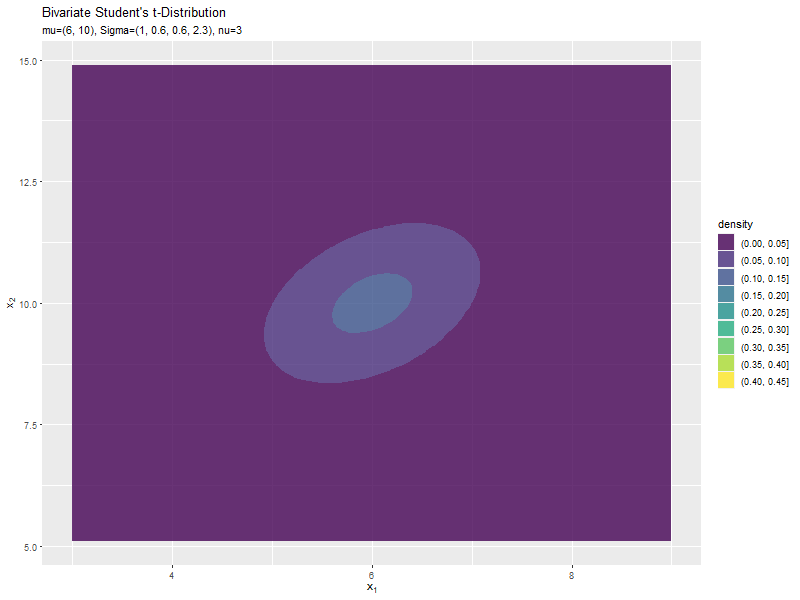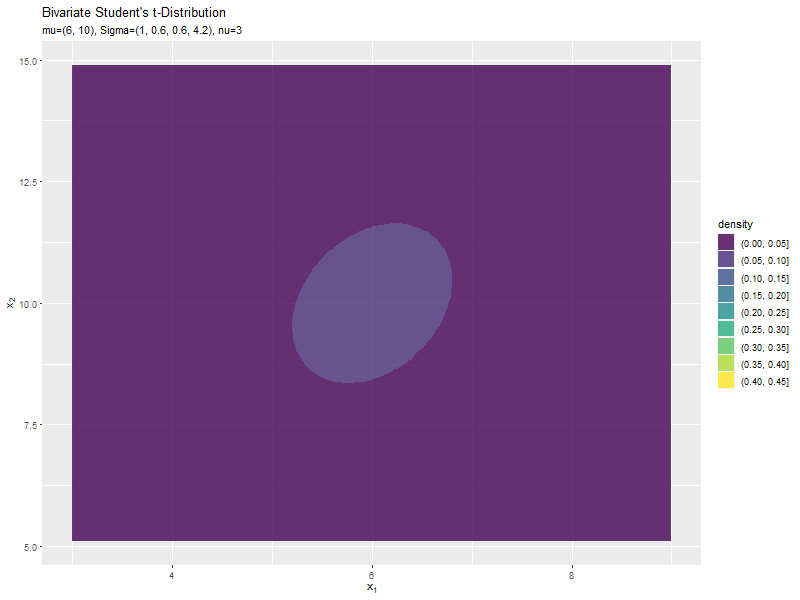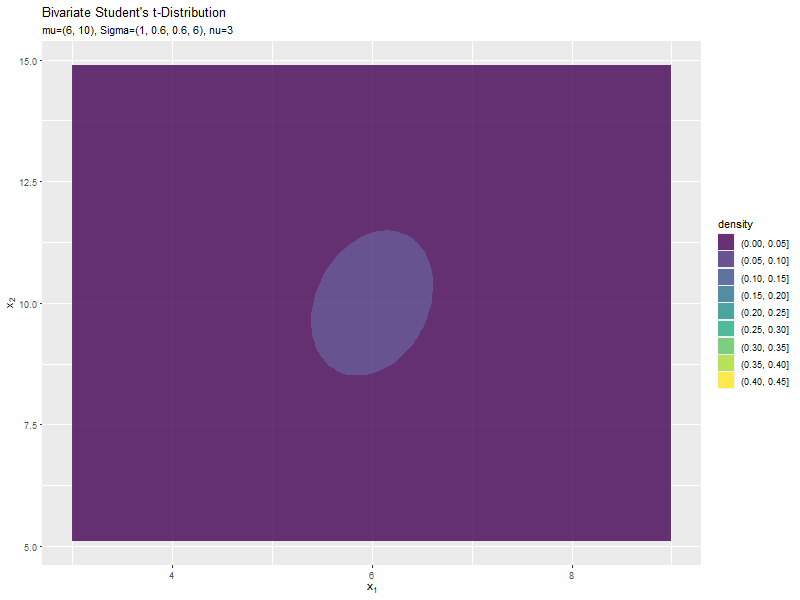
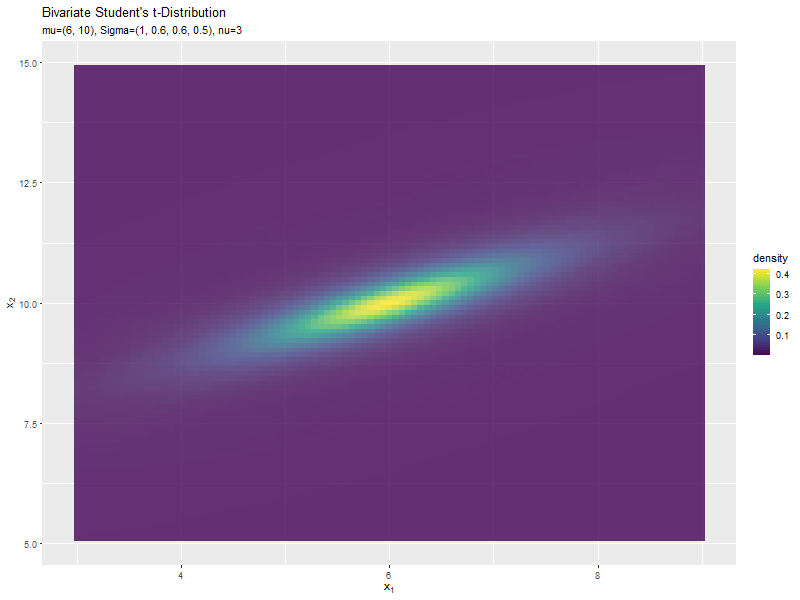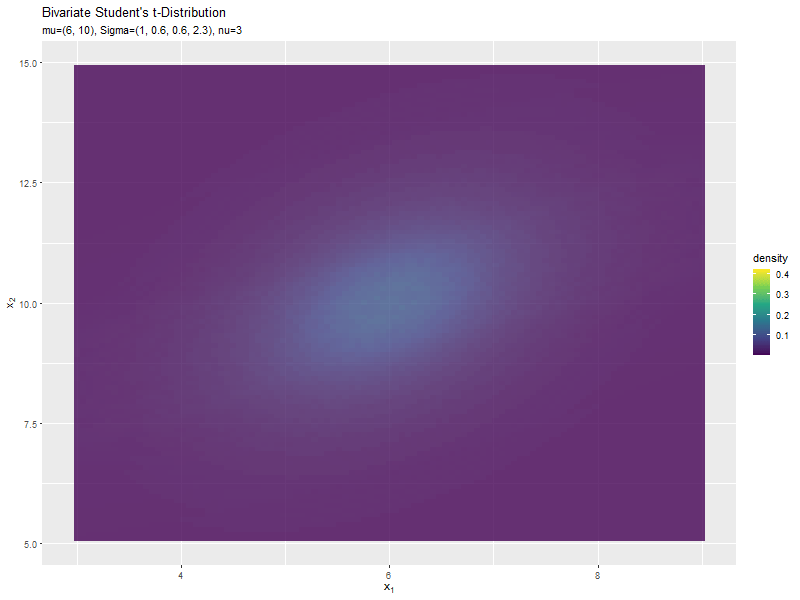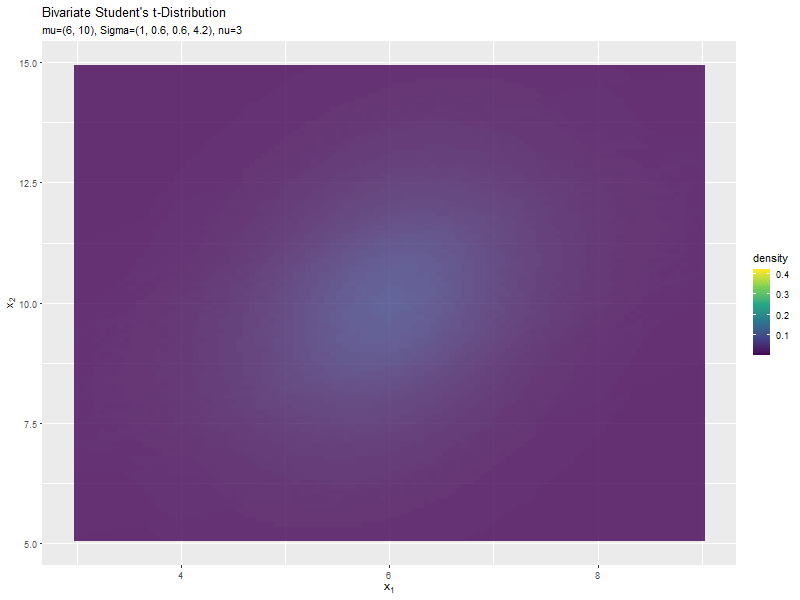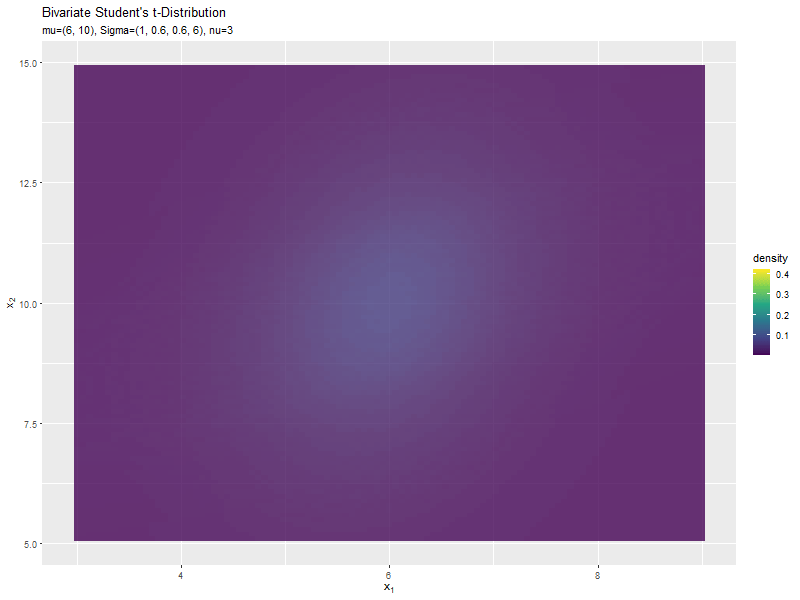
$\sigma_{2,2}$の値に応じて、y軸方向に広がるのが分かります。
スケール行列(1,2成分)の影響
両軸のスケール$\sigma_{1,2}, \sigma_{2,1}$の値を変化させ、$\nu, \boldsymbol{\mu}, \sigma_{1,1}, \sigma_{2,2}$を固定します。
・コード(クリックで展開)
# 次元数を設定 D <- 2 # 自由度を指定 nu <- 3 # 位置ベクトルを指定 mu_d <- c(6, 10) # x軸・y軸のスケールパラメータを指定 sigma_11 <- 4 sigma_22 <- 10 # x・y軸のスケールパラメータとして利用する値を指定 sigma_12_vals <- seq(from = -5, to = 5, by = 0.1) |> round(digits = 1) # フレーム数を設定 frame_num <- length(sigma_12_vals) frame_num
## [1] 101
値の間隔が一定になるように$\sigma_{1,2} = \sigma_{2,1}$の値をsigma_12_valsとして作成します。また、$\sigma_{1,1}, \sigma_{2,2}$をsigma_11, sigma_22として値を指定します。
パラメータごとに分布を計算します。
# xの値を作成 x_1_vals <- seq( from = mu_d[1] - sqrt(sigma_11) * 3, to = mu_d[1] + sqrt(sigma_11) * 3, length.out = 101 ) x_2_vals <- seq( from = mu_d[2] - sqrt(sigma_22) * 3, to = mu_d[2] + sqrt(sigma_22) * 3, length.out = 101 ) # パラメータごとに多次元t分布を計算 anime_dens_df <- tidyr::expand_grid( sigma_12 = sigma_12_vals, # パラメータ x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(sigma_12) |> # 分布の計算用にグループ化 dplyr::mutate( density = mvnfast::dmvt( X = as.matrix(cbind(x_1, x_2)), mu = mu_d, sigma = matrix(c(sigma_11, unique(sigma_12), unique(sigma_12), sigma_22), nrow = D, ncol = D), df = nu ), # 確率密度 parameter = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma_11, ", ", sigma_12, ", ", sigma_12, ", ", sigma_22, "), nu=", nu) |> factor(levels = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma_11, ", ", sigma_12_vals, ", ", sigma_12_vals, ", ", sigma_22, "), nu=", nu)) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_dens_df
## # A tibble: 1,530,150 × 5 ## nu x_1 x_2 density parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 0.1 3 4 0.000467 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## 2 0.1 3 4.12 0.000477 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## 3 0.1 3 4.24 0.000487 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## 4 0.1 3 4.36 0.000497 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## 5 0.1 3 4.48 0.000507 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## 6 0.1 3 4.6 0.000517 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## 7 0.1 3 4.72 0.000527 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## 8 0.1 3 4.84 0.000538 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## 9 0.1 3 4.96 0.000548 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## 10 0.1 3 5.08 0.000558 mu=(6, 10), Sigma=(1, 0.6, 0.6, 4), nu=0.1 ## # … with 1,530,140 more rows
「自由度の影響」のnu, nu_valsとsigma_12, sigma_12_valsを入れ換えるように処理します。
「自由度の影響」のコードで作図できます。
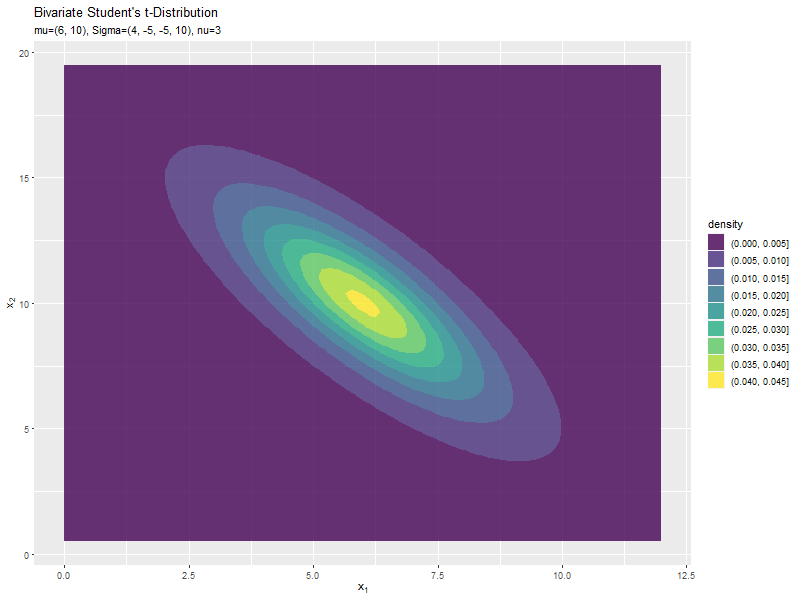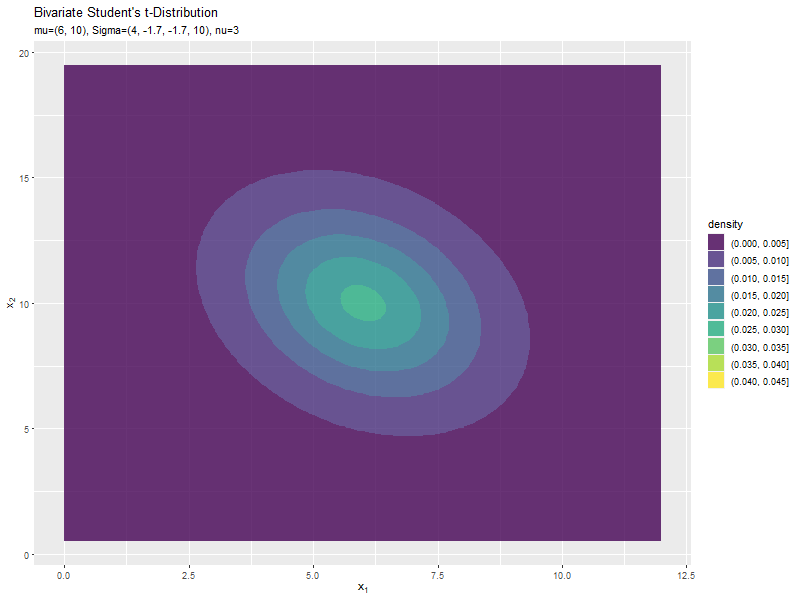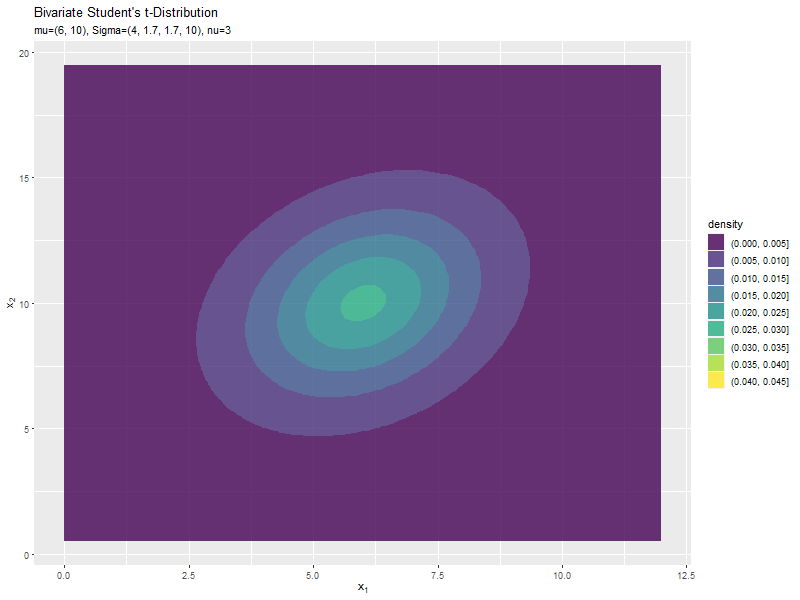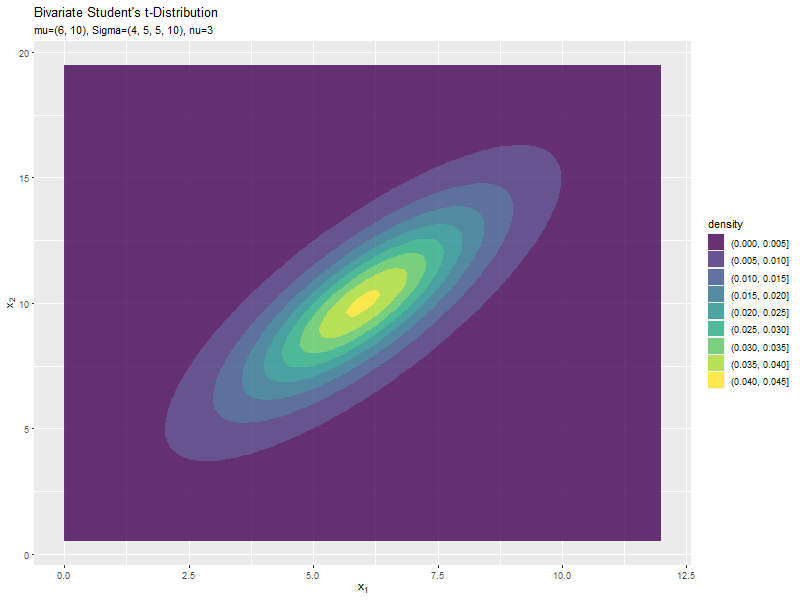
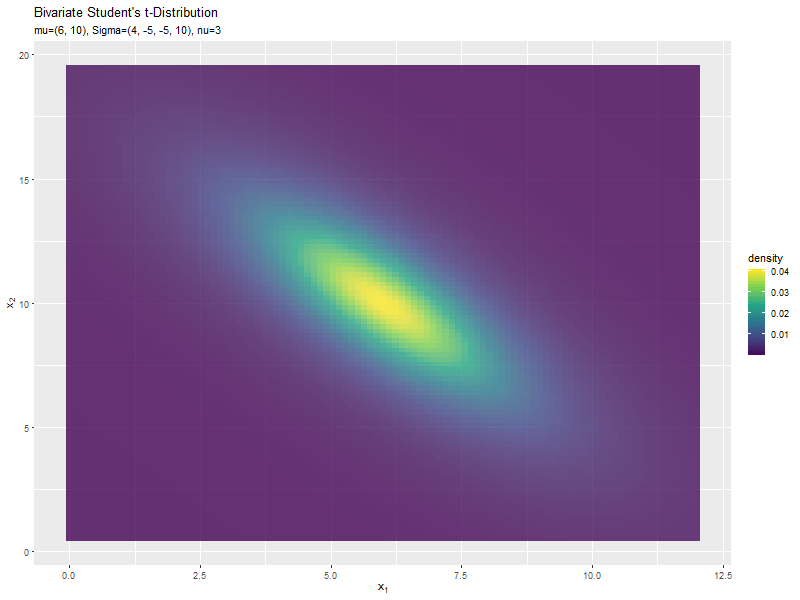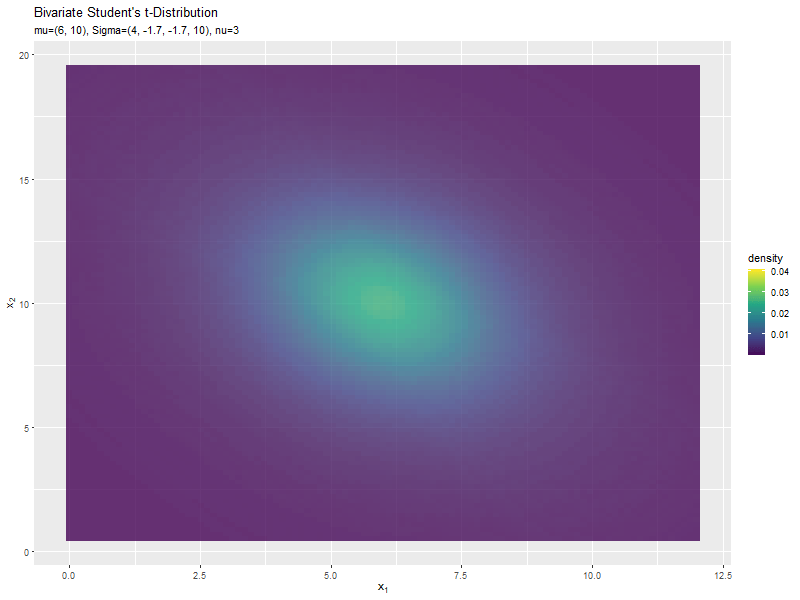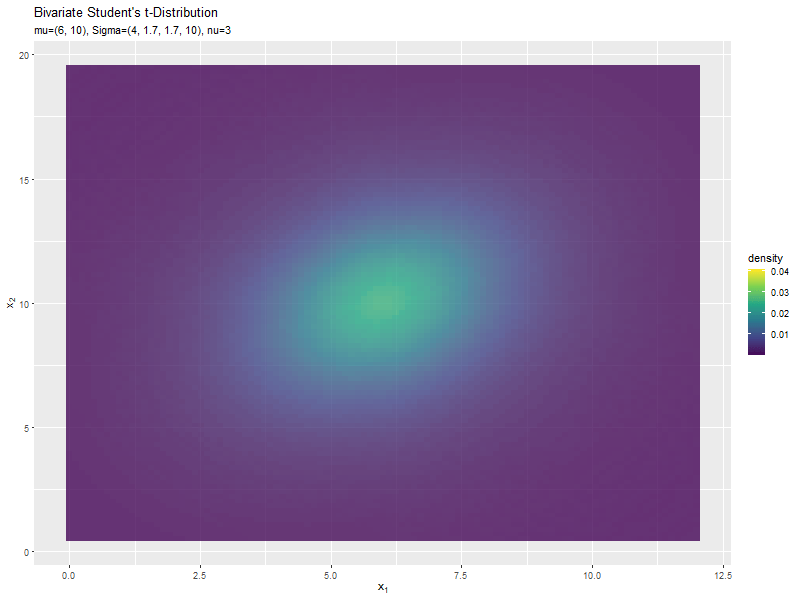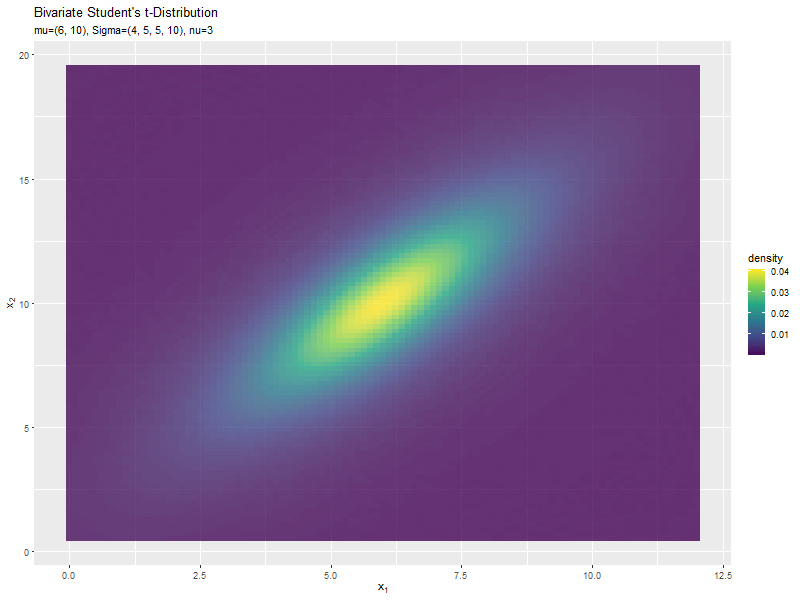
$\sigma_{1,2}$の値に応じて、x軸とy軸の広がる方向が変化するのが分かります。
この記事では、多次元スチューデントのt分布の作図を確認しました。
参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上』,丸善出版,2012年.
おわりに
半分コピペで済んでしまって書いてて面白くなかったです(コピペはコピペで面倒で決して楽ではないです)。出来上がりもガウス分布と代り映えしないし、なので自由度のアニメーションが一番やって良かったです。ガウス分布と比較してみたら面白くなりますかね。エントロピーの可視化とかと合わせてやってみたいです、いつか。
2022年11月30日は、モーニング娘。'22の加賀楓さんの23歳のお誕生日です🍁♨先ほどアップされたMVを観ましょう聴きましょう。
卒コンまでもうあとわずか、つつがなく卒業を迎えられますように。
【次の内容】
つづかない