はじめに
『ゼロから作るDeep Learning 4 ――強化学習編』の独学時のまとめノートです。初学者の補助となるようにゼロつくシリーズの4巻の内容に解説を加えていきます。本と一緒に読んでください。
この記事は、5.2節の内容です。状態価値関数をモンテカルロ法により逐次更新する方法を確認します。
【前節の内容】
【他の記事一覧】
【この記事の内容】
5.2 モンテカルロ法による方策評価
モンテカルロ法を用いた状態価値関数の計算(方策評価)を考えます。収益の計算や割引率、指数移動平均については「2.3:収益と状態価値関数【ゼロつく4のノート】 - からっぽのしょこ」を参照してください。
5.2.1 価値関数をモンテカルロ法で求める
まずは、状態価値関数の計算を数式で確認します。
・数式の確認
時刻$t$の収益は、割引率$0 \leq \gamma \leq 1$を用いて、次の式で計算するのでした(2.3.2項・3.1.2項)。
また、状態価値関数は、現在の状態が$s$のときの収益$G$の期待値で定義されました(2.3.3項)。
真の状態価値関数$v_{\pi}(s)$を求めるには、方策$\pi$が既知である必要があります。
そこで、方策が未知の場合は、サンプリングした収益$G^{(i)}$の標本平均を状態価値関数の推定値$V_{\pi}(s)$とします。
ここで、$i$回目のエピソードで得られた収益を$G^{(i)}$で表します。
標本平均をインクリメンタルに求める場合は、次の式を繰り返し計算します(1.3.2項・5.4.1項)。
$n$回更新した状態価値関数の推定値($n$個の収益の標本平均)を$V_n(s)$で表します。
5.2.2-3 モンテカルロ法の効率の良い実装
次は、状態価値関数の計算をプログラムで確認します。5.3節のシミュレーションを1エピソード行い状態価値の推定値を求めます。5.3節とあわせて読んでください。
利用するライブラリを読み込みます。
# ライブラリを読み込み import numpy as np from collections import defaultdict import matplotlib.pyplot as plt from matplotlib.colors import LinearSegmentedColormap from matplotlib.animation import FuncAnimation
推移をアニメーションで確認するのにanimationモジュールを利用します。不要であれば省略してください。
また、3×4マスのグリッドワールドのクラスGridWorldを読み込みます。
# 実装済みのクラスと関数を読み込み import sys sys.path.append('../deep-learning-from-scratch-4-master') from common.gridworld import GridWorld from ch05.mc_eval import RandomAgent
実装済みクラスの読み込みについては「3.6.1:MNISTデータセットの読み込み【ゼロつく1のノート(Python)】 - からっぽのしょこ」、GridWorldクラスについては「4.2.1:GridWorldクラスの実装:評価と改善に関するメソッド【ゼロつく4のノート】 - からっぽのしょこ」「4.2.1:GridWorldクラスの実装:可視化に関するメソッド【ゼロつく4のノート】 - からっぽのしょこ」、RandomAgentクラスについては「5.4.2項」を参照してください。(図が出力されますが?無視します。)
グリッドワールドとマルコフ法によるエージェントのインスタンスを作成して、1エピソードの処理を実行します。
# 環境・エージェントのインスタンスを作成 env = GridWorld() agent = RandomAgent() # スタートの状態を設定 state = env.reset() print(state) # 試行回数(時刻)を初期化 t = 0 # ヒートマップの色付け用の値を初期化 vmax = 0.0 vmin = 0.0 # 1エピソードのシミュレーション while True: # 試行回数をカウント t += 1 # 確率論的方策に従い行動を決定 action = agent.get_action(state) # サンプルデータを取得 next_state, reward, done = env.step(action) # 結果を記録 agent.add(state, action, reward) # ゴールに着いた場合 if done: # 状態価値関数を計算 agent.eval() # 最大値・最小値を保存 vmax = max([vmax] + list(agent.V.values())) vmin = min([vmin] + list(agent.V.values())) # シミュレーションを終了 break # 状態を更新 state = next_state # サンプルデータを複製 memory_lt = agent.memory.copy() # ゴールマスのダミーのサンプルを記録 memory_lt.append((next_state, '_', 0.0)) # 試行回数を保存 T = t # 試行回数を表示 print('iteration :', T) print(next_state)
(2, 0)
iteration : 39
(0, 3)
この記事では、スタートのマス(最初の状態)を$L_{2,0}$、ゴールのマスを$L_{0,3}$で表します。ゴールマスに辿り着くとエピソードを終了します。問題設定や処理の詳細は5.3.3項を参照してください。
agentのmemoryに保存されているT個のサンプルデータ(状態・行動・報酬)を取り出してmemory_ltとします。また作図用に、最終的な状態(ゴールマス)のデータを含めるため、行動と報酬をダミーの値として格納しておきます。
memory_ltからマスのインデックスと報酬を取り出して、それぞれの配列を作成します。
# x軸の値・y軸の値・報酬の受け皿を初期化 memory_x = np.empty(T+1) memory_y = np.empty(T+1) memory_r = np.empty(T+1) # x軸の値・y軸の値・報酬を配列に格納 for t in range(len(memory_lt)): # 時刻tの状態(マスのインデックス)・行動・報酬を取得 (y, x), a, r = memory_lt[t] # 値を格納 memory_x[t] = x memory_y[t] = y memory_r[t] = r print(memory_x[:10]) print(memory_y[:10]) print(memory_r[:10])
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[2. 1. 1. 0. 0. 0. 0. 0. 1. 2.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
状態のタプルをアンパックして受け取り、それぞれ配列に格納します。
この配列は、リスト内包表記を使って次のようにも処理できます(intかfloatかが変わってますが)。
# x軸の値・y軸の値・報酬を配列に格納 memory_x = np.array([memory_lt[t][0][1] for t in range(T+1)]) memory_y = np.array([memory_lt[t][0][0] for t in range(T+1)]) memory_r = np.array([memory_lt[t][2] for t in range(T+1)]) print(memory_x[:10]) print(memory_y[:10]) print(memory_r[:10])
[0 0 0 0 0 0 0 0 0 0]
[2 1 1 0 0 0 0 0 1 2]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
1エピソードで推定した状態価値関数をヒートマップで確認します。
# 状態価値関数のヒートマップを作成
env.render_v(v=agent.V)
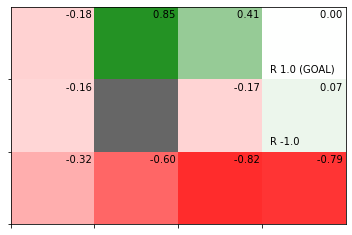
各マスの状態価値の計算過程を確認していきます。
まずは、エージェントが遷移した状態(通ったマス)を確認します。
・作図コード(クリックで展開)
# マップのサイズを取得 xs = env.width ys = env.height # グラフの設定 plt.figure(figsize=(12, 9), facecolor='white') # 図の設定 plt.suptitle('state transition', fontsize=20) # 全体のタイトル plt.title('t='+str(T) + ', total reward:'+str(np.sum(memory_r)), fontsize=15, loc='left') # タイトル plt.xticks(ticks=np.arange(xs)) # x軸の目盛位置 plt.yticks(ticks=np.arange(ys), labels=ys-np.arange(ys)-1) # y軸の目盛位置 plt.xlim(xmin=0, xmax=xs) # x軸の範囲 plt.ylim(ymin=0, ymax=ys) # y軸の範囲 plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False) # 軸ラベル plt.grid() # グリッド線 # マス(状態)ごとに処理 for state in env.states(): # マスのインデックスを取得 y, x = state # 報酬を抽出 r = env.reward_map[y, x] # 報酬がある場合 if r != 0 and r is not None: # 報酬ラベル用の文字列を作成 txt = 'R ' + str(r) # ゴールの場合 if state == env.goal_state: # 報酬ラベルにゴールを追加 txt = txt + ' (GOAL)' # 報酬ラベルを描画 plt.text(x=x+0.1, y=ys-y-0.9, s=txt, ha='left', va='bottom', fontsize=15) # 壁のマスの場合 if state == env.wall_state: # 壁を描画 rect = plt.Rectangle(xy=(x, ys-y-1), width=1, height=1, fc=(0.4, 0.4, 0.4, 1.0)) # 長方形を作成 plt.gca().add_patch(rect) # 重ねて描画 # 壁以外のマス場合 else: # 各状態の遷移回数ラベルを描画 cnts_txt = 'n=' + str(agent.cnts[state]) plt.text(x=x+0.1, y=ys-y-0.1, s=cnts_txt, ha='left', va='top', size=15) # 線が重ならないようにするための値を作成 d = np.linspace(0.1, 0.9, num=T+1) # エージェントの軌跡を描画 plt.plot(memory_x+d, ys-memory_y-1.0+d) plt.scatter(x=memory_x+d, y=ys-memory_y-1.0+d, marker='h') plt.show()
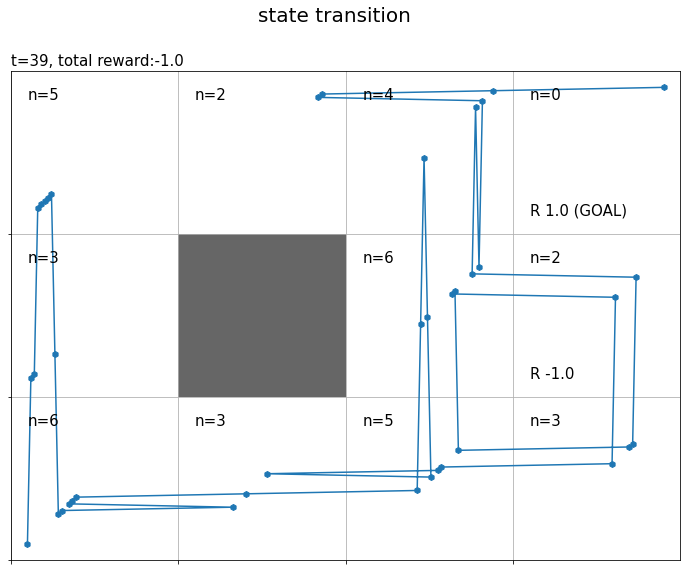
状態の遷移を青線、各状態に遷移した回数を$n$で示します。
(最終的な)各状態の遷移回数はagentのcntsに記録されています。
このグラフをアニメーションで確認します。
・作図コード(クリックで展開)
# 各状態の遷移回数を初期化 cnts = defaultdict(lambda: 0) # グラフを初期化 fig = plt.figure(figsize=(12, 9), facecolor='white') # 図の設定 fig.suptitle('state transition', fontsize=20) # 全体のタイトル # 作図処理を関数として定義 def update(t): # 前フレームのグラフを初期化 plt.cla() # t回目の状態・報酬を取得 state, _, reward = memory_lt[t] # 時刻tの状態の遷移回数をカウントアップ if t+1<= T: # ゴールマスを除く cnts[state] += 1 # 総報酬を計算 total_reward = np.sum(memory_r[:t+1]) # マス(状態)ごとに処理 for state in env.states(): # マスのインデックスを取得 y, x = state # 報酬を抽出 r = env.reward_map[y, x] # 報酬がある場合 if r != 0 and r is not None: # 報酬ラベル用の文字列を作成 txt = 'R ' + str(r) # ゴールの場合 if state == env.goal_state: # 報酬ラベルにゴールを追加 txt = txt + ' (GOAL)' # 報酬ラベルを描画 plt.text(x=x+0.1, y=ys-y-0.9, s=txt, ha='left', va='bottom', fontsize=12) # 壁のマスの場合 if state == env.wall_state: # 壁を描画 rect = plt.Rectangle(xy=(x, ys-y-1), width=1, height=1, fc=(0.4, 0.4, 0.4, 1.0)) # 長方形を作成 plt.gca().add_patch(rect) # 重ねて描画 # 壁以外のマス場合 else: # 各状態の遷移回数ラベルを描画 cnts_txt = 'n=' + str(cnts[state]) plt.text(x=x+0.1, y=ys-y-0.1, s=cnts_txt, ha='left', va='top', size=12) # 最後以外の場合 if t+1 <= T: # t回目のインデックス・行動を取得 (y, x), action, _ = agent.memory[t] # 矢印の描画用のリストを作成 arrows = ['↑', '↓', '←', '→'] offsets = [(0, 0.1), (0, -0.1), (-0.1, 0), (0.1, 0)] # 矢印の描画用の値を抽出 arrow = arrows[action] offset = offsets[action] # 方策ラベル(矢印)を描画 plt.text(x=x+0.5+offset[0], y=ys-y-0.5+offset[1], s=arrow, ha='center', va='center', size=50) # 線が重ならないようにするための値を作成 d = np.linspace(0.1, 0.9, num=T+1) # エージェントの軌跡を描画 plt.plot(memory_x[:t+1]+d[:t+1], ys-memory_y[:t+1]-1.0+d[:t+1]) plt.scatter(x=memory_x[:t+1]+d[:t+1], y=ys-memory_y[:t+1]-1.0+d[:t+1], marker='h') # グラフの設定 if t+1 <= T: # ゴールマスを除く plt.title('t='+str(t+1) + ', total reward:'+str(total_reward), loc='left') # タイトル else: plt.title('t='+str(T) + ', total reward:'+str(total_reward), loc='left') # タイトル plt.xticks(ticks=np.arange(xs)) # x軸の目盛位置 plt.yticks(ticks=np.arange(ys), labels=ys-np.arange(ys)-1) # y軸の目盛位置 plt.xlim(xmin=0, xmax=xs) # x軸の範囲 plt.ylim(ymin=0, ymax=ys) # y軸の範囲 plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False) # 軸ラベル plt.grid() # グリッド線 # gif画像を作成 anime = FuncAnimation(fig, update, frames=T+1, interval=500) # gif画像を保存 anime.save('RandomAgent.gif')
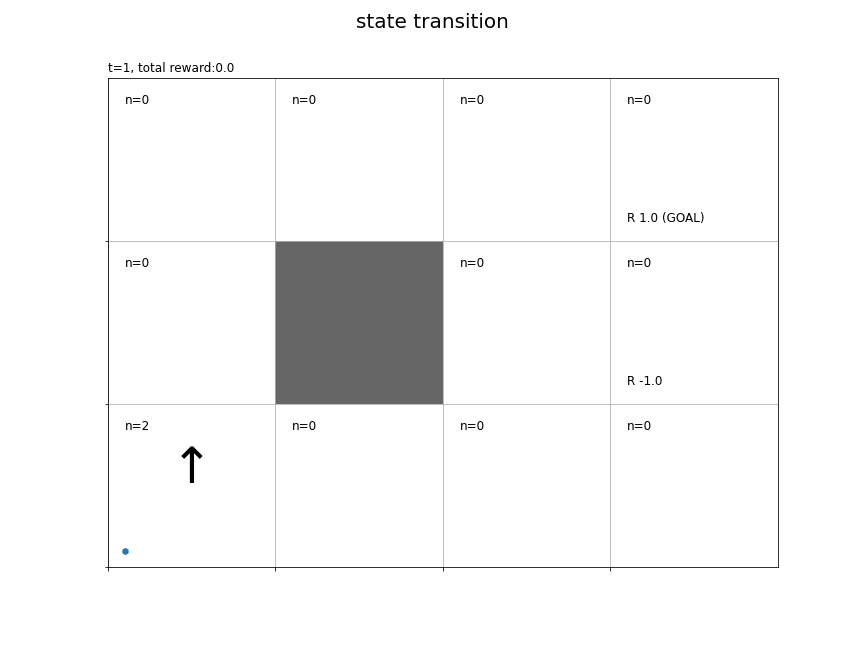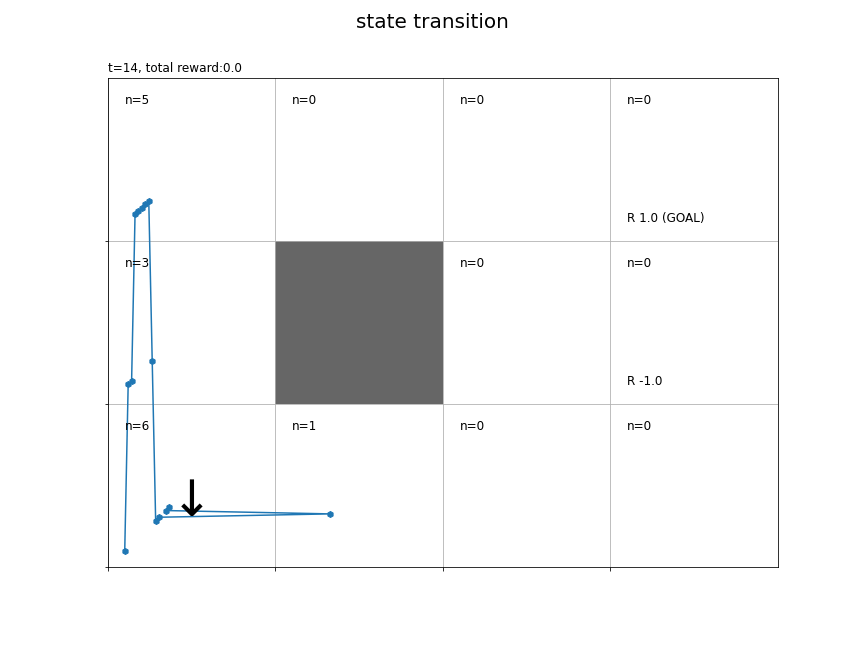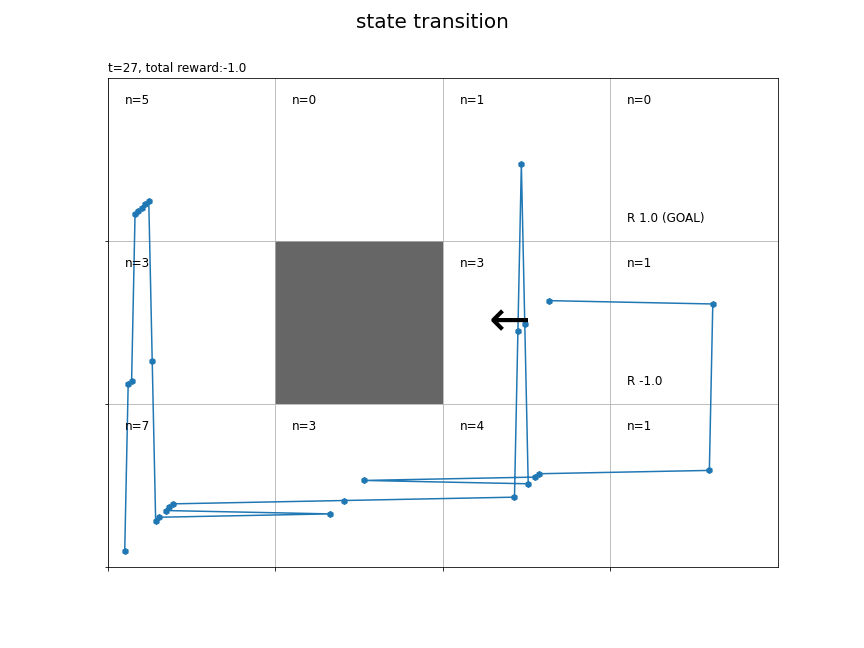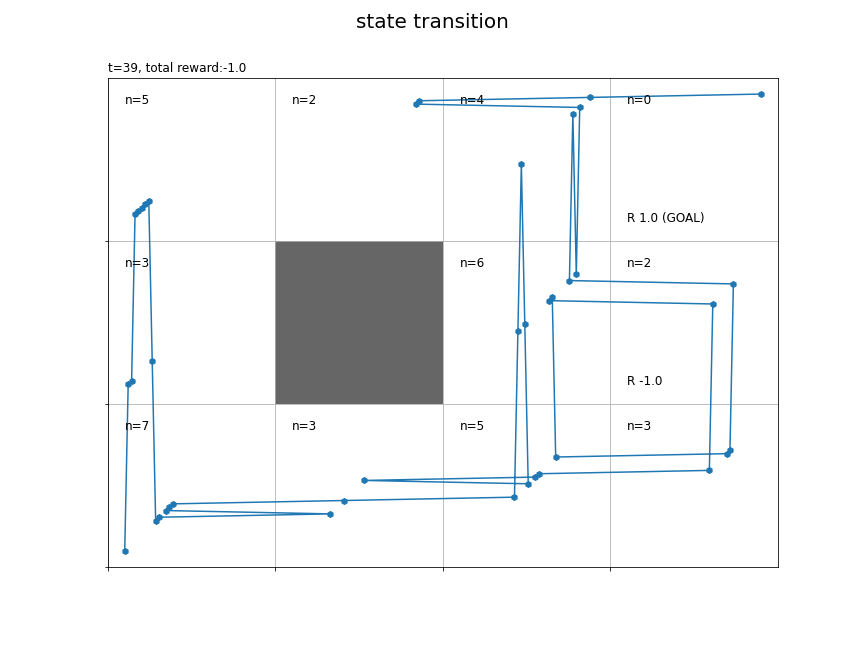
各時刻の行動を矢印で示します。各時刻の作図処理を関数update()として定義して、FuncAnimation()でアニメーション(gif画像)を作成します。
各状態の遷移回数をcntsに記録しておきます。
続いて、時刻ごとに、その時刻の状態(エージェントがいるマス)の収益を計算します。
・作図コード(クリックで展開)
# 各状態の遷移回数を初期化 cnts = defaultdict(lambda: 0) # グラフを初期化 fig = plt.figure(figsize=(12, 9), facecolor='white') # 図の設定 fig.suptitle('return', fontsize=20) # 全体のタイトル # 作図処理を関数として定義 def update(t): # 前フレームのグラフを初期化 plt.cla() # T-t回目の状態・報酬を取得 state, _, reward = agent.memory[-t-1] # 時刻tの状態の遷移回数をカウントアップ cnts[state] += 1 # マス(状態)ごとに処理 for state in env.states(): # マスのインデックスを取得 y, x = state # 報酬を抽出 r = env.reward_map[y, x] # 報酬がある場合 if r != 0 and r is not None: # 報酬ラベル用の文字列を作成 txt = 'R ' + str(r) # ゴールの場合 if state == env.goal_state: # 報酬ラベルにゴールを追加 txt = txt + ' (GOAL)' # 報酬ラベルを描画 plt.text(x=x+0.1, y=ys-y-0.9, s=txt, ha='left', va='bottom', fontsize=15) # 壁のマスの場合 if state == env.wall_state: # 壁を描画 rect = plt.Rectangle(xy=(x, ys-y-1), width=1, height=1, fc=(0.4, 0.4, 0.4, 1.0)) # 長方形を作成 plt.gca().add_patch(rect) # 重ねて描画 # 壁以外のマス場合 else: # 各状態となった回数ラベルを描画 cnts_txt = 'n=' + str(cnts[state]) plt.text(x=x+0.1, y=ys-y-0.1, s=cnts_txt, ha='left', va='top', size=15) # 線が重ならないようにするための値を作成 d = np.linspace(0.1, 0.9, num=T+1) # エージェントの軌跡を描画 plt.plot(memory_x[-t-2:]+d[-t-2:], ys-memory_y[-t-2:]-1.0+d[-t-2:]) plt.scatter(x=memory_x[-t-2:]+d[-t-2:], y=ys-memory_y[-t-2:]-1.0+d[-t-2:], marker='h') # T-t回目のインデックス・行動を取得 (y, x), _, reward = agent.memory[-t-1] # 収益を計算 G = np.sum(memory_r[:-1][-t-1:] * agent.gamma**np.arange(t+1)) # 収益ラベルを描画 return_txt = '$G^{('+str(cnts[(y, x)])+')}_{L_{'+str(y)+',' + str(x)+'}}='+str(np.round(G, 3))+'$' plt.text(x=x+0.5, y=ys-y-0.5, s=return_txt, ha='center', va='center', size=15) # グラフの設定 plt.title('t='+str(T-t) + ', $\gamma='+str(agent.gamma)+'$', loc='left') # タイトル plt.xticks(ticks=np.arange(xs)) # x軸の目盛位置 plt.yticks(ticks=np.arange(ys), labels=ys-np.arange(ys)-1) # y軸の目盛位置 plt.xlim(xmin=0, xmax=xs) # x軸の範囲 plt.ylim(ymin=0, ymax=ys) # y軸の範囲 plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False) # 軸ラベル plt.grid() # グリッド線 # gif画像を作成 anime = FuncAnimation(fig, update, frames=T, interval=500) # gif画像を保存 anime.save('Return.gif')
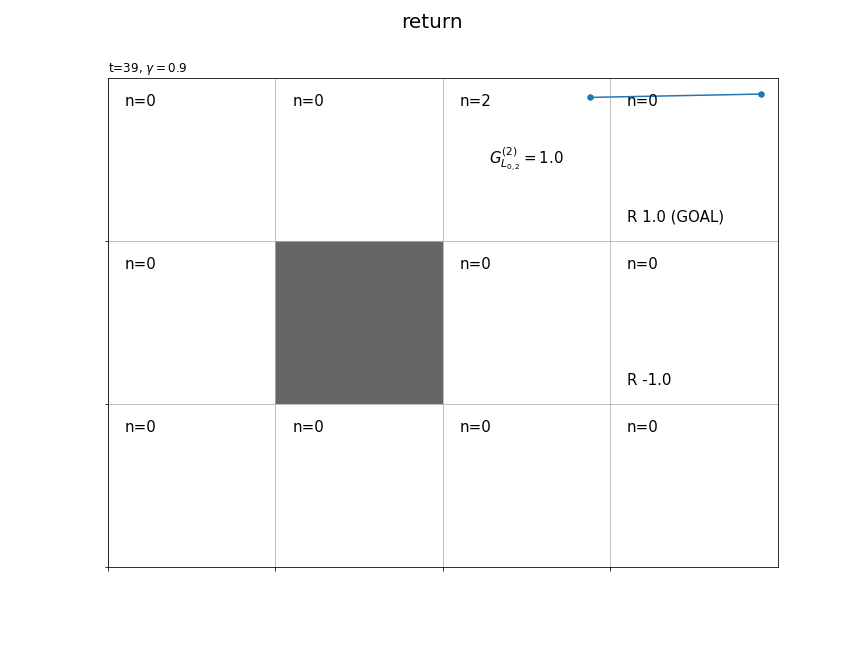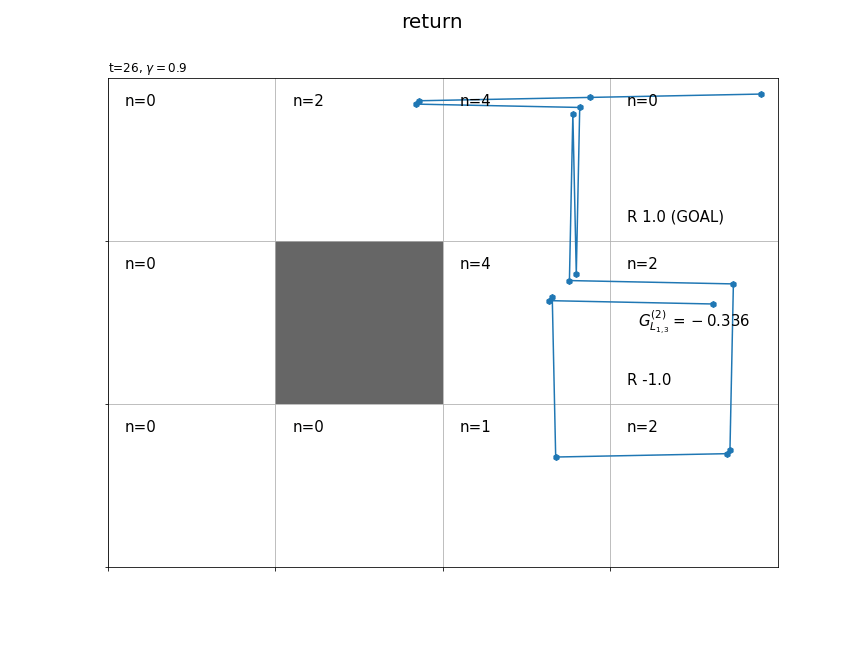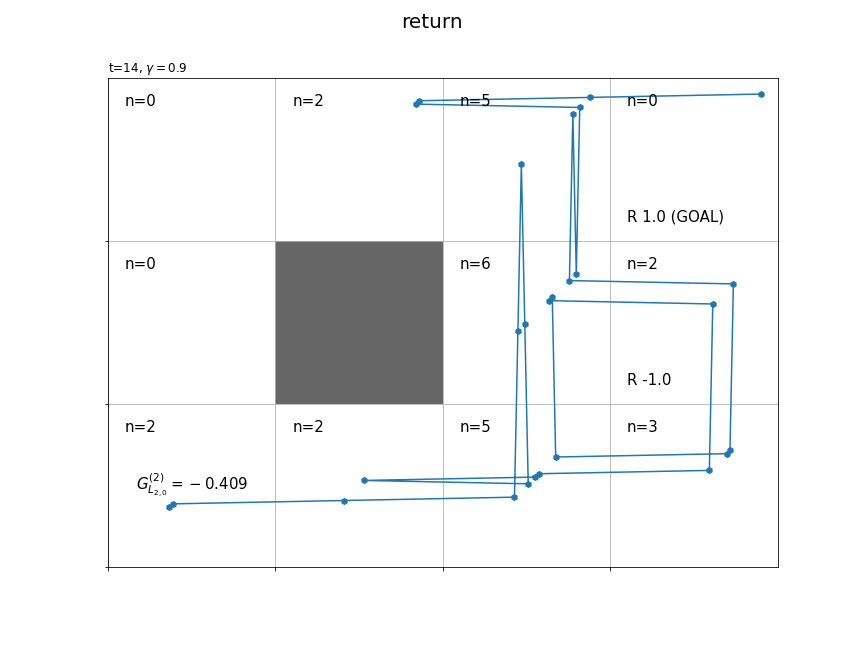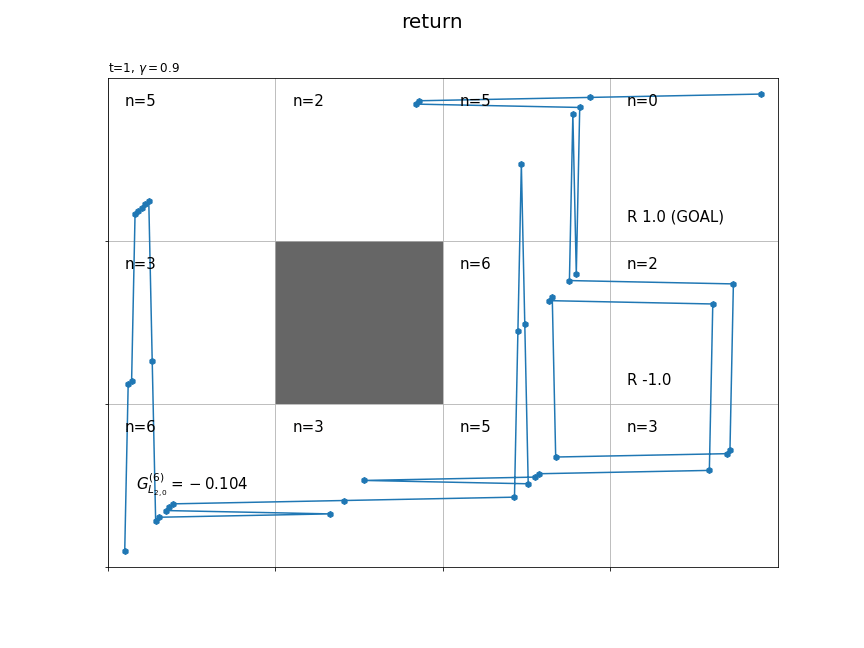
(今後登場するかは分かりませんが、)時刻$t$の状態$S_t$が$L_{h,w}$マスのときの収益を$G_{L_{h,w}}$で表すことにします。また、各状態の収益のサンプルは$n$個得られます。そこで、$i$番目の収益のサンプルを$G_{L_{h,w}}^{(i)}$で表します。
時刻1からTを逆順に計算することで、全ての時刻また経路上の全ての状態で式(3.3)によりインクリメンタルに計算できます。
各状態においてn回収益が計算される(n個のサンプルが得られる)のが分かります。
最後に、時刻ごとに、各状態(マス)の収益の標本平均を計算して、状態価値の推定値を求めます。
・作図コード(クリックで展開)
# 色付け用に最小値・最大値を再設定 vmax = max(vmax, abs(vmin)) vmin = -1 * vmax vmax = 1 if vmax < 1 else vmax vmin = -1 if vmin > -1 else vmin # カラーマップを設定 color_list = ['red', 'white', 'green'] cmap = LinearSegmentedColormap.from_list('colormap_name', color_list) # 状態価値の計算用のオブジェクトを初期化 cnts = defaultdict(lambda: 0) V = defaultdict(lambda: 0.0) V_arr = np.zeros((ys, xs)) # グラフを初期化 fig = plt.figure(figsize=(12, 9), facecolor='white') # 図の設定 fig.suptitle('state-value', fontsize=20) # 全体のタイトル # 作図処理を関数として定義 def update(t): # 前フレームのグラフを初期化 plt.cla() # T-t回目の状態・報酬を取得 state, _, reward = agent.memory[-t-1] # 収益を計算 G = np.sum(memory_r[:-1][-t-1:] * agent.gamma**np.arange(t+1)) # 時刻tの状態の遷移回数をカウントアップ cnts[state] += 1 # 状態価値を計算 V[state] += (G - V[state]) / cnts[state] V_arr[state] = V[state] # 状態価値のヒートマップを描画 plt.pcolormesh(np.flipud(V_arr), cmap=cmap, vmin=vmin, vmax=vmax) # ヒートマップ # マス(状態)ごとに処理 for state in env.states(): # マスのインデックスを取得 y, x = state # 報酬を抽出 r = env.reward_map[y, x] # 報酬がある場合 if r != 0 and r is not None: # 報酬ラベル用の文字列を作成 txt = 'R ' + str(r) # ゴールの場合 if state == env.goal_state: # 報酬ラベルにゴールを追加 txt = txt + ' (GOAL)' # 報酬ラベルを描画 plt.text(x=x+0.1, y=ys-y-0.9, s=txt, ha='left', va='bottom', fontsize=15) # 壁のマスの場合 if state == env.wall_state: # 壁を描画 rect = plt.Rectangle(xy=(x, ys-y-1), width=1, height=1, fc=(0.4, 0.4, 0.4, 1.0)) # 長方形を作成 plt.gca().add_patch(rect) # 重ねて描画 # 壁以外のマス場合 else: # 各状態となった回数ラベルを描画 #cnts_txt = 'n=' + str(cnts[state]) #plt.text(x=x+0.1, y=ys-y-0.1, s=cnts_txt, # ha='left', va='top', size=15) # 状態価値ラベルを描画 value_txt = '$V_{'+str(cnts[state])+'}(L_{'+str(y)+','+str(x)+'})=' + str(np.round(V_arr[y, x], 2))+'$' plt.text(x=x+0.9, y=ys-y-0.1, s=value_txt, ha='right', va='top', fontsize=15) # 線が重ならないようにするための値を作成 d = np.linspace(0.1, 0.9, num=T+1) # エージェントの軌跡を描画 plt.plot(memory_x[-t-2:]+d[-t-2:], ys-memory_y[-t-2:]-1.0+d[-t-2:]) plt.scatter(x=memory_x[-t-2:]+d[-t-2:], y=ys-memory_y[-t-2:]-1.0+d[-t-2:], marker='h') # 後からt回目のインデックス・行動を取得 (y, x), _, reward = agent.memory[-t-1] # 収益ラベルを描画 return_txt = '$G^{('+str(cnts[(y, x)])+')}_{L_{'+str(y)+','+str(x)+'}}=' + str(np.round(G, 3))+'$' plt.text(x=x+0.5, y=ys-y-0.5, s=return_txt, ha='center', va='center', size=15) # グラフの設定 plt.title('t='+str(T-t) + ', $\gamma='+str(agent.gamma)+'$', loc='left') # タイトル plt.xticks(ticks=np.arange(xs)) # x軸の目盛位置 plt.yticks(ticks=np.arange(ys), labels=ys-np.arange(ys)-1) # y軸の目盛位置 plt.xlim(xmin=0, xmax=xs) # x軸の範囲 plt.ylim(ymin=0, ymax=ys) # y軸の範囲 plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False) # 軸ラベル plt.grid() # グリッド線 # gif画像を作成 anime = FuncAnimation(fig, update, frames=T, interval=500) # gif画像を保存 anime.save('StateValue.gif')
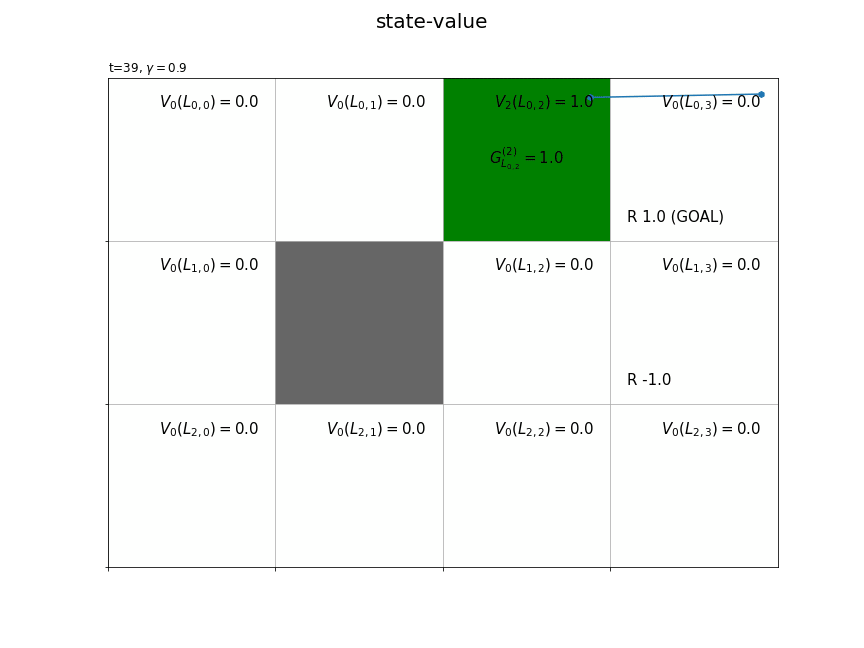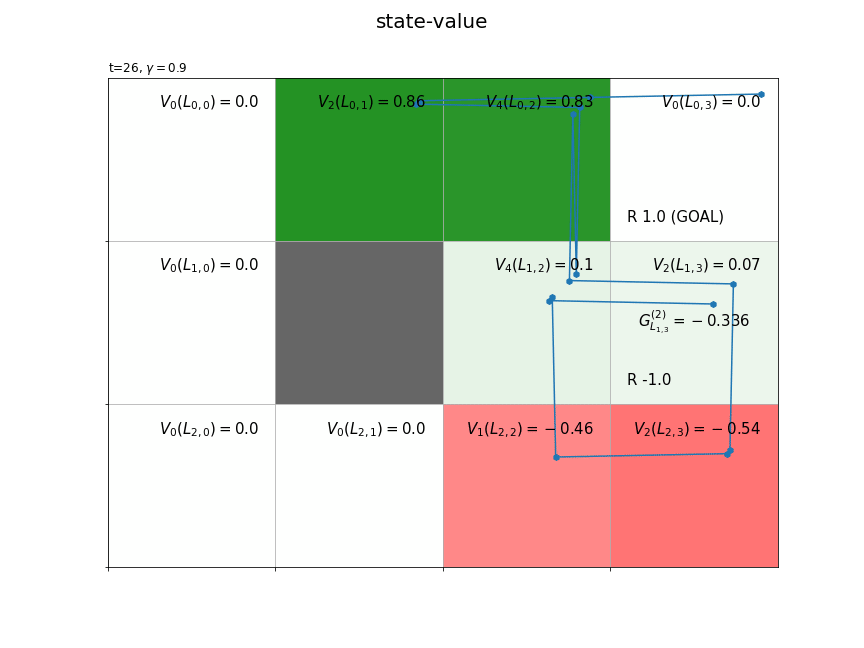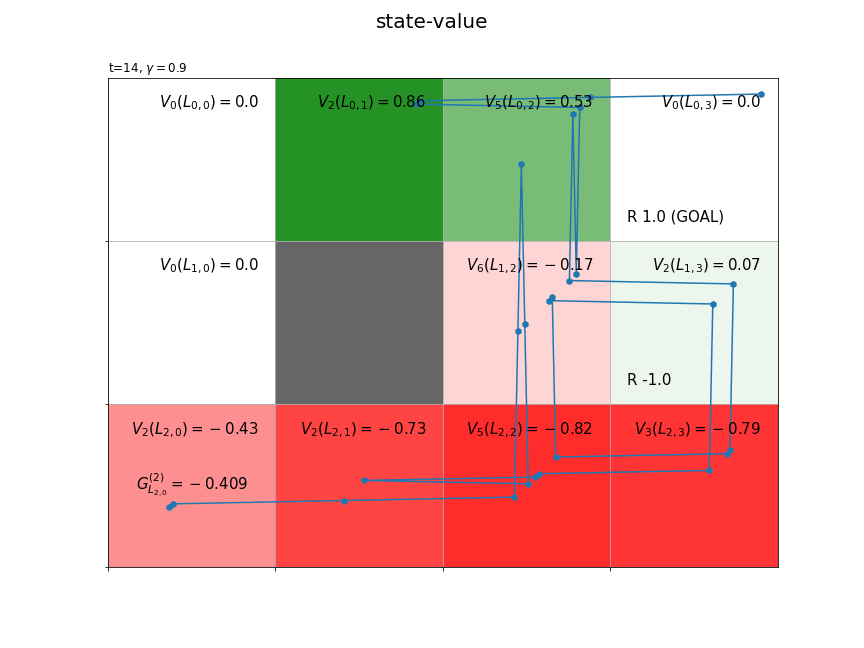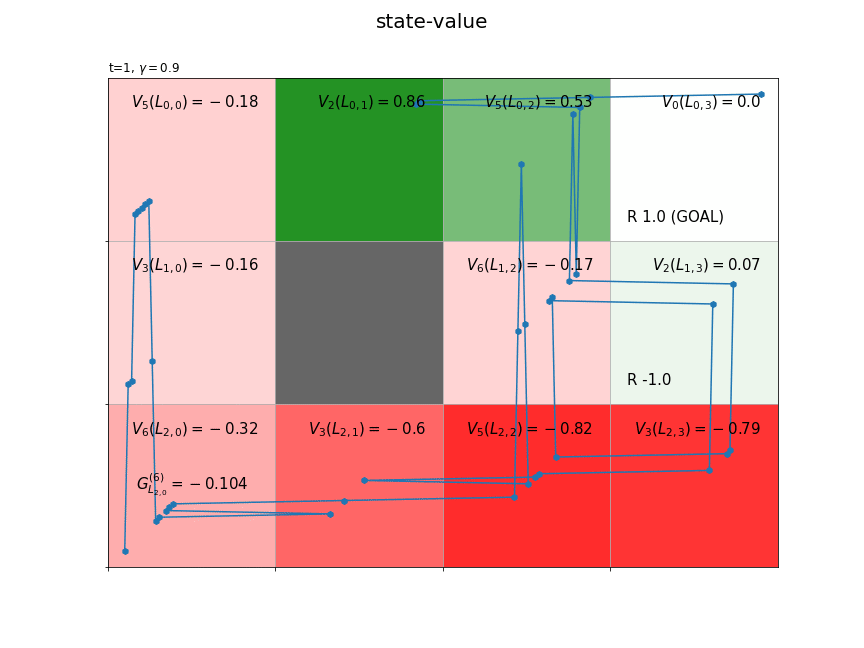
方策$\pi$に従い行動が決まるとき、$L_{h,w}$マスの推定状態価値を$V_{\pi}(L_{h,w})$で表します。収益のサンプル$G_{L_{h,w}}^{(i)}$が得られる度に、$L_{h,w}$マスの状態価値を更新します。$n$個のサンプルによって求めた($n$回更新した)状態価値を$V_n(L_{h,w})$で表します。
状態価値関数の値は、推定処理用にディクショナリV、作図処理用にNumPy配列V_arrを作成しておきます。新たなに得られた収益Gを使って、式(5.2')により時刻tの状態stateの状態価値V[state], V_arr[state]を更新します。
以上が、1エピソードで行う状態価値関数の推定処理です。インクリメンタルに収益を計算することで、1エピソードでT個のサンプルが得られました。また、各状態の状態価値と遷移回数を保存しておけば、今回のエピソードで得られたサンプルデータを捨てても、次回のエピソードで得られるサンプルデータを用いて状態価値関数を更新できます。
・別のエピソードの結果
複数エピソードで更新したものではなく、それぞれ別のシミュレーションの結果です。
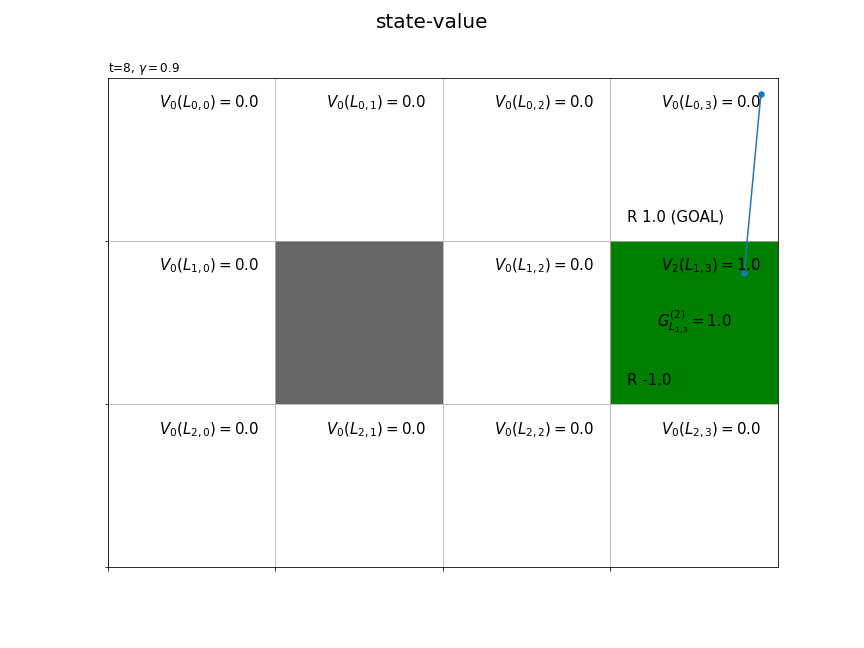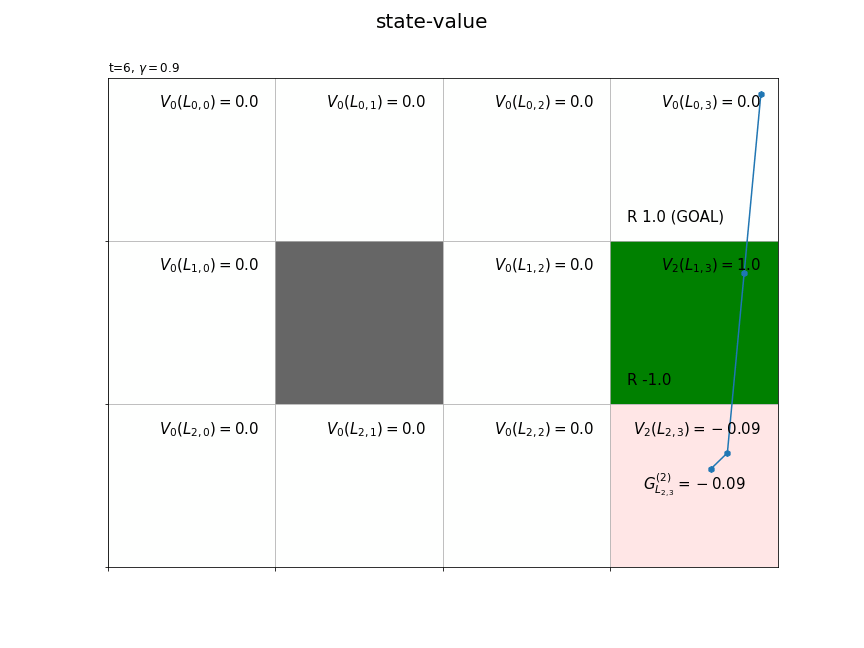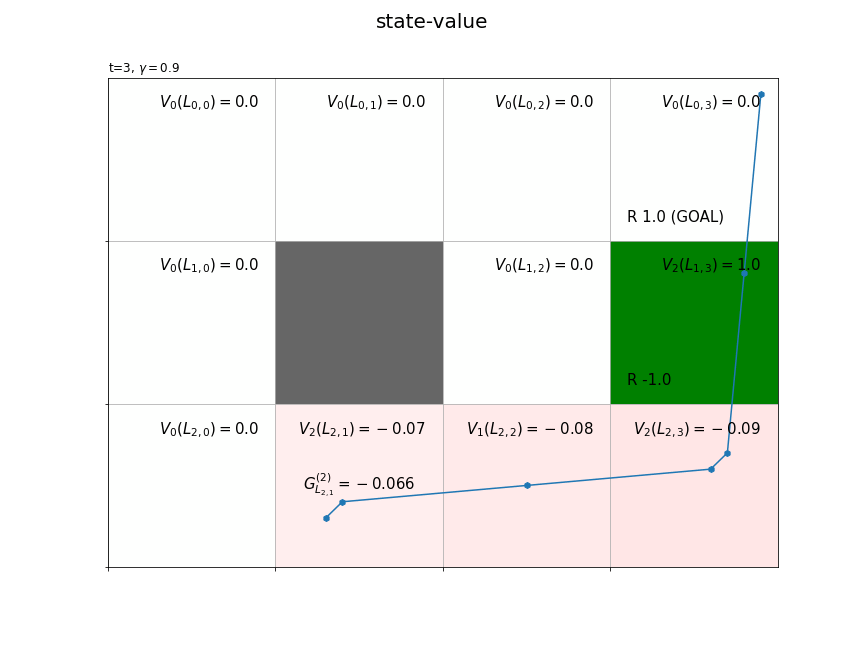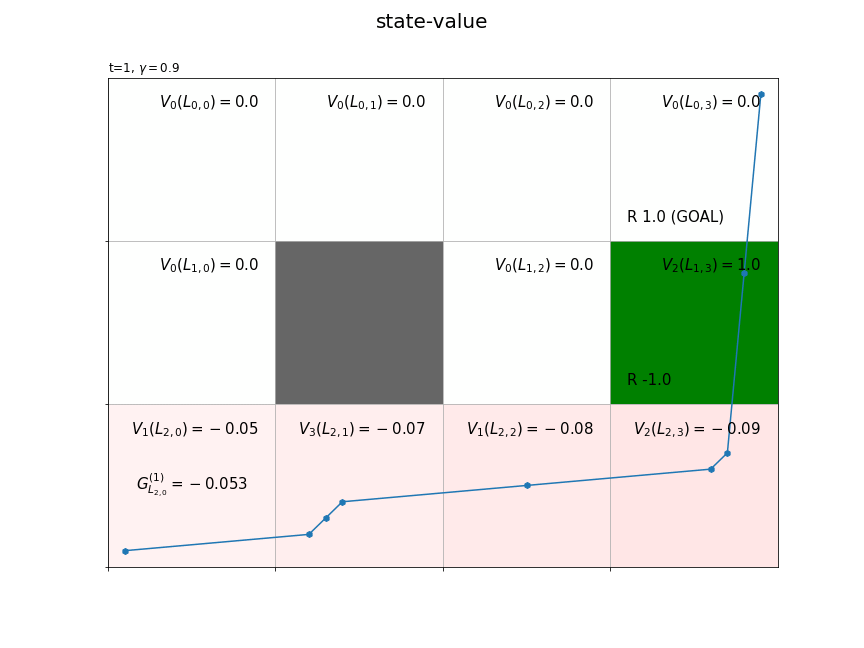



この節では、モンテカルロ法による状態価値関数の計算をインクリメンタルに行う方法を確認しました。次節では、モンテカルロ法による状態価値関数の計算を実装します。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning 4 ――強化学習編』オライリー・ジャパン,2022年.
- サポートページ:GitHub - oreilly-japan/deep-learning-from-scratch-4
おわりに
この節を深掘りするつもりはなかったのですが、5.3節以降を実装していても逐次処理感がよく分からなかったので、戻って咀嚼することにしました。
で、図5-9の内容をグリッドワールドに対応付けようと頑張りましたが、これが私の表現力の限界でした。
あ、4か月以上あきましたがベルマン方程式の導出時の傷が癒えてきたので5章を進めます。
【次節の内容】