はじめに
『ゼロから作るDeep Learning 4 ――強化学習編』の独学時のまとめノートです。初学者の補助となるようにゼロつくシリーズの4巻の内容に解説を加えていきます。本と一緒に読んでください。
この記事は、4.4節の内容です。方策反復法を実装して最適方策を求めます。
【前節の内容】
【他の記事一覧】
【この記事の内容】
4.4 方策反復法の実装
3×4マスのグリッドワールド(図4-8)に対して、方策反復法により最適方策を求めます。反復方策法のアルゴリズムについては「4.3:方策反復法【ゼロつく4のノート】 - からっぽのしょこ」を参照してください。
利用するライブラリを読み込みます。
# 利用するライブラリを読み込み import numpy as np from collections import defaultdict # 追加ライブラリ import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation from matplotlib.colors import LinearSegmentedColormap
MatplotlibライブラリのanimationモジュールからFuncAnimationを使って、推移の確認用のアニメーションを作成します。その際に、colorsモジュールからLinearSegmentedColormapも使います。不要であれば省略してください。
また、3×4マスのグリッドワールドのクラスGridWorldを読み込みます。
# 実装済みのクラスと関数を読み込み import sys sys.path.append('../deep-learning-from-scratch-4-master') from common.gridworld import GridWorld from ch04.policy_eval import policy_eval
GridWorldクラスについては「4.2.1:GridWorldクラスの実装【ゼロつく4のノート】 - からっぽのしょこ」、polcy_eval関数については「4.2.3:反復方策評価の実装【ゼロつく4のノート】 - からっぽのしょこ」を参照してください。
4.4.1 方策の改善
状態価値関数をgreedy化して方策を更新(改善)します。方策の改善については4.3.1項を参照してください。
・argmaxの実装
greedyな方策を得るには、行動価値関数が最大となる行動を得る必要があります。まずは、その計算(処理)に利用する関数を実装します。ディクショナリから最大値のキーを抽出する処理を関数argmax()として実装します。
・処理の確認
argmax()の内部で行われる処理を確認します。
ある状態の方策を想定したディクショナリを作成します。
# ディクショナリを作成 dic = {0: 0.4, 1: 0.05, 2: 0.4, 3: 0.15} print(dic.keys()) print(dic.values())
dict_keys([0, 1, 2, 3])
dict_values([0.4, 0.05, 0.4, 0.15])
全ての状態の方策を格納したディクショナリpiではなく、piに格納されている1つのディクショナリに対応します。
ディクショナリから最大値のキーを抽出します。
# 最大値を取得 max_value = max(dic.values()) print('max value :', max_value) # 最大値のキーを初期化 max_key = 0 # 要素ごとに処理 for key, value in dic.items(): # 最大値であればキーを更新 if value == max_value: max_key = key # 更新されたキーと値を表示 print('key', max_key, ': value', value)
max value : 0.4
key 0 : value 0.4
key 2 : value 0.4
for文とitems()メソッドを使って、ディクショナリからキーkeyと値valueを順番に取り出して処理します。
取り出した値が最大値であれば、そのキーをmax_keyとして保存します。最大値が複数ある場合は、最後のキーがmax_keyに保存されます。
抽出した最大値のキーを指定することで、ディクショナリから最大値を取り出せます。
# 最大値を抽出 print(dic[max_key])
0.4
これにより、行動価値関数(の計算結果)のディクショナリから価値(値)が最大となる行動(キー)を抽出できます。
・実装
処理の確認ができたので、最大値のキーを抽出する処理を関数として実装します。argmax関数の定義については、次のページを参照してください。
実装した関数を試してみましょう。
# ディクショナリを作成 dic = {0: 0.4, 1: 0.05, 2: 0.4, 3: 0.15} # 最大値となるキーを抽出 max_key = argmax(dic) print(max_key) print(dic[max_key])
2
0.4
処理の確認時と同じ結果が得られました。
以上で、価値が最大となる行動を抽出する関数を実装できました。次は、状態価値関数をgreedy化する関数を実装します。
・greedy_policyの実装
次は、状態価値関数をgreedy化する処理を関数greedy_policy()として実装します。
・計算式の確認
関数内で行う計算について数式で確認します。
方策反復法による方策の更新式(状態価値関数のgreedy化)は、次の式でした(4.3.1項)。
図4-8の問題設定では、決定論的に状態が遷移するので、次の式になります。
・処理の確認
続いて、greedy_policy()の内部で行われる処理を確認します。
引数に指定する(関数内で利用する)オブジェクトを作成します。
# グリッドワールドのインスタンスを作成 env = GridWorld() # 全ての状態価値関数を初期化 V = defaultdict(lambda: 0) # 割引率を指定 gamma = 0.9
GridWorldクラスのインスタンスenvを作成します。
全てのマスの状態価値関数の初期値を0として格納したディクショナリVを作成します。
割引率gammaを指定します。
初期値による状態価値関数のヒートマップを確認しましょう。
# 状態価値関数のヒートマップを作図
env.render_v(v=V)

全ての状態(マス)で初期値が0なので、全て白色になっています。
状態価値関数をgreedy化して方策を更新します。
# 全ての方策を初期化 pi = {} # 状態ごとに処理 for state in env.states(): # 行動価値関数を初期化 action_values = {} # 行動ごとに処理 for action in env.actions(): # 次の状態を取得 next_state = env.next_state(state, action) # 報酬を取得 r = env.reward(state, action, next_state) # 行動価値関数を計算:式(4.8)の波括弧 value = r + gamma * V[next_state] # 行動価値を格納 action_values[action] = value # 行動価値が最大の行動を抽出:式(4.8) max_action = argmax(action_values) # 決定論的方策(疑似の確率論的方策)を作成 action_probs = {0: 0, 1: 0, 2: 0, 3: 0} # 初期化 action_probs[max_action] = 1.0 # (疑似の確率論的)方策を格納 pi[state] = action_probs # 結果を確認 print(list(pi.keys())) # 状態 print([argmax(probs) for probs in pi.values()]) # greedyな行動
[(0, 0), (0, 1), (0, 2), (0, 3), (1, 0), (1, 1), (1, 2), (1, 3), (2, 0), (2, 1), (2, 2), (2, 3)]
[3, 3, 3, 3, 3, 3, 2, 0, 3, 3, 3, 3]
for文とstate()メソッドを使って、状態ごとに処理します。
さらに、for文とactions()メソッドを使って、行動ごとに処理します。
next_state()メソッドで次の状態、reward()メソッドで報酬を取得して、行動価値関数(決定論的方策の更新式)(4.8)の波括弧部分を計算して、valueとします。
全ての行動の価値をaction_valuesに格納して、価値が最大となる行動をargmax()で抽出します。
抽出した行動を取る確率が1でそれ以外の確率を0とした疑似的な確率論的方策actions_probsを作成して、全ての状態の方策piに格納します。
得られた(更新した)方策を可視化します。
# 方策を可視化
env.render_v(v=V, policy=pi)

各状態(マス)の方策が1つの行動になっています。
argmax()の内部では、上下左右の順番に最大値を検索し、最大値が複数ある場合は後に処理される行動(キー)を抽出するのでした。また、全ての状態価値関数の初期値を0にしたので、この時点での更新式(4.8)の計算は報酬(リンゴと爆弾のマス)のみに影響します。よって、報酬のマスに隣接しないマス(状態)では、最後に処理される右の行動が選ばれます。また、リンゴ(正の報酬)のマスに隣接するマスではそちらへ移動(遷移)する行動が選ばれ、爆弾(負の報酬)のマスに隣接するマスではそちらを避ける行動のうち最後に処理される行動が選ばれます。
以上が、方策反復法において方策を1回更新する処理です。
・実装
処理の確認ができたので、状態価値関数をgreedy化する処理を関数として実装します。greedy_policy関数の定義については、argmax関数のときと同じページを参照してください。
実装した関数を試してみましょう。
# グリッドワールドのインスタンスを作成 env = GridWorld() # 全ての状態価値関数を初期化 V = defaultdict(lambda: 0) # 割引率を指定 gamma = 0.9 # 状態価値関数をgreedy化した方策を計算 pi = greedy_policy(V, env, gamma) # 方策を可視化 env.render_v(v=V, policy=pi)

処理の確認時と同じ結果が得られました。
以上で、状態価値関数をgreedy化して方策を更新する処理を実装できました。次は、方策の評価と改善を収束するまで繰り返す関数を実装します。
4.4.2 評価と改善を繰り返す
4.2.3項で実装したpolicy_eval()で方策を評価し、4.4.1項で実装したgreedy_policy()で方策を改善する処理を繰り返して、最適方策と最適状態価値関数を求めます。
・policy_iter関数の実装
最後に、方策反復法により状態価値関数と方策を収束するまで更新する関数policy_iter()として実装します。
・処理の確認
policy_iter()の内部で行われる処理を確認します。
引数に指定する(関数内で利用する)オブジェクトを作成します。
# グリッドワールドのインスタンスを作成 env = GridWorld() # 割引率を指定 gamma = 0.9 # 閾値を指定 threshold = 0.001
GridWorldクラスのインスタンスenvを作成します。
割引率gammaと閾値thresholdを指定します。
方策反復法によって、方策が改善されなくなるまで更新を繰り返します。
# 全ての方策を初期化 pi = defaultdict(lambda: {0: 0.25, 1: 0.25, 2: 0.25, 3: 0.25}) # 全ての状態価値関数を初期化 V = defaultdict(lambda: 0) # 記録用のリストを初期化 trace_pi = [pi] # 初期値を記録 trace_V = [{state: 0 for state in env.states()}] # 初期値を記録 # 試行回数のカウントを初期化 cnt = 0 # 繰り返し処理 while True: # 方策を評価(状態価値関数を計算):式(4.3) V = policy_eval(pi, V, env, gamma, threshold) # 方策を改善(状態価値関数をgreedy化して方策を計算):式(4.8) new_pi = greedy_policy(V, env, gamma) # 方策が改善されくなると終了 if new_pi == pi: break # (疑似の確率論的)方策を更新 pi = new_pi # 試行回数をカウント cnt += 1 # 更新値を記録 trace_pi.append(pi.copy()) trace_V.append(V.copy()) # 途中経過を表示 print('===', 'iter', cnt, '===') print('state-value', np.round(list(V.values()), 2)) # 状態価値 print('max policy', [argmax(probs) for probs in pi.values()]) # greedyな行動
=== iter 1 ===
state-value [ 0.03 -0.03 0.1 0.21 -0.5 0. -0.1 -0.22 -0.14 -0.43 -0.37 -0.78]
max policy [3, 3, 3, 3, 0, 0, 0, 0, 0, 2, 2, 2]
=== iter 2 ===
state-value [0.81 0.73 0.9 1. 0.9 0. 0.66 0.59 0.81 0.53 1. 0.48]
max policy [3, 3, 3, 3, 0, 3, 0, 0, 0, 2, 0, 2]
=== iter 3 ===
state-value [0.81 0.73 0.9 1. 0.9 0. 0.66 0.59 0.81 0.81 1. 0.73]
max policy [3, 3, 3, 3, 0, 3, 0, 0, 0, 3, 0, 2]
=== iter 4 ===
state-value [0.81 0.73 0.9 1. 0.9 0. 0.66 0.73 0.81 0.81 1. 0.73]
max policy [3, 3, 3, 3, 0, 3, 0, 0, 3, 3, 0, 2]
4.2.3項で実装したpolicy_eval()で方策を評価(式(4.3)で状態価値関数を推定)します。
greedy_policy()で方策を改善(式(4.8)で状態価値関数をgreedy化)して、new_Vとします。
更新前の方策piと更新後の方策new_piに変化がなければ、while文による繰り返し処理をbreakで終了します。変化があれば、方策piを更新します(書き換えます)。
途中経過の出力を見ると、4回更新されたのが分かります。
収束した状態価値関数と方策(最適状態価値関数と最適方策)のヒートマップを作成します。
# 状態価値関数と方策を可視化
env.render_v(v=V, policy=pi)

爆弾(負の報酬)のマスを避けて、ゴール(正の報酬)のマスに近付く行動になっています。負の報酬を避けられたことで、ランダムな方策(4.2節)のときと異なり、全ての状態で価値関数が正の値(マスが緑色)になっています。また、ゴールのマスから離れるほど状態価値が小さくなっています。
これは割引率の影響で、次のようにして計算(再現)できます。
# ゴールのマスまでの距離を指定 n = np.arange(5) # 報酬を指定 r = 1 # 報酬を割引 print(np.round(r * gamma**n, 2))
[1. 0.9 0.81 0.73 0.66]
詳しくは2.3.2項を参照してください。
・更新推移の可視化
ここまでで、繰り返しの更新処理を確認できました。続いて、途中経過をアニメーションで確認します。
状態価値関数と方策のヒートマップのアニメーションを作成します。
・作図コード(クリックで展開)
# グリッドマップのサイズを取得 xs = env.width ys = env.height # 最後の状態価値の最小値・最大値を取得 vmin = min(trace_V[-1].values()) vmax = max(trace_V[-1].values()) # 色付け用に最小値・最大値を再設定 vmax = max(vmax, abs(vmin)) vmin = -1 * vmax if vmax < 1: vmax = 1 if vmin > -1: vmin = -1 # カラーマップを設定 color_list = ['red', 'white', 'green'] cmap = LinearSegmentedColormap.from_list('colormap_name', color_list) # 図を初期化 fig = plt.figure(figsize=(9, 6)) # 図の設定 plt.suptitle('Policy Iteration', fontsize=20) # 全体のタイトル # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i回目の更新値を取得 pi = trace_pi[i] V = trace_V[i] # ディクショナリを配列に変換 v = np.zeros((env.shape)) for state, value in V.items(): v[state] = value # 状態価値のヒートマップを描画 plt.pcolormesh(np.flipud(v), cmap=cmap, vmin=vmin, vmax=vmax) # ヒートマップ # マス(状態)ごとに処理 for state in env.states(): # インデックスを取得 y, x = state # 報酬を抽出 r = env.reward_map[state] # 報酬がある場合 if r != 0 and r is not None: # 報酬ラベル用の文字列を作成 txt = 'R ' + str(r) # ゴールの場合 if state == env.goal_state: # 報酬ラベルにゴールを追加 txt = txt + ' (GOAL)' # 報酬ラベルを描画 plt.text(x=x+0.1, y=ys-y-0.9, s=txt) # 壁以外の場合 if state != env.wall_state: # 状態価値ラベルを描画 plt.text(x=x+0.4, y=ys-y-0.15, s='{:12.2f}'.format(v[y, x])) # 確率が最大の行動を抽出 actions = pi[state] max_actions = [k for k, v in actions.items() if v == max(actions.values())] # 矢印の描画用のリストを作成 arrows = ['↑', '↓', '←', '→'] offsets = [(0, 0.1), (0, -0.1), (-0.1, 0), (0.1, 0)] # 行動ごとに処理 for action in max_actions: # 矢印の描画用の値を抽出 arrow = arrows[action] offset = offsets[action] # ゴールの場合 if state == env.goal_state: # 描画せず次の状態へ continue # 方策ラベル(矢印)を描画 plt.text(x=x+0.45+offset[0], y=ys-y-0.5+offset[1], s=arrow, fontsize=20) # 壁の場合 if state == env.wall_state: # 壁を描画 plt.gca().add_patch(plt.Rectangle(xy=(x, ys-y-1), width=1, height=1, fc=(0.4, 0.4, 0.4, 1.0))) # 長方形を重ねる # マスを描画 plt.xticks(ticks=np.arange(xs)) # x軸の目盛位置 plt.yticks(ticks=np.arange(ys)) # y軸の目盛位置 plt.xlim(xmin=0, xmax=xs) # x軸の範囲 plt.ylim(ymin=0, ymax=ys) # y軸の範囲 plt.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False) # 軸ラベル plt.grid() # グリッド線 plt.title('iter:'+str(i), loc='left') # タイトル # gif画像を作成 anime = FuncAnimation(fig, update, frames=len(trace_V), interval=500) # gif画像を保存 anime.save('policy_iter.gif')
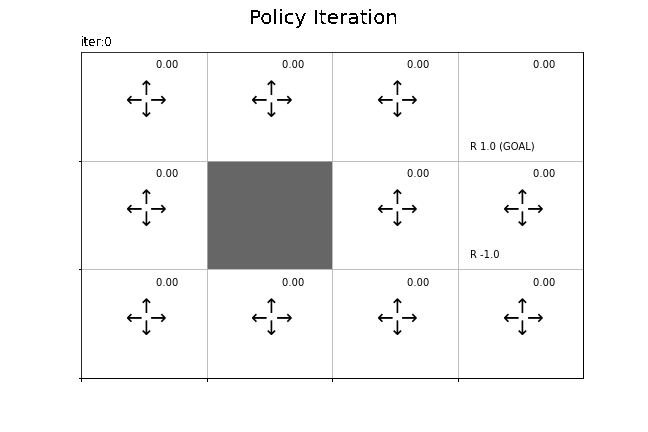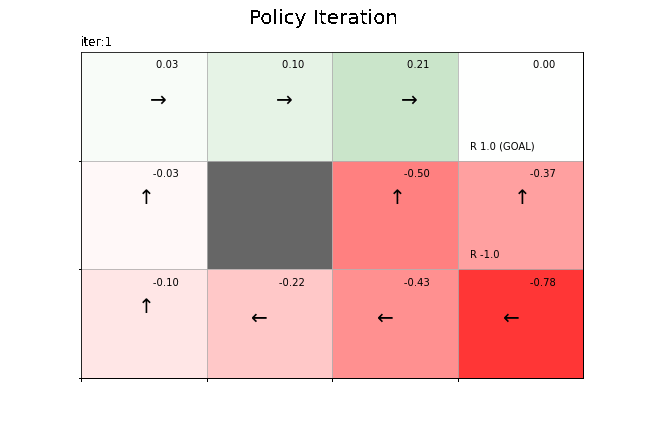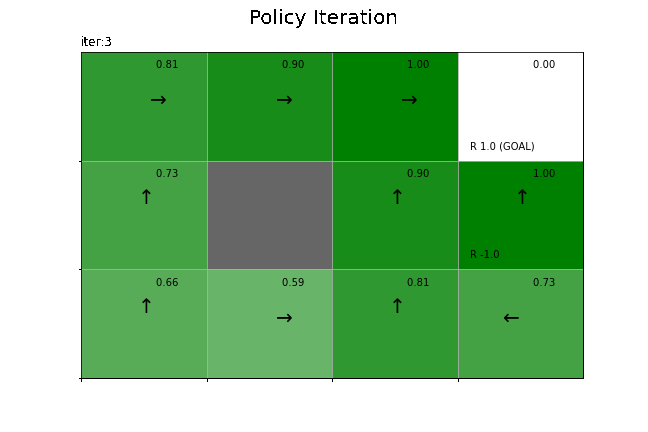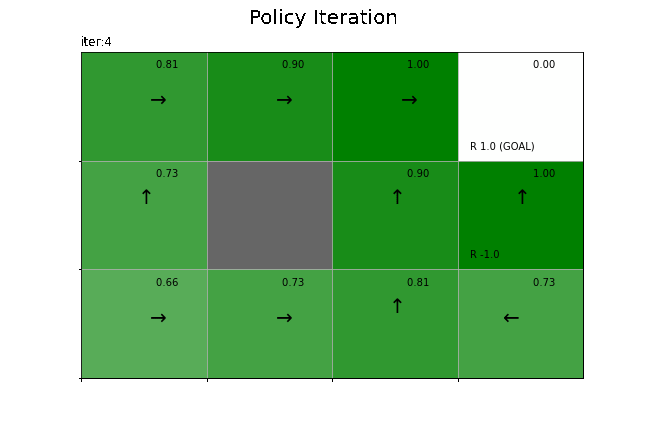
状態価値関数の更新値の推移をグラフで確認します。
・作図コード(クリックで展開)
# 更新回数を取得 max_iter = len(trace_V) # 状態数を取得 state_size = env.reward_map.size # 作図用の配列を作成 trace_V_arr = np.zeros((max_iter, state_size)) for i in range(max_iter): # i回目の更新値を抽出 V = trace_V[i] # 配列に格納 trace_V_arr[i] = list(V.values()) # 状態価値関数の推移を作図 plt.figure(figsize=(8, 6)) for s in range(env.reward_map.size): plt.plot(np.arange(max_iter), trace_V_arr[:, s]) plt.xlabel('iteration') plt.ylabel('state-value') plt.suptitle('Policy Ieration', fontsize=20) plt.title('$\gamma='+str(gamma)+'$', loc='left') plt.grid() plt.show()

アニメーションでは、状態価値を色の濃淡で表しました。こちらは、y軸で表しています。
・実装
処理の確認ができたので、方策反復法を関数として実装します。policy_iter関数の定義については、argmax関数のときと同じページを参照してください。
(render_v()の引数は更新後の方策new_piの方がいいのでは?最後のグラフでは一致するけど。)
実装した関数を試してみましょう。
# グリッドワールドのインスタンスを作成 env = GridWorld() # 割引率を指定 gamma = 0.9 # 閾値を指定 threshold = 0.001 # 最適方策を計算:式(4.8)の繰り返し pi = policy_iter(env, gamma, threshold, is_render=True)

処理の確認時と同じ結果が得られました。
この例の問題設定では、最適方策が2つ存在すると本に書いてあります。これはスタート(左下)のマスから「右右上上右」と「上上右右右」です。どちらのルートも行動価値が同じなことからも分かります。実装した関数で得られた(このグラフの)スタートマスの行動が「上」ではなく「右」なのは、上下左右の順番に処理するargmax()が検索順が後の「右」を出力するからですね。
この節では、方策反復法を実装しました。これにより、方策の評価と改善を繰り返して最適方策を得られました。次節では、価値反復法により最適方策を得ることを考えます。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning 4 ――強化学習編』オライリー・ジャパン,2022年.
- サポートページ:GitHub - oreilly-japan/deep-learning-from-scratch-4
おわりに
最適方策が求まりました。というわけで、これで4章での目標は達成です。次節ではもう少し効率化した?方法で同じく最適方策を求めます。
【次節の内容】