はじめに
機械学習で登場する確率分布について色々な角度から理解したいシリーズです。
ベータ関数のグラフをPythonで作成します。
【前の内容】
【他の記事一覧】
【この記事の内容】
ベータ関数の作図
ベータ関数(Beta Function)の計算を確認して、グラフを作成します。
利用するライブラリを読み込みます。
# 利用するライブラリ import numpy as np from scipy.special import gamma, gammaln, beta # ガンマ関数, 対数ガンマ関数, ベータ関数 import matplotlib.pyplot as plt
定義式の確認
まずは、ベータ関数の定義式を確認します。
ベータ関数は、次の式で定義されます。
ここで、$\Gamma(x)$はガンマ関数です。ガンマ関数については「ガンマ関数の性質の導出 - からっぽのしょこ」を参照してください。
ベータ関数の計算
続いて、ベータ関数の計算方法を確認します。
SciPyライブラリのspecialモジュールのガンマ関数gamma()を使って計算します。
# 変数の値を指定 a = 2.1 b = 3.2 # ガンマ関数によりベータ関数の計算 z = gamma(a) * gamma(b) / gamma(a + b) print(z)
0.06661713159437423
ガンマ関数の定義式
を計算します。
対数ガンマ関数gammaln()を使って計算します。
# 対数ガンマ関数によりベータ関数の計算 log_z = gammaln(a) + gammaln(b) - gammaln(a + b) z = np.exp(log_z) print(z)
0.06661713159437421
対数をとった定義式
を計算します。
計算結果の指数をとります。
指数と対数の性質より$\exp(\log x) = x$です。
ベータ関数beta()を使って計算します。
# ベータ関数の計算 z = beta(a, b) print(z)
0.06661713159437423
$x$が0または負の整数の場合は計算できません。
# ベータ関数を計算:(計算できない) print(beta(2.5, 0.0)) print(beta(-2.0, 2.5))
inf
inf
ベータ関数の計算を確認できました。次は、ベータ関数を可視化します。
グラフの作成
MatplotlibライブラリのPyPlotモジュールを利用して、ベータ関数のグラフを作成します。
非負の値の場合
まずは、0より大きい実数$\alpha, \beta$を範囲として、ベータ関数を計算します。
# x軸とy軸の値を指定:(a > 0, b > 0) a_vals = np.arange(start=0.01, stop = 3.0, step=0.01) b_vals = np.arange(start=0.01, stop = 3.0, step=0.01) print(a_vals[:5]) print(b_vals[:5])
[0.01 0.02 0.03 0.04 0.05]
[0.01 0.02 0.03 0.04 0.05]
x軸($\alpha$)の値を作成してa_vals、y軸($\beta$)の値を作成してb_valsとします。
格子点に変換します。
# 格子状の点を作成 a_grid, b_grid = np.meshgrid(a_vals, b_vals) print(a_grid[:5, :5]) print(b_grid[:5, :5]) print(a_grid.shape)
[[0.01 0.02 0.03 0.04 0.05]
[0.01 0.02 0.03 0.04 0.05]
[0.01 0.02 0.03 0.04 0.05]
[0.01 0.02 0.03 0.04 0.05]
[0.01 0.02 0.03 0.04 0.05]]
[[0.01 0.01 0.01 0.01 0.01]
[0.02 0.02 0.02 0.02 0.02]
[0.03 0.03 0.03 0.03 0.03]
[0.04 0.04 0.04 0.04 0.04]
[0.05 0.05 0.05 0.05 0.05]]
(299, 299)
np.meshgrid()でa_vals, b_valsの全ての組み合わせを持つ配列を作成してa_grid, b_gridとします。
ベータ関数を計算します。
# ベータ関数の計算 z_grid = beta(a_grid, b_grid) print(z_grid[:5, :5])
[[199.96757732 149.95171626 133.2694139 124.92066437 119.90546205]
[149.95171626 99.93608768 83.25401521 74.90549309 69.89051572]
[133.2694139 83.25401521 66.5721701 58.22387282 53.20911788]
[124.92066437 74.90549309 58.22387282 49.87579792 44.86126291]
[119.90546205 69.89051572 53.20911788 44.86126291 39.84694542]]
作成したa_grid, b_gridを用いて、beta()でベータ関数の計算をします。
ベータ関数のグラフを作成します。
# ベータ関数を作図 fig = plt.figure(figsize=(9, 8)) ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_surface(a_grid, b_grid, z_grid, cmap='jet', alpha=0.6) # 曲面図 ax.contour(a_grid, b_grid, z_grid, cmap='jet', offset=z_grid.min()) # 等高線図 ax.set_xlabel('$\\alpha$') # x軸ラベル ax.set_ylabel('$\\beta$') # y軸ラベル ax.set_zlabel('$B(\\alpha, \\beta)$') # z軸ラベル fig.suptitle('Beta Function', fontsize=20) # 全体のタイトル plt.show() # 描画
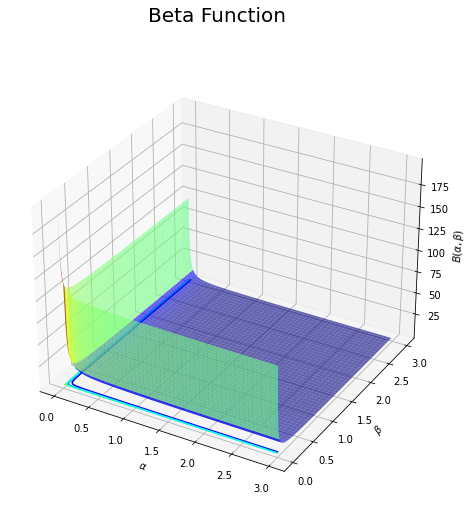
$\alpha = 0$と$\beta = 0$の垂線に漸近しているのが分かります。
負の値を含む場合
続いて、負の実数も含めて、ベータ関数を計算します。
# x軸とy軸の値を指定:(0と負の整数は計算できない) a_vals = np.arange(start=-2.0, stop=2.0, step=0.001) b_vals = np.arange(start=-2.0, stop=2.0, step=0.001) # 格子状の点を作成 a_grid, b_grid = np.meshgrid(a_vals, b_vals) print(a_grid.shape) # ベータ関数の計算 z_grid = beta(a_grid, b_grid) print(np.round(z_grid[:5, :5], 2))
(4000, 4000)
[[ inf inf inf inf inf]
[ inf 11985.97 8984.2 7981.27 7478.05]
[ inf 8984.2 5985.94 4985.34 4484.16]
[ inf 7981.27 4985.34 3985.91 3485.6 ]
[ inf 7478.05 4484.16 3485.6 2985.88]]
0と負の整数のとき、計算結果がinfになります。
グラフに表示しない値をマスクします。
# 閾値を指定 threshold = 10.0 # 閾値外の値をマスク z_mask_grid = np.ma.masked_where((z_grid < -threshold) | (z_grid > threshold), z_grid) print(z_mask_grid[:5, :5])
[[-- -- -- -- --]
[-- -- -- -- --]
[-- -- -- -- --]
[-- -- -- -- --]
[-- -- -- -- --]]
閾値thresholdを指定して、その範囲外の値の要素をnp.ma.masked_where()でマスクします。第1引数にマスクする条件、第2引数にマスクしない場合に返す値を指定します。この例では、$y < - \mathrm{threshold}$、$\mathrm{threshold} < y$の値をマスクします。複数の条件A, Bの一方でも該当する要素をマスクする場合は、(A) | (B)と書きます。
ベータ関数のグラフを作成します。
# ベータ関数を作図 fig = plt.figure(figsize=(9, 8)) ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_surface(a_grid, b_grid, z_mask_grid, cmap='jet', alpha=0.6) # 曲面図 ax.contour(a_grid, b_grid, z_mask_grid, cmap='jet', offset=z_mask_grid.min()) # 等高線図 ax.set_xlabel('$\\alpha$') # x軸ラベル ax.set_ylabel('$\\beta$') # y軸ラベル ax.set_zlabel('$B(\\alpha, \\beta)$') # z軸ラベル fig.suptitle('Beta Function', fontsize=20) # 全体のタイトル ax.set_zlim(zmin=z_mask_grid.min(), zmax=threshold) # z軸の表示範囲 #ax.view_init(elev=90, azim=270) # 表示アングル plt.show() # 描画
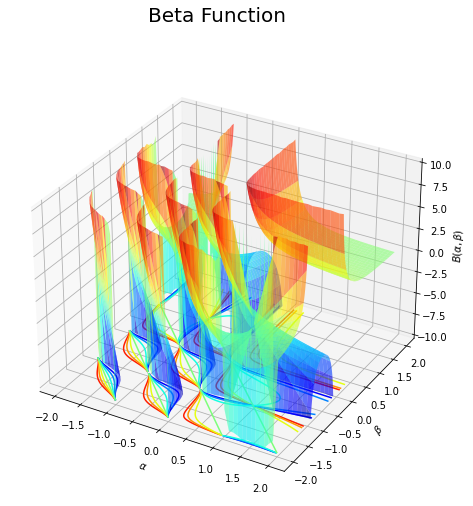
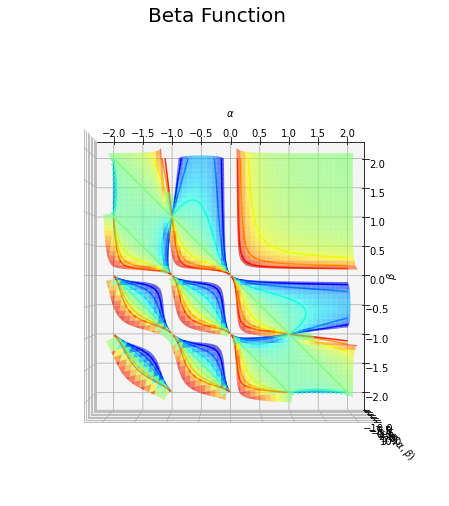
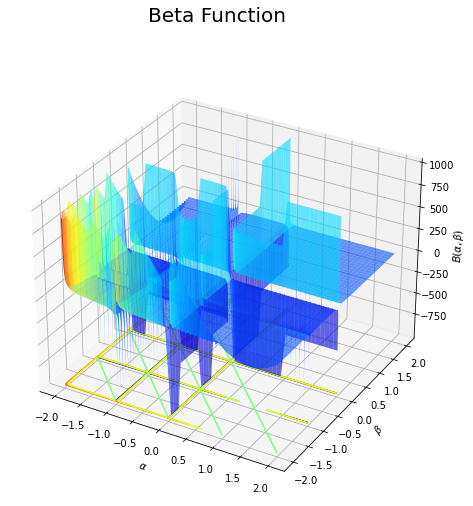

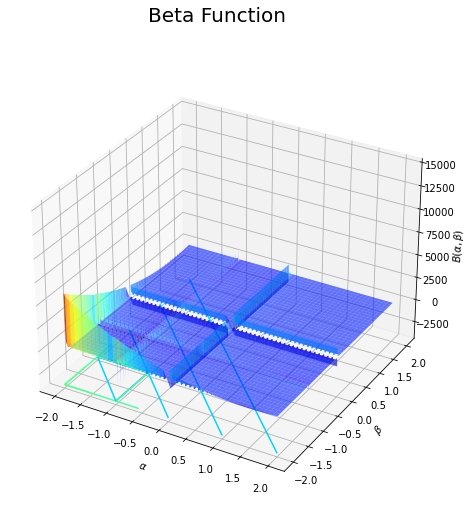
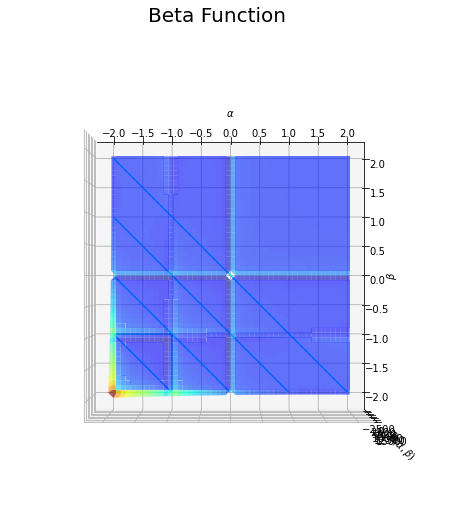
各軸の値が負の整数と0の点において、不連続なグラフになっているのが分かります。
参考文献
- 岩田具治『トピックモデル』(機械学習プロフェッショナルシリーズ)講談社,2015年.
おわりに
とりあえずこれで一区切りにして分布の方に戻ります。
【次の内容】
つづく