はじめに
機械学習で登場する確率分布について色々な角度から理解したいシリーズです。
この記事では、R言語でポアソン分布の乱数を生成します。
【前の内容】
【他の記事一覧】
【この記事の内容】
ポアソン分布の乱数生成
ポアソン分布(Poisson Distribution)の乱数を生成します。ポアソン分布については「ポアソン分布の定義式の確認 - からっぽのしょこ」を参照してください。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(gganimate)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているため、ggplot2は読み込む必要があります。
magrittrパッケージのパイプ演算子%>%ではなく、ベースパイプ(ネイティブパイプ)演算子|>を使っています。%>%に置き換えても処理できます。
分布の変化をアニメーション(gif画像)で確認するのにgganimateパッケージを利用します。不要であれば省略してください。
サンプリング
ポアソン分布の乱数を生成します。
ポアソン分布のパラメータ$\lambda$とデータ数$N$を設定します。
# パラメータを指定 lambda <- 4.5 # データ数(サンプルサイズ)を指定 N <- 1000
発生回数の期待値$\lambda > 0$とデータ数(サンプルサイズ)$N$を指定します。
ポアソン分布に従う乱数を生成します。
# ポアソン分布に従う乱数を生成 x_n <- rpois(n = N, lambda = lambda) head(x_n)
## [1] 6 6 7 6 6 6
ポアソン分布の乱数はrpois()で生成できます。データ数の引数nにN、パラメータの引数lambdaにlmandaを指定します。
乱数の可視化
生成した乱数を集計してヒストグラムを作成します。
サンプルの値を集計します。
# xの値を作成 x_vals <- seq(from = 0, to = max(x_n) + 3) # サンプルを集計 freq_df <- tidyr::tibble(x = x_n) |> # 乱数を格納 dplyr::count(x, name = "frequency") |> # 度数を測定 dplyr::right_join(tidyr::tibble(x = x_vals), by = "x") |> # 全てのパターンに追加 dplyr::mutate(frequency = tidyr::replace_na(frequency, 0)) # サンプルにない場合の欠損値を0に置換 freq_df
## # A tibble: 19 × 2 ## x frequency ## <int> <int> ## 1 0 8 ## 2 1 48 ## 3 2 104 ## 4 3 161 ## 5 4 192 ## 6 5 161 ## 7 6 147 ## 8 7 88 ## 9 8 47 ## 10 9 25 ## 11 10 11 ## 12 11 4 ## 13 12 2 ## 14 13 1 ## 15 15 1 ## 16 14 0 ## 17 16 0 ## 18 17 0 ## 19 18 0
サンプリングした値x_nをデータフレームに格納して、count()で重複をカウントします。
サンプルx_nにない値はデータフレームに含まれないため、right_join()で0からMの整数を持つデータフレームに結合します。サンプルにない場合は、度数列frequencyが欠損値NAになるので、replace_na()で0に置換します。(この処理は、作図自体には影響しません。サブタイトルに度数を表示するのに必要な処理です。)
サンプルのヒストグラムを作成します。
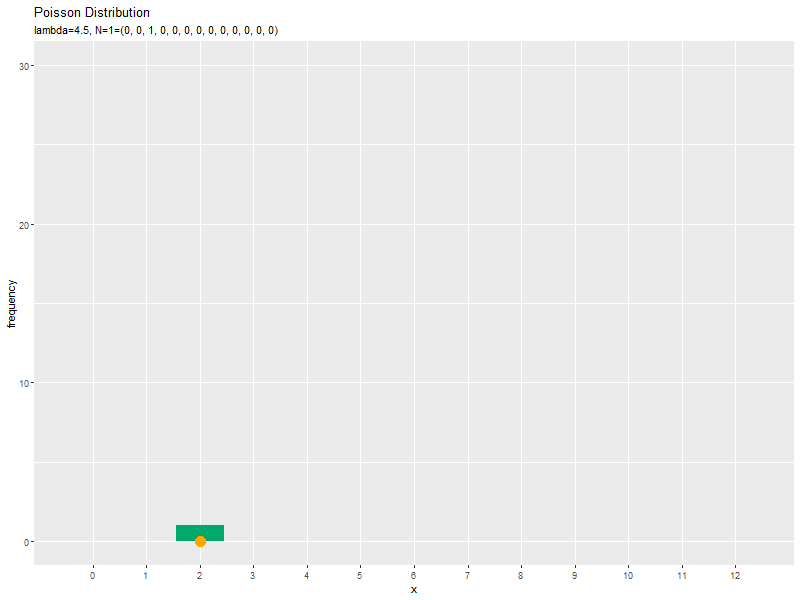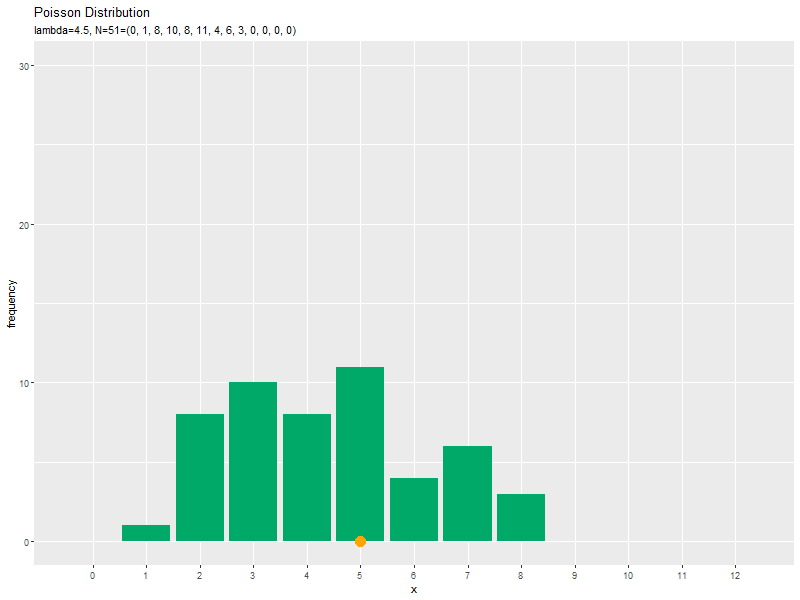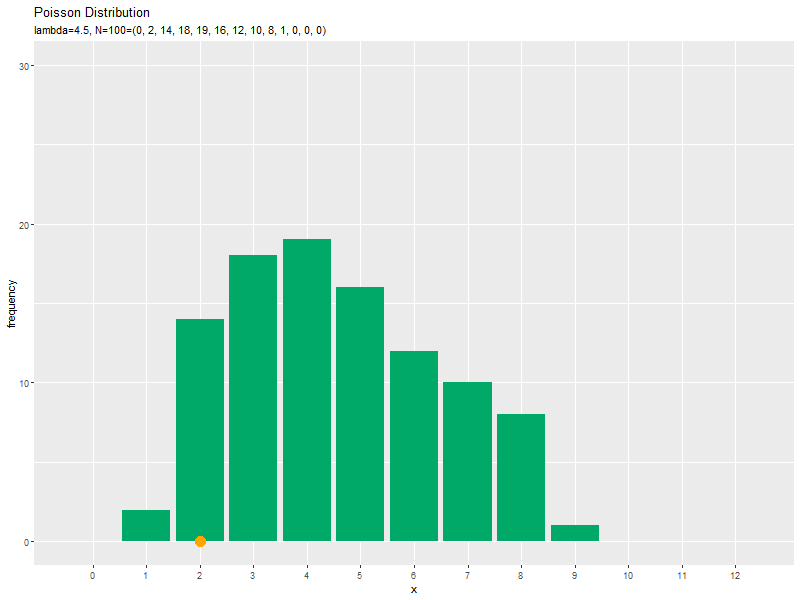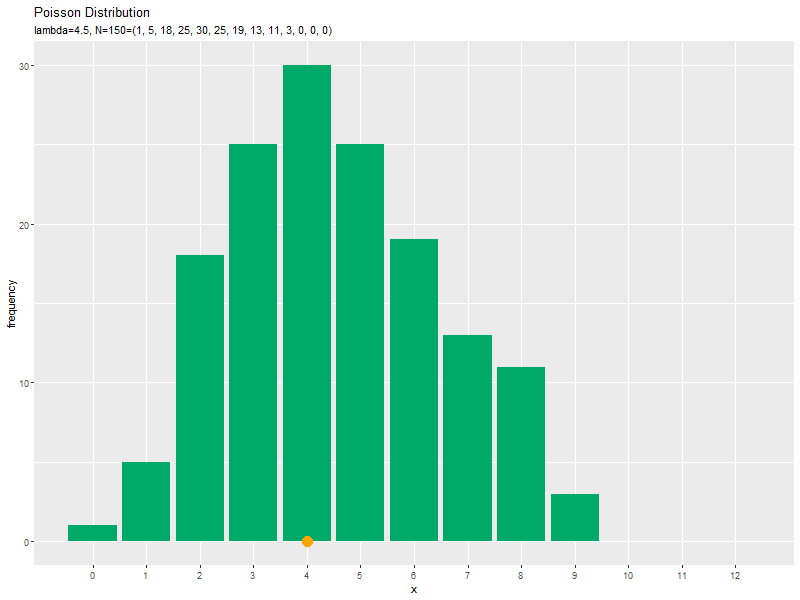
# サンプルのヒストグラムを作成:度数 ggplot(data = freq_df, mapping = aes(x = x, y = frequency)) + # データ geom_bar(stat = "identity", fill = "#00A968") + # 度数 scale_x_continuous(breaks = x_vals, minor_breaks = FALSE) + # x軸目盛 labs(title = "Poisson Distribution", subtitle = paste0("lambda=", lambda, ", N=", N), x = "x", y = "frequency") # ラベル
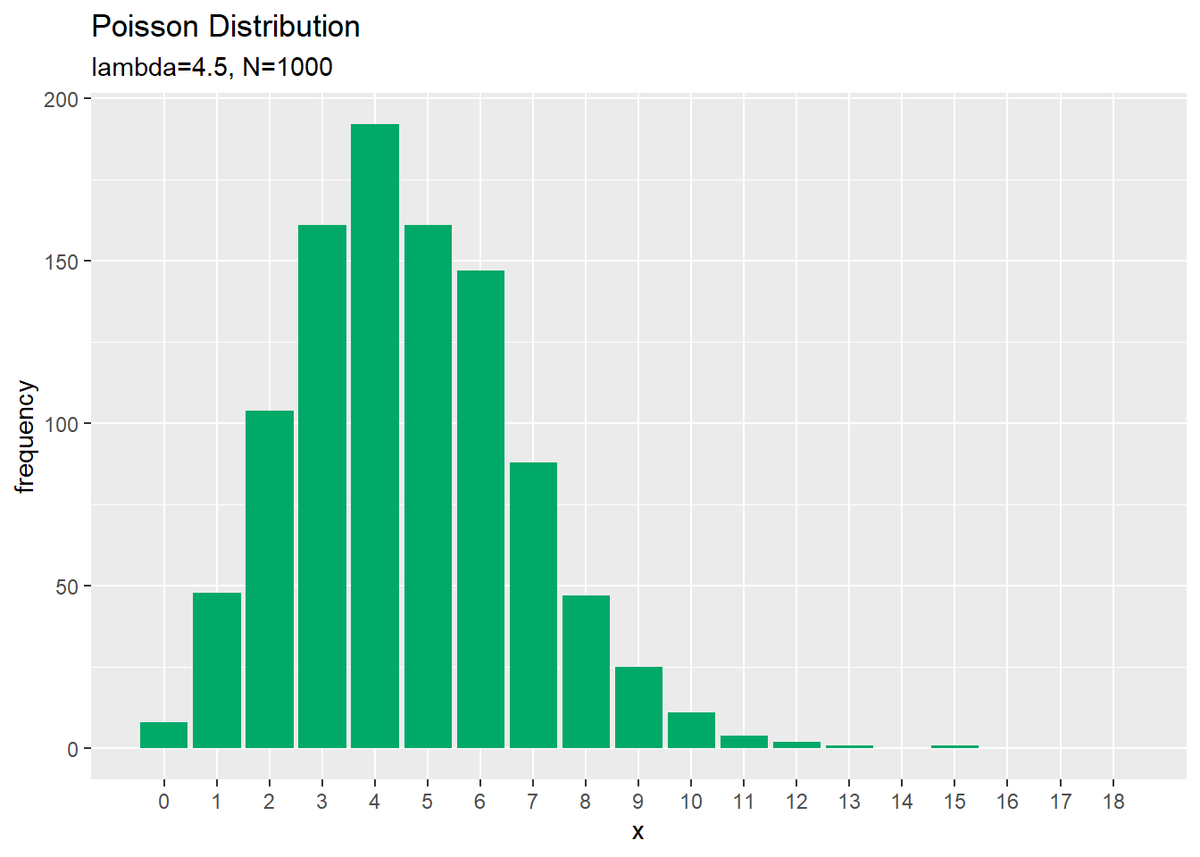
度数を高さとする棒グラフを作成します。
相対度数を分布と重ねて描画します。
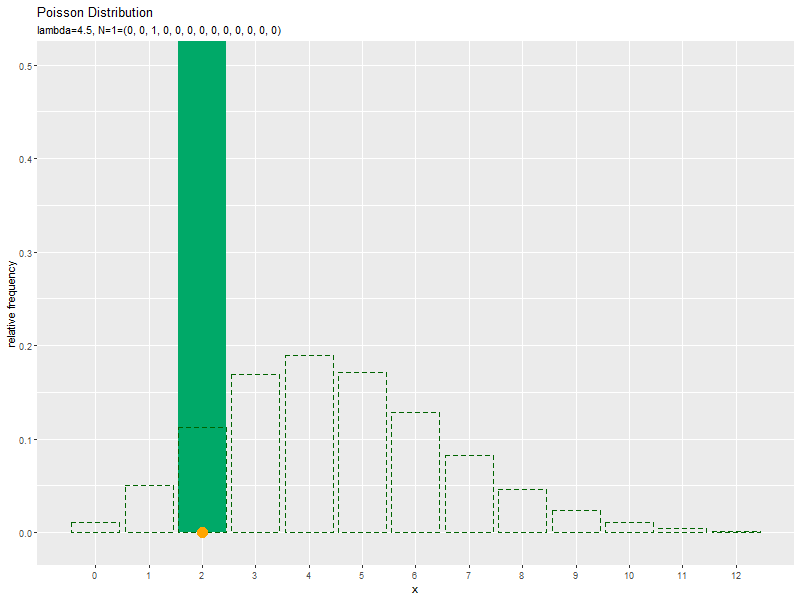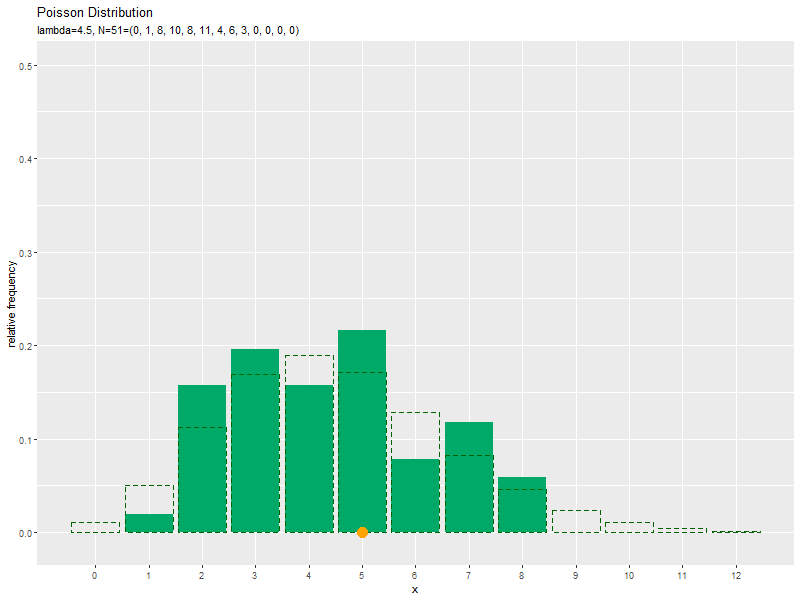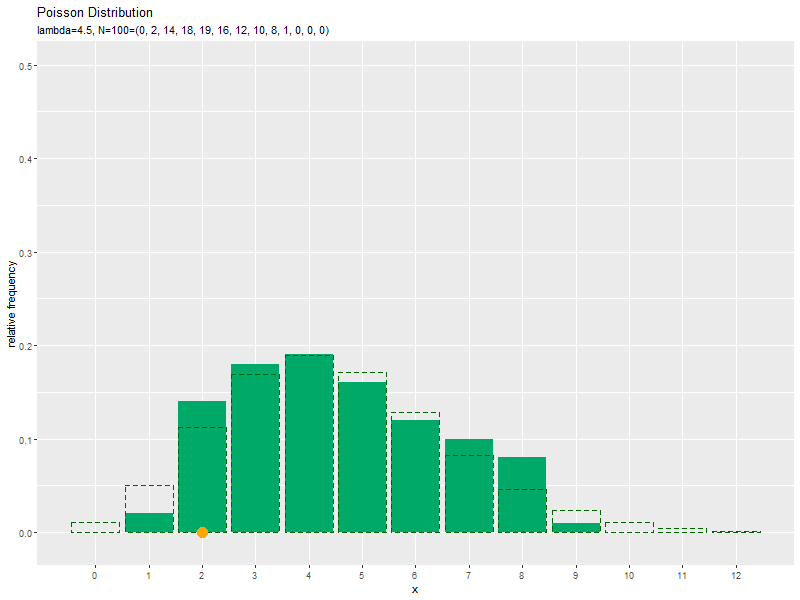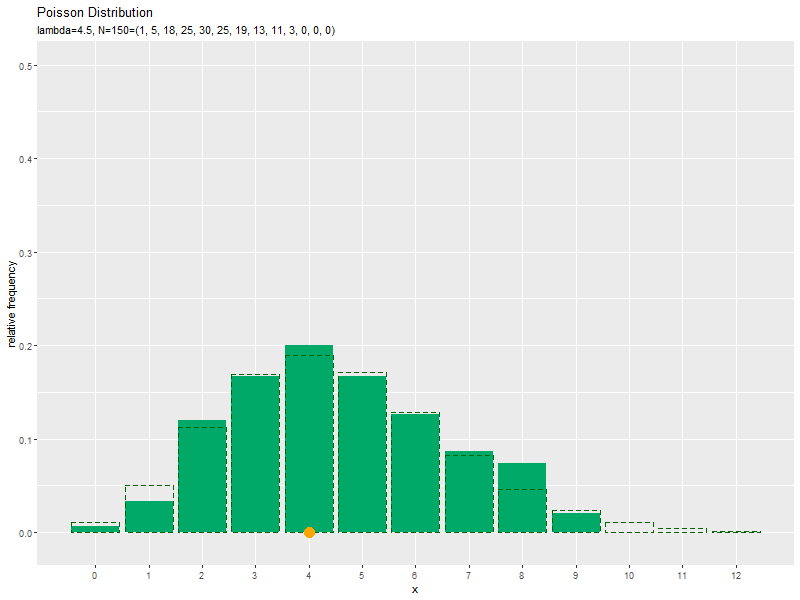
# ポアソン分布を計算 prob_df <- tidyr::tibble( x = x_vals, # 確率変数 probability = dpois(x = x_vals, lambda = lambda) # 確率 ) # サンプルのヒストグラムを作成:相対度数 ggplot() + geom_bar(data = freq_df, mapping = aes(x = x, y = frequency/N), stat = "identity", fill = "#00A968") + # 相対度数 geom_bar(data = prob_df, mapping = aes(x = x, y = probability), stat = "identity", alpha = 0, color = "darkgreen", linetype = "dashed") + # 元の分布 scale_x_continuous(breaks = x_vals, minor_breaks = FALSE) + # x軸目盛 labs( title = "Bernoulli Distribution", subtitle = parse( text = paste0( "list(lambda==", lambda, ", N==(list(", paste0(freq_df[["frequency"]], collapse = ", "), ")))") ), x = "x", y = "relative frequency" ) # ラベル
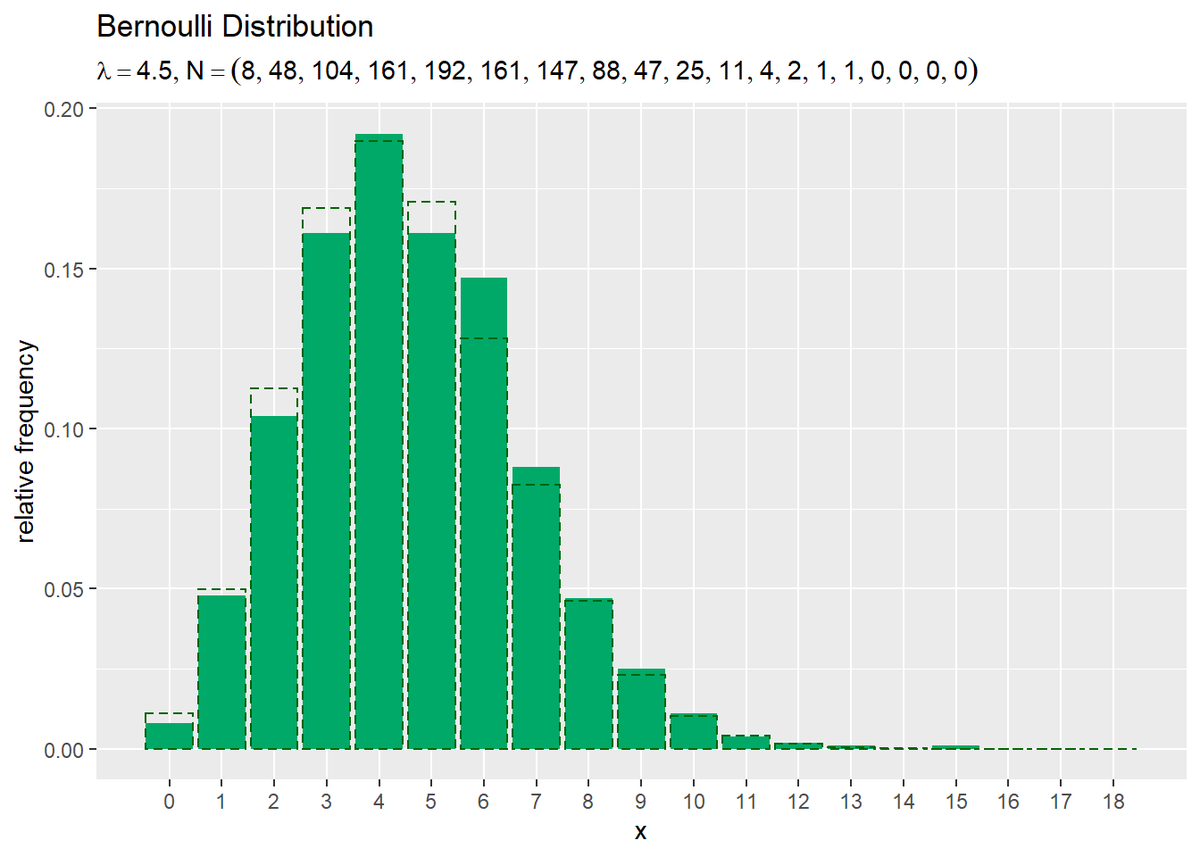
度数frequencyをデータ数Nで割った相対度数を高さとする棒グラフを作成します。
ギリシャ文字などの記号を使った数式を表示する場合は、expression()の記法を使います。等号は"=="、複数の(数式上の)変数を並べるには"list(変数1, 変数2)"とします。(プログラム上の)変数の値を使う場合は、parse()のtext引数に指定します。
データ数(サンプルサイズ)が十分に増えると、ヒストグラムの形が分布の形に近付きます。
乱数と分布の関係をアニメーションで可視化
次は、サンプルサイズとヒストグラムの形状の関係をアニメーションで確認します。
・作図コード(クリックで展開)
パラメータ$\lambda$とデータ数$N$を指定して、ポアソン分布の乱数を生成します。
# パラメータを指定 lambda <- 4.5 # データ数を指定 N <- 1000 # ポアソン分布に従う乱数を生成 x_n <- rpois(n = N, lambda = lambda) head(x_n)
## [1] 2 3 7 3 3 5
x_nのn番目の要素を、n回目にサンプリングされた値とみなします。アニメーションのn番目のフレームでは、n個のサンプルx_n[1:n]のヒストグラムを描画します。
サンプリング回数ごとに、確率変数の値x_valsごとの度数を求めます。
# xの値を作成 x_vals <- seq(from = 0, to = max(x_n) + 3) # サンプルを集計 freq_df <- tibble::tibble( x = x_n, # サンプル n = 1:N, # データ番号 frequency = 1 # 集計用の値 ) |> # 乱数を格納 dplyr::right_join(tidyr::expand_grid(x = x_vals, n = 1:N), by = c("x", "n")) |> # 全てのパターンに結合 dplyr::mutate(frequency = tidyr::replace_na(frequency, replace = 0)) |> # サンプルにない場合の欠損値を0に置換 dplyr::arrange(n, x) |> # 集計用に昇順に並べ替え dplyr::group_by(x) |> # 集計用にグループ化 dplyr::mutate(frequency = cumsum(frequency)) |> # 累積和を計算 dplyr::ungroup() # グループ化を解除 freq_df
## # A tibble: 1,950 × 3 ## x n frequency ## <int> <int> <dbl> ## 1 0 1 0 ## 2 1 1 0 ## 3 2 1 1 ## 4 3 1 0 ## 5 4 1 0 ## 6 5 1 0 ## 7 6 1 0 ## 8 7 1 0 ## 9 8 1 0 ## 10 9 1 0 ## # … with 1,940 more rows
サンプルx_n、データ番号(サンプリング回数)1:N、度数計算用の値1をデータフレームに格納します。各データ番号において、実際にサンプリングされた値がデータフレームに含まれます。
$x$の値とデータ番号の全ての組み合わせをexpand_grid()で作成して、そこにサンプルをright_join()で結合します。サンプルにない場合は、frequency列が欠損値NAになるので、replace_na()で0に置換します。
x列($x$の値)でグループ化して、frequency列(サンプルは1でそれ以外は0)の累積和をcumsum()で計算して、各試行回数までの度数を求めます。
ヒストグラムの作図に利用する集計結果が得られました。以降は、グラフの装飾のための処理です。
$x$の値(x_valseの各要素)ごとの度数を使って、フレーム切替用のラベルを作成します。
# フレーム切替用のラベルを作成 label_vec <- freq_df |> tidyr::pivot_wider( id_cols = n, names_from = x, names_prefix = "x", values_from = frequency ) |> # 度数列を展開 tidyr::unite(col = "label", dplyr::starts_with("x"), sep = ", ") |> # 度数情報をまとめて文字列化 dplyr::mutate( label = paste0("lambda=", lambda, ", N=", n, "=(", label, ")") |> (\(.){factor(., levels = .)})() ) |> # パラメータ情報をまとめて因子型に変換 dplyr::pull(label) # ベクトルとして取得 head(label_vec)
## [1] lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## [2] lambda=4.5, N=2=(0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## [3] lambda=4.5, N=3=(0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0) ## [4] lambda=4.5, N=4=(0, 0, 1, 2, 0, 0, 0, 1, 0, 0, 0, 0, 0) ## [5] lambda=4.5, N=5=(0, 0, 1, 3, 0, 0, 0, 1, 0, 0, 0, 0, 0) ## [6] lambda=4.5, N=6=(0, 0, 1, 3, 0, 1, 0, 1, 0, 0, 0, 0, 0) ## 150 Levels: lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ...
pivot_wider()で、x列(x_vals)の値ごとの度数列に展開します。データ番号(サンプリング回数)の列nとx_valsに対応したM+1個の列になります。
度数列の値をunite()で文字列としてまとめて、さらにpaste0()でパラメータの値と結合し、因子型に変換します。因子型への変換処理では、無名関数function()の省略記法\()を使って、(\(x){引数xを使った具体的な処理})()としています。直前のパイプ演算子を%>%にすると、行全体(\(引数){処理})()を{}の中の処理に置き換えられます(置き換えられるように引数名を.にしています)。
作成したラベル列をpull()でベクトルとして取り出します。
集計結果のデータフレームにフレーム切替用のラベル列を追加します。
# フレーム切替用のラベルを追加 anime_freq_df <- freq_df |> tibble::add_column(parameter = rep(label_vec, each = length(x_vals))) anime_freq_df
## # A tibble: 1,950 × 4 ## x n frequency parameter ## <int> <int> <dbl> <fct> ## 1 0 1 0 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 2 1 1 0 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 3 2 1 1 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 4 3 1 0 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 5 4 1 0 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 6 5 1 0 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 7 6 1 0 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 8 7 1 0 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 9 8 1 0 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 10 9 1 0 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## # … with 1,940 more rows
label_vecの各要素をM+1個(x_valsの要素数)に複製して、add_column()で列として追加します。
(M+1)×N行のデータフレームになります。これをヒストグラムの描画に使います。
サンプルと対応するラベルをデータフレームに格納します。
# サンプルを格納 anime_data_df <- tibble::tibble( x = x_n, # サンプル parameter = label_vec # フレーム切替用ラベルを追加 ) anime_data_df
## # A tibble: 150 × 2 ## x parameter ## <int> <fct> ## 1 2 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 2 3 lambda=4.5, N=2=(0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 3 7 lambda=4.5, N=3=(0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0) ## 4 3 lambda=4.5, N=4=(0, 0, 1, 2, 0, 0, 0, 1, 0, 0, 0, 0, 0) ## 5 3 lambda=4.5, N=5=(0, 0, 1, 3, 0, 0, 0, 1, 0, 0, 0, 0, 0) ## 6 5 lambda=4.5, N=6=(0, 0, 1, 3, 0, 1, 0, 1, 0, 0, 0, 0, 0) ## 7 3 lambda=4.5, N=7=(0, 0, 1, 4, 0, 1, 0, 1, 0, 0, 0, 0, 0) ## 8 2 lambda=4.5, N=8=(0, 0, 2, 4, 0, 1, 0, 1, 0, 0, 0, 0, 0) ## 9 4 lambda=4.5, N=9=(0, 0, 2, 4, 1, 1, 0, 1, 0, 0, 0, 0, 0) ## 10 6 lambda=4.5, N=10=(0, 0, 2, 4, 1, 1, 1, 1, 0, 0, 0, 0, 0) ## # … with 140 more rows
N行のデータフレームになります。各サンプリングにおけるサンプルの値を描画するのに使います。
ポアソン分布を計算して、データ数分に複製し、対応するラベルを追加します。
# ポアソン分布の情報を複製 anime_prob_df <- tibble::tibble( x = x_vals, # 確率変数 probability = dpois(x = x_vals, lambda = lambda), # 確率 num = N # 複製数 ) |> tidyr::uncount(num) |> # データ数分に複製 tibble::add_column(parameter = rep(label_vec, times = length(x_vals))) |> # フレーム切替用ラベルを追加 dplyr::arrange(parameter) # サンプリング回数ごとに並べ替え anime_prob_df
## # A tibble: 1,950 × 3 ## x probability parameter ## <int> <dbl> <fct> ## 1 0 0.0111 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 2 1 0.0500 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 3 2 0.112 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 4 3 0.169 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 5 4 0.190 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 6 5 0.171 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 7 6 0.128 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 8 7 0.0824 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 9 8 0.0463 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## 10 9 0.0232 lambda=4.5, N=1=(0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) ## # … with 1,940 more rows
確率分布の情報とデータ数Nをデータフレームに格納して、uncount()で複製します。
(M+1)×N行のデータフレームになります。これを分布の棒グラフを描画するのに使います。
サンプルのヒストグラムのアニメーション(gif画像)を作成します。
# ポアソン乱数のヒストグラムのアニメーションを作図:度数 anime_freq_graph <- ggplot() + geom_bar(data = anime_freq_df, mapping = aes(x = x, y = frequency), stat = "identity", fill = "#00A968") + # 度数 geom_point(data = anime_data_df, mapping = aes(x = x, y = 0), color = "orange", size = 5) + # サンプル gganimate::transition_manual(parameter) + # フレーム scale_x_continuous(breaks = x_vals, minor_breaks = FALSE) + # x軸目盛 labs(title = "Poisson Distribution", subtitle = "{current_frame}", x = "x", y = "frequency") # ラベル # gif画像を作成 gganimate::animate(anime_freq_graph, nframes = N, fps = 10, width = 800, height = 600)
transition_manual()にフレームの順序を表す列を指定します。この例では、因子型のラベルのレベルの順に描画されます。
animate()のフレーム数の引数nframesにデータ数(サンプルサイズ)、フレームレートの引数fpsに1秒当たりのフレーム数を指定します。fps引数の値が大きいほどフレームが早く切り替わります。ただし、値が大きいと指定した通りに動作しません。
相対度数を分布と重ねたアニメーションを作成します。
# ポアソン乱数のヒストグラムのアニメーションを作図:相対度数 anime_prop_graph <- ggplot() + geom_bar(data = anime_freq_df, mapping = aes(x = x, y = frequency/n), stat = "identity", fill = "#00A968") + # 相対度数 geom_bar(data = anime_prob_df, mapping = aes(x = x, y = probability), stat = "identity", alpha = 0, color = "darkgreen", linetype = "dashed") + # 元の分布 geom_point(data = anime_data_df, mapping = aes(x = x, y = 0), color = "orange", size = 5) + # サンプル gganimate::transition_manual(parameter) + # フレーム scale_x_continuous(breaks = x_vals, minor_breaks = FALSE) + # x軸目盛 coord_cartesian(ylim = c(-0.01, 0.5)) + # y軸の表示範囲 labs(title = "Poisson Distribution", subtitle = "{current_frame}", x = "x", y = "relative frequency") # ラベル # gif画像を作成 gganimate::animate(anime_prop_graph, nframes = N, fps = 10, width = 800, height = 600)
サンプルが増えるに従って、ヒストグラムが元の分布に近付くのを確認できます。
この記事では、ポアソン分布の乱数を確認しました。
参考文献
- 須山敦志『ベイズ推論による機械学習入門』(機械学習スタートアップシリーズ)杉山将監修,講談社,2017年.
おわりに
記事を分割しました。
- 2022.07.19:加筆修正しました。
【次の内容】
つづく