はじめに
機械学習で登場する確率分布について色々な角度から理解したいシリーズです。
この記事では、R言語で1次元ガウス分布(一変量正規分布)のグラフを作成します。
【前の内容】
【他の記事一覧】
【この記事の内容】
1次元ガウス分布の乱数生成
1次元分布(Gaussian Distribution)の乱数を生成します。ガウス分布については「1次元ガウス分布の定義式の確認 - からっぽのしょこ」を参照してください。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(gganimate)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているため、ggplot2は読み込む必要があります。
magrittrパッケージのパイプ演算子%>%ではなく、ベースパイプ(ネイティブパイプ)演算子|>を使っています。%>%に置き換えても処理できます。
分布の変化をアニメーション(gif画像)で確認するのにgganimateパッケージを利用します。不要であれば省略してください。
サンプリング
ガウス分布の乱数を生成します。
ガウス分布のパラメータ$\mu, \sigma$とデータ数$N$を設定します。
# 平均パラメータを指定 mu <- 2 # 標準偏差パラメータを指定 sigma <- 2.5 # データ数(サンプルサイズ)を指定 N <- 1000
平均パラメータ(実数)$\mu$、精度パラメータ(正の実数)$\sigma$とデータ数(サンプルサイズ)$N$を指定します。
ガウス分布に従う乱数を生成します。
# ガウス分布に従う乱数を生成 x_n <- rnorm(n = N, mean = mu, sd = sigma) head(x_n)
## [1] 2.55048161 -0.04747142 2.19561314 -3.66976768 0.01840773 3.23607231
ガウス分布の乱数は、rnorm()で生成できます。データ数(サンプルサイズ)の引数nにN、平均の引数meanにmu、標準偏差の引数sdにsigmaを指定します。
乱数の可視化
サンプルのヒストグラムを作成します。
# サンプルを格納 data_df <- tidyr::tibble(x = x_n) # サンプルのヒストグラムを作成:度数 ggplot(data = data_df, mapping = aes(x = x, y = ..count..)) + # データ geom_histogram(bins = 30, fill = "#00A968") + # ヒストグラム labs( title = "Gaussian Distribution", subtitle = paste0("mu=", mu, ", sigma=", sigma, ", N=", N), # (文字列表記用) #subtitle = parse(text = paste0("list(mu==", mu, ", sigma==", sigma, ", N==", N, ")")), # (数式表記用) x = "x", y = "frequency" ) # ラベル
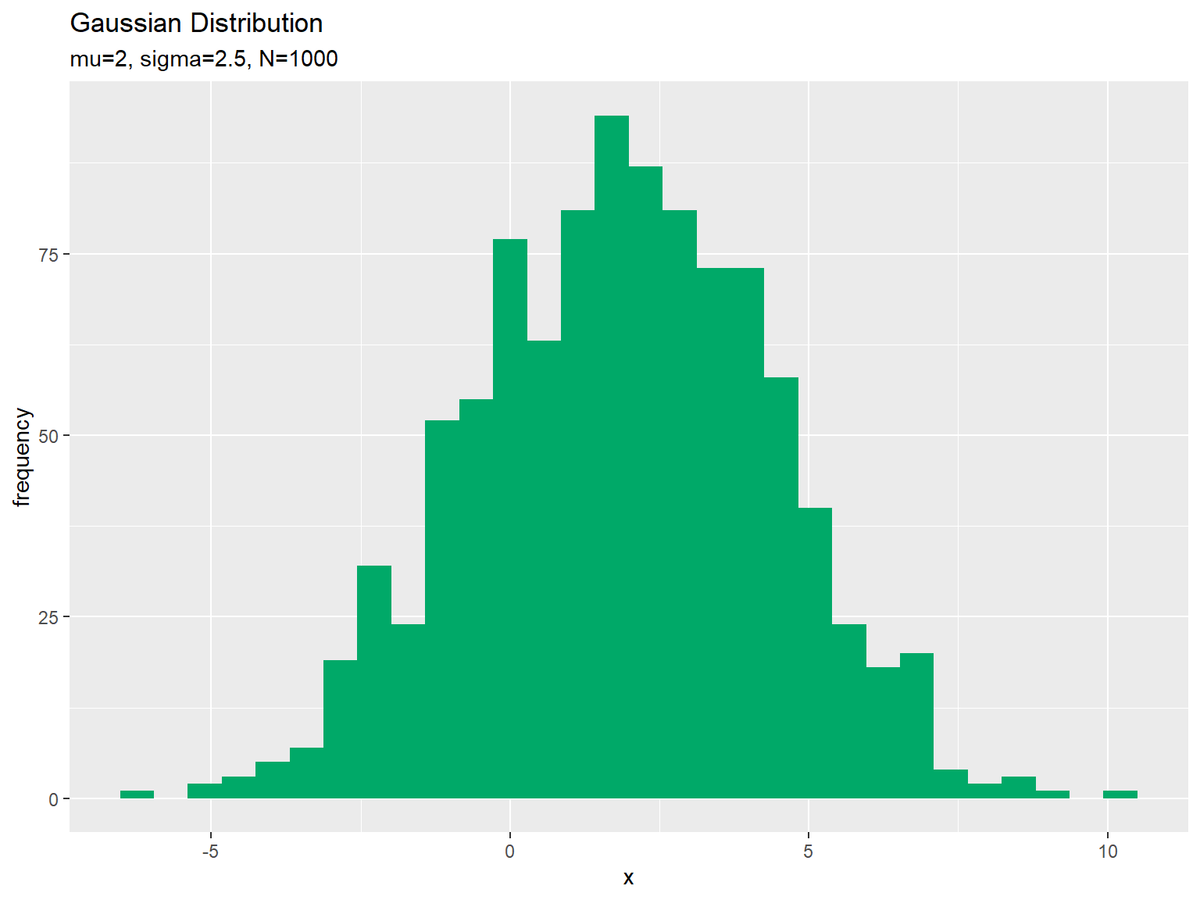
サンプルをデータフレームに格納して、geom_histgram()でヒストグラムを描画します。デフォルト(y = ..count..)では、度数のヒストグラムを作成します。集計の範囲については、バーの数の引数binsまたはバーのサイズの引数binwidthを指定します。
ギリシャ文字などの記号を使った数式を表示する場合は、expression()の記法を使います。等号は"=="、複数の(数式上の)変数を並べるには"list(変数1, 変数2)"とします。(プログラム上の)変数の値を使う場合は、parse()のtext引数に指定します。
サンプルの密度を確率分布と重ねて描画します。
# xの値を作成 x_vals <- seq(from = mu-sigma * 4, to = mu+sigma * 4, length.out = 251) # ガウス分布を計算 dens_df <- tidyr::tibble( x = x_vals, # 確率変数 density = dnorm(x = x_vals, mean = mu, sd = sigma) # 確率密度 ) # サンプルのヒストグラムを作成:密度 ggplot() + geom_histogram(data = data_df, mapping = aes(x = x, y = ..density..), bins = 30, fill = "#00A968") + # ヒストグラム geom_line(data = dens_df, mapping = aes(x = x, y = density), color = "darkgreen", size = 1, linetype = "dashed") + # 元の分布 labs(title = "Gaussian Distribution", subtitle = parse(text = paste0("list(mu==", mu, ", sigma==", sigma, ", N==", N, ")")), # 数式で表示 x = "x", y = "density") # ラベル
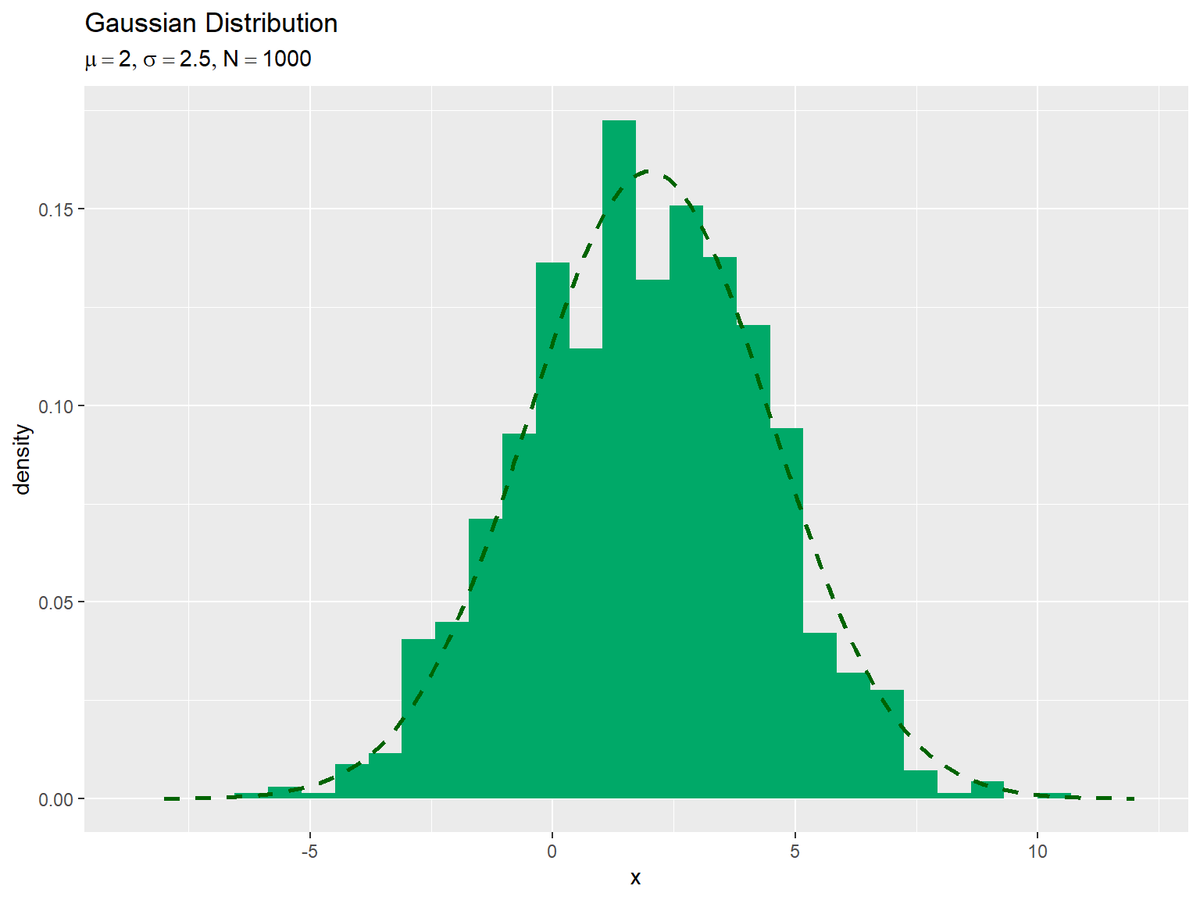
geom_histogram()のy軸の引数yに..density..を指定すると、密度に変換したヒストグラムを描画します。
データ数(サンプルサイズ)が十分に増えると、ヒストグラムの形が分布の形に近付きます。
乱数と分布の関係をアニメーションで可視化
次は、サンプルサイズとヒストグラムの形状の関係をアニメーションで確認します。
パラメータ$\mu, \sigma$とデータ数$N$を指定して、ガウス分布の乱数を生成します。
・作図コード(クリックで展開)
# 平均パラメータを指定 mu <- 2 # 標準偏差パラメータを指定 sigma <- 2.5 # データ数(フレーム数)を指定 N <- 100 # ガウス分布に従う乱数を生成 x_n <- rnorm(n = N, mean = mu, sd = sigma) head(x_n)
## [1] -3.086761 6.154742 2.905464 2.149756 -1.574255 2.382001
x_nのn番目の要素を、n回目にサンプリングされた値とみなします。アニメーションのn番目のフレームでは、n個のサンプルx_n[1:n]のヒストグラムを描画します。
サンプリング回数ごとに、それまでのサンプルを持つデータフレームを作成します。
# サンプルを複製して格納 anime_freq_df <- tidyr::tibble( x = rep(x_n, times = N), # サンプル n = rep(1:N, times = N), # データ番号 frame = rep(1:N, each = N) # フレーム番号 ) |> dplyr::filter(n <= frame) |> # サンプリング回数以前のサンプルを抽出 dplyr::mutate( parameter = paste0("mu=", mu, ", sigma=", sigma, ", N=", frame) |> factor(levels = paste0("mu=", mu, ", sigma=", sigma, ", N=", 1:N)) ) # フレーム切替用ラベルを追加 anime_freq_df
## # A tibble: 5,050 × 4 ## x n frame parameter ## <dbl> <int> <int> <fct> ## 1 -3.09 1 1 mu=2, sigma=2.5, N=1 ## 2 -3.09 1 2 mu=2, sigma=2.5, N=2 ## 3 6.15 2 2 mu=2, sigma=2.5, N=2 ## 4 -3.09 1 3 mu=2, sigma=2.5, N=3 ## 5 6.15 2 3 mu=2, sigma=2.5, N=3 ## 6 2.91 3 3 mu=2, sigma=2.5, N=3 ## 7 -3.09 1 4 mu=2, sigma=2.5, N=4 ## 8 6.15 2 4 mu=2, sigma=2.5, N=4 ## 9 2.91 3 4 mu=2, sigma=2.5, N=4 ## 10 2.15 4 4 mu=2, sigma=2.5, N=4 ## # … with 5,040 more rows
データ番号(n列)は1からNの整数がN回繰り返すように、フレーム番号(frame列)は1からNの整数がN個ずつ並ぶように作成します。サンプルはデータ番号に対応するように複製します。
フレーム番号ごとに、それ以下の番号のサンプルをfilter()で抽出します。
フレーム番号をデータ番号として、フレーム切替用のラベル列を作成します。これにより、各フレーム(サンプリング回数)ごとにそれ以前のサンプルを使ってグラフを作成できます。ラベルが文字列型だと文字列の基準で順序が決まるので、因子型にしてサンプリング回数に応じたレベル(順序)を設定します。
このデータフレームは、ヒストグラムを描画するのに使います。
サンプルと対応するラベルをデータフレームに格納します。
# サンプルを格納 anime_data_df <- tidyr::tibble( x = x_n, # サンプル n = 1:N, # データ番号 parameter = paste0("mu=", mu, ", sigma=", sigma, ", N=", 1:N) |> factor(levels = paste0("mu=", mu, ", sigma=", sigma, ", N=", 1:N)) # フレーム切替用ラベル ) anime_data_df
## # A tibble: 100 × 3 ## x n parameter ## <dbl> <int> <fct> ## 1 -3.09 1 mu=2, sigma=2.5, N=1 ## 2 6.15 2 mu=2, sigma=2.5, N=2 ## 3 2.91 3 mu=2, sigma=2.5, N=3 ## 4 2.15 4 mu=2, sigma=2.5, N=4 ## 5 -1.57 5 mu=2, sigma=2.5, N=5 ## 6 2.38 6 mu=2, sigma=2.5, N=6 ## 7 1.91 7 mu=2, sigma=2.5, N=7 ## 8 3.18 8 mu=2, sigma=2.5, N=8 ## 9 6.03 9 mu=2, sigma=2.5, N=9 ## 10 -1.31 10 mu=2, sigma=2.5, N=10 ## # … with 90 more rows
このデータフレームは、各サンプリングにおけるサンプルの値を描画するのに使います。
サンプルのヒストグラムのアニメーション(gif画像)を作成します。
# サンプルのヒストグラムのアニメーションのアニメーションを作図:度数 anime_freq_graph <- ggplot() + # geom_histogram(data = anime_freq_df, mapping = aes(x = x), breaks = seq(from = min(x_vals), to = max(x_vals), length.out = 30), fill = "#00A968") + # ヒストグラム geom_point(data = anime_data_df, mapping = aes(x = x, y = 0), color = "orange", size = 6) + # サンプル gganimate::transition_manual(parameter) + # フレーム labs(title = "Gaussian Distribution", subtitle = "{current_frame}", x = "x", y = "frequency") # ラベル # gif画像を作成 gganimate::animate(anime_freq_graph, nframes = N, fps = 10, width = 800, height = 600)
集計範囲を固定するために、geom_histogram()のbreaks引数に区切り位置を指定します。この例では、seq()を使ってx_valsの最小値から最大値の範囲を30等分しています。
transition_manual()にフレームの順序を表す列を指定します。この例では、因子型のラベルのレベルの順に描画されます。
animate()のフレーム数の引数nframesにデータ数(サンプルサイズ)、フレームレートの引数fpsに1秒当たりのフレーム数を指定します。fps引数の値が大きいほどフレームが早く切り替わります。
サンプルの密度を確率分布と重ねたアニメーションを作成します。
# xの値を作成 x_vals <- seq(from = mu-sigma * 4, to = mu+sigma * 4, length.out = 251) # ガウス分布を計算 dens_df <- tidyr::tibble( x = x_vals, # 確率変数 density = dnorm(x = x_vals, mean = mu, sd = sigma) # 確率密度 ) # サンプルのヒストグラムのアニメーションのアニメーションを作図:密度 anime_freq_graph <- ggplot() + # geom_histogram(data = anime_freq_df, mapping = aes(x = x, y = ..density..), breaks = seq(from = min(x_vals), to = max(x_vals), length.out = 30), fill = "#00A968") + # ヒストグラム geom_point(data = anime_data_df, mapping = aes(x = x, y = 0), color = "orange", size = 6) + # サンプル geom_line(data = dens_df, mapping = aes(x = x, y = density), color = "darkgreen", size = 1, linetype = "dashed") + # 元の分布 gganimate::transition_manual(parameter) + # フレーム coord_cartesian(ylim = c(0, max(dens_df[["density"]])*2)) + # 軸の表示範囲 labs(title = "Gaussian Distribution", subtitle = "{current_frame}", x = "x", y = "density") # ラベル # gif画像を作成 gganimate::animate(anime_freq_graph, nframes = N, fps = 10, width = 800, height = 600)
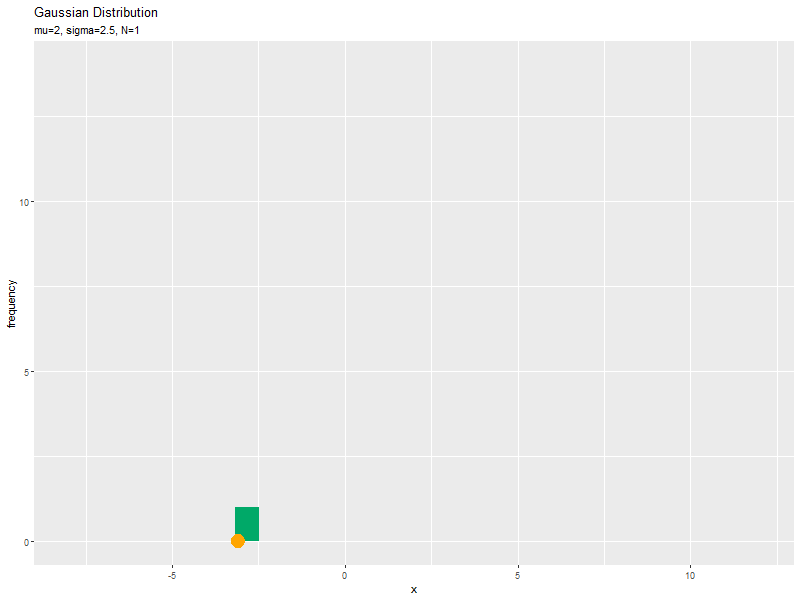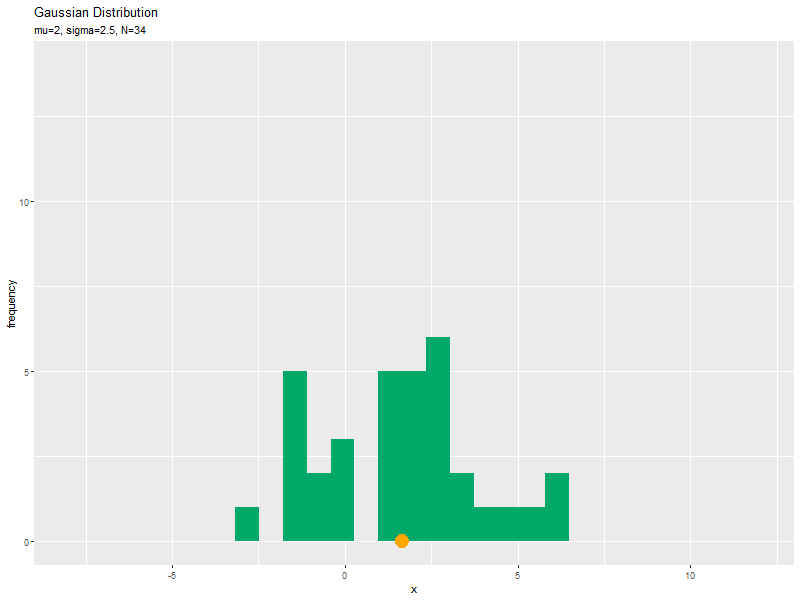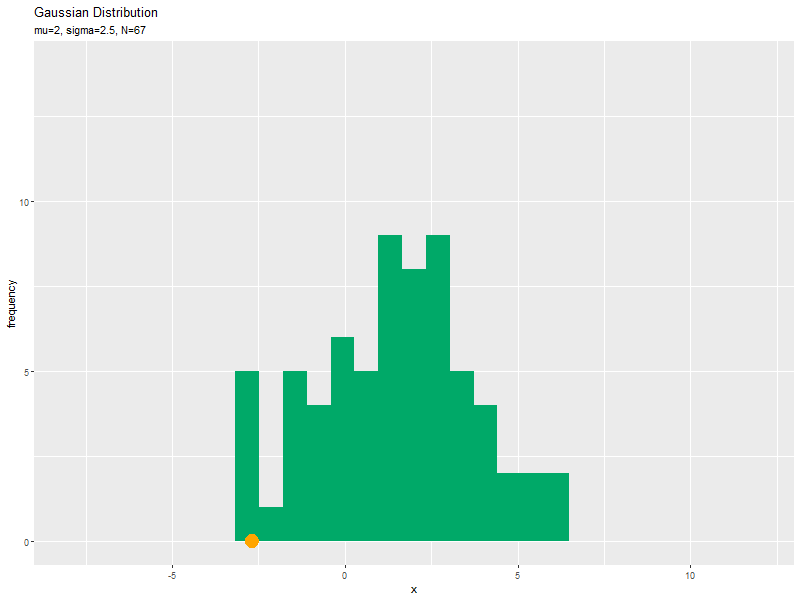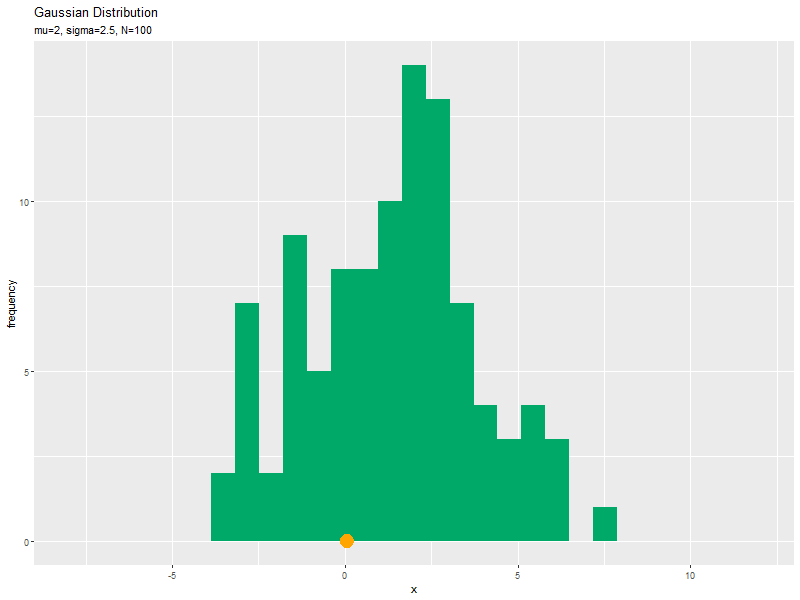
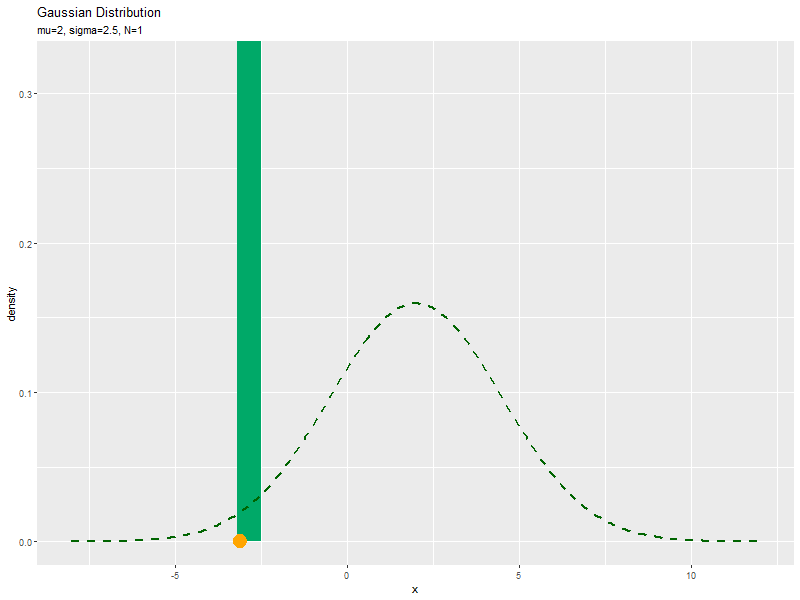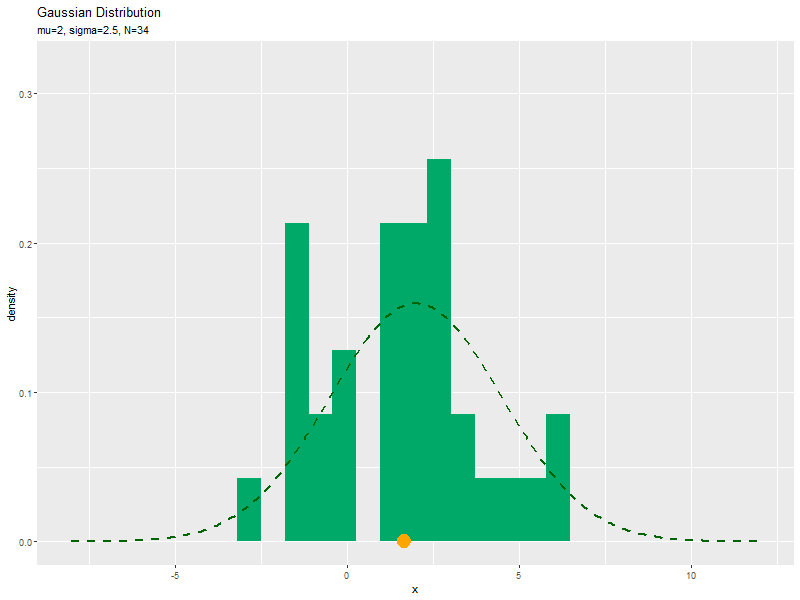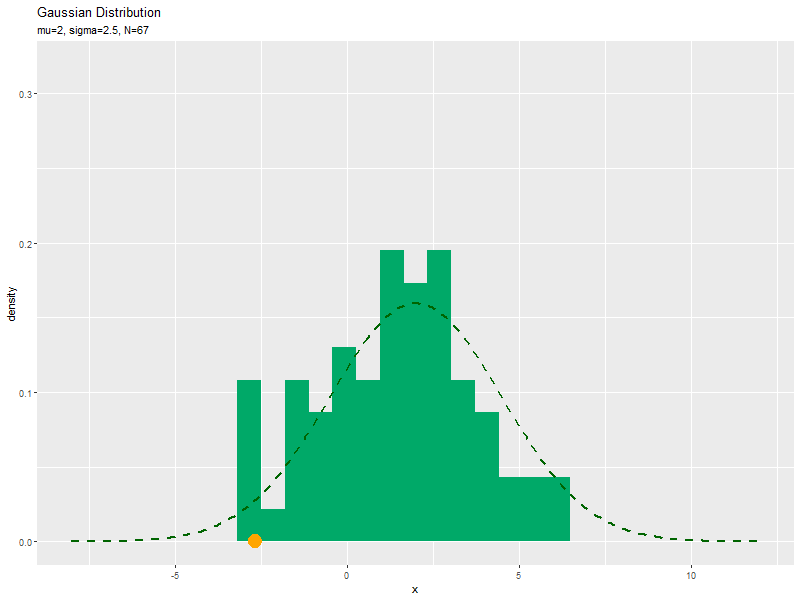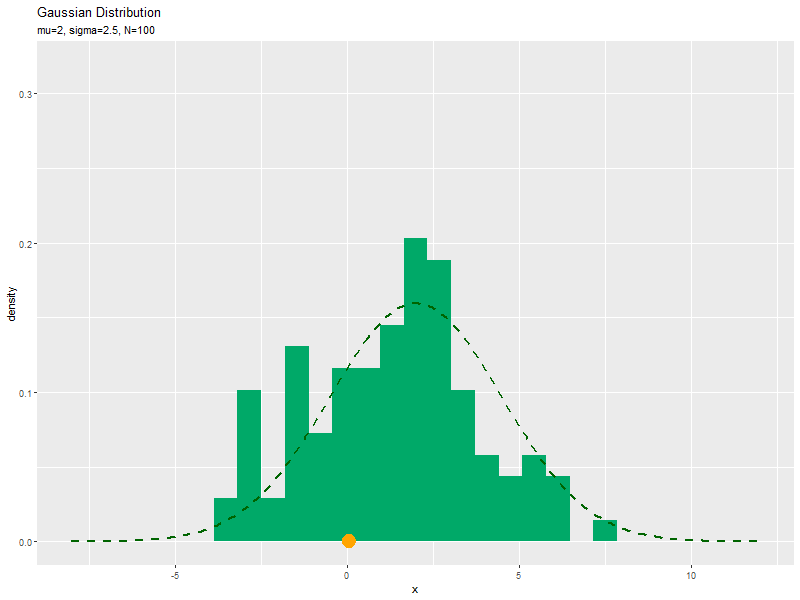
サンプルが増えるに従って、ヒストグラムが元の分布に近付くのを確認できます。
この記事では、1次元ガウス分布の乱数生成を確認しました。次は、ガウス分布から確率分布を生成します。
参考文献
- 須山敦志『ベイズ推論による機械学習入門』(機械学習スタートアップシリーズ)杉山将監修,講談社,2017年.
おわりに
加筆修正の際に「ガウス分布の作図」から記事を分割しました。
【次の内容】