はじめに
この記事は、「Rのカレンダー | Advent Calendar 2021 - Qiita」の11日目の記事です。
『パターン認識と機械学習』の独学時のまとめです。一連の記事は「数式の行間埋め」または「R・Pythonでのスクラッチ実装」からアルゴリズムの理解を補助することを目的としています。本とあわせて読んでください。
この記事は、3.1.4項「正則化最小二乗法」の内容です。ラッソ回帰(Lasso回帰)の最尤推定をR言語で実装します。
【数式読解編】
【前節の内容】
【他の節一覧】
【この節の内容】
・ラッソ回帰の実装
ラッソ回帰(L1正則化)を実装します。線形基底関数モデルについては「【R】3.1.1:線形基底関数モデルの実装【PRMLのノート】 - からっぽのしょこ」を参照してください。
この記事では、ラッソ回帰により観測データから真のモデルを推定(近似)します。
利用するパッケージを読み込みます。
# 3.1.4項で利用するパッケージ library(tidyverse)
・関数の準備
パラメータの更新に利用する関数を作成しておきます。
# ラッソ回帰の重みパラメータの最尤解を計算する関数を作成 soft_thresholding <- function(S, lambda, phi_x_n) { # 条件に応じて値を計算 if(S > lambda) { # S > λの場合の計算 w <- (S - lambda) / sum(phi_x_n^2) } else if(S < -lambda) { # S < -λの場合の計算 w <- (S + lambda) / sum(phi_x_n^2) } else { # -λ =< S =< λの場合 w <- 0 } return(w) }
ラッソ回帰では、条件によってパラメータの更新式が異なります。また、繰り返し更新します。
何度も複雑な処理をすることになるので、次の計算を行う処理を関数にしておきます。
詳しくは、パラメータ推定のところで解説します。
・モデルの設定とデータの生成
データを生成する関数を設定して、利用するデータを人工的に生成します。処理の流れは3.1.1項と同じなので、詳しくはそちらを参照してください。
データ生成関数(推定対象の関数)と基底関数を作成します。
# 真の関数を作成 y_true <- function(x) { # 計算式を指定 y <- sin(2 * pi * x) return(y) } # 多項式基底関数を作成 phi_poly <- function(x, m) { # m乗を計算 y <- x^m return(y) } # 計画行列を作成 Phi <- function(x_n, M) { # 変数を初期化 x_nm <- matrix(0, nrow = length(x_n), ncol = M) # m列目を計算 for(m in 0:(M-1)) { x_nm[, m+1] <- phi_poly(x_n, m) } return(x_nm) }
この例では、多項式基底関数を使います。ガウス基底関数やシグモイド基底関数を使う場合は3.1.1項を参照してください。
真のモデルの精度パラメータを指定して出力を計算します。
# データの範囲を指定 x_min <- 0 x_max <- 1 # 作図用のxの値を作成 x_vals <- seq(x_min, x_max, by = 0.01) # 真の精度パラメータを指定 beta_true <- 3 sigma_true <- sqrt(1 / beta_true) # 真の標準偏差 # 真のモデルを計算 model_df <- tidyr::tibble( x = x_vals, # x軸の値 y = y_true(x_vals), # y軸の値 minus_sigma = y - 2 * sigma_true, # μ - 2σ plus_sigma = y + 2 * sigma_true # μ + 2σ )
設定したモデルに従って、データを生成します。
# データ数を指定 N <- 100 # (観測)データを生成 x_n <- runif(n = N, min = x_min, max = x_max) # 入力 t_n <- y_true(x_n) + rnorm(n = N, mean = 0, sd = sigma_true) # 出力 # 観測データをデータフレームに格納 data_df <- tidyr::tibble( x_n = x_n, # 入力 t_n = t_n # 出力 )
$N$個の観測データ(入力値$\mathbf{x} = \{x_1, \cdots, x_N\}$と目標値$\mathbf{t} = \{t_1, \cdots, t_N\}$)を作成できました。
・最尤推定
正則化しない場合と正則化する場合のそれぞれで最尤推定を行いパラメータ$\mathbf{w} = (w_0, w_1, \cdots, w_{M-1})^{\top}$を求めて、結果を比較します。
パラメータの数(基底関数の数)$M$を指定して、入力値を基底関数により変換します。
# 重みパラメータの次元数(基底関数の数)を指定 M <- 6 # 基底関数により入力を変換 phi_x_nm <- Phi(x_n, M)
計画行列
をphi_x_nmとします。また、$\boldsymbol{\phi}(x_n)$は$\boldsymbol{\Phi}$の$n$行目です。
・正則化しない場合
まずは、正則化を行わない場合の重みパラメータと分散パラメータの最尤解を計算します。
# 重みパラメータの最尤解を計算 w_ml_m <- solve(t(phi_x_nm) %*% phi_x_nm) %*% t(phi_x_nm) %*% t_n %>% as.vector() # 分散パラメータの最尤解を計算 sigma2_ml <- sum((t_n - phi_x_nm %*% w_ml_m)^2) / N # 精度パラメータの最尤解を計算 beta_ml <- 1 / sigma2_ml # 確認 w_ml_m beta_ml
## [1] 0.02112813 7.16151989 1.75034675 -83.49166179 128.76367082 ## [6] -54.41141148 ## [1] 2.330755
重みパラメータ、分散パラメータ、精度パラメータをそれぞれ次の式で計算します。
ただし、$t_n - \mathbf{w}^{\top} \phi(x_n)$の計算を$N$個同時に行うため、$\mathbf{t} - \boldsymbol{\Phi} \mathbf{w}$で計算しています。
推定した線形回帰のパラメータを使って回帰曲線を計算します。
# 推定したパラメータによるモデルを計算 ml_df <- tidyr::tibble( x = x_vals, # x軸の値 t = Phi(x_vals, M) %*% w_ml_m %>% as.vector(), # y軸の値 minus_sigma = t - 2 * sqrt(sigma2_ml), # μ - 2σ plus_sigma = t + 2 * sqrt(sigma2_ml) # μ + 2σ ) # 確認 head(ml_df)
## # A tibble: 6 x 4 ## x t minus_sigma plus_sigma ## <dbl> <dbl> <dbl> <dbl> ## 1 0 0.0211 -1.29 1.33 ## 2 0.01 0.0928 -1.22 1.40 ## 3 0.02 0.164 -1.15 1.47 ## 4 0.03 0.235 -1.07 1.55 ## 5 0.04 0.305 -1.00 1.62 ## 6 0.05 0.374 -0.936 1.68
未知の入力値(x軸の値)$x_{*}$に対する予測値(y軸の値)$t_{*}$を次の式で計算します。
さらに、分散パラメータsigma2_mlを使って、推定した精度を求めます。
ここまでは、3.1.1項と同様の処理です。
・正則化する場合
続いて、正則化を行う場合の重みパラメータと分散パラメータの最尤解を計算します。ラッソ回帰の最尤解は直接求められないので、座標降下法により要素ごとに値を繰り返し更新します。
# 繰り返し回数を指定 max_iter <- 100 # 正則化係数を指定 lambda <- 0.5 # 重みパラメータを初期化 w_lasso_m <- runif(n = M, min = -5, max = 5) # 範囲を指定 # 座標降下法による推定 for(i in 1:max_iter) { # バイアスパラメータを0に置換:(バイアスを正則化項に含めない場合の処理) w_lasso_m[1] <- 0 # バイアスパラメータの最尤解を計算:(バイアスを正則化項に含めない場合の処理) w_lasso_m[1] <- sum(t_n - phi_x_nm %*% w_lasso_m) / N # パラメータを要素ごとに更新 for(m in 2:M) { # (バイアスを正則化項に含める場合は1からMに変更) # m番目のパラメータを0に置換 w_lasso_m[m] <- 0 # 分子の項を計算 S <- sum((t_n - phi_x_nm %*% w_lasso_m) * phi_x_nm[, m]) # 重みパラメータの最尤解を計算 w_lasso_m[m] <- soft_thresholding(S, lambda, phi_x_nm[, m]) } } # ラッソ回帰の分散パラメータの最尤解を計算 sigma2_lasso <- sum((t_n - phi_x_nm %*% w_lasso_m)^2) / N # リッジ回帰の精度パラメータの最尤解を計算 beta_lasso <- 1 / sigma2_lasso # 確認 w_lasso_m beta_lasso
## [1] 1.0459172 -0.5627309 -3.7555834 0.0000000 0.6832504 2.2706207 ## [1] 1.934952
まずは、バイアスパラメータ(0番目のパラメータ)$w_0$を計算します。
ただし、正則化項にバイアスを含める場合はこの処理は行いません。
内積の計算$\sum_{j=1}^{M-1} w_j \phi_j(x_n)$は、$j = 1, \cdots, M-1$です。バイアス$w_0$を含めないことに注意してください。
そこで、(インデックスは1からなので)1番目の要素w_lasso_m[1]の値を0にしてから計算します。
また$N$個同時に処理するため、丸括弧の計算を$\mathbf{t} - \boldsymbol{\Phi} \mathbf{w}_{\backslash 0}$で行います。$w_0 = 0$(0番目の要素を0)としたパラメータを$\mathbf{w}_{\backslash 0} = (0, w_1, \cdots, w_{M-1})$で表しました(が、これはもう登場しません)。
次に、バイアスを除く重みパラメータの各要素を順番に計算します。
ただし、正則化項にバイアスを含める場合はバイアスについてもこちらの更新式で計算します。そのため、for(m in 1:M)に変更する必要があります。
こちらの内積$\sum_{j \neq m} w_j \phi_j(x_n)$は、更新対象のインデックス$m$を含めない$j = 0, 1, \cdots, m-1, m+1, \cdots, M-1$です。
そこで、$m$番目の要素w_lasso_m[m]の値を0にしてから計算します。
また一度に処理するため、丸括弧の計算を$\mathbf{t} - \boldsymbol{\Phi} \mathbf{w}_{\backslash m}$で行います。$w_m = 0$としたパラメータを$\mathbf{w}_{\backslash m} = (w_0, w_1, \cdots, w_{m-1}, 0, w_{m+1}, \cdots, w_{M-1})$で表しました(が、ほんとにもう登場しません)。
場合分けの計算は、始めに作成した関数soft_thresholding()で行います。
この2つの処理によって、全てのパラメータw_lasso_mが更新されます。この処理をmax_iterに指定した回数繰り返すことで、徐々に最尤解に近付けていきます。
最後に、分散パラメータ、精度パラメータを計算します。
こちらの内積には$M$個全て使います。また、$N$個同時に計算(処理)します。
推定したリッジ回帰のパラメータを使って回帰曲線を計算します。
# 推定したパラメータによるモデルを計算 lasso_df <- tidyr::tibble( x = x_vals, # x軸の値 t = Phi(x_vals, M) %*% w_lasso_m %>% as.vector(), # y軸の値 minus_sigma = t - 2 * sqrt(sigma2_lasso), # μ - 2σ plus_sigma = t + 2 * sqrt(sigma2_lasso) # μ + 2σ ) # 確認 head(lasso_df)
## # A tibble: 6 x 4 ## x t minus_sigma plus_sigma ## <dbl> <dbl> <dbl> <dbl> ## 1 0 1.05 -0.392 2.48 ## 2 0.01 1.04 -0.398 2.48 ## 3 0.02 1.03 -0.405 2.47 ## 4 0.03 1.03 -0.412 2.46 ## 5 0.04 1.02 -0.420 2.46 ## 6 0.05 1.01 -0.429 2.45
先ほどと同様に、y軸の値を計算します。
以上がラッソ回帰の推定処理です。推定したパラメータの要素がいくつか0になっているのを確認できます。
・推定結果の確認
ラッソ回帰により推定した回帰曲線(近似曲線)を作図します。
# 推定したパラメータによるモデルを作図 ggplot() + geom_point(data = data_df, aes(x = x_n, y = t_n)) + # 観測データ geom_line(data = model_df, aes(x = x, y = y), color = "cyan4") + # 真のモデル geom_ribbon(data = model_df, aes(x = x, ymin = minus_sigma, ymax = plus_sigma), fill = "cyan4", alpha = 0.1, color = "cyan4", linetype = "dotted") + # 真のノイズ範囲 geom_line(data = ml_df, aes(x = x, y = t), color = "blue", linetype ="dashed") + # 推定したモデル:(正則化なし) geom_line(data = lasso_df, aes(x = x, y = t), color = "blue") + # 推定したモデル:(L1正則化) geom_ribbon(data = lasso_df, aes(x = x, ymin = minus_sigma, ymax = plus_sigma), fill = "blue", alpha = 0.1, color = "blue", linetype = "dotted") + # 推定したノイズ範囲 #ylim(c(-5, 5)) + # y軸の表示範囲 labs(title = "Lasso Regression", subtitle = paste0("N=", N, ", M=", M, ", q=", 1, ", lambda=", lambda, ", w=(", paste0(round(w_lasso_m, 2), collapse = ", "), ")", ", beta=", round(beta_lasso, 2)), x = "x", y = "t")

緑の実線が真のモデル、青の実線がラッソ回帰(L1正則化)による近似曲線、青の破線が正則化なしの近似曲線です。
この例だと、正則化しない方がうまく近似できていますね。
$\lambda$の値が大きいほど、正則化の効果が強まります。
3つの条件によって変わるパラメータの更新式をグラフで確認します。
# 正則化係数との大小関係によりパラメータを計算 subdiff_df <- tidyr::tibble( S = seq(-2, 2, by = 0.01), # 分子の項 w = dplyr::case_when( S > lambda ~ (S - lambda) / sum(phi_x_nm[, m]^2), S < -lambda ~ (S + lambda) / sum(phi_x_nm[, m]^2), TRUE ~ 0 ) # 重みパラメータ ) # 確認 head(subdiff_df)
## # A tibble: 6 x 2 ## S w ## <dbl> <dbl> ## 1 -2 -0.126 ## 2 -1.99 -0.125 ## 3 -1.98 -0.125 ## 4 -1.97 -0.124 ## 5 -1.96 -0.123 ## 6 -1.95 -0.122
分子の項$S$の値が変化したときのパラメータ$w_k$の値の変化を計算します。
$S$と$w_k$のグラフを作図します。
# 正則化係数との大小関係によるパラメータのグラフを作成 ggplot(subdiff_df, aes(x = S, y = w)) + geom_line() + # 重みパラメータ labs(title = expression(paste(w[k] == 0, " (", - lambda <= S, ", ", S <= lambda, ")")), subtitle = paste0("lambda=", lambda), y = expression(w[k]))

$S < - \lambda$と$S > \lambda$の範囲では、$S$と$w_k$は比例関係にあるのが分かります。$- \lambda < S < \lambda$の範囲だと、$w_k$が0になります。よって、$\lambda$が大きいほど$w_k$が0になりやすいのを確認できます。
正則化の効果を見るために、観測データ数を減らしパラメータ数を増やして、過学習が起きやすい設定にしてみます。

正則化していない方(青の破線)はデータに過剰に適合しています。正則化している方(青の実線)は過剰適合を回避できています。
以上でラッソ回帰を実装できました。
・おまけ:正則化係数と回帰曲線の関係
最後に、正則化係数と回帰曲線(近似曲線)の関係をアニメーションで確認します。
・作図コード(クリックで展開)
アニメーション(gif画像)の作成にgganimateパッケージを利用します。
# 追加パッケージ library(gganimate)
for()ループで正則化係数$\lambda$の値を変更しながら繰り返しパラメータと回帰曲線を計算します。
# 使用するlambdaの値を作成 lambda_vals <- seq(0, 0.5, by = 0.002) # 重みパラメータを初期値を生成 #w_init_m <- runif(n = M, min = -5, max = 5) # 範囲を指定 # lambdaごとに最尤解を計算 anime_lasso_df <- dplyr::tibble() for(lambda in lambda_vals) { # 重みパラメータを初期化 w_lasso_m <- w_init_m # 座標降下法による推定 for(i in 1:max_iter) { # バイアスパラメータを0に置換:(バイアスを正則化項に含めない場合の処理) w_lasso_m[1] <- 0 # バイアスパラメータの最尤解を計算:(バイアスを正則化項に含めない場合の処理) w_lasso_m[1] <- sum(t_n - phi_x_nm %*% w_lasso_m) / N # パラメータを要素ごとに更新 for(m in 2:M) { # (バイアスを正則化項に含める場合は1からMに変更) # m番目のパラメータを0に置換 w_lasso_m[m] <- 0 # 分子の項を計算 S <- sum((t_n - phi_x_nm %*% w_lasso_m) * phi_x_nm[, m]) # 重みパラメータの最尤解を計算 w_lasso_m[m] <- soft_thresholding(S, lambda, phi_x_nm[, m]) } } # ラッソ回帰の分散パラメータの最尤解を計算 sigma2_lasso <- sum((t_n - phi_x_nm %*% w_lasso_m)^2) / N # ラッソ回帰の精度パラメータの最尤解を計算 beta_lasso <- 1 / sigma2_lasso # 推定したパラメータによるモデルを計算 tmp_lasso_df <- tidyr::tibble( x = x_vals, # x軸の値 t = Phi(x_vals, M) %*% w_lasso_m %>% as.vector(), # y軸の値 minus_sigma = t - 2 * sqrt(sigma2_lasso), # μ - 2σ plus_sigma = t + 2 * sqrt(sigma2_lasso), # μ + 2σ label = paste0( "lambda=", lambda, ", w=(", paste0(round(w_lasso_m, 2), collapse = ", "), ")", ", beta=", round(beta_lasso, 2) ) %>% as.factor() # フレーム切替用のラベル ) # 結果を結合 anime_lasso_df <- rbind(anime_lasso_df, tmp_lasso_df) } # 確認 head(anime_lasso_df)
## # A tibble: 6 x 5 ## x t minus_sigma plus_sigma label ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 0 0.458 -0.451 1.37 lambda=0, w=(0.46, 1.94, -4.46, -2.09, -0.~ ## 2 0.01 0.477 -0.432 1.39 lambda=0, w=(0.46, 1.94, -4.46, -2.09, -0.~ ## 3 0.02 0.495 -0.414 1.40 lambda=0, w=(0.46, 1.94, -4.46, -2.09, -0.~ ## 4 0.03 0.512 -0.397 1.42 lambda=0, w=(0.46, 1.94, -4.46, -2.09, -0.~ ## 5 0.04 0.528 -0.381 1.44 lambda=0, w=(0.46, 1.94, -4.46, -2.09, -0.~ ## 6 0.05 0.543 -0.366 1.45 lambda=0, w=(0.46, 1.94, -4.46, -2.09, -0.~
$\lambda$として使う値を作成してlambda_valsとします。
lambda_valsから値を順番に取り出して、パラメータの最尤解を求めて回帰曲線を計算します。計算結果はanime_lasso_dfに追加していきます。
パラメータの初期値が変わらないようにw_init_mとして固定しておきます。
作図してgif画像として出力します。
# 推定したパラメータによるモデルを作図 anime_graph <- ggplot() + geom_point(data = data_df, aes(x = x_n, y = t_n)) + # 観測データ geom_line(data = model_df, aes(x = x, y = y), color = "cyan4") + # 真のモデル geom_ribbon(data = model_df, aes(x = x, ymin = minus_sigma, ymax = plus_sigma), fill = "cyan4", alpha = 0.1, color = "cyan4", linetype = "dotted") + # 真のノイズ範囲 geom_line(data = ml_df, aes(x = x, y = t), color = "blue", linetype ="dashed") + # 推定したモデル:(正則化なし) geom_line(data = anime_lasso_df, aes(x = x, y = t), color = "blue") + # 推定したモデル:(L1正則化) geom_ribbon(data = anime_lasso_df, aes(x = x, ymin = minus_sigma, ymax = plus_sigma), fill = "blue", alpha = 0.1, color = "blue", linetype = "dotted") + # 推定したノイズ範囲 gganimate::transition_manual(label) + # フレーム ylim(c(-3, 3)) + # y軸の表示範囲 labs(title = "Lasso Regression", subtitle = "{current_frame}", x = "x", y = "t") # gif画像に変換 gganimate::animate(anime_graph, nframes = length(lambda_vals), fps = 10)
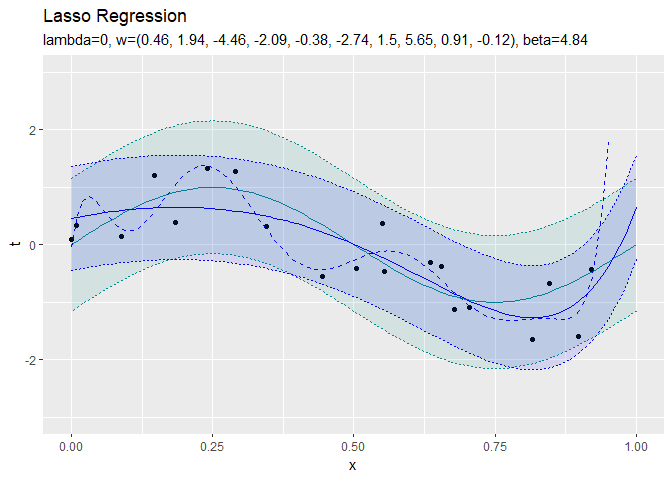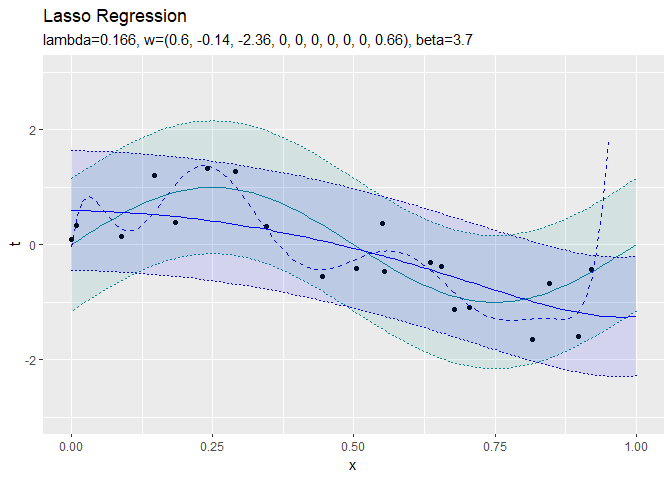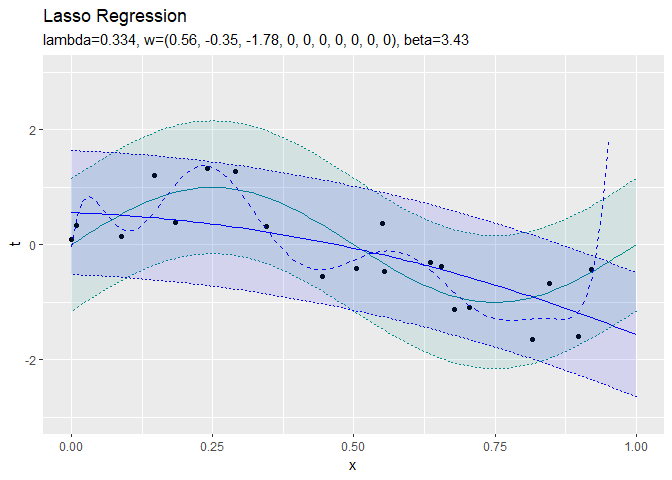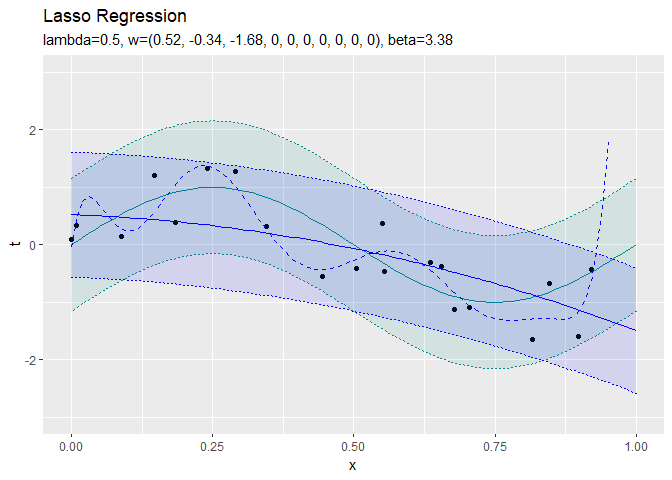
正則化係数が大きくなるほど、値が0のパラメータが増えていき、回帰曲線がシンプルになっていくことから、正則化の効果が強まるのを確認できます。
($\lambda = 0$でも正規化しない最尤解と一致しない理由をもう少し考えたいけど、今回はここまで。)
Enjoy!
参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上下』,丸善出版,2012年.
おわりに
2回目のアドカレ参加、今年は2つ投稿する。来年は1人アドカレをやる。
2021年12月11日は、BEYOOOOONDSとSeasoningSの平井美葉さんの22歳のお誕生日です!!!
ギャップがたまらんのよ。
【次節の内容】
【関連する内容】