はじめに
『パターン認識と機械学習』の独学時のまとめです。一連の記事は「数式の行間埋め」または「R・Pythonでのスクラッチ実装」からアルゴリズムの理解を補助することを目的としています。本とあわせて読んでください。
この記事は、3.1.4項「正則化最小二乗法」の内容です。ラッソ回帰(Lasso回帰)の正則化項と最尤解の関係をR言語で可視化します。
【数式読解編】
【前節の内容】
【他の節一覧】
【この節の内容】
・ラッソ回帰の正則化項と最尤解の関係
「二乗和誤差関数・正則化項」と「重みパラメータの最尤解」との関係をグラフで確認します。L1正則化項については「【R】3.1.4.0:Lpノルムの作図【PRMLのノート】 - からっぽのしょこ」、ラッソ回帰の実装については「【R】3.1.4.b:ラッソ回帰の実装【PRMLのノート】 - からっぽのしょこ」を参照してください。
利用するパッケージを読み込みます。
# 3.1.4項で利用するパッケージ library(tidyverse)
・関数の準備
パラメータの更新に利用する関数を作成しておきます。
# ラッソ回帰の重みパラメータの最尤解を計算する関数を作成 soft_thresholding <- function(S, lambda, phi_x_n) { # 条件に応じて値を計算 if(S > lambda) { # S > λの場合の計算 w <- (S - lambda) / sum(phi_x_n^2) } else if(S < -lambda) { # S < -λの場合の計算 w <- (S + lambda) / sum(phi_x_n^2) } else { # -λ =< S =< λの場合 w <- 0 } return(w) }
ラッソ回帰では、条件によってパラメータの更新式が異なります。また、繰り返し更新します。
何度も複雑な処理をすることになるので、次の計算を行う処理を関数にしておきます。
詳しくは、パラメータ推定のところで解説します。
・モデルの設定とデータの生成
データ生成関数と基底関数を作成します。
# 真の関数を指定 y_true <- function(x) { # 計算式を指定 y <- sin(pi * x) return(y) } # 基底関数を指定 Phi <- function(x) { # 計算式を指定 phi_x <- cbind(x, x^2) return(phi_x) }
この例では、多項式基底関数を使います。また、2次元のグラフで可視化するため$M = 2$とし、バイアス$w_0$含めません($\phi_0(x) = 1$としません)。
データを生成して基底関数で変換します。
# データ数を指定 N <- 50 # (観測)データを生成 x_n <- runif(n = N, min = 0, max = 1) # 入力 t_n <- y_true(x_n) + rnorm(n = N, mean = 0, sd = 1) # 出力 # 基底関数により入力を変換 phi_x_nm <- Phi(x_n) # 確認 phi_x_nm[1:5, ]
## x ## [1,] 0.9462595 0.89540698 ## [2,] 0.8638488 0.74623471 ## [3,] 0.2317932 0.05372807 ## [4,] 0.4302496 0.18511476 ## [5,] 0.1467278 0.02152905
$N$個の観測データ(入力値$\mathbf{x} = \{x_1, \cdots, x_N\}$と目標値$\mathbf{t} = \{t_1, \cdots, t_N\}$)を作成して、計画行列
をphi_x_nmとします。また、$\boldsymbol{\phi}(x_n)$は$\boldsymbol{\Phi}$の$n$行目です。
作図用のパラメータの点を作成して、二乗和誤差関数と正則化項を計算します。
# 値を設定:(固定) q <- 1 # パラメータの次元数を設定:(固定) M <- 2 # 作図用のwの範囲を指定 w_i <- seq(-5, 5, by = 0.1) # 作図用のwの点を作成 w_im <- expand.grid(w_i, w_i) %>% as.matrix() # 正則化項を計算 E_df <- tidyr::tibble( w_1 = w_im[, 1], # x軸の値 w_2 = w_im[, 2], # y軸の値 E_D = colSums((t_n - phi_x_nm %*% t(w_im))^2) / N, # 二乗和誤差 E_W = abs(w_1)^q + abs(w_2)^q # 正則化項 ) # 確認 head(E_df)
## # A tibble: 6 x 4 ## w_1 w_2 E_D E_W ## <dbl> <dbl> <dbl> <dbl> ## 1 -5 -5 30.6 10 ## 2 -4.9 -5 30.0 9.9 ## 3 -4.8 -5 29.4 9.8 ## 4 -4.7 -5 28.8 9.7 ## 5 -4.6 -5 28.1 9.6 ## 6 -4.5 -5 27.5 9.5
パラメータの各要素$w_1, w_2$の値を作成してw_iとします。
w_iの全ての組み合わせを持つように点$\mathbf{w} = (w_1, w_2)^{\top}$を作成しw_imとします。w_imの各行は$\mathbf{w}$がとり得る点に対応します。
w_imの行数はw_iの2乗になります。処理が重い場合はw_iを調整してください。
二乗和誤差関数(誤差項)とL1正則化項(L1ノルム)を計算します。
二乗和誤差関数とL1正則化項の等高線図を作成します。
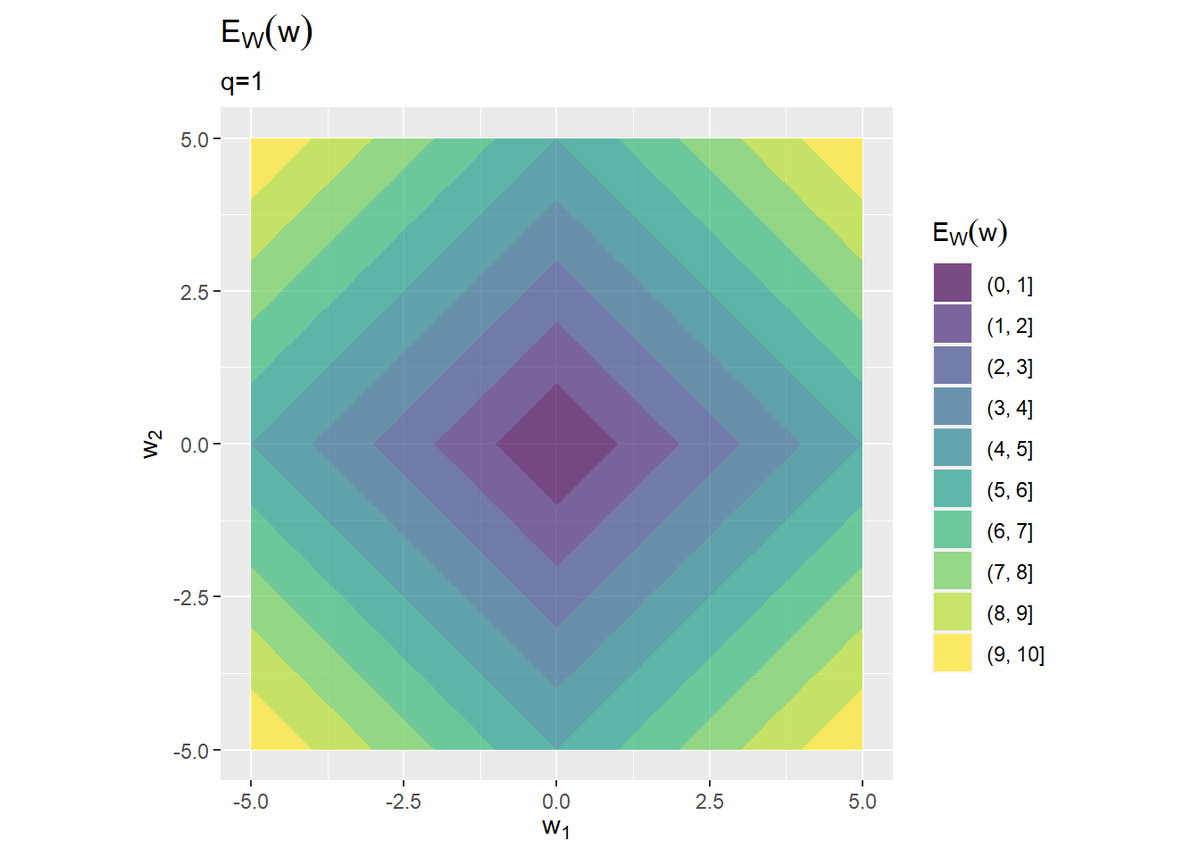
# 二乗和誤差関数の等高線図を作成 ggplot(E_df, aes(x = w_1, y = w_2)) + geom_contour_filled(aes(z = E_D, fill = ..level..), alpha = 0.7) + # 二乗和誤差関数:(塗りつぶし) #geom_contour(aes(z = E_D, color = ..level..)) + # 二乗和誤差関数:(等高線) coord_fixed(ratio = 1) + # アスペクト比 labs(title = expression(E[D](w)), subtitle = paste0("q=", q), x = expression(w[1]), y = expression(w[2]), fill = expression(E[D](w))) # 正則化項の等高線図を作成 ggplot(E_df, aes(x = w_1, y = w_2)) + geom_contour_filled(aes(z = E_W, fill = ..level..), alpha = 0.7) + # 正則化項:(塗りつぶし) #geom_contour(aes(z = E_W, color = ..level..)) + # 正則化項:(等高線) coord_fixed(ratio = 1) + # アスペクト比 labs(title = expression(E[W](w)), subtitle = paste0("q=", q), x = expression(w[1]), y = expression(w[2]), fill = expression(E[W](w)))
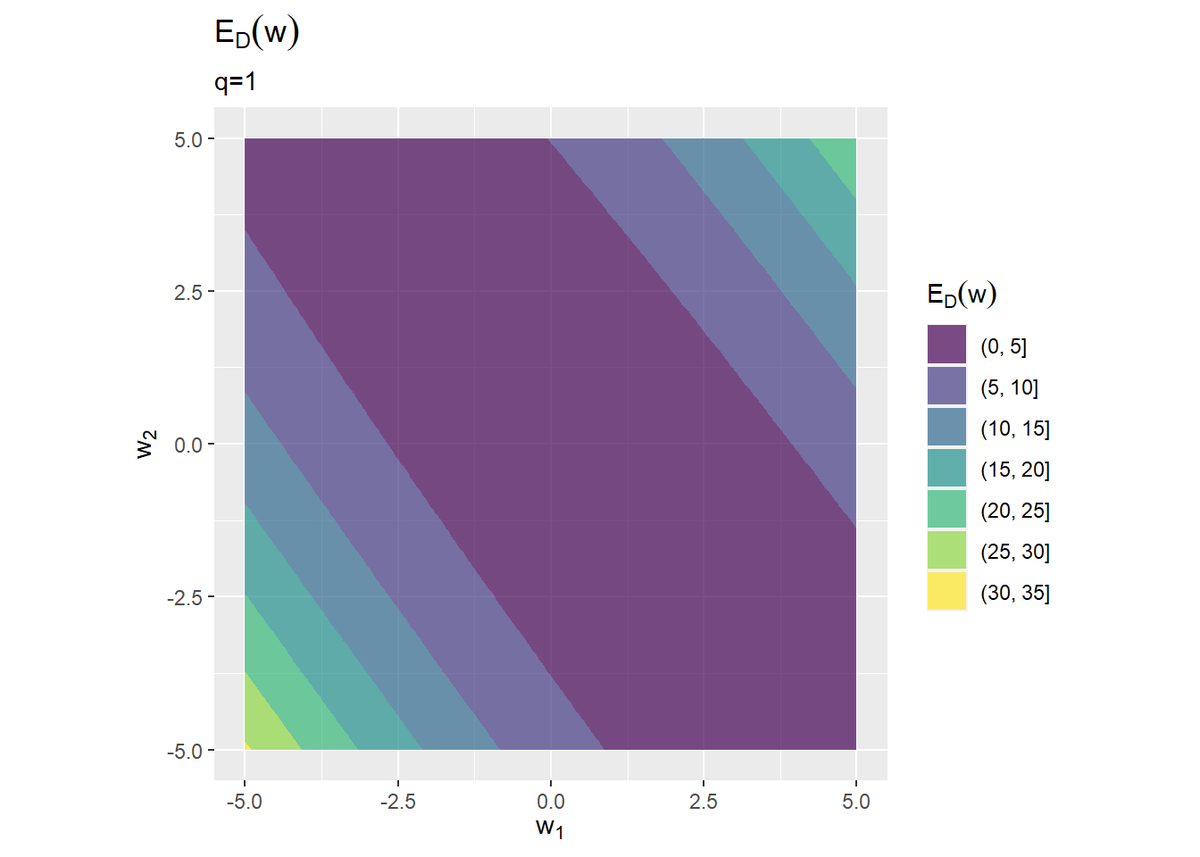
二乗和誤差関数は観測データに依存して形が決まります。
L1正則化項のグラフを真上から見るとひし形をしていて、原点$\mathbf{w} = (0, 0)$のとき最小の0になります。
・最尤推定
座標降下法によりラッソ回帰のパラメータの最尤解を1要素ずつ繰り返し計算します。
# 繰り返し回数を指定 max_iter <- 50 # 正則化係数を指定 lambda <- 5 # 重みパラメータを初期化 w_lasso_m <- runif(n = M, min = -5, max = 5) # 座標降下法による推定 for(i in 1:max_iter) { # パラメータを要素ごとに更新 for(m in 1:M) { # m番目のパラメータを0に置換 w_lasso_m[m] <- 0 # 分子の項を計算 S <- sum((t_n - phi_x_nm %*% w_lasso_m) * phi_x_nm[, m]) # 重みパラメータの最尤解を計算 w_lasso_m[m] <- soft_thresholding(S, lambda, phi_x_nm[, m]) } }
重みパラメータの各要素を順番に計算します。
内積の計算$\sum_{j \neq m} w_j \phi_j(x_n)$は、更新対象のインデックス$m$を含めない$j = 1, \cdots, m-1, m+1, \cdots, M$です。
そこで、$m$番目の要素w_lasso_m[m]の値を0にしてから計算します。
また一度に処理するため、丸括弧の計算を$\mathbf{t} - \boldsymbol{\Phi} \mathbf{w}_{\backslash m}$で行います。$w_m = 0$としたパラメータを$\mathbf{w}_{\backslash m} = (w_1, \cdots, w_{m-1}, 0, w_{m+1}, \cdots, w_M)$で表しました(この例だと$M = 2$だけど)。
場合分けの計算は、始めに作成した関数soft_thresholding()で行います。
正則化なしの最尤解も計算して、データフレームに格納します。
# 重みパラメータの最尤解を計算 w_ml_m <- solve(t(phi_x_nm) %*% phi_x_nm) %*% t(phi_x_nm) %*% t_n %>% as.vector() # 重みパラメータをデータフレームに格納 w_df <- tidyr::tibble( w_1 = c(w_lasso_m[1], w_ml_m[1]), # x軸の値 w_2 = c(w_lasso_m[2], w_ml_m[2]), # y軸の値 method = factor(c("lasso", "ml"), levels = c("lasso", "ml")) # ラベル ) # 確認 w_df
## # A tibble: 2 x 3 ## w_1 w_2 method ## <dbl> <dbl> <fct> ## 1 0.343 0 lasso ## 2 3.76 -4.29 ml
正規化なしの最尤解は次の式で計算します。
重みパラメータの最尤解をプロットします。
# 推定したパラメータによる誤差項を計算 E_D <- sum((t_n - phi_x_nm %*% w_lasso_m)^2) / N E_W <- sum(abs(w_lasso_m)^q) # 最尤解を作図 ggplot() + geom_contour_filled(data = E_df, aes(x = w_1, y = w_2, z = E_D, fill = ..level..), alpha = 0.7) + # 二乗和誤差関数:(塗りつぶし) geom_contour(data = E_df, aes(x = w_1, y = w_2, z = E_D), color = "blue", breaks = E_D) + # 二乗和誤差関数:(等高線) geom_contour(data = E_df, aes(x = w_1, y = w_2, z = E_W), color = "red", breaks = E_W) + # 正則化項:(等高線) geom_point(data = w_df, aes(x = w_1, y = w_2, color = method), shape = 4, size = 5) + # パラメータの最尤解 coord_fixed(ratio = 1) + # アスペクト比 labs(title = "Lasso Regression", subtitle = paste0("lambda=", lambda, ", w_lasso=(", paste0(round(w_lasso_m, 2), collapse = ", "), ")", ", w_ml=(", paste0(round(w_ml_m, 2), collapse = ", "), ")"), x = expression(w[1]), y = expression(w[2]), fill = expression(E[D](w)))
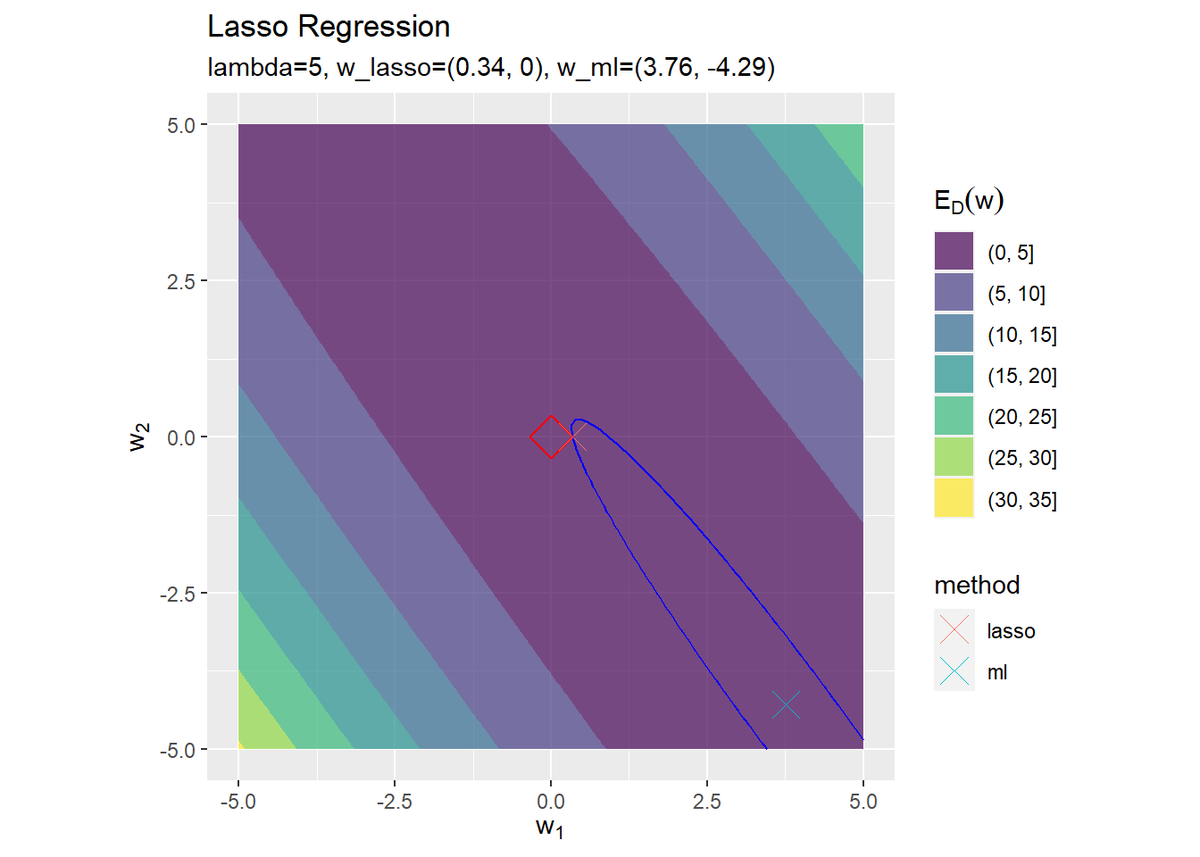
青色のバツ印が正則化なしの最尤解、赤井のバツ印が正則化ありの最尤解です。
ラッソ回帰の最尤解を使って二乗和誤差関数E_Dと正則化項E_Wを計算します。
それぞれbreaks引数に指定すると、その値となる等高線を引けます。最尤解を接点として2つの等高線が接しているのが分かります。
二乗和誤差関数と正則化項を加えた誤差関数の等高線図を作成します。
# 誤差関数を作図 ggplot(E_df, aes(x = w_1, y = w_2)) + geom_contour_filled(aes(z = E_D+lambda*E_W, fill = ..level..)) + # 二乗和誤差関数:(塗りつぶし) geom_contour(aes(z = E_D), color = "blue", alpha = 0.7, linetype = "dashed") + # 二乗和誤差関数:(等高線) geom_contour(aes(z = E_W), color = "red", alpha = 0.7, linetype = "dashed") + # 正則化項:(等高線) coord_fixed(ratio = 1) + # アスペクト比 labs(title = expression(E(w) == E[D](w) + lambda * E[w](w)), subtitle = paste0("q=", q, ", lambda=", lambda), x = expression(w[1]), y = expression(w[2]), fill = expression(E(w)))
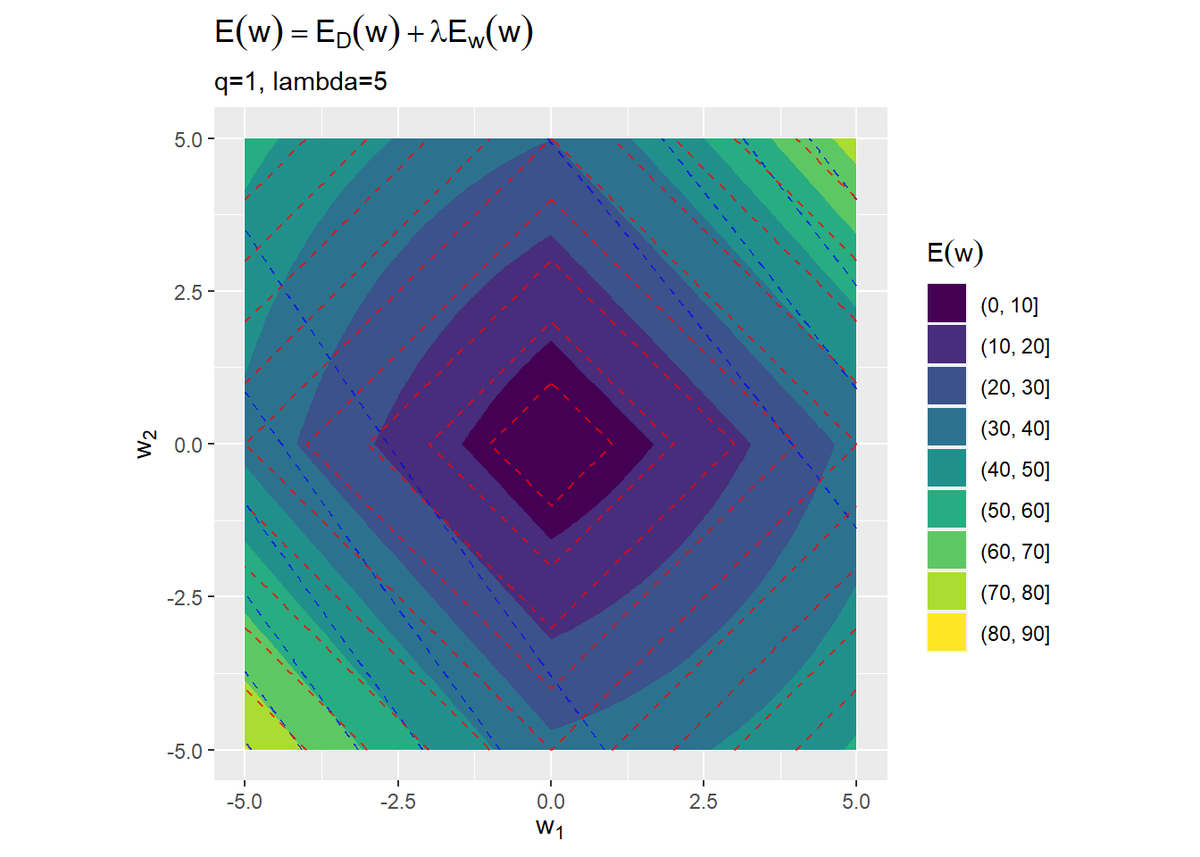
$\lambda$によってどちらの影響を強く受けるのかを調整できます。
・おまけ:正則化係数と最尤解の関係
最後に、正則化係数と最尤解の関係をアニメーションで確認します。
・コード(クリックで展開)
アニメーション(gif画像)の作成にgganimateパッケージを利用します。
# 追加パッケージ library(gganimate)
接線のアニメーション用に細かい$\mathbf{w}$の点を作成します。
# 接線用に細かいwの点を作成 w_vals <- seq(-5, 5, by = 0.005) # 刻み幅を変更 w_point <- expand.grid(w_vals, w_vals) %>% as.matrix() hd_E_df <- tidyr::tibble( w_1 = w_point[, 1], # x軸の値 w_2 = w_point[, 2], # y軸の値 E_D = colSums((t_n - phi_x_nm %*% t(w_point))^2) / N, # 二乗和誤差 E_W = abs(w_1)^q + abs(w_2)^q # 正則化項 )
この例だと、誤差項と正則化項の等高線の接線を描画するのに細かい点が必要です。しかしw_imを細かくすると、塗りつぶし等高線用のデータフレームanime_E_dfの行数が無駄に増えてしまいます。そこで、E_dfとは別にhd_E_dfとして作成しておきます。
for()ループで正則化係数lambdaの値を変更して繰り返しパラメータを計算して、接線となる等高線を計算します。
# 使用するlambdaの値を作成 lambda_vals <- seq(0, 15, by = 0.1) # 重みパラメータを初期値を生成 w_init_m <- runif(n = M, min = -5, max = 5) # lambdaごとに最尤解を計算 anime_w_df <- tidyr::tibble() # パラメータの最尤解 anime_E_D_df <- tidyr::tibble() # 誤差項:(接線) anime_E_W_df <- tidyr::tibble() # 正則化項:(接線) anime_E_df <- tidyr::tibble() # 誤差関数 for(lambda in lambda_vals) { # 重みパラメータを初期化 w_lasso_m <- w_init_m # 座標降下法による推定 for(i in 1:max_iter) { # m番目パラメータを更新 for(m in 1:M) { # m番目のパラメータを0に置換 w_lasso_m[m] <- 0 # 分子の項を計算 S <- sum((t_n - phi_x_nm %*% w_lasso_m) * phi_x_nm[, m]) # 重みパラメータの最尤解を計算 w_lasso_m[m] <- soft_thresholding(S, lambda, phi_x_nm[, m]) } } # 推定したパラメータによる誤差項を計算 E_D_val <- sum((t_n - phi_x_nm %*% w_lasso_m)^2) / N # 二乗和誤差 E_W_val <- sum(abs(w_lasso_m)^q) # 正則化項 # アニメーション用のラベルを作成 label <- paste0( "lambda=", lambda, ", E=", round(E_D_val + lambda * E_W_val, 2), ", E_D=", round(E_D_val, 2), ", E_W=", round(E_W_val, 2) ) # 推定したパラメータをデータフレームに格納 tmp_w_df <- tidyr::tibble( w_1 = c(w_lasso_m[1], w_ml_m[1]), # x軸の値 w_2 = c(w_lasso_m[2], w_ml_m[2]), # y軸の値 method = factor(c("lasso", "ml"), levels = c(c("lasso", "ml"))), # ラベル label = as.factor(label) # フレーム切替用のラベル ) # 結果を結合 anime_w_df <- rbind(anime_w_df, tmp_w_df) # 接線となる誤差項の等高線を抽出 anime_E_D_df <- hd_E_df %>% dplyr::select(w_1, w_2, E_D) %>% # 利用する列を抽出 dplyr::mutate( E_D = dplyr::if_else(round(E_D, 2) == round(E_D_val, 2), true = round(E_D_val, 2), false = 0) ) %>% # 接線となる誤差項の点以外を0に置換 cbind(label = as.factor(label)) %>% # フレーム切替用のラベル列を追加 rbind(anime_E_D_df, .) %>% # 結合 dplyr::filter(E_D > 0) # 接線となる誤差項の点を抽出:(最後でないと接線となる点がなかった時にエラーになる) # 接線となる正則化項の等高線を抽出 anime_E_W_df <- hd_E_df %>% dplyr::select(w_1, w_2, E_W) %>% # 利用する列を抽出 dplyr::mutate( E_W = dplyr::if_else(round(E_W, 2) == round(E_W_val, 2), true = round(E_W_val, 2), false = 0) ) %>% # 接線となる正則化項の点以外を0に置換 cbind(label = as.factor(label)) %>% # フレーム切替用のラベル列を追加 rbind(anime_E_W_df, .) %>% # 結合 dplyr::filter(E_W > 0) # 接線となる正則化項の点を抽出:(最後でないと接線となる点がなかった時にエラーになる) # アニメーション用に複製 anime_E_df <- E_df %>% dplyr::mutate(E = E_D + lambda * E_W) %>% #dplyr::select(w_1, w_2, E) %>% # 使用する列を抽出 cbind(label = as.factor(label)) %>% # フレーム切替用のラベル列を追加 rbind(anime_E_df, .) # 結合 # 途中経過を表示 #message("\r", rep(" ", 30), appendLF = FALSE) # 前回のメッセージを初期化 #message("\r", "lambda=", lambda, " (", round(lambda / max(lambda_vals) * 100, 2), "%)", appendLF = FALSE) } # 確認 head(anime_E_df) head(anime_E_D_df) head(anime_E_W_df)
## w_1 w_2 E_D E_W E label ## 1 -5.0 -5 30.64384 10.0 30.64384 lambda=0, E=1.03, E_D=1.03, E_W=7.59 ## 2 -4.9 -5 30.00881 9.9 30.00881 lambda=0, E=1.03, E_D=1.03, E_W=7.59 ## 3 -4.8 -5 29.38066 9.8 29.38066 lambda=0, E=1.03, E_D=1.03, E_W=7.59 ## 4 -4.7 -5 28.75940 9.7 28.75940 lambda=0, E=1.03, E_D=1.03, E_W=7.59 ## 5 -4.6 -5 28.14502 9.6 28.14502 lambda=0, E=1.03, E_D=1.03, E_W=7.59 ## 6 -4.5 -5 27.53753 9.5 27.53753 lambda=0, E=1.03, E_D=1.03, E_W=7.59 ## w_1 w_2 E_D label ## 1 4.140 -4.820 1.03 lambda=0, E=1.03, E_D=1.03, E_W=7.59 ## 2 4.145 -4.820 1.03 lambda=0, E=1.03, E_D=1.03, E_W=7.59 ## 3 4.125 -4.815 1.03 lambda=0, E=1.03, E_D=1.03, E_W=7.59 ## 4 4.130 -4.815 1.03 lambda=0, E=1.03, E_D=1.03, E_W=7.59 ## 5 4.135 -4.815 1.03 lambda=0, E=1.03, E_D=1.03, E_W=7.59 ## 6 4.140 -4.815 1.03 lambda=0, E=1.03, E_D=1.03, E_W=7.59 ## w_1 w_2 E_W label ## 1 -2.590 -5.000 7.59 lambda=0, E=1.03, E_D=1.03, E_W=7.59 ## 2 2.590 -5.000 7.59 lambda=0, E=1.03, E_D=1.03, E_W=7.59 ## 3 -2.595 -4.995 7.59 lambda=0, E=1.03, E_D=1.03, E_W=7.59 ## 4 2.595 -4.995 7.59 lambda=0, E=1.03, E_D=1.03, E_W=7.59 ## 5 -2.600 -4.990 7.59 lambda=0, E=1.03, E_D=1.03, E_W=7.59 ## 6 2.600 -4.990 7.59 lambda=0, E=1.03, E_D=1.03, E_W=7.59
$\lambda$として使う値lambda_valsを作成します。
lambda_valsから値を順番に取り出して、パラメータの最尤解を計算します。計算結果はanime_w_dfに追加していきます。
パラメータの初期値が変わらないようにw_init_mとして固定しておきます。
最尤解を接点とする誤差項と正則化項の接線となる点を抽出して、それぞれanime_E_D_df, anime_E_W_dfに追加します。
誤差関数のデータフレームについても、同じ試行(フレーム)のlabel列を持つように複製しておく必要があります。
作図してgif画像として出力します。
# 誤差項と最尤解の関係を作図 anime_graph <- ggplot() + geom_contour_filled(data = anime_E_df, aes(x = w_1, y = w_2, z = E_D, fill = ..level..), alpha = 0.7) + # 誤差項:(塗りつぶし等高線) geom_contour(data = E_df, aes(x = w_1, y = w_2, z = E_W), color = "red", linetype = "dashed", breaks = seq(1, 3, by = 1)) + # 正則化項:(等高線) geom_point(data = anime_E_D_df, aes(x = w_1, y = w_2), color = "blue", shape = ".", size = 0.1) + # 誤差項:(接線) geom_point(data = anime_E_W_df, aes(x = w_1, y = w_2), color = "red", shape = ".", size = 0.1) + # 正則化項:(接線) geom_point(data = anime_w_df, aes(x = w_1, y = w_2, color = method), shape = 4, size = 5) + # パラメータの最尤解 gganimate::transition_manual(label) + # フレーム coord_fixed(ratio = 1) + # アスペクト比 labs(title = "Lasso Regression", subtitle = "{current_frame}", x = expression(w[1]), y = expression(w[2]), fill = expression(E[D](w))) # gif画像に変換 gganimate::animate(anime_graph, nframes = length(lambda_vals), fps = 10)
# 誤差項と最尤解の関係を作図 anime_graph <- ggplot() + geom_contour_filled(data = anime_E_df, aes(x = w_1, y = w_2, z = E, fill = ..level..), alpha = 0.7) + # 誤差関数:(塗りつぶし等高線) geom_contour(data = E_df, aes(x = w_1, y = w_2, z = E_D), color = "blue", linetype = "dashed", breaks = seq(1, 10, length.out = 3)) + # 誤差項:(等高線) geom_contour(data = E_df, aes(x = w_1, y = w_2, z = E_W), color = "red", linetype = "dashed", breaks = seq(1, 3, by = 1)) + # 正則化項:(等高線) geom_point(data = anime_E_D_df, aes(x = w_1, y = w_2), color = "blue", shape = ".", size = 0.1) + # 誤差項:(接線) geom_point(data = anime_E_W_df, aes(x = w_1, y = w_2), color = "red", shape = ".", size = 0.1) + # 正則化項:(接線) geom_point(data = anime_w_df, aes(x = w_1, y = w_2, color = method), shape = 4, size = 5) + # パラメータの最尤解 gganimate::transition_manual(label) + # フレーム coord_fixed(ratio = 1) + # アスペクト比 labs(title = "Lasso Regression", subtitle = "{current_frame}", x = expression(w[1]), y = expression(w[2]), fill = expression(E(w))) # gif画像に変換 gganimate::animate(anime_graph, nframes = length(lambda_vals), fps = 10)
接線(等高線の一本)だけをgeom_contour()で引くのは非効率なので、散布図geom_point()で線に見えるように引くことにします。
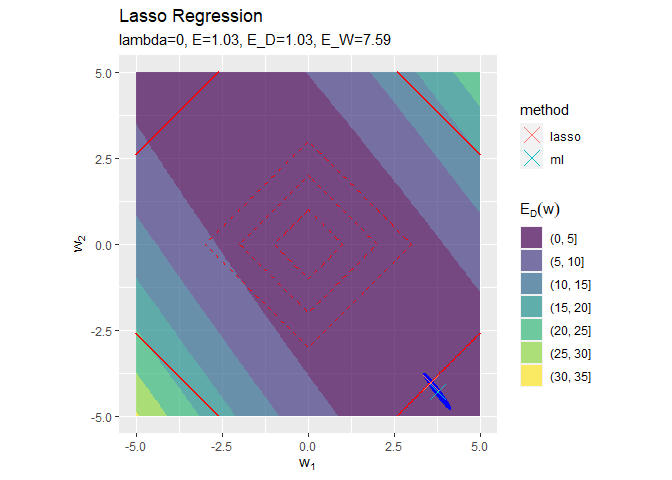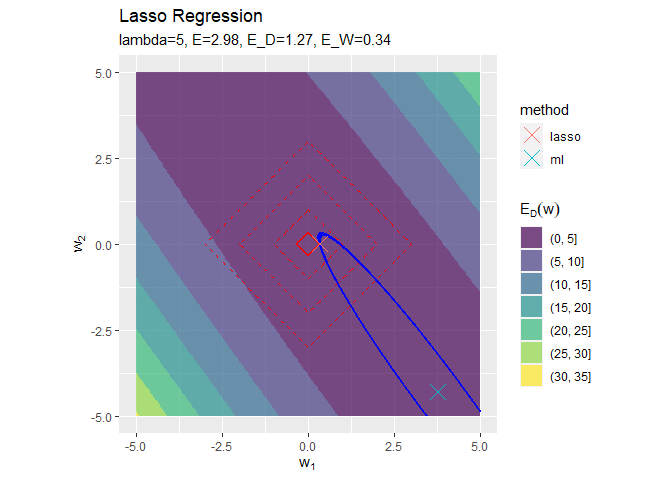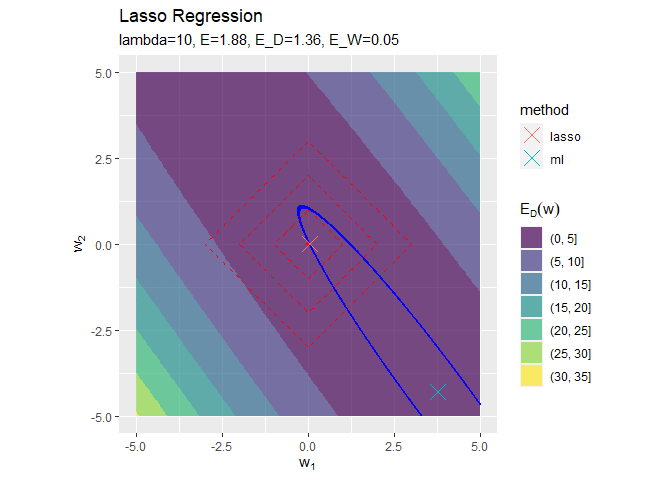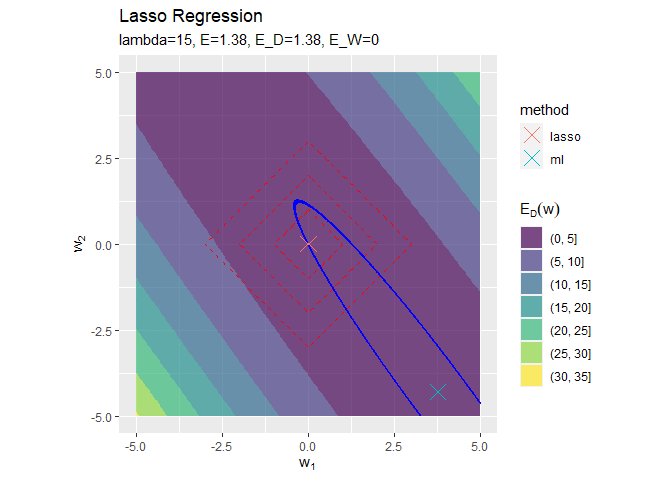
正則化係数が大きくなるほど「二乗和誤差関数が最小となる点(青色のバツ印)」から「正則化項の最小値となる点(赤色の四角の中心)」に移動しているのを確認できます。
また、必ずひし形の頂点と接する(パラメータが0になる)わけではないことも分かります。
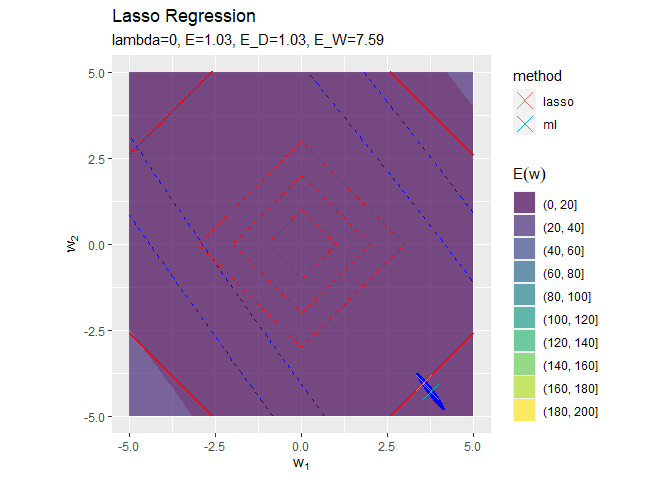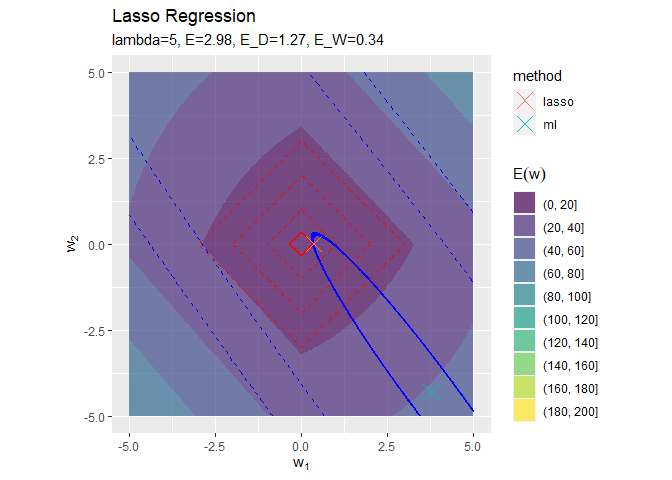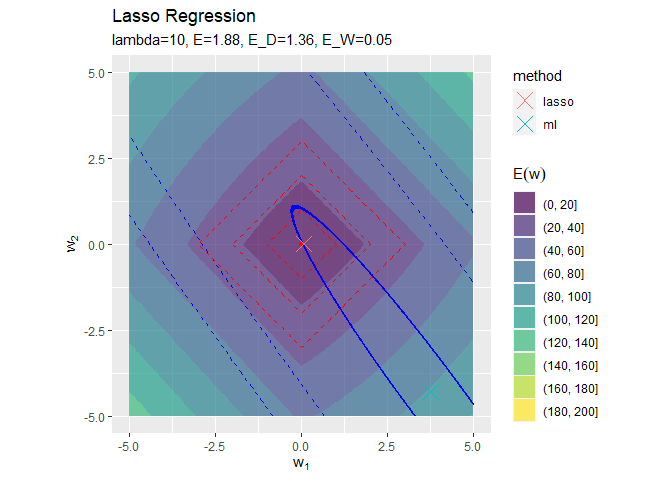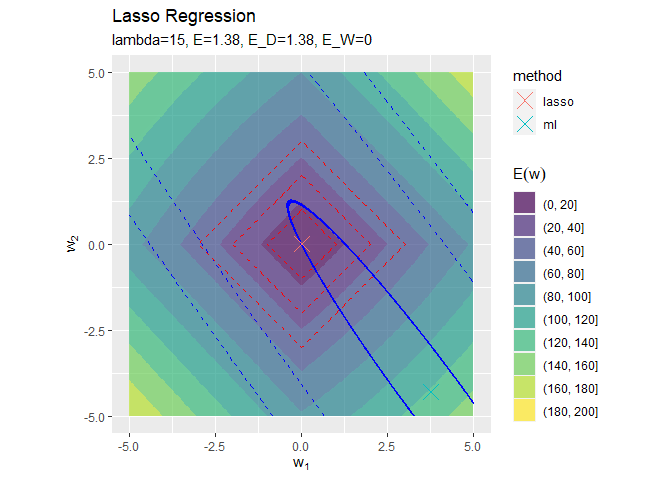
正則化係数が大きくなるほど誤差関数に対する正則化項の影響が強くなっているのを確認できます。
参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上下』,丸善出版,2012年.
おわりに
明日のアドカレネタに続く。
こちらはパラメータの最尤解自体をプロットします。次のはパラメータの最尤解を使った回帰曲線をプロットします。色んな角度から見ると理解が深まるよね。
佳林ちゃん卒業から1年かぁ。
【関連する内容】