はじめに
『ベイズ推論による機械学習入門』の学習時のノートです。「数式の行間を読んでみた」とそれを「RとPythonで組んでみた」によって、「数式」と「プログラム」から理解するのが目標です。
省略してある内容等ありますので、本とあわせて読んでください。
この記事では、「尤度関数を平均と精度が未知の多次元ガウス分布(多変量正規分布)」、「事前分布をガウス・ウィシャート分布」とした場合の「パラメータの事後分布」と「未観測値の予測分布」の計算をR言語で実装します。
【数式読解編】
【前の節の内容】
【他の節の内容】
【この節の内容】
3.4.3 多次元ガウス分布の学習と予測:平均・精度が未知の場合
尤度関数を多次元ガウス分布(Multivariate Gaussian Distribution)・多変量正規分布(Multivariate Normal Distribution)、事前分布をガウス・ウィシャート分布(Gaussian-Wishart Distribution)とするモデルに対するベイズ推論を実装します。人工的に生成したデータを用いて、ガウス分布の平均パラメータを推定し、また未観測データに対する予測分布を求めます。
ガウス分布については「多次元ガウス分布の定義式 - からっぽのしょこ」を参照してください。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(mvnfast) library(gganimate)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているため、ggplot2は読み込む必要があります。
magrittrパッケージのパイプ演算子%>%ではなく、ネイティブパイプ(ベースパイプ)演算子|>を使っています。%>%に置き換えても処理できます。
学習の推移をアニメーション(gif画像)で確認するのにgganimateパッケージを利用します。不要であれば省略してください。
ベイズ推論の実装
まずは、モデルを設定して、データを生成します。生成したデータを用いて、事後分布のパラメータを計算します。さらに、事後分布のパラメータを用いて、予測分布のパラメータを計算します。
生成分布の設定
データの生成分布(真の分布)として、多次元ガウス分布$\mathcal{N}(\mathbf{x}_n | \boldsymbol{\mu}, \boldsymbol{\Lambda}^{-1})$を設定します。
ガウス分布のグラフ作成については「【R】2次元ガウス分布の作図 - からっぽのしょこ」、ウィシャート分布の可視化については「【R】ウィシャート分布の可視化 - からっぽのしょこ」を参照してください。
真の分布($D$次元ガウス分布)のパラメータ$\boldsymbol{\mu}, \boldsymbol{\Sigma} = \boldsymbol{\Lambda}^{-1}$を設定します。この例では2次元のグラフで表現するため、次元数を$D = 2$とします。パラメータの計算自体は次元数に関わらず行えます。
# 次元数を指定 D <- 2 # 真の平均ベクトルを指定 mu_truth_d <- c(25, 50) # 真の分散共分散行列を指定 sigma_truth_dd <- matrix(c(900, -100, -100, 400), nrow = D, ncol = D) # 真の精度行列を計算 lambda_truth_dd <- solve(sigma_truth_dd) lambda_truth_dd
## [,1] [,2] ## [1,] 0.0011428571 0.0002857143 ## [2,] 0.0002857143 0.0025714286
平均ベクトル$\boldsymbol{\mu} = (\mu_1, \mu_2)^{\top}$をmu_truth_dとして値を指定します。
分散共分散行列$\boldsymbol{\Sigma} = (\sigma_1^2, \sigma_{2,1}, \sigma_{1,2}, \sigma_2^2)$をsigma_truth_ddとして値を指定します。$\sigma_d$は$x_d$の標準偏差、$\sigma_d^2$は$x_d$の分散、$\sigma_{i,j} = \sigma_{j,i}$は$x_i, x_j$の共分散であり、$\sigma_d^2$は正の実数、$\sigma_{i,j}$は実数、また$\boldsymbol{\Sigma}$は正定値行列を満たす必要があります。
精度行列$\boldsymbol{\Lambda} = \boldsymbol{\Sigma}^{-1}$を計算してlambda_truth_ddとします。逆行列はsolve()で計算できます。
mu_truth_d, lambda_truth_ddが真の値であり、この値を求めるのがここでの目的です。
真の分布の確率変数がとり得る値$\mathbf{x}$を作成します。
# グラフ用のxの値を作成 x_1_vec <- seq( mu_truth_d[1] - sqrt(sigma_truth_dd[1, 1]) * 3, mu_truth_d[1] + sqrt(sigma_truth_dd[1, 1]) * 3, length.out = 201 ) x_2_vec <- seq( mu_truth_d[2] - sqrt(sigma_truth_dd[2, 2]) * 3, mu_truth_d[2] + sqrt(sigma_truth_dd[2, 2]) * 3, length.out = 201 ) # グラフ用のxの点を作成 x_mat <- tidyr::expand_grid( x_1 = x_1_vec, x_2 = x_2_vec ) |> # 格子点を作成 as.matrix() # マトリクスに変換 head(x_mat)
## x_1 x_2 ## [1,] -65 -10.0 ## [2,] -65 -9.4 ## [3,] -65 -8.8 ## [4,] -65 -8.2 ## [5,] -65 -7.6 ## [6,] -65 -7.0
$x_1$(x軸)の値をx_1_vals、$x_2$(y軸)の値をx_2_valsとします。この例では、それぞれ平均を中心に標準偏差の3倍を範囲とします。
x_1_valsとx_2_valsの要素の全ての組み合わせ(格子状の点)をexpand_grid()で作成します。データフレームが出力されるので、as.matrix()でマトリクスに変換してx_matとします。x_matの各行が点$\mathbf{x} = (x_1, x_2)^{\top}$に対応します。
真の分布を計算して、作図用のデータフレームを作成します。
# 真の分布(多次元ガウス分布)を計算:式(2.72) model_dens_df <- tibble::tibble( x_1 = x_mat[, 1], # x軸の値 x_2 = x_mat[, 2], # y軸の値 dens = mvnfast::dmvn(X = x_mat, mu = mu_truth_d, sigma = sigma_truth_dd) # 確率密度 ) model_dens_df
## # A tibble: 40,401 × 3 ## x_1 x_2 dens ## <dbl> <dbl> <dbl> ## 1 -65 -10 0.00000000549 ## 2 -65 -9.4 0.00000000611 ## 3 -65 -8.8 0.00000000680 ## 4 -65 -8.2 0.00000000756 ## 5 -65 -7.6 0.00000000839 ## 6 -65 -7 0.00000000931 ## 7 -65 -6.4 0.0000000103 ## 8 -65 -5.8 0.0000000114 ## 9 -65 -5.2 0.0000000126 ## 10 -65 -4.6 0.0000000140 ## # … with 40,391 more rows
x_matの行ごとに確率密度を計算します。多次元ガウス分布の確率密度は、mvnfastパッケージのdmvn()で計算できます。確率変数の引数Xにx_mat、平均ベクトルの引数muにmu_truth_d、分散共分散行列の引数sigmaにsigma_truth_ddまたはlambda_truth_ddの逆行列を指定します。
真の分布のグラフを作成します。
# パラメータラベル用の文字列を作成 model_param_text <- paste0( "list(mu==(list(", paste(round(mu_truth_d, 1), collapse = ", "), "))", ", Lambda==(list(", paste(round(lambda_truth_dd, 5), collapse = ", "), ")))" ) # 真の分布を作図 ggplot() + geom_contour(data = model_dens_df, mapping = aes(x = x_1, y = x_2, z = dens, color = ..level..)) + # 真の分布:(等高線図) #geom_contour_filled(data = model_dens_df, mapping = aes(x = x_1, y = x_2, z = dens, fill = ..level..), alpha = 0.8) + # 真の分布:(塗りつぶし等高線図) labs(title = "Multivariate Gaussian Distribution", subtitle = parse(text = model_param_text), color = "density", fill = "density", x = expression(x[1]), y = expression(x[2]))
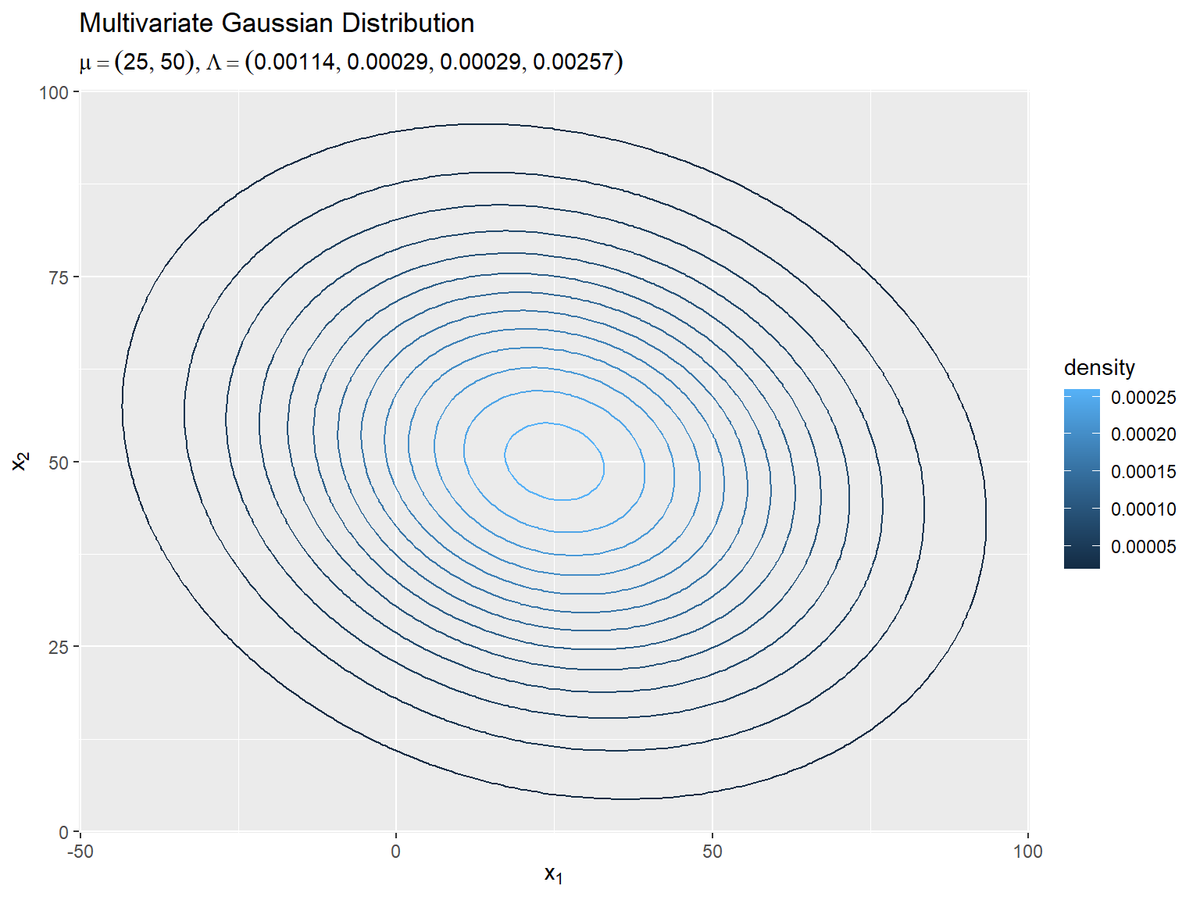
geom_contour()またはgeom_contour_filled()で等高線グラフを描画します。
真のパラメータを求めることは、真の分布を求めることを意味します。
前節のように、事前分布や事後分布に関して、精度行列の期待値(ウィシャート分布の期待値)の逆行列(分散共分散行列の期待値)によるマハラノビス距離の等高線グラフと、楕円形になるマハラノビス距離の等高線の軸によって可視化します。
比較のため、真の分散共分散行列を用いてマハラノビス距離とその軸のグラフを作成します。
真の分散共分散行列$\boldsymbol{\Sigma}$を用いて、マハラノビス距離を計算します。
# 真のΛによるマハラノビス距離を計算 model_delta_df <- tibble::tibble( x_1 = x_mat[, 1], # x軸の値 x_2 = x_mat[, 2], # y軸の値 delta = mahalanobis(x = x_mat, center = mu_truth_d, cov = sigma_truth_dd) |> sqrt() # 距離 ) model_delta_df
## # A tibble: 40,401 × 3 ## x_1 x_2 delta ## <dbl> <dbl> <dbl> ## 1 -65 -10 4.65 ## 2 -65 -9.4 4.62 ## 3 -65 -8.8 4.60 ## 4 -65 -8.2 4.58 ## 5 -65 -7.6 4.56 ## 6 -65 -7 4.53 ## 7 -65 -6.4 4.51 ## 8 -65 -5.8 4.49 ## 9 -65 -5.2 4.46 ## 10 -65 -4.6 4.44 ## # … with 40,391 more rows
マハラノビス距離の2乗をmahalanobis()で計算します。変数の引数Xにx_mat、平均ベクトルの引数centerにmu_truth_d、分散共分散行列の引数covにsigma_truth_ddまたはlambda_truth_ddを指定します。精度行列を使う場合はinverted = TRUEを指定します。
計算結果の平方根をとりマハラノビス距離を計算します。平方根はsqrt()で計算できます。
真の分散共分散行列$\boldsymbol{\Sigma}$の固有値と固有ベクトルを用いて、楕円(マハラノビス距離の等高線)の軸を計算します。
# 真のΛの固有値・固有ベクトルを計算 model_eigen <- eigen(sigma_truth_dd) model_lmd_d <- model_eigen[["values"]] model_u_dd <- model_eigen[["vectors"]] |> t() # 真のΛによる楕円の軸を計算 model_axis_df <- tibble::tibble( xend = mu_truth_d[1] + model_u_dd[, 1] * sqrt(model_lmd_d), # x軸の値 yend = mu_truth_d[2] + model_u_dd[, 2] * sqrt(model_lmd_d) # y軸の値 ) model_axis_df
## # A tibble: 2 × 2 ## xend yend ## <dbl> <dbl> ## 1 -4.77 55.7 ## 2 21.3 30.8
固有値$\lambda_d$と固有ベクトル$\mathbf{u}_d = (u_{d,1}, u_{d,2})^{\top}$をeigen()で計算します。リストが出力されるので、"values"で固有値(をまとめたベクトル)、"vectors"で固有ベクトル(をまとめたマトリクス)を取り出します。数式での成分と合わせるために転置しておきます。
軸番号(長軸か短軸か)を$i$、次元(x軸かy軸か)を$j$として、軸の先端の点を$\mu_i + u_{j,i} \sqrt{\lambda_j}$で計算します。
真の分散共分散行列によるマハラノビス距離の等高線とその軸のグラフを作成します。
# 等高線を引く値を指定 break_vals <- seq(0, ceiling(max(model_delta_df[["delta"]])), by = 0.5) # 真の分散共分散行列による距離と軸を作図 ggplot() + geom_contour(data = model_delta_df, aes(x = x_1, y = x_2, z = delta, color = ..level..), breaks = break_vals) + # 真のΛによる距離:(等高線図) #geom_contour_filled(data = model_delta_df, aes(x = x_1, y = x_2, z = delta, fill = ..level..), # breaks = break_vals, alpha = 0.8) + # 真のΛによる距離:(塗りつぶし等高線図) geom_segment(data = model_axis_df, mapping = aes(x = mu_truth_d[1], y = mu_truth_d[2], xend = xend, yend = yend, linetype = "model"), color = "red", size = 1, arrow = arrow(length = unit(10, "pt"))) + # 真のΛによる軸 scale_linetype_manual(breaks = "model", values = "solid", labels = "true model", name = "axis") + # (凡例表示用の黒魔術) coord_fixed(ratio = 1) + # アスペクト比 labs(title = "Mahalanobis Distance", subtitle = parse(text = model_param_text), color = "distance", fill = "distance", x = expression(x[1]), y = expression(x[2]))
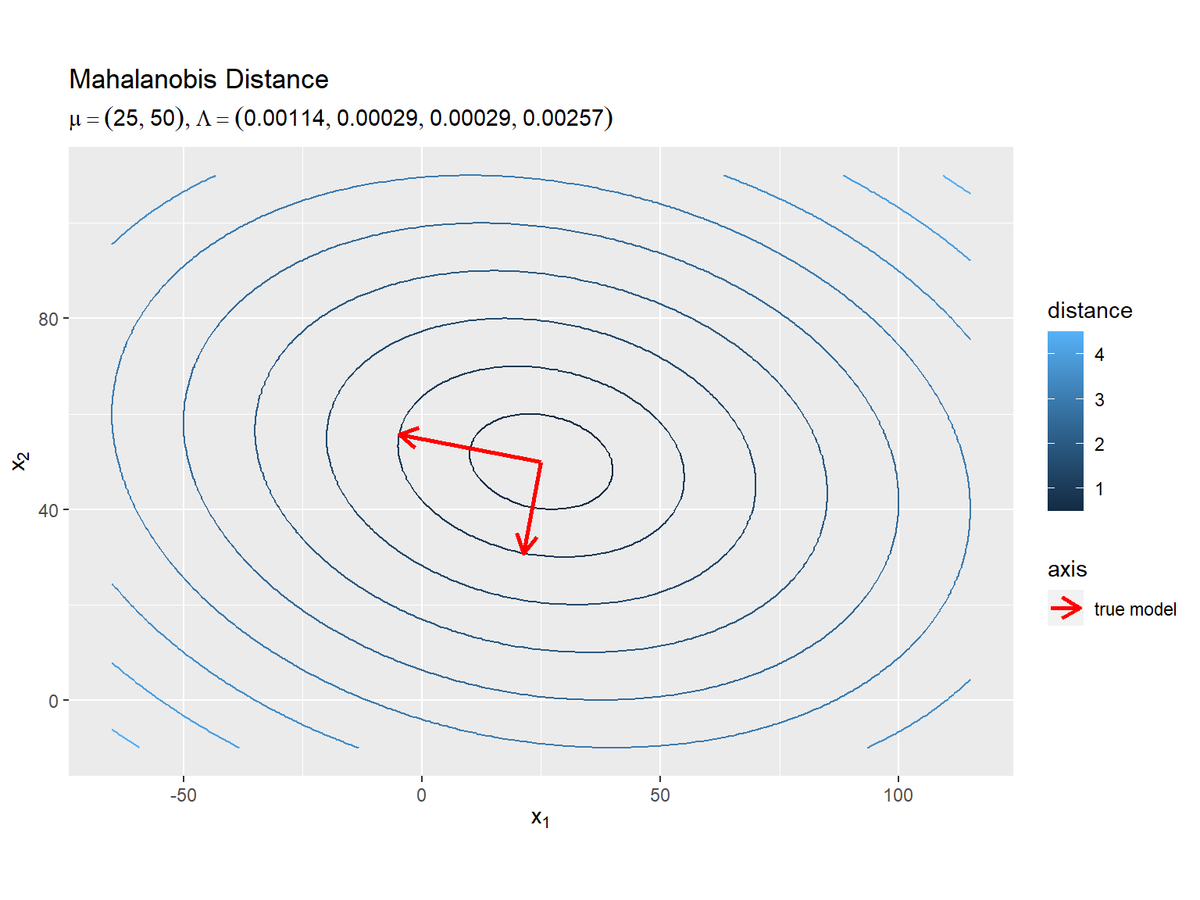
geom_segment()で軸(線分)を描画します。線分の始点の引数x, yにmu_dの値、終点の引数xend, yendにxend, yend列を指定します。
データの生成
続いて、構築したモデルに従って観測データ$\mathbf{X} = \{\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_N\}$、$\mathbf{x}_n = (x_{n,1}, x_{n,2}, \cdots, x_{n,D})^{\top}$を生成します。
ガウス分布の乱数生成については「【R】多次元ガウス分布の乱数生成 - からっぽのしょこ」を参照してください。
多次元ガウス分布に従う$N$個のデータをランダムに生成します。
# (観測)データ数を指定 N <- 100 # 多次元ガウス分布に従うデータを生成 x_nd <- mvnfast::rmvn(n = N, mu = mu_truth_d, sigma = sigma_truth_dd) head(x_nd)
## [,1] [,2] ## [1,] -18.6154597 52.06612 ## [2,] 32.1689748 27.59413 ## [3,] 29.0538979 48.44592 ## [4,] 9.6052187 65.05754 ## [5,] 0.1474273 26.82536 ## [6,] -3.4585826 42.03643
多次元ガウス分布に従う乱数は、mvnfastパッケージのrmvn()で生成できます。データ数の引数nにN、平均ベクトルの引数muにmu_truth_d、分散共分散行列の引数sigmaにsigma_truth_ddまたはlambda_truth_ddの逆行列を指定します。生成したN個のデータをx_ndとします。
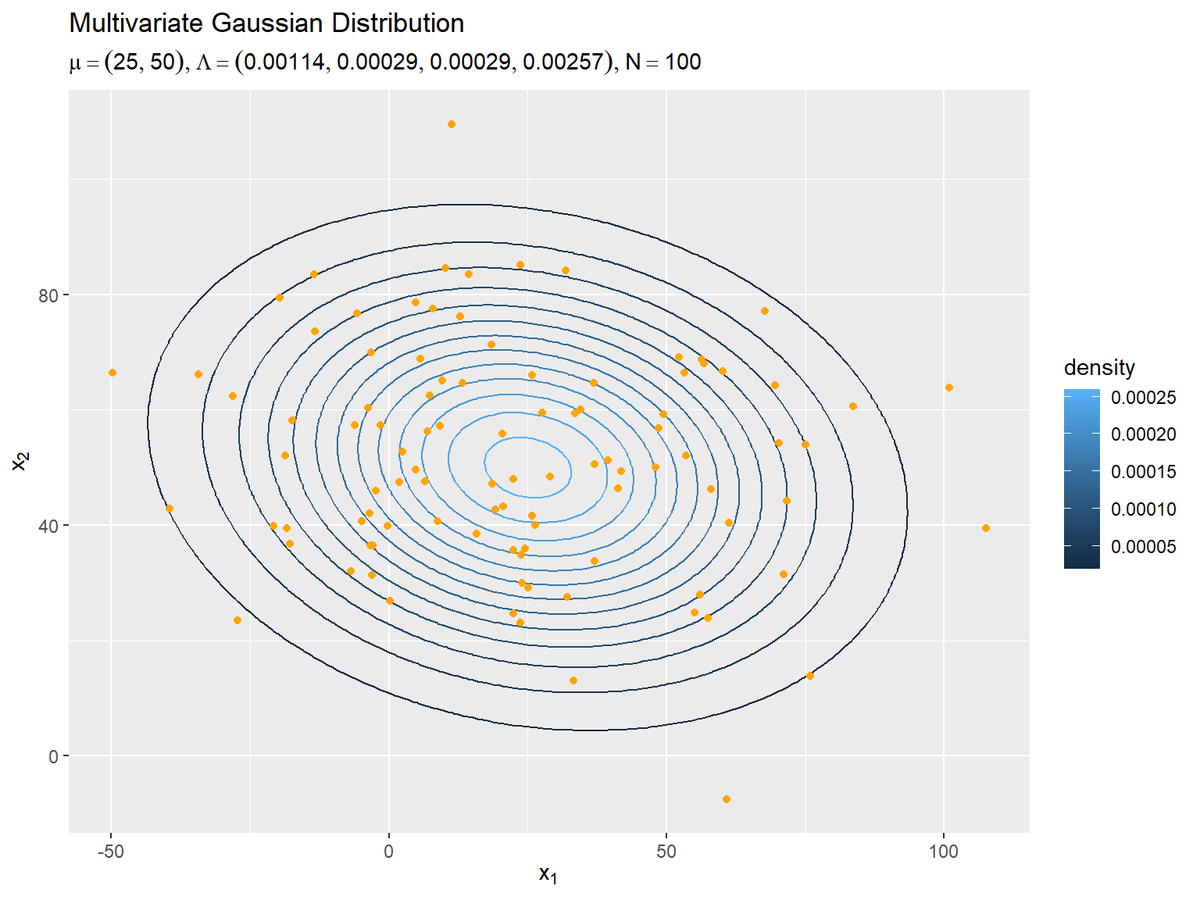
観測データの散布図を真の分布と重ねて確認します。
# 観測データを格納 data_df <- tibble::tibble( x_1 = x_nd[, 1], # x軸の値 x_2 = x_nd[, 2] # y軸の値 ) # パラメータラベル用の文字列を作成 sample_param_text <- paste0( "list(mu==(list(", paste(round(mu_truth_d, 1), collapse = ", "), "))", ", Lambda==(list(", paste(round(lambda_truth_dd, 5), collapse = ", "), "))", ", N==", N, ")" ) # 観測データの散布図を作成 ggplot() + geom_contour(data = model_dens_df, aes(x = x_1, y = x_2, z = dens, color = ..level..)) + # 真の分布:(等高線図) #geom_contour_filled(data = model_dens_df, aes(x = x_1, y = x_2, z = dens, fill = ..level..), alpha = 0.8) + # 真の分布:(塗りつぶし等高線図) geom_point(data = data_df, aes(x = x_1, y = x_2), color = "orange") + # 観測データ labs(title = "Multivariate Gaussian Distribution", subtitle = parse(text = sample_param_text), color = "density", fill = "density", x = expression(x[1]), y = expression(x[2]))
事前分布の設定
次は、尤度に対する共役事前分布を設定します。多次元ガウス分布の平均パラメータ$\boldsymbol{\mu}$と精度パラメータ$\boldsymbol{\Lambda}$の同時事前分布$p(\boldsymbol{\mu}, \boldsymbol{\Lambda})$としてガウス・ウィシャート分布$\mathrm{NW}(\boldsymbol{\mu}, \boldsymbol{\Lambda} | \mathbf{m}, \beta, \nu, \mathbf{W})$を設定します。
$\boldsymbol{\mu}, \boldsymbol{\Lambda}$の事前分布(ガウス・ウィシャート分布)のパラメータ(超パラメータ)$\mathbf{m}, \beta, \nu, \mathbf{W}$を設定します。
# μの事前分布の平均ベクトルを指定 m_d <- c(0, 0) # μの事前分布の精度行列の係数を指定 beta <- 1 # Λの事前分布の自由度を指定 nu <- D # Λの事前分布の逆スケール行列を指定 w_dd <- diag(D) * 0.00005
多次元ガウス分布の平均ベクトル$\mathbf{m} = (m_1, m_2)^{\top}$をm_d、精度行列の係数$\beta$をbetaとして値を指定します。$\beta$は$\beta > 0$を満たす必要があります。
ウィシャート分布の自由度$\nu$をnu、逆スケール行列$\mathbf{W} = (w_{1,1}, w_{2,1}, w_{1,2}, w_{2,2})$をw_ddとして値を指定します。$\nu$は$\nu > D - 1$、$\mathbf{W}$は正定値行列を満たす必要があります。
$\boldsymbol{\mu}$の事前分布の期待値(平均ベクトルの期待値)と、$\boldsymbol{\Lambda}$の事前分布の期待値(精度行列の期待値)を計算します。
# μの期待値を計算:式(2.76) E_mu_d <- m_d # Λの期待値を計算:式(2.89) E_lambda_dd <- nu * w_dd # μの事前分布の分散共分散行列を計算 E_sigma_mu_dd <- solve(beta * E_lambda_dd) E_mu_d; E_lambda_dd; E_sigma_mu_dd
## [1] 0 0 ## [,1] [,2] ## [1,] 1e-04 0e+00 ## [2,] 0e+00 1e-04 ## [,1] [,2] ## [1,] 10000 0 ## [2,] 0 10000
多次元ガウス分布の期待値とウィシャート分布の期待値を次の式で計算します。
また、$\boldsymbol{\Lambda}$の期待値と$\beta$の積の逆行列$(\beta \mathbb{E}[\boldsymbol{\Lambda}])^{-1}$を、$\boldsymbol{\mu}$の事前分布の分散共分散行列$\boldsymbol{\Sigma}_{\boldsymbol{\mu}} = (\beta \boldsymbol{\Lambda})^{-1}$の期待値とします。
$\boldsymbol{\mu}$の事前分布の確率変数がとり得る値$\boldsymbol{\mu}$を作成します。
# グラフ用のμの値を作成 mu_1_vec <- seq( mu_truth_d[1] - sqrt(E_sigma_mu_dd[1, 1]), mu_truth_d[1] + sqrt(E_sigma_mu_dd[1, 1]), length.out = 301 ) mu_2_vec <- seq( mu_truth_d[2] - sqrt(E_sigma_mu_dd[2, 2]), mu_truth_d[2] + sqrt(E_sigma_mu_dd[2, 2]), length.out = 301 ) # グラフ用のμの点を作成 mu_mat <- tidyr::expand_grid( mu_1 = mu_1_vec, mu_2 = mu_2_vec ) |> # 格子点を作成 as.matrix() # マトリクスに変換 head(mu_mat)
## mu_1 mu_2 ## [1,] -75 -50.00000 ## [2,] -75 -49.33333 ## [3,] -75 -48.66667 ## [4,] -75 -48.00000 ## [5,] -75 -47.33333 ## [6,] -75 -46.66667
$\mathbf{x}$と同様に、$\boldsymbol{\mu} = (\mu_1, \mu_2)^{\top}$がとり得る値を作成してmu_matとします。この例では、真の値を中心に事前分布の標準偏差の期待値を範囲とします。
$\boldsymbol{\mu}$の事前分布を計算します。
# μの事前分布(多次元ガウス分布)を計算:式(2.72) prior_dens_df <- tibble::tibble( mu_1 = mu_mat[, 1], # x軸の値 mu_2 = mu_mat[, 2], # y軸の値 dens = mvnfast::dmvn(X = mu_mat, mu = m_d, sigma = E_sigma_mu_dd) # 確率密度 ) prior_dens_df
## # A tibble: 90,601 × 3 ## mu_1 mu_2 dens ## <dbl> <dbl> <dbl> ## 1 -75 -50 0.0000106 ## 2 -75 -49.3 0.0000106 ## 3 -75 -48.7 0.0000107 ## 4 -75 -48 0.0000107 ## 5 -75 -47.3 0.0000107 ## 6 -75 -46.7 0.0000108 ## 7 -75 -46 0.0000108 ## 8 -75 -45.3 0.0000108 ## 9 -75 -44.7 0.0000109 ## 10 -75 -44 0.0000109 ## # … with 90,591 more rows
真の分布と同様に、mu_matの行ごとに確率密度を計算します。
$\boldsymbol{\mu}$の事前分布のグラフを作成します。
# 真のμを格納 param_df <- tibble::tibble( mu_1 = mu_truth_d[1], # x軸の値 mu_2 = mu_truth_d[2] # y軸の値 ) # パラメータラベル用の文字列を作成 prior_N_param_text <- paste0( "list(m==(list(", paste(round(m_d, 1), collapse = ", "), "))", ", beta==", beta, ", E(Lambda)==(list(", paste(round(E_lambda_dd, 5), collapse = ", "), ")))" ) # μの事前分布を作図 ggplot() + geom_contour(data = prior_dens_df, mapping = aes(x = mu_1, y = mu_2, z = dens, color = ..level..)) + # μの事前分布:(等高線図) #geom_contour_filled(data = prior_dens_df, mapping = aes(x = mu_1, y = mu_2, z = dens, fill = ..level..), alpha = 0.8) + # μの事前分布:(塗りつぶし等高線図) geom_point(data = param_df, mapping = aes(x = mu_1, y = mu_2, shape = "param"), color = "red", size = 6) + # 真のμ scale_shape_manual(breaks = "param", values = 4, labels = "true parameter", name = "") + # (凡例表示用の黒魔術) labs(title = "Multivariate Gaussian Distribution", subtitle = parse(text = prior_N_param_text), color = "density", fill = "density", x = expression(mu[1]), y = expression(mu[2]))
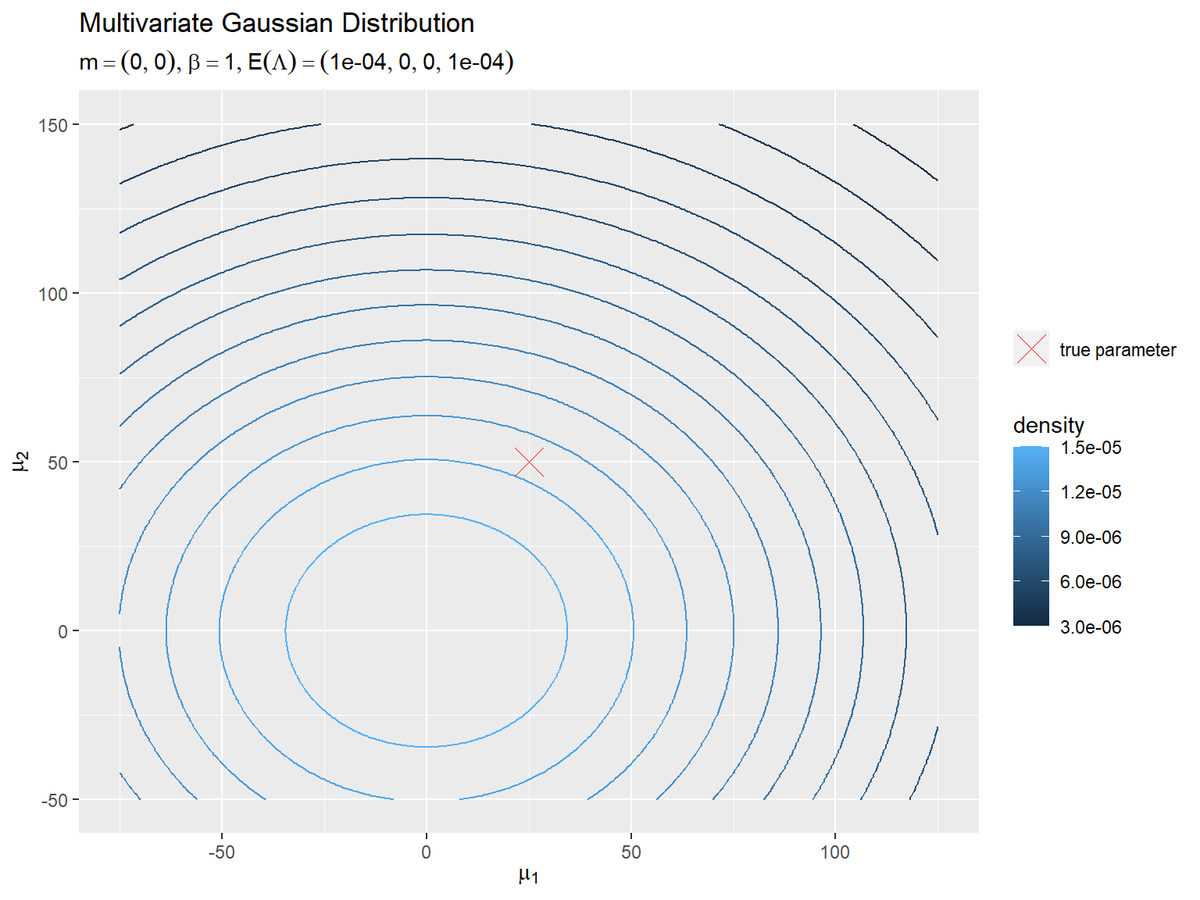
$\boldsymbol{\mu}$の真の値を赤色のバツ印で示します。
精度行列の期待値$\mathbb{E}[\boldsymbol{\Lambda}]$を用いて、マハラノビス距離を計算します。
# Λの期待値によるマハラノビス距離を計算 prior_delta_df <- tibble::tibble( x_1 = x_mat[, 1], # x軸の値 x_2 = x_mat[, 2], # y軸の値 delta_W = mahalanobis(x = x_mat, center = mu_truth_d, cov = E_lambda_dd, inverted = TRUE) |> sqrt(), # 真のμからの距離 delta_NW = mahalanobis(x = x_mat, center = E_mu_d, cov = E_lambda_dd, inverted = TRUE) |> sqrt() # μの期待値からの距離 ) prior_delta_df
## # A tibble: 40,401 × 4 ## x_1 x_2 delta_W delta_NW ## <dbl> <dbl> <dbl> <dbl> ## 1 -65 -10 1.08 0.658 ## 2 -65 -9.4 1.08 0.657 ## 3 -65 -8.8 1.08 0.656 ## 4 -65 -8.2 1.07 0.655 ## 5 -65 -7.6 1.07 0.654 ## 6 -65 -7 1.07 0.654 ## 7 -65 -6.4 1.06 0.653 ## 8 -65 -5.8 1.06 0.653 ## 9 -65 -5.2 1.06 0.652 ## 10 -65 -4.6 1.05 0.652 ## # … with 40,391 more rows
真の分布のときと同様にして、2パターンの距離を計算します。
1つ目は$\boldsymbol{\Lambda}$の事後分布(ウィシャート分布)の可視化用に、真の平均ベクトルmu_truth_dと精度行列の期待値E_lambda_ddを使って距離を計算してdelta_W列とします。2つ目は$\boldsymbol{\mu}$と$\boldsymbol{\Lambda}$の同時事後分布(ガウス-ウィシャート分布)の可視化用に、平均ベクトルの期待値E_mu_dと精度行列の期待値E_lambda_ddを使って距離を計算してdelta_NW列とします。
精度行列の期待値$\mathbb{E}[\boldsymbol{\Lambda}]$の逆行列を用いて、楕円の軸を計算します。
# Λの期待値の固有値・固有ベクトルを計算 prior_eigen <- eigen(solve(E_lambda_dd)) prior_lmd_d <- prior_eigen[["values"]] prior_u_dd <- prior_eigen[["vectors"]] |> t() # Λの期待値による楕円の軸を計算 prior_axis_df <- tibble::tibble( # 真のμからの軸 xend_W = mu_truth_d[1] + prior_u_dd[, 1] * sqrt(prior_lmd_d), yend_W = mu_truth_d[2] + prior_u_dd[, 2] * sqrt(prior_lmd_d), # μの期待値からの軸 xend_NW = E_mu_d[1] + prior_u_dd[, 1] * sqrt(prior_lmd_d), yend_NW = E_mu_d[2] + prior_u_dd[, 2] * sqrt(prior_lmd_d) ) prior_axis_df
## # A tibble: 2 × 4 ## xend_W yend_W xend_NW yend_NW ## <dbl> <dbl> <dbl> <dbl> ## 1 25 150 0 100 ## 2 -75 50 -100 0
こちらも真の分布のときと同様にして、2パターンの軸を計算します。
$\boldsymbol{\Lambda}$の事後分布(ウィシャート分布)の可視化用に、真の平均ベクトルmu_truth_dを始点(軸の交点)とする軸を計算してxend_W, yend_W列とします。また、$\boldsymbol{\mu}$と$\boldsymbol{\Lambda}$の同時事後分布(ガウス-ウィシャート分布)の可視化用に、平均ベクトルの期待値E_mu_dを始点とする軸を計算してxend_NW, yend_NW列とします。
$\boldsymbol{\Lambda}$の事前分布の期待値(精度行列の期待値)によるマハラノビス距離の等高線とその軸のグラフを作成します。
# パラメータラベル用の文字列を作成 prior_W_param_text <- paste0( "list(nu==", nu, ", W==(list(", paste(w_dd, collapse = ", "), ")))" ) # Λの事前分布の期待値による距離と軸を作図 ggplot() + geom_contour(data = model_delta_df, mapping = aes(x = x_1, y = x_2, z = delta, color = ..level..), breaks = break_vals, alpha = 0.5, linetype = "dashed") + # 真のΛによる距離 geom_contour(data = prior_delta_df, mapping = aes(x = x_1, y = x_2, z = delta_W, color = ..level..), breaks = break_vals) + # Λの期待値による距離 geom_segment(data = model_axis_df, mapping = aes(x = mu_truth_d[1], y = mu_truth_d[2], xend = xend, yend = yend, linetype = "model"), color = "red", size = 1, arrow = arrow(length = unit(10, "pt"))) + # 真のΛによる軸 geom_segment(data = prior_axis_df, mapping = aes(x = mu_truth_d[1], y = mu_truth_d[2], xend = xend_W, yend = yend_W, linetype = "prior"), color = "blue", size = 1, arrow = arrow(length = unit(10, "pt"))) + # Λの期待値による軸 scale_linetype_manual(breaks = c("prior", "model"), values = c("solid", "dashed"), labels = c("prior", "true model"), name = "axis") + # (凡例表示用の黒魔術) guides(linetype = guide_legend(override.aes = list(color = c("blue", "red"), size = c(0.5, 0.5), linetype = c("solid", "dashed")))) + # (凡例表示用の黒魔術) coord_fixed(ratio = 1) + # アスペクト比 labs(title = "Mahalanobis Distance", subtitle = parse(text = prior_W_param_text), color = "distance", x = expression(x[1]), y = expression(x[2]))
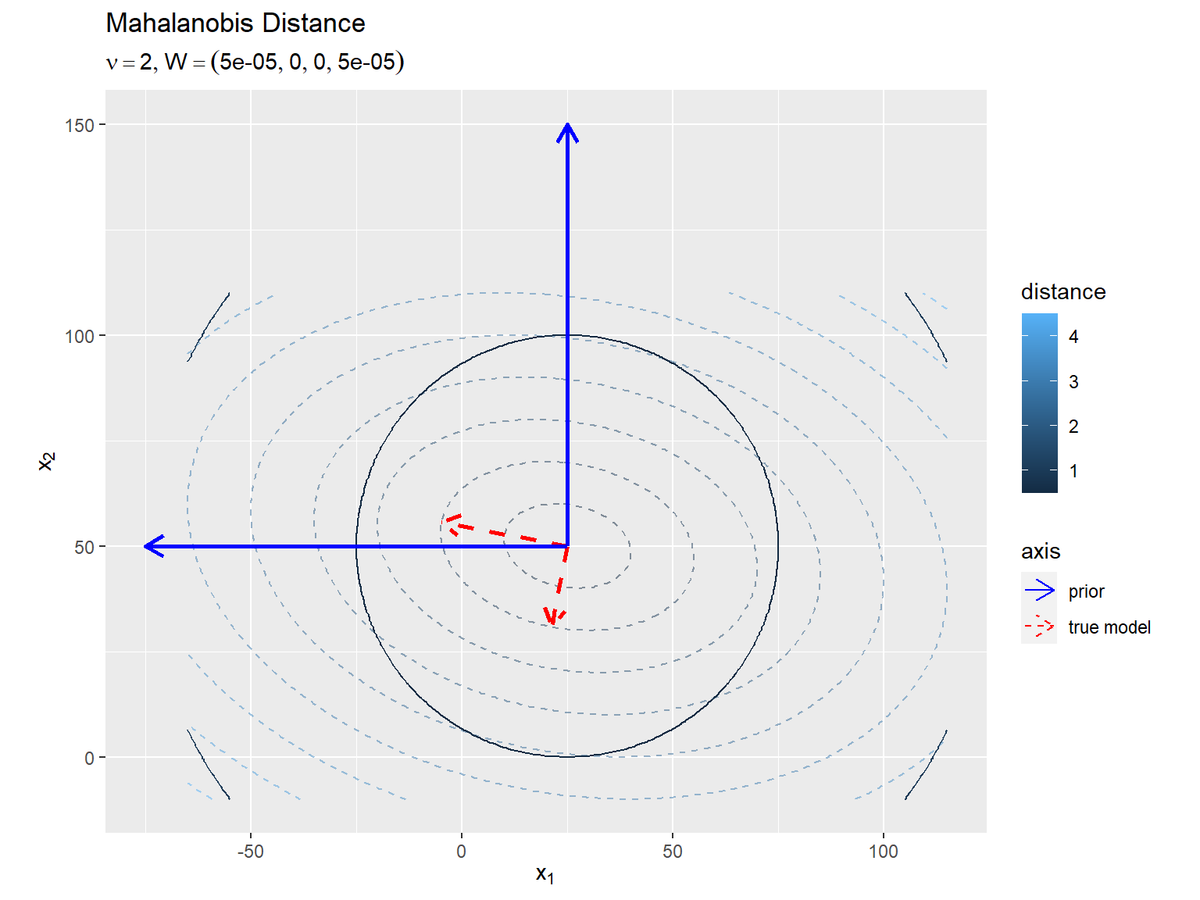
真の精度行列による等高線と軸を破線で重ねて描画します。
このグラフはウィシャート分布の可視化に対応します。
同様に、$\boldsymbol{\mu}, \boldsymbol{\Lambda}$の事前分布の期待値(平均ベクトルと精度行列の期待値)によるマハラノビス距離の等高線とその軸のグラフを作成します。
# パラメータラベル用の文字列を作成 prior_NW_param_text <- paste0( "list(m==(list(", paste(round(m_d, 1), collapse = ", "), "))", ", beta==", beta, ", nu==", nu, ", W==(list(", paste(w_dd, collapse = ", "), ")))" ) # μとΛの事前分布の期待値による距離と軸を作図 ggplot() + geom_contour(data = model_delta_df, mapping = aes(x = x_1, y = x_2, z = delta, color = ..level..), breaks = break_vals, alpha = 0.5, linetype = "dashed") + # 真のμとΛによる距離 geom_contour(data = prior_delta_df, mapping = aes(x = x_1, y = x_2, z = delta_NW, color = ..level..), breaks = break_vals) + # μとΛの期待値による距離 geom_segment(data = model_axis_df, mapping = aes(x = mu_truth_d[1], y = mu_truth_d[2], xend = xend, yend = yend, linetype = "model"), color = "red", size = 1, arrow = arrow(length = unit(10, "pt"))) + # 真のμとΛによる軸 geom_segment(data = prior_axis_df, mapping = aes(x = E_mu_d[1], y = E_mu_d[2], xend = xend_NW, yend = yend_NW, linetype = "prior"), color = "blue", size = 1, arrow = arrow(length = unit(10, "pt"))) + # μとΛの期待値による軸 scale_linetype_manual(breaks = c("prior", "model"), values = c("solid", "dashed"), labels = c("prior", "true model"), name = "axis") + # (凡例表示用の黒魔術) guides(linetype = guide_legend(override.aes = list(color = c("blue", "red"), size = c(0.5, 0.5), linetype = c("solid", "dashed")))) + # (凡例表示用の黒魔術) coord_fixed(ratio = 1) + # アスペクト比 labs(title = "Mahalanobis Distance", subtitle = parse(text = prior_NW_param_text), color = "distance", x = expression(x[1]), y = expression(x[2]))
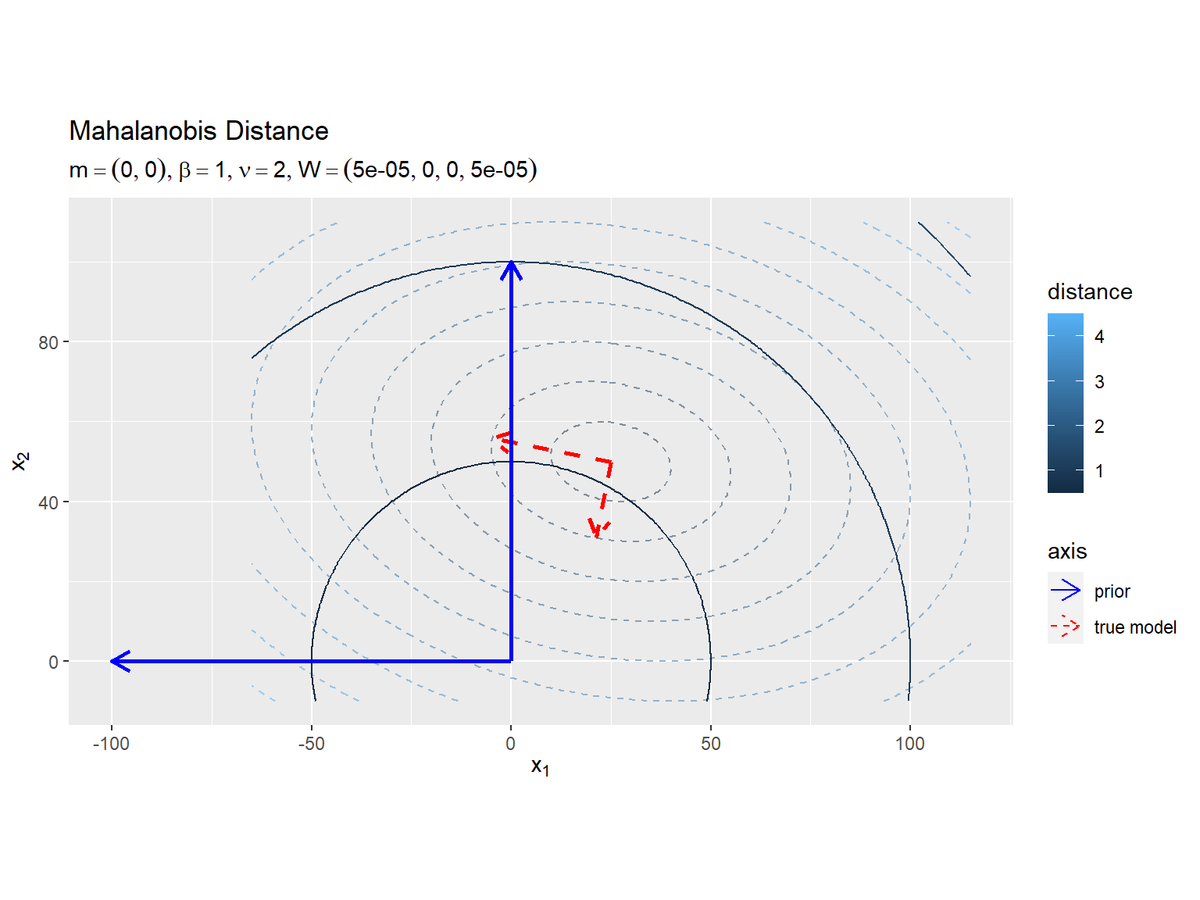
このグラフはガウス-ウィシャート分布の可視化に対応します。
距離の等高線の中心・軸の交点の位置が異なるだけで形状は同じです。
事後分布の計算
観測データ$\mathbf{X}$から平均パラメータ$\boldsymbol{\mu}$と精度パラメータ$\boldsymbol{\Lambda}$の同時事後分布$p(\boldsymbol{\mu}, \boldsymbol{\Lambda} | \mathbf{X}) = \mathrm{NW}(\boldsymbol{\mu} | \hat{\mathbf{m}}, \hat{\beta}, \hat{\nu}, \hat{\mathbf{W}})$を求めます(平均パラメータ$\boldsymbol{\mu}$と精度パラメータ$\boldsymbol{\Lambda}$を分布推定します)。
観測データ$\mathbf{X}$を用いて、$\boldsymbol{\mu}$の事後分布(ガウス分布)のパラメータ$\hat{\mathbf{m}}, \hat{\beta}$を計算します。
# μの事後分布の精度行列の係数を計算:式(3.129) beta_hat <- N + beta # μの事後分布の平均ベクトルを計算:式(3.129) m_hat_d <- (colSums(x_nd) + beta * m_d) / beta_hat m_hat_d; beta_hat
## [1] 22.28693 51.05404 ## [1] 101
$\boldsymbol{\mu}$の事後分布のパラメータを次の式で計算します。
また、$\boldsymbol{\Lambda}$の事後分布(ウィシャート分布)のパラメータ$\hat{\nu}, \hat{\mathbf{W}}$を計算します。
# Λの事後分布の自由度を計算:式(3.133) nu_hat <- N + nu # Λの事後分布の逆スケール行列を計算:式(3.133) term_x <- t(x_nd) %*% as.matrix(x_nd) term_m <- beta * as.matrix(m_d) %*% t(m_d) term_m_hat <- beta_hat * as.matrix(m_hat_d) %*% t(m_hat_d) w_hat_dd <- solve(term_x + term_m - term_m_hat + solve(w_dd)) nu_hat; w_hat_dd
## [1] 102 ## [,1] [,2] ## [1,] 8.638388e-06 9.376961e-07 ## [2,] 9.376961e-07 1.725548e-05
$\boldsymbol{\Lambda}$の事後分布のパラメータを次の式で計算します。
ただし、$\sum_{n=1}^N \mathbf{x}_n \mathbf{x}_n^{\top}$の計算について、$\mathbf{X}^{\top} \mathbf{X}$で計算しています。
$\boldsymbol{\mu}$の事後分布の期待値(平均ベクトルの期待値)と、$\boldsymbol{\Lambda}$の事後分布の期待値(精度行列の期待値)を計算します。
# μの期待値を計算:式(2.76) E_mu_hat_d <- m_hat_d # Λの期待値を計算:式(2.89) E_lambda_hat_dd <- nu_hat * w_hat_dd E_mu_hat_d; E_lambda_hat_dd
## [1] 22.28693 51.05404 ## [,1] [,2] ## [1,] 0.0008811156 0.000095645 ## [2,] 0.0000956450 0.001760059
事前分布のときと同様に計算してE_mu_hat_d, E_lambda_hat_ddとします。
$\boldsymbol{\mu}$の事後分布を計算します。
# μの事後分布(多次元ガウス分布)を計算:式(2.72) posterior_dens_df <- tibble::tibble( mu_1 = mu_mat[, 1], # x軸の値 mu_2 = mu_mat[, 2], # y軸の値 dens = mvnfast::dmvn(X = mu_mat, mu = m_hat_d, sigma = solve(beta_hat * E_lambda_hat_dd)) # 確率密度 ) posterior_dens_df
## # A tibble: 90,601 × 3 ## mu_1 mu_2 dens ## <dbl> <dbl> <dbl> ## 1 -75 -50 0 ## 2 -75 -49.3 0 ## 3 -75 -48.7 0 ## 4 -75 -48 0 ## 5 -75 -47.3 0 ## 6 -75 -46.7 0 ## 7 -75 -46 0 ## 8 -75 -45.3 0 ## 9 -75 -44.7 0 ## 10 -75 -44 0 ## # … with 90,591 more rows
更新した超パラメータm_hat_d, lambda_lambda_hat_ddを使って、事前分布のときと同様にして処理します。
$\boldsymbol{\mu}$の事後分布のグラフを作成します。
# パラメータラベル用の文字列を作成 posterior_N_param_text <- paste0( "list(N ==", N, ", hat(m)==(list(", paste(round(m_hat_d, 1), collapse = ", "), "))", ", hat(beta)==", beta_hat, ", E(Lambda)==(list(", paste(round(E_lambda_hat_dd, 5), collapse = ", "), ")))" ) # μの事後分布を作図 ggplot() + geom_contour(data = posterior_dens_df, mapping = aes(x = mu_1, y = mu_2, z = dens, color = ..level..)) + # μの事後分布:(等高線図) #geom_contour_filled(data = posterior_dens_df, mapping = aes(x = mu_1, y = mu_2, z = dens, fill = ..level..), alpha = 0.8) + # μの事後分布:(塗りつぶし等高線図) geom_point(data = param_df, mapping = aes(x = mu_1, y = mu_2), color = "red", size = 6, shape = 4) + # 真のμ #coord_cartesian(xlim = c(min(mu_1_vec), max(mu_1_vec)), ylim = c(min(mu_2_vec), max(mu_2_vec))) + # 表示範囲 labs(title = "Multivariate Gaussian Distribution", subtitle = parse(text = posterior_N_param_text), color = "density", fill = "density", x = expression(mu[1]), y = expression(mu[2]))
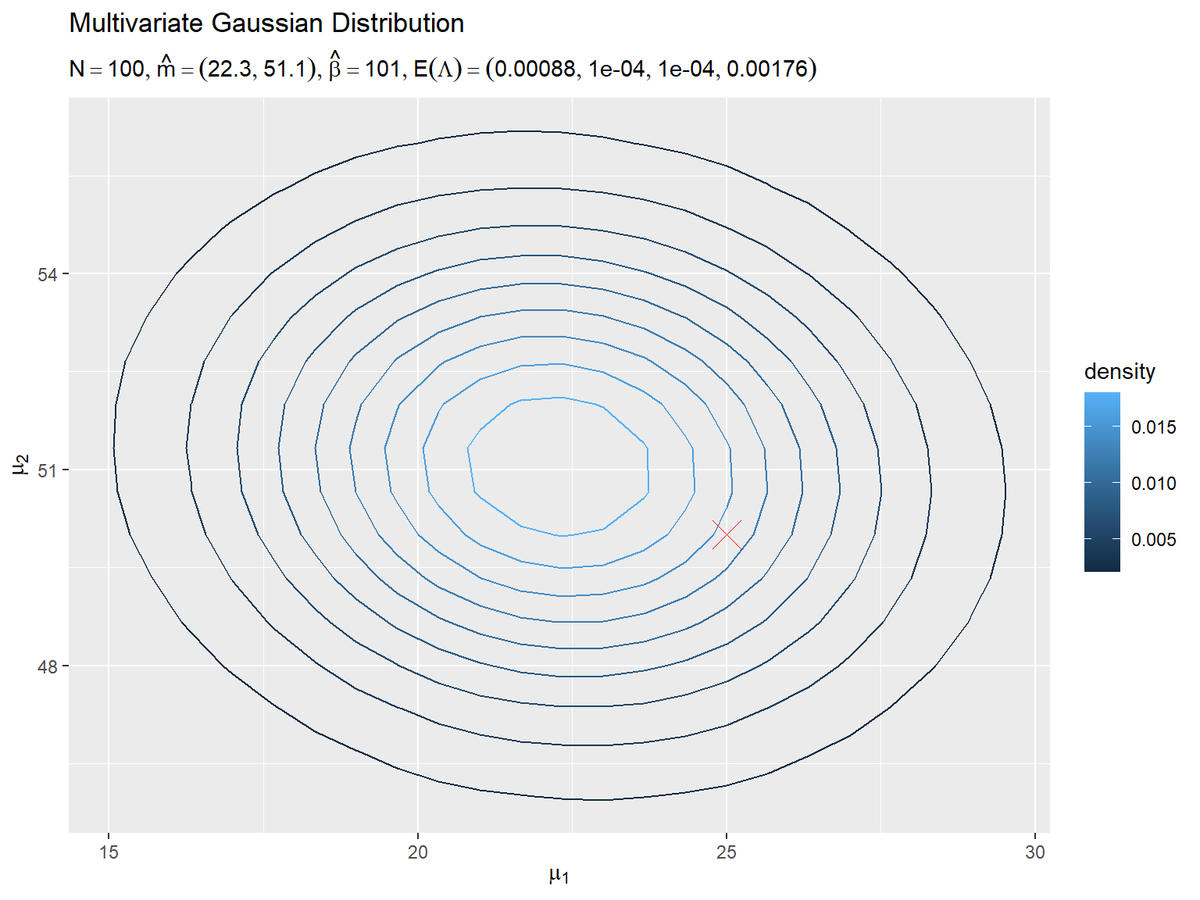
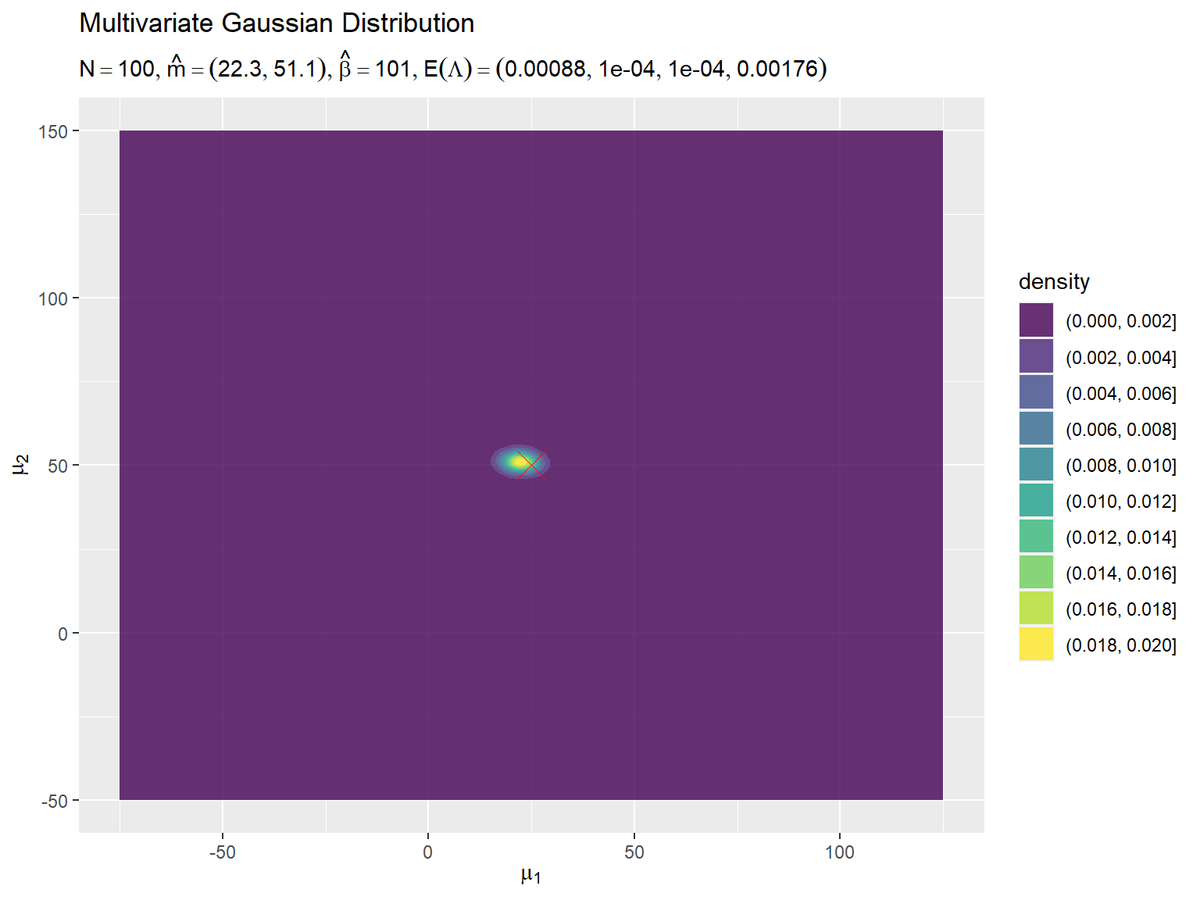
$\boldsymbol{\mu}$の真の値付近をピークとする分布を推定できています。上の図は、下の図を拡大した図になっています。そのため、描画に使う点の数が少なく、等高線が角張っています。
精度行列の期待値$\mathbb{E}[\boldsymbol{\Lambda}]$を用いて、マハラノビス距離を計算します。
# Λの期待値によるマハラノビス距離を計算 posterior_delta_df <- tibble::tibble( x_1 = x_mat[, 1], # x軸の値 x_2 = x_mat[, 2], # y軸の値 delta_W = mahalanobis(x = x_mat, center = mu_truth_d, cov = E_lambda_hat_dd, inverted = TRUE) |> sqrt(), # 真のμからの距離 delta_NW = mahalanobis(x = x_mat, center = E_mu_hat_d, cov = E_lambda_hat_dd, inverted = TRUE) |> sqrt() # μの期待値からの距離 ) posterior_delta_df
## # A tibble: 40,401 × 4 ## x_1 x_2 delta_W delta_NW ## <dbl> <dbl> <dbl> <dbl> ## 1 -65 -10 3.81 3.78 ## 2 -65 -9.4 3.79 3.76 ## 3 -65 -8.8 3.77 3.74 ## 4 -65 -8.2 3.76 3.73 ## 5 -65 -7.6 3.74 3.71 ## 6 -65 -7 3.72 3.69 ## 7 -65 -6.4 3.70 3.67 ## 8 -65 -5.8 3.68 3.65 ## 9 -65 -5.2 3.67 3.64 ## 10 -65 -4.6 3.65 3.62 ## # … with 40,391 more rows
事前分布のときと同様にして処理します。
精度行列の期待値$\mathbb{E}[\boldsymbol{\Lambda}]$の逆行列を用いて、楕円の軸を計算します。
# Λの期待値の固有値・固有ベクトルを計算 posterior_eigen <- eigen(solve(E_lambda_hat_dd)) posterior_lmd_d <- posterior_eigen[["values"]] posterior_u_dd <- posterior_eigen[["vectors"]] |> t() # Λの期待値による楕円の軸を計算 posterior_axis_df <- tibble::tibble( # 真のμからの軸 xend_W = mu_truth_d[1] + posterior_u_dd[, 1] * sqrt(posterior_lmd_d), yend_W = mu_truth_d[2] + posterior_u_dd[, 2] * sqrt(posterior_lmd_d), # μの期待値からの軸 xend_NW = E_mu_hat_d[1] + posterior_u_dd[, 1] * sqrt(posterior_lmd_d), yend_NW = E_mu_hat_d[2] + posterior_u_dd[, 2] * sqrt(posterior_lmd_d) ) posterior_axis_df
## # A tibble: 2 × 4 ## xend_W yend_W xend_NW yend_NW ## <dbl> <dbl> <dbl> <dbl> ## 1 -8.69 53.6 -11.4 54.7 ## 2 22.5 26.4 19.7 27.4
事前分布のときと同様にして処理します。
$\boldsymbol{\Lambda}$の事後分布の期待値(精度行列の期待値)によるマハラノビス距離の等高線とその軸のグラフを作成します。
# パラメータラベル用の文字列を作成 posterior_W_param_text <- paste0( "list(N==", N, ", hat(nu)==", nu_hat, ", hat(W)==(list(", paste(round(w_hat_dd, 6), collapse = ", "), ")))" ) # Λの事後分布の期待値による距離と軸を作図 ggplot() + geom_contour(data = model_delta_df, aes(x = x_1, y = x_2, z = delta, color = ..level..), breaks = break_vals, alpha = 0.5, linetype = "dashed") + # 真のΛによる距離 geom_contour(data = posterior_delta_df, aes(x = x_1, y = x_2, z = delta_W, color = ..level..), breaks = break_vals) + # Λの期待値による距離 geom_segment(data = model_axis_df, mapping = aes(x = mu_truth_d[1], y = mu_truth_d[2], xend = xend, yend = yend, linetype = "model"), color = "red", size = 1, arrow = arrow(length = unit(10, "pt"))) + # 真のΛによる軸 geom_segment(data = posterior_axis_df, mapping = aes(x = mu_truth_d[1], y = mu_truth_d[2], xend = xend_W, yend = yend_W, linetype = "posterior"), color = "blue", size = 1, arrow = arrow(length = unit(10, "pt"))) + # Λの期待値による軸 scale_linetype_manual(breaks = c("posterior", "model"), values = c("solid", "dashed"), labels = c("posterior", "true model"), name = "axis") + # (凡例表示用の黒魔術) guides(linetype = guide_legend(override.aes = list(color = c("blue", "red"), size = c(0.5, 0.5), linetype = c("solid", "dashed")))) + # (凡例表示用の黒魔術) coord_fixed(ratio = 1) + # アスペクト比 labs(title = "Mahalanobis Distance", subtitle = parse(text = posterior_W_param_text), color = "distance", x = expression(x[1]), y = expression(x[2]))
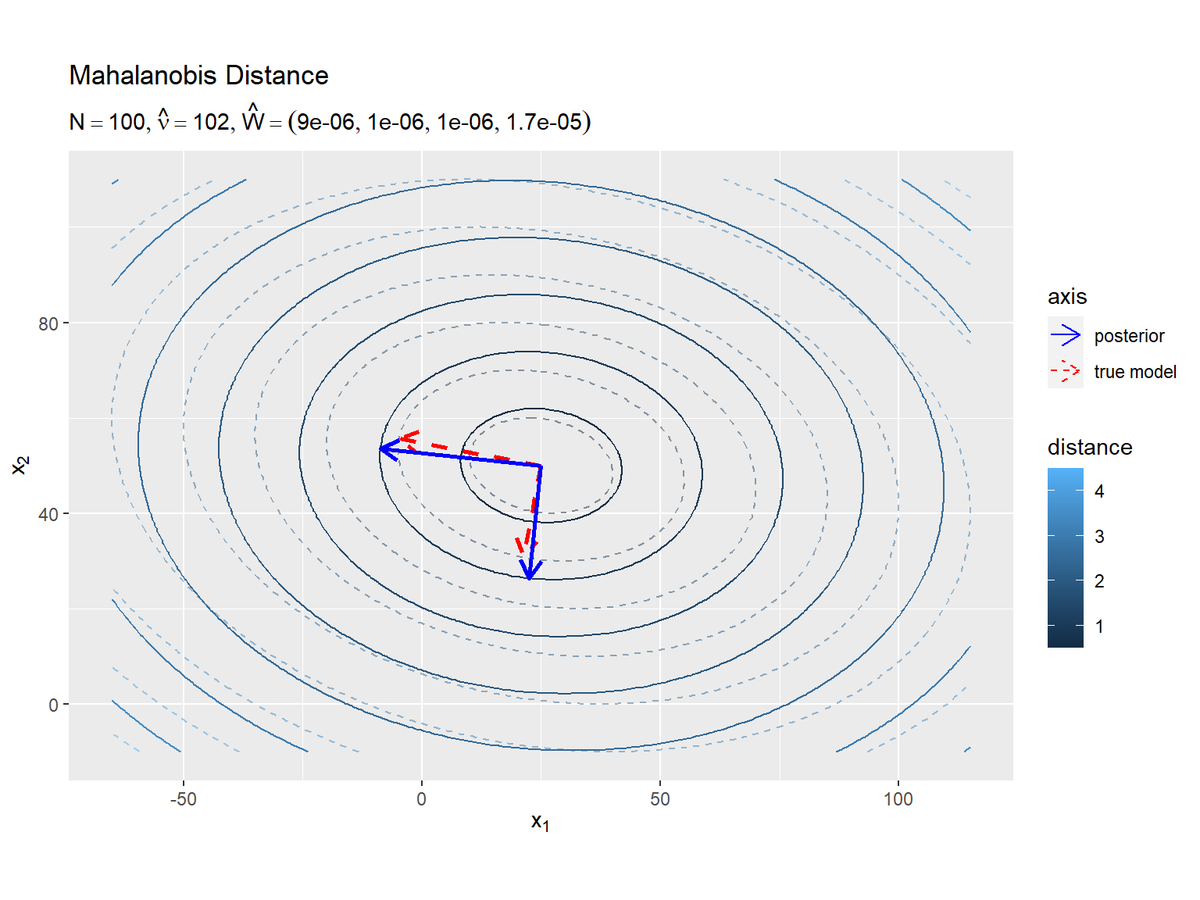
軸の方向が近付いていることから精度パラメータを推定できているのが分かります。
同様に、$\boldsymbol{\mu}, \boldsymbol{\Lambda}$の事後分布の期待値(平均ベクトルと精度行列の期待値)によるマハラノビス距離の等高線とその軸のグラフを作成します。
# パラメータラベル用の文字列を作成 posterior_NW_param_text <- paste0( "list(N==", N, ", hat(m)==(list(", paste(round(m_hat_d, 1), collapse = ", "), "))", ", hat(beta)==", beta_hat, ", hat(nu)==", nu_hat, ", hat(W)==(list(", paste(round(w_hat_dd, 6), collapse = ", "), ")))" ) # Λの事後分布の期待値による距離と軸を作図 ggplot() + geom_contour(data = model_delta_df, aes(x = x_1, y = x_2, z = delta, color = ..level..), breaks = break_vals, alpha = 0.5, linetype = "dashed") + # 真のΛによる距離 geom_contour(data = posterior_delta_df, aes(x = x_1, y = x_2, z = delta_NW, color = ..level..), breaks = break_vals) + # Λの期待値による距離 geom_segment(data = model_axis_df, mapping = aes(x = mu_truth_d[1], y = mu_truth_d[2], xend = xend, yend = yend, linetype = "model"), color = "red", size = 1, arrow = arrow(length = unit(10, "pt"))) + # 真のΛによる軸 geom_segment(data = posterior_axis_df, mapping = aes(x = E_mu_hat_d[1], y = E_mu_hat_d[2], xend = xend_NW, yend = yend_NW, linetype = "posterior"), color = "blue", size = 1, arrow = arrow(length = unit(10, "pt"))) + # Λの期待値による軸 scale_linetype_manual(breaks = c("posterior", "model"), values = c("solid", "dashed"), labels = c("posterior", "true model"), name = "axis") + # (凡例表示用の黒魔術) guides(linetype = guide_legend(override.aes = list(color = c("blue", "red"), size = c(0.5, 0.5), linetype = c("solid", "dashed")))) + # (凡例表示用の黒魔術) coord_fixed(ratio = 1) + # アスペクト比 labs(title = "Mahalanobis Distance", subtitle = parse(text = posterior_NW_param_text), color = "distance", x = expression(x[1]), y = expression(x[2]))
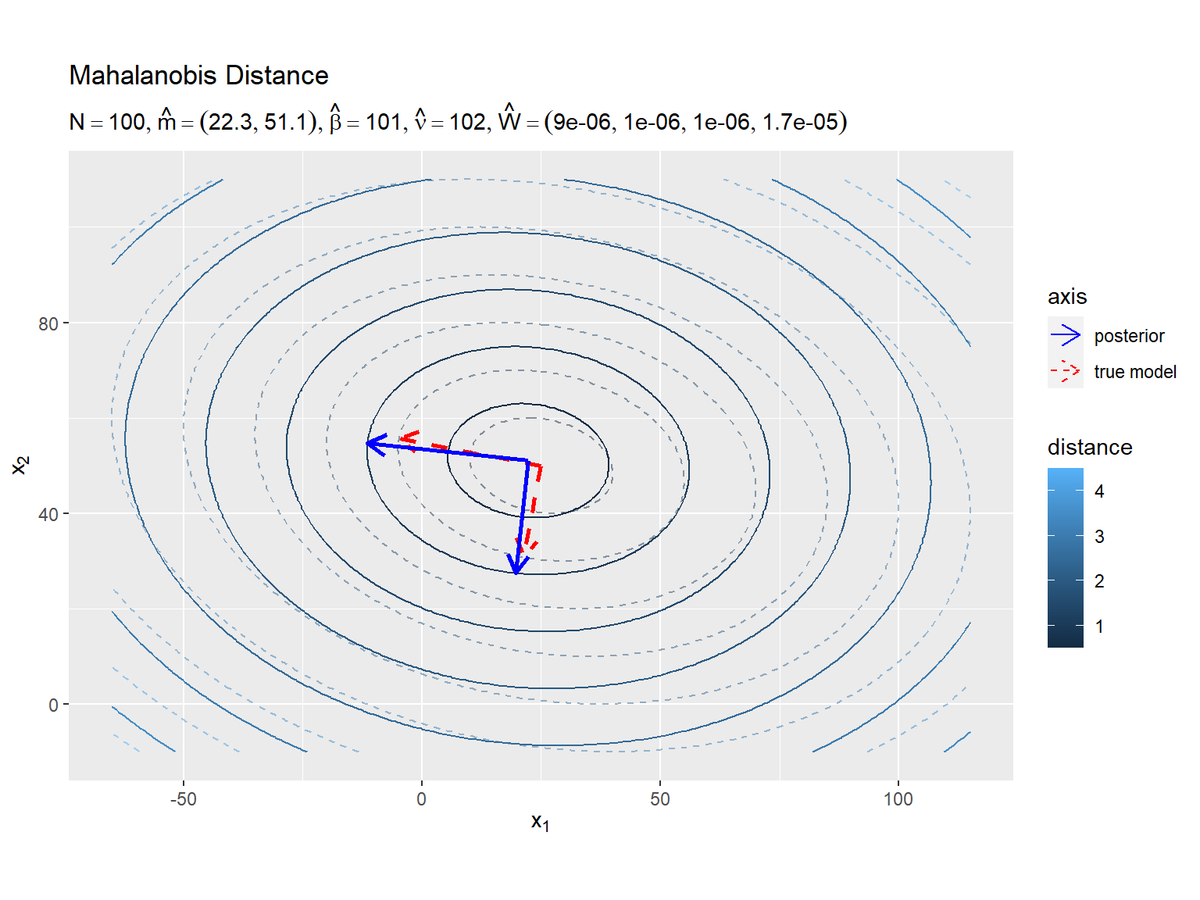
軸の始点と方向が近付いていることから平均パラメータと精度パラメータを推定できているのが分かります。
予測分布の計算
最後に、(観測データ$\mathbf{X}$から求めた)事後分布のパラメータ$\hat{\mathbf{m}}, \hat{\beta}, \hat{\nu}, \hat{\mathbf{W}}$から未観測のデータ$\mathbf{x}_{*}$の予測分布$p(\mathbf{x}_{*} | \mathbf{X}) = \mathrm{St}(\mathbf{x}_{*} | \hat{\boldsymbol{\mu}}_s, \hat{\boldsymbol{\Lambda}}_s, \hat{\nu}_s)$を求めます。予測分布は多次元スチューデントのt分布になります。
$\boldsymbol{\mu}, \boldsymbol{\Lambda}$の事後分布のパラメータ$\hat{\mathbf{m}}, \hat{\beta}, \hat{\nu}, \hat{\mathbf{W}}$を用いて、予測分布($D$次元スチューデントのt分布)のパラメータ$\hat{\boldsymbol{\mu}}_s, \hat{\boldsymbol{\Lambda}}_s, \hat{\nu}_s$を計算します。
# 予測分布の位置ベクトルを計算:式(3.140') mu_s_hat_d <- m_hat_d # 予測分布の逆スケール行列を計算:式(3.140') lambda_s_hat_dd <- (1 - D + nu_hat) * beta_hat / (1 + beta_hat) * w_hat_dd # 予測分布の自由度ルを計算:式(3.140') nu_s_hat <- 1 - D + nu_hat mu_s_hat_d; lambda_s_hat_dd; nu_s_hat
## [1] 22.28693 51.05404 ## [,1] [,2] ## [1,] 0.0008639235 0.0000937788 ## [2,] 0.0000937788 0.0017257175 ## [1] 101
予測分布のパラメータを次の式で計算します。
予測分布を計算します。
# 予測分布(多次元t分布)を計算:式(3.121) predict_dens_df <- tibble::tibble( x_1 = x_mat[, 1], # x軸の値 x_2 = x_mat[, 2], # y軸の値 dens = mvnfast::dmvt(X = x_mat, mu = mu_s_hat_d, sigma = solve(lambda_s_hat_dd), df = nu_s_hat) # 確率密度 ) predict_dens_df
## # A tibble: 40,401 × 3 ## x_1 x_2 dens ## <dbl> <dbl> <dbl> ## 1 -65 -10 0.000000240 ## 2 -65 -9.4 0.000000256 ## 3 -65 -8.8 0.000000271 ## 4 -65 -8.2 0.000000288 ## 5 -65 -7.6 0.000000306 ## 6 -65 -7 0.000000324 ## 7 -65 -6.4 0.000000344 ## 8 -65 -5.8 0.000000364 ## 9 -65 -5.2 0.000000386 ## 10 -65 -4.6 0.000000408 ## # … with 40,391 more rows
x_matの値ごとに確率密度を計算します。多次元のスチューデントのt分布の確率密度は、mvnfastパッケージのdmvt()で計算できます。確率変数の引数Xにx_mat、位置ベクトルの引数muにmu_s_hat_d、スケール行列の引数sigmaにlambda_s_hat_ddの逆行列、自由度の引数dfにnu_s_hatを指定します。lambda_s_hat_ddは逆スケール行列です。
予測分布のグラフを真の分布と重ねて作成します。
# パラメータラベル用の文字列を作成 predict_param_text <- paste0( "list(N==", N, ", hat(mu)[s]==(list(", paste0(mu_s_hat_d, collapse = ", "), "))", ", hat(Lambda)[s]==(list(", paste(round(lambda_s_hat_dd, 5), collapse = ", "), "))", ", hat(nu)[s]==", nu_s_hat, ")" ) # 予測分布を作図 ggplot() + geom_contour(data = model_dens_df, aes(x = x_1, y = x_2, z = dens, color = ..level..), alpha = 0.5, linetype = "dashed") + # 真の分布 geom_contour(data = predict_dens_df, aes(x = x_1, y = x_2, z = dens, color = ..level..)) + # 予測分布 labs(title = "Multivariate Student's t Distribution", subtitle = parse(text = predict_param_text), color = "density", x = expression(x[1]), y = expression(x[2]))
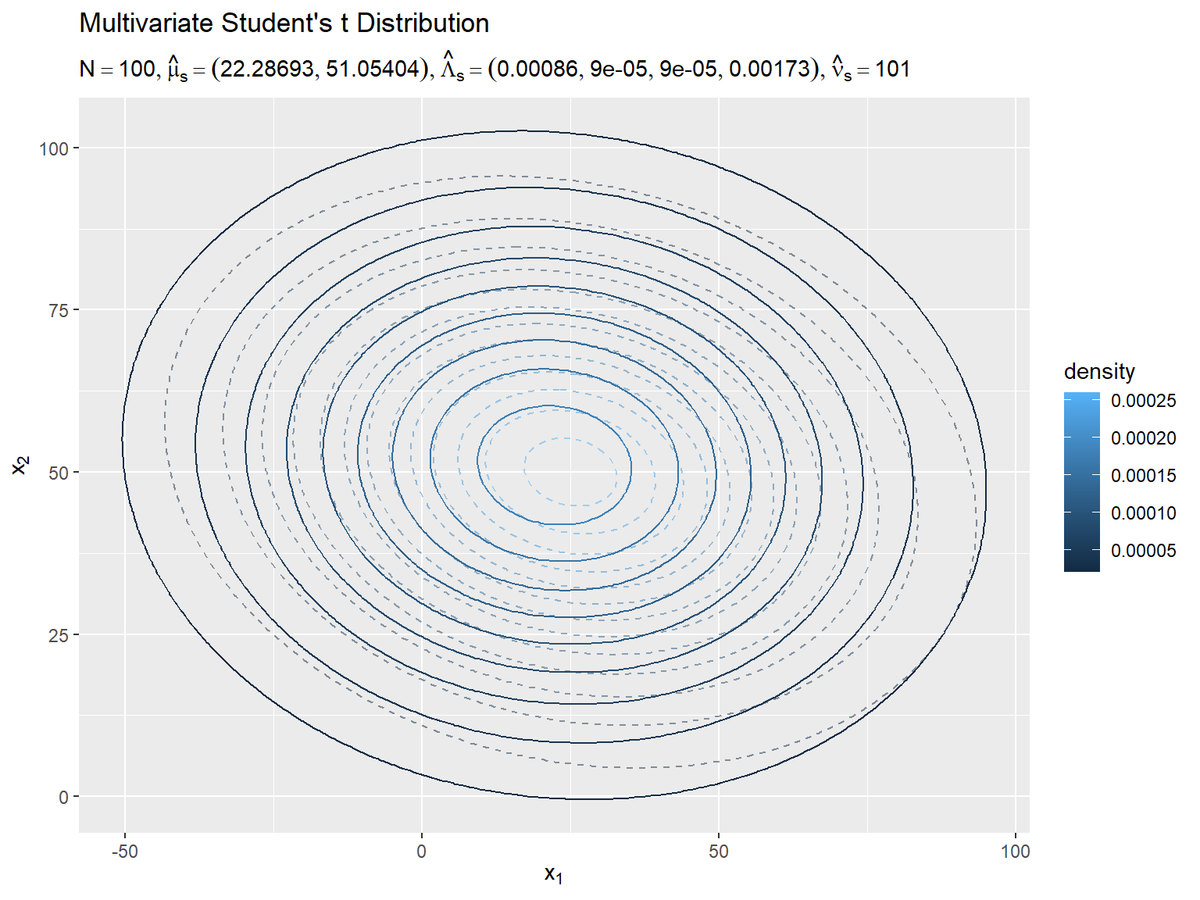
真の分布の等高線を破線で示します。
観測データが増えると、予測分布が真の分布に近付きます。
以上で、ガウス分布のベイズ推論を実装できました。
学習推移の可視化
gganimateパッケージを利用して、パラメータの推定値(更新値)の推移(分布の変化)をアニメーション(gif画像)で確認します。
モデルの設定
真の分布のパラメータ$\boldsymbol{\mu}, \boldsymbol{\Lambda}$と、事前分布のパラメータ(の初期値)$\mathbf{m}, \beta, \nu, \mathbf{W}$、試行回数$N$を設定します。
# 次元数を指定 D <- 2 # 真の平均ベクトルを指定 mu_truth_d <- c(25, 50) # 真の分散共分散行列を指定 sigma_truth_dd <- matrix(c(900, -100, -100, 400), nrow = D, ncol = D) # 真の精度行列を計算 lambda_truth_dd <- solve(sigma_truth_dd) # μの事前分布の平均ベクトルを指定 m_d <- c(0, 0) # μの事前分布の精度行列の係数を指定 beta <- 1 # Λの事前分布の自由度を指定 nu <- D # Λの事前分布の逆スケール行列を指定 w_dd <- diag(D) * 0.00005 # データ数(試行回数)を指定 N <- 100
「ベイズ推論の実装」と同じく、パラメータを指定します。
・コード(クリックで展開)
真の分布の確率変数がとり得る値$\mathbf{x}$、事前分布がとり得る値$\boldsymbol{\mu}$を作成します。
# μの期待値を計算:式(2.76) E_mu_d <- m_d # Λの期待値を計算:式(2.89) E_lambda_dd <- nu * w_dd # μの事前分布の分散共分散行列を計算 E_sigma_mu_dd <- solve(beta * E_lambda_dd) # グラフ用のμの値を作成 mu_1_vec <- seq( mu_truth_d[1] - sqrt(E_sigma_mu_dd[1, 1]), mu_truth_d[1] + sqrt(E_sigma_mu_dd[1, 1]), length.out = 201 ) mu_2_vec <- seq( mu_truth_d[2] - sqrt(E_sigma_mu_dd[2, 2]), mu_truth_d[2] + sqrt(E_sigma_mu_dd[2, 2]), length.out = 201 ) # グラフ用のμの点を作成 mu_mat <- tidyr::expand_grid(mu_1 = mu_1_vec, mu_2 = mu_2_vec) |> # 格子点を作成 as.matrix() # マトリクスに変換 # グラフ用のxの値を作成 x_1_vec <- seq( mu_truth_d[1] - sqrt(sigma_truth_dd[1, 1]) * 3, mu_truth_d[1] + sqrt(sigma_truth_dd[1, 1]) * 3, length.out = 201 ) x_2_vec <- seq( mu_truth_d[2] - sqrt(sigma_truth_dd[2, 2]) * 3, mu_truth_d[2] + sqrt(sigma_truth_dd[2, 2]) * 3, length.out = 201 ) # グラフ用のxの点を作成 x_mat <- tidyr::expand_grid(x_1 = x_1_vec, x_2 = x_2_vec) |> # 格子点を作成 as.matrix() # マトリクスに変換
確率変数がとり得る値(x軸とy軸の値)を作成します。グラフが粗い場合や処理が重い場合は、mu_*_vec, x_*_vecの要素数(by引数の値)または値の間隔(length.out引数の値)を調整してください。
推論処理:for関数による処理
for()を使って、1データずつ生成してパラメータの更新を繰り返し処理します。前ステップで求めた事後分布(のパラメータ)を次ステップの事前分布(のパラメータ)として用いる逐次学習をイメージしやすいです。
・コード(クリックで展開)
超パラメータの初期値を使って、$\boldsymbol{\mu}$の事前分布を計算します。
# μの事前分布を計算:式(2.72) anime_posterior_dens_df <- tibble::tibble( mu_1 = mu_mat[, 1], mu_2 = mu_mat[, 2], dens = mvnfast::dmvn(X = mu_mat, mu = m_d, sigma = solve(beta * nu * w_dd)), # 確率密度 param = paste0( "N=", 0, ", m=(", paste(round(m_d, 1), collapse = ", "), ")", ", beta=", beta, ", E[lambda]=(", paste0(round(nu * w_dd, 5), collapse = ", "), ")" ) |> as.factor() # フレーム切替用ラベル ) anime_posterior_dens_df
## # A tibble: 40,401 × 4 ## mu_1 mu_2 dens param ## <dbl> <dbl> <dbl> <fct> ## 1 -75 -50 0.0000106 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 2 -75 -49 0.0000107 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 3 -75 -48 0.0000107 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 4 -75 -47 0.0000108 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 5 -75 -46 0.0000108 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 6 -75 -45 0.0000109 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 7 -75 -44 0.0000109 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 8 -75 -43 0.0000110 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 9 -75 -42 0.0000110 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 10 -75 -41 0.0000110 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## # … with 40,391 more rows
現在のパラメータを文字列結合し因子型に変換して、フレーム切替用のラベル列とします。
超パラメータの初期値を使って、$\boldsymbol{\Lambda}$の事前分布の期待値によるマハラノビス距離を計算します。
# Λの期待値によるマハラノビス距離を計算 anime_posterior_delta_df <- tibble::tibble( x_1 = x_mat[, 1], # x軸の値 x_2 = x_mat[, 2], # y軸の値 delta_W = mahalanobis(x = x_mat, center = mu_truth_d, cov = E_lambda_dd, inverted = TRUE) |> sqrt(), # 真のμからの距離 delta_NW = mahalanobis(x = x_mat, center = E_mu_d, cov = E_lambda_dd, inverted = TRUE) |> sqrt(), # μの期待値からの距離 param_W = paste0( "N=", 0, ", nu=", nu, ", W=(", paste0(round(w_dd, 6), collapse = ", "), ")" ) |> as.factor(), # フレーム切替用ラベル:(Λの事後分布) param_NW = paste0( "N=", 0, ", m=(", paste(round(m_d, 1), collapse = ", "), ")", ", beta=", beta, ", nu=", nu, ", W=(", paste0(round(w_dd, 6), collapse = ", "), ")" ) |> as.factor() # フレーム切替用ラベル:(μとΛの事後分布) ) anime_posterior_delta_df
## # A tibble: 40,401 × 6 ## x_1 x_2 delta_W delta_NW param_W param_NW ## <dbl> <dbl> <dbl> <dbl> <fct> <fct> ## 1 -65 -10 1.08 0.658 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## 2 -65 -9.4 1.08 0.657 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## 3 -65 -8.8 1.08 0.656 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## 4 -65 -8.2 1.07 0.655 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## 5 -65 -7.6 1.07 0.654 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## 6 -65 -7 1.07 0.654 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## 7 -65 -6.4 1.06 0.653 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## 8 -65 -5.8 1.06 0.653 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## 9 -65 -5.2 1.06 0.652 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## 10 -65 -4.6 1.05 0.652 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## # … with 40,391 more rows
同様に、フレーム切替用のラベル列を作成します。
また、楕円の軸を計算します。
# Λの期待値の固有値・固有ベクトルを計算 prior_eigen <- eigen(solve(E_lambda_dd)) prior_lmd_d <- prior_eigen[["values"]] prior_u_dd <- prior_eigen[["vectors"]] |> t() # Λの期待値による楕円の軸を計算 anime_posterior_axis_df <- tibble::tibble( # Λの期待値による軸 xend_W = mu_truth_d[1] + prior_u_dd[, 1] * sqrt(prior_lmd_d), yend_W = mu_truth_d[2] + prior_u_dd[, 2] * sqrt(prior_lmd_d), # μとΛの期待値による軸 xstart_NW = E_mu_d[1], ystart_NW = E_mu_d[2], xend_NW = E_mu_d[1] + prior_u_dd[, 1] * sqrt(prior_lmd_d), yend_NW = E_mu_d[2] + prior_u_dd[, 2] * sqrt(prior_lmd_d), param_W = paste0( "N=", 0, ", nu=", nu, ", W=(", paste0(round(w_dd, 6), collapse = ", "), ")" ) |> as.factor(), # フレーム切替用ラベル:(Λの事後分布) param_NW = paste0( "N=", 0, ", m=(", paste(round(m_d, 1), collapse = ", "), ")", ", beta=", beta, ", nu=", nu, ", W=(", paste0(round(w_dd, 6), collapse = ", "), ")" ) |> as.factor() # フレーム切替用ラベル:(μとΛの事後分布) ) anime_posterior_axis_df
## # A tibble: 2 × 8 ## xend_W yend_W xstart_NW ystart_NW xend_NW yend_NW param_W param_NW ## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <fct> <fct> ## 1 25 150 0 0 0 100 N=0, nu=2, W=(5e-0… N=0, m=… ## 2 -75 50 0 0 -100 0 N=0, nu=2, W=(5e-0… N=0, m=…
anime_posterior_delta_dfと対応するラベル列を作成します。
事前分布のパラメータを使って、予測分布のパラメータと予測分布を計算します。
# 初期値による予測分布のパラメータを計算:式(3.140) mu_s_d <- m_d lambda_s_dd <- (nu - 1) * beta / (1 + beta) * w_dd nu_s <- nu - 1 # 初期値による予測分布を計算:式(3.121) anime_predict_dens_df <- tibble::tibble( x_1 = x_mat[, 1], x_2 = x_mat[, 2], dens = mvnfast::dmvt( X = x_mat, mu = mu_s_d, sigma = solve(lambda_s_dd), df = nu_s ), param = paste0( "N=", 0, ", mu_s=(", paste(round(mu_s_d, 1), collapse = ", "), ")", ", lambda_s=(", paste(round(lambda_s_dd, 5), collapse = ", "), ")", ", nu_s=", nu_s ) |> as.factor() # フレーム切替用ラベル ) anime_predict_dens_df
## # A tibble: 40,401 × 4 ## x_1 x_2 dens param ## <dbl> <dbl> <dbl> <fct> ## 1 -65 -10 0.00000341 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## 2 -65 -9.4 0.00000341 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## 3 -65 -8.8 0.00000341 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## 4 -65 -8.2 0.00000341 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## 5 -65 -7.6 0.00000342 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## 6 -65 -7 0.00000342 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## 7 -65 -6.4 0.00000342 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## 8 -65 -5.8 0.00000342 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## 9 -65 -5.2 0.00000342 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## 10 -65 -4.6 0.00000342 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## # … with 40,391 more rows
こちらもフレーム切替用のラベル列を作成します。
パラメータの更新処理をN回繰り返します。
# 観測データの受け皿を初期化 x_nd <- matrix(NA, nrow = N, ncol = D) # ベイズ推論 for(n in 1:N) { # 多次元ガウス分布に従うデータを生成 x_nd[n, ] <- mvnfast::rmvn(n = 1, mu = mu_truth_d, sigma = sigma_truth_dd) |> as.vector() # μの事後分布のパラメータを更新:式(3.129) old_beta <- beta old_m_d <- m_d beta <- 1 + beta m_d <- (x_nd[n, ] + old_beta * m_d) / beta # Λの事後分布のパラメータを更新:式(3.133) term_x <- x_nd[n, ] %*% t(x_nd[n, ]) term_m <- old_beta * old_m_d %*% t(old_m_d) term_m_hat <- beta * m_d %*% t(m_d) w_dd <- solve( term_x + term_m - term_m_hat + solve(w_dd) ) nu <- 1 + nu # μの事前分布を計算:式(2.72) tmp_posterior_dens_df <- tibble::tibble( mu_1 = mu_mat[, 1], mu_2 = mu_mat[, 2], dens = mvnfast::dmvn(X = mu_mat, mu = m_d, sigma = solve(beta * nu * w_dd)), # 確率密度 param = paste0( "N=", n, ", m=(", paste(round(m_d, 1), collapse = ", "), ")", ", beta=", beta, ", E[lambda]=(", paste0(round(nu * w_dd, 5), collapse = ", "), ")" ) |> as.factor() # フレーム切替用ラベル ) # μの期待値を計算 E_mu_d <- m_d # Λの期待値を計算:式(2.89) E_lambda_dd <- nu * w_dd # Λの期待値によるマハラノビス距離を計算 tmp_posterior_delta_df <- tibble::tibble( x_1 = x_mat[, 1], # x軸の値 x_2 = x_mat[, 2], # y軸の値 delta_W = mahalanobis(x = x_mat, center = mu_truth_d, cov = E_lambda_dd, inverted = TRUE) |> sqrt(), # 真のμからの距離 delta_NW = mahalanobis(x = x_mat, center = E_mu_d, cov = E_lambda_dd, inverted = TRUE) |> sqrt(), # μの期待値からの距離 param_W = paste0( "N=", n, ", nu=", nu, ", W=(", paste0(round(w_dd, 6), collapse = ", "), ")" ) |> as.factor(), # フレーム切替用ラベル:(Λの事後分布) param_NW = paste0( "N=", n, ", m=(", paste(round(m_d, 1), collapse = ", "), ")", ", beta=", beta, ", nu=", nu, ", W=(", paste0(round(w_dd, 6), collapse = ", "), ")" ) |> as.factor() # フレーム切替用ラベル:(μとΛの事後分布) ) # Λの期待値の固有値・固有ベクトルを計算 posterior_eigen <- eigen(solve(E_lambda_dd)) posterior_lmd_d <- posterior_eigen[["values"]] posterior_u_dd <- posterior_eigen[["vectors"]] |> t() # Λの期待値による楕円の軸を計算 tmp_posterior_axis_df <- tibble::tibble( # μとΛの期待値による軸 xend_W = mu_truth_d[1] + posterior_u_dd[, 1] * sqrt(posterior_lmd_d), yend_W = mu_truth_d[2] + posterior_u_dd[, 2] * sqrt(posterior_lmd_d), # μとΛの期待値による軸 xstart_NW = E_mu_d[1], ystart_NW = E_mu_d[2], xend_NW = E_mu_d[1] + posterior_u_dd[, 1] * sqrt(posterior_lmd_d), yend_NW = E_mu_d[2] + posterior_u_dd[, 2] * sqrt(posterior_lmd_d), param_W = paste0( "N=", n, ", nu=", nu, ", W=(", paste0(round(w_dd, 6), collapse = ", "), ")" ) |> as.factor(), # フレーム切替用ラベル:(Λの事後分布) param_NW = paste0( "N=", n, ", m=(", paste(round(m_d, 1), collapse = ", "), ")", ", beta=", beta, ", nu=", nu, ", W=(", paste0(round(w_dd, 6), collapse = ", "), ")" ) |> as.factor() # フレーム切替用ラベル:(μとΛの事後分布) ) # 予測分布のパラメータを更新:式(1.40) mu_s_d <- m_d lambda_s_dd <- (nu - 1) * beta / (1 + beta) * w_dd nu_s <- nu - 1 # 初期値による予測分布を計算:式(3.121) tmp_predict_dens_df <- tibble::tibble( x_1 = x_mat[, 1], x_2 = x_mat[, 2], dens = mvnfast::dmvt(X = x_mat, mu = mu_s_d, sigma = solve(lambda_s_dd), df = nu_s), param = paste0( "N=", n, ", mu_s=(", paste(round(mu_s_d, 1), collapse = ", "), ")", ", lambda_s=(", paste(round(lambda_s_dd, 5), collapse = ", "), ")", ", nu_s=", nu_s ) |> as.factor() # フレーム切替用ラベル ) # 推論結果を結合 anime_posterior_dens_df <- rbind(anime_posterior_dens_df, tmp_posterior_dens_df) anime_posterior_delta_df <- rbind(anime_posterior_delta_df, tmp_posterior_delta_df) anime_posterior_axis_df <- rbind(anime_posterior_axis_df, tmp_posterior_axis_df) anime_predict_dens_df <- rbind(anime_predict_dens_df, tmp_predict_dens_df) # 動作確認 #print(paste0("n=", n, " (", round(n / N * 100, 1), "%)")) }
超パラメータに関して、$\hat{\mathbf{m}}, \hat{\mathbf{W}}$に対応するmu_hat_d, w_hat_ddなどを新たに作るのではなく、mu_d, w_ddを繰り返し更新(上書き)していきます。これにより、事後分布のパラメータの計算式(3.129),(3.133)の$N$と$\sum_{n=1}^N$の計算は、ループ処理によってN回繰り返し1とx_nd[n, ]を加えることで行います。n回目のループ処理のときには、n-1回分の1とx_nd[n, ]が既にbetaやw_ddに加えられています。
更新したパラメータを使って事後分布と予測分布を計算して、それぞれ計算結果をanime_***_dfに結合していきます。
結果を確認します。
# 確認 head(x_nd)
## [,1] [,2] ## [1,] 26.95426 72.39050 ## [2,] -20.32012 60.45478 ## [3,] 16.21622 47.71549 ## [4,] -21.59416 50.49566 ## [5,] 35.83564 40.76963 ## [6,] 30.97469 57.18002
anime_posterior_dens_d
## # A tibble: 4,080,501 × 4 ## mu_1 mu_2 dens param ## <dbl> <dbl> <dbl> <fct> ## 1 -75 -50 0.0000106 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 2 -75 -49 0.0000107 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 3 -75 -48 0.0000107 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 4 -75 -47 0.0000108 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 5 -75 -46 0.0000108 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 6 -75 -45 0.0000109 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 7 -75 -44 0.0000109 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 8 -75 -43 0.0000110 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 9 -75 -42 0.0000110 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 10 -75 -41 0.0000110 N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## # … with 4,080,491 more rows
anime_posterior_delta_dff; anime_posterior_axis_df
## # A tibble: 4,080,501 × 6 ## x_1 x_2 delta_W delta_NW param_W param_NW ## <dbl> <dbl> <dbl> <dbl> <fct> <fct> ## 1 -65 -10 1.08 0.658 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## 2 -65 -9.4 1.08 0.657 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## 3 -65 -8.8 1.08 0.656 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## 4 -65 -8.2 1.07 0.655 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## 5 -65 -7.6 1.07 0.654 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## 6 -65 -7 1.07 0.654 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## 7 -65 -6.4 1.06 0.653 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## 8 -65 -5.8 1.06 0.653 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## 9 -65 -5.2 1.06 0.652 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## 10 -65 -4.6 1.05 0.652 N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0)… ## # … with 4,080,491 more rows ## # A tibble: 202 × 8 ## xend_W yend_W xstart_NW ystart_NW xend_NW yend_NW param_W param_NW ## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <fct> <fct> ## 1 25 150 0 0 0 100 N=0, nu=2, W=(5e-… N=0, m=… ## 2 -75 50 0 0 -100 0 N=0, nu=2, W=(5e-… N=0, m=… ## 3 55.5 132. 13.5 36.2 44.0 118. N=1, nu=3, W=(4.9… N=1, m=… ## 4 -51.5 78.5 13.5 36.2 -63.0 64.7 N=1, nu=3, W=(4.9… N=1, m=… ## 5 41.1 124. 2.21 44.3 18.3 119. N=2, nu=4, W=(4.7… N=2, m=… ## 6 -45.9 65.3 2.21 44.3 -68.7 59.6 N=2, nu=4, W=(4.7… N=2, m=… ## 7 41.5 116. 5.71 45.1 22.2 111. N=3, nu=5, W=(4.7… N=3, m=… ## 8 -38.1 65.7 5.71 45.1 -57.4 60.9 N=3, nu=5, W=(4.7… N=3, m=… ## 9 41.4 110. 0.251 46.2 16.7 106. N=4, nu=6, W=(4.6… N=4, m=… ## 10 -33.1 65.9 0.251 46.2 -57.8 62.1 N=4, nu=6, W=(4.6… N=4, m=… ## # … with 192 more rows
anime_predict_dens_df
## # A tibble: 4,080,501 × 4 ## x_1 x_2 dens param ## <dbl> <dbl> <dbl> <fct> ## 1 -65 -10 0.00000341 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## 2 -65 -9.4 0.00000341 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## 3 -65 -8.8 0.00000341 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## 4 -65 -8.2 0.00000341 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## 5 -65 -7.6 0.00000342 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## 6 -65 -7 0.00000342 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## 7 -65 -6.4 0.00000342 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## 8 -65 -5.8 0.00000342 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## 9 -65 -5.2 0.00000342 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## 10 -65 -4.6 0.00000342 N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s… ## # … with 4,080,491 more rows
それぞれ「mu_mat, x_matの行数」掛ける「N+1」行のデータフレームになります。行数が増えすぎないように注意してください。
作図処理
事後分布と予測分布の推移をそれぞれアニメーションで可視化します。
・コード(クリックで展開)
まずは、$\boldsymbol{\mu}$の事後分布に関して可視化します。
観測データと対応するラベルをデータフレームに格納します。
# 観測データを格納 anime_data_df <- tibble::tibble( x_1 = c(NA, x_nd[, 1]), x_2 = c(NA, x_nd[, 2]), param = anime_posterior_dens_df[["param"]] |> unique() # フレーム切替用ラベル ) anime_data_df
## # A tibble: 101 × 3 ## x_1 x_2 param ## <dbl> <dbl> <fct> ## 1 NA NA N=0, m=(0, 0), beta=1, E[lambda]=(1e-04, 0, 0, 1e-04) ## 2 27.0 72.4 N=1, m=(13.5, 36.2), beta=2, E[lambda]=(0.00015, -1e-05, -1e-05… ## 3 -20.3 60.5 N=2, m=(2.2, 44.3), beta=3, E[lambda]=(0.00019, 0, 0, 0.00017) ## 4 16.2 47.7 N=3, m=(5.7, 45.1), beta=4, E[lambda]=(0.00024, 0, 0, 0.00022) ## 5 -21.6 50.5 N=4, m=(0.3, 46.2), beta=5, E[lambda]=(0.00027, 0, 0, 0.00026) ## 6 35.8 40.8 N=5, m=(6.2, 45.3), beta=6, E[lambda]=(0.00031, 0, 0, 3e-04) ## 7 31.0 57.2 N=6, m=(9.7, 47), beta=7, E[lambda]=(0.00034, -1e-05, -1e-05, 0… ## 8 4.81 41.2 N=7, m=(9.1, 46.3), beta=8, E[lambda]=(0.00038, -1e-05, -1e-05,… ## 9 -6.46 67.2 N=8, m=(7.4, 48.6), beta=9, E[lambda]=(0.00042, 0, 0, 0.00042) ## 10 -14.4 45.1 N=9, m=(5.2, 48.2), beta=10, E[lambda]=(0.00046, 0, 0, 0.00047) ## # … with 91 more rows
事前分布には観測データが影響しないので欠損値NAとして、anime_posterior_dfのラベル列と合わせて格納します。
参考として、各試行における観測データを描画するのに使います。
$\boldsymbol{\mu}$の事後分布の推移のアニメーションを作成します。
# 真のμを格納 param_df <- tibble::tibble( mu_1 = mu_truth_d[1], # x軸の値 mu_2 = mu_truth_d[2] # y軸の値 ) # μの事後分布のアニメーションを作図 posterior_graph <- ggplot() + geom_contour(data = anime_posterior_dens_df, mapping = aes(x = mu_1, y = mu_2, z = dens, color = ..level..)) + # μの事後分布 #geom_contour_filled(data = anime_posterior_dens_df, mapping = aes(x = mu_1, y = mu_2, z = dens, fill = ..level..), alpha = 0.8) + # μの事後分布 geom_point(data = param_df, mapping = aes(x = mu_1, y = mu_2), color = "red", size = 6, shape = 4) + # 真のμ geom_point(data = anime_data_df, mapping = aes(x = x_1, y = x_2), color = "orange", size = 3) + # 観測データ gganimate::transition_manual(param) + # フレーム #coord_cartesian(xlim = c(min(mu_1_vec), max(mu_2_vec)), ylim = c(min(mu_2_vec), max(mu_2_vec))) + # 表示範囲 labs(title = "Multivariate Gaussian Distribution", subtitle = "{current_frame}", color = "density", fill = "density", x = expression(mu[1]), y = expression(mu[2])) # gif画像を作成 gganimate::animate(posterior_graph, nframes = N+1+10, end_pause = 10, fps = 10, width = 800, height = 600)
フレームの順番を示す列をtransition_manual()に指定して、animate()でgif画像を作成します。事前分布(初期値)を含むため、フレーム数はN+1です。
続いて、$\boldsymbol{\Lambda}$の事後分布に関して可視化します。
anime_posterior_delta_dfまたはanime_posterior_axis_dfのラベル列を使って観測データを格納します。
# 観測データを格納 anime_data_df <- tibble::tibble( x_1 = c(NA, x_nd[, 1]), # x軸の値 x_2 = c(NA, x_nd[, 2]), # y軸の値 param_W = anime_posterior_delta_df[["param_W"]] |> unique(), # フレーム切替用ラベル:(Λの事後分布) param_NW = anime_posterior_delta_df[["param_NW"]] |> unique() # フレーム切替用ラベル:(μとΛの事後分布) ) anime_data_df
## # A tibble: 101 × 4 ## x_1 x_2 param_W param_NW ## <dbl> <dbl> <fct> <fct> ## 1 NA NA N=0, nu=2, W=(5e-05, 0, 0, 5e-05) N=0, m=(0, 0), … ## 2 27.0 72.4 N=1, nu=3, W=(4.9e-05, -2e-06, -2e-06, 4.4e-05) N=1, m=(13.5, 3… ## 3 -20.3 60.5 N=2, nu=4, W=(4.7e-05, -1e-06, -1e-06, 4.3e-05) N=2, m=(2.2, 44… ## 4 16.2 47.7 N=3, nu=5, W=(4.7e-05, -1e-06, -1e-06, 4.3e-05) N=3, m=(5.7, 45… ## 5 -21.6 50.5 N=4, nu=6, W=(4.6e-05, -1e-06, -1e-06, 4.3e-05) N=4, m=(0.3, 46… ## 6 35.8 40.8 N=5, nu=7, W=(4.4e-05, 0, 0, 4.3e-05) N=5, m=(6.2, 45… ## 7 31.0 57.2 N=6, nu=8, W=(4.3e-05, -1e-06, -1e-06, 4.3e-05) N=6, m=(9.7, 47… ## 8 4.81 41.2 N=7, nu=9, W=(4.3e-05, -1e-06, -1e-06, 4.3e-05) N=7, m=(9.1, 46… ## 9 -6.46 67.2 N=8, nu=10, W=(4.2e-05, 0, 0, 4.2e-05) N=8, m=(7.4, 48… ## 10 -14.4 45.1 N=9, nu=11, W=(4.1e-05, 0, 0, 4.2e-05) N=9, m=(5.2, 48… ## # … with 91 more rows
参考として、各試行における観測データを描画するのに使います。
$\boldsymbol{\Lambda}$の事後分布の期待値によるマハラノビス距離とその軸の推移のアニメーションを作成します。
# 真のΛによるマハラノビス距離を計算 model_delta_df <- tibble::tibble( x_1 = x_mat[, 1], # x軸の値 x_2 = x_mat[, 2], # y軸の値 delta = mahalanobis(x = x_mat, center = mu_truth_d, cov = lambda_truth_dd, inverted = TRUE) |> sqrt() # 距離 ) # 真のΛの固有値・固有ベクトルを計算 model_eigen <- eigen(sigma_truth_dd) model_lmd_d <- model_eigen[["values"]] model_u_dd <- model_eigen[["vectors"]] |> t() # 真のΛによる楕円の軸を計算 model_axis_df <- tibble::tibble( xend = mu_truth_d[1] + model_u_dd[, 1] * sqrt(model_lmd_d), # x軸の値 yend = mu_truth_d[2] + model_u_dd[, 2] * sqrt(model_lmd_d) # y軸の値 ) # 等高線を引く値を指定 break_vals <- seq(0, ceiling(max(model_delta_df[["delta"]])), by = 0.5) # Λの事後分布の期待値による距離と軸のアニメーションを作図 anime_posterior_graph <- ggplot() + geom_contour(data = model_delta_df, aes(x = x_1, y = x_2, z = delta, color = ..level..), breaks = break_vals, alpha = 0.5, linetype = "dashed") + # 真のΛによる距離 geom_contour(data = anime_posterior_delta_df, aes(x = x_1, y = x_2, z = delta_W, color = ..level..), breaks = break_vals) + # Λの期待値による距離 geom_segment(data = model_axis_df, mapping = aes(x = mu_truth_d[1], y = mu_truth_d[2], xend = xend, yend = yend, linetype = "model"), color = "red", size = 1, arrow = arrow(length = unit(10, "pt"))) + # 真のΛによる軸 geom_segment(data = anime_posterior_axis_df, mapping = aes(x = mu_truth_d[1], y = mu_truth_d[2], xend = xend_W, yend = yend_W, linetype = "posterior"), color = "blue", size = 1, arrow = arrow(length = unit(10, "pt"))) + # μとΛの期待値による軸 geom_point(data = anime_data_df, mapping = aes(x = x_1, y = x_2), color = "orange", size = 3) + # 観測データ gganimate::transition_manual(param_W) + # フレーム scale_linetype_manual(breaks = c("posterior", "model"), values = c("solid", "dashed"), labels = c("posterior", "true model"), name = "axis") + # (凡例表示用の黒魔術) guides(linetype = guide_legend(override.aes = list(color = c("blue", "red"), size = c(0.5, 0.5), linetype = c("solid", "dashed")))) + # (凡例表示用の黒魔術) coord_fixed(ratio = 1, xlim = c(min(x_1_vec), max(x_1_vec)), ylim = c(min(x_2_vec), max(x_2_vec))) + # アスペクト比 labs(title = "Mahalanobis Distance", subtitle = "{current_frame}", color = "distance", x = expression(x[1]), y = expression(x[2])) # gif画像を作成 gganimate::animate(anime_posterior_graph, nframes = N+1+10, end_pause = 10, fps = 10, width = 800, height = 600)
同様に、$\boldsymbol{\mu}$と$\boldsymbol{\Lambda}$の同時事後分布の期待値によるマハラノビス距離とその軸の推移のアニメーションを作成します。
# μとΛの事後分布の期待値による距離と軸のアニメーションを作図 anime_posterior_graph <- ggplot() + geom_contour(data = model_delta_df, aes(x = x_1, y = x_2, z = delta, color = ..level..), breaks = break_vals, alpha = 0.5, linetype = "dashed") + # 真のΛによる距離 geom_contour(data = anime_posterior_delta_df, aes(x = x_1, y = x_2, z = delta_NW, color = ..level..), breaks = break_vals) + # μとΛの期待値による距離 geom_segment(data = model_axis_df, mapping = aes(x = mu_truth_d[1], y = mu_truth_d[2], xend = xend, yend = yend, linetype = "model"), color = "red", size = 1, arrow = arrow(length = unit(10, "pt"))) + # 真のΛによる軸 geom_segment(data = anime_posterior_axis_df, mapping = aes(x = xstart_NW, y = ystart_NW, xend = xend_NW, yend = yend_NW, linetype = "posterior"), color = "blue", size = 1, arrow = arrow(length = unit(10, "pt"))) + # Λの期待値による軸 geom_point(data = anime_data_df, mapping = aes(x = x_1, y = x_2), color = "orange", size = 3) + # 観測データ gganimate::transition_manual(param_NW) + # フレーム scale_linetype_manual(breaks = c("posterior", "model"), values = c("solid", "dashed"), labels = c("posterior", "true model"), name = "axis") + # (凡例表示用の黒魔術) guides(linetype = guide_legend(override.aes = list(color = c("blue", "red"), size = c(0.5, 0.5), linetype = c("solid", "dashed")))) + # (凡例表示用の黒魔術) coord_fixed(ratio = 1, xlim = c(min(x_1_vec), max(x_1_vec)), ylim = c(min(x_2_vec), max(x_2_vec))) + # アスペクト比 labs(title = "Mahalanobis Distance", subtitle = "{current_frame}", color = "distance", x = expression(x[1]), y = expression(x[2])) # gif画像を作成 gganimate::animate(anime_posterior_graph, nframes = N+1+10, end_pause = 10, fps = 10, width = 800, height = 600)
最後に、予測分布に関して可視化します。
anime_predict_dfのラベル列を使って観測データを格納します。
# 観測データを格納 anime_data_df <- tibble::tibble( x_1 = c(NA, x_nd[, 1]), x_2 = c(NA, x_nd[, 2]), param = anime_predict_dens_df[["param"]] |> unique() # フレーム切替用ラベル ) anime_data_df
## # A tibble: 101 × 3 ## x_1 x_2 param ## <dbl> <dbl> <fct> ## 1 NA NA N=0, mu_s=(0, 0), lambda_s=(2e-05, 0, 0, 2e-05), nu_s=1 ## 2 27.0 72.4 N=1, mu_s=(13.5, 36.2), lambda_s=(7e-05, 0, 0, 6e-05), nu_s=2 ## 3 -20.3 60.5 N=2, mu_s=(2.2, 44.3), lambda_s=(0.00011, 0, 0, 1e-04), nu_s=3 ## 4 16.2 47.7 N=3, mu_s=(5.7, 45.1), lambda_s=(0.00015, 0, 0, 0.00014), nu_s=4 ## 5 -21.6 50.5 N=4, mu_s=(0.3, 46.2), lambda_s=(0.00019, 0, 0, 0.00018), nu_s=5 ## 6 35.8 40.8 N=5, mu_s=(6.2, 45.3), lambda_s=(0.00022, 0, 0, 0.00022), nu_s=6 ## 7 31.0 57.2 N=6, mu_s=(9.7, 47), lambda_s=(0.00026, 0, 0, 0.00026), nu_s=7 ## 8 4.81 41.2 N=7, mu_s=(9.1, 46.3), lambda_s=(3e-04, -1e-05, -1e-05, 0.00031… ## 9 -6.46 67.2 N=8, mu_s=(7.4, 48.6), lambda_s=(0.00034, 0, 0, 0.00034), nu_s=9 ## 10 -14.4 45.1 N=9, mu_s=(5.2, 48.2), lambda_s=(0.00038, 0, 0, 0.00038), nu_s=… ## # … with 91 more rows
各試行における観測データを描画するのに使います。
また、各試行までの観測データを格納します。
# 観測データを複製して格納 anime_alldata_df <- tidyr::expand_grid( frame = 1:N, # フレーム番号 n = 1:N # 試行回数 ) |> # 全ての組み合わせを作成 dplyr::filter(n < frame) |> # フレーム番号以前のデータを抽出 dplyr::mutate( x_1 = x_nd[n, 1], x_2 = x_nd[n, 2], param = unique(anime_predict_dens_df[["param"]])[frame+1] # フレーム切替用ラベル ) anime_alldata_df
## # A tibble: 4,950 × 5 ## frame n x_1 x_2 param ## <int> <int> <dbl> <dbl> <fct> ## 1 2 1 27.0 72.4 N=2, mu_s=(2.2, 44.3), lambda_s=(0.00011, 0, 0, 1e-0… ## 2 3 1 27.0 72.4 N=3, mu_s=(5.7, 45.1), lambda_s=(0.00015, 0, 0, 0.00… ## 3 3 2 -20.3 60.5 N=3, mu_s=(5.7, 45.1), lambda_s=(0.00015, 0, 0, 0.00… ## 4 4 1 27.0 72.4 N=4, mu_s=(0.3, 46.2), lambda_s=(0.00019, 0, 0, 0.00… ## 5 4 2 -20.3 60.5 N=4, mu_s=(0.3, 46.2), lambda_s=(0.00019, 0, 0, 0.00… ## 6 4 3 16.2 47.7 N=4, mu_s=(0.3, 46.2), lambda_s=(0.00019, 0, 0, 0.00… ## 7 5 1 27.0 72.4 N=5, mu_s=(6.2, 45.3), lambda_s=(0.00022, 0, 0, 0.00… ## 8 5 2 -20.3 60.5 N=5, mu_s=(6.2, 45.3), lambda_s=(0.00022, 0, 0, 0.00… ## 9 5 3 16.2 47.7 N=5, mu_s=(6.2, 45.3), lambda_s=(0.00022, 0, 0, 0.00… ## 10 5 4 -21.6 50.5 N=5, mu_s=(6.2, 45.3), lambda_s=(0.00022, 0, 0, 0.00… ## # … with 4,940 more rows
フレーム番号と試行回数(データ番号)の全ての組み合わせを作成して、フレーム番号未満のデータを抽出します。フレーム切替用のラベルは、フレーム番号を使って抽出します。
各試行以前のデータを描画するのに使うので、フレーム番号が2からになります。
予測分布の推移のアニメーションを作成します。
# 真の分布(多次元ガウス分布)を計算:式(2.72) model_dens_df <- tibble::tibble( x_1 = x_mat[, 1], x_2 = x_mat[, 2], dens = mvnfast::dmvn(X = x_mat, mu = mu_truth_d, sigma = sigma_truth_dd) # 確率密度 ) # 予測分布を作図 anime_predict_graph <- ggplot() + geom_contour(data = model_dens_df, aes(x = x_1, y = x_2, z = dens, color = ..level..), alpha = 0.5, linetype = "dashed") + # 真の分布 geom_contour(data = anime_predict_dens_df, aes(x = x_1, y = x_2, z = dens, color = ..level..)) + # 予測分布 geom_point(data = anime_alldata_df, aes(x = x_1, y = x_2), color ="orange", alpha = 0.5) + # 過去の観測データ geom_point(data = anime_data_df, aes(x = x_1, y = x_2), color ="orange", size = 3) + # 観測データ gganimate::transition_manual(param) + # フレーム labs(title = "Multivariate Student's t Distribution", subtitle = "{current_frame}", color = "density", x = expression(x[1]), y = expression(x[2])) # gif画像を作成 gganimate::animate(anime_predict_graph, nframes = N+1+10, end_pause = 10, fps = 10, width = 800, height = 600)
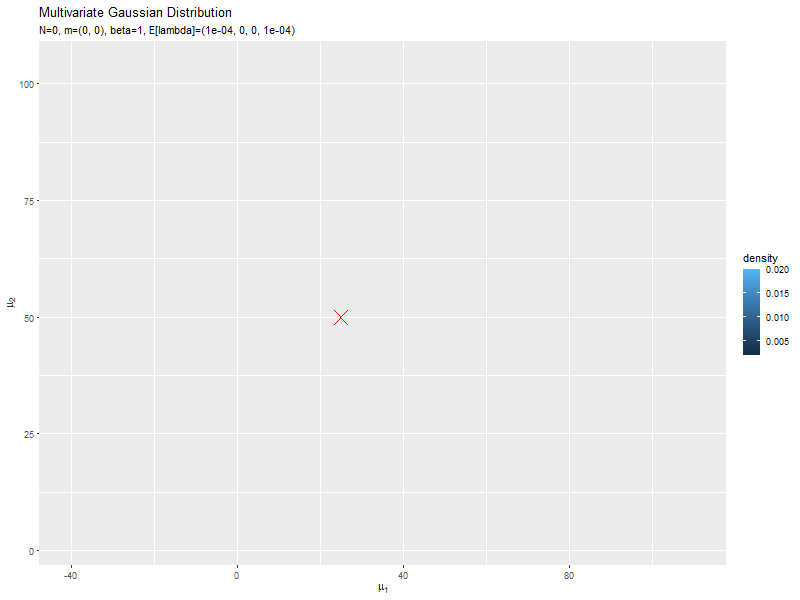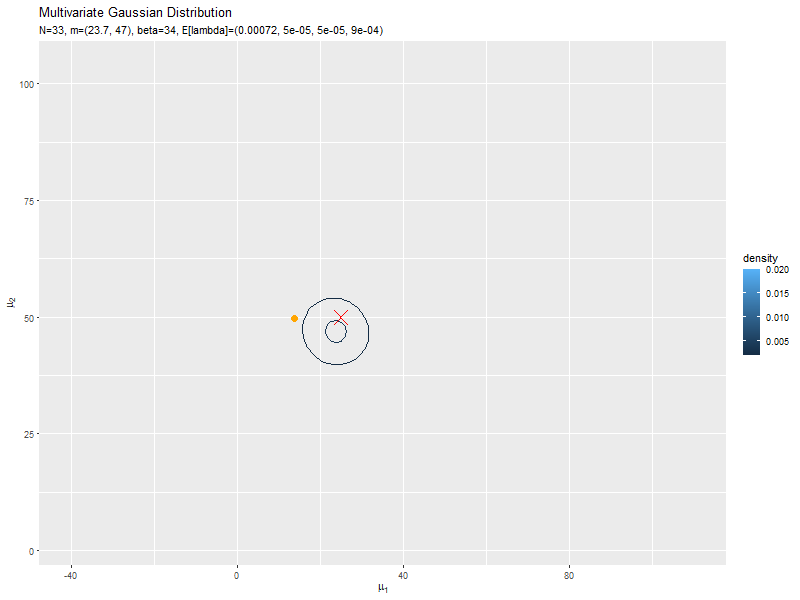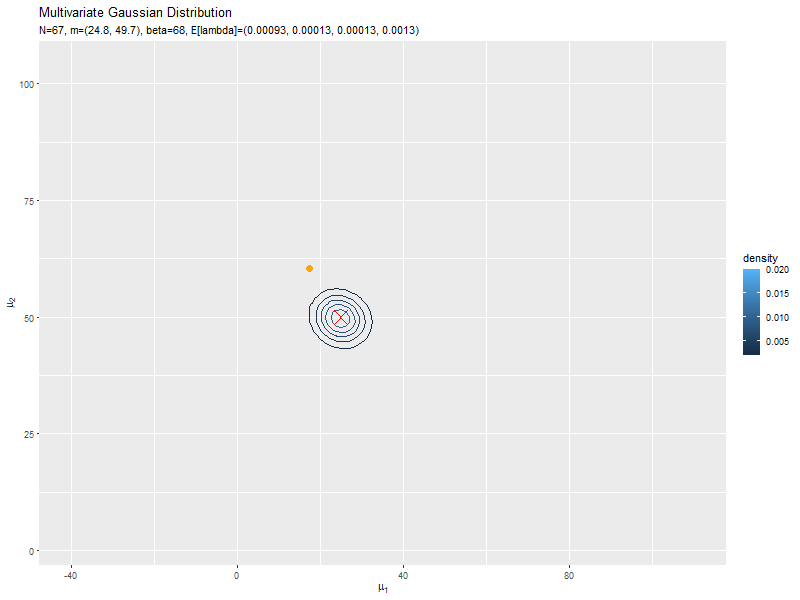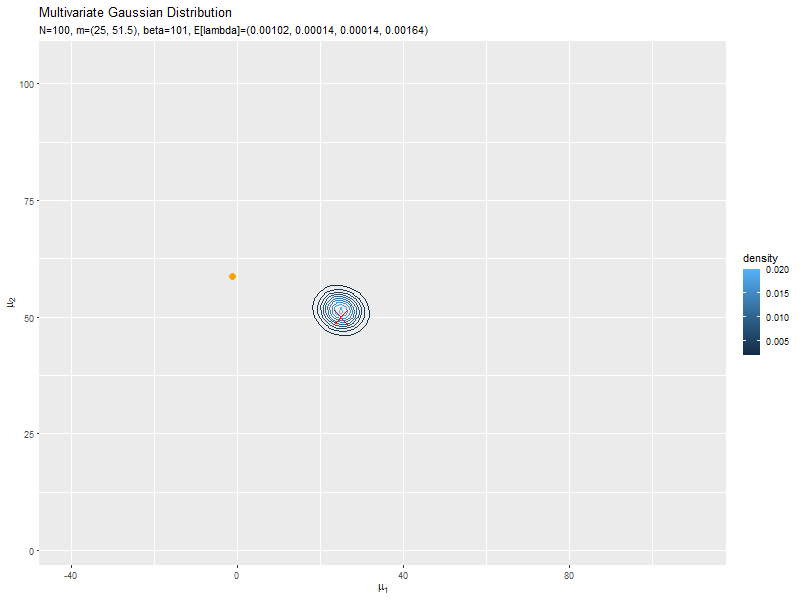

データが増えるにつれて、真のパラメータ付近の確率密度が大きくなっていくのを確認できます。
始めの頃は、分散が大きく確率密度が小さいため、等高線が描画されていません。
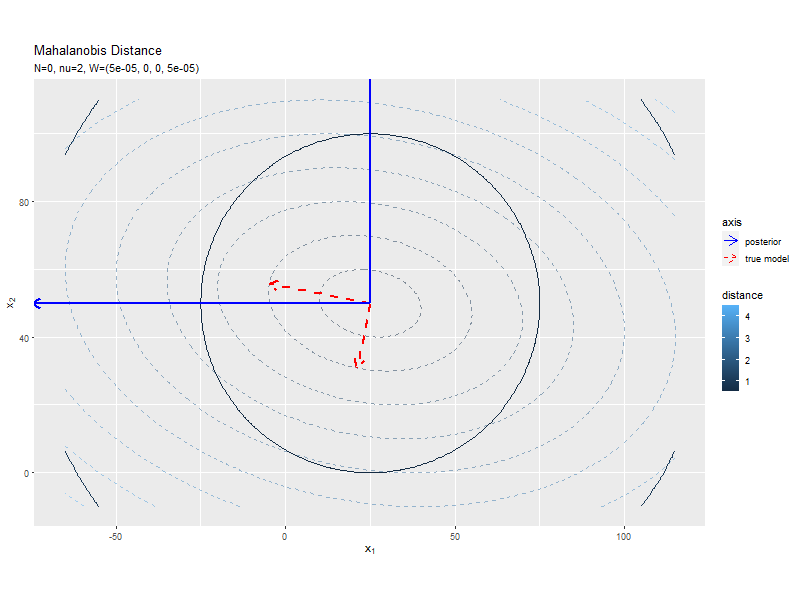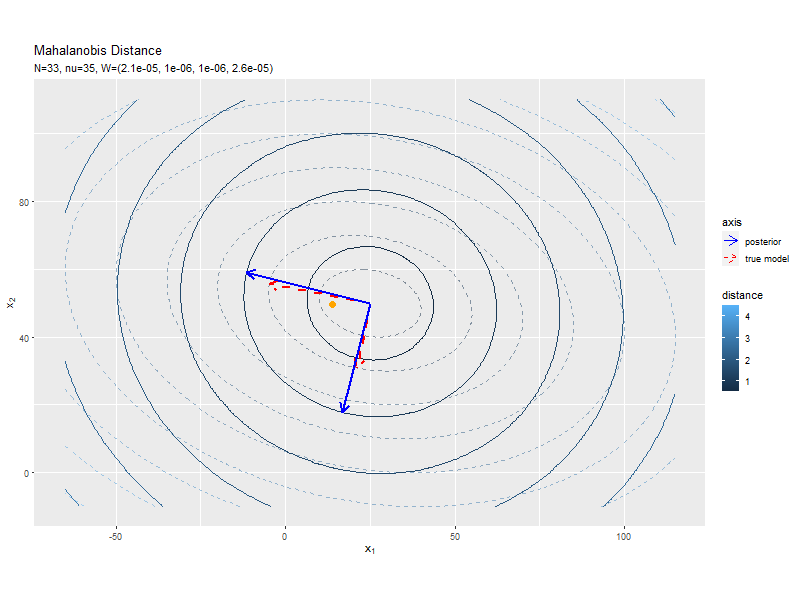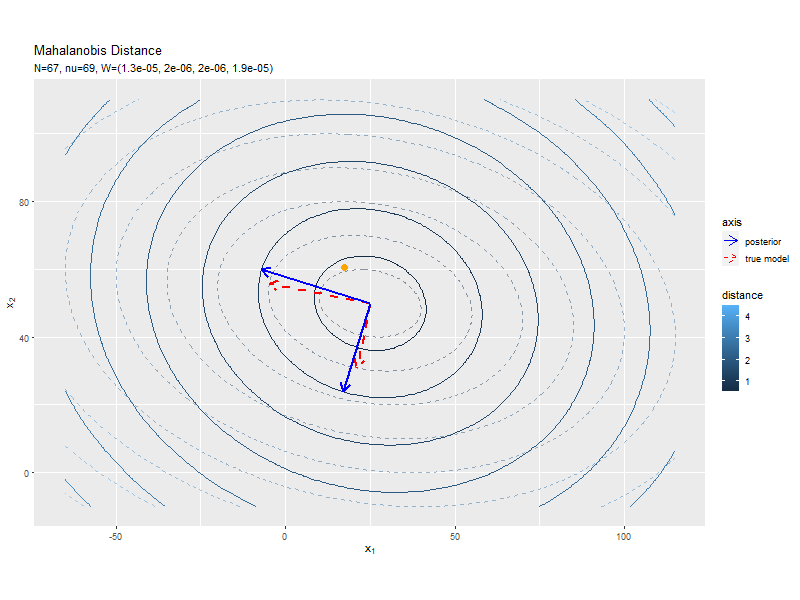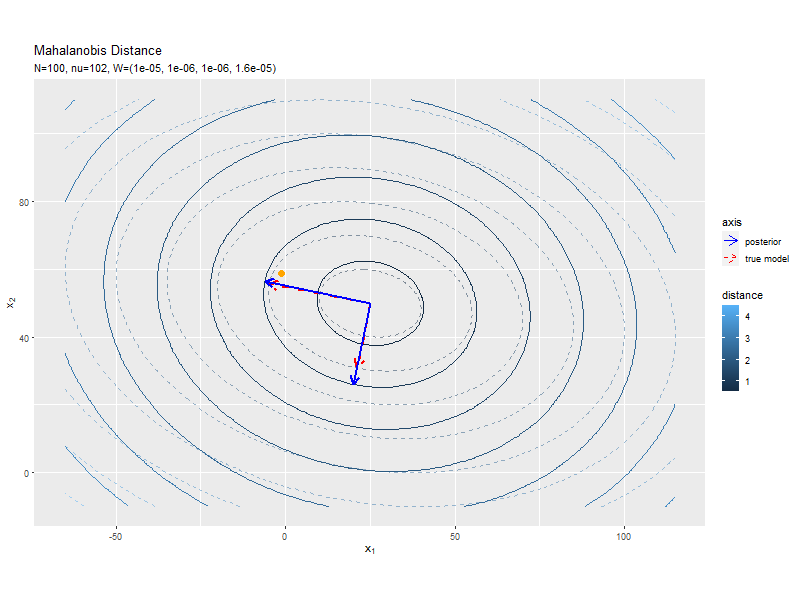
データが増えるにつれて、真の精度行列による軸に近付いていくを確認できます。
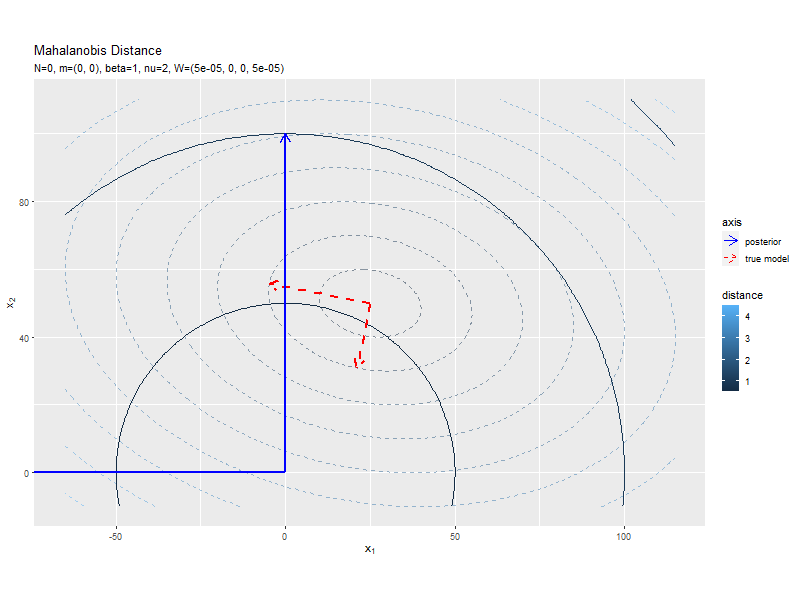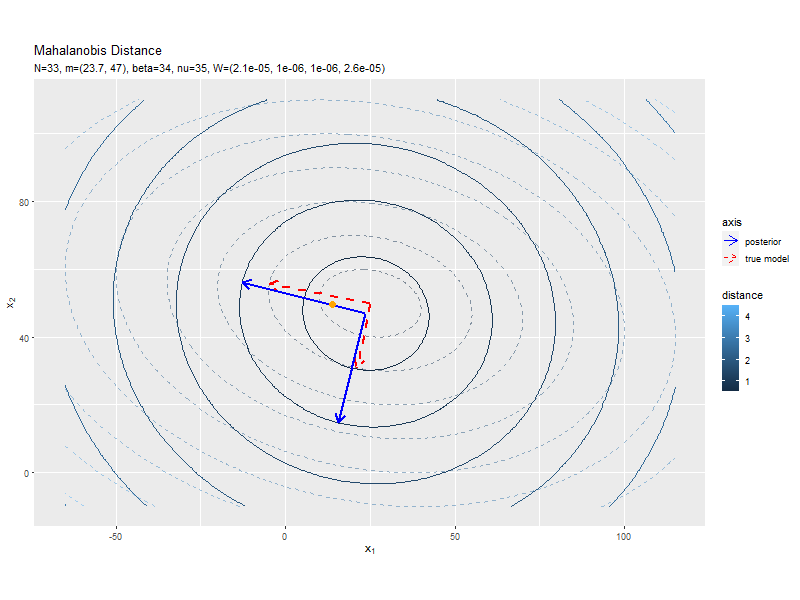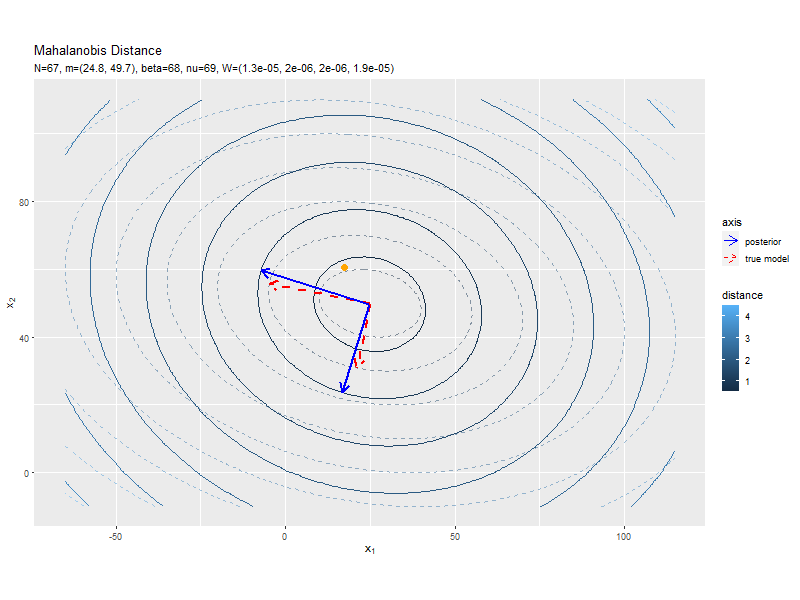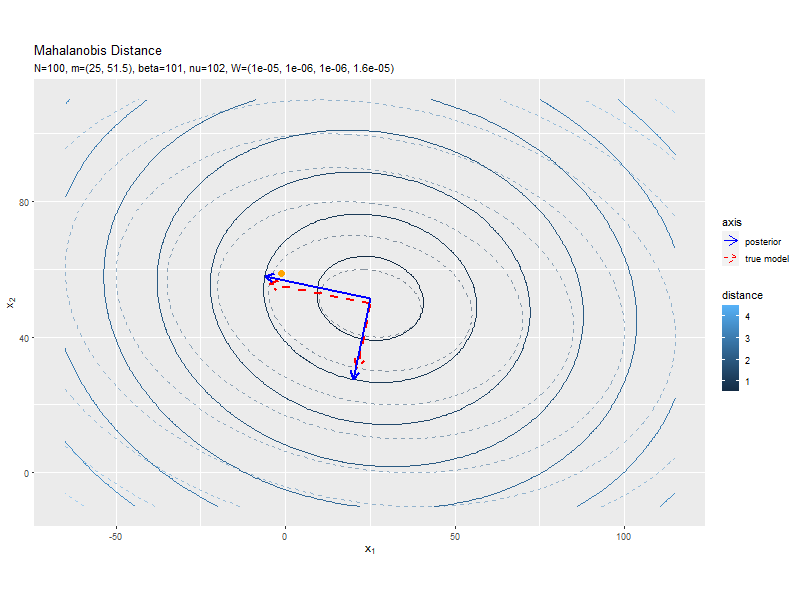
等高線の中心と軸の形が真のパラメータによるものに近付いていくを確認できます。

新たなデータによって平均(分布の中心)と精度(分布の広がり具合)が推移しているのを確認できます。
参考文献
- 須山敦志『ベイズ推論による機械学習入門』(機械学習スタートアップシリーズ)杉山将監修,講談社,2017年.
おわりに
データに従って変形する予測分布を見てると落ち着く。ところで、事後分布のアニメーションが何か少し変な気が、予測分布はアニメーションの方だとうまくいってるけどメインの方が何か変な気がする(データ数が前2つよりも多めに必要なんだと思う)。
- 2021/04/12:加筆修正しました。その際に数式読解編と記事を分割しました。
- 2022/09/23:加筆修正しました。
分かりやすくなったはずなんだけどなぁ、作図用のコードが増えすぎて本筋の内容が埋もれてしまった感があります。頑張って読んでください。
これで一区切り、カテゴリ分布を飛ばしたけど。
【次の節の内容】