はじめに
『パターン認識と機械学習』の独学時のまとめです。一連の記事は「数式の行間埋め」または「R・Pythonでのスクラッチ実装」からアルゴリズムの理解を補助することを目的としています。本とあわせて読んでください。
この記事は、3.1.1項「最尤推定と最小二乗法」の内容です。線形基底関数モデルの最尤推定をR言語で実装します。
【数理読解編】
【前節の内容】
【他の節一覧】
【この節の内容】
・Rで実装
線形基底関数モデルの最尤推定を実装します。
利用するパッケージを読み込みます。
# 3.1.1項で利用するパッケージ library(tidyverse)
・モデルの設定
まずは、データを生成する関数を設定します。
データ生成関数(推定対象の関数)を指定します。
# 真の関数を作成 y_true <- function(x) { # 計算式を指定 y <- sin(2 * pi * x) return(y) }
この例では、$y = \sin(2 \pi x)$とします。
作図用にx軸の点を作成します。
# データの範囲を指定 x_min <- 0 x_max <- 1 # 作図用のxの値を作成 x_vec <- seq(x_min, x_max, 0.01)
グラフとして表示するx軸の範囲を最小値x_min・最大値x_maxに指定して、x軸の点を作成します。
x_min, x_maxはデータの生成時にも使用します。
真のパラメータを指定します。
# 真の精度パラメータを指定 beta_true <- 3 # 真の標準偏差を計算 sigma_true <- sqrt(1 / beta_true) sigma_true
## [1] 0.5773503
真のガウスノイズ$\epsilon \sim \mathcal{N}(\epsilon | 0, \beta^{-1})$の精度(分散の逆数)$\beta$をbeta_trueとして指定します。
また、標準偏差$\sigma = \sqrt{\frac{1}{\beta}}$を計算して、sigma_trueとします。(標準偏差を直接指定しても問題ありません。)
真の関数の出力を計算します。
# 真のモデルを計算 model_df <- tidyr::tibble( x = x_vec, # x軸の値 y = y_true(x), # y軸の値 minus_sigma = y - 2 * sigma_true, # μ - 2σ plus_sigma = y + 2 * sigma_true # μ + 2σ ) # 確認 head(model_df)
## # A tibble: 6 x 4 ## x y minus_sigma plus_sigma ## <dbl> <dbl> <dbl> <dbl> ## 1 0 0 -1.15 1.15 ## 2 0.01 0.0628 -1.09 1.22 ## 3 0.02 0.125 -1.03 1.28 ## 4 0.03 0.187 -0.967 1.34 ## 5 0.04 0.249 -0.906 1.40 ## 6 0.05 0.309 -0.846 1.46
作図用に計算結果をデータフレームに格納します。
また、ノイズの範囲の目安として、期待値$y$から標準偏差の2倍の範囲を計算します。
真の関数を作図します。
# 真のモデルを作図 ggplot() + geom_line(data = model_df, aes(x = x, y = y), color = "cyan4") + # 真のモデル geom_ribbon(data = model_df, aes(x = x, ymin = minus_sigma, ymax = plus_sigma), fill = "cyan4", alpha = 0.1, color = "cyan4", linetype = "dotted") + # 真のノイズ範囲 labs(title = expression(t == sin(2 * pi * x)), subtitle = paste0("beta=", beta_true), x = "x", y = "t")
geom_line()で折れ線グラフを描画します。
また、geom_ribbon()で$2 \sigma$の範囲を描画します。
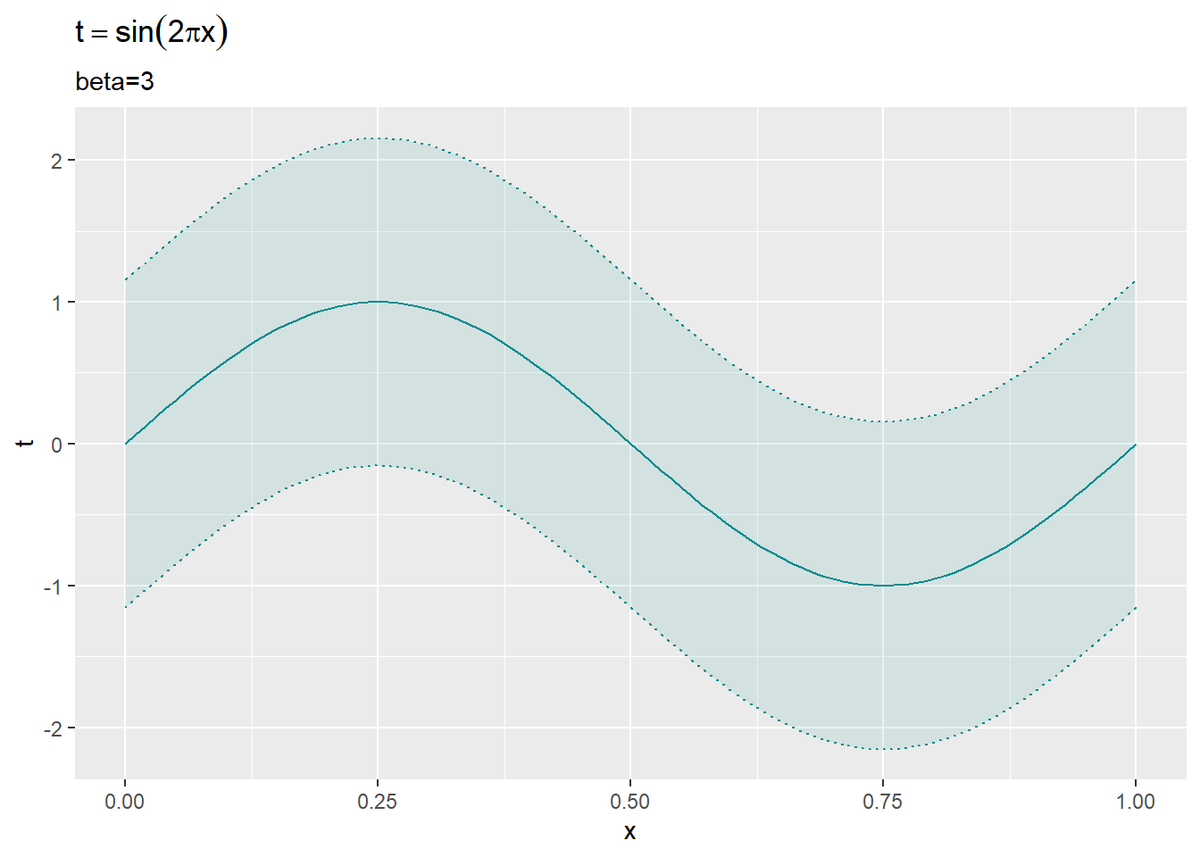
この曲線を推定(近似)するのが目標です。
・基底関数の設定
次に、3種類の基底関数(多項式基底関数・ガウス基底関数・シグモイド基底関数)を作成します。基底関数については「【R】3.1.0:基底関数の作図【PRMLのノート】 - からっぽのしょこ」を参照してください。
多項式基底関数を作成します。
# 多項式基底関数を作成 phi_poly <- function(x, m) { # m乗を計算 y <- x^m return(y) }
多項式$\sum_{m=0}^{M-1} w_m \phi_m(x)$について、$m$番目の基底関数を次の式とします。
多項式基底関数の計算を行う計画行列を作成します。
# 計画行列を作成 Phi_poly <- function(x_n, M) { # 変数を初期化 x_nm <- matrix(0, nrow = length(x_n), ncol = M) # m列目を計算 for(m in 0:(M-1)) { x_nm[, m+1] <- phi_poly(x_n, m) } return(x_nm) }
計画行列$\boldsymbol{\Phi}$は、$\boldsymbol{\Phi}_{m,n} = \phi_m(x_n)$である行列です。
計画行列は、$N$次元ベクトルの入力変数$\mathbf{x}$を、非線形関数(基底関数)により値を変換し、また$N \times M$の行列に変換します。
同様に、ガウス基底関数とその計画行列を作成します。
# ガウス基底関数を作成 phi_gauss <- function(x, mu = 0, s = 0.2) { # ガウス関数の計算 y <- exp(-(x - mu)^2 / (2 * s^2)) return(y) } # 計画行列を作成 Phi_gauss <- function(x_n, M) { # M-1個のパラメータを指定 mu_m <- seq(0, 1, length.out = M-1) s <- 0.1 # 変数を初期化 x_nm <- matrix(1, nrow = length(x_n), ncol = M) # (1行目を除く)m列目を計算 for(m in 1:(M-1)) { x_nm[, m+1] <- phi_gauss(x_n, mu = mu_m[m], s = s) } return(x_nm) }
ガウス基底関数は、次の式で定義されます。
ただし、$\phi_0(x) = 1$です。そのため、x_nmの初期値を1として2列目以降を計算します。
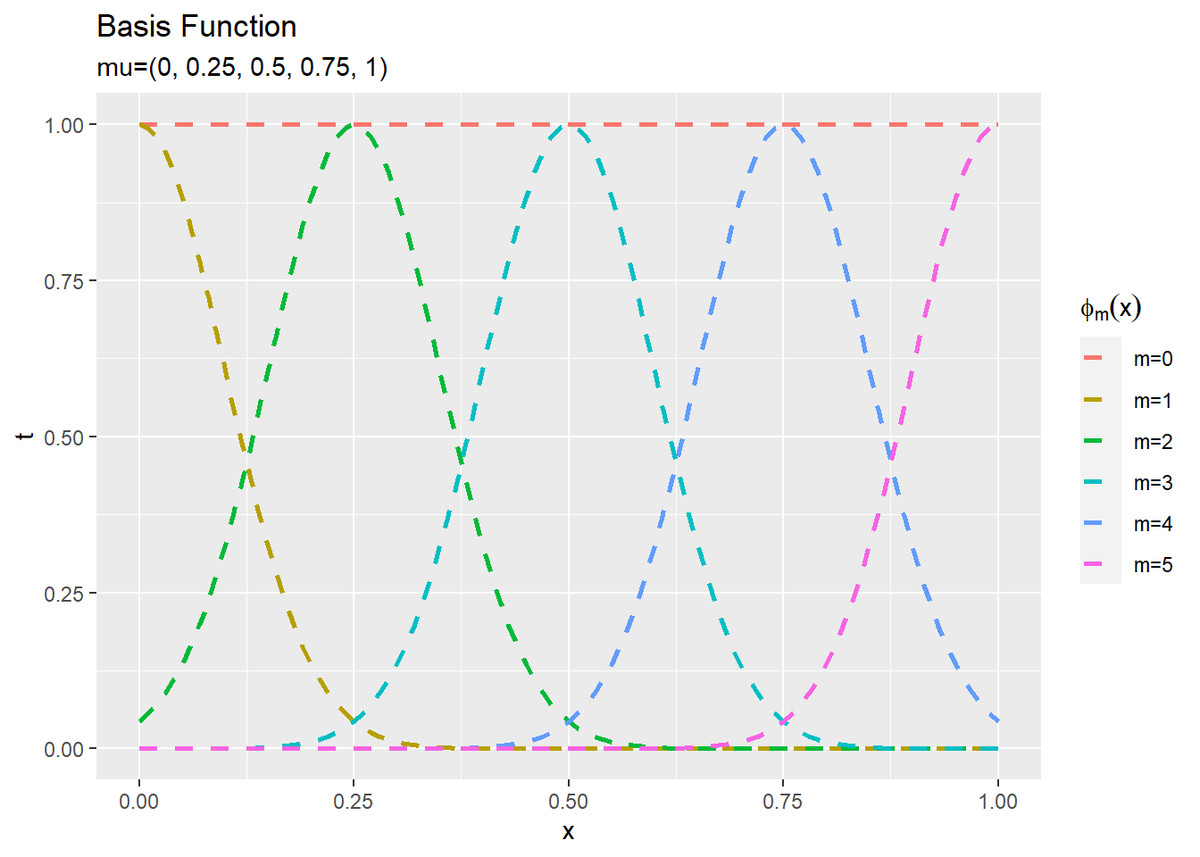
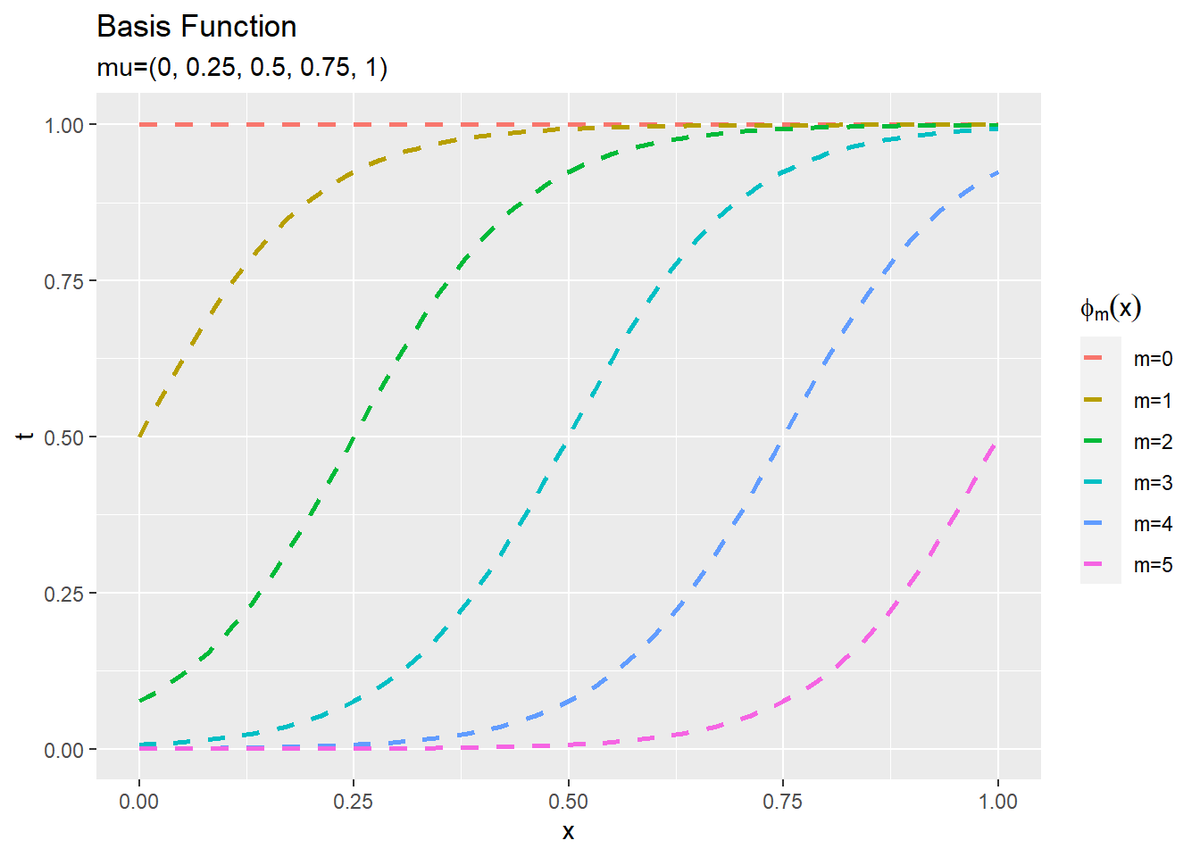
この例では、$M - 1$個のパラメータ$\boldsymbol{\mu} = (\mu_1, \mu_2, \cdots, \mu_{M-1})$をx_min, x_maxと同じ範囲で等間隔に刻んだ値を指定します。また、全ての基底関数で$s = 0.1$とします。(適切な設定の仕方は知らない。)
シグモイド基底関数とその計画行列を作成します。
# シグモイド基底関数を作成 phi_sigmoid <- function(x, mu = 0, s = 0.1) { # 入力を標準化 a <- (x - mu) / s # ロジスティックシグモイド関数の計算 y <- 1 / (1 + exp(-a)) return(y) } # 計画行列を作成 Phi_sigmoid <- function(x_n, M) { # M-1個のパラメータを指定 mu_m <- seq(0, 1, length.out = M-1) s <- 0.1 # 変数を初期化 x_nm <- matrix(1, nrow = length(x_n), ncol = M) # (1行目を除く)m列目を計算 for(m in 1:(M-1)) { x_nm[, m+1] <- phi_sigmoid(x_n, mu = mu_m[m], s = s) } return(x_nm) }
シグモイド基底関数は、次の式で定義されます。
こちらも、$\phi_0(x) = 1$です。
また、パラメータ$\boldsymbol{\mu}$も同様に設定します。
ロジスティックシグモイド関数$\sigma(a)$によって、出力は$0 \leq \phi_m(x) \leq 1$になります。
・データの生成
観測データを人工的に作成します。
観測データを作成します。
# データ数を指定 N <- 100 # (観測)データを生成 x_n <- runif(n = N, min = x_min, max = x_max) # 入力 t_n <- y_true(x_n) + rnorm(n = N, mean = 0, sd = sigma_true) # 出力
最小値x_min・最大値x_maxの一様乱数に従って入力データ$\mathbf{x} = \{x_1, x_2, \cdots, x_N\}$を生成します。
真の関数y_true()の出力に平均0・精度$\beta$のガウス乱数$\epsilon$を加えて、目標値$\mathbf{t} = \{t_1, t_2, \cdots, t_N\}$を作成します。
作図用に観測データをデータフレームに格納します。
# 観測データをデータフレームに格納 data_df <- tidyr::tibble( x_n = x_n, # 入力 t_n = t_n # 出力 ) # 確認 head(data_df)
## # A tibble: 6 x 2 ## x_n t_n ## <dbl> <dbl> ## 1 0.189 0.535 ## 2 0.491 0.451 ## 3 0.402 -0.00414 ## 4 0.0683 0.729 ## 5 0.00980 0.472 ## 6 0.365 0.854
観測データの散布図を作成します。
# 観測データの散布図を作成 ggplot() + geom_point(data = data_df, aes(x = x_n, y = t_n)) + # 観測データ geom_line(data = model_df, aes(x = x, y = y), color = "cyan4") + # 真のモデル geom_ribbon(data = model_df, aes(x = x, ymin = minus_sigma, ymax = plus_sigma), fill = "cyan4", alpha = 0.1, color = "cyan4", linetype = "dotted") + # 真のノイズ範囲 labs(title = expression(t[n] == sin(2 * pi * x[n]) + epsilon[n]), subtitle = paste0("N=", N, ", beta=", beta_true), x = "x", y = "t")
geom_point()で散布図を描画します。
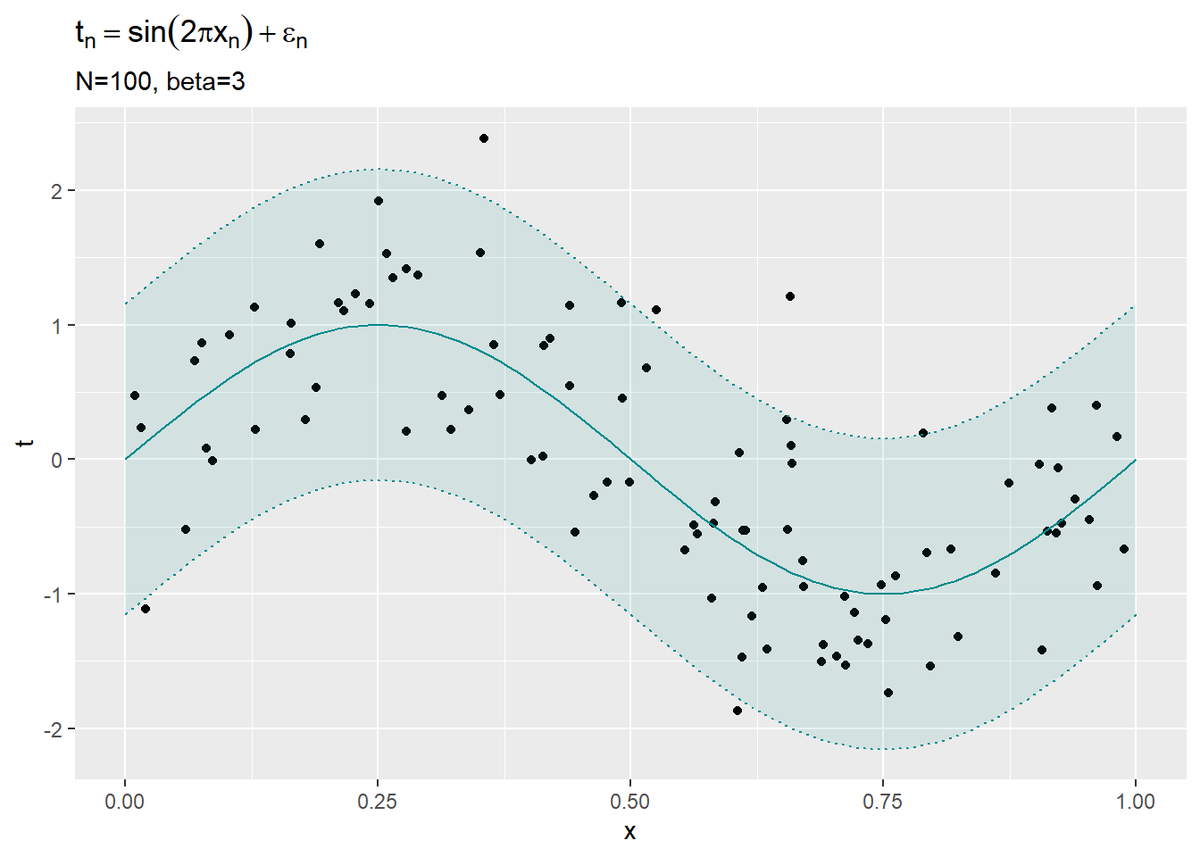
x軸の各点において、y軸方向に平均$\sin(2 \pi x)$・精度$\beta$のガウス分布$\mathcal{N}(t | \sin(2 \pi x), \beta^{-1})$になっています。
各データが概ね$2 \sigma$の範囲に収まっているのを確認できます。
・最尤推定
3つの基底関数を用いて、線形基底関数モデルの最尤推定を行います。
・多項式基底関数の場合
多項式基底関数を用いて推定します。
利用する基底関数を設定します。
# 基底関数を設定 Phi <- Phi_poly
関数Phi()として、Phi_poly()を複製します。
パラメータの最尤推定量を計算します。
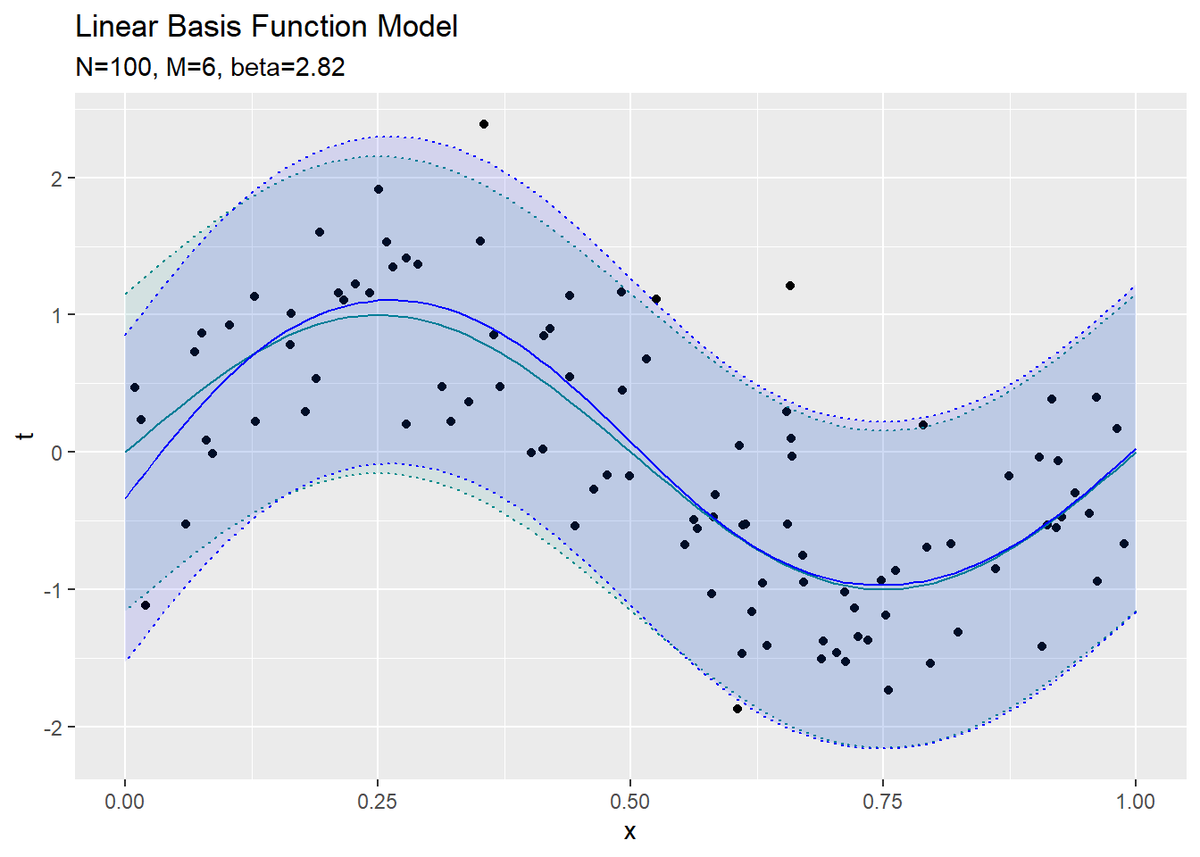
# 重みパラメータの次元数(基底関数の数)を指定 M <- 6 # 基底関数により入力を変換 phi_x_nm <- Phi(x_n, M) # 重みパラメータの最尤推定量を計算 w_hat_m <- solve(t(phi_x_nm) %*% phi_x_nm) %*% t(phi_x_nm) %*% t_n %>% as.vector() # 分散パラメータの最尤推定量を計算 sigma2_hat <- sum((t_n - t(w_hat_m) %*% t(phi_x_nm))^2) / N # 精度パラメータの最尤推定量を計算 beta_hat <- 1 / sigma2_hat # 確認 w_hat_m beta_hat
## [1] -0.2056304 5.4922731 27.3589219 -160.3611065 216.1241900 ## [6] -88.5846208 ## [1] 2.844453
尤度関数を最大化する重みパラメータ$\mathbf{w}_{\mathrm{ML}}$と分散パラメータ$\frac{1}{\beta_{\mathrm{ML}}}$を次の式で計算します。
ただし、$t_n - \mathbf{w}^{\top} \phi(\mathbf{x}_n)$の計算を$N$個同時に行うため、$\mathbf{t} - \mathbf{w}^{\top} \boldsymbol{\Phi}^{\top}$で計算しています。
sigma2_hatの逆数が精度パラメータの最尤推定量$\beta_{\mathrm{ML}}$になります。これは計算する必要はありません。
推定したパラメータを用いて、モデルの出力を計算します。
# 推定したパラメータによるモデルを計算 ml_df <- tidyr::tibble( x = x_vec, # x軸の値 t = t(w_hat_m) %*% t(Phi(x, M)) %>% as.vector(), # y軸の値 minus_sigma = t - 2 * sqrt(sigma2_hat), # μ - 2σ plus_sigma = t + 2 * sqrt(sigma2_hat) # μ + 2σ ) # 確認 head(ml_df)
## # A tibble: 6 x 4 ## x t minus_sigma plus_sigma ## <dbl> <dbl> <dbl> <dbl> ## 1 0 -0.206 -1.39 0.980 ## 2 0.01 -0.148 -1.33 1.04 ## 3 0.02 -0.0861 -1.27 1.10 ## 4 0.03 -0.0204 -1.21 1.17 ## 5 0.04 0.0481 -1.14 1.23 ## 6 0.05 0.119 -1.07 1.30
推定した重みパラメータ$\mathbf{w}_{\mathrm{ML}}$を使って、y軸の値を次の式で計算します。
また、分散パラメータsigma2_hat(精度パラメータ$\beta_{\mathrm{ML}}$)を用いて、推定した精度を求めます。
近似曲線を作図します。
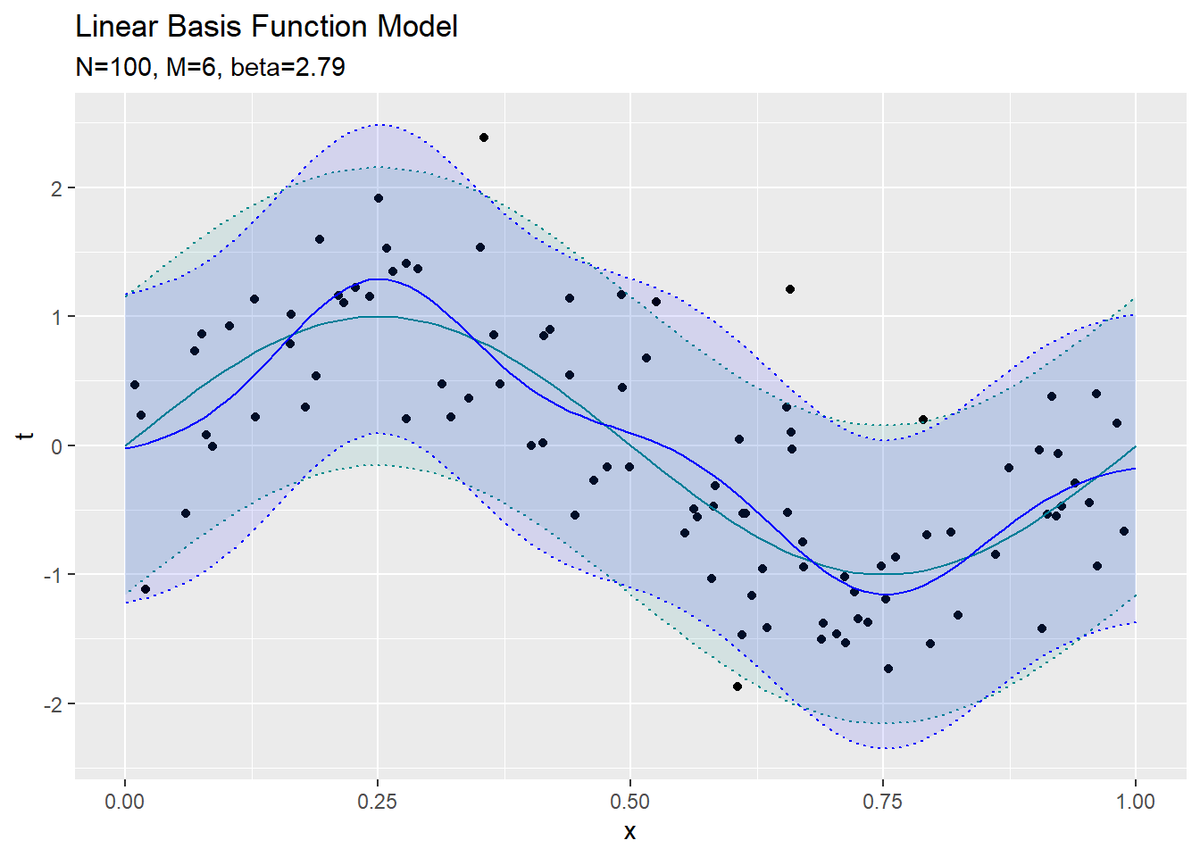
# 推定したパラメータによるモデルを作図 ggplot() + geom_point(data = data_df, aes(x = x_n, y = t_n)) + # 観測データ geom_line(data = model_df, aes(x = x, y = y), color = "cyan4") + # 真のモデル geom_ribbon(data = model_df, aes(x = x, ymin = minus_sigma, ymax = plus_sigma), fill = "cyan4", alpha = 0.1, color = "cyan4", linetype = "dotted") + # 真のノイズ範囲 geom_line(data = ml_df, aes(x = x, y = t), color = "blue") + # 推定したモデル geom_ribbon(data = ml_df, aes(x = x, ymin = minus_sigma, ymax = plus_sigma), fill = "blue", alpha = 0.1, color = "blue", linetype = "dotted") + # 推定したノイズの範囲 #ylim(c(-5, 5)) + labs(title = "Linear Basis Function Model", subtitle = paste0("N=", N, ", M=", M, ", beta=", round(beta_hat, 2)), x = "x", y = "t")
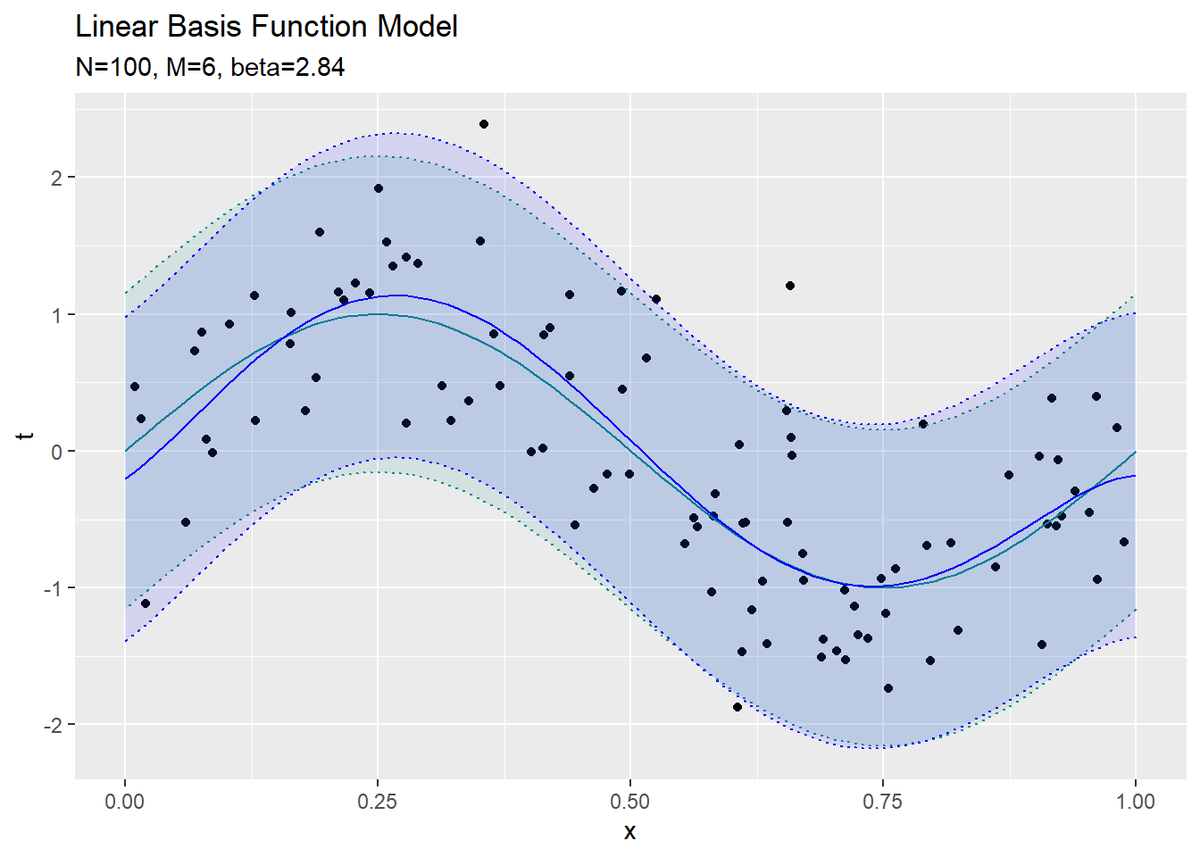
真のモデルを近似できているのが分かります。
最後に、基底関数と重みと近似曲線の関係を確認します。
$M$個の基底関数をそれぞれ計算してデータフレームに格納します。
# M個の基底関数を計算 phi_df <- Phi(x_vec, M) %>% # 基底関数 dplyr::as_tibble(.name_repair = "unique") %>% # データフレームに変換 dplyr::rename_with(.fn = ~paste0("m=", 0:(M-1)), .cols = 1:M) %>% # 列名を付与 cbind(x = x_vec) %>% # x軸の値を結合 tidyr::pivot_longer( cols = -x, names_to = "phi", names_transform = list(phi = as.factor), values_to = "phi_x" ) # long型に変換 # 確認 tail(phi_df)
## # A tibble: 6 x 3 ## x phi phi_x ## <dbl> <fct> <dbl> ## 1 1 m=0 1 ## 2 1 m=1 1 ## 3 1 m=2 1 ## 4 1 m=3 1 ## 5 1 m=4 1 ## 6 1 m=5 1
$M$個の基底関数のグラフを作成します。
# M個の基底関数を作図 ggplot() + geom_line(data = phi_df, aes(x = x, y = phi_x, color = phi), linetype = "dashed", size = 1) + # 基底関数 labs(title = "Basis Function", subtitle = paste0("mu=(", paste0(round(seq(0, 1, length.out = M-1), 2), collapse = ", "), ")"), x = "x", y = "t", color = expression(phi[m](x)))
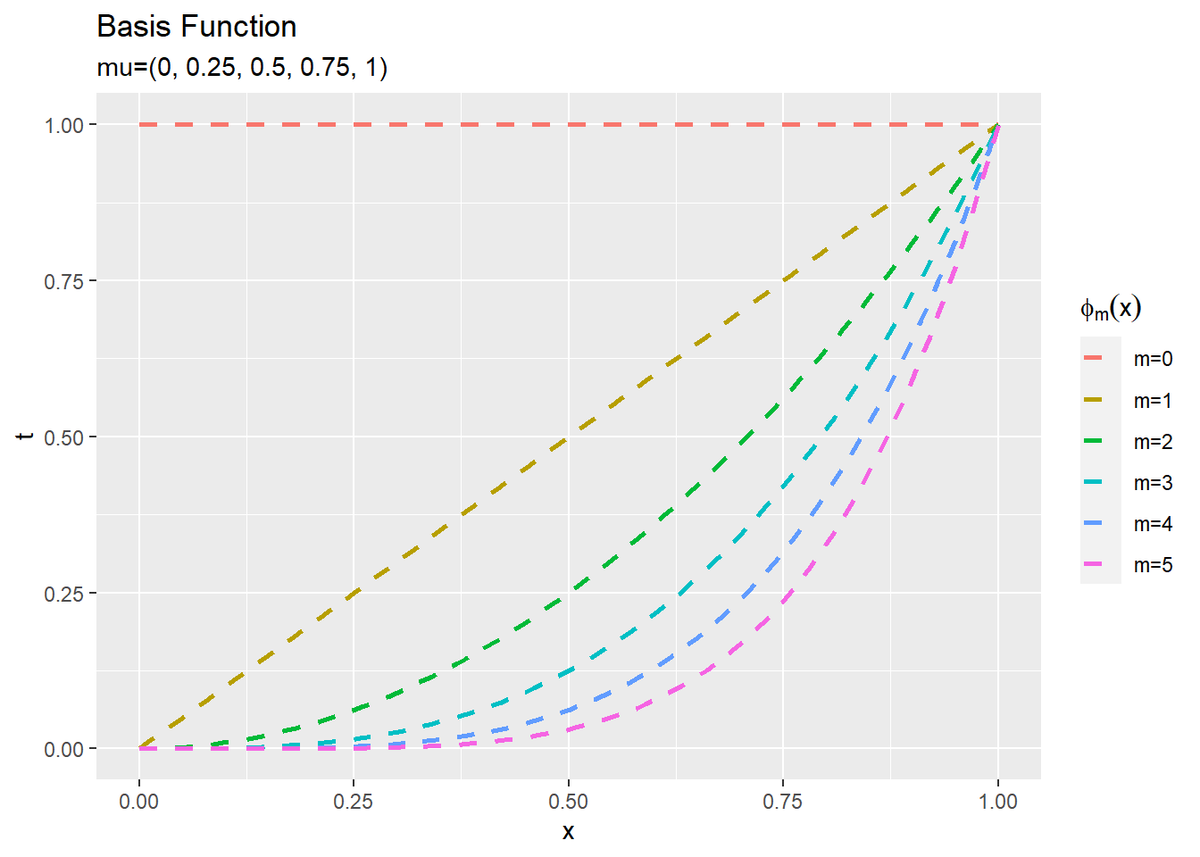
基底関数ごとに対応するパラメータで重み付けします。
# M個の基底関数を重み付け phi_w_df <- t(w_hat_m * t(Phi(x_vec, M))) %>% # 基底関数ごとに重み付け dplyr::as_tibble(.name_repair = "unique") %>% # データフレームに変換 dplyr::rename_with(.fn = ~paste0("m=", 0:(M-1)), .cols = 1:M) %>% # 列名を付与 cbind(x = x_vec) %>% # x軸の値を結合 tidyr::pivot_longer( cols = -x, names_to = "phi", names_transform = list(phi = as.factor), values_to = "phi_x" ) # long型に変換 # 確認 tail(phi_w_df)
## # A tibble: 6 x 3 ## x phi phi_x ## <dbl> <fct> <dbl> ## 1 1 m=0 -0.206 ## 2 1 m=1 5.49 ## 3 1 m=2 27.4 ## 4 1 m=3 -160. ## 5 1 m=4 216. ## 6 1 m=5 -88.6
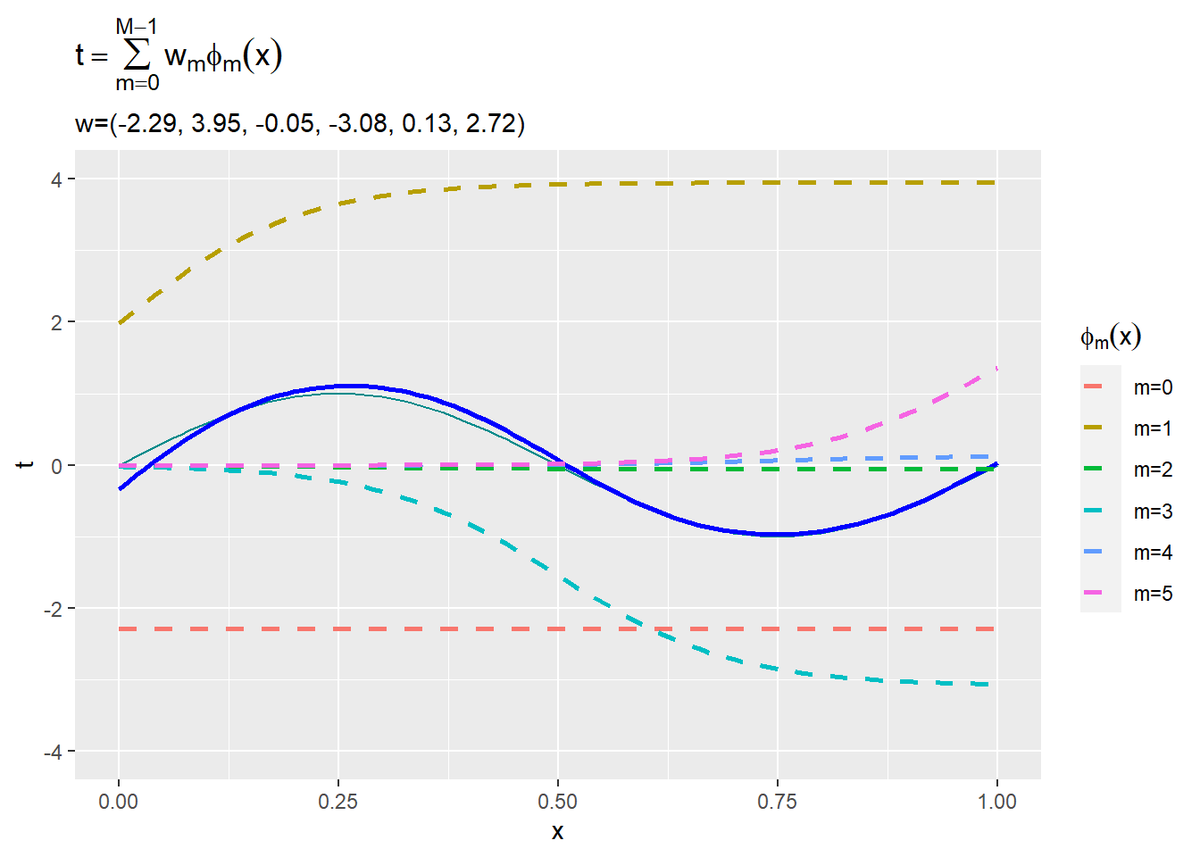
重み付けした$M$個の基底関数と近似曲線のグラフを作成します。
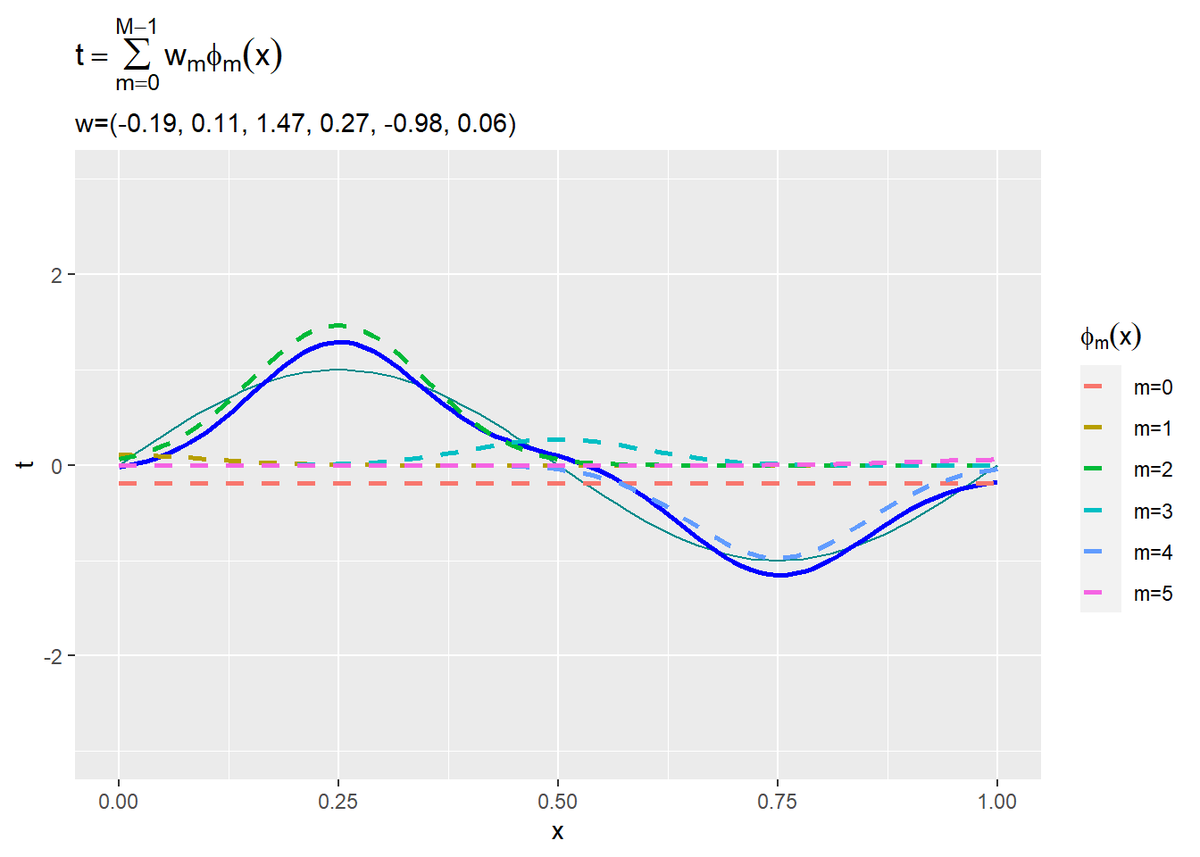
# 重み付けしたM個の基底関数を作図 ggplot() + geom_line(data = model_df, aes(x = x, y = y), color = "cyan4") + # 真のモデル geom_line(data = ml_df, aes(x = x, y = t), color = "blue", size = 1) + # 推定したモデル geom_line(data = phi_w_df, aes(x = x, y = phi_x, color = phi), linetype = "dashed", size = 1) + # 基底関数 ylim(c(-5, 5)) + labs(title = expression(t == sum(w[m] * phi[m](x), m==0, M-1)), subtitle = paste0("w=(", paste0(round(w_hat_m, 2), collapse = ", "), ")"), x = "x", y = "t", color = expression(phi[m](x)))
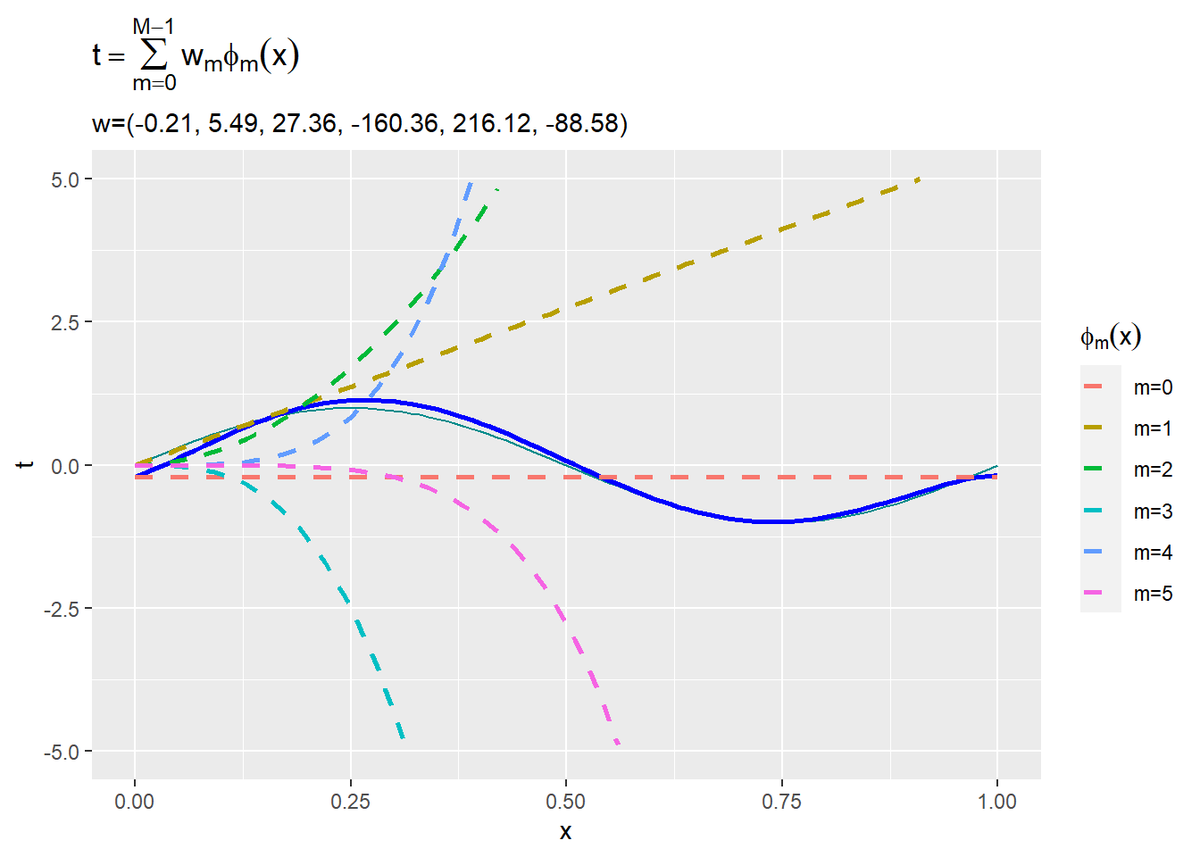
$M$個の基底関数をy軸方向に和をとった値が近似曲線(青色の実線)になります。パラメータの大小によって各基底関数の影響が変わります。また、負の値であればy軸方向に反転します。
1つの水平線$\phi_0(x)$と$M - 1$個のガウス曲線$\phi_m(x)\ (m = 1, \cdots, M-1)$によって、近似曲線(青色の実線)が構成されているのが分かります。
以上が、多項式基底関数を用いた線形基底関数モデルの最尤推定です。
・ガウス基底関数の場合
続いて、ガウス基底関数を用いて行います。
ガウス基底関数の計画行列Phi_gauss()を設定します。
# 基底関数を設定 Phi <- Phi_gauss
先ほどのコードで推定できます。
・シグモイド基底関数の場合
最後に、シグモイド基底関数を用いて行います。
シグモイド基底関数の計画行列Phi_sigmoid()を設定します。
# 基底関数を設定 Phi <- Phi_sigmoid
こちらもそのまま処理できます。
以上で、線形基底関数モデルの最尤推定を実装できました。
参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上下』,丸善出版,2012年.
おわりに
これを組んでみてようやく基底関数が入力にどう影響してるのかを理解できた。
この記事の投稿前日と当日にアップされたMVをぜひ観てください!
【次節の内容】