はじめに
「プログラミング」学習初手『ゼロから作るDeep Learning』民のための実装攻略ノートです。『ゼロつく1』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
関数やクラスとして実装される処理の塊を細かく分解して、1つずつ処理を確認しながらゆっくりと組んでいきます。
この記事は、6.1.2項「SGD」の内容になります。SGD(確率的勾配降下法)をPythonで実装します。またその学習過程を確認します。
【前節の内容】
【他の節の内容】
【この節の内容】
6.1.2 SGD
5章では、誤差逆伝播法による勾配の計算をクラスとして実装しました。この節では、求めた勾配を用いてパラメータを更新する勾配法について注目します。勾配降下法については「4.4.0:勾配【ゼロつく1のノート(数学)】 - からっぽのしょこ」で説明しました。またデータの一部をランダムに取り出して行う勾配降下法を確率的勾配降下法(SGD)と呼ぶのでした。この節ではSGDの発展形ともいえる手法について説明します。
パラメータの更新でこれまで使ってきたSGD(確率的勾配降下法)をクラスとして実装します。
・更新式の確認
重みパラメータを$\mathbf{W}$、損失関数を$L$、$\mathbf{W}$に関する損失関数の勾配$\frac{\partial L}{\partial \mathbf{W}}$をとすると、SGDは次の式でした。
ここで$\eta$は学習率(ステップサイズ)です。また$\leftarrow$は、右辺の計算によって左辺の値を更新することを表します。
式(6.1)について、$\mathbf{W}$の$j,k$要素に注目すると更新式は
となります。表記は異なりますが式(4.7)と同じことです。
勾配降下法では、現在のパラメータから学習率で割り引いた勾配を引くことでパラメータを更新します。これは勾配(傾き)が正の値であれば変数$w_{jk}$が小さくなるほど関数の値が小さくなり、逆に勾配が負の値であれば変数を大きなるほど関数の値が小さくなるためでした。詳しくは4.4.1項を参考にしてください。
・実装
では何度も扱った処理なので、早速クラスとして実装します。
# この項で利用するライブラリを読み込む import numpy as np import matplotlib.pyplot as plt
# 確率的勾配降下法の実装 class SGD: # インスタンス変数を定義 def __init__(self, lr=0.01): self.lr = lr # 学習率 # パラメータの更新メソッドを定義 def update(self, params, grads): # パラメータごとに値を更新 for key in params.keys(): params[key] -= self.lr * grads[key] # 式(6.1)
学習率はインスタンスの作成時に引数lrに指定し、インスタンス変数として値を保持します。
パラメータと勾配はどちらもディクショナリ変数として更新メソッド.update()の使用時に引数に指定します。
・アルゴリズムの確認
SGDにより関数
の最小値となる$x,\ y$を探索します。この関数の勾配(偏微分)は
になります。
まずは関数(6.2)とその勾配をそれぞれ関数として定義しておきます。
# 式(6.2) def f(x, y): return x ** 2 / 20.0 + y ** 2 # 式(6.2)の勾配 def df(x, y): # 偏微分 dx = x / 10.0 # df / dx dy = 2.0 * y # df / dy return dx, dy # (値を2つ出力!)
元の関数は作図に、勾配はもちろんパラメータの更新に利用します。
ちなみにこの関数を等高線図にすると次のようになります。
# 等高線用の値 x = np.arange(-10, 10, 0.01) # x軸の値 y = np.arange(-5, 5, 0.01) # y軸の値 X, Y = np.meshgrid(x, y) # 格子状の点に変換 Z = f(X, Y) # 作図 plt.contour(X, Y, Z) # 等高線 plt.plot(0, 0, '+') # 最小値の点 plt.xlim(-10, 10) # x軸の範囲 plt.ylim(-10, 10) # y軸の範囲 plt.xlabel("x") # x軸ラベル plt.ylabel("y") # y軸ラベル plt.title("$f(x, y) = \\frac{1}{20} x^2 + y^2$", fontsize=20) # タイトル plt.show()

原点がこの関数の最小値になります。また原点付近が横に広くなだらかに(勾配が小さく)なっていることが確認できます。
初期値は点$(-7, 2)$とします。これまでと同様に、パラメータ(変数)params、パラメータごとの勾配gradsのディクショナリ変数を作成して、どちらもパラメータ名をキーとして値を格納します。
学習率を指定して、SGDクラスのインスタンスを作成します。
# パラメータの初期値を指定 params = {} params['x'] = -7.0 params['y'] = 2.0 # 勾配の初期値を指定 grads = {} grads['x'] = 0 grads['y'] = 0 # 学習率を指定 lr = 0.95 # インスタンスを作成 optimizer = SGD(lr=lr)
試行回数を指定して、学習を行います。また、パラメータの更新値を記録するためのリスト型の変数を用意しておきます。値の追加は.append()を使います。
# 試行回数を指定 iter_num = 30 # 更新値の記録用リストを初期化 x_history = [] y_history = [] # 初期値を保存 x_history.append(params['x']) y_history.append(params['y']) # 関数の最小値を探索 for _ in range(iter_num): # 勾配を計算 grads['x'], grads['y'] = df(params['x'], params['y']) # パラメータを更新 optimizer.update(params, grads) # パラメータを記録 x_history.append(params['x']) y_history.append(params['y'])
勾配を計算し、gradsに格納している値をそれぞれ上書きします。そしてSGDクラスの更新メソッド.update()にparamsとgradsを指定して、パラメータを更新します。
更新値の推移を先ほどの等高線グラフに重ねて確認しましょう。
# 作図 plt.plot(x_history, y_history, 'o-') # パラメータの推移 plt.contour(X, Y, Z) # 等高線 plt.plot(0, 0, '+') # 最小値の点 plt.xlim(-10, 10) # x軸の範囲 plt.ylim(-10, 10) # y軸の範囲 plt.xlabel("x") # x軸ラベル plt.ylabel("y") # y軸ラベル plt.title("SGD", fontsize=20) # タイトル plt.text(6, 7.5, "$\\eta=$" + str(lr) + "\niteration:" + str(iter_num)) # メモ plt.show()
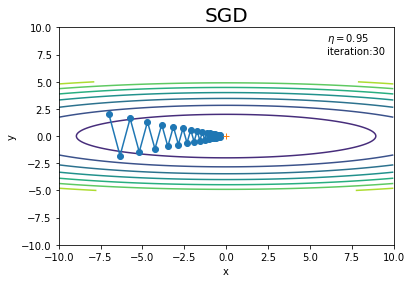
ジグザク(最小値とは異なる向き)に移動しています(図6-3)。このように非効率な経路を辿っているということは、最小値となるパラメータを効率よく探索できているとは言えません。つまり効率的に学習が進んでいないということです。
学習率や試行回数を変更して試してみましょう!
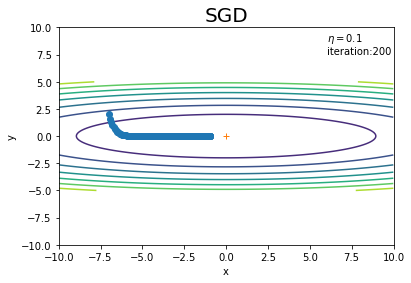
学習率を小さくすると経路はよくなりましたが、その分必要な更新回数が増えました。
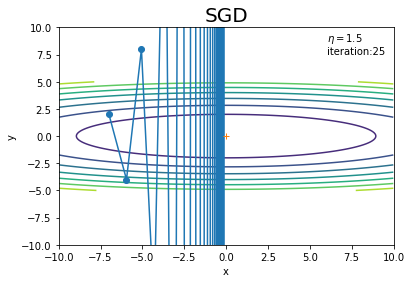
学習率が大きいと発散してしまいます。一応最小値をの上を通っていますが、これでは最小値となるパラメータに収束しません。
アルゴリズムの選択も重要ですが、ハイパーパラメータの値を変更して確認することも必須です。
次からは、SGDの問題点を改善するために考えられた手法を見ていきます。
参考文献
おわりに
確率的勾配降下法の基本形を実装しました!これ自体は何度も使ったものですね。
章を跨ぎましたが途切れず続けます!
【次節の内容】
