はじめに
『ゼロから作るDeep Learning 4 ――強化学習編』の独学時のまとめノートです。初学者の補助となるようにゼロつくシリーズの4巻の内容に解説を加えていきます。本と一緒に読んでください。
この記事は、7.3.1項から7.2.3項の内容です。DeZeroを利用して2層のニューラルネットワークの学習を実装します。
【前節の内容】
【他の記事一覧】
【この記事の内容】
7.3 ニューラルネットワーク
DeZeroライブラリを使って、ニューラルネットワークの学習を実装します。DeZeroフレームワークについては「『ゼロから作るDeep Learning 3』の学習ノート:記事一覧 - からっぽのしょこ」を参照してください。
利用するライブラリを読み込みます。
# ライブラリを読み込み import numpy as np from dezero import Variable import dezero.functions as F # 追加ライブラリ import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation
更新推移をアニメーションで確認するのにmatplotlibのモジュールを利用します。不要であれば省略してください。
7.3.1 非線形なデータセット
まずは、学習に利用するトイ・データセットを作成します。
乱数を使ってデータセットを作成します。
# データ数を指定 N = 100 # トイ・データを生成 x_data = np.random.rand(N) y_data = np.sin(2 * np.pi * x_data) + np.random.rand(N) print(np.round(x_data[:10], 3)) print(np.round(y_data[:10], 3))
[0.154 0.099 0.637 0.81 0.266 0.552 0.097 0.856 0.514 0.909]
[ 1.607 1.17 -0.131 -0.203 1.873 0.604 1.136 -0.312 0.459 0.265]
0から1の一様乱数をnp.random.rand()で生成して、sin関数np.sim()で非線形な変換を行い、データを作成します。
データセットを散布図で確認します。
# トイ・データセットの散布図を作成 plt.figure(figsize=(8, 6), facecolor='white') plt.scatter(x_data, y_data) plt.xlabel('x') plt.ylabel('y') plt.title('N=' + str(N), loc='left') plt.suptitle('$x_n \sim U(0, 1),\ y_n = \sin(2 \pi x_n) + r_n,\ r_n \sim U(0, 1)$', fontsize=15) plt.grid() plt.show()

このデータに合うような曲線を求めます。
7.3.2 線形変換と活性化関数
学習の前に、線形変換と活性化関数を可視化します。
x軸の値を作成します。
# x軸の値を作成 x_line = np.linspace(-5, 5, num=251) print(x_line[:10])
[-5. -4.96 -4.92 -4.88 -4.84 -4.8 -4.76 -4.72 -4.68 -4.64]
恒等関数のグラフを作成します。
# 恒等関数のグラフを作成 plt.figure(figsize=(8, 6), facecolor='white') plt.plot(x_line, x_line, label='identity') plt.xlabel('x') plt.ylabel('f(x)') plt.suptitle('Identity Function', fontsize=20) plt.title('$f(x) = x$', loc='left') plt.legend() plt.grid() plt.show()

x軸の値をそのままy軸の値にします。
パラメータ$W, b$を指定して、線形変換を行います。
# 重みとバイアスを指定 W = np.array([[-6.0]]) b = np.array([10.0]) # 線形変換を計算 y_linear = F.linear(x_line.reshape((-1, 1)), W, b).data.flatten() print(np.round(y_linear[:10], 3))
[40. 39.76 39.52 39.28 39.04 38.8 38.56 38.32 38.08 37.84]
線形変換したグラフを作成します。
# パラメータラベルを作成 param_label = 'f(x) = x W + b' param_label += ', W='+str(W.item()) + ', b='+str(b.item()) # 線形変換のグラフを作成 plt.figure(figsize=(8, 6), facecolor='white') plt.plot(x_line, y_linear, label='linear') plt.xlabel('x') plt.ylabel('f(x)') plt.suptitle('Linear Transformation', fontsize=20) plt.title('$'+param_label+'$', loc='left') plt.legend() plt.grid() plt.show()

縦軸の値を見ると、恒等関数のグラフの傾きを変えて並行移動したグラフなのを確認できます。
シグモイド関数・ReLU関数・tanh関数を計算します。
# 活性化関数を計算 y_sigmoid = F.sigmoid(x_line).data y_relu = F.relu(x_line).data y_tanh = F.tanh(x_line).data print(np.round(y_sigmoid[:10], 3)) print(y_relu[:10]) print(np.round(y_tanh[:10], 3))
[0.007 0.007 0.007 0.008 0.008 0.008 0.008 0.009 0.009 0.01 ]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[-1. -1. -1. -1. -1. -1. -1. -1. -1. -1.]
シグモイド関数・ReLU関数・tanh関数のグラフを作成します。
# 活性化関数のグラフを作成 plt.figure(figsize=(8, 6), facecolor='white') plt.plot(x_line, y_sigmoid, label='sigmoid') plt.plot(x_line, y_relu, label='relu') plt.plot(x_line, y_tanh, label='tanh') plt.xlabel('x') plt.ylabel('f(x)') plt.suptitle('Activation Function', fontsize=20) plt.legend() plt.grid() plt.ylim(-1.1, 1.6) plt.show()
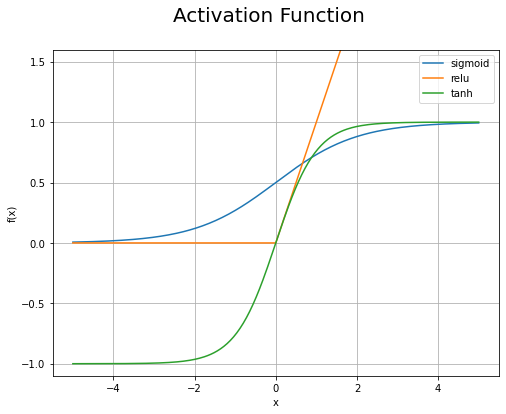
非線形なグラフに変換されたのを確認できます。
7.3.3 ニューラルネットワークの実装
次は、勾配降下法によるニューラルネットワークの学習を実装します。2乗和誤差の順伝播については「4.2.1:2乗和誤差の実装【ゼロつく1のノート(実装)】 - からっぽのしょこ」、逆伝播については「ステップ42:平均2乗誤差の逆伝播の導出【ゼロつく3のノート(数学)】 - からっぽのしょこ」を参照してください。
2層のニューラルネットワークを関数として定義します。
# 2層のニューラルネットワークを作成 def predict(x, W1, b1, W2, b2): # 入力層の計算 y = F.linear(x, W1, b1) y = F.sigmoid(y) # 出力層の計算 y = F.linear(y, W2, b2) return y
(推移の確認用にパラメータを引数に受け取れるように変更しています。)
勾配降下法により損失関数(平均2乗誤差)が最小となるパラメータを求めます。
# 試行回数を指定 iters = 10000 # 学習率を指定 lr = 0.2 # 入力層・中間層・出力層のサイズを指定 I = 1 H = 10 O = 1 # トイ・データセットをVariableインスタンス化 x = Variable(x_data.reshape((N, 1))) y = Variable(y_data.reshape((N, 1))) # パラメータを初期化 W1 = Variable(0.01 * np.random.randn(I, H)) b1 = Variable(np.zeros(H)) W2 = Variable(0.01 * np.random.randn(H, O)) b2 = Variable(np.zeros(O)) # 推移の確認用のリストを初期化 trace_loss = [] trace_W1 = [W1.data[0].copy()] trace_b1 = [b1.data.copy()] trace_W2 = [W2.data[:, 0].copy()] trace_b2 = [b2.data.copy()] # 繰り返し学習 for i in range(iters): # 予測値(ニューラルネットワーク)を計算 y_pred = predict(x, W1, b1, W2, b2) # 損失を計算 loss = F.mean_squared_error(y, y_pred) # 勾配を初期化 W1.cleargrad() b1.cleargrad() W2.cleargrad() b2.cleargrad() # 勾配(逆伝播)を計算 loss.backward() # 勾配降下法により値を更新 W1.data -= lr * W1.grad.data b1.data -= lr * b1.grad.data W2.data -= lr * W2.grad.data b2.data -= lr * b2.grad.data # 更新値を保存 trace_loss.append(loss.data) trace_W1.append(W1.data[0].copy()) trace_b1.append(b1.data.copy()) trace_W2.append(W2.data[:, 0].copy()) trace_b2.append(b2.data.copy()) # 一定回数ごとに損失を表示 if (i+1) % 500 == 0: print('iter '+str(i+1) + ': loss='+str(loss.data))
iter 500: loss=0.30211289065520647
iter 1000: loss=0.30073685826954427
iter 1500: loss=0.2992192046855335
iter 2000: loss=0.2971914354822332
iter 2500: loss=0.2941692064271711
iter 3000: loss=0.28935923935116054
iter 3500: loss=0.28126872262591945
iter 4000: loss=0.26658176067891737
iter 4500: loss=0.2397161151662756
iter 5000: loss=0.19536020385747033
iter 5500: loss=0.13291263069552484
iter 6000: loss=0.0889304082395797
iter 6500: loss=0.07558437518097162
iter 7000: loss=0.07264561120281264
iter 7500: loss=0.07171635866267119
iter 8000: loss=0.07124027465304014
iter 8500: loss=0.07093348130993946
iter 9000: loss=0.0707139882921757
iter 9500: loss=0.07054616926238644
iter 10000: loss=0.07041141080786444
処理の内容については本を参照してください。
学習したパラメータを使って、データごとの予測値と平均2乗誤差を計算します。
# 予測値を計算 y_pred = predict(x, W1, b1, W2, b2) print(np.round(y_pred.data[:10].flatten(), 3)) # 損失を計算 last_loss = F.mean_squared_error(y, y_pred).data print(last_loss)
[ 1.275 1.065 -0.306 -0.34 1.557 0.199 1.06 -0.213 0.505 -0.037]
0.0704111664483751
最終的なパラメータW1, b1, W2, b2における損失は、trace_lossに含まれていないので、計算してlast_lossとします。
損失関数の推移をグラフで確認します。
# 損失関数の推移を作図 plt.figure(figsize=(8, 6), facecolor='white') plt.plot(np.arange(iters+1), trace_loss+[last_loss]) plt.xlabel('iteration') plt.ylabel('loss') plt.suptitle('Mean Squared Error', fontsize=20) plt.title('lr='+str(lr), loc='left') plt.grid() plt.show()

最後の値last_lossをリストに格納して、過去の値trace_lossと+演算子で結合して描画します。
損失が0に近付いていくことから学習が進んでいるのが分かります。
回帰曲線を計算します。
# 回帰曲線を計算 x_line = np.linspace(0, 1, num=101) y_line = predict(x_line.reshape((-1, 1)), W1, b1, W2, b2).data.flatten() print(np.round(x_line[:10], 3)) print(np.round(y_line[:10], 3))
[0. 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09]
[0.646 0.69 0.733 0.776 0.82 0.862 0.905 0.947 0.989 1.03 ]
x軸の値x_lineを作成して、要素ごとに予測値を計算します。内積を計算できるように形状を合わせる必要があります。
トイ・データセットの散布図に、回帰曲線を重ねて描画します。
# 残差を計算 y_residual = y_pred.data.flatten() - y_data # パラメータラベルを作成 param_label = 'iter:' + str(iters) param_label += ', lr=' + str(lr) param_label += ', loss='+str(np.round(last_loss, 3)) # 回帰曲線を計算 plt.figure(figsize=(12, 9), facecolor='white') plt.quiver(x_data, y_data, np.repeat(0, N), y_residual, scale_units='xy', scale=1, units='dots', width=0.1, headwidth=0.1, fc='none', ec='gray', linewidth=1.5, linestyle=':', label='residual') # 残差 plt.scatter(x_data, y_data, label='data') # データ plt.plot(x_line, y_line, color='red', label='predict') # 回帰曲線 plt.xlabel('x') plt.ylabel('y') plt.suptitle('Neural Network', fontsize=20) plt.title(param_label, loc='left') plt.grid() plt.legend() plt.show()

データごとに観測値と予測値の差を計算して、plt.quiver()で線分を描画します。
回帰曲線の推移をアニメーションで確認します。
・作図コード(クリックで展開)
# フレーム数を指定 frame_num = 100 # 1フレーム当たりの試行回数を設定 iter_per_frame = iters // frame_num # 図を初期化 fig = plt.figure(figsize=(12, 9), facecolor='white') fig.suptitle('Neural Network', fontsize=20) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i回目のパラメータを取得 W1 = trace_W1[i*iter_per_frame].reshape((I, H)) b1 = trace_b1[i*iter_per_frame] W2 = trace_W2[i*iter_per_frame].reshape((H, O)) b2 = trace_b2[i*iter_per_frame] # 予測値を計算 y_pred = predict(x, W1, b1, W2, b2) # 残差を計算 y_residual = y_pred.data.flatten() - y_data # 回帰曲線を計算 y_line = predict(x_line.reshape((-1, 1)), W1, b1, W2, b2).data.flatten() # パラメータラベルを作成 param_label = 'iter:' + str(i*iter_per_frame) param_label += ', lr=' + str(lr) if i*iter_per_frame < iters: param_label += ', loss='+str(np.round(trace_loss[i*iter_per_frame], 5)) else: param_label += ', loss='+str(np.round(last_loss, 5)) # 回帰曲線を描画 plt.quiver(x_data, y_data, np.repeat(0, N), y_residual, scale_units='xy', scale=1, units='dots', width=0.1, headwidth=0.1, fc='none', ec='gray', linewidth=1.5, linestyle=':', label='residual') # 残差 plt.scatter(x_data, y_data, label='data') # データ plt.plot(x_line, y_line, color='red', label='predict') # 回曲直線 plt.xlabel('x') plt.ylabel('y') plt.title(param_label, loc='left') plt.grid() plt.legend() # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # gif画像を保存 ani.save('TwoLayerNet.gif')
フレームごとにtrace_*からi番目の値を取り出して回帰曲線を描画する処理を関数update()として定義して、FuncAnimation()でアニメーション(gif画像)を作成します。
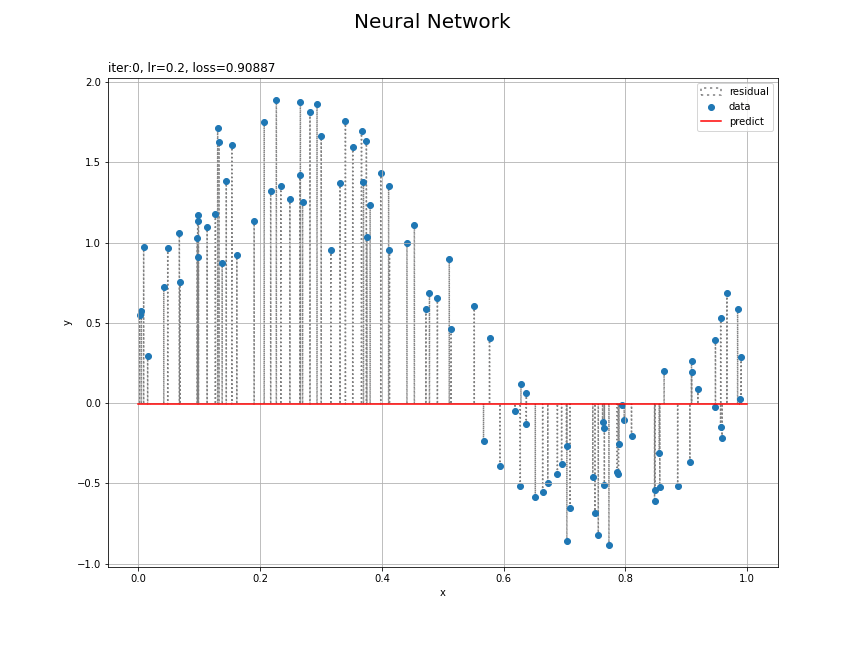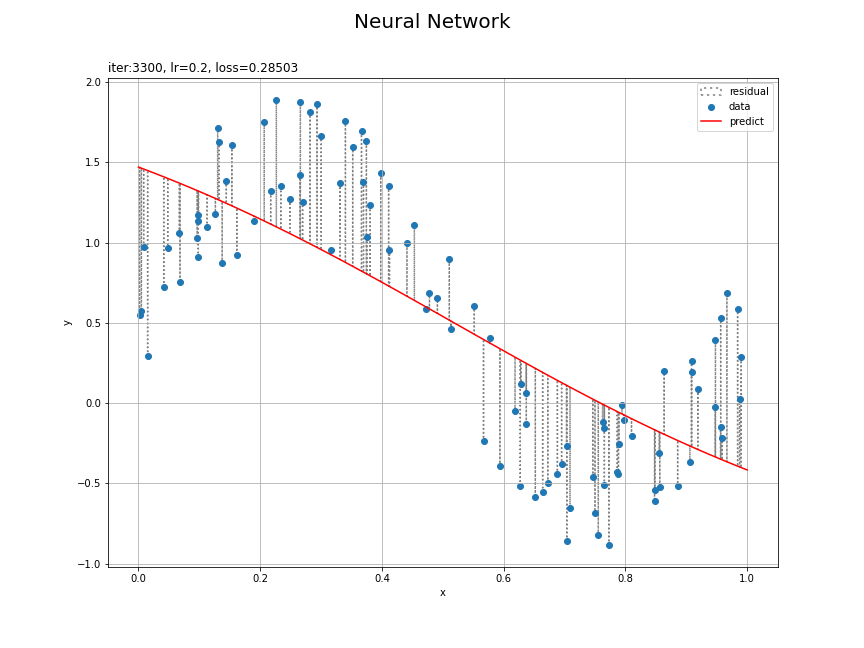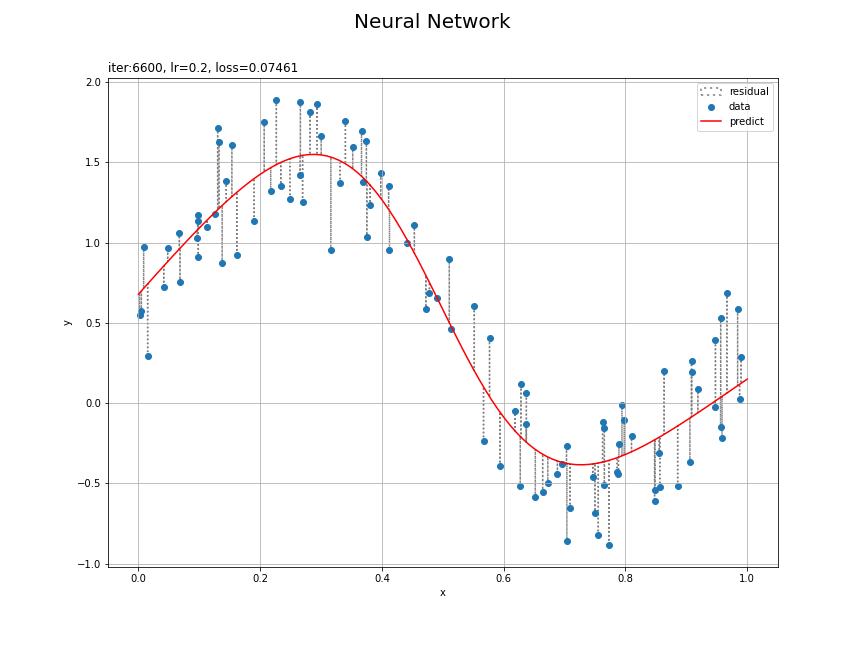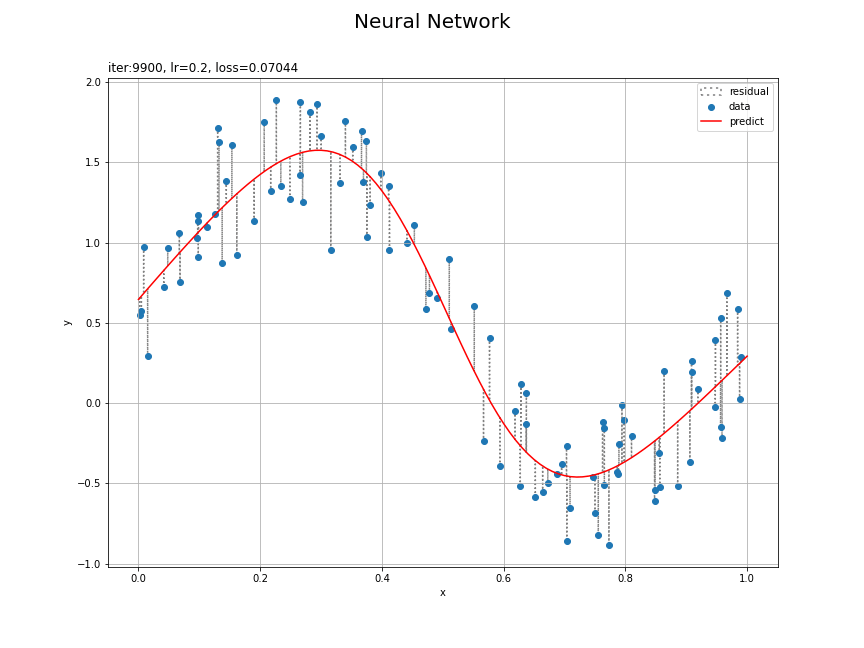
データへの当てはまりがよくなる様子を確認できます。
各パラメータの更新値の推移をグラフで確認します。
・作図コード(クリックで展開)
# 入力層の重みパラメータの更新値の推移を作図 plt.figure(figsize=(8, 6), facecolor='white') for h in range(H): w_vals = np.array(trace_W1)[:, h] plt.plot(np.arange(iters+1), w_vals, label='$w_'+str(h)+'$') plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('input layer parameters', fontsize=20) plt.title('lr='+str(lr), loc='left') plt.grid() plt.legend() plt.show()
# 入力層のバイアスパラメータの更新値の推移を作図 plt.figure(figsize=(8, 6), facecolor='white') for h in range(H): b_vals = np.array(trace_b1)[:, h] plt.plot(np.arange(iters+1), b_vals, label='$b_'+str(h)+'$') plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('input layer parameters', fontsize=20) plt.title('lr='+str(lr), loc='left') plt.grid() plt.legend() plt.show()
# 出力層の重みパラメータの更新値の推移を作図 plt.figure(figsize=(8, 6), facecolor='white') for h in range(H): w_vals = np.array(trace_W2)[:, h] plt.plot(np.arange(iters+1), w_vals, label='$w_'+str(h)+'$') plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('output layer parameters', fontsize=20) plt.title('lr='+str(lr), loc='left') plt.grid() plt.legend() plt.show()
# 出力層のバイアスパラメータの更新値の推移を作図 plt.figure(figsize=(8, 6), facecolor='white') plt.plot(np.arange(iters+1), np.array(trace_b2).flatten(), label='$b_0$') plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('output layer parameters', fontsize=20) plt.title('lr='+str(lr), loc='left') plt.grid() plt.legend() plt.show()




この項では、DeZeroの基本的なクラスを使って2層のニューラルネットワークを実装しました。次項では、最適化手法を比較します。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning 4 ――強化学習編』オライリー・ジャパン,2022年.
- サポートページ:GitHub - oreilly-japan/deep-learning-from-scratch-4
おわりに
ほぼ同じ内容を書いたことがある気がしますがまぁ②、、
【次節の内容】