はじめに

　R言語を使って、円関数の定義や公式を可視化して理解しようシリーズです。

　この記事では、アルキメデスの渦巻きのグラフを作成します。

【前の内容】

www.anarchive-beta.com

【他の記事一覧】

www.anarchive-beta.com

【この記事の内容】

はじめに
アルキメデスの螺旋の可視化
参考書籍
おわりに

アルキメデスの螺旋の可視化

　sin関数(サイン関数・sine function)とcos関数(コサイン関数・cosine function)を用いて定義されるアルキメデスの螺旋(アルキメデスの渦巻き・Archimedes' spiral)をグラフで確認します。

　利用するパッケージを読み込みます。

# 利用パッケージ
library(tidyverse)
library(gganimate)

　この記事では、基本的に パッケージ名::関数名() の記法を使うので、パッケージの読み込みは不要です。ただし、作図コードについてはパッケージ名を省略するので、 ggplot2 を読み込む必要があります。
　また、ネイティブパイプ演算子 |> を使います。magrittr パッケージのパイプ演算子 %>% に置き換えられますが、その場合は magrittr を読み込む必要があります。

定義式の確認

　まずは、アルキメデスの螺旋の定義を数式で確認します。
　sin関数については「【R】sin関数の可視化 - からっぽのしょこ」、cos関数については「【R】cos関数の可視化 - からっぽのしょこ」、度数法と弧度法の角度については「【R】円周の作図 - からっぽのしょこ」を参照してください。

　アルキメデスの螺旋は、sin関数とcos関数を用いて、次の式で定義されます。

$\displaystyle \begin{align} &\quad r = a \theta \\ &\left\{ \begin{aligned} x &= r \cos \theta \\ y &= r \sin \theta \end{aligned} \right. \end{align}$

　変数 $\theta$ は弧度法における角度(ラジアン)です。度数法における角度を $\theta^{\circ}$ とすると、 $\theta = \frac{2 \pi}{360^{\circ}} \theta^{\circ}$ の関係です。 $\pi$ は円周率です。
　螺旋の形状は定数(パラメータ) $a$ によって決まります。実数 $a$ は螺旋の間隔や全体のサイズに影響します。
　 $r$ は中心からの距離で、 $\theta$ に応じて変化します。

アルキメデスの螺旋の作図

　次は、アルキメデスの螺旋のグラフを作成して、変数(ラジアン)と座標(曲線上の点)の関係を確認します。

螺旋の作図

　アルキメデスの螺旋のグラフを作成します。

　パラメータを指定して、螺旋の描画用のデータフレームを作成します。

# パラメータを指定
a <- 1

# 周回数を指定
lap_num <- 4

# 螺旋用のラジアン(弧度法の角度)を作成
t_vec <- seq(from = 0, to = lap_num*2*pi, length.out = 1000) # 正の範囲
#t_vec <- seq(from = -lap_num*2*pi, to = 0, length.out = 1000) # 負の範囲
#t_vec <- seq(from = -lap_num*pi, to = lap_num*pi, length.out = 1000) # 正と負の範囲

# 螺旋の座標を作成
spiral_df <- tibble::tibble(
  t = t_vec, # ラジアン
  r = a * t, # ノルム
  x = r * cos(t), # x座標
  y = r * sin(t), # y座標
  sgn_t_flag = t >= 0 # 角度の正負
)
spiral_df

　周回数 lap_num を指定して、螺旋の座標計算用のラジアン $\theta$ を作成します。 $2 \pi$ の範囲で1周します。
　実数 $a$ を指定して、原点からの距離(変数ごとの係数) $r = a \theta$ を計算し、x軸の値 $x = r \cos \theta$ とy軸の値 $y = r \sin \theta$ を計算します。

・作図コード(クリックで展開)

　グラフサイズや軸線用の値を設定します。

# グラフサイズを設定
axis_size <- c(spiral_df[["x"]], spiral_df[["y"]]) |> 
  abs() |> 
  max() |> 
  ceiling()

# 目盛間隔を設定
step_val <- 15

# 軸線数を設定
if(axis_size%%step_val == 0) {
  
  # グラフサイズと最大目盛が一致する場合
  circle_num <- axis_size %/% step_val
} else {
  
  # グラフサイズと最大目盛が一致しない場合
  circle_num <- axis_size %/% step_val + 1
  
  # グラフサイズを拡大
  axis_size <- max(axis_size, circle_num*step_val)
}
axis_size; circle_num

　ノルム軸線の目盛間隔(円ごとの半径の間隔)を step_val、軸線数(円の数)を circle_num とします。作図時に自動で設定されるx軸・y軸の目盛間隔と同じ値にすると見栄えがよくなります。
　螺旋のx軸・y軸の最大値とノルム軸の最大値からグラフサイズの半分を axis_size とします。

　ノルム軸線(円)の描画用のデータフレームを作成します。

# ノルム軸線の座標を作成
coord_circle_df <- tidyr::expand_grid(
  r = 1:circle_num * step_val, 
  t = seq(from = 0, to = 2*pi, length.out = 361), 
) |> # 半径ごとにラジアンを複製
  dplyr::mutate(
    x = r * cos(t), 
    y = r * sin(t)
  )
coord_circle_df

　半径が step_val 間隔の circle_num 個の円周の座標を計算します。外側の円周の半径は axis_size になります。

　角度軸線(斜線)の描画用のデータフレームを作成します。

# 半円における目盛数(分母の値)を指定
denom <- 6

# 角度軸線の座標を作成
coord_oblique_df <- tibble::tibble(
  i = seq(from = 0, to = 2*denom-1, by = 1), # 目盛位置番号(分子の値)
  t = i / denom * pi, 
  r = axis_size, # ノルム軸線の最大値
  x = r * cos(t), 
  y = r * sin(t), 
  t_label = paste0("frac(", i, ", ", denom, ")~pi"), # 角度ラベル
  h = 1 - (x/r * 0.5 + 0.5), 
  v = 1 - (y/r * 0.5 + 0.5)
)
coord_oblique_df

　ノルム軸線の外側の円周上を等間隔の 2 * denom 個に分割した点の座標を計算します。denom を $n$ とすると、目盛間隔は $\frac{1}{n} \pi$ になります。また $i, n$ を整数として、 $\frac{i}{n} \pi$ と $\frac{i + 2 n}{n} \pi = \frac{i}{n} \pi + 2 \pi$ の目盛位置が一致します。

　螺旋のグラフを作成します。

# ラベル用の文字列を作成
fnc_label <- paste0(
  "list(", 
  "r == a * theta, ", 
  "a == ", a, 
  ")"
)

# 螺旋を作図
add_size <- 2
ggplot() + 
  geom_path(data = coord_circle_df, 
            mapping = aes(x = x, y = y, group = r), 
            color = "white") + # ノルム軸線
  geom_segment(data = coord_oblique_df, 
               mapping = aes(x = 0, y = 0, xend = x, yend = y, group = i), 
               color = "white") + # 角度軸線
  geom_text(data = coord_oblique_df, 
            mapping = aes(x = x, y = y, label = t_label, hjust = h, vjust = v), 
            parse = TRUE) + # 角度目盛ラベル
  geom_path(data = spiral_df, 
            mapping = aes(x = x, y = y), 
            linewidth = 1) + # 螺旋
  coord_fixed(ratio = 1, 
              xlim = c(-axis_size-add_size, axis_size+add_size), 
              ylim = c(-axis_size-add_size, axis_size+add_size)) + 
  labs(title = "Archimedes' spiral", 
       subtitle = parse(text = fnc_label), 
       x = expression(x == r ~ cos~theta), 
       y = expression(y == r ~ sin~theta))

　(x軸方向に値が増減するため geom_line() ではなく、) geom_path() で螺旋を描画します。

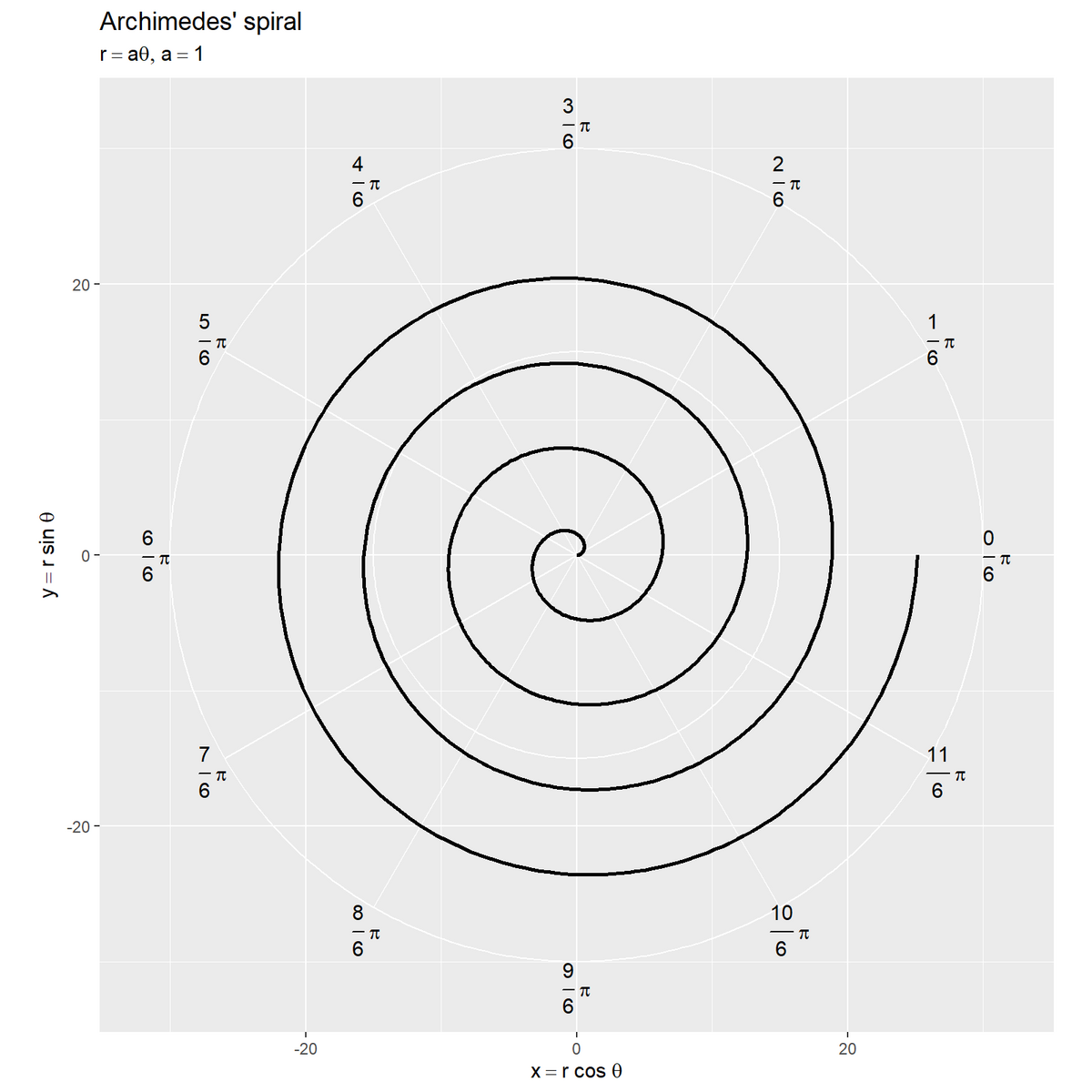
　 $2 \pi$ の間隔で1周するので、線の間隔は $2 a \pi$ で一定になります。

　以上で、アルキメデスの螺旋を描画できました。次からは、変数やパラメータによる螺旋への影響を確認していきます。

角度と座標の関係

　アルキメデスの螺旋上を移動する点のアニメーションを作成します。

・作図コード(クリックで展開)

　フレーム数を指定して、螺旋上の点の描画用のデータフレームを作成します。

# フレーム数を指定
frame_num <- 300

# 螺旋上の点用のラジアンを作成
t_vals <- seq(from = min(t_vec), to = max(t_vec), length.out = frame_num+1)[1:frame_num]

# 螺旋上の点の座標を作成
angle_point_df <- tibble::tibble(
  frame_i = 1:frame_num, # フレーム番号
  t = t_vals, 
  r = a * t, 
  x = r * cos(t), 
  y = r * sin(t), 
  var_label = paste0(
    "list(", 
    "a == ", a, ", ", 
    "theta == ", round(t/pi, digits = 2), " * pi, ", 
    "r == ", round(r, digits = 2), 
    ")"
  ) # 変数ラベル
)
angle_point_df

　フレーム数 frame_num を指定して、螺旋の座標計算用のラジアン t_vec の範囲を等間隔に frame_num 個に分割して、螺旋上の点の座標計算用のラジアン t_vals を作成します。

　角度を示す線分の描画用のデータフレームを作成します。

# 反転フラグを設定
neg_flag <- FALSE

# 角度線の座標を作成
angle_oblique_df <- dplyr::bind_rows(
  # 角度用の斜線
  tibble::tibble(
    frame_i = 1:frame_num, 
    t = t_vals, 
    r = a * t, 
    x = dplyr::if_else(r >= 0, true = axis_size*cos(t), false = -axis_size*cos(t)), 
    y = dplyr::if_else(r >= 0, true = axis_size*sin(t), false = -axis_size*sin(t)), 
    type = "origin"
  ), 
  # 反転した角度用の斜線
  tibble::tibble(
    frame_i = 1:frame_num, 
    t = t_vals, 
    r = a * t, 
    x = dplyr::case_when(
      neg_flag == FALSE ~ NA, 
      r <  0 ~ axis_size * cos(t), 
      r >= 0 ~ -axis_size * cos(t)
    ), 
    y = dplyr::case_when(
      neg_flag == FALSE ~ NA, 
      r <  0 ~ axis_size * sin(t), 
      r >= 0 ~ -axis_size * sin(t)
    ), 
    type = "negation"
  )
)
angle_oblique_df

　 $\theta$ に応じて、半径が axis_size の円周上の点の座標を計算します。 $r$ が負の値の場合は、螺旋が反転するので、半径を -axis_size とします。
　 $r$ が正負の値を含む場合は、反転した点の座標も格納します。(全ての場合を共通のコードで処理するために、)反転した座標を含めるかどうかを neg_flag で設定します。

　螺旋と角度線上の点の描画用のデータフレームを作成します。

# 角度線上の点の座標を作成
r_min <- a * min(t_vec)
r_max <- a * max(t_vec)
point_df <- tidyr::expand_grid(
  frame_i = 1:frame_num, 
  lap_i   = (-lap_num):(lap_num-1) # 点番号
) |> # フレームごとに点を複製
  dplyr::mutate(
    tmp_t = t_vals[frame_i] %% (2*pi), # 単位円相当のラジアン
    t = lap_i * 2*pi + tmp_t, 
    r = a * t, 
    x = r * cos(t), 
    y = r * sin(t),   
    sgn_t_flag = t >= 0 # 角度の正負
  ) |> 
  dplyr::filter(r >= r_min, r <= r_max) # 螺旋上の点を抽出
point_df

　 $\theta$ の前後 $2 \pi$ 間隔 $\theta + 2 i \pi$ の点の座標を計算します。 $i$ は整数で、lap_i 列とします。
　lap_i 列は、 $r$ が正の値のみの場合は 0 から lap_num - 1、負の値のみの場合は -lap_num から -1、正負の値を含む場合は ceiling(-0.5 * lap_num) から floor(0.5 * lap_num - 1) の整数です。(全ての場合を共通のコードで処理するために、)-lap_num から lap_num - 1 の整数を用いて座標を計算し、r の最小値から最大値の点(行)を取り出します。

　螺旋上の点のアニメーションを作成します。

# 螺旋上の点のアニメーションを作図
add_size <- 2
anim <- ggplot() + 
  geom_path(data = coord_circle_df, 
            mapping = aes(x = x, y = y, group = r), 
            color = "white") + # ノルム軸線
  geom_segment(data = coord_oblique_df, 
               mapping = aes(x = 0, y = 0, xend = x, yend = y, group = i), 
               color = "white") + # 角度軸線
  geom_segment(mapping = aes(x = c(-Inf, 0), y = c(0, -Inf), 
                             xend = c(Inf, 0), yend = c(0, Inf)), 
               arrow = arrow(length = unit(10, units = "pt"), ends = "last")) + # x・y軸線
  geom_text(data = coord_oblique_df, 
            mapping = aes(x = x, y = y, label = t_label, hjust = h, vjust = v), 
            parse = TRUE) + # 角度目盛ラベル
  geom_path(data = spiral_df, 
            mapping = aes(x = x, y = y, color = sgn_t_flag), 
            linewidth = 0.5) + # 螺旋
  geom_segment(data = angle_oblique_df,
               mapping = aes(x = 0, y = 0, xend = x, yend = y, linetype = type),
               linewidth = 1) + # 角度用の補助線
  geom_point(data = angle_point_df, 
             mapping = aes(x = x, y = y), 
             size = 5) + # 螺旋上の点
  geom_point(data = point_df, 
             mapping = aes(x = x, y = y, color = sgn_t_flag), 
             size = 4, shape = "circle open") + # 角度用の補助線上の点
  geom_text(data = angle_point_df, 
            mapping = aes(x = -Inf, y = Inf, label = var_label), 
            parse = TRUE, hjust = 0, vjust = -0.5) + # 変数ラベル
  gganimate::transition_manual(frames = frame_i) + # フレーム切替
  scale_color_manual(breaks = c("TRUE", "FALSE"), 
                     values = c("blue", "red"), 
                     labels = c(expression(theta >= 0), expression(theta < 0)), 
                     name = expression(sgn~theta)) + # 角度の正負
  scale_linetype_manual(breaks = c("origin", "negation"), 
                        values = c("solid", "dashed"), guide = "none") + # 角度の正負
  coord_fixed(ratio = 1, clip = "off", 
              xlim = c(-axis_size-add_size, axis_size+add_size), 
              ylim = c(-axis_size-add_size, axis_size+add_size)) + 
  labs(title = "Archimedes' spiral", 
       subtitle = "", # (変数ラベルの表示用)
       x = expression(x == r ~ cos~theta), 
       y = expression(y == r ~ sin~theta))

# gif画像を作成
gganimate::animate(
  plot = anim, 
  nframes = frame_num, fps = 10, 
  width = 600, height = 600, 
  renderer = gganimate::gifski_renderer()
)

　gganimate パッケージを利用してアニメーション(gif画像)を作成します。
　transition_manual() のフレーム制御の引数 frames にフレーム番号列 frame_i を指定します。
　animate() の plot 引数にグラフオブジェクト、nframes 引数にフレーム数 frame_num を指定して、gif画像を作成します。また、fps 引数に1秒当たりのフレーム数を指定できます。

　gganimate を利用したフレーム切り替えでは、フレームに応じてサブタイトルを変更できますが、その際に expression() を使えないので、geom_text() を使って疑似的にサブタイトルの位置にパラメータラベルを表示しています。
　coord_***() に clip = "off" を指定すると、描画領域外(余白領域)に描画できます。

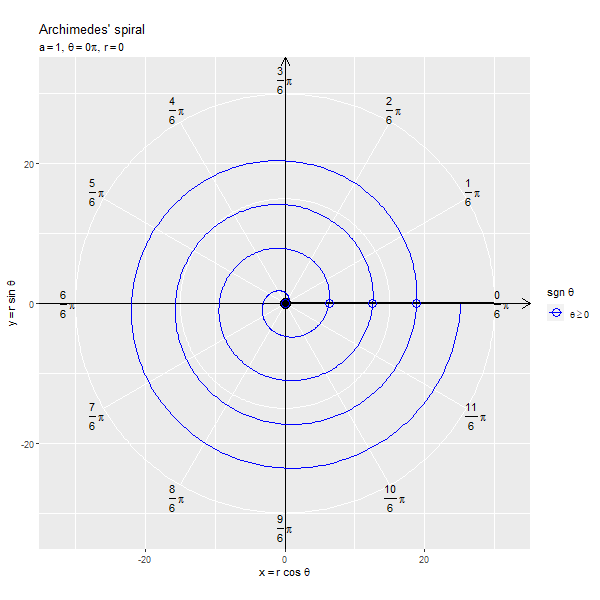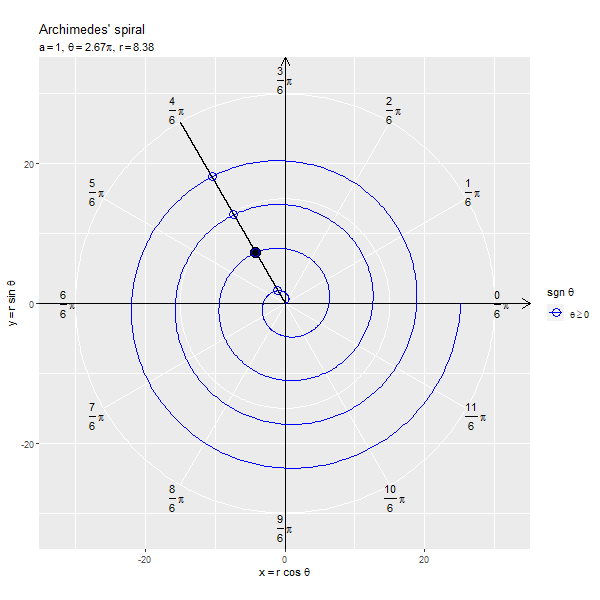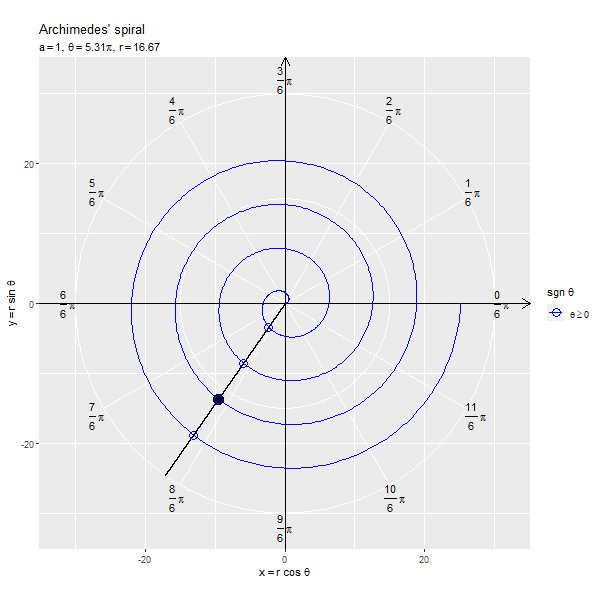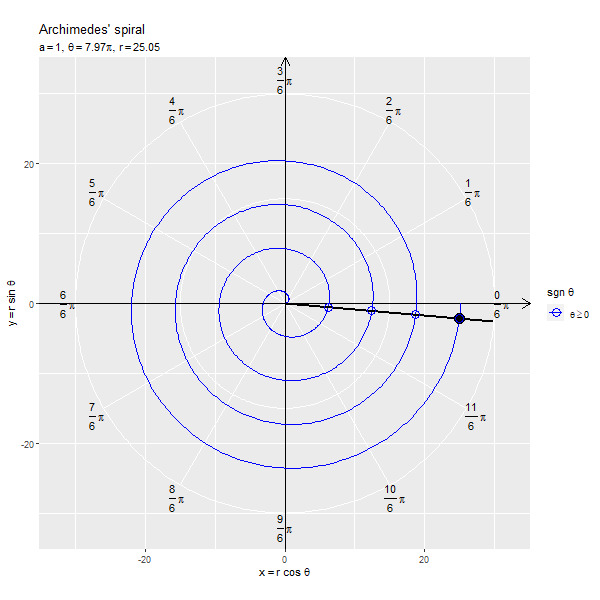
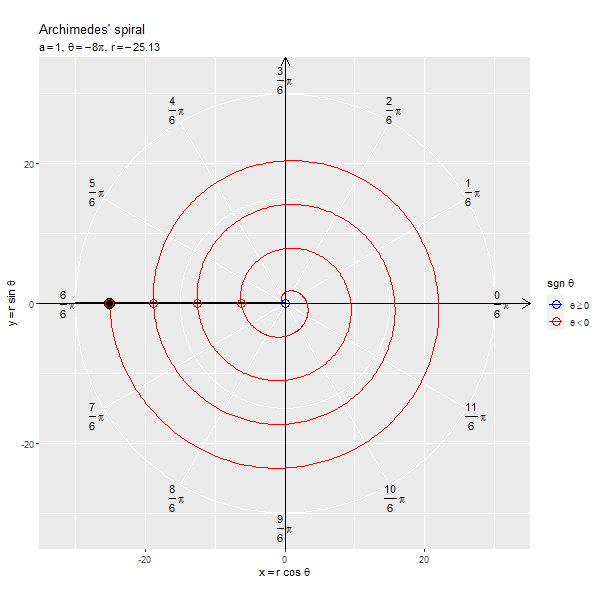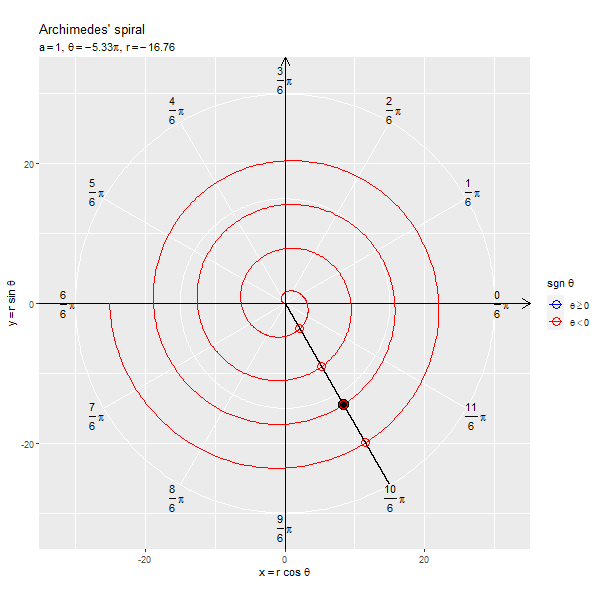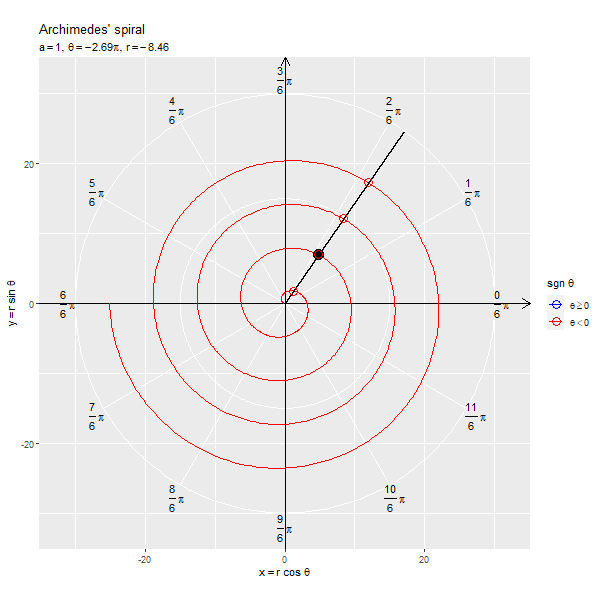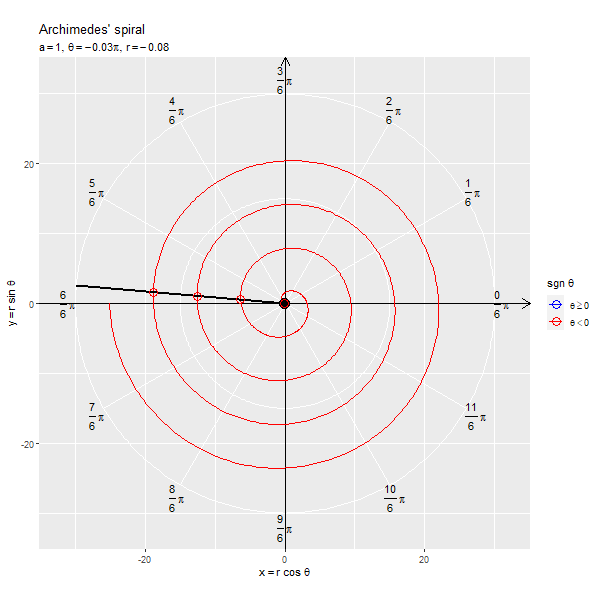
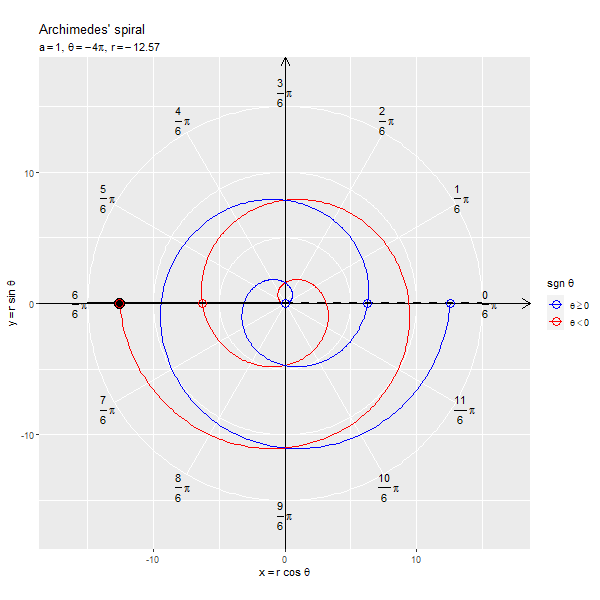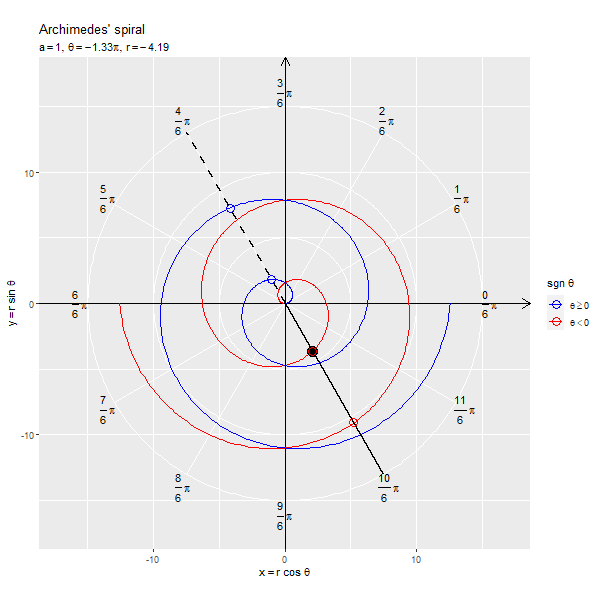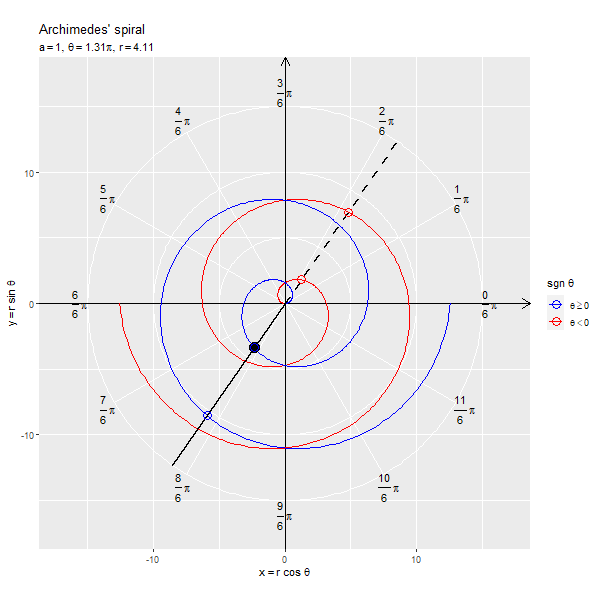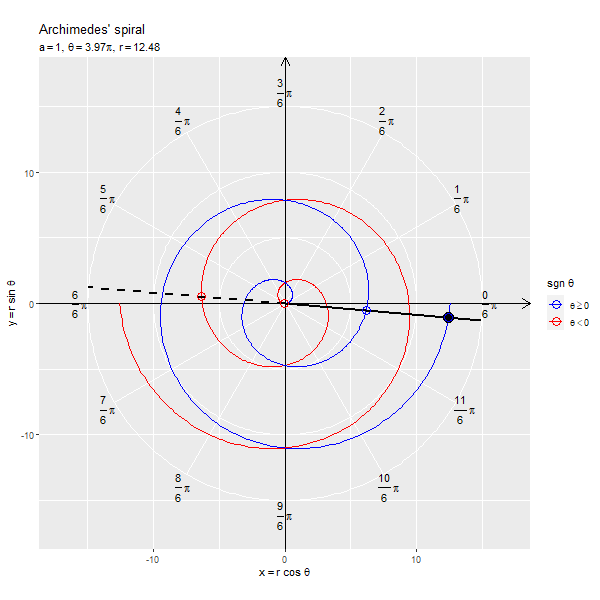
　フレームごとの $\theta$ の点を黒色の点で示します。原点と $\theta$ の点を通る半直線を黒色の線分、 $r$ が正の値と負の値を含む場合は反転した点を通る半直線を破線の線分で示します。
　x軸線の正の部分と半直線の偏角が変数 $\theta$ に対応します。
　 $\theta + 2 i \pi$ の点( $i$ を整数として $\theta$ の前後 $2 \pi$ 間隔の点)が線分上に並ぶのを確認できます。

パラメータと形状の関係

　続いて、定数(パラメータ)の値の変化に応じたグラフを作成して、パラメータと螺旋の形状の関係を確認します。

・作図コード(クリックで展開)

　フレーム数とパラメータを指定して、螺旋の描画用のデータフレームを作成します。

# フレーム数を指定
frame_num <- 201

# パラメータを指定
a_vals <- seq(from = -10, to = 10, length.out = frame_num)

# 周回数を指定
lap_num <- 10

# 螺旋の座標を作成
anim_spiral_df <- tidyr::expand_grid(
  frame_i = 1:frame_num, 
  t       = seq(from = 0, to = lap_num*2*pi, length.out = 1000)
) |> # フレームごとにラジアンを複製
  dplyr::mutate(
    a = a_vals[frame_i], 
    r = a * t, 
    x = r * cos(t), 
    y = r * sin(t)
  )
anim_spiral_df

## # A tibble: 201,000 × 6
##    frame_i      t     a      r      x       y
##      <int>  <dbl> <dbl>  <dbl>  <dbl>   <dbl>
##  1       1 0        -10  0      0      0     
##  2       1 0.0629   -10 -0.629 -0.628 -0.0395
##  3       1 0.126    -10 -1.26  -1.25  -0.158 
##  4       1 0.189    -10 -1.89  -1.85  -0.354 
##  5       1 0.252    -10 -2.52  -2.44  -0.626 
##  6       1 0.314    -10 -3.14  -2.99  -0.973 
##  7       1 0.377    -10 -3.77  -3.51  -1.39  
##  8       1 0.440    -10 -4.40  -3.98  -1.88  
##  9       1 0.503    -10 -5.03  -4.41  -2.43  
## 10       1 0.566    -10 -5.66  -4.78  -3.04  
## # ℹ 200,990 more rows

　フレーム数 frame_num を指定して、frame_num 個の値を指定します。
　フレーム番号( 1 から frame_num までの整数)とラジアンの値の組み合わせを expand_grid() で作成します。パラメータの値ごとに螺旋用のラジアンを複製できます。

　目安として用いる螺旋上の点の描画用のデータフレームを作成します。

# 点数を指定
point_num <- lap_num * 4 + 1

# 螺旋上の点の座標を作成
anim_point_df <- tidyr::expand_grid(
  frame_i = 1:frame_num, 
  t       = seq(
    from = min(anim_spiral_df[["t"]]), 
    to   = max(anim_spiral_df[["t"]]), 
    length.out = point_num
  )
) |> # フレームごとにラジアンを複製
  dplyr::mutate(
    a = a_vals[frame_i], 
    r = a * t, 
    x = r * cos(t), 
    y = r * sin(t)
  )
anim_point_df

## # A tibble: 8,241 × 6
##    frame_i     t     a      r         x         y
##      <int> <dbl> <dbl>  <dbl>     <dbl>     <dbl>
##  1       1  0      -10    0    0         0       
##  2       1  1.57   -10  -15.7 -9.62e-16 -1.57e+ 1
##  3       1  3.14   -10  -31.4  3.14e+ 1 -3.85e-15
##  4       1  4.71   -10  -47.1  8.66e-15  4.71e+ 1
##  5       1  6.28   -10  -62.8 -6.28e+ 1  1.54e-14
##  6       1  7.85   -10  -78.5 -2.40e-14 -7.85e+ 1
##  7       1  9.42   -10  -94.2  9.42e+ 1 -3.46e-14
##  8       1 11.0    -10 -110.   4.71e-14  1.10e+ 2
##  9       1 12.6    -10 -126.  -1.26e+ 2  6.16e-14
## 10       1 14.1    -10 -141.  -7.79e-14 -1.41e+ 2
## # ℹ 8,231 more rows

　螺旋の対応関係の確認用に、変数(ラジアン)に関して一定間隔に点を描画することにします。
　点の数 point_num を指定し point_num 個のラジアンの値を作成して、螺旋の座標計算と同様に処理します。

　パラメータラベルの描画用のデータフレームを作成します。

# パラメータラベル用の文字列を作成
anim_label_df <- tibble::tibble(
  frame_i = 1:frame_num, # フレーム番号
  a       = a_vals, 
  param_label = paste0("a == ", round(a, digits = 2)) # パラメータラベル
)
anim_label_df

## # A tibble: 201 × 3
##    frame_i     a param_label
##      <int> <dbl> <chr>      
##  1       1 -10   a == -10   
##  2       2  -9.9 a == -9.9  
##  3       3  -9.8 a == -9.8  
##  4       4  -9.7 a == -9.7  
##  5       5  -9.6 a == -9.6  
##  6       6  -9.5 a == -9.5  
##  7       7  -9.4 a == -9.4  
##  8       8  -9.3 a == -9.3  
##  9       9  -9.2 a == -9.2  
## 10      10  -9.1 a == -9.1  
## # ℹ 191 more rows

　フレームごとにパラメータラベル用の文字列を作成します。

　グラフサイズや軸線用の値を設定します。

# グラフサイズを指定
axis_size <- 50

# 目盛間隔を指定
step_val <- 12.5

# 軸線数を設定
circle_num <- axis_size %/% step_val
circle_num

## [1] 4

　グラフサイズ(の半分の値) axis_size、ノルム軸線の目盛間隔 step_val と軸線数 circle_num を指定します。この例では、x軸・y軸とノルム軸の最大値を指定して、螺旋などが超える場合は表示しない(枠外になる)ことにします。

　ノルム軸線と角度軸線の描画用のデータフレームを作成します。

# ノルム軸線の座標を作成
coord_circle_df <- tidyr::expand_grid(
  r = 1:circle_num * step_val, 
  t = seq(from = 0, to = 2*pi, length.out = 361), 
) |> # 半径ごとにラジアンを複製
  dplyr::mutate(
    x = r * cos(t), 
    y = r * sin(t)
  )

# 半円における目盛数(分母の値)を指定
denom <- 6

# 角度軸線の座標を作成
coord_oblique_df <- tibble::tibble(
  i = seq(from = 0, to = 2*denom-1, by = 1), # 目盛位置番号(分子の値)
  t = i / denom * pi, 
  r = circle_num * step_val, # ノルム軸線の最大値
  x = r * cos(t), 
  y = r * sin(t), 
  t_label = paste0("frac(", i, ", ", denom, ")~pi"), # 角度ラベル
  h = 1 - (x/r * 0.5 + 0.5), 
  v = 1 - (y/r * 0.5 + 0.5)
)

　「螺旋の作図」のときと同様にして、処理します。ただし、ノルム軸の最大値の設定の仕方が変わっています。

　螺旋のアニメーションを作成します。

# ラベル用の文字列を作成
fnc_label <- "r == a * theta"

# 螺旋のアニメーションを作図
anim <- ggplot() + 
  geom_path(data = coord_circle_df, 
            mapping = aes(x = x, y = y, group = r), 
            color = "white") + # ノルム軸線
  geom_segment(data = coord_oblique_df, 
               mapping = aes(x = 0, y = 0, xend = x, yend = y, group = i), 
               color = "white") + # 角度軸線
  geom_path(data = anim_spiral_df, 
            mapping = aes(x = x, y = y, color = t/pi), 
            linewidth = 1) + # 螺旋
  geom_point(data = anim_point_df, 
             mapping = aes(x = x, y = y, color = t/pi), 
             size = 4) + # 螺旋上の点
  geom_label(data = anim_label_df, 
             mapping = aes(x = -Inf, y = Inf, label = param_label), 
             parse = TRUE, hjust = 0, vjust = 1, alpha = 0.5, label.r = unit(0, units = "pt")) + # パラメータラベル
  gganimate::transition_manual(frames = frame_i) + # フレーム切替
  coord_fixed(ratio = 1, 
              xlim = c(-axis_size, axis_size), 
              ylim = c(-axis_size, axis_size)) + 
  labs(title = "Archimedes' spiral", 
       subtitle = parse(text = fnc_label), 
       color = expression(frac(theta, pi)), 
       x = expression(x == r ~ cos~theta), 
       y = expression(y == r ~ sin~theta))

# gif画像を作成
gganimate::animate(
  plot = anim, 
  nframes = frame_num, fps = 10, 
  width = 600, height = 600, 
  renderer = gganimate::gifski_renderer()
)

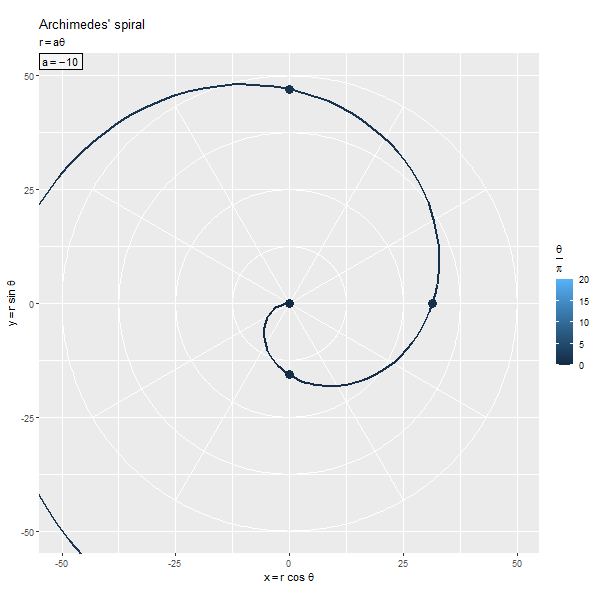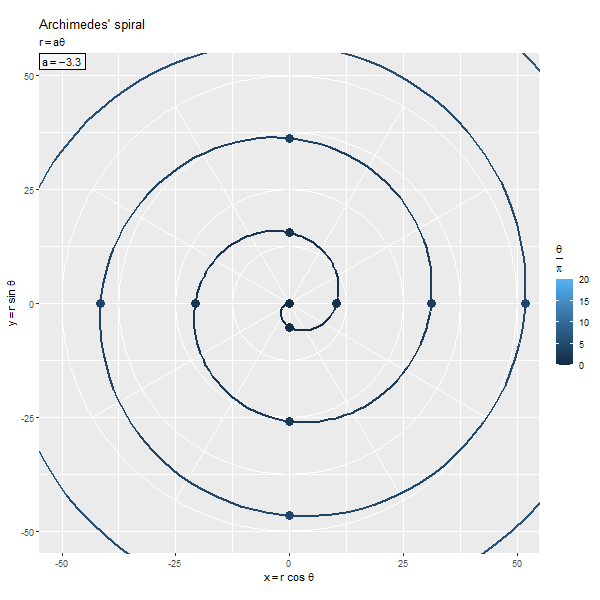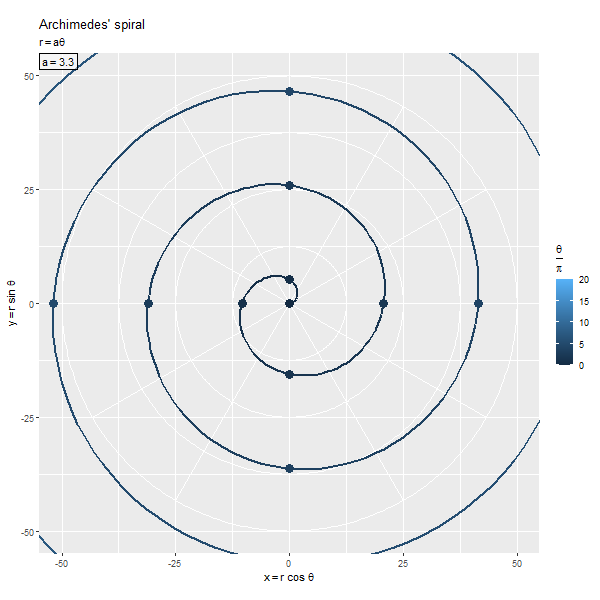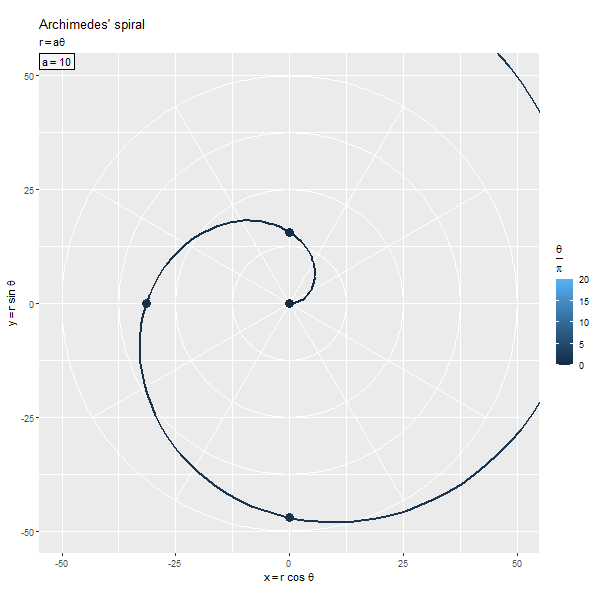
　 $a$ の絶対値が大きいほど、 $r$ の絶対値が大きくなるため、螺旋のサイズが大きくなります。 $a$ の符号によってx軸・y軸に対して反転します。

アルキメデスの螺旋とsin曲線・cos曲線の関係

　最後は、アルキメデスの螺旋とsin関数・cos関数の曲線のグラフを作成して、変数(ラジアン)と座標や定数(パラメータ)と形状の関係を確認します。
　作図コードについては「GitHub - anemptyarchive/Mathematics: 数学ノート」の「spiral > code > archimedes_spiral.R」、作図の解説については「【R】cos関数の可視化 - からっぽのしょこ」などを参照してください。

変数と座標の関係

　変数に応じて移動するアルキメデスの螺旋・sin曲線・cos曲線上の点のアニメーションを作成します。

　螺旋上の点(黒色の点)のx軸方向の変化(青色の点)とy軸方向の変化(赤色の点)が、それぞれcos関数曲線上の点とsin関数曲線上の点に対応しているのを確認できます。
　 $\theta$ の絶対値が大きいほど、 $r$ の絶対値が大きくなるため、曲線の振幅が大きくなります。

パラメータと形状の関係

　パラメータに応じて変化するアルキメデスの螺旋・sin曲線・cos曲線のアニメーションを作成します。

　対応関係の目安として、 $\theta$ に応じて曲線を色付けし、一定間隔で点を打っています。
　螺旋のx軸方向の形状とy軸方向の形状が、それぞれcos関数曲線の形状とsin関数曲線の形状に対応しているのを確認できます。
　 $a$ の絶対値が大きいほど、 $r$ の絶対値が大きくなるため、曲線の振幅が大きくなります。 $a$ の符号によってそれぞれの軸に対して反転します。

　この記事では、アルキメデスの螺旋のグラフを作成しました。次の記事では、対数螺旋のグラフを作成します。

参考書籍

『曲線と曲面（改訂版）－微分幾何的アプローチ－』梅原雅顕・山田光太郎,裳華房,2015年.

おわりに

　螺旋(2次元の場合は渦巻と呼ぶっぽい?)も円関数で描けるんですね。言われてみればそりゃそうだという気もしましたが。
　というわけで、前回のリサージュ曲線の記事から円関数シリーズの拡張編の開始です。コード的にはこっちを先に書き始めてましたが、諸事情によりあっちを先に記事化しました。

　たまたま螺旋の記事を見かけたのがきっかけなのですが、なんでそれをやってみようと思ったかというと、10年ぶりくらいにNARUTOを読んでいるところだったからです。

　2023年10月18日は、つばきファクトリーの福田真琳さんの19歳のお誕生日であり、Juice=Juiceの入江里咲さんの18歳のお誕生日でもあります！

　グループは違いますがハロプロの同期で、お二人とも賢くバランスを取れる可愛らしい方です。そして何と言うか、私の心の隙間にピッタリ嵌るかのように日々の癒しを与えてくれるアイドルです。

【次の内容】

からっぽのしょこ

読んだら書く！書いたら読む！同じ事は二度調べ(たく)ない

【R】アルキメデスの螺旋の可視化

はじめに

アルキメデスの螺旋の可視化

定義式の確認

アルキメデスの螺旋の作図

螺旋の作図

角度と座標の関係

パラメータと形状の関係

アルキメデスの螺旋とsin曲線・cos曲線の関係

変数と座標の関係

パラメータと形状の関係

参考書籍

おわりに