はじめに

　調べても分からなかったので自分なりにやってみる黒魔術シリーズです。もっといい方法があれば教えてください。

　この記事では、ggplot2パッケージを利用してn分木のグラフを作成します。

【前の内容】

www.anarchive-beta.com

【他の内容】

www.anarchive-beta.com

【目次】

はじめに
ggplot2でn分木を作図したい
- n分木の作成
  - 座標計算用の関数
  - 作図
おわりに

ggplot2でn分木を作図したい

　gplot2パッケージを利用して、n分木(多分木・n進木・nアレイツリー・n-ary tree)のグラフを作成する。

　利用するパッケージを読み込む。

# 利用パッケージ
library(tidyverse)

　この記事では、基本的に パッケージ名::関数名() の記法を使っているので、パッケージを読み込む必要はない。ただし、作図コードについてはパッケージ名を省略しているので、ggplot2 を読み込む必要がある。
　また、ネイティブパイプ演算子 |> を使っている。magrittr パッケージのパイプ演算子 %>% に置き換えても処理できるが、その場合は magrittr を読み込む必要がある。

n分木の作成

　最初のノード(要素)のインデックスを1として、「上から下」また「左から右」方向に欠損なくノード(要素)が並ぶn分木のグラフを作成する。ノードごとに分岐数が異なるツリーは扱わない。
　インデックスを0から割り当てる場合は「二分木を作図したい」を参照のこと。

座標計算用の関数

　まずは、作図に利用する関数を実装しておく。

　ノードの深さをカウントする関数を作成する。

# 深さカウント関数を作成
count_depth <- function(index, base, depth_cnt = 0) {
  
  # 親インデックスを計算
  parent_index <- ceiling(index / base) - 1
  
  # 深さをカウント
  depth_cnt <- depth_cnt + 1
  
  # 親が根なら終了
  if(parent_index <= 0) return(depth_cnt)
  
  # 深さを計算
  depth_cnt <- count_depth(parent_index, base, depth_cnt)
  
  # 深さを出力
  return(depth_cnt)
}

# 確認
count_depth(index = 8, base = 2, depth_cnt = 0)

## [1] 3

　深さを求めるインデックス $i$ と分岐数 $b$ を受け取り、親ノードのインデックス $j = \lceil \frac{i}{b} \rceil - 1$ を計算する。 $\lceil x \rceil$ は、天井関数(ceiling())で、 $x$ 以上の最小の整数(小数点以下の切り上げ)を表す。
　親ノードが根ノードになるまで再帰的に処理して、親ノードの数を深さとして出力する。

　ノードインデックスを入力して、深さを出力する関数を作成する。

# 深さ計算関数(スカラ)を作成
index_to_depth <- function(index, base) {
  
  # 深さを作成
  depth_cnt <- 0
  
  # 根なら終了
  if(index == 0) return(depth_cnt)
  
  # 深さを計算
  depth_cnt <- count_depth(index, base, depth_cnt)
  
  # 深さを出力
  return(depth_cnt)
}

# 確認
index_to_depth(index = 8, base = 2)

## [1] 3

　ノードのインデックスを受け取り、count_depth() で深さをカウントして出力する。根ノード(インデックスが0)の場合は 0 を出力する。

　複数のインデックスを入力して、それぞれの深さを出力する関数を作成する。

# 深さ計算関数(ベクトル)を作成
depth <- function(index, base) {
  
  # 深さの受け皿を初期化
  depth <- rep(0, times = length(index))
  
  # 要素ごとに処理
  for(i in seq_along(index)) {
    
    # 深さを計算
    depth[i] <- index_to_depth(index[i], base)
  }
  
  # 深さを出力
  return(depth)
}

# 確認
depth(index = c(4, 8, 16), base = 2)

## [1] 2 3 4

　複数個のインデックスをベクトルとして受け取り、それぞれ index_to_depth() で深さをカウントしてベクトルとして出力する。

　ノードの深さを入力して、インデックスの最小値を出力する関数を作成する。

# 最小インデックス計算関数(スカラ)を作成
depth_to_min_index <- function(depth, base) {
  
  # インデックスの最小値を初期化
  index <- 0
  
  # 根なら終了
  if(depth == 0) return(index)
  
  # 深さごとに処理
  for(h in 1:depth) {
    
    # インデックスの最小値を計算
    index <- index * base + 1
  }
  
  # 最小インデックスを出力
  return(index)
}

# 確認
depth_to_min_index(depth = 4, base = 2)

## [1] 7

　ノードの深さ $h$ と分岐数 $b$ を受け取り、その深さにおける最小(左端)のノードのインデックス $k$ を計算して出力する。根ノード(深さが0)の場合は 0 を出力する。
　根ノード(深さが $h = 0$ のノード)のインデックスを $k^{(0)} = 0$ とすると、各深さのインデックスの最小値は $k^{(h)} = b k^{(h-1)} + 1$ で求まる。つまり、初期値を $k^{(0)} = 0$ として、1つ浅い深さ $h - 1$ におけるインデックスの最小値 $k^{(h-1)}$ を分岐数 $b$ 倍して $1$ を加えた値を、求めたい深さ $h$ 回繰り返して計算する。

　複数の深さを入力して、それぞれの最小インデックスを出力する関数を作成する。

# 最小インデックス計算関数(ベクトル)を作成
min_index <- function(depth, base) {
  
  # インデックスの受け皿を作成
  index <- rep(0, times = length(depth))
  
  # 要素ごとに処理
  for(i in seq_along(depth)) {
    
    # 最小インデックスを計算
    index[i] <- depth_to_min_index(depth[i], base)
  }
  
  # 最小インデックスを出力
  return(index)
}

# 確認
min_index(depth = c(2, 3, 4), base = 2)

## [1]  3  7 15

　複数個の深さをベクトルとして受け取り、それぞれ depth_to_min_index() で最小インデックスを計算してベクトルとして出力する。

作図

　次は、用意した関数を使って各ノードやエッジの座標を求めて、ツリーを作成する。

　ノード数を指定して、値を作成する。

# 分岐数を指定
b <- 2

# ノード数を指定
N <- 61

# (簡易的に)値を作成
a <- 1:N
head(a)

## [1] 1 2 3 4 5 6

　ノード(頂点・節)の数を整数 N として、N 個の値を数値(などの)ベクトル a として作成する。a のみが与えられる場合は、a の要素数を N とする。

　ノードの描画用のデータフレームを作成する。

# ラベル位置の調整値を指定
d <- 0.6

# ノードの座標を作成
node_df <- tibble::tibble(
  value   = a, 
  index   = 0:(N-1), 
  depth   = depth(index, b), 
  col_idx = index - min_index(depth, b) + 1, # 深さごとのノード番号
  coord_x = (col_idx * 2 - 1) * 1/(min_index(depth+1, b) - min_index(depth, b)), 
  label_offset = dplyr::case_when(
    depth >= 5 ~ 0.5 - d, # 指定した深さ以降は全て指定した位置に配置:(深さと符号を指定)
    (index-1)%%b <  0.5*b ~ 0.5 + d, # 中より左の分岐は左に配置
    (index-1)%%b >= 0.5*b ~ 0.5 - d  # 中と右の分岐は右に配置
  ) # ラベル位置を左右にズラす
)
node_df

## # A tibble: 61 × 6
##    value index depth col_idx coord_x label_offset
##    <int> <int> <dbl>   <dbl>   <dbl>        <dbl>
##  1     1     0     0       1   1             -0.1
##  2     2     1     1       1   0.5            1.1
##  3     3     2     1       2   1.5           -0.1
##  4     4     3     2       1   0.25           1.1
##  5     5     4     2       2   0.75          -0.1
##  6     6     5     2       3   1.25           1.1
##  7     7     6     2       4   1.75          -0.1
##  8     8     7     3       1   0.125          1.1
##  9     9     8     3       2   0.375         -0.1
## 10    10     9     3       3   0.625          1.1
## # ℹ 51 more rows

　この例では、根ノードのインデックスを $i = 0$ 、深さを $h = 0$ とする。

　各ノード(要素) $v_i$ の値 $a_i$ とインデックス $i$ をデータフレームに格納して、深さ $h$ を depth() で計算する。
　各深さにおけるノード番号(位置)を $k$ 、左端のノードの(全体における)インデックスを $i^{(h)}_{\mathrm{min}}$ で表すことにする。 $i^{(h)}_{\mathrm{min}}$ を min_index() で計算して、左からの位置は $k = i - i^{(h)}_{\mathrm{min}} + 1$ で求まる。
　各分岐をシンメトリーに描画する場合は、深さごとに、ノード数個 $i^{(h+1)}_{\mathrm{min}} - i^{(h)}_{\mathrm{min}}$ に等間隔 $\frac{1}{i^{(h+1)}_{\mathrm{min}} - i^{(h)}_{\mathrm{min}}}$ に分割した $2 k - 1$ 番目の位置にノードを配置する。このとき、x軸の範囲は0から2になる。
　ラベル位置の調整用の値を作成する。この例では、インデックスが偶数の場合は左にズラすために0.5以上の値、奇数の場合は右にズラすために0.5以下の値を格納する。ただし、ノード数が多くなるとラベルが重なりやすくなるので、一定の深さ以降は一方向にズラす。

　エッジの描画用のデータフレームを作成する。

# エッジの座標を作成
edge_df <- dplyr::bind_rows(
  # 子ノードの座標
  node_df |> 
    dplyr::filter(depth > 0) |> # 根を除去
    dplyr::mutate(
      edge_id   = index, 
      node_type = "childe" # (確認用)
    ), 
  # 親ノードの座標
  node_df |> 
    dplyr::filter(depth > 0) |> # 根を除去
    dplyr::mutate(
      edge_id   = index, 
      node_type = "parent", # (確認用)
      depth   = depth - 1, 
      index   = ceiling(index / b) - 1, 
      col_idx = index - min_index(depth, b) + 1, # 深さごとのノード番号
      coord_x = (col_idx * 2 - 1) * 1/(min_index(depth+1, b) - min_index(depth, b)), 
    )
) |> 
  dplyr::select(!label_offset) |> 
  dplyr::arrange(edge_id, depth)
edge_df

## # A tibble: 120 × 7
##    value index depth col_idx coord_x edge_id node_type
##    <int> <dbl> <dbl>   <dbl>   <dbl>   <int> <chr>    
##  1     2     0     0       1    1          1 parent   
##  2     2     1     1       1    0.5        1 childe   
##  3     3     0     0       1    1          2 parent   
##  4     3     2     1       2    1.5        2 childe   
##  5     4     1     1       1    0.5        3 parent   
##  6     4     3     2       1    0.25       3 childe   
##  7     5     1     1       1    0.5        4 parent   
##  8     5     4     2       2    0.75       4 childe   
##  9     6     2     1       2    1.5        5 parent   
## 10     6     5     2       3    1.25       5 childe   
## # ℹ 110 more rows

　親子ノードを結ぶエッジ(辺・枝)の描画用に、子ノードのインデックスを $i$ 、親ノードのインデックスを $j$ として、子ノード $v_i$ と親ノード $v_j$ の座標データをそれぞれ作成して結合する。
　子ノードのデータは、各ノードのデータ node_df から根ノードのデータ(行)を取り除く。
　親ノードのデータは、各ノードのデータから根ノードのデータを取り除いて親ノードのデータを計算する。親ノードの深さは $h_{(\mathrm{parent})} = h_{(\mathrm{childe})} - 1$ 、インデックスは $j = \lceil \frac{i}{b} \rceil - 1$ で求まる。座標などは $j$ を用いて先ほどと同様にして計算する。
　元のノードのインデックスをエッジIDとする。

　nアレイツリーを作成する。

# ツリーの高さを取得
max_h <- depth(N-1, b)

# 縦方向の余白の調整値を指定
d <- 0.1

# 二分木を作図
ggplot() + 
  geom_path(data = edge_df, 
            mapping = aes(x = coord_x, y = depth, group = edge_id), 
            linewidth = 1) + # エッジ
  geom_point(data = node_df, 
             mapping = aes(x = coord_x, y = depth), 
             size = 10, shape = "circle filled", fill = "white", stroke = 1) + # ノード
  # geom_text(data = node_df, 
  #           mapping = aes(x = coord_x, y = depth, label = value), 
  #           size = 5) + # 値ラベル
  geom_text(data = node_df, 
            mapping = aes(x = coord_x, y = depth, label = paste0("a[", index, "]")), parse = TRUE, 
            size = 4) + # 要素ラベル
  geom_text(data = node_df, 
            mapping = aes(x = coord_x, y = depth, label = index, hjust = label_offset), 
            size = 4, vjust = -1.5, color = "blue") + # 位置ラベル
  scale_x_continuous(labels = NULL, name = "") + 
  scale_y_reverse(breaks = 0:max_h, minor_breaks = FALSE) + 
  coord_cartesian(xlim = c(0, 2), ylim = c(max_h+d, -d)) + # 表示範囲
  labs(title = paste0(b, "-ary tree"), 
       subtitle = paste0("height = ", max_h), 
       y = "depth")

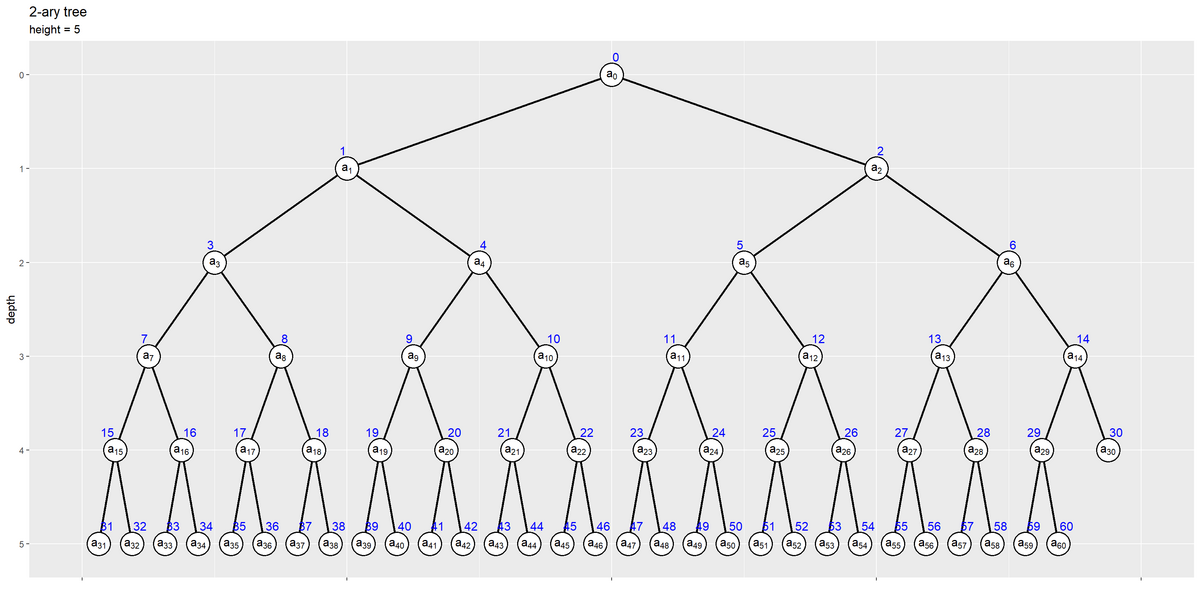
　エッジとして geom_path() で線分を描画する。線分間が繋がらないように、group 引数にエッジIDを指定する。
　ノードとして geom_point() で点を描画する。枠線と枠内を色分けする場合は、shape 引数に "*** filled" の形状を指定する。
　ラベルを geom_text() でテキストを描画する。ノードやエッジと重ならないように表示する場合は、hjust, vjust 引数に値を指定する。この例では、深さが4まではインデックスが偶数なら左、奇数なら右に、深さが5からは全て右にズラしている。
　深さ(y軸の値)が大きくなるほど下になるように、scale_y_reverse() でy軸を反転する。

　他の分岐数のツリーも同様にして作成できる。

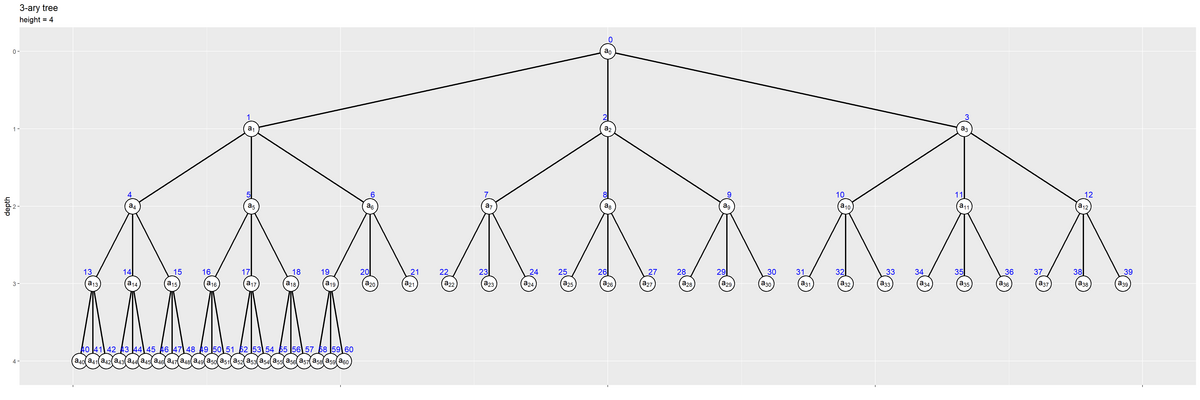
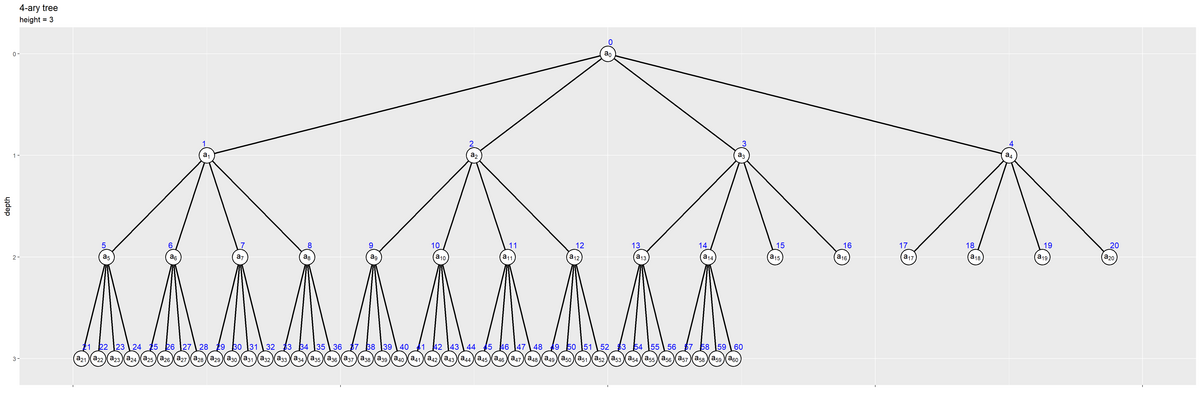
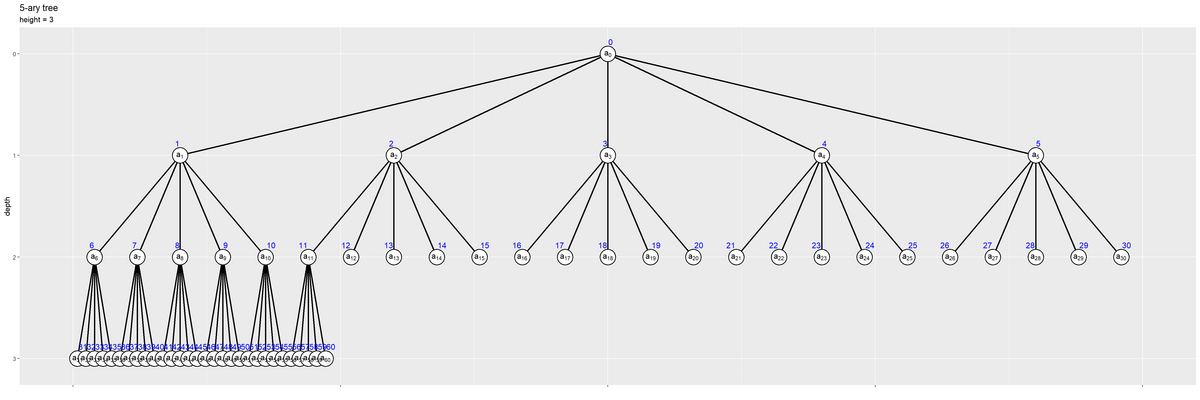
　分岐数 b の他に、ラベル位置などの設定(調整値)などを変更している。

　この記事では、n分木のグラフを作成した。

おわりに

　ヒープソートの理解のためにバイナリツリーの図を作りたかっただけなんですが、根のインデックスが0だとどうやるんだろう、2より多く分岐したらどうなるんだろうかと気になってしまって、気付いたら作ってました。
　ノードごとにバラバラに分岐する場合も気になるんですが、さすがに面倒臭さが極まりそうなので止めておきます。

　NNの文脈で活性化関数によって非線形な変換を云々とあってなるほど～と気楽に思ったものですが、深さごとのインデックスの最小値を求めようとしたら、親子のインデックスの関係式 $i_{(\mathrm{childe})} = b i_{(\mathrm{parent})} + 1$ の+1がなんと面倒なことか。二分木であればどの深さでも一発で計算できたのに、この計算のための関数を用意する必要がありました。この厄介さを実感できただけでも実装してみた甲斐があったと思うことにします。まさか一発で計算できたりしませんよね。