はじめに
機械学習で登場する確率分布について色々な角度から理解したいシリーズです。
この記事では、R言語を使って2次元ガウス分布の分散共分散行列とユークリッド距離・マハラノビス距離の関係をグラフで確認します。
【前の内容】
【数式読解編】
【他の記事一覧】
【この記事の内容】
分散共分散行列とユークリッド距離・マハラノビス距離の関係の可視化
分散共分散行列(Variance–Covariance Matrix)とユークリッド距離(Euclidean Distance)・マハラノビス距離(Mahalanobis Dostance)の関係を2次元ガウス分布を用いて可視化します。分散共分散行列と距離の関係については「https://www.anarchive-beta.com/entry/2022/08/29/080000」を参照してください。
利用するパッケージを読み込みます。
library(tidyverse) library(mvnfast) library(ggrepel)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているため、ggplot2は読み込む必要があります。
magrittrパッケージのパイプ演算子%>%ではなく、ベースパイプ(ネイティブパイプ)演算子|>を使っています。%>%に置き換えても処理できます。
サンプルの距離の可視化
2次元ガウス分布の乱数を生成して、サンプルごとのユークリッド距離とマハラノビス距離を可視化します。2次元ガウス分布のグラフ作成については「2次元ガウス分布の作図」、乱数生成については「多次元ガウス分布の乱数生成」を参照してください。
ガウス分布のパラメータ$\boldsymbol{\mu}, \boldsymbol{\Sigma}$を設定します。この例では、2次元のグラフで可視化するため、次元数を$D = 2$とします。
# 平均ベクトルを指定 mu_d <- c(6, 10) # 分散共分散行列を指定 sigma_dd <- matrix(c(1, 0.6, 0.6, 1.5), nrow = 2, ncol = 2)
平均ベクトル$\boldsymbol{\mu} = (\mu_1, \mu_2)$、分散共分散行列$\boldsymbol{\Sigma} = (\sigma_1^2, \sigma_{2,1}, \sigma_{1,2}, \sigma_2^2)$を指定します。
平均$\mu_d$は実数、分散$\sigma_d^2$は非負の実数、共分散$\sigma_{1,2}$は実数、また$\boldsymbol{\Sigma}$は正定値行列を満たす必要があります。
設定したパラメータに応じて、ガウス分布の確率変数がとり得る値$\mathbf{x}$を作成します。
# xの値を作成 x_1_vals <- seq( from = mu_d[1] - sqrt(sigma_dd[1, 1]) * 3, to = mu_d[1] + sqrt(sigma_dd[1, 1]) * 3, length.out = 100 ) x_2_vals <- seq( from = mu_d[2] - sqrt(sigma_dd[2, 2]) * 3, to = mu_d[2] + sqrt(sigma_dd[2, 2]) * 3, length.out = 100 ) # xの点を作成 x_mat <- tidyr::expand_grid( x_1 = x_1_vals, # x軸の値 x_2 = x_2_vals # y軸の値 ) |> # 格子点を作成 as.matrix() # マトリクスに変換 head(x_mat)
## x_1 x_2 ## [1,] 3 6.325765 ## [2,] 3 6.399992 ## [3,] 3 6.474219 ## [4,] 3 6.548446 ## [5,] 3 6.622673 ## [6,] 3 6.696900
$x_1$(x軸)の値をx_1_vals、$x_2$(y軸)の値をx_2_valsとします。この例では、それぞれ平均を中心に標準偏差の3倍を範囲とします。
x_1_valsとx_2_valsの要素の全ての組み合わせ(格子状の点)をexpand_grid()で作成します。データフレームが出力されるので、as.matrix()でマトリクスに変換してx_matとします。x_matの各行が点$\mathbf{x} = (x_1, x_2)$に対応します。
$\mathbf{x}$の点ごとの確率密度を計算します。
# 多次元ガウス分布を計算 dens_df <- tibble::tibble( x_1 = x_mat[, 1], # x軸の値 x_2 = x_mat[, 2], # y軸の値 density = mvnfast::dmvn(X = x_mat, mu = mu_d, sigma = sigma_dd) # 確率密度 ) dens_df
## # A tibble: 10,000 × 3 ## x_1 x_2 density ## <dbl> <dbl> <dbl> ## 1 3 6.33 0.000355 ## 2 3 6.40 0.000400 ## 3 3 6.47 0.000448 ## 4 3 6.55 0.000501 ## 5 3 6.62 0.000556 ## 6 3 6.70 0.000615 ## 7 3 6.77 0.000676 ## 8 3 6.85 0.000740 ## 9 3 6.92 0.000807 ## 10 3 6.99 0.000875 ## # … with 9,990 more rows
多次元ガウス分布の確率密度は、mvnfastパッケージのdmvn()で計算できます。確率変数の引数Xにx_mat、平均の引数muにmu_d、共分散の引数sigmaにsigma_ddを指定します。
$\mathbf{x}$の点ごとのユークリッド距離とマハラノビス距離を計算します。
# 点ごとに距離を計算 dist_df <- tibble::tibble( x_1 = x_mat[, 1], # x軸の値 x_2 = x_mat[, 2], # y軸の値 euclidean = apply((t(x_mat) - mu_d)^2, 2, sum) |> sqrt(), # ユークリッド距離 mahalanobis = t(t(x_mat)-mu_d) %*% solve(sigma_dd) %*% (t(x_mat)-mu_d) |> diag() |> sqrt() # マハラノビス距離 ) dist_df
## # A tibble: 10,000 × 4 ## x_1 x_2 euclidean mahalanobis ## <dbl> <dbl> <dbl> <dbl> ## 1 3 6.33 4.74 3.48 ## 2 3 6.40 4.69 3.44 ## 3 3 6.47 4.63 3.41 ## 4 3 6.55 4.57 3.38 ## 5 3 6.62 4.52 3.34 ## 6 3 6.70 4.46 3.31 ## 7 3 6.77 4.41 3.28 ## 8 3 6.85 4.35 3.26 ## 9 3 6.92 4.30 3.23 ## 10 3 6.99 4.25 3.21 ## # … with 9,990 more rows
ユークリッド距離とマハラノビス距離は、それぞれ次の式で定義されます。
転置はt()、逆行列の計算はsolve()、行列の積の計算は%*%演算子で行えます。
ただし、複数個の$\mathbf{x}$を同時に処理するために、適宜転置して計算する必要があります。また、二次形式(平方根の中)の計算において全ての点の組み合わせで処理されます。そのため、同じ点による計算結果(対角要素)をdaig()で取り出します。
作図用の$\mathbf{x}$に関して処理できました。次は、サンプル$\mathbf{x}_n$に関して処理します。
ガウス分布に従う乱数を生成します。
# データ数(サンプルサイズ)を指定 N <- 10 # 多次元ガウス分布に従う乱数を生成 x_nd <- mvnfast::rmvn(n = N, mu = mu_d, sigma = sigma_dd) head(x_nd)
## [,1] [,2] ## [1,] 5.218377 11.229742 ## [2,] 5.064676 9.457486 ## [3,] 6.726710 10.932408 ## [4,] 7.832292 11.036711 ## [5,] 5.191408 9.939346 ## [6,] 5.664115 7.568301
多次元ガウス分布の乱数は、mvnfastパッケージのrmvn()で生成できます。データ数の引数nにN、平均の引数muにmu_d、共分散の引数sigmaにsigma_ddを指定します。
生成した値をN個のサンプルx_ndとします。x_ndの各行が$\mathbf{x}_n = (x_{n,1}, x_{n,2})$に対応します。
サンプル$\mathbf{x}_n$ごとにユークリッド距離とマハラノビス距離を計算します。
# サンプルごとに距離を計算 data_df <- tibble::tibble( n = factor(1:N), # データ番号 x_1 = x_nd[, 1], # x軸の値 x_2 = x_nd[, 2], # y軸の値 euclidean = apply((t(x_nd) - mu_d)^2, 2, sum) |> sqrt(), # ユークリッド距離 mahalanobis = t(t(x_nd)-mu_d) %*% solve(sigma_dd) %*% (t(x_nd)-mu_d) |> diag() |> sqrt(), # マハラノビス距離 coord_label = paste0("x=(", round(x_1, 1), ", ", round(x_2, 1), ")"), # 座標ラベル dist_label = paste0("ED=", round(euclidean, 2), "\nMD=", round(mahalanobis, 2)) # 距離ラベル ) data_df
## # A tibble: 10 × 7 ## n x_1 x_2 euclidean mahalanobis coord_label dist_label ## <fct> <dbl> <dbl> <dbl> <dbl> <chr> <chr> ## 1 1 5.22 11.2 1.46 1.77 x=(5.2, 11.2) "ED=1.46\nMD=1.77" ## 2 2 5.06 9.46 1.08 0.935 x=(5.1, 9.5) "ED=1.08\nMD=0.94" ## 3 3 6.73 10.9 1.18 0.863 x=(6.7, 10.9) "ED=1.18\nMD=0.86" ## 4 4 7.83 11.0 2.11 1.83 x=(7.8, 11) "ED=2.11\nMD=1.83" ## 5 5 5.19 9.94 0.811 0.901 x=(5.2, 9.9) "ED=0.81\nMD=0.9" ## 6 6 5.66 7.57 2.45 2.12 x=(5.7, 7.6) "ED=2.45\nMD=2.12" ## 7 7 5.65 10.6 0.695 0.838 x=(5.6, 10.6) "ED=0.7\nMD=0.84" ## 8 8 5.78 10.5 0.504 0.591 x=(5.8, 10.5) "ED=0.5\nMD=0.59" ## 9 9 6.41 10.5 0.662 0.483 x=(6.4, 10.5) "ED=0.66\nMD=0.48" ## 10 10 6.64 11.6 1.71 1.30 x=(6.6, 11.6) "ED=1.71\nMD=1.3"
先ほどと同様に計算します。こちらは、色分け用の因子型のデータ番号列と、グラフに載せる情報として座標と距離のラベル列を作成します。
作図用のデータフレームを作成できました。次は、作図処理を行います。
生成分布の確率密度の等高線と、ユークリッド距離とマハラノビス距離の等高線に、サンプルを重ねたグラフを作成します。
# 距離の等高線のプロット位置を指定 dist_vals <- seq(from = 1, to = 5, by = 1) # パラメータラベルを作成:(数式表示用) math_text <- paste0( "list(", "mu==group('(', list(", paste0(mu_d, collapse = ", "), "), ')')", ", Sigma==group('(', list(", paste0(sigma_dd, collapse = ", "), "), ')')", ")" ) # サンプルごとのユークリッド距離とマハラノビス距離の可視化 ggplot() + geom_contour_filled(data = dens_df, mapping = aes(x = x_1, y = x_2, z = density, fill = ..level..), alpha = 0.5) + # 2次元ガウス分布 geom_contour(data = dist_df, mapping = aes(x = x_1, y = x_2, z = euclidean, linetype = "ed"), breaks = dist_vals, color = "pink", size = 1) + # ユークリッド距離 geom_contour(data = dist_df, mapping = aes(x = x_1, y = x_2, z = mahalanobis, linetype = "md"), breaks = dist_vals, color = "skyblue", size = 1) + # マハラノビス距離 geom_segment(data = data_df, mapping = aes(x = mu_d[1], y = mu_d[2], xend = x_1, yend = x_2, color = n), arrow = arrow(length = unit(5, "pt"), type = "closed"), show.legend = FALSE) + # 期待値とサンプルの線分 geom_point(data = data_df, mapping = aes(x = x_1, y = x_2, color = n), alpha = 0.8, size = 5, show.legend = FALSE) + # サンプル ggrepel::geom_label_repel(data = data_df, mapping = aes(x = x_1, y = x_2, color = n, label = paste0(coord_label, "\n", dist_label)), alpha = 0.8, size = 2.5, label.padding = unit(3, "pt"), box.padding = unit(10, "pt"), point.padding = unit(10, "pt"), min.segment.length = 0, max.overlaps = Inf, show.legend = FALSE) + # サンプルラベル coord_fixed(ratio = 1) + # アスペクト比 scale_linetype_manual(breaks = c("ed", "md"), values = c("solid", "solid"), labels = c("euclidean", "mahalanobis"), name = "distance") + # (凡例表示用の黒魔術) guides(linetype = guide_legend(override.aes = list(color = c("pink", "skyblue")))) + # (凡例表示用の黒魔術) labs(title ="Maltivariate Gaussian Distribution", subtitle = parse(text = math_text), # (数式表示用) color = "x", fill = "density", x = expression(x[1]), y = expression(x[2]))
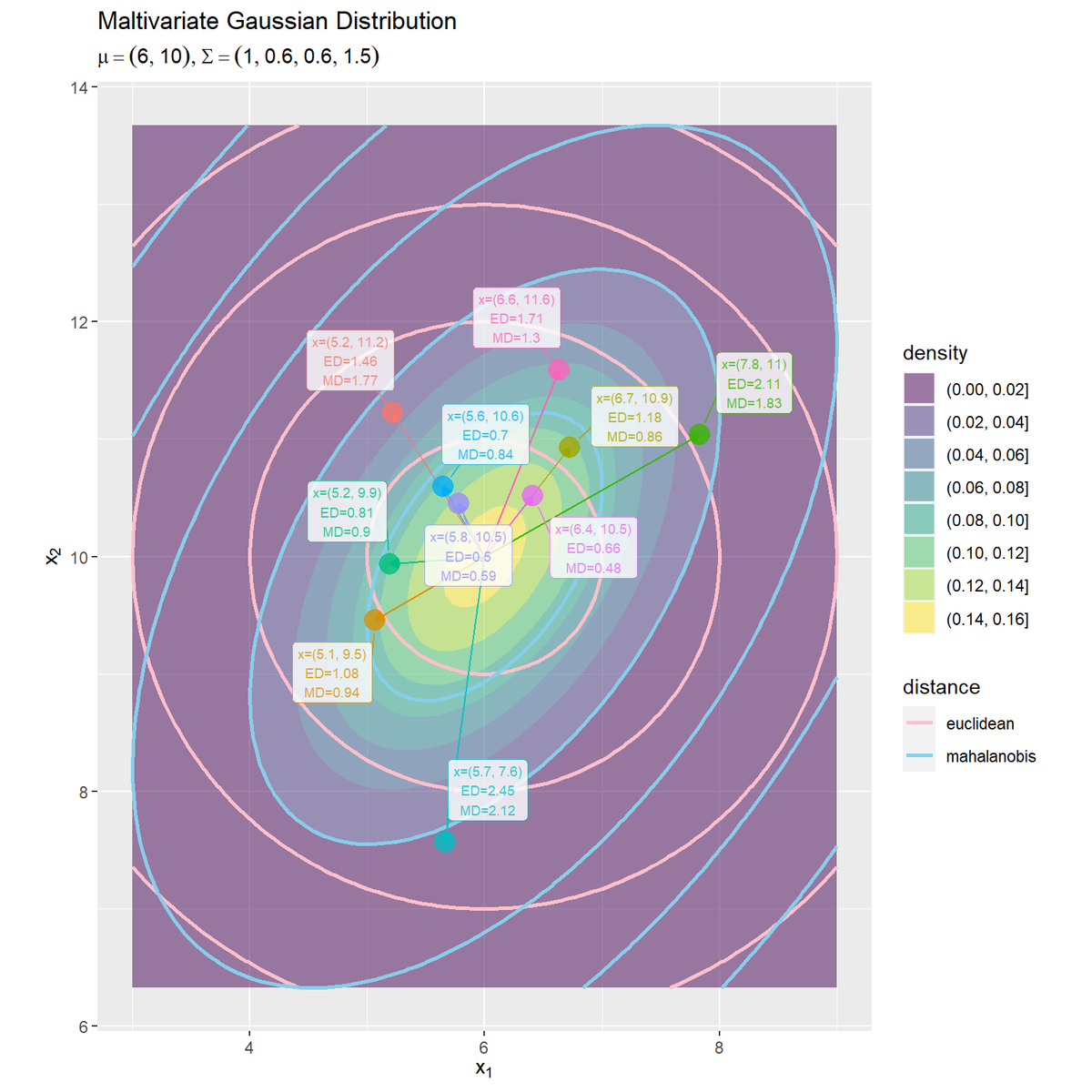
確率密度の塗りつぶし等高線図をgeom_contour_filled()で描画します。
ユークリッド距離とマハラノビス距離の等高線図をそれぞれgeom_contour()で描画します。線を引くz軸の値の引数breaksに値を指定します。この例では、1から5の整数とします。
期待値(距離が0の点)と各サンプルを結ぶ線分をgeom_segment()で描画します。
サンプルの散布図をgeom_point()で描画します。
サンプルごとの距離をggrepelパッケージのgeom_label_repel()でラベルとして表示します。
ユークリッド距離の等高線は、アスペクト比が1のとき円になります。グラフのアスペクト比はcoord_fixed()のratio引数で指定できます。
続いて、ユークリッド距離とマハラノビス距離が等しい等高線を1本だけ引いて比較します。
線を引く距離を指定して、それぞれの距離の内外のサンプルを判別します。
# 距離を指定 dist <- 1.5 # 指定した範囲の内外を判定 data_df2 <- data_df |> dplyr::mutate( color_flag = dplyr::case_when( euclidean <= dist & mahalanobis <= dist ~ "both", euclidean <= dist ~ "euclid", mahalanobis <= dist ~ "mahal", TRUE ~ "none" ) # 色分け用フラグ ) data_df2
## # A tibble: 10 × 8 ## n x_1 x_2 euclidean mahalanobis coord_label dist_label color_flag ## <fct> <dbl> <dbl> <dbl> <dbl> <chr> <chr> <chr> ## 1 1 5.22 11.2 1.46 1.77 x=(5.2, 11.2) "ED=1.46\nM… euclid ## 2 2 5.06 9.46 1.08 0.935 x=(5.1, 9.5) "ED=1.08\nM… both ## 3 3 6.73 10.9 1.18 0.863 x=(6.7, 10.9) "ED=1.18\nM… both ## 4 4 7.83 11.0 2.11 1.83 x=(7.8, 11) "ED=2.11\nM… none ## 5 5 5.19 9.94 0.811 0.901 x=(5.2, 9.9) "ED=0.81\nM… both ## 6 6 5.66 7.57 2.45 2.12 x=(5.7, 7.6) "ED=2.45\nM… none ## 7 7 5.65 10.6 0.695 0.838 x=(5.6, 10.6) "ED=0.7\nMD… both ## 8 8 5.78 10.5 0.504 0.591 x=(5.8, 10.5) "ED=0.5\nMD… both ## 9 9 6.41 10.5 0.662 0.483 x=(6.4, 10.5) "ED=0.66\nM… both ## 10 10 6.64 11.6 1.71 1.30 x=(6.6, 11.6) "ED=1.71\nM… mahal
case_when()で場合分けして色分け用のラベルを作成します(距離の内外で色分けする必要はありません)。
確率密度と距離の等高線にサンプルを重ねなグラフを作成します。
# ユークリッド距離とマハラノビス距離の比較 ggplot() + geom_contour_filled(data = dens_df, mapping = aes(x = x_1, y = x_2, z = density, fill = ..level..), alpha = 0.5) + # 2次元ガウス分布 geom_contour(data = dist_df, mapping = aes(x = x_1, y = x_2, z = euclidean, linetype = "ed"), breaks = dist, color = "pink", size = 1) + # ユークリッド距離 geom_contour(data = dist_df, mapping = aes(x = x_1, y = x_2, z = mahalanobis, linetype = "md"), breaks = dist, color = "skyblue", size = 1) + # マハラノビス距離 geom_point(data = data_df2, mapping = aes(x = x_1, y = x_2, color = color_flag), alpha = 0.8, size = 5, show.legend = FALSE) + # サンプル geom_label(mapping = aes(x = min(x_1_vals), y = max(x_2_vals), label = paste0("dist:", dist)), hjust = 0) + # 距離ラベル coord_fixed(ratio = 1) + # アスペクト比 scale_color_manual(breaks = c("both", "euclid", "mahal", "none"), values = c("#00A968", "pink", "skyblue", "gray")) + # サンプルの色 scale_linetype_manual(breaks = c("ed", "md"), values = c("solid", "solid"), labels = c("euclidean", "mahalanobis"), name = "distance") + # (凡例表示用の黒魔術) guides(linetype = guide_legend(override.aes = list(color = c("pink", "skyblue")))) + # (凡例表示用の黒魔術) labs(title ="Maltivariate Gaussian Distribution", subtitle = parse(text = math_text), color = "x", fill = "density", x = expression(x[1]), y = expression(x[2]))
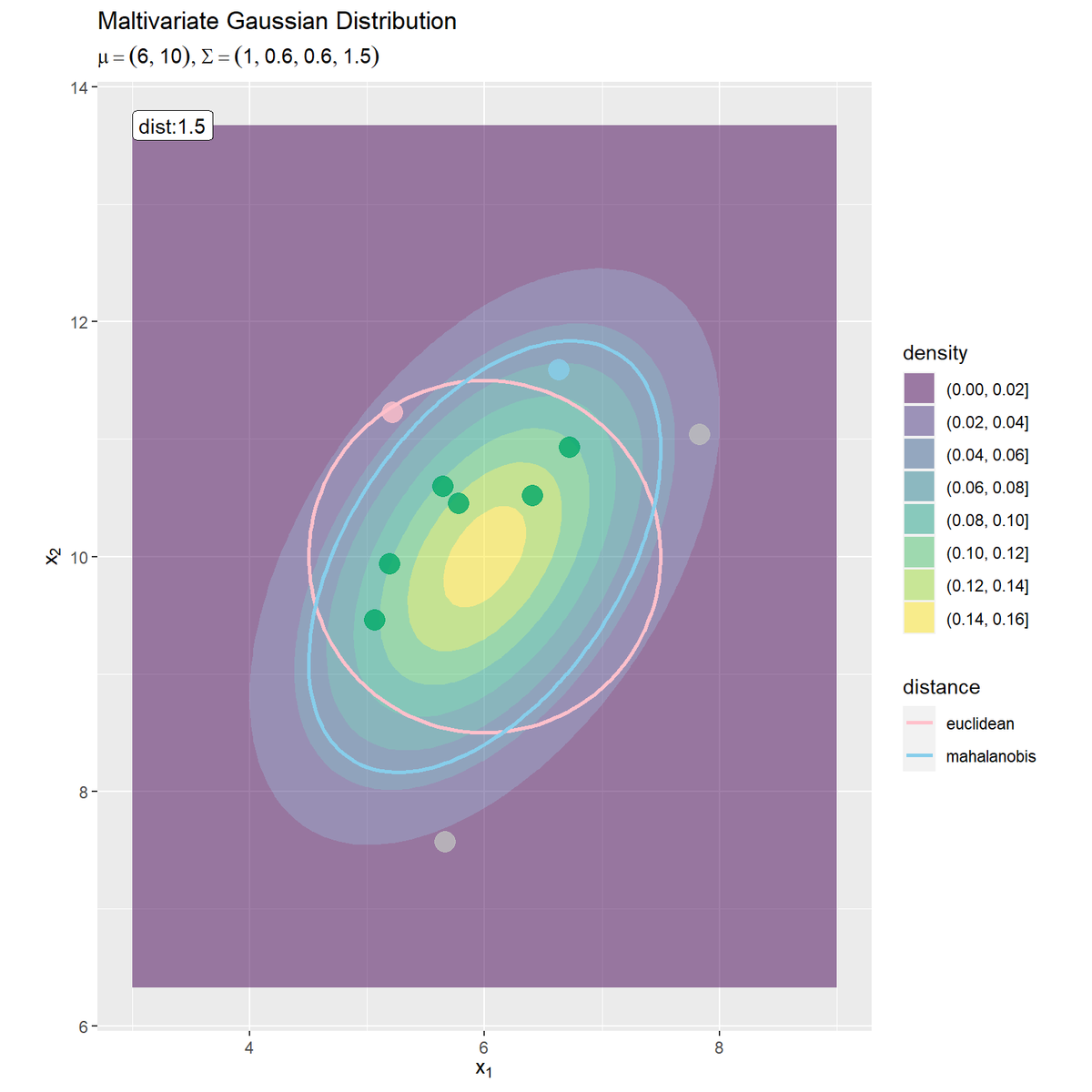
サンプルの色分けを設定する場合は、scale_color_manual()のbreaks引数にラベルの文字列、values引数に色を指定します。
・分散共分散行列が単位行列の場合
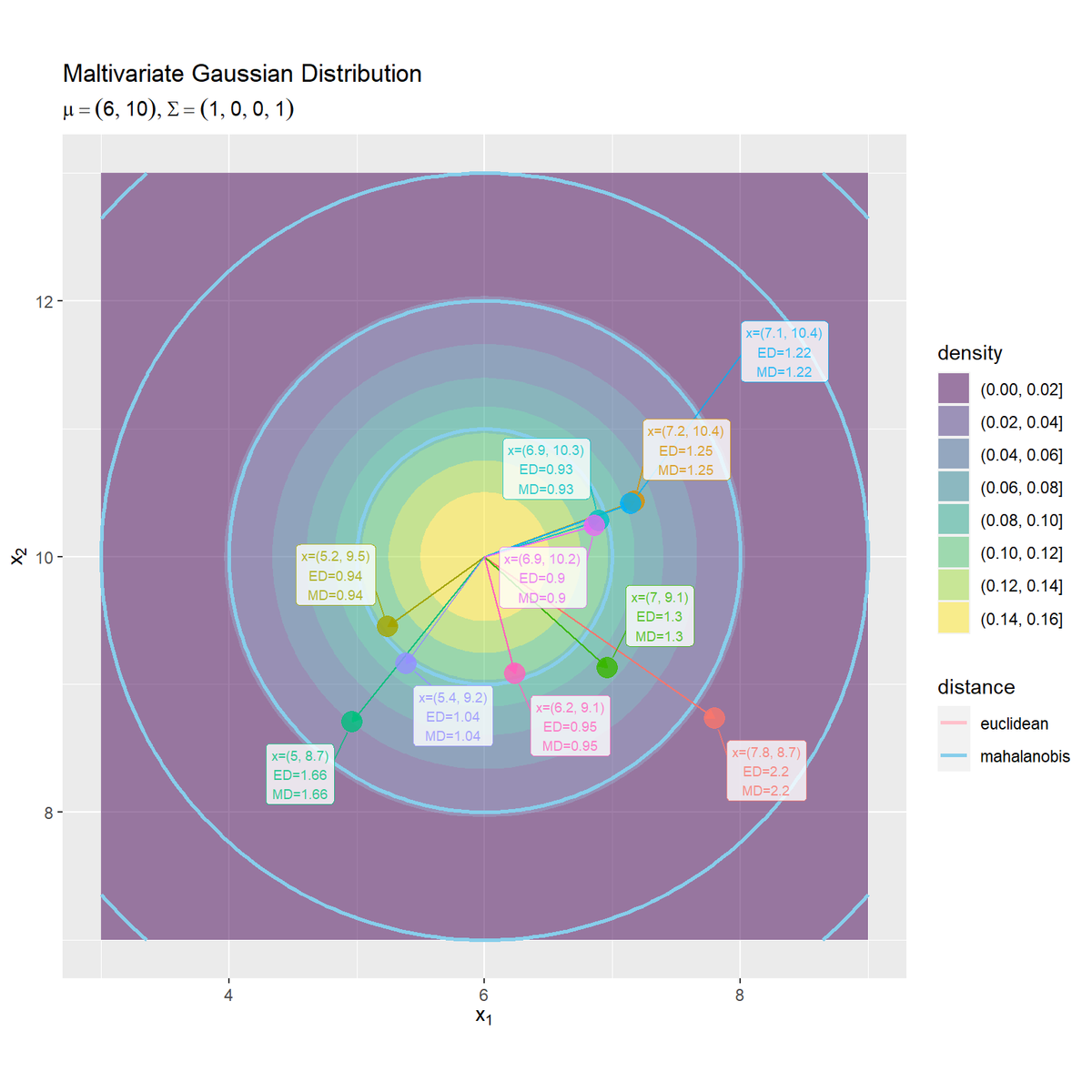
確率密度(の等高線)とマハラノビス距離(の等高線)が対応しているのが分かります。
分散共分散行列が単位行列の場合、ユークリッド距離とマハラノビス距離が一致します。
パラメータと距離の関係をアニメーションで可視化
パラメータの値を少しずつ変化させて、ユークリッド距離とマハラノビス距離の等高線の変化をアニメーションで確認します。
分散(1軸)の影響
まずは、x軸方向の分散$\sigma_1^2$の値を変化させ、$\sigma_{1,2}, \sigma_{2,1}, \sigma_2^2$を固定します。
・作図コード(クリックで展開)
# 平均ベクトルを指定 mu_d <- c(0, 0) # x軸の分散として利用する値を指定 sigma2_1_vals <- seq(from = 0.5, to = 5, by = 0.1) |> round(2) # y軸の分散を指定 sigma2_2 <- 2 # 共分散を指定 sigma_12 <- 0.6 # フレーム数を確認 length(sigma2_1_vals)
## [1] 46
値の間隔が一定になるように$\sigma_1^2$の値をsigma2_1_valsとして作成します。パラメータごとにフレームを切り替えるので、sigma2_1_valsの要素数がアニメーションのフレーム数になります。
また、共分散$\sigma_{1,2} = \sigma_{2,1}$をsigma2_2、y軸方向の分散$\sigma_2^2$をsigma2_2として値を指定します。
設定したパラメータに応じて確率変数の値$\mathbf{x}$を作成して、パラメータごとに分布を計算します。
# xの値を作成 x_1_vals <- seq( from = mu_d[1] - sqrt(max(sigma2_1_vals)) * 2, to = mu_d[1] + sqrt(max(sigma2_1_vals)) * 2, length.out = 100 ) x_2_vals <- seq( from = mu_d[2] - sqrt(sigma2_2) * 3, to = mu_d[2] + sqrt(sigma2_2) * 3, length.out = 100 ) # xの点を作成 x_mat <- tidyr::expand_grid( x_1 = x_1_vals, x_2 = x_2_vals ) |> # 格子点を作成 as.matrix() # マトリクスに変換 # パラメータごとに多次元ガウス分布を計算 anime_dens_df <- tidyr::expand_grid( sigma2_1 = sigma2_1_vals, x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(sigma2_1) |> # 確率密度の計算用にグループ化 dplyr::mutate( density = mvnfast::dmvn( X = x_mat, mu = mu_d, sigma = matrix(c(unique(sigma2_1), sigma_12, sigma_12, sigma2_2), nrow = 2, ncol = 2) ), # 確率密度 parameter = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2, ")") |> factor(levels = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1_vals, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_dens_df
## # A tibble: 460,000 × 5 ## sigma2_1 x_1 x_2 density parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 0.5 -4.47 -4.24 2.50e-10 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) ## 2 0.5 -4.47 -4.16 2.32e-10 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) ## 3 0.5 -4.47 -4.07 2.13e-10 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) ## 4 0.5 -4.47 -3.99 1.95e-10 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) ## 5 0.5 -4.47 -3.90 1.77e-10 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) ## 6 0.5 -4.47 -3.81 1.60e-10 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) ## 7 0.5 -4.47 -3.73 1.44e-10 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) ## 8 0.5 -4.47 -3.64 1.28e-10 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) ## 9 0.5 -4.47 -3.56 1.14e-10 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) ## 10 0.5 -4.47 -3.47 1.01e-10 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) ## # … with 459,990 more rows
パラメータsigma2_1_valsと確率変数x_1_vals, x_2_valsの要素の全ての組み合わせをexpand_grid()を作成します。これにより、パラメータごとにx_matを複製できます。
パラメータ列sigma2_1でグループ化することで、x_matごとに確率密度を計算できます。
パラメータごとにフレーム切替用のラベルを作成します。文字列型だと文字列の基準で順序が決まるので、因子型にしてパラメータに応じたレベル(順序)を設定します。
同様に、パラメータごとに描画範囲全体の距離を計算します。
# パラメータごとに距離を計算 anime_dist_df <- tidyr::expand_grid( sigma2_1 = sigma2_1_vals, x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(sigma2_1) |> # 距離の計算用にグループ化 dplyr::mutate( euclidean = apply((t(x_mat) - mu_d)^2, 2, sum) |> sqrt(), # ユークリッド距離 mahalanobis = t(t(x_mat)-mu_d) %*% solve(matrix(c(unique(sigma2_1), sigma_12, sigma_12, sigma2_2), nrow = 2, ncol = 2)) %*% (t(x_mat)-mu_d) |> diag() |> sqrt(), # マハラノビス距離 parameter = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2, ")") |> factor(levels = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1_vals, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() |> # グループ化を解除 tidyr::pivot_longer( cols = c(euclidean, mahalanobis), names_to = "type", values_to = "distance" ) # 距離の列をまとめる anime_dist_df
## # A tibble: 920,000 × 6 ## sigma2_1 x_1 x_2 parameter type distance ## <dbl> <dbl> <dbl> <fct> <chr> <dbl> ## 1 0.5 -4.47 -4.24 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) euclidean 6.16 ## 2 0.5 -4.47 -4.24 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) mahalanobis 6.40 ## 3 0.5 -4.47 -4.16 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) euclidean 6.11 ## 4 0.5 -4.47 -4.16 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) mahalanobis 6.41 ## 5 0.5 -4.47 -4.07 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) euclidean 6.05 ## 6 0.5 -4.47 -4.07 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) mahalanobis 6.43 ## 7 0.5 -4.47 -3.99 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) euclidean 5.99 ## 8 0.5 -4.47 -3.99 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) mahalanobis 6.44 ## 9 0.5 -4.47 -3.90 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) euclidean 5.93 ## 10 0.5 -4.47 -3.90 mu=(0, 0), Sigma=(0.5, 0.6, 0.6, 2) mahalanobis 6.46 ## # … with 919,990 more rows
「サンプルの距離の可視化」と同様に計算した2つの距離の列をpivot_longer()でまとめます。
等高線のアニメーション(gif画像)を作成します。
# 距離の等高線のプロット位置を指定 dist_vals <- seq(from = 0, to = 10, by = 1) # ユークリッド距離とマハラノビス距離のアニメーションを作図 anime_dist_graph <- ggplot() + geom_contour_filled(data = anime_dens_df, mapping = aes(x = x_1, y = x_2, z = density, fill = ..level..), alpha = 0.5) + # 2次元ガウス分布 geom_contour(data = anime_dist_df, mapping = aes(x = x_1, y = x_2, z = distance, color = type), breaks = dist_vals, size = 1) + # 距離 gganimate::transition_manual(parameter) + # フレーム coord_fixed(ratio = 1) + # アスペクト比 scale_color_manual(breaks = c("euclidean", "mahalanobis"), values = c("pink", "skyblue"), name = "distance") + # 線の色 labs(title ="Maltivariate Gaussian Distribution", subtitle = "{current_frame}", fill = "density", x = expression(x[1]), y = expression(x[2])) # gif画像を作成 gganimate::animate(anime_dist_graph, nframes = length(sigma2_1_vals), fps = 10, width = 800, height = 800)
transition_manual()にフレームの順序を表す列を指定します。この例では、因子型のラベルのレベルの順に描画されます。
animate()のフレーム数の引数nframesにパラメータ数、フレームレートの引数fpsに1秒当たりのフレーム数を指定します。fps引数の値が大きいほどフレームが早く切り替わります。ただし、値が大きいと意図通りに動作しません。
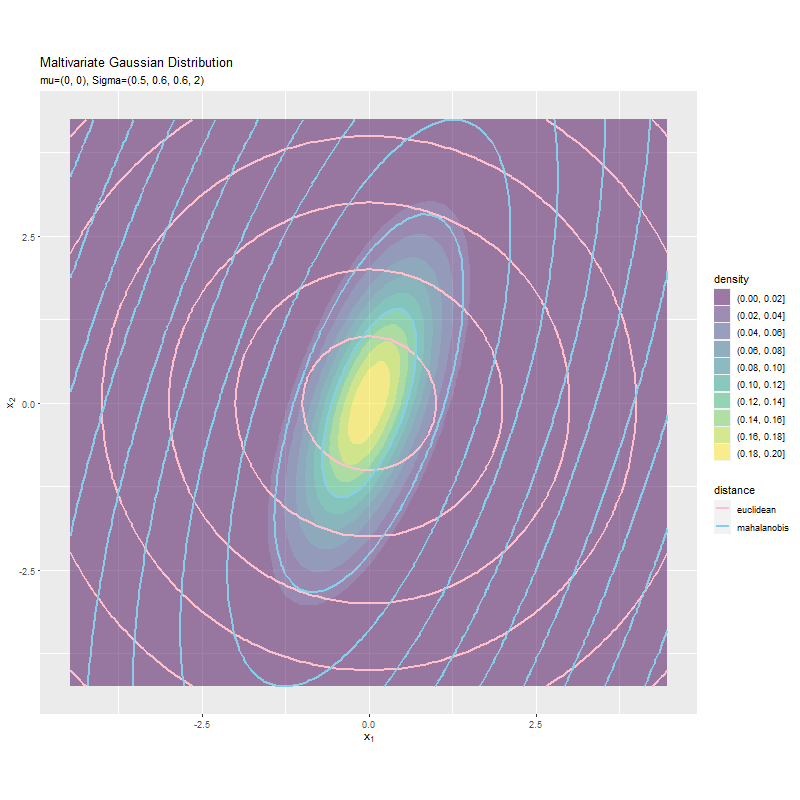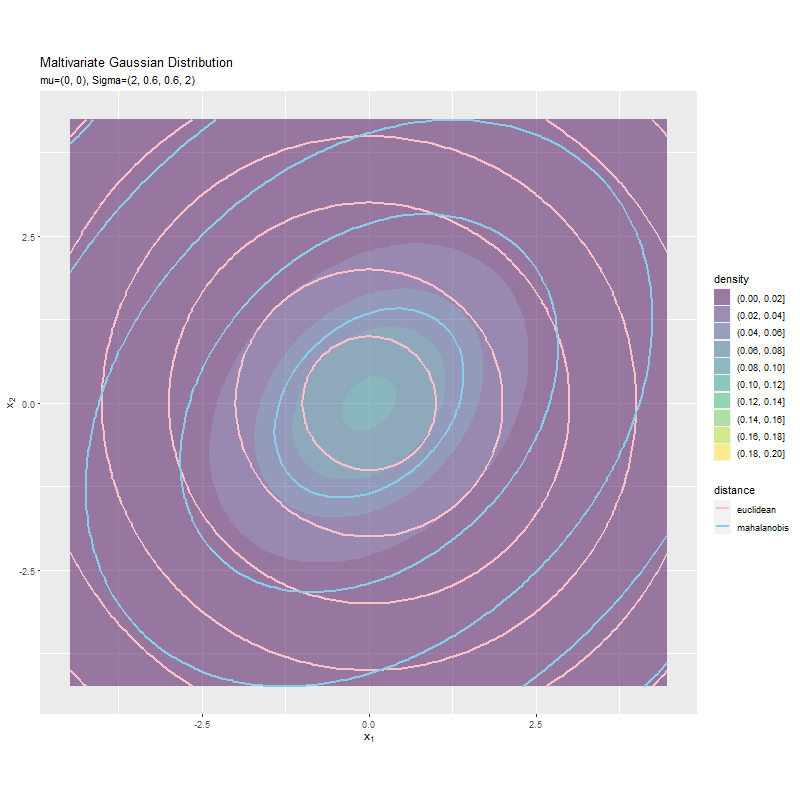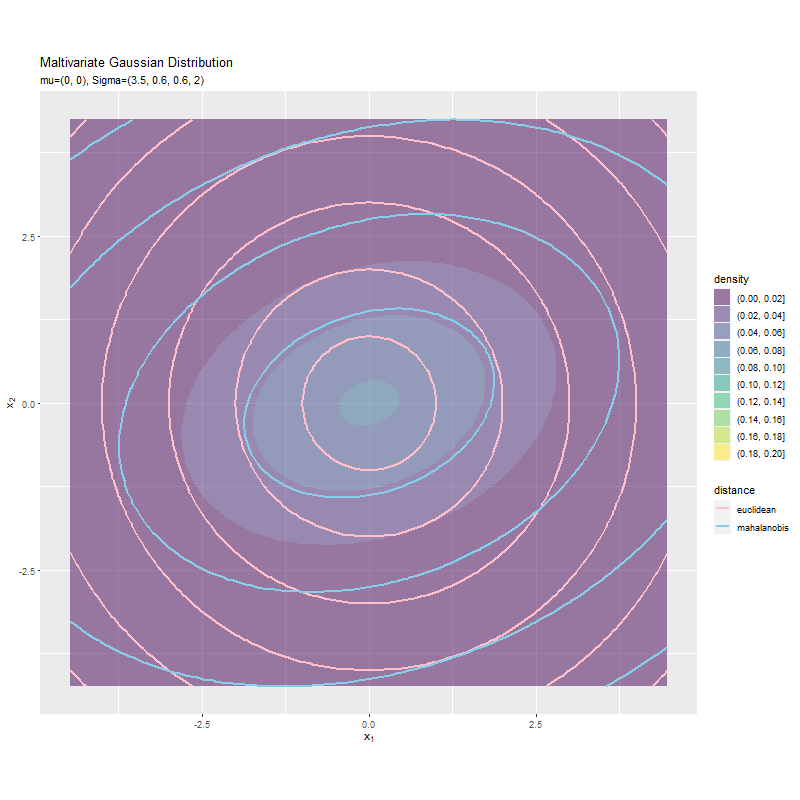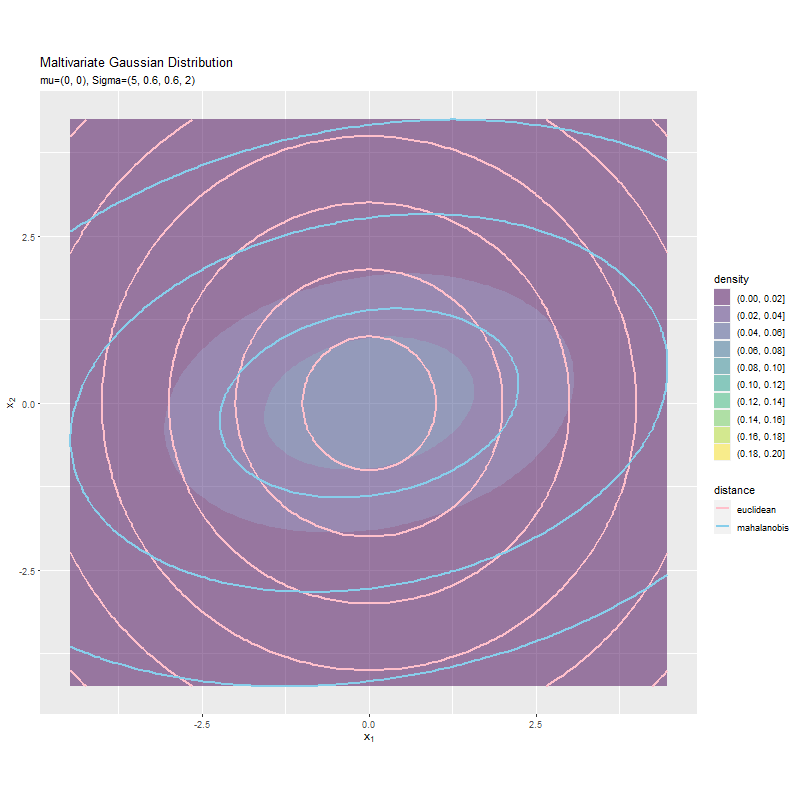
$\sigma_1^2$が大きくなるほど、x軸方向のマハラノビス距離が変化しています。ユークリッド距離は変化しません。これは計算式に$\boldsymbol{\Sigma}$を含まないためです。
分散(2軸)の影響
次は、y軸方向の分散$\sigma_2^2$の値を変化させ、$\sigma_1^2, \sigma_{1,2}, \sigma_{2,1}$を固定します。
・作図コード(クリックで展開)
# 平均ベクトルを指定 mu_d <- c(0, 0) # x軸の分散を指定 sigma2_1 <- 2 # y軸の分散として利用する値を指定 sigma2_2_vals <- seq(from = 0.5, to = 5, by = 0.1) |> round(2) # 共分散を指定 sigma_12 <- 0.6 # フレーム数を確認 length(sigma2_2_vals)
## [1] 46
値の間隔が一定になるように$\sigma_2^2$の値をsigma2_2_valsとして作成します。
また、x軸方向の分散$\sigma_1^2$をsigma2_1として値を指定します。
確率変数の値を作成して、パラメータごとに分布を計算します。
# xの値を作成 x_1_vals <- seq( from = mu_d[1] - sqrt(sigma2_1) * 3, to = mu_d[1] + sqrt(sigma2_1) * 3, length.out = 100 ) x_2_vals <- seq( from = mu_d[2] - sqrt(max(sigma2_2_vals)) * 2, to = mu_d[2] + sqrt(max(sigma2_2_vals)) * 2, length.out = 100 ) # xの点を作成 x_mat <- tidyr::expand_grid( x_1 = x_1_vals, x_2 = x_2_vals ) |> # 格子点を作成 as.matrix() # マトリクスに変換 # パラメータごとに多次元ガウス分布を計算 anime_dens_df <- tidyr::expand_grid( sigma2_2 = sigma2_2_vals, x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(sigma2_2) |> # 確率密度の計算用にグループ化 dplyr::mutate( density = mvnfast::dmvn( X = x_mat, mu = mu_d, sigma = matrix(c(sigma2_1, sigma_12, sigma_12, unique(sigma2_2)), nrow = 2, ncol = 2) ), # 確率密度 parameter = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2, ")") |> factor(levels = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2_vals, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_dens_df
## # A tibble: 460,000 × 5 ## sigma2_2 x_1 x_2 density parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 0.5 -4.24 -4.47 2.50e-10 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) ## 2 0.5 -4.24 -4.38 6.10e-10 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) ## 3 0.5 -4.24 -4.29 1.45e- 9 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) ## 4 0.5 -4.24 -4.20 3.35e- 9 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) ## 5 0.5 -4.24 -4.11 7.57e- 9 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) ## 6 0.5 -4.24 -4.02 1.67e- 8 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) ## 7 0.5 -4.24 -3.93 3.57e- 8 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) ## 8 0.5 -4.24 -3.84 7.47e- 8 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) ## 9 0.5 -4.24 -3.75 1.52e- 7 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) ## 10 0.5 -4.24 -3.66 3.02e- 7 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) ## # … with 459,990 more rows
「分散(1軸)の影響」と同様に処理します。
パラメータごとに描画範囲全体の距離を計算します。
# パラメータごとに距離を計算 anime_dist_df <- tidyr::expand_grid( sigma2_2 = sigma2_2_vals, x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(sigma2_2) |> # 距離の計算用にグループ化 dplyr::mutate( euclidean = apply((t(x_mat) - mu_d)^2, 2, sum) |> sqrt(), # ユークリッド距離 mahalanobis = t(t(x_mat)-mu_d) %*% solve(matrix(c(sigma2_1, sigma_12, sigma_12, unique(sigma2_2)), nrow = 2, ncol = 2)) %*% (t(x_mat)-mu_d) |> diag() |> sqrt(), # マハラノビス距離 parameter = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2, ")") |> factor(levels = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2_vals, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() |> # グループ化を解除 tidyr::pivot_longer( cols = c(euclidean, mahalanobis), names_to = "type", values_to = "distance" ) # 距離の列をまとめる anime_dist_df
## # A tibble: 920,000 × 6 ## sigma2_2 x_1 x_2 parameter type distance ## <dbl> <dbl> <dbl> <fct> <chr> <dbl> ## 1 0.5 -4.24 -4.47 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) euclidean 6.16 ## 2 0.5 -4.24 -4.47 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) mahalanobis 6.40 ## 3 0.5 -4.24 -4.38 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) euclidean 6.10 ## 4 0.5 -4.24 -4.38 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) mahalanobis 6.26 ## 5 0.5 -4.24 -4.29 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) euclidean 6.03 ## 6 0.5 -4.24 -4.29 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) mahalanobis 6.12 ## 7 0.5 -4.24 -4.20 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) euclidean 5.97 ## 8 0.5 -4.24 -4.20 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) mahalanobis 5.98 ## 9 0.5 -4.24 -4.11 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) euclidean 5.91 ## 10 0.5 -4.24 -4.11 mu=(0, 0), Sigma=(2, 0.6, 0.6, 0.5) mahalanobis 5.85 ## # … with 919,990 more rows
「分散(1軸)の影響」と同様に処理します。
「分散(1軸)の影響」のコードで作図できます。フレーム数はsigma2_2_valsの要素数です。
# gif画像を作成 gganimate::animate(anime_dist_graph, nframes = length(sigma2_2_vals), fps = 10, width = 800, height = 800)
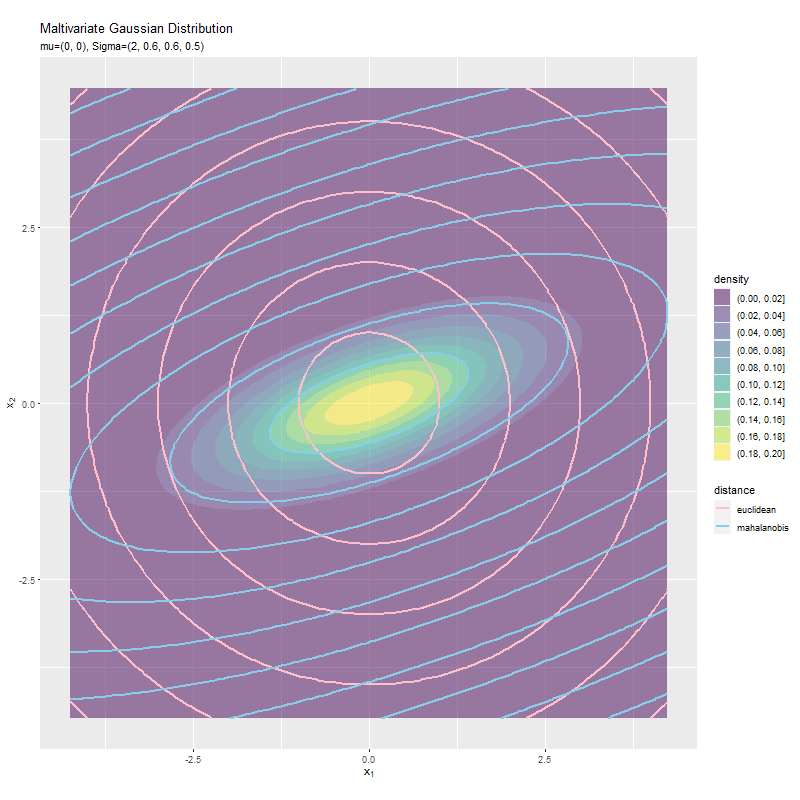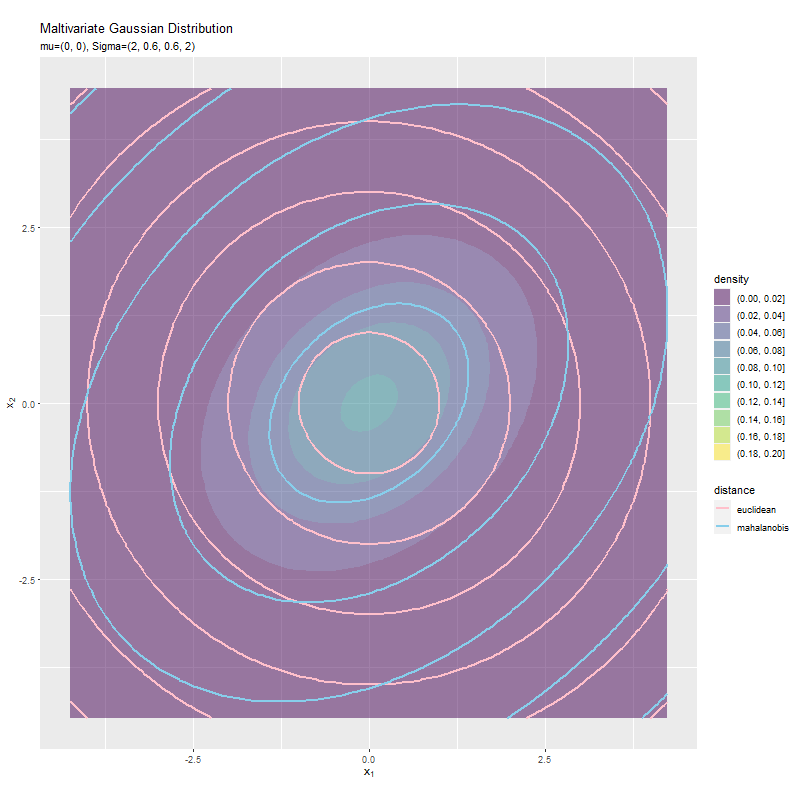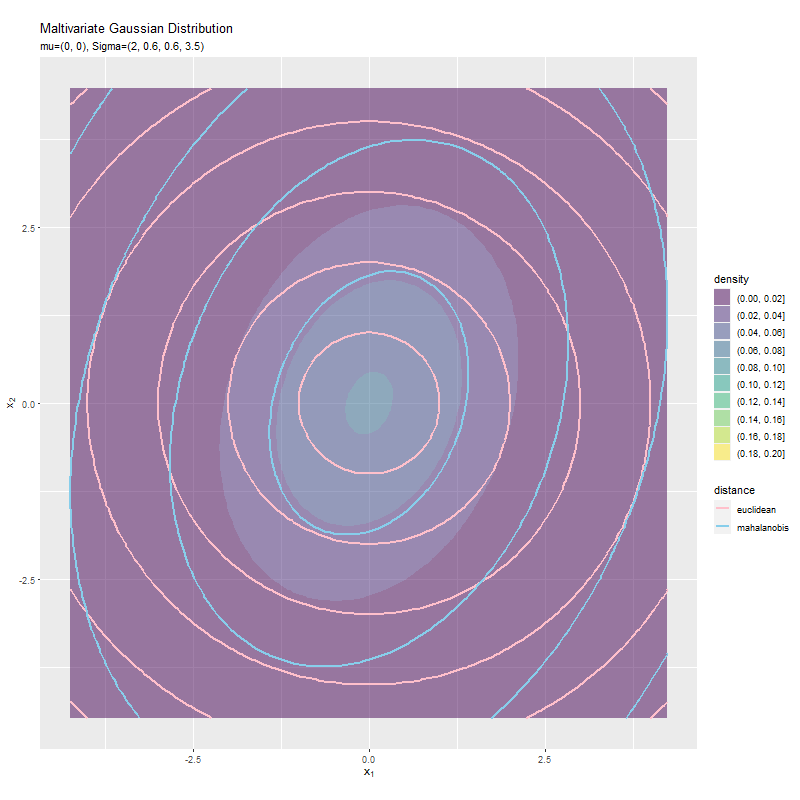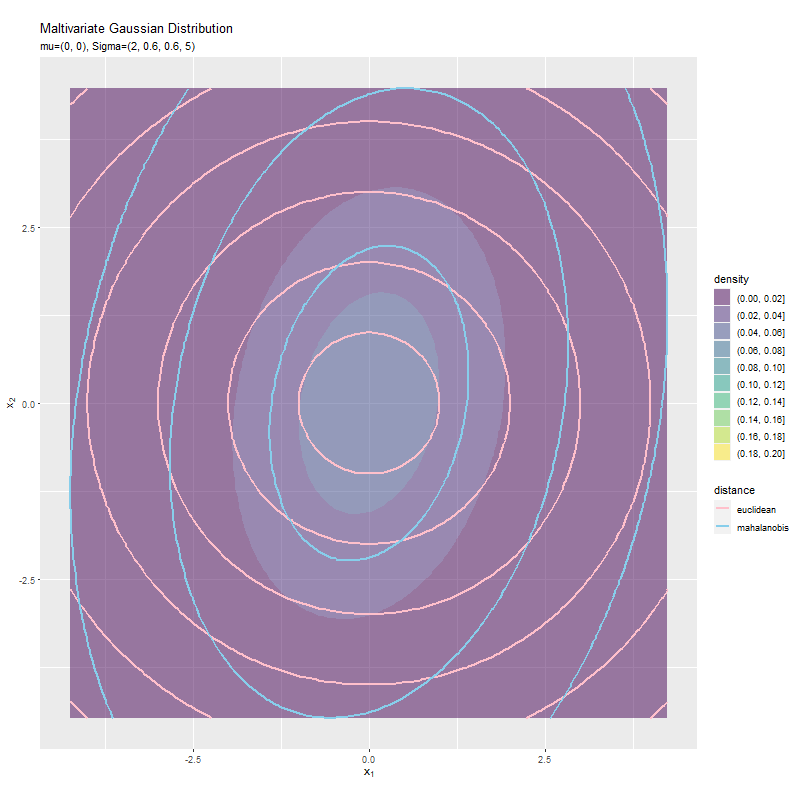
$\sigma_2^2$が大きくなるほど、y軸方向のマハラノビス距離が変化しています。
共分散の影響
最後に、共分散$\sigma_{1,2} = \sigma_{2,1}$の値を変化させ、$\sigma_1^2, \sigma_2^2$を固定します。
・作図コード(クリックで展開)
# 平均ベクトルを指定 mu_d <- c(0, 0) # 分散を指定 sigma2_1 <- 3 sigma2_2 <- 4.5 # 共分散を指定として利用する値を指定 sigma_12_vals <- seq(from = -2, to = 2, by = 0.1) |> round(2) # フレーム数を確認 length(sigma_12_vals)
## [1] 41
値の間隔が一定になるように$\sigma_{1,2}$の値をsigma_12_valsとして作成します。
確率変数の値を作成して、パラメータごとに分布を計算します。
# xの値を作成 x_1_vals <- seq( from = mu_d[1] - sqrt(sigma2_1) * 3, to = mu_d[1] + sqrt(sigma2_1) * 3, length.out = 100 ) x_2_vals <- seq( from = mu_d[2] - sqrt(sigma2_2) * 3, to = mu_d[2] + sqrt(sigma2_2) * 3, length.out = 100 ) # xの点を作成 x_mat <- tidyr::expand_grid( x_1 = x_1_vals, x_2 = x_2_vals ) |> # 格子点を作成 as.matrix() # マトリクスに変換 # パラメータごとに多次元ガウス分布を計算 anime_dens_df <- tidyr::expand_grid( sigma_12 = sigma_12_vals, x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(sigma_12) |> # 確率密度の計算用にグループ化 dplyr::mutate( density = mvnfast::dmvn( X = x_mat, mu = mu_d, sigma = matrix(c(sigma2_1, unique(sigma_12), unique(sigma_12), sigma2_2), nrow = 2, ncol = 2) ), # 確率密度 parameter = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2, ")") |> factor(levels = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12_vals, ", ", sigma_12_vals, ", ", sigma2_2, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() # グループ化を解除 anime_dens_df
## # A tibble: 410,000 × 5 ## sigma_12 x_1 x_2 density parameter ## <dbl> <dbl> <dbl> <dbl> <fct> ## 1 -2 -5.20 -6.36 1.36e-10 mu=(0, 0), Sigma=(3, -2, -2, 4.5) ## 2 -2 -5.20 -6.24 2.03e-10 mu=(0, 0), Sigma=(3, -2, -2, 4.5) ## 3 -2 -5.20 -6.11 3.00e-10 mu=(0, 0), Sigma=(3, -2, -2, 4.5) ## 4 -2 -5.20 -5.98 4.41e-10 mu=(0, 0), Sigma=(3, -2, -2, 4.5) ## 5 -2 -5.20 -5.85 6.46e-10 mu=(0, 0), Sigma=(3, -2, -2, 4.5) ## 6 -2 -5.20 -5.72 9.40e-10 mu=(0, 0), Sigma=(3, -2, -2, 4.5) ## 7 -2 -5.20 -5.59 1.36e- 9 mu=(0, 0), Sigma=(3, -2, -2, 4.5) ## 8 -2 -5.20 -5.46 1.96e- 9 mu=(0, 0), Sigma=(3, -2, -2, 4.5) ## 9 -2 -5.20 -5.34 2.81e- 9 mu=(0, 0), Sigma=(3, -2, -2, 4.5) ## 10 -2 -5.20 -5.21 4.01e- 9 mu=(0, 0), Sigma=(3, -2, -2, 4.5) ## # … with 409,990 more rows
「分散(1軸)の影響」と同様に処理します。
パラメータごとに描画範囲全体の距離を計算します。
# パラメータごとに距離を計算 anime_dist_df <- tidyr::expand_grid( sigma_12 = sigma_12_vals, x_1 = x_1_vals, x_2 = x_2_vals ) |> # パラメータごとに格子点を複製 dplyr::group_by(sigma_12) |> # 距離の計算用にグループ化 dplyr::mutate( euclidean = apply((t(x_mat) - mu_d)^2, 2, sum) |> sqrt(), # ユークリッド距離 mahalanobis = t(t(x_mat)-mu_d) %*% solve(matrix(c(sigma2_1, unique(sigma_12), unique(sigma_12), sigma2_2), nrow = 2, ncol = 2)) %*% (t(x_mat)-mu_d) |> diag() |> sqrt(), # マハラノビス距離 parameter = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12, ", ", sigma_12, ", ", sigma2_2, ")") |> factor(levels = paste0("mu=(", mu_d[1], ", ", mu_d[2], "), Sigma=(", sigma2_1, ", ", sigma_12_vals, ", ", sigma_12_vals, ", ", sigma2_2, ")")) # フレーム切替用ラベル ) |> dplyr::ungroup() |> # グループ化を解除 tidyr::pivot_longer( cols = c(euclidean, mahalanobis), names_to = "type", values_to = "distance" ) # 距離の列をまとめる anime_dist_df
## # A tibble: 820,000 × 6 ## sigma_12 x_1 x_2 parameter type distance ## <dbl> <dbl> <dbl> <fct> <chr> <dbl> ## 1 -2 -5.20 -6.36 mu=(0, 0), Sigma=(3, -2, -2, 4.5) euclidean 8.22 ## 2 -2 -5.20 -6.36 mu=(0, 0), Sigma=(3, -2, -2, 4.5) mahalanobis 6.29 ## 3 -2 -5.20 -6.24 mu=(0, 0), Sigma=(3, -2, -2, 4.5) euclidean 8.12 ## 4 -2 -5.20 -6.24 mu=(0, 0), Sigma=(3, -2, -2, 4.5) mahalanobis 6.22 ## 5 -2 -5.20 -6.11 mu=(0, 0), Sigma=(3, -2, -2, 4.5) euclidean 8.02 ## 6 -2 -5.20 -6.11 mu=(0, 0), Sigma=(3, -2, -2, 4.5) mahalanobis 6.16 ## 7 -2 -5.20 -5.98 mu=(0, 0), Sigma=(3, -2, -2, 4.5) euclidean 7.92 ## 8 -2 -5.20 -5.98 mu=(0, 0), Sigma=(3, -2, -2, 4.5) mahalanobis 6.10 ## 9 -2 -5.20 -5.85 mu=(0, 0), Sigma=(3, -2, -2, 4.5) euclidean 7.82 ## 10 -2 -5.20 -5.85 mu=(0, 0), Sigma=(3, -2, -2, 4.5) mahalanobis 6.03 ## # … with 819,990 more rows
「分散(1軸)の影響」と同様に処理します。
「分散(1軸)の影響」のコードで作図できます。フレーム数はsigma_12_valsの要素数です。
# gif画像を作成 gganimate::animate(anime_dist_graph, nframes = length(sigma_12_vals), fps = 10, width = 800, height = 800)
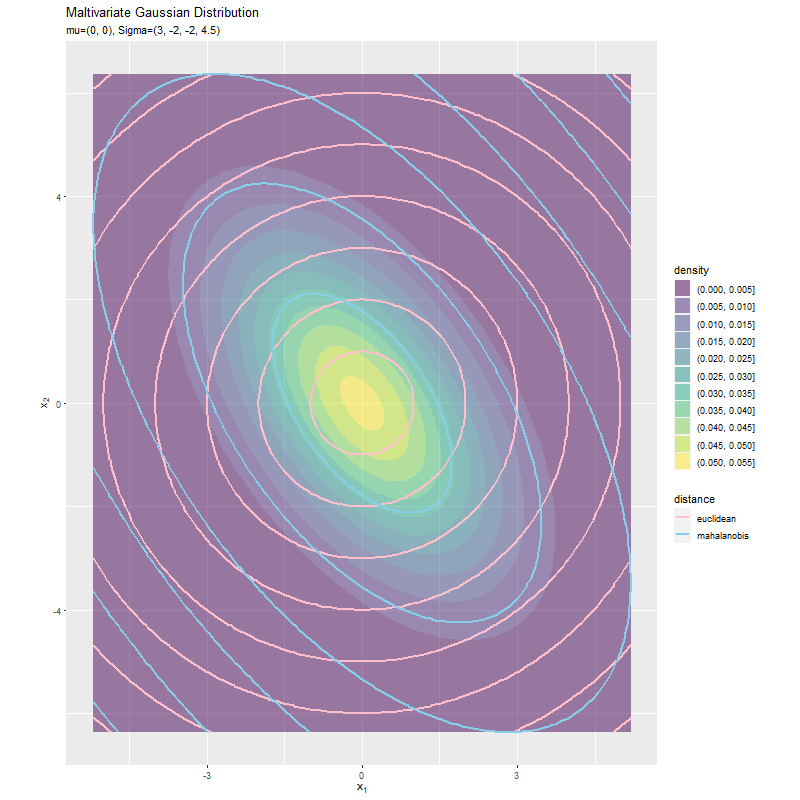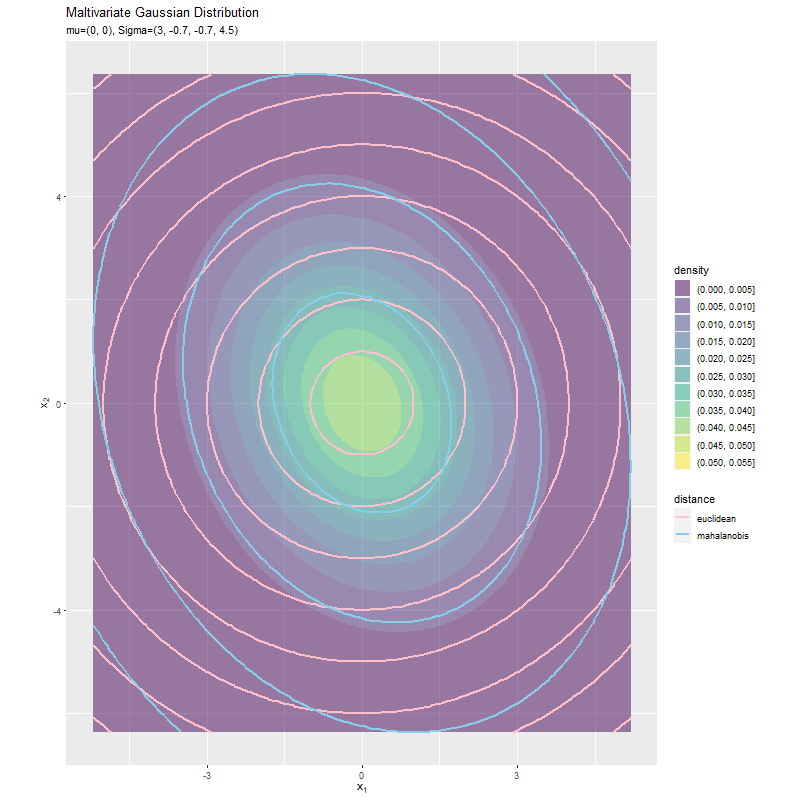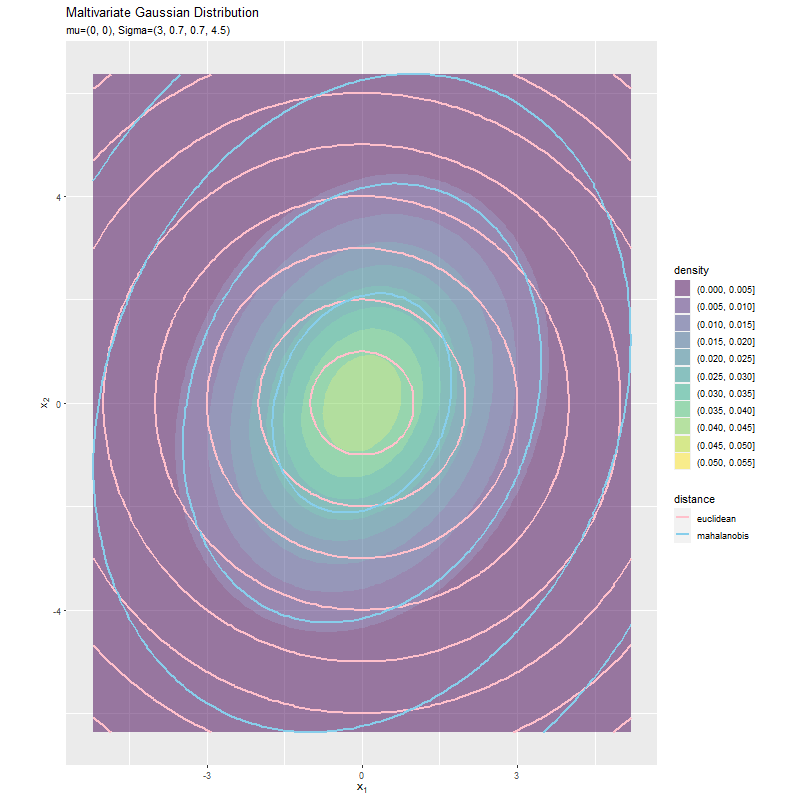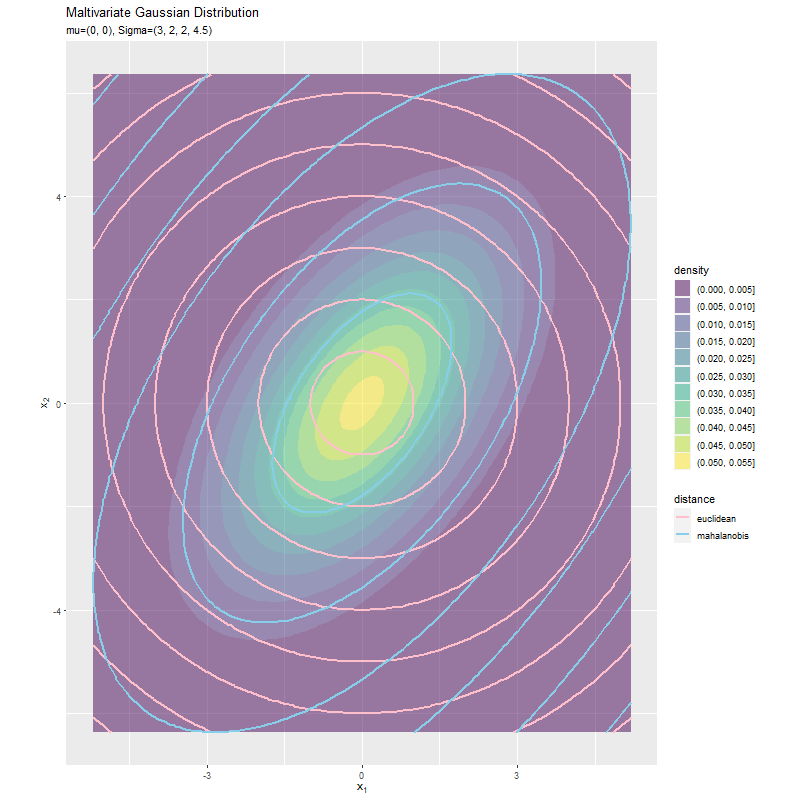
$\sigma_{1,2}$の値に応じて、マハラノビス距離の楕円の向きが変化しています。
参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上』,丸善出版,2012年.
おわりに
マハラノビス距離が3の等高線が意図せず描画範囲(平均から標準偏差の3倍)で推移することに気付いたので理由を考えてみたくなったのですが、これ以上脱線する余裕はないのであった。
1枚目のグラフに関して、等高線図と散布図でcolor引数を使いつつ等高線図の内容だけを凡例に表示させたくて色々試した結果、linetype引数を経由して凡例の表示を弄るという黒魔術的な実装をしてしまいました。適切な方法があれば教えてください。ggplotを色々扱えるようになったことと、グラフの出来には満足してます。
【次の内容】