【Python】多項分布の作図

はじめに

　機械学習で登場する確率分布について色々な角度から理解したいシリーズです。

　多項分布の計算とグラフの作成をPythonで行います。

【前の内容】

www.anarchive-beta.com

【他の記事一覧】

www.anarchive-beta.com

【目次】

多項分布

　多項分布(Multinomial Distribution)の計算と作図を行います。

　利用するライブラリを読み込みます。

# 利用するライブラリ
import numpy as np
from scipy.stats import multinomial # 多項分布
from scipy.special import gamma, loggamma # ガンマ関数, 対数ガンマ関数
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

　分布の変化をアニメーション(gif画像)で確認するのにmatplotlibライブラリのanimationモジュールを利用します。不要であれば省略してください。

定義式の確認

　まずは、多項分布の定義式を確認します。

　多項分布は、次の式で定義されます。詳しくは「多項分布の定義式 - からっぽのしょこ」を参照してください。

$$ \mathrm{Mult}(\boldsymbol{x} | M, \boldsymbol{\phi}) = \frac{ M! }{ x_1! x_2! \cdots x_V! } \prod_{v=1}^V \phi_v^{x_v} $$

　ここで、$x_v$はクラス$v$が出現した回数、$M$は試行回数、$\phi_v$はクラス$v$の出現確率です。
　確率変数の値$\mathbf{x} = (x_1, \cdots, x_V)$は、$x_v \in \{1, \cdots, V\}$、$\sum_{v=1}^V x_v = M$となります。パラメータ$\boldsymbol{\phi} = (\phi_1, \cdots, \phi_V)$は、$\phi_v \in (0, 1)$、$\sum_{v=1}^V \phi_v = 1$を満たす必要があります。

　この式の対数をとると、次の式になります。

$$ \log \mathrm{Mult}(\boldsymbol{x} | N, \boldsymbol{\phi}) = \log M! + \sum_{v=1}^V \Bigl\{ x_v \log \phi_v - \log x_v! \Bigr\} $$

　多項分布のクラス$v$における平均と分散は、次の式で計算できます。詳しくは「多項分布の平均と分散の導出 - からっぽのしょこ」を参照してください。

$$ \begin{aligned} \mathbb{E}[x_v] &= N \phi_v \\ \mathbb{V}[x_v] &= N \phi_v (1 - \phi_v) \end{aligned} $$

　これらの計算を行いグラフを作成します。

確率の計算

　多項分布に従う確率を計算する方法をいくつか確認します。

　パラメータを設定します。

# パラメータを指定
phi_v = np.array([0.3, 0.5, 0.2])

# 確率変数の値を指定
x_v = np.array([2.0, 3.0, 1.0])

# データ数を計算
M = np.sum(x_v)

　多項分布のパラメータ$\boldsymbol{\phi} = (\phi_1, \cdots, \phi_V)$、$0 \leq \phi_v \leq 1$、$\sum_{v=1}^V \phi_v = 1$、試行回数$M$、確率変数がとり得る値$\mathbf{x} = (x_1, \cdots, x_V)$、$x_v \in \{0, 1, \cdots, M\}$、$\sum_{v=1}^V x_v = M$を指定します。設定した値に従う確率を計算します。

　まずは、定義式から確率を計算します。

# 定義式により確率を計算
C = gamma(M + 1.0) / np.prod(gamma(x_v + 1.0))
prob = C * np.prod(phi_v**x_v)
print(prob)

0.13499999999999998

　多項分布の定義式

$$ \begin{aligned} C_{\mathrm{Mult}} &= \frac{M!}{\prod_{v=1}^V x_v!} \\ \mathrm{Mult}(\mathbf{x} | M, \boldsymbol{\phi}) &= C_{\mathrm{Mult}} \prod_{v=1}^V \phi_v^{x_v} \end{aligned} $$

で計算します。$C_{\mathrm{Mult}}$は、多項分布の正規化係数です。
　階乗$x!$の計算は、ガンマ関数$\Gamma(x + 1) = x!$に置き換えて計算します。ガンマ関数は、SciPyライブラリのspecialモジュールのgamma()で計算できます。

　対数をとった定義式から計算します。

# 対数をとった定義式により確率を計算
log_C = loggamma(M + 1.0) - np.sum(loggamma(x_v + 1.0))
log_prob = log_C + np.sum(x_v * np.log(phi_v))
prob = np.exp(log_prob)
print(prob, log_prob)

0.13500000000000006 -2.002480500543707

　対数をとった定義式

$$ \begin{aligned} \log C_{\mathrm{Mult}} &= \log M! - \sum_{v=1}^V \log x_v! \\ \log \mathrm{Mult}(\mathbf{x} | M, \boldsymbol{\phi}) &= \log C_{\mathrm{Mult}} + \sum_{v=1}^V x_v \log \phi_v \end{aligned} $$

を計算します。
　対数をとったガンマ関数はloggamma()で計算できます。
　計算結果の指数をとると確率が得られます。

$$ \mathrm{Mult}(\mathbf{x} | M, \boldsymbol{\phi}) = \exp \Bigr( \log \mathrm{Mult}(\mathbf{x} | M, \boldsymbol{\phi}) \Bigr) $$

　指数と対数の性質より$\exp(\log x) = x$です。

　次は、SciPyライブラリのモジュールを使って確率を計算します。
　多項分布のモジュールmultinomialの確率計算メソッドpmf()を使って計算します。

# 多項分布の関数により確率を計算
prob = multinomial.pmf(x=x_v, n=M, p=phi_v)
print(prob)

0.13500000000000018

　出現頻度の引数xにx_v、試行回数の引数をn = M、出現確率の引数pにphi_vを指定します。

　logpmf()だと対数をとった確率を計算します。

# 多項分布の対数をとった関数により確率を計算
log_prob = multinomial.logpmf(x=x_v, n=M, p=phi_v)
prob = np.exp(log_prob)
print(prob, log_prob)

0.13500000000000018 -2.0024805005437063

　計算結果の指数をとると確率が得られます。

統計量の計算

　多項分布の平均と分散を計算します。

　クラス$v$の平均を計算します。

# クラス番号を指定
v = 1

# クラスvの平均を計算
E_x = M * phi_v[v]
print(E_x)

3.0

　多項分布の各クラスの平均は、次の式で計算できます。

$$ \mathbb{E}[x_v] = N \phi_v $$

　クラス$v$の分散を計算します。

# クラスvの分散を計算
V_x = M * phi_v[v] * (1.0 - phi_v[v])
print(V_x)

1.5

　多項分布の各クラスの分散は、次の式で計算できます。

$$ \mathbb{V}[x_v] = N \phi_v (1 - \phi_v) $$

グラフの作成

　MatplotlibライブラリのPyPlotモジュールを利用して多項分布のグラフを作成します。

・分布の計算

　作図に利用する$\mathbf{x} = (x_1, x_2, x_3)$の値を作成します。ここでは、3次元のグラフで描画するため$V = 3$とします。3D棒グラフについては「3D棒グラフの作図 - からっぽのしょこ」を参照してください。

# 試行回数を指定
M = 10

# 作図用のxの値を作成
x_vals = np.arange(M + 1)

# 格子点を作成
X1, X2 = np.meshgrid(x_vals, x_vals)

# 作図用のxの点を作成
x1_vals = X1.flatten()
x2_vals = X2.flatten()
x3_vals = np.where(x1_vals+x2_vals <= M, M - (x1_vals+x2_vals), 0.0)

# 計算用のxの点を作成
x_points = np.stack([x1_vals, x2_vals, x3_vals], axis=1)
print(x_points[:5])
print(x_points.shape)

[[ 0.  0. 10.]
 [ 1.  0.  9.]
 [ 2.  0.  8.]
 [ 3.  0.  7.]
 [ 4.  0.  6.]]
(121, 3)

　$\mathbf{x}$の各要素$x_v$がとり得る値(0からMの整数)をx_valsとします。
　x_valsの全ての組み合わせを持つように$x_1, x_2$を作成します。np.meshgrid()で全ての組み合わせを作成します。結果は2次元配列になるので、flatten()で1次元配列に並び替えます。
　np.where()を使って$x_3$を作成します。$x_1 + x_2 + x_3 = M$となるように$x_3$の値を決めます。ただし、$x_1 + x_2 > M$となる場合は、$x_3 = 0$とします。

　$x_1, x_2, x_3$の値x1_vals, x2_vals, x3_valsを列とする配列を作成します。x_pointsの各行が1つの点$\mathbf{x}$に対応します。

　作成した$\mathbf{x}$ごとの確率を計算します。

# 分布を計算
probability = multinomial.pmf(x=x_points, n=M, p=phi_v)
print(probability[:5])
print(np.sum(probability))

[1.02400e-07 1.53600e-06 1.03680e-05 4.14720e-05 1.08864e-04]
1.0000000000000004

　x_pointsの行ごとの確率を返します。
　分布の総和は1になります。

　作図用の点と対応する確率が得られたので、分布を描画していきます。

・行ごとに色付け

　y軸($x_2$)の値ごとに色を変えて描画します。

# カラーマップを設定
cm = plt.get_cmap('hsv')

# 多項分布を作図
fig = plt.figure(figsize=(12, 9)) # 図の設定
ax = fig.add_subplot(projection='3d') # 3D用の設定
ax.bar3d(x=x1_vals - 0.5, y=x2_vals - 0.5, z=np.zeros_like(x1_vals), 
         dx=1.0, dy=1.0, dz=probability, 
         color=cm(x2_vals / M), alpha=0.5, shade=True) # 3D棒グラフ
ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')
ax.set_zlabel('probability')
fig.suptitle('Maltinomial Distribution', fontsize=20)
ax.set_title('$\phi=(' + ', '.join([str(phi) for phi in phi_v]) + '), M=' + str(M) + '$', loc='left')
#ax.view_init(elev=90, azim=270) # 表示アングル
plt.show()

多項分布のグラフ

　$x_2$の値x2_valsを最大値のMで割って正規化した値を、色(RGB)情報に変換してcolor引数に指定します。

　$x_2 = 5$における$M + 1$個の点($x_1 = 0, \cdots, M$)を確認してみます。

# 確認
print(x_points[55:66])
print(probability[55:66])

[[ 0.  5.  5.]
 [ 1.  5.  4.]
 [ 2.  5.  3.]
 [ 3.  5.  2.]
 [ 4.  5.  1.]
 [ 5.  5.  0.]
 [ 6.  5.  0.]
 [ 7.  5.  0.]
 [ 8.  5.  0.]
 [ 9.  5.  0.]
 [10.  5.  0.]]
[0.00252    0.0189     0.0567     0.08505    0.0637875  0.01913625
 0.         0.         0.         0.         0.        ]

　$\mathbf{x} = (x_1, x_2, x_3)$について、$(6, 5, 0)$から$(10, 5, 0)$は、$\mathbf{x}$がとり得ない値なので確率が0になっています。

　そこで、$\mathbf{x}$がとり得ない点をマスクします。

# xがとり得ない値の要素をマスク
x2_mask_vals = np.ma.masked_where(condition=x1_vals+x2_vals > M, a=x2_vals)
probability_mask = np.ma.masked_where(condition=x1_vals+x2_vals > M, a=probability)
print(x1_vals[55:66])
print(x2_mask_vals[55:66])
print(probability_mask[55:66])

[ 0  1  2  3  4  5  6  7  8  9 10]
[5 5 5 5 5 5 -- -- -- -- --]
[0.002520000000000002 0.018899999999999986 0.05670000000000003
 0.08504999999999999 0.06378750000000005 0.019136250000000018 -- -- -- --
 --]

　np.ma.masked_where()で$x_1 + x_2 > M$の要素をマスクします。第1引数に条件式(の結果)を、第2引数に対象の配列を指定します。Trueの要素をマスクして返します。
　マスクされた要素は--と表示されます。

　先ほどと同様に作図します。

# カラーマップを設定
cm = plt.get_cmap('hsv')

# 多項分布を作図
fig = plt.figure(figsize=(12, 9)) # 図の設定
ax = fig.add_subplot(projection='3d') # 3D用の設定
ax.bar3d(x=x1_vals - 0.5, y=x2_vals - 0.5, z=np.zeros_like(x1_vals), 
         dx=1.0, dy=1.0, dz=probability_mask, 
         color=cm(x2_mask_vals / M), alpha=0.5, shade=True) # 3D棒グラフ
ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')
ax.set_zlabel('probability')
fig.suptitle('Maltinomial Distribution', fontsize=20)
ax.set_title('$\phi=(' + ', '.join([str(phi) for phi in phi_v]) + '), M=' + str(M) + '$', loc='left')
#ax.view_init(elev=90, azim=270) # 表示アングル
plt.show()

多項分布のグラフ

　マスクされた点が黒色になっています。

　次は、マスクではなく消去します。

# xがとり得ない値の要素を削除
x1_del_vals = np.delete(arr=x1_vals, obj=x1_vals+x2_vals > M)
x2_del_vals = np.delete(arr=x2_vals, obj=x1_vals+x2_vals > M)
probability_del = np.delete(arr=probability, obj=x1_vals+x2_vals > M)
print(x1_del_vals[45:55])
print(x2_del_vals[45:55])
print(probability_del[45:55])

[0 1 2 3 4 5 0 1 2 3]
[5 5 5 5 5 5 6 6 6 6]
[0.00252    0.0189     0.0567     0.08505    0.0637875  0.01913625
 0.00525    0.0315     0.070875   0.070875  ]

　np.delete()の第1引数に対象の配列を、第2引数に条件式(の結果)を指定すると、Trueの要素を削除して返します。

　これまでと同様に作図します。

# カラーマップを設定
cm = plt.get_cmap('hsv')

# 多項分布を作図
fig = plt.figure(figsize=(12, 9)) # 図の設定
ax = fig.add_subplot(projection='3d') # 3D用の設定
ax.bar3d(x=x1_del_vals - 0.5, y=x2_del_vals - 0.5, z=np.zeros_like(x1_del_vals), 
         dx=1.0, dy=1.0, dz=probability_del, 
         color=cm(x2_del_vals / M), alpha=0.5, shade=True) # 3D棒グラフ
ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')
ax.set_zlabel('probability')
fig.suptitle('Maltinomial Distribution', fontsize=20)
ax.set_title('$\phi=(' + ', '.join([str(phi) for phi in phi_v]) + '), M=' + str(M) + '$', loc='left')
#ax.view_init(elev=90, azim=270) # 表示アングル
plt.show()

多項分布のグラフ

　$x_1 + x_2 > M$の範囲が描画されなくなりました。

・確率に応じて色付け

　先ほどは、点の位置によって色分けしました。今度は、各点の確率の大小によって色を変えて描画します。

# カラーマップを設定
cm = plt.get_cmap('jet')

# 多項分布を作図
fig = plt.figure(figsize=(12, 9)) # 図の設定
ax = fig.add_subplot(projection='3d') # 3D用の設定
ax.bar3d(x=x1_del_vals - 0.5, y=x2_del_vals - 0.5, z=np.zeros_like(x1_del_vals), 
         dx=1.0, dy=1.0, dz=probability_del, 
         color=cm(probability_del / np.max(probability_del)), alpha=0.5, shade=True) # 3D棒グラフ
ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')
ax.set_zlabel('probability')
fig.suptitle('Maltinomial Distribution', fontsize=20)
ax.set_title('$\phi=(' + ', '.join([str(phi) for phi in phi_v]) + '), M=' + str(M) + '$', loc='left')
#ax.view_init(elev=0, azim=300) # 表示アングル:(横から)
#ax.view_init(elev=90, azim=270) # 表示アングル:(上から)
plt.show()

多項分布のグラフ

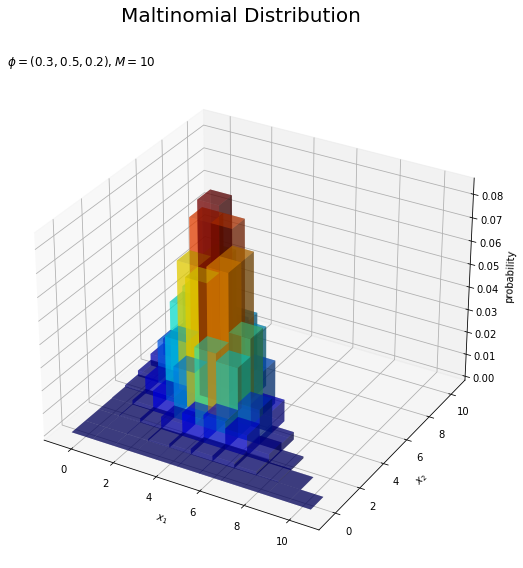
　各点の確率probabilityを最大値で割って正規化した値を、色(RGB)情報に変換してcolor引数に指定します。

　続いて、統計量の情報を重ねて描画します。

# 補助線用の値を作成
vals = np.arange(-1, M + 2)
zeros = np.repeat(0.0, len(vals))

# 補助線用の統計量を計算
E_x1 = M * phi_v[0]
V_x1 = M * phi_v[0] * (1.0 - phi_v[0])
s_x1 = np.sqrt(V_x1)
E_x2 = M * phi_v[1]
V_x2 = M * phi_v[1] * (1.0 - phi_v[1])
s_x2 = np.sqrt(V_x2)

# カラーマップを設定
cm = plt.get_cmap('jet')

# 多項分布を作図
fig = plt.figure(figsize=(12, 9)) # 図の設定
ax = fig.add_subplot(projection='3d') # 3D用の設定
ax.bar3d(x=x1_del_vals - 0.5, y=x2_del_vals - 0.5, z=np.zeros_like(x1_del_vals), 
         dx=1.0, dy=1.0, dz=probability_del, 
         color=cm(probability_del / np.max(probability_del)), alpha=0.5, shade=False) # 分布
ax.plot(xs=np.repeat(E_x1, len(vals)), ys=vals, zs=zeros, color='#00A968', linestyle='--', label='$E[x_v]$') # クラス1の平均
ax.plot(xs=np.repeat(E_x1 - s_x1, len(vals)), ys=vals, zs=zeros, color='#00A968', linestyle=':', label='$E[x_v] \pm \sqrt{V[x_v]}$') # クラス1の平均 + 標準偏差
ax.plot(xs=np.repeat(E_x1 + s_x1, len(vals)), ys=vals, zs=zeros, color='#00A968', linestyle=':') # クラス1の平均 + 標準偏差
ax.plot(xs=vals, ys=np.repeat(E_x2, len(vals)), zs=zeros, color='#00A968', linestyle='--') # クラス2の平均
ax.plot(xs=vals, ys=np.repeat(E_x2 - s_x2, len(vals)), zs=zeros, color='#00A968', linestyle=':') # クラス2の平均 + 標準偏差
ax.plot(xs=vals, ys=np.repeat(E_x2 + s_x2, len(vals)), zs=zeros, color='#00A968', linestyle=':') # クラス2の平均 + 標準偏差
ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')
ax.set_zlabel('probability')
fig.suptitle('Maltinomial Distribution', fontsize=20)
ax.set_title('$\phi=(' + ', '.join([str(phi) for phi in phi_v]) + '), M=' + str(M) + '$', loc='left')
ax.set_xticks(ticks=x_vals) # x軸目盛
ax.set_yticks(ticks=x_vals) # y軸目盛
ax.legend() # 凡例
#ax.view_init(elev=90, azim=270) # 表示アングル
plt.show()

多項分布のグラフ

　各クラス(軸)$x_1, x_2$の平均(破線)が交差する点が確率の最大値であるのが分かります。
　また、平均を中心に標準偏差の範囲(破線)で山が高く(赤に近い色に)なっているのが分かります。

パラメータと分布の形状の関係

　パラメータ$\boldsymbol{\phi}$と試行回数$M$が及ぼす分布への影響をアニメーション(gif画像)で可視化します。

・パラメータの影響

　まずは、パラメータ$\boldsymbol{\phi}$の値を少しずつ変更して、分布の変化をアニメーションで確認します。

・作図コード(クリックで展開)

　作図に利用する$\boldsymbol{\phi} = (\phi_1, \phi_2, \phi_3)$の値を作成します。

# 作図用のphiの値を作成
phi_vals = np.arange(start=0.0, stop=1.01, step=0.01)

# 作図用のphiの点を作成
phi_points = np.stack([
    phi_vals, 
    (1.0 - phi_vals) * 0.6, # 配分を指定
    (1.0 - phi_vals) * 0.4 # 配分を指定
], axis=1)
print(phi_points[:5])
print(np.sum(phi_points[:5], axis=1))
print(phi_points.shape)

[[0.    0.6   0.4  ]
 [0.01  0.594 0.396]
 [0.02  0.588 0.392]
 [0.03  0.582 0.388]
 [0.04  0.576 0.384]]
[1. 1. 1. 1. 1.]
(101, 3)

　$\phi_1$がとり得る値を作成してphi_valsとします。
　$\phi_1 + \phi_2 + \phi_3 = 1$なので、$1 - \phi_1$は$\phi_1$以外の確率の和$\phi_2 + \phi_3$です。よって、1 - phi_valsを分割して$\phi_2, \phi_3$の値とします。
　$\phi_1, \phi_2, \phi_3$の値を列とする配列を作成します。

　「グラフの作成」と同様に$\mathbf{x} = (x_1, x_2, x_3)$の値を作成します。

# 試行回数を指定
M = 10

# 作図用のxの値を作成
x_vals = np.arange(M + 1)

# 格子点を作成
X1, X2 = np.meshgrid(x_vals, x_vals)

# 作図用のxの点を作成:(xがとり得ない値を消去する場合)
x1_vals = np.delete(X1.flatten(), obj=(X1 + X2).flatten() > M)
x2_vals = np.delete(X2.flatten(), obj=(X1 + X2).flatten() > M)

# 作図用のxの点を作成:(全ての組み合わせを描画する場合)
#x1_vals = X1.flatten()
#x2_vals = X2.flatten()
x3_vals = np.where(x1_vals+x2_vals <= M, M - (x1_vals+x2_vals), 0.0)

# 計算用のxの点を作成
x_points = np.stack([x1_vals, x2_vals, x3_vals], axis=1)
print(x_points[:5])
print(x_points.shape)

[[ 0.  0. 10.]
 [ 1.  0.  9.]
 [ 2.  0.  8.]
 [ 3.  0.  7.]
 [ 4.  0.  6.]]
(66, 3)

　gif画像を作成します。

# カラーマップの設定
cm = plt.get_cmap('jet')

# カラーマップの最大値を指定
p_max = 0.15

# 図を初期化
fig = plt.figure(figsize=(12, 8)) # 図の設定
ax = fig.add_subplot(projection='3d') # 3D用の設定
fig.suptitle('Multinomial Distribution', fontsize=20)

# 作図処理を関数として定義
def update(i):
    # 前フレームのグラフを初期化
    plt.cla()
    
    # i番目のパラメータを取得
    phi_v = phi_points[i]
    
    # i番目のパラメータによる分布を計算
    probability = multinomial.pmf(x=x_points, n=M, p=phi_v)
    
    # xがとり得ない値の要素をマスク:(xがとり得ない値をマスクする場合)
    #probability = np.ma.masked_where(x1_vals + x2_vals > M, probability)
    
    # 多項分布を作図
    ax.bar3d(x=x1_vals - 0.45, y=x2_vals - 0.45, z=np.zeros_like(x1_vals), 
             dx=0.9, dy=0.9, dz=probability, 
             color=cm(probability / p_max), alpha=0.5, shade=True) # 3D棒グラフ
    ax.set_xlabel('$x_1$')
    ax.set_ylabel('$x_2$')
    ax.set_zlabel('probability')
    ax.set_title('$\phi=(' + ', '.join([str(phi) for phi in np.round(phi_v, 2)]) + ')' +
                 ', M=' + str(M) + '$', loc='left')
    ax.set_zlim(0.0, p_max) # z軸の表示範囲
    #ax.view_init(elev=0, azim=315) # 表示アングル

# gif画像を作成
anime_prob = FuncAnimation(fig, update, frames=len(phi_vals), interval=50)

# gif画像を保存
anime_prob.save('Multinomial_prob_phi.gif')

多項分布とパラメータの関係

　$\phi_2$の値が大きいほど$x_2$が大きい確率が高く、$\phi_1$が大きくなるほど$x_1$が大きい確率が高くなるのを確認できます。

・試行回数の影響

　続いて、$\boldsymbol{\phi}$を固定して$M$を変更したときの、分布の変化をアニメーションで確認します。

・作図コード(クリックで展開)

# パラメータを指定
phi_v = np.array([0.3, 0.5, 0.2])

# 試行回数の最大値を指定
M_max = 50

# カラーマップの設定
cm = plt.get_cmap('jet')

# カラーマップの最大値を指定
p_max = 0.1

# 図を初期化
fig = plt.figure(figsize=(12, 8)) # 図の設定
ax = fig.add_subplot(projection='3d') # 3D用の設定
fig.suptitle('Multinomial Distribution', fontsize=20)

# 作図処理を関数として定義
def update(M):
    # 前フレームのグラフを初期化
    plt.cla()
    
    # 1からMに変換
    M += 1
    
    # 作図用のxの値を作成
    x_vals = np.arange(M + 1)
    
    # 格子状のxの点を作成
    X1, X2 = np.meshgrid(x_vals, x_vals)
    
    # 作図用のxの点を作成:(xがとり得ない値を消去する場合)
    x1_vals = np.delete(X1.flatten(), obj=(X1 + X2).flatten() > M)
    x2_vals = np.delete(X2.flatten(), obj=(X1 + X2).flatten() > M)
    
    # 作図用のxの点を作成:(全ての組み合わせを描画する場合)
    #x1_vals = X1.flatten()
    #x2_vals = X2.flatten()
    x3_vals = np.where(x1_vals+x2_vals <= M, M - (x1_vals+x2_vals), 0.0)
    
    # 計算用のxの点を作成
    x_points = np.stack([x1_vals, x2_vals, x3_vals], axis=1)
    
    # 分布を計算
    probability = multinomial.pmf(x=x_points, n=M, p=phi_v)
    
    # xがとり得ない値の要素をマスク:(xがとり得ない値をマスクする場合)
    #probability = np.ma.masked_where(x1_vals + x2_vals > M, probability)
    
    # 多項分布を作図
    ax.bar3d(x=x1_vals - 0.45, y=x2_vals - 0.45, z=np.zeros_like(x1_vals), 
             dx=0.9, dy=0.9, dz=probability, 
             color=cm(probability / p_max), alpha=0.5, shade=True) # 3D棒グラフ
    ax.set_xlabel('$x_1$')
    ax.set_ylabel('$x_2$')
    ax.set_zlabel('probability')
    ax.set_title('$\phi=(' + ', '.join([str(phi) for phi in phi_v]) + ')' +
                 ', M=' + str(M) + '$', loc='left')
    ax.set_zlim(0.0, p_max) # z軸の表示範囲
    #ax.view_init(elev=0, azim=315) # 表示アングル

# gif画像を作成
anime_prob = FuncAnimation(fig, update, frames=M_max, interval=100)

# gif画像を保存
anime_prob.save('Multinomial_prob_M.gif')

多項分布と試行回数の関係

　試行回数$M$が増えるに従って、$x_1, x_2$が大きいほど確率が高くなる(山が右上に移動する)のを確認できます。ただし、$\mathbf{x}$がとり得る値の範囲も広がっていくため、全体における相対的な山の位置は変わりません。また分布の総和は1なので、$\mathbf{x}$がとり得る値が増えるほど1つの点の確率(z軸の値)が小さくなります。

乱数の生成

　多項分布の乱数を生成してヒストグラムを確認します。

　パラメータを指定して、多項分布に従う乱数を生成します。

# パラメータを指定
phi_v = np.array([0.3, 0.5, 0.2])

# 試行回数を指定
M = 10

# データ数を指定
N = 1000

# 多項分布に従う乱数を生成
x_nv = np.random.multinomial(n=M, pvals=phi_v, size=N)
print(x_nv[:5])
print(x_nv.shape)

[[2 5 3]
 [3 5 2]
 [3 4 3]
 [1 5 4]
 [2 6 2]]
(1000, 3)

　多項分布の乱数生成関数np.random.multinomial()の試行回数の引数nにM、出現確率(パラメータ)の引数pvalsにphi、データ数(サンプルサイズ)の引数sizeにNを指定します。

　$\mathbf{x}$がとり得る値を作成します。

# 作図用のxの値を作成
x_vals = np.arange(M + 1)

# 格子点を作成
X1, X2 = np.meshgrid(x_vals, x_vals)

# 作図用のxの点を作成:(xがとり得ない値を消去する場合)
x1_vals = np.delete(X1.flatten(), obj=(X1 + X2).flatten() > M)
x2_vals = np.delete(X2.flatten(), obj=(X1 + X2).flatten() > M)

# 作図用のxの点を作成:(全ての組み合わせを描画する場合)
#x1_vals = X1.flatten()
#x2_vals = X2.flatten()
x3_vals = np.where(x1_vals+x2_vals <= M, M - (x1_vals+x2_vals), 0.0)

# 計算用のxの点を作成
x_points = np.stack([x1_vals, x2_vals, x3_vals], axis=1)
print(x_points[:5])
print(x_points.shape)

[[ 0.  0. 10.]
 [ 1.  0.  9.]
 [ 2.  0.  8.]
 [ 3.  0.  7.]
 [ 4.  0.  6.]]
(66, 3)

　「グラフの作成」での$\mathbf{x}$の点と同じです。

　サンプルを集計します。

# 重複するサンプルをカウント
uni_sample, uni_freq = np.unique(x_nv, return_counts=True, axis=0)
print(uni_sample[:5])
print(uni_freq[:5])

[[0 3 7]
 [0 5 5]
 [0 6 4]
 [0 7 3]
 [0 8 2]]
[ 1  5  4 10  6]

　np.unique()で重複するサンプル(行)をカウントします。第1引数に指定した配列から重複する要素を取り除いて返します。軸の引数axisに0を指定すると、行ごとに重複を調べます。return_countsをTrueにすると、重複する個数を返します。

　サンプルとして得られなかった点はグラフに描画されないため、頻度0として補完します。

# サンプルにないxの点と結合
frequency = np.zeros(len(x_points))
for j, x_v in enumerate(uni_sample):
    for i, x_point in enumerate(x_points):
        # 作図用の点とサンプルが一致すれば頻度を代入
        if all(x_point == x_v):
            frequency[i] = uni_freq[j]
            break
print(x_points[11:21])
print(frequency[11:21])

[[0. 1. 9.]
 [1. 1. 8.]
 [2. 1. 7.]
 [3. 1. 6.]
 [4. 1. 5.]
 [5. 1. 4.]
 [6. 1. 3.]
 [7. 1. 2.]
 [8. 1. 1.]
 [9. 1. 0.]]
[0. 0. 0. 0. 3. 1. 3. 1. 1. 0.]

　全ての要素を0として、x_pointsに対応した出現頻度frequencyを作成します。
　重複を除いたサンプルuni_sampleと全ての点x_pointsの各行(点)を順番にマッチして、一致すれば頻度をfrequencyに移します。サンプルに含まれない場合は、対応する要素が0のままになり出現しなかったことを表します。

　x_nvとx_pointsを総当たりでマッチすると次のように処理できます。

# 乱数を集計:(総当たり)
frequency = np.zeros(len(x_points))
for i, x_point in enumerate(x_points):
    frequency[i] = np.sum([all(x_point == x_v) for x_v in x_nv])
print(frequency[11:21])

[0. 0. 0. 0. 3. 1. 3. 1. 1. 0.]

　データ数が増えると処理時間に多少の差が出ます。

　マスクする場合は次の処理を追加します。

# xがとり得ない値の要素をマスク:(xがとり得ない値をマスクする場合)
#frequency = np.ma.masked_where(x1_vals + x2_vals > M, frequency)

　ヒストグラムを作成します。

# カラーマップの設定
cm = plt.get_cmap('jet')

# サンプルのヒストグラムを作成
fig = plt.figure(figsize=(12, 9)) # 図の設定
ax = fig.add_subplot(projection='3d') # 3D用の設定
ax.bar3d(x=x1_vals - 0.45, y=x2_vals - 0.45, z=np.zeros_like(x1_vals), 
         dx=1.0, dy=1.0, dz=frequency, 
         color=cm(frequency / np.max(frequency)), alpha=0.5, shade=True) # ヒストグラム
ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')
ax.set_zlabel('frequency')
fig.suptitle('Maltinomial Distribution', fontsize=20)
ax.set_title('$\phi=(' + ', '.join([str(phi) for phi in phi_v]) + ')' + 
             ', M=' + str(M) + ', N=' + str(N) + '$', loc='left')
#ax.view_init(elev=0, azim=315) # 表示アングル
plt.show()

多項分布の乱数のヒストグラム

　構成比を作図します。

# サンプルの構成比を計算
proportion = frequency / N

# サンプルの構成比を作図
fig = plt.figure(figsize=(12, 9)) # 図の設定
ax = fig.add_subplot(projection='3d') # 3D用の設定
ax.bar3d(x=x1_vals - 0.45, y=x2_vals - 0.45, z=np.zeros_like(x1_vals), 
         dx=1.0, dy=1.0, dz=proportion, 
         color=cm(proportion / np.max(proportion)), alpha=0.5, shade=True) # 構成比
ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')
ax.set_zlabel('proportion')
fig.suptitle('Maltinomial Distribution', fontsize=20)
ax.set_title('$\phi=(' + ', '.join([str(phi) for phi in phi_v]) + ')' + 
             ', M=' + str(M) + ', N=' + str(N) + '$', loc='left')
#ax.view_init(elev=0, azim=315) # 表示アングル
plt.show()

　頻度frequencyをデータ数Nで割り、各値の構成比を計算します。

多項分布の乱数の構成比

　データ数が十分に増えると分布のグラフに形が近づきます。

　サンプルサイズとヒストグラムの変化をアニメーションで確認します。乱数を1つずつ取り出して作図します。

　ヒストグラムのアニメーションを作成します。

・作図コード(クリックで展開)

# フレーム数を指定
N_frame = 150

# 図を初期化
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(projection='3d') # 3D用の設定
fig.suptitle('Maltinomial Distribution', fontsize=20)

# カラーマップの設定
cm = plt.get_cmap('jet')

# 頻度の最大値を取得
uni_arr, uni_freq = np.unique(x_nv[:N_frame], return_counts=True, axis=0)
z_max = np.max(uni_freq)

# 作図処理を関数として定義
def update(n):
    # 前フレームのグラフを初期化
    plt.cla()
    
    # n個のサンプルをカウント
    uni_arr, uni_freq = np.unique(x_nv[:(n+1)], return_counts=True, axis=0)
    
    # サンプルにないxの点と結合
    frequency = np.zeros(len(x_points))
    for i, x_v in enumerate(uni_arr):
        for j, x_point in enumerate(x_points):
            # 作図用の点とサンプルが一致すれば頻度を代入
            if all(x_point == x_v):
                frequency[j] = uni_freq[i]
                break
    
    # xが取らない値をマスク
    frequency = np.ma.masked_where(x1_vals + x2_vals > M, frequency)
    
    # n番目のサンプルの値を取得
    x1, x2 = x_nv[n, [0, 1]]
    
    # n番目のサンプルの頻度を取得
    x_idx = np.where(np.all(x_points == x_nv[n], axis=1) == True)[0][0]
    z = frequency[x_idx]
    
    # サンプルのヒストグラムを作成
    ax.bar3d(x=x1_vals - 0.5, y=x2_vals - 0.5, z=np.zeros_like(x1_vals), 
             dx=1.0, dy=1.0, dz=frequency, 
             color=cm(frequency / z_max), alpha=0.5, shade=True) # ヒストグラム
    ax.scatter(x1, x2, z + 0.1, color='orange', s=100) # サンプル
    ax.set_xlabel('$x_1$')
    ax.set_ylabel('$x_2$')
    ax.set_zlabel('frequency')
    ax.set_title('$\phi=(' + ', '.join([str(phi) for phi in phi_v]) + ')' + 
                 ', M=' + str(M) + ', N=' + str(n) + '$', loc='left')
    ax.set_zlim(0.0, z_max) # z軸の表示範囲
    ax.view_init(elev=0, azim=300) # 表示アングル:(横から)
    #ax.view_init(elev=90, azim=270) # 表示アングル:(上から)

# gif画像を作成
anime_freq = FuncAnimation(fig, update, frames=N_frame, interval=100)

# gif画像を保存
anime_freq.save('Multinomial_freq.gif')

多項分布の乱数のヒストグラムの推移

　構成比のアニメーションを作成します。

・作図コード(クリックで展開)

# フレーム数を指定
N_frame = 150

# 図を初期化
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(projection='3d') # 3D用の設定
fig.suptitle('Maltinomial Distribution', fontsize=20)

# カラーマップの設定
cm = plt.get_cmap('jet')

# 構成比の最大値を取得
uni_arr, uni_freq = np.unique(x_nv[:N_frame], return_counts=True, axis=0)
p_max = np.max(uni_freq) / N
p_max = 0.2

# 作図処理を関数として定義
def update(n):
    # 前フレームのグラフを初期化
    plt.cla()
    
    # n個のサンプルをカウント
    uni_arr, uni_freq = np.unique(x_nv[:(n+1)], return_counts=True, axis=0)
    
    # サンプルにないxの点と結合
    frequency = np.zeros(len(x_points))
    for i, x_v in enumerate(uni_arr):
        for j, x_point in enumerate(x_points):
            # 作図用の点とサンプルが一致すれば頻度を代入
            if all(x_point == x_v):
                frequency[j] = uni_freq[i]
                break
    
    # サンプルの構成比を計算
    proportion = frequency / (n + 1)
    
    # xが取らない値をマスク
    proportion = np.ma.masked_where(x1_vals + x2_vals > M, proportion)
    
    # n番目のサンプルの値を取得
    x1, x2 = x_nv[n, [0, 1]]
    
    # n番目のサンプルの頻度を取得
    x_idx = np.where(np.all(x_points == x_nv[n], axis=1) == True)[0][0]
    z = proportion[x_idx]
    
    # サンプルの構成比を作成
    ax.bar3d(x=x1_vals - 0.5, y=x2_vals - 0.5, z=np.zeros_like(x1_vals), 
             dx=1.0, dy=1.0, dz=proportion, 
             color=cm(proportion / p_max), alpha=0.5, shade=True) # 構成比
    ax.scatter(x1, x2, z, color='orange', s=100) # サンプル
    ax.set_xlabel('$x_1$')
    ax.set_ylabel('$x_2$')
    ax.set_zlabel('proportion')
    ax.set_title('$\phi=(' + ', '.join([str(phi) for phi in phi_v]) + ')' + 
                 ', M=' + str(M) + ', N=' + str(n) + '$', loc='left')
    ax.set_zlim(0.0, p_max) # z軸の表示範囲
    #ax.view_init(elev=0, azim=300) # 表示アングル:(横から)
    #ax.view_init(elev=90, azim=270) # 表示アングル:(上から)

# gif画像を作成
anime_prop = FuncAnimation(fig, update, frames=N_frame, interval=100)

# gif画像を保存
anime_prop.save('Multinomial_prop.gif')

多項分布の乱数の構成比の推移

　サンプルが増えるに従って、元の分布に近付いていくのを確認できます。

　以上で、多項分布を確認できました。

参考文献

• 岩田具治『トピックモデル』(機械学習プロフェッショナルシリーズ)講談社,2015年.

おわりに

　加筆修正の際に青トピシリーズから独立させました。

　いつも、数式を解く→実装する→解説を書く→ブログに転載の順に進めるのですが、解説を書いている間に実装を変更したり他の可視化を試したくなったりするのが常で、書いては消しての解説文。分布に含まない点をマスクするのも削除するのも後から思い付いて書き足しました。さらに、R→Pythonの順に進めることが多いのですが、Pythonで思い付いたことをRの方にも反映しようとするとブログとMarkdownのノートとスクリプトの3つを変更しないといけなくてまぁ大変。
　何が言いたいかというと、上手くやれるツールや技術があるんだろうけどそれを調べるのもまた面倒で後回しにしているのをそろそろちゃんとしないとなと思いました。そもそも大した目的もなく勉強しているので勉強に効率を求める気はないのですが、面倒なのはモチベに影響して困ります。努力を続けるための努力とな、あぁ分身したい。

　2022年1月19日は、アンジュルムの伊勢鈴蘭さんの18歳の誕生日です。

　あざといキャラって色々大変だろうけど大きな何かに実を結んでほしい。

【次の内容】

つづく