はじめに
「機械学習・深層学習」初学者のための『ゼロから作るDeep Learning』の攻略ノートです。『ゼロつくシリーズ』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
ニューラルネットワーク内部の計算について、数学的背景の解説や計算式の導出を行い、また実際の計算結果やグラフで確認していきます。
この記事は、4.3.3項「偏微分」の内容です。偏微分の定義を説明します。
【前節の内容】
【他の記事一覧】
【この記事の内容】
4.3.3 偏微分
前項では、1変数の関数の微分を確認しました。この項では、複数の変数を持つ関数の微分を解説します。多変数関数の微分を偏微分と言います。
利用するライブラリを読み込みます。
# 4.3.3項で利用するライブラリ import numpy as np import matplotlib.pyplot as plt
・数式の確認
まずは、偏微分の定義を確認します。
2つの変数$x,\ y$の関数$f(x, y)$の微分を考えます。複数の変数の内、1つの変数に注目して他の変数を定数とみなして(値を固定して)微分することを偏微分と言います。微分については4.3.1項を参照してください。
$x$についての$f(x, y)$の偏微分を$\frac{\partial f(x, y)}{\partial x}$で表し、次の式で定義されます。
この式は、$x$の微小な変化に対する$f(x, y)$の変化の割合を表します。$h$は微小な値です。$\frac{\partial f(x, y)}{\partial x}$を偏導関数とも呼びます。
同様に、$y$についての偏微分は次の式です。
微分と同様に、ある変数がほんの少し変化したときの関数の変化を表しています。
微分は$d$で表しましたが、偏微分では$\partial$で表記します。$\partial$は、dに対応するギリシャ文字$\delta$の筆記体です。また、$\frac{\partial f(x, y)}{\partial x}$を簡易的に$f_x(x, y)$と表記することもあります(この本では登場しません)。
$x$についての偏微分のことを、単に「$x$に関する微分」と言うこともあります。
・グラフで確認
次に、関数と偏微分(接線の傾き)の関係をグラフで確認します。3Dプロットについては「3Dプロットの作図【ゼロつく1のノート(Python)】 - からっぽのしょこ」を参照してください。
この例では、2つの変数$x_0,\ x_1$の2乗和
の偏微分を考えます。
作図用の$x_0,\ x_1$の値を作成します。
# 作図用の値を作成 x0_vals = np.arange(-3.0, 3.5, 0.5) x1_vals = np.arange(-3.0, 3.5, 0.5) # 格子状の点に変換 X0_vals, X1_vals = np.meshgrid(x0_vals, x1_vals) print(X0_vals[0:5, 0:5]) print(X1_vals[0:5, 0:5])
[[-3. -2.5 -2. -1.5 -1. ]
[-3. -2.5 -2. -1.5 -1. ]
[-3. -2.5 -2. -1.5 -1. ]
[-3. -2.5 -2. -1.5 -1. ]
[-3. -2.5 -2. -1.5 -1. ]]
[[-3. -3. -3. -3. -3. ]
[-2.5 -2.5 -2.5 -2.5 -2.5]
[-2. -2. -2. -2. -2. ]
[-1.5 -1.5 -1.5 -1.5 -1.5]
[-1. -1. -1. -1. -1. ]]
プロットするx軸とy軸の値をそれぞれx0_vals, x1_valsとして作成します。この例では、-3から3の範囲の0.5間隔の値とします。
作成した値をnp.meshgrid()で格子状の点となる2つの配列に変換します。X0_valsは行方向に、X1_valsは列方向に値が変化します。X0_valsとX1_valsは同じ形状になります。X0_valsはx軸の値、X1_valsはy軸の値です。
X0_valsとX1_valsの2乗和を計算します。
# 2乗和を計算 Z_vals = X0_vals**2 + X1_vals**2 print(Z_vals[0:5, 0:5])
[[18. 15.25 13. 11.25 10. ]
[15.25 12.5 10.25 8.5 7.25]
[13. 10.25 8. 6.25 5. ]
[11.25 8.5 6.25 4.5 3.25]
[10. 7.25 5. 3.25 2. ]]
同じ位置の要素同士で2乗和が計算されます。Z_valsはz軸の値です。
2乗和の関数$f(x_0, x_1)$を3Dグラフで可視化します。
# 2乗和のグラフを作成 fig = plt.figure(figsize=(8, 8)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_wireframe(X0_vals, X1_vals, Z_vals) # ワイヤーフレーム図 ax.set_xlabel('$x_0$') # x軸ラベル ax.set_ylabel('$x_1$') # y軸ラベル ax.set_zlabel('f(x)') # z軸ラベル ax.set_title('$f(x) = x_0^2 + x_1^2$', fontsize=20) # タイトル plt.show()

4.3.2項の$f(x) = x^2$のグラフのy軸を360°回転させたようなイメージです。
$x_0 = 2,\ x_1 = 1$のときの$x_1$についての偏微分$\frac{\partial f(x_0, x_1)}{\partial x_1}$を求めてみます。
$x_0$を固定した2乗和の関数を作成しておきます。また作図時に利用するため、関数に指定した値を持つ変数x0を作成しておきます。
# 接点(x0, x1, f(x))のx0を指定 x0 = 2.0 # x0を固定した2乗和の関数を作成 def f1(x1): # x0の値を指定 x0 = 2.0 # 2乗和を計算 return x0**2 + x1**2
この関数は$x_0$と$x_1$の2乗和を計算しますが、$x_0$は固定されているため、$x_1$の関数と言えますね。ちなみに、解析的に求めた$x_1$の偏微分は、$\frac{\partial f(x_0, x_1)}{\partial x_1} = 2 x_1$です
よって、「4.3.1-2:数値微分【ゼロつく1のノート(数学)】 - からっぽのしょこ」で実装した数値微分を計算する関数numerical_diff()を使って、偏微分$\frac{\partial f(x_0, x_1)}{\partial x_1}$を計算できます。
# 接点(x0, x1, f(x))のx1を指定 x1 = 1.5 # x1についての偏微分を計算 dx1 = numerical_diff(f1, x1) print(dx1)
3.00000000000189
$x_0 = 2, x_1 = 1.5$のときの$x_1$についての偏微分$\frac{\partial f(x_0, x_1)}{\partial x_1} = 2 * 1.5 = 3$が求まりました。
$\frac{\partial f(x_0, x_1)}{\partial x_1}$は、$f(x_0, x_1)$上の点$(x_0, x_1, f(x_0, x_1))$における$x_1$軸方向の接線の傾きです。
4.3.2項のときと同様に、切片も求めて、接線を引いてみましょう。
# 切片を計算 b1 = f1(x1) - dx1 * x1 print(b1) # 接線のz軸の値を計算 tangent_line = dx1 * x1_vals + b1 print(tangent_line)
1.749999999997165
[-7.25 -5.75 -4.25 -2.75 -1.25 0.25 1.75 3.25 4.75 6.25 7.75 9.25
10.75]
$f(x_0, x_1)$のグラフに接線を重ねて表示します。
# 接線を作図 fig = plt.figure(figsize=(8, 8)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_wireframe(X0_vals, X1_vals, Z_vals, label='$f(x_0, x_1)$') # 対象の関数 ax.plot(np.repeat(x0, len(x1_vals)), x1_vals, tangent_line, color='orange', label='$f_x(x_1, x_2)$') # 接線 ax.set_xlabel('$x_0$') # x軸ラベル ax.set_ylabel('$x_1$') # y軸ラベル ax.set_zlabel('f(x)') # z軸ラベル ax.set_title('$(x_0, x_1, f(x))=(' + str(x0) + ', ' + str(x1) + ', ' + str(np.round(f1(x1), 1)) + ')' + ', dx_1=' + str(np.round(dx1, 2)) + '$', loc='left') # 接点に関する値 fig.suptitle('$f(x) = x_0^2 + x_1^2$', fontsize=20) # 全体のタイトル ax.legend() # 凡例 #ax.view_init(elev=20, azim=340) # 表示アングル plt.show()
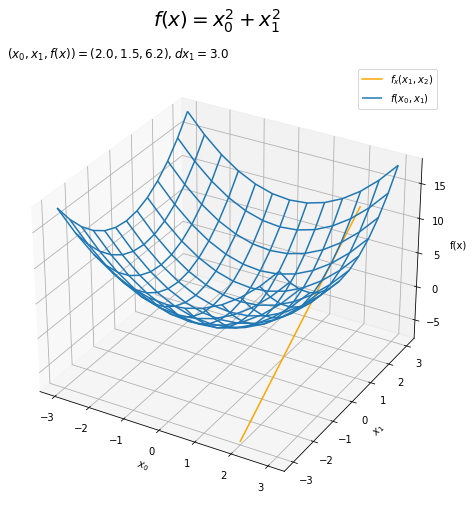

(2つの3Dプロットを2次元的に重ねて表示しているだけのようで、どの角度からでも正しい位置関係に見えるわけではなさそうです。)
3Dのグラフを$x_0 = 2$で(接線に沿って)切断した断面図は、横軸が$x_1$で縦軸が$f(x_0, x_1)$の2Dのグラフになります。
# 接線を作図 plt.figure(figsize=(8, 6)) plt.plot(x1_vals, f1(x1_vals), label='$f(x_0, x_1)$') plt.plot(x1_vals, tangent_line, label='$f_{x_0}(x_0, x_1)$') #plt.scatter(x1, f1(x1)) plt.xlabel('$x_1$') # x軸ラベル plt.ylabel('f(x)') # y軸ラベル plt.suptitle('$f(x_0, x_1) = x_0^2 + x_1^2$', fontsize=20) # タイトル plt.title('$(x_0, x_1, f(x))=(' + str(x0) + ', ' + str(x1) + ', ' + str(np.round(f1(x1), 1)) + ')' + ', dx_1=' + str(np.round(dx1, 2)) + '$', loc='left') # 接点に関する値 plt.grid() # グリッド線 plt.legend() # 凡例 plt.ylim(0, 14) # y軸の表示範囲 plt.show()

$x_1$についての偏微分$\frac{\partial f(x_0, x_1)}{\partial x_1}$が、$f(x_0, x_1)$上の点$(x_0, x_1, f(x_0, x_1))$における$x_1$軸方向の傾きなのを確認できます。
この節では、微分を確認しました。次節では、各変数の偏微分をまとめた勾配について説明します。
参考文献
おわりに
加筆修正の際に記事を分割しました。
【次節の内容】
