6.1.4：Momentum【ゼロつく1のノート(実装)】

はじめに

　「プログラミング」学習初手『ゼロから作るDeep Learning』民のための実装攻略ノートです。『ゼロつく1』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。

　関数やクラスとして実装される処理の塊を細かく分解して、1つずつ処理を確認しながらゆっくりと組んでいきます。

　この記事は、6.1.4項「Momentum」の内容になります。Momentum SGDを説明し、Pythonで実装します。またその学習過程を確認します。

【前節の内容】

www.anarchive-beta.com

【他の節の内容】

www.anarchive-beta.com

【この節の内容】

はじめに
6.1.4 Momentum
参考文献
おわりに

6.1.4 Momentum

　MormentumあるいはMormentum SGDとは、SGD(確率的勾配降下法)に「運動量(モーメンタム)」という考え方を導入した手法です。SGDでは、更新の度に「止まった」ボールがその地点の勾配に従い傾斜を転がるイメージでした。Momentumでは、これまでの更新の「転がり具合」を(ある程度)保ったまま、それに加えて現地点の勾配に従い傾斜を転がるイメージです。

・更新式の確認

　重みパラメータを$\mathbf{W}$、損失関数を$L$、$\mathbf{W}$に関する損失関数の勾配を$\frac{\partial L}{\partial \mathbf{W}}$とすると、Momentumは次の式になります。

$$ \mathbf{v} \leftarrow \alpha \mathbf{v} - \eta \frac{\partial L}{\partial \mathbf{W}} \tag{6.3} $$

　ここで、$\mathbf{v}$は「速度」に対応する変数で、その調整項を$\alpha$とします。$\alpha$は「速度」に対して「摩擦(抵抗)」と言えます。また勾配の影響力を調整する学習率(ステップサイズ)を$\eta$とします。

　勾配によって更新した$\mathbf{v}$を用いてパラメータを更新します。

$$ \mathbf{W} \leftarrow \mathbf{W} + \mathbf{v} \tag{6.4} $$

　式(6.3),(6.4)の$j,k$要素に注目すると更新式は

$$ \begin{aligned} v_{jk} &\leftarrow \alpha v_{jk} - \eta \frac{\partial L}{\partial w_{jk}} \\ w_{jk} &\leftarrow w_{jk} + v_{jk} \end{aligned} $$

となります。

　ちなみに$\leftarrow$は、右辺の計算によって左辺の変数を更新することを表しています。不気味であれば右肩に括弧付きの数字で更新回数を示すことで、次のように等式でも表せます。

$$ \begin{aligned} v_{jk}^{(t)} &= \alpha v_{jk}^{(t-1)} - \eta \frac{\partial L}{\partial w_{jk}^{(t-1)}} \\ w_{jk}^{(t)} &= w_{jk}^{(t-1)} + v_{jk}^{(t)} \end{aligned} $$

　これは$t$回目の更新によって現在の値($t-1$回目の更新値)$v_{jk}^{(t-1)},\ w_{jk}^{(t-1)}$を更新することを表しています。右肩の記号が恐ろしければ矢印の方で理解しましょう。

　プログラミングっぽく$w_{jk} = w_{jk} + v_{jk}$と書くと、$v_{jk}$が0でないと式が成立しないことになるという不都合があるだけのことです。

　式(6.3),(6.4)についてもう少し考えてみましょう。

　$\alpha$が0のとき$\mathbf{v}$の影響がなくなり、$\mathbf{v} = - \eta \frac{\partial L}{\partial \mathbf{W}}$となります(これは等式で大丈夫ですね)。これを式(6.4)に代入すると

$$ \mathbf{W} \leftarrow \mathbf{W} - \eta \frac{\partial L}{\partial \mathbf{W}} \tag{6.1} $$

SGDの更新式になります。このことからもMomentumがSGDを拡張した手法であることを確認できます。

　式(6.3)の初回の更新について考えてみます。更新式は$\mathbf{v}^{(1)} = \alpha \mathbf{v}^{(0)} - \eta \frac{\partial L}{\partial \mathbf{W}^{(0)}}$と表せます。(このことを今から確認するのですが、$\mathbf{v}$は過去の勾配の情報であるため初回は過去の情報がないことから)$\mathbf{v}$の初期値$\mathbf{v}^{(0)}$を0とすると、この式は

$$ \mathbf{v}^{(1)} = - \eta \frac{\partial L}{\partial \mathbf{W}^{(0)}} $$

になります。

　次に2回目の更新を考えます。式は$\mathbf{v}^{(2)} = \alpha \mathbf{v}^{(1)} - \eta \frac{\partial L}{\partial \mathbf{W}^{(1)}}$ですね。この式に1回目の更新値(上の式)を代入すると

$$ \mathbf{v}^{(2)} = - \alpha \eta \frac{\partial L}{\partial \mathbf{W}^{(0)}} - \eta \frac{\partial L}{\partial \mathbf{W}^{(1)}} $$

となります。

　ではこれを3回目の更新式$\mathbf{v}^{(3)} = \alpha \mathbf{v}^{(2)} - \eta \frac{\partial L}{\partial \mathbf{W}^{(2)}}$に代入すると

$$ \begin{aligned} \mathbf{v}^{(3)} &= \alpha \left( - \alpha \eta \frac{\partial L}{\partial \mathbf{W}^{(0)}} - \eta \frac{\partial L}{\partial \mathbf{W}^{(1)}} \right) - \eta \frac{\partial L}{\partial \mathbf{W}^{(2)}} \\ &= - \alpha^2 \eta \frac{\partial L}{\partial \mathbf{W}^{(0)}} - \alpha \eta \frac{\partial L}{\partial \mathbf{W}^{(1)}} - \eta \frac{\partial L}{\partial \mathbf{W}^{(2)}} \end{aligned} $$

となります。1つ目の項の$\alpha^2$は$\alpha$の2乗のことです。

　ではでは$T$回更新を繰り返すと

$$ \begin{aligned} \mathbf{v}^{(T)} &= - \alpha^{T-1} \eta \frac{\partial L}{\partial \mathbf{W}^{(0)}} - \alpha^{T-2} \eta \frac{\partial L}{\partial \mathbf{W}^{(1)}} - \cdots - \alpha \eta \frac{\partial L}{\partial \mathbf{W}^{(T-2)}} - \eta \frac{\partial L}{\partial \mathbf{W}^{(T-1)}} \\ &= - \eta \left( \alpha^{T-1} \frac{\partial L}{\partial \mathbf{W}^{(0)}} + \alpha^{T-2} \frac{\partial L}{\partial \mathbf{W}^{(1)}} + \cdots + \alpha^1 \frac{\partial L}{\partial \mathbf{W}^{(T-2)}} + \alpha^0 \frac{\partial L}{\partial \mathbf{W}^{(T-1)}} \right) \\ &= - \eta \sum_{t=1}^T \alpha^{T-t} \frac{\partial L}{\partial \mathbf{W}^{(t-1)}} \end{aligned} $$

となります。最後の2つの項について$\alpha^{T-(T-1)} = \alpha$、$\alpha^{T-T} = \alpha^0 = 1$です。

　これを用いると$\mathbf{W}$の$T$回目の更新値は

$$ \begin{align} \mathbf{W}^{(T)} &= \mathbf{W}^{(T-1)} + \mathbf{v}^{(T)} \tag{6.4}\\ &= \mathbf{W}^{(T-1)} - \eta \sum_{t=1}^T \alpha^{T-t} \frac{\partial L}{\partial \mathbf{W}^{(t-1)}} \end{align} $$

で計算できることが分かります。

　つまりMomentumでは、これまでの全ての勾配の情報を$\mathbf{v}$として保存します。そしてその過去の勾配の情報を利用してパラメータを更新します。ただし$0 \leq \alpha < 1$なので、古い勾配ほど値が割り引かれて影響力がなくなります。また$\alpha$の値が大きいほど過去の情報を重視することになります。

・実装

　更新式の確認ができたので、Momentum SGDを実装します。

# この項で利用するライブラリを読み込む
import numpy as np
import matplotlib.pyplot as plt

　学習率$\eta$と$\mathbf{v}$の調整項$\alpha$は、どちらもインスタンスの作成時にそれぞれ引数lr、momentumとして指定し、インスタンス変数として値を保持します。デフォルト値として、よく用いられる値を設定しておきます。

　$\mathbf{v}$はパラメータ$\mathbf{W}$と同じ形状にする必要があるため、インスタンス作成時はNoneを定義してインスタンス変数だけ作成しておきます。更新メソッドの使用時に渡されるパラメータ(とパラメータごとの勾配)と同じ形状で全ての要素が0の変数を作成し、ディクショナリ型のインスタンス変数vに格納します。

# Momentumの実装
class Momentum:
    
    # インスタンス変数を定義
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr # 学習率
        self.momentum = momentum # vの調整項
        self.v = None # 速度
    
    # パラメータの更新メソッドを定義
    def update(self, params, grads):
        # vを初期化
        if self.v is None: # 初回のみ
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val) # 全ての要素が0
        
        # パラメータごとに値を更新
        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key] # 式(6.3)
            params[key] += self.v[key] # 式(6.4)

　更新式に従いパラメータごとに値を更新します。パラメータと勾配はどちらもディクショナリ変数として更新メソッド.update()の使用時に引数に指定します。

・アルゴリズムの確認

　Momentumにより関数

$$ f(x, y) = \frac{1}{20} x^2 + y^2 \tag{6.2} $$

の最小値となる$x,\ y$を探索します。この関数の勾配(偏微分)は

$$ \frac{\partial f(x, y)}{\partial x} = \frac{1}{10} x ,\ \frac{\partial f(x, y)}{\partial y} = 2 y $$

になります。

　まずは関数(6.2)とその勾配をそれぞれ関数として定義しておきます。

# 式(6.2)
def f(x, y):
    return x ** 2 / 20.0 + y ** 2

# 式(6.2)の勾配(偏微分)
def df(x, y):
    # 偏微分
    dx = x / 10.0 # df / dx
    dy = 2.0 * y # df / dy
    return dx, dy # (値を2つ出力！)

　元の関数は作図に、勾配はもちろんパラメータの更新に利用します。

　ちなみにこの関数を等高線図にすると次のようになります。

# 等高線用の値
x = np.arange(-10, 10, 0.01) # x軸の値
y = np.arange(-5, 5, 0.01) # y軸の値
X, Y = np.meshgrid(x, y) # 格子状の点に変換
Z = f(X, Y)

# 作図
plt.contour(X, Y, Z) # 等高線
plt.plot(0, 0, '+') # 最小値の点
plt.xlim(-10, 10) # x軸の範囲
plt.ylim(-10, 10) # y軸の範囲
plt.xlabel("x") # x軸ラベル
plt.ylabel("y") # y軸ラベル
plt.title("$f(x, y) = \\frac{1}{20} x^2 + y^2$", fontsize=20) # タイトル
plt.show()

　原点がこの関数の最小値になります。また原点付近が横に広くなだらかに(勾配が小さく)なっていることが確認できます。

　初期値は点$(-7, 2)$とします。これまでと同様に、パラメータ(変数)params、パラメータごとの勾配gradsのディクショナリ変数を作成して、パラメータ名をキーとして値を格納します。

　学習率$\eta$と$\mathbf{v}$の調整項$\alpha$を指定して、Momentumクラスのインスタンスを作成します。

# パラメータの初期値を指定
params = {}
params['x'] = -7.0
params['y'] = 2.0

# 勾配の初期値を指定
grads = {}
grads['x'] = 0
grads['y'] = 0

# 学習率を指定
lr = 0.1

# モーメンタムを指定
momentum = 0.9

# インスタンスを作成
optimizer = Momentum(lr=lr, momentum=momentum)

　試行回数を指定して、学習を行います。また、パラメータの更新値を記録するためのリスト型の変数を用意しておきます。値の追加は.append()を使います。

# 試行回数を指定
iter_num = 30

# 更新値の記録用リストを初期化
x_history = []
y_history = []

# 初期値を保存
x_history.append(params['x'])
y_history.append(params['y'])

# 関数の最小値を探索
for _ in range(iter_num):
    
    # 勾配を計算
    grads['x'], grads['y'] = df(params['x'], params['y'])
    
    # パラメータを更新
    optimizer.update(params, grads)
    
    # パラメータを記録
    x_history.append(params['x'])
    y_history.append(params['y'])

　勾配を計算し、gradsに格納している値をそれぞれ上書きします。そしてMomentumクラスの更新メソッド.update()にparamsとgradsを指定して、パラメータを更新します。

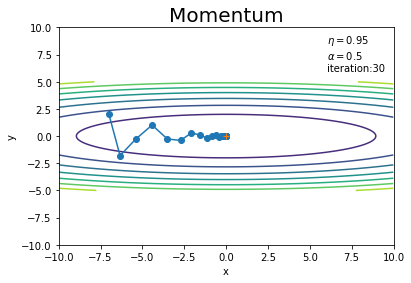
　更新値の推移を先ほどの等高線グラフに重ねて確認しましょう。

# 作図
plt.plot(x_history, y_history, 'o-') # パラメータの推移
plt.contour(X, Y, Z) # 等高線
plt.plot(0, 0, '+') # 最小値の点
plt.xlim(-10, 10) # x軸の範囲
plt.ylim(-10, 10) # y軸の範囲
plt.xlabel("x") # x軸ラベル
plt.ylabel("y") # y軸ラベル
plt.title("Momentum", fontsize=20) # タイトル
plt.text(6, 6, "$\\eta=$" + str(lr) + "\n$\\alpha=$" + str(momentum) + "\niteration:" + str(iter_num)) # メモ
plt.show()

　SGDのとき(図6-3)よりもジグザク度合いが軽減されています。ただし過去の勾配の影響を受けるため、最小値の点(勾配が0になっても)ピタリと止まることができずに行き過ぎています(図6-5)。

　学習率や試行回数を変更して試してみましょう！

　更新回数を増やすと、最近の勾配に従い方向転換して関数が最小になる点に戻っていることが分かります。

　$\alpha$を0にすると、SGDと(式が同じになるので)同じ経路を辿ります(図6-3)。

　$\mathbf{v}$の働きを見るため、$\alpha$の値を変えてみます。

　モーメンタムについてざっくりとイメージしてみます。

　初期値の点$(-7, 2)$の勾配では、「y軸のマイナス方向」にそこそこかつ「x軸のプラス方向」に少し力が働き、点(パラメータ)が移動します。$\mathbf{v}$の初期値は0なので、図6-3と同じだけ移動します(同じ更新値となります)。
　2回目の更新では、「y軸のプラス方向」にそこそこかつ「x軸のプラス方向」に少し力が働きます。しかし前回の運動量の影響を受けて、「y軸方向の力は打ち消し合い」また「x軸方向の力は加算」されます。
　3回目の更新では、y軸方向の力はほとんど生まれません。よって$\alpha$で割り引かれた前回の運動量のままに進んでいます。

　過去の勾配を上手く利用することでSGDよりも効率よく学習を進められます。

　ハイパーパラメータの設定も効率的な最適化にとって重要です。

　SGDに「運動量」という概念を導入したMomentum SGDについて確認できました。次はまた別のアプローチでSGDを発展させた手法を取り上げます。

参考文献

斎藤康毅『ゼロから作るDeep Learning』オライリー・ジャパン,2016年.

おわりに

　数式を弄るときは記事を分けていたのですが、この節の内容だと分けるほどの文量にならなかったので悩みました。記号が多いので複雑に見えますが、やっている式変形自体は基本的なものなので、一緒に載せることにしました。あ、勾配の計算自体はそれなりの難易度ですね、あくまでここで行った式変形の話です。
　それと、この節の5つの似たような手法の特徴や違いを理解するには、数式を比較するのが分かりやすいと思います。実際読んでみてどうでしょうか？想定読者をどこに置くのかも微妙に悩みます。

　プログラムだけでなく数式からも確認できたら、アルゴリズムの理解がより深まるのは確かなので、心に余裕があるときに他の記事もチラリと読んでみてください。少なくとも(1年半前まで全く勉強していなかった)私が理解できるくらいには噛み砕いて解説しているつもりです。折角書いたので是非(本音)！あでも、かなり激しい内容も一部あるのでそれはうまいこと避けてください！
　とはいえ、数式弄りに時間をとられていると(私のように)そもそもの勉強が進まなくなるので、バランス良くやっていきましょう。。

【次節の内容】