はじめに
「Python」初学者のための『ゼロから作るDeep Learning』攻略ノートです。『ゼロつく1』の学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
本を進めるにあたって必要となるPython文法や利用する関数について、その機能や使い方、補足情報を確認していきます。
この記事では、2変数の関数の勾配をベクトルで可視化する方法を解説します。
【他の記事一覧】
【この節の内容】
・矢印プロットの作図
MatplotlibのPyPlotモジュールを利用して、2変数の関数の勾配を矢印プロットで可視化します。
この記事では、2変数$x,\ y$(または$x_0,\ x_1$)の2乗和$f(x, y) = x^2 + y^2$を例とします。
$x,\ y$に関する偏微分をまとめた勾配$(\frac{\partial f(x, y)}{\partial x}, \frac{\partial f(x, y)}{\partial y})$を矢印プロット化します。
次のライブラリを利用します。
# 利用するライブラリ import numpy as np import matplotlib.pyplot as plt
・quiver関数の確認
plt.quiver()は、2Dのグラフと3Dのグラフで処理が変わります。まずは、それぞれの処理を確認します。
・2D quiver
2次元のグラフにおけるplt.quiver()の処理を確認します。
2次元の矢印プロットは、plt.quiver(X, Y, U, V)で作成します。
引数X, Yは、矢印の始点$(x, y)$の値です。引数U, Vは、それぞれベクトルのx成分とy成分です。つまり、点(X, Y)からx軸方向にU、y軸方向にV変化した点$(x + u, y + v)$が矢印の終点になります。各引数には、スカラでも配列でも指定できます。
始点$(x, y)$と変化量$u,\ v$の値を指定します。
# 始点(x, y)を指定 x, y = 1.0, 1.0 # 各次元の変化量を指定 u, v = 2.0, 3.0
始点のx軸の値をx、y軸の値をyとして値を指定します。
また、始点x, yからのx軸方向への変化量をu、y軸方向への変化量をvとして値を指定します。
plt.quiver()で矢印プロットを作成します。
# 矢印プロットを作成 plt.figure(figsize=(6, 6)) # 図の設定 plt.quiver(x, y, u, v, angles='xy', scale_units='xy', scale=1) # 矢印プロット plt.scatter(x, y, label='(x, y)') # 始点 plt.scatter(x + u, y + v, label='(x+u, y+v)') # 終点 plt.xlabel('x') # x軸ラベル plt.ylabel('y') # y軸ラベル plt.title('quiver(x, y, u, v)', fontsize=20) # タイトル plt.grid() # グリッド線 plt.legend() # 凡例 plt.xlim(0, 5) # x軸の表示範囲 plt.ylim(0, 5) # y軸の表示範囲 plt.show()

引数にangles='xy'、scale_units='xy'、scale=1を指定すると、u, vの通りにベクトルが描画されます。
引数を指定しないと(デフォルトでは)、次のように自動で調整されます。
# 矢印プロットを作成 plt.figure(figsize=(6, 6)) # 図の設定 plt.quiver(x, y, u, v) # 矢印プロット plt.xlabel('x') # x軸ラベル plt.ylabel('y') # y軸ラベル plt.title('quiver(x, y, u, v)', fontsize=20) plt.grid() # グリッド線 plt.xlim(0, 5) # x軸の表示範囲 plt.ylim(0, 5) # y軸の表示範囲 plt.show()

勾配を可視化する際には、デフォルトの設定で作図します。
・3D quiver
3次元のグラフにおけるplt.quiver()の処理を確認します。
3次元の矢印プロットは、plt.quiver(X, Y, Z, U, V, W)で作成します。
引数X, Y, Zは、矢印の始点$(x, y, z)$の値です。引数U, V, Wは、それぞれベクトルのx・y・z成分です。つまり、点(X, Y, Z)からx軸方向にU、y軸方向にV、z軸方向にW変化した点$(x + u, y + v, z + w)$が矢印の終点になります。各引数には、スカラでも配列でも指定できます。
始点$(x, y, z)$と変化量$u,\ v,\ w$の値を指定します。
# 始点(x, y, z)の座標を指定 x, y, z = 1.0, 1.0, 1.0 # 各次元の変化量を指定 u, v, w = 2.0, 2.0, 2.0
plt.quiver()で矢印プロットを作成します。
# 矢印プロットを作成 fig = plt.figure(figsize=(8, 8)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3Dプロットの設定 ax.quiver(x, y, z, u, v, w, arrow_length_ratio=0.1) # 矢印プロット ax.scatter(x, y, z, label='(x, y, z)') # 始点 ax.scatter(x + u, y + v, z + w, label='(x+u, y+v, z+w)') # 終点 ax.set_xlabel('x') # x軸ラベル ax.set_ylabel('y') # y軸ラベル ax.set_zlabel('z') # z軸ラベル ax.set_title('quiver(x, y, z, u, v, w)', fontsize=20) # タイトル ax.legend() # 凡例 ax.set_xlim(0, 5) # x軸の表示範囲 ax.set_ylim(0, 5) # y軸の表示範囲 ax.set_zlim(0, 5) # z軸の表示範囲 plt.show()

分かりにくいので、補助線などを入れてみます(この図は再現する必要はありません)。
・コード(クリックで展開)
# 補助線用の値を作成 x_vals = np.arange(5) y_vals = np.arange(5) z_vals = np.arange(5)
# 図の設定 fig = plt.figure(figsize=(8, 8)) ax = fig.add_subplot(projection='3d') # 始点(x, y, z) ax.scatter(x, y, z, color='orange', s=100) ax.text(x, y, z, s='(x, y, z)', fontsize=15) # 終点(x+u, y+v, z+w) ax.scatter(x+u, y+v, z+w, color='orange', s=100) ax.text(x+u, y+v, z+w, s='(x+u, y+v, z+w)', fontsize=15) # 経路のベクトル ax.quiver(x, y, z, u, 0, 0, linestyle='--', arrow_length_ratio=0.1) # x軸 ax.quiver(x+u, y, z, 0, v, 0, linestyle='--', arrow_length_ratio=0.1) # y軸 ax.quiver(x+u, y+v, z, 0, 0, w, linestyle='--', arrow_length_ratio=0.1) # z軸 ax.text(x+0.5*u, y, z, s='u', fontsize=15) ax.text(x+u, y+0.5*v, z, s='v', fontsize=15) ax.text(x+u, y+v, z+0.5*w, s='w', fontsize=15) # 始点と終点を結ぶベクトル ax.quiver(x, y, z, u, v, w, arrow_length_ratio=0.1) # 始点(x, y, z)の補助線 plt.plot([min(x_vals.min(), x+u), max(x_vals.max(), x+u)], [y, y], [z, z], color='black', linestyle=':') # x軸 plt.plot([x, x], [min(y_vals.min(), y+v), max(y_vals.max(), y+v)], [z, z], color='black', linestyle=':') # y軸 plt.plot([x, x], [y, y], [min(z_vals.min(), z+w), max(z_vals.max(), z+w)], color='black', linestyle=':') # z軸 # 終点(x+u, y+v, z+w)の補助線 #plt.plot([min(x_vals.min(), x+u), max(x_vals.max(), x+u)], [y+v, y+v], [z+w, z+w], # color='black', linestyle=':') # x軸 #plt.plot([x+u, x+u], [min(y_vals.min(), y+v), max(y_vals.max(), y+v)], [z+w, z+w], # color='black', linestyle=':') # y軸 #plt.plot([x+u, x+u], [y+v, y+v], [min(z_vals.min(), z+w), max(z_vals.max(), z+w)], # color='black', linestyle=':') # z軸 # ラベル ax.set_xlabel('x') # x軸 ax.set_ylabel('y') # y軸 ax.set_zlabel('z') # z軸 ax.set_title('quiver(x, y, z, u, v, w)', fontsize=20) # タイトル # 表示 plt.show()

以上がplt.quiver()の基本的な使い方です。
・勾配の可視化
次は、2変数関数$f(x, y)$の勾配$(\frac{\partial f(x, y)}{\partial x}, \frac{\partial f(x, y)}{\partial y})$を矢印プロットで表現します。重複する内容は省略しているので、「3Dプロットの作図【ゼロつく1のノート(Python)】 - からっぽのしょこ」も参照してください。
・作図用の点
作図に利用する点(配列)を作成します。
$x,\ y$としてプロットする値(x軸とy軸の値)をx, yとして作成し、格子状の点X, Yに変換して、2乗和Zを計算します。
# x軸とy軸の値を作成 x = np.arange(-3, 4) y = np.arange(-3, 4) # 格子状の点を作成 X, Y = np.meshgrid(x, y) # 2乗和を計算 Z = X**2 + Y**2 print(Z) print(Z.shape)
[[18 13 10 9 10 13 18]
[13 8 5 4 5 8 13]
[10 5 2 1 2 5 10]
[ 9 4 1 0 1 4 9]
[10 5 2 1 2 5 10]
[13 8 5 4 5 8 13]
[18 13 10 9 10 13 18]]
(7, 7)
プロット時にベクトルが細かくなりすぎないように、この例では-3から3の整数とします。
作成した値をnp.meshgrid()で格子状の点に変換します。
偏微分$\frac{\partial f(x, y)}{\partial x},\ \frac{\partial f(x, y)}{\partial y}$を計算して、それぞれdX, dYとします。(微分の記号のdを付けて区別します。)
# 勾配(偏微分)を計算 dX = 2 * X dY = 2 * Y print(dX[:2, :]) print(dY[:, :2])
[[-6 -4 -2 0 2 4 6] [-6 -4 -2 0 2 4 6]] [[-6 -6] [-4 -4] [-2 -2] [ 0 0] [ 2 2] [ 4 4] [ 6 6]]
2乗和は、次の式でした。
「$x$に関する$f(x, y)$の微分$\frac{\partial f(x, y)}{\partial x}$」と「$y$に関する$f(x, y)$の微分$\frac{\partial f(x, y)}{\partial y}$」は、それぞれ次の式で計算できます。
詳しくは、「5.2:連鎖率【ゼロつく1のノート(数学)】 - からっぽのしょこ」を参照してください。また、$\frac{\partial f(x, y)}{\partial x},\ \frac{\partial f(x, y)}{\partial y}$をそれぞれ簡易的に$f_x(x, y),\ f_y(x, y)$でも表記します。下付き文字が、偏微分した変数を表します。
同様に、関数$f(x, y)$を等高線で作図するのに使うx・y・z軸の値fX, fY, fZを作成します。(関数:functionのfで区別します。)
# x軸とy軸の値を作成 fx = np.arange(-3, 3.1, 0.1) fy = np.arange(-3, 3.1, 0.1) # 格子状の点を作成 fX, fY = np.meshgrid(fx, fy) # 2乗和を計算 fZ = fX**2 + fY**2 print(fZ) print(fZ.shape)
[[18. 17.41 16.84 ... 16.84 17.41 18. ]
[17.41 16.82 16.25 ... 16.25 16.82 17.41]
[16.84 16.25 15.68 ... 15.68 16.25 16.84]
...
[16.84 16.25 15.68 ... 15.68 16.25 16.84]
[17.41 16.82 16.25 ... 16.25 16.82 17.41]
[18. 17.41 16.84 ... 16.84 17.41 18. ]]
(61, 61)
この例では、x・y軸ともに-3から3までの範囲で0.1刻みの値を作成します。等高線を綺麗に描くにはある程度細かい値が必要なので、X, Y, Zとは別に用意しておきます。
以上で、必要な値(配列)を用意できました。では可視化を行っていきます。
・2次元矢印プロットの作成
勾配を2次元の矢印プロットで可視化します。
勾配の値dX, dYを使って作図します。
# 2Dの矢印プロットを作成 plt.figure(figsize=(8, 8)) # 図の設定 plt.quiver(X, Y, -dX, -dY) # 矢印プロット plt.xlabel('x') # x軸ラベル plt.ylabel('y') # y軸ラベル plt.title('Gradient', fontsize=20) # タイトル plt.grid() # グリッド線 plt.show()

偏微分はその点における接線の傾きを表します。また、勾配ベクトル$(\frac{\partial f(x, y)}{\partial x},\ \frac{\partial f(x, y)}{\partial y})$は関数$f(x, y)$を最大化する方向を表します。勾配降下法では$f(x, y)$を最小化する方向が知りたいので、dX, dYに-を付けて符号を反転させる($+$と$-$を入れ変える)ことで、勾配ベクトルとは反対の方向に矢印が向くようにします。
関数$f(x, y)$と勾配の関係が分かりやすいように、等高線図と重ねて表示します。
# ベクトル図を作成 plt.figure(figsize=(8, 8)) # 図の設定 plt.contourf(fX, fY, fZ, alpha=0.5) # 塗りつぶし等高線図 plt.quiver(X, Y, -dX, -dY) # ベクトル図 plt.xlabel('x') # x軸ラベル plt.ylabel('y') # y軸ラベル plt.title('Gradient', fontsize=20) # タイトル plt.grid() # グリッド線 plt.show()

矢印の長さが勾配の大きさに対応しています。そのため、等高線の間隔が狭い位置ほど矢印が長くなります。矢印の長さの設定については、最後に少しだけ確認します。
また、勾配ベクトルは等高線に直交します。
・3次元矢印プロットの作成
勾配を3次元の矢印プロットで可視化します。
勾配の値(偏微分)dX, dYは、x軸とy軸方向に変化する値でした。3次元のグラフを作成するために、z軸方向の変化量Wを計算します。
# z軸方向の勾配の値を計算 W = np.sqrt(dX**2 + dY**2) + 1e-7
(これはいったい何を計算してるんだ?ノルム?これで勾配を割る理由も分からん。)
Wは割り算に使うので、0を含んでいると警告メッセージが表示されます。微小な値1e-7を加えておくと、0除算を回避できます。
勾配の値dX, dYとWを使って作図します。
# 3Dベクトル図を作成 fig = plt.figure(figsize=(8, 8)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_wireframe(X, Y, Z, alpha=0.5, label='f(x, y)') # 対象の関数(粗い) ax.contourf(fX, fY, fZ, alpha=0.5, offset=0) # 対称の関数(細かい) ax.quiver(X, Y, Z, -dX/W, -dY/W, -W, color='black', pivot='tail', arrow_length_ratio=0.1, length=0.5, label='(dx, dy)') # 勾配 ax.set_xlabel('x') # x軸ラベル ax.set_ylabel('y') # y軸ラベル ax.set_zlabel('z') # z軸ラベル ax.legend() # 凡例 #ax.view_init(elev=90, azim=270) # 表示アングル plt.show()


真上から見た図は、2次元のグラフのようになります。ただし、2D・3Dどちらのベクトルも長さが調整されているので一致しません。これについては、次で確認します。
・2D quiverと3D quiverの対応関係
関数$f(x, y)$と接線・接平面、勾配ベクトルの関係を確認します。また、2Dと3Dのベクトルの長さについて確認します。(ただし、私の理解が追い付いていないのでスッキリ解決しません。むしろ教えて下さい。)
(そもそも本編には登場しない内容なので、読むだけで良いと思います。)
変数$x,\ y$の2乗和$f(x, y) = x^2 + y^2$を計算する関数を作成しておきます。
# 2乗和の関数を作成 def f(x, y): return x**2 + y**2
$f(x, y)$上の点$(x, y, z)$をそれぞれpx, py, pzとします。px, pyの値を指定して、$z = f(x, y)$でpzを計算します。(点:pointのpです。)
# 接点(x, y, z)の値を指定 px = 1.0 py = 2.0 # zを計算 pz = f(px, py) print(pz)
5.0
この例では、$x = 1,\ y = 2$とします。$z = f(x, y) = 5$です。
この点$(1, 2, 5)$を接点として、接線と接平面を求めます。
点(px, py, pz)における勾配(偏微分)を計算します。
# 接点の勾配(dx, dy)を計算 dpx = 2 * px dpy = 2 * py print(dpx) print(dpy)
2.0
4.0
$x = 1, y = 2$における偏微分は$\frac{\partial f(x, y)}{\partial x} = 2 x = 2$、$\frac{\partial f(x, y)}{\partial y} = 2 y = 4$です。
$\frac{\partial f(x, y)}{\partial x},\ \frac{\partial f(x, y)}{\partial y}$は、それぞれx軸方向とy軸方向の接線の傾きを表します。
x軸方向とy軸方向の接線の切片を計算します。
# 接線の切片を計算 bx = f(px, py) - dpx * px by = f(px, py) - dpy * py print(bx) print(by)
3.0
-3.0
x軸方向の接線の傾きを$a_x$、切片を$b_x$とすると、接線は$z = a_x x + b_x$で表せます。この式を$b_x$について整理すると、$b_x = z - a_x x$で切片を計算できるのが分かります。
よって、$x = 1,\ y = 2$のとき、$z = f(x, y) = 5$、$a_x = \frac{\partial f(x, y)}{\partial x} = 2$を代入すると、$b_x = 5 - 2 * 1 = 3$が求まります。
y軸方向についても同様に計算できます。
傾きdpx, dpyと接線bx, byが求まったので、x軸方向とy軸方向の接線を計算します。
# 接線を計算 tangent_line_x = dpx * x + bx tangent_line_y = dpy * y + by print(tangent_line_x) print(tangent_line_y)
[-3. -1. 1. 3. 5. 7. 9.]
[-15. -11. -7. -3. 1. 5. 9.]
x軸の値xの要素ごとに、$z = a_x x + b_x$の計算をして、x軸方向の接線のz軸の値tangent_line_xを求めます。y軸方向の接線についても同様に計算します。
続いて、接平面を計算します。
# 接平面を計算
tangent_plane = dpx * (X - px) + dpy * (Y - py) + f(px, py)
接点を$(x_p, y_p, z_p)$とすると、接平面は次の式で計算できます。
仰々しく見えますが、偏微分$\frac{\partial f(x, y)}{\partial x},\ \frac{\partial f(x, y)}{\partial y}$をそれぞれ傾き$a_x,\ a_y$に置き換えると
係数と変数のペアと定数という接線と同じような式の形です。
関数$f(x, y)$のグラフに接線と接平面を重ねて描画します。
# 対象の関数と勾配ベクトルを作図 fig = plt.figure(figsize=(8, 8)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_wireframe(X, Y, Z, label='f(x, y)') # 対象の関数 ax.scatter(px, py, pz, s=100, c='black', label='(x, y, z)') # 接点 ax.plot_wireframe(X, Y, tangent_plane, color='orange', alpha=0.5) # 接平面 ax.plot(x, np.repeat(py, len(x)), tangent_line_x, color='red', linewidth=2.5, label='$f_x(x, y)$') # x0軸方向の接線 ax.plot(np.repeat(px, len(y)), y, tangent_line_y, color='green', linewidth=2.5, label='$f_y(x, y)$') # x1軸方向の接線 ax.set_xlabel('x') # x軸ラベル ax.set_ylabel('y') # y軸ラベル ax.set_zlabel('z') # z軸ラベル ax.legend() # 凡例 plt.show()

x軸方向の接線(赤線)とy軸方向の接線(緑線)をそれぞれ並行移動させたものが接平面(オレンジ線)です。
勾配ベクトルは、接平面上のベクトルです。
接点における勾配のz軸方向の変化量wを計算します。
# z軸方向の変化量を計算 wx = np.sqrt(dpx**2 + 0) wy = np.sqrt(0 + dpy**2) w = np.sqrt(dpx**2 + dpy**2) print(w)
4.47213595499958
同様に、x軸方向にだけ変化した(y軸方向への変化が0の)ときのz軸方向の変化量をwxとします。その逆の、y軸方向にだけ変化した(x軸方向への変化が0の)ときのz軸方向の変化量をwyとします。
勾配に関するベクトルも重ねて描画します。(これも確認用に作成する図です。)
・コード(クリックで展開)
## 対象の関数と勾配ベクトルを作図 # 設定 fig = plt.figure(figsize=(8, 8)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 # 関数 ax.plot_wireframe(X, Y, Z, alpha=0.5, label='f(x, y)') # 対象の関数 ax.scatter(px, py, pz, s=100, c='black', label='(x, y, z)') # 接点 # 接平面 ax.plot_wireframe(X, Y, tangent_plane, color='orange', alpha=0.5) # 接平面 ax.plot(x, np.repeat(py, len(x)), tangent_line_x, color='red', alpha=0.5, linewidth=2.5, linestyle='--', label='$f_x(x, y)$') # x軸方向の接線 ax.plot(np.repeat(px, len(y)), y, tangent_line_y, color='green', alpha=0.5, linewidth=2.5, linestyle='--', label='$f_y(x, y)$') # y軸方向の接線 # ベクトル ax.quiver(px, py, pz, -dpx/w, -dpy/w, -w, color='black', linewidth=2.5, arrow_length_ratio=0.1, length=1, label='(dx, dy)') # 勾配方向のベクトル ax.quiver(px, py, pz, -dpx/wx, 0, -wx, color='red', linewidth=2.5, arrow_length_ratio=0.1, length=1, label='(dx, 0)') # x軸方向のベクトル ax.quiver(px, py, pz, 0, -dpy/wy, -wy, color='green', linewidth=2.5, arrow_length_ratio=0.1, length=1, label='(0, dy)') # y軸方向のベクトル # ラベル ax.set_xlabel('x') # x軸ラベル ax.set_ylabel('y') # y軸ラベル ax.set_zlabel('z') # z軸ラベル ax.legend() # 凡例 #ax.view_init(elev=90, azim=270) # 表示アングル plt.show()
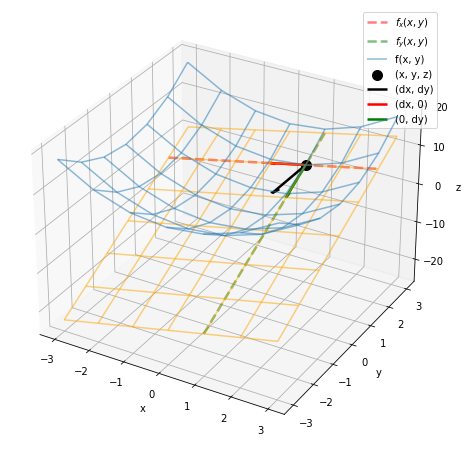
2つの接線上のベクトルは、勾配ベクトル(黒色)との関係を見るためのものです。描画する必要はありません。
さて、関数と接線・接平面、勾配ベクトルの関係が分かりました(いや分からん)。次のは、この3D矢印プロットで描画される勾配ベクトルと、最初に作成した2D矢印プロットで描画される勾配ベクトルとの対応を確認します。
・3次元空間用の調整を行う場合
・コード(クリックで展開)
2Dグラフの方も3Dグラフと同様に、x軸とy軸の変化量dpx, dpyをz軸の変化量w, wx, wyで割ります。
# 2Dの勾配ベクトルを作図 # 設定 plt.figure(figsize=(6, 6)) # 図の設定 # 関数 plt.contour(fX, fY, fZ) # 対象の関数 plt.scatter(px, py, label='(x, y, z)') # 接点 # 接線 plt.hlines(y=py, xmin=x.min(), xmax=x.max(), color='red', linestyle='--', label="f '(x)") # x軸方向の接線 plt.vlines(x=px, ymin=y.min(), ymax=y.max(), color='green', linestyle='--', label="f '(y)") # y軸方向の接線 # ベクトル plt.quiver(px, py, -dpx/w, -dpy/w, angles='xy', scale_units='xy', scale=1, label='(dx, dy)') # 勾配ベクトル plt.quiver(px, py, -dpx/wx, 0, angles='xy', scale_units='xy', scale=1, color='red', label='(dx, 0)') # x軸方向のベクトル plt.quiver(px, py, 0, -dpy/wy, angles='xy', scale_units='xy', scale=1, color='green', label='(0, dy)') # y軸方向のベクトル # ラベル plt.xlabel('x') # x軸ラベル plt.ylabel('y') # y軸ラベル plt.grid() # グリッド線 plt.legend() # 凡例 plt.show()


3Dグラフの方は先ほどのグラフを真上から見たものです。
同じ調整を行ったので、ベクトルの長さや向きが一致しています。
・値を調整しない場合
・コード(クリックで展開)
x軸とy軸の変化量dpx, dpyをz軸の変化量w, wx, wyで割るのを止めてみます。
## 対象の関数と勾配ベクトルを作図 # 設定 fig = plt.figure(figsize=(8, 8)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 # 関数 ax.plot_wireframe(X, Y, Z, alpha=0.5, label='f(x, y)') # 対象の関数 ax.scatter(px, py, pz, s=100, c='black', label='(x, y, z)') # 接点 # 接平面 ax.plot_wireframe(X, Y, tangent_plane, color='orange', alpha=0.5) # 接平面 ax.plot(x, np.repeat(py, len(x)), tangent_line_x, color='red', alpha=0.5, linewidth=2.5, linestyle='--', label="f '(x)") # x軸方向の接線 ax.plot(np.repeat(px, len(y)), y, tangent_line_y, color='green', alpha=0.5, linewidth=2.5, linestyle='--', label="f '(y)") # y軸方向の接線 # ベクトル ax.quiver(px, py, pz, -dpx, -dpy, -w, color='black', linewidth=2.5, arrow_length_ratio=0.1, length=1, label='(dx, dy)') # 勾配方向のベクトル ax.quiver(px, py, pz, -dpx, 0, -wx, color='red', linewidth=2.5, arrow_length_ratio=0.1, length=1, label='(dx, 0)') # x軸方向のベクトル ax.quiver(px, py, pz, 0, -dpy, -wy, color='green', linewidth=2.5, arrow_length_ratio=0.1, length=1, label='(0, dy)') # y軸方向のベクトル # ラベル ax.set_xlabel('x') # x軸ラベル ax.set_ylabel('y') # y軸ラベル ax.set_zlabel('z') # z軸ラベル ax.legend() # 凡例 ax.view_init(elev=90, azim=270) # 表示アングル plt.show()
勾配dpx, dpyの値のままの図(引数angles='xy'、scale_units='xy'、scale=1を指定した図)を作成します。
## 2Dのベクトルを作図 # 設定 plt.figure(figsize=(6, 6)) # 図の設定 # 関数 plt.contour(fX, fY, fZ) # 対象の関数 plt.scatter(px, py, label='(x, y, z)') # 接点 # 接線 plt.hlines(y=py, xmin=x.min(), xmax=y.max(), color='red', linestyle='--', label="f '(x)") # x軸方向の接線 plt.vlines(x=px, ymin=y.min(), ymax=x.max(), color='green', linestyle='--', label="f '(y)") # y軸方向の接線 # ベクトル plt.quiver(px, py, -dpx, -dpy, angles='xy', scale_units='xy', scale=1, label='(dx, dy)') # 勾配ベクトル plt.quiver(px, py, -dpx, 0, angles='xy', scale_units='xy', scale=1, color='red', label='(dx, 0)') # x軸方向のベクトル plt.quiver(px, py, 0, -dpy, angles='xy', scale_units='xy', scale=1, color='green', label='(0, dy)') # y軸方向のベクトル # ラベル plt.xlabel('x') # x軸ラベル plt.ylabel('y') # y軸ラベル plt.grid() # グリッド線 plt.legend() # 凡例 plt.show()


ただし、z軸方向の調整がされていないため、別のアングルで見るとベクトルの向きが関数に対応していません。
・デフォルトの補正の場合
・コード(クリックで展開)
# 2Dのベクトルを作図 # 設定 plt.figure(figsize=(6, 6)) # 図の設定 # 関数 plt.contour(fX, fY, fZ) # 対象の関数 plt.scatter(px, py, label='(x, y, z)') # 接点 # 接線 plt.hlines(y=py, xmin=x.min(), xmax=y.max(), color='red', linestyle='--', label="f '(x)") # x軸方向の接線 plt.vlines(x=px, ymin=y.min(), ymax=x.max(), color='green', linestyle='--', label="f '(y)") # y軸方向の接線 # ベクトル plt.quiver(px, py, -dpx, -dpy, label='(dx, dy)') # 勾配ベクトル # ラベル plt.xlabel('x') # x軸ラベル plt.ylabel('y') # y軸ラベル plt.grid() # グリッド線 plt.legend() # 凡例 plt.show()

この図が、1つの点に対しての勾配のプロットです。これを複数の点X, Y, Zで行ったものが「2次元矢印プロット」で作成した図です。
以上で、2Dと3Dプロットを使って2変数関数の勾配を可視化できました。これらの図は6.1節にてもう一度だけ登場します。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning』オライリー・ジャパン,2016年.
おわりに
勾配ベクトルを3次元空間にプロットする際の、z軸方向の変化量Wの計算が分かりませんでした。これって高校数学?大学数学?何の分野を調べればいいのかも分かりません。
あと私の頭は、3次元の情報を自在に操ってイメージできるようにはできていないようで中々大変です。
記事投稿日の前日に公開された(半セルフ)カバー動画をぜひ観て・聴いてください!
それぞれのグループを卒業・解散してソロ活動のお二人がこの曲を歌うのって中々来るものがある。
【関連する記事】