はじめに
「Python」初学者のための『ゼロから作るDeep Learning』攻略ノートです。『ゼロつくシリーズ』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
本を進めるにあたって必要となるPython文法や利用する関数について、その機能や使い方、補足情報を確認していきます。
この記事では、2変数の関数を3次元のグラフで可視化する方法を解説します。
【他の記事一覧】
【この節の内容】
・3Dプロットの作図
MatplotlibのPyPlotモジュールを利用して、2変数の関数を3Dのグラフで可視化します。
この記事では、2変数$x,\ y$(または$x_0,\ x_1$)の2乗和$z = x^2 + y^2$を例とします。
次のライブラリを利用します。
# 利用するライブラリ import numpy as np import matplotlib.pyplot as plt #from mpl_toolkits.mplot3d import Axes3D
3Dプロットの作図にmpl_toolkits.mplot3dを読み込む必要があるとかないとかというのを見たのでメモをとして書いておきます。
・meshgrid関数の確認
3Dプロットを作成するには、格子状の点(x軸とy軸の値が直交する点)を用意する必要があります。そこでまずは、格子点を作成する関数np.meshgrid()を確認しておきます。
「x軸の値($x$の値)」と「y軸の値($y$の値)」を1次元配列として作成します。
# x軸の値を作成 x = np.array([1, 3, 5, 7, 9]) print(x) print(x.shape) # y軸の値を作成 y = np.array([2, 4, 6, 8]) print(y) print(y.shape)
[1 3 5 7 9]
(5,)
[2 4 6 8]
(4,)
この例では、分かりやすいように奇数と偶数の配列を作成しました。また、要素数が同じにならないようにもしています。
np.meshgrid()を使って、格子状の点を作成します。
# 格子状の点を作成 X, Y = np.meshgrid(x, y) print(X) print(X.shape) print(Y) print(Y.shape)
[[1 3 5 7 9]
[1 3 5 7 9]
[1 3 5 7 9]
[1 3 5 7 9]]
(4, 5)
[[2 2 2 2 2]
[4 4 4 4 4]
[6 6 6 6 6]
[8 8 8 8 8]]
(4, 5)
np.meshgrid()は、2つの配列を出力します(正確には、入力した数と同じ数です)。
1つ目の配列Xは、第1引数の配列xを行方向に複製した2次元配列になります。2つ目の配列Yは、第2引数の配列yを列方向に複製した2次元配列になります。XとYは同じ形状です。
変数名は、元の1次元配列を小文字x、変換後の2次元配列を大文字Xや小文字を2つxxで表現するのが慣例のようです。
XとYの要素を並べて確認しましょう。
# 確認 print(X.flatten()) print(Y.flatten())
[1 3 5 7 9 1 3 5 7 9 1 3 5 7 9 1 3 5 7 9]
[2 2 2 2 2 4 4 4 4 4 6 6 6 6 6 8 8 8 8 8]
xとyの要素に関して全ての組み合わせができます。
XとYの2乗和を計算します。
# 2乗和を計算 Z = X**2 + Y**2 print(Z) print(Z.shape)
[[ 5 13 29 53 85]
[ 17 25 41 65 97]
[ 37 45 61 85 117]
[ 65 73 89 113 145]]
(4, 5)
同じ位置の要素を2乗した和が求まります。計算結果Zも同じ形状の配列になります。
以上が作図前に行う処理です。
作成した点を簡単にグラフで確認しておきましょう。
xをx軸の値、yをy軸の値として散布図にしてみます。
# xとyの点を確認 plt.scatter(x[:4], y) # 散布図 plt.xlabel('x') # x軸ラベル plt.ylabel('y') # y軸ラベル #plt.xticks(x) # x軸目盛 #plt.yticks(y) # y軸目盛 plt.grid() # グリッド線 plt.show()
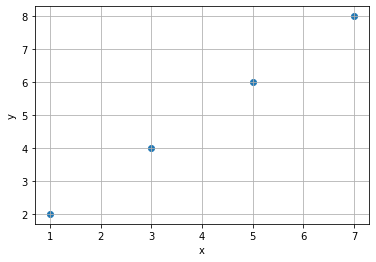
散布図は、plt.scatter()で作成します。xとyの要素数が異なるため、同じ数になるように調整しています。
続いて、Xをx軸の値、Yをy軸の値として散布図にしてみます。
# XとYの点を確認 plt.scatter(X, Y) # 散布図 plt.xlabel('x') # x軸ラベル plt.ylabel('y') # y軸ラベル #plt.xticks(x) # x軸目盛 #plt.yticks(y) # y軸目盛 plt.grid() # グリッド線 plt.show()
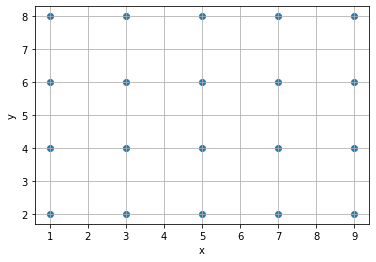
碁盤の目のようになっています。これを格子点と呼びます。
・作図用の点
処理の確認ができたので、実際に作図するための点(配列)を作成します。
x軸の値とy軸の値を設定します。
# x軸とy軸の値を作成 x = np.arange(-5, 5.1, 0.1) y = np.arange(-5, 5.1, 0.1) print(x[:10]) print(x.shape)
[-5. -4.9 -4.8 -4.7 -4.6 -4.5 -4.4 -4.3 -4.2 -4.1]
(101,)
この例では、x軸とy軸ともに-5から5までを範囲として、0.1刻みの値を作成します。
格子状の点を作成します。
# 格子状の点を作成 X, Y = np.meshgrid(x, y) print(X) print(X.shape) print(Y) print(Y.shape)
[[-5. -4.9 -4.8 ... 4.8 4.9 5. ]
[-5. -4.9 -4.8 ... 4.8 4.9 5. ]
[-5. -4.9 -4.8 ... 4.8 4.9 5. ]
...
[-5. -4.9 -4.8 ... 4.8 4.9 5. ]
[-5. -4.9 -4.8 ... 4.8 4.9 5. ]
[-5. -4.9 -4.8 ... 4.8 4.9 5. ]]
(101, 101)
[[-5. -5. -5. ... -5. -5. -5. ]
[-4.9 -4.9 -4.9 ... -4.9 -4.9 -4.9]
[-4.8 -4.8 -4.8 ... -4.8 -4.8 -4.8]
...
[ 4.8 4.8 4.8 ... 4.8 4.8 4.8]
[ 4.9 4.9 4.9 ... 4.9 4.9 4.9]
[ 5. 5. 5. ... 5. 5. 5. ]]
(101, 101)
XとYの2乗和を計算します。
# 2乗和を計算 Z = X**2 + Y**2 print(Z) print(Z.shape)
[[50. 49.01 48.04 ... 48.04 49.01 50. ]
[49.01 48.02 47.05 ... 47.05 48.02 49.01]
[48.04 47.05 46.08 ... 46.08 47.05 48.04]
...
[48.04 47.05 46.08 ... 46.08 47.05 48.04]
[49.01 48.02 47.05 ... 47.05 48.02 49.01]
[50. 49.01 48.04 ... 48.04 49.01 50. ]]
(101, 101)
これで準備が整いました。続いて、2乗和の関数を2次元の図と3次元の図で可視化していきます。
・等高線図
等高線グラフによって、3次元の情報を2次元のグラフで可視化します。
等高線図を作成します。
# 等高線図を作成 plt.figure(figsize=(7, 6)) plt.contour(X, Y, Z) # 等高線図 plt.xlabel('x') # x軸ラベル plt.ylabel('y') # y軸ラベル plt.title('$z = x^2 + y^2$', fontsize=20) # タイトル plt.colorbar() # z軸の値 plt.show()
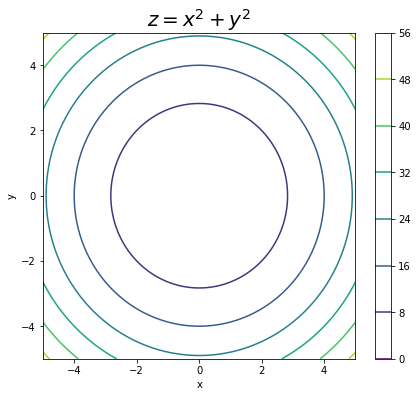
等高線図は、plt.contour()で作成します。
plt.contourf()を使うと、等高線の間を塗りつぶします。
# 塗りつぶし等高線図を作成 plt.figure(figsize=(7, 6)) plt.contourf(X, Y, Z) # 塗りつぶし等高線図 plt.xlabel('x') # x軸ラベル plt.ylabel('y') # y軸ラベル plt.title('$z = x^2 + y^2$', fontsize=20) # タイトル plt.colorbar() # z軸の値 plt.show()
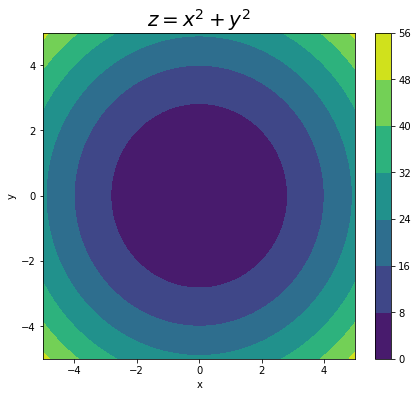
alpha引数に0から1の値を指定することで、透過度を調整できます。
# 塗りつぶし等高線図を作成 plt.figure(figsize=(7, 6)) plt.contourf(X, Y, Z, alpha=0.5) # 塗りつぶし等高線図 plt.xlabel('x') # x軸ラベル plt.ylabel('y') # y軸ラベル plt.title('$z = x^2 + y^2$', fontsize=20) # タイトル plt.colorbar() # z軸の値 plt.show()
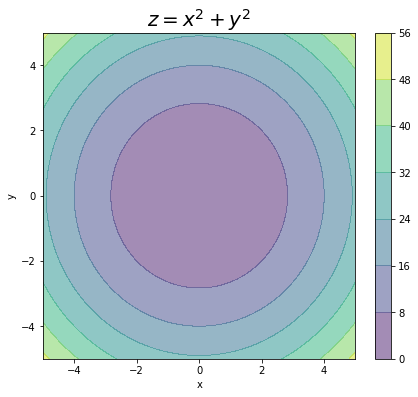
0に近いほど色が薄く、1に近いほど色が濃くなります。
・3Dプロット
続いて、3次元のグラフで可視化します。
ところで、MatplotlibにはMATLAB-styleとOOP-styleの2つの記述方法があります。
MATLAB-styleは、これまで書いてきた方法で、plt.plot()やplt.title()のように関数を重ねて記述します。
OOP-styleは、オブジェクト指向(object-oriented programing)で扱います。図をfigやaxのオブジェクトとして作成し、ax.plot()やax.title()のようにメソッドを使って記述します。
3Dプロットに関しては、(この書き方しか見付けられなかったので)OOP-styleで作成します。複雑な図や細かい調整ができることもあり、OOP-styleが推奨されています。
このシリーズの記事では、基本的な図しか書かないことやとっつきやすさを優先して、MATLAB-styleで記述します。(何より私がこっちでしか書けないので。)
ワイヤーフレーム図を作成します。
# ワイヤーフレーム図を作成 fig = plt.figure(figsize=(8, 8)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_wireframe(X, Y, Z) # ワイヤーフレーム図 ax.set_xlabel('x') # x軸ラベル ax.set_ylabel('y') # y軸ラベル ax.set_zlabel('z') # z軸ラベル plt.show()
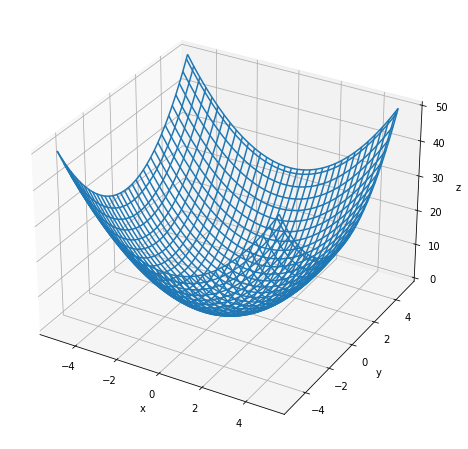
ワイヤーフレーム図は、ax.plot_wireframe()で作成します。
ax.view_init(elev, azim)で、表示する図の角度を変更できます。
# ワイヤーフレーム図を作成 fig = plt.figure(figsize=(8, 8)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_wireframe(X, Y, Z, label='label') # ワイヤーフレーム図 ax.set_xlabel('x') # x軸ラベル ax.set_ylabel('y') # y軸ラベル ax.set_zlabel('z') # z軸ラベル ax.set_title('title', loc='center', fontsize=20) # グラフタイトル fig.suptitle('suptitle', fontsize=20) # 図全体のタイトル ax.legend() # 凡例 ax.view_init(elev=20, azim=240) # 表示アングル plt.show()
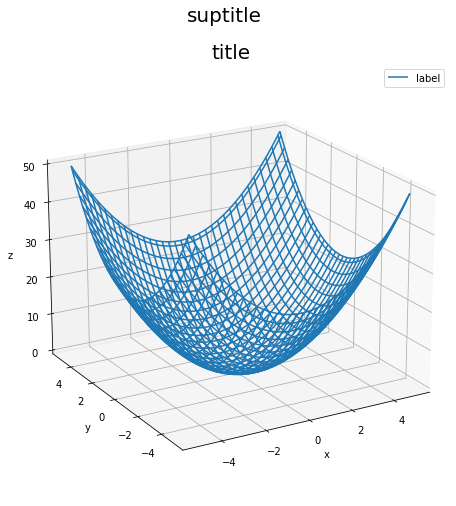
elevに縦方向の角度、azimに横方向の角度を指定できます。
他にも様々な加工を行えます。(ax.set_zlim()等は、背後の軸・目盛には影響するけどプロット自体には影響しないようです。なのでグラフ部分がはみ出ます。)
本には登場しませんが、他のグラフもいくつか載せておきます。(ただし、○○図という名称は私が雰囲気で呼んでいるだけです。正しい名称があれば教えてください。)
ワイヤーフレーム図でも色を付けられるのですが少し手間がかかるようなので、曲面図を作成します。
# 曲面図を作成 fig = plt.figure(figsize=(8, 8)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_surface(X, Y, Z, cmap='jet') # 曲面図 ax.set_xlabel('x') # x軸ラベル ax.set_ylabel('y') # y軸ラベル ax.set_zlabel('z') # z軸ラベル plt.show()
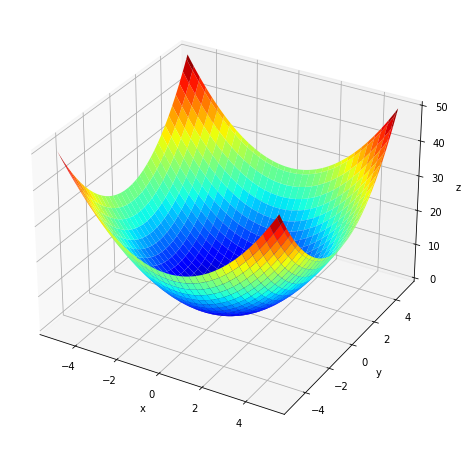
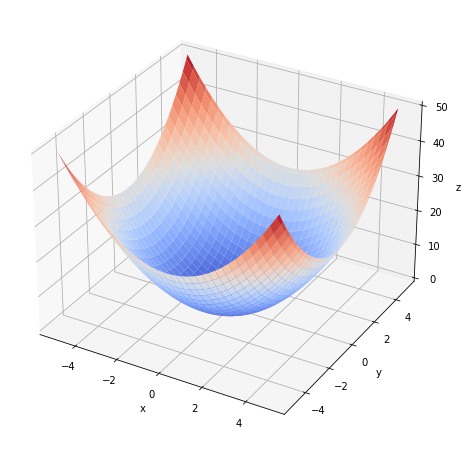
曲面図は、ax.plot_surface()で作成します。
カラーマップ引数cmapに色名を指定できます。左の図はjet、右の図はcoolwarmを指定したグラフです。
colorbar()でカラーバーを表示できます。
# 曲面図を作成 fig = plt.figure(figsize=(8, 8)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 surf = ax.plot_surface(X, Y, Z, cmap='viridis') # 曲面図 ax.set_xlabel('x') # x軸ラベル ax.set_ylabel('y') # y軸ラベル ax.set_zlabel('z') # z軸ラベル fig.colorbar(surf, shrink=0.5, aspect=10) # カラーバー plt.show()
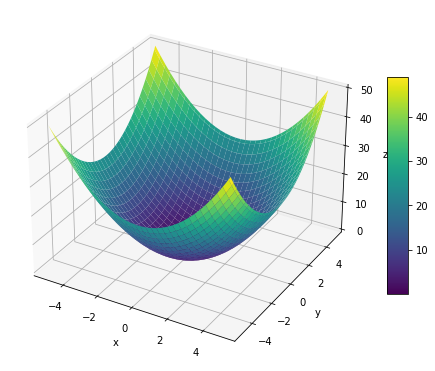
サイズは、引数shrink, aspectで調整できます。shrinkは、図全体に対するカラーバーの高さの比率です。aspectは、カラーバーの横幅に対する高さの比です。
3次元の等高線図も作成できます。
# 等高線図を作成 fig = plt.figure(figsize=(8, 8)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.contour(X, Y, Z) # 等高線図 ax.set_xlabel('x') # x軸ラベル ax.set_ylabel('y') # y軸ラベル ax.set_zlabel('z') # z軸ラベル plt.show()
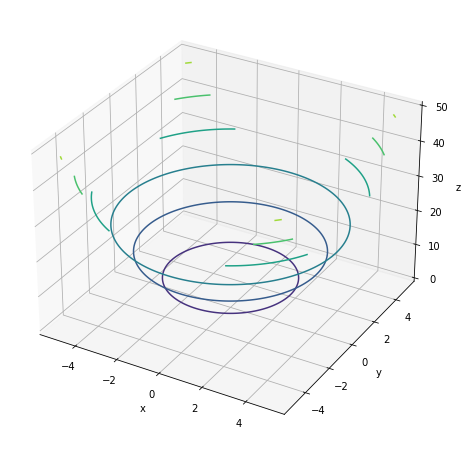
(ax.contourf()はなんか微妙だったので省略。)
他のグラフと重ねて描画することもできます。
# 3Dプロットを作成 fig = plt.figure(figsize=(8, 8)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_surface(X, Y, Z, cmap='jet') # 曲面図 ax.contour(X, Y, Z, cmap='jet', offset=0) # 等高線図 #ax.contourf(X, Y, Z, alpha=0.5, cmap='jet', offset=0) # 塗りつぶし等高線図 ax.set_xlabel('x') # x軸ラベル ax.set_ylabel('y') # y軸ラベル ax.set_zlabel('z') # z軸ラベル plt.show()
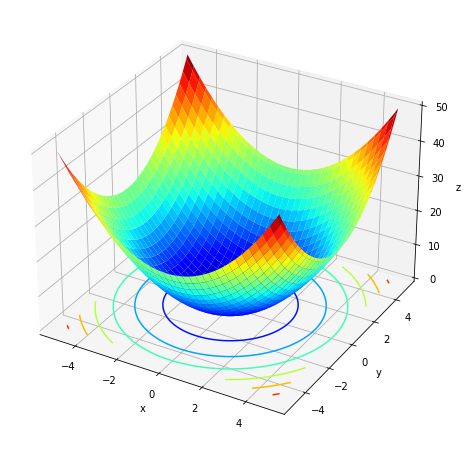
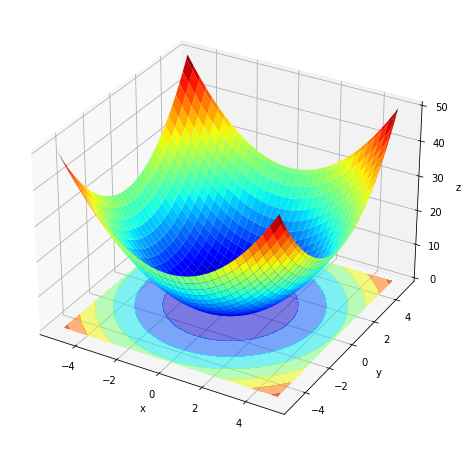
左の図はax.contour()、右の図はax.contourf()で作成したグラフも表示しています。等高線を描画する平面の高さ(z軸の値)をoffsetに指定します。
等高線図でもcmapを指定できます。
3Dの散布図も作成できます。
# 散布図を作成 fig = plt.figure(figsize=(8, 8)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3Dプロットの準備 ax.scatter(X, Y, Z, c=Z, cmap='jet') # 散布図 ax.set_xlabel('x') # x軸ラベル ax.set_ylabel('y') # y軸ラベル ax.set_zlabel('z') # z軸ラベル plt.show()

散布図は、格子状の点でなくても作図できます。
以上で、3Dプロットを使って2変数の関数を可視化できました。主に、勾配降下法によるパラメータの更新値の推移を確認するのに利用します。次は、矢印プロットを使って勾配を可視化します。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning』オライリー・ジャパン,2016年.
おわりに
ゼロからDL1巻を始めて1年ちょっとが経ち、3巻まで読み終わりました。そしてPython歴も1年とちょっとになりました。ので、1巻の記事から加筆修正していきます。なんてったってPython歴1か月の頃から書き始めたシリーズですからね。気になるところだらけです。早急にやり遂げたい。
とは言いつつ記事の修正って結構大変で、普通に1つ記事を書くのと同じだけ疲れます。間をとって(?)notebook上で少し書いて放置していた内容を完成させるところから始めました。
そんなこんなでこれがゼロつくシリーズの2周目最初の更新です。そろそろfigとaxで書く方を覚えないとなー。
2021年7月13日は、モーニング娘。の元リーダー道重さゆみさんの32歳のお誕生日です!!!
おめでとうございます!!当時はアイドルというものにカケラも興味がなく、あんまり知りませんでした。今となってはタイムマシンがあれば卒コンを観に行きたい日々を過ごしています。
【関連する記事】