はじめに
『ゼロから作るDeep Learning 3』の初学者向け攻略ノートです。『ゼロつく3』の学習の補助となるように適宜解説を加えていきます。本と一緒に読んでください。
本で省略されているクラスや関数の内部の処理を1つずつ解説していきます。
この記事は、主にステップ42「線形回帰」を補足する内容です。
DeZeroのモジュールを利用して線形回帰を実装します。
【前ステップの内容】
【他の記事一覧】
【この記事の内容】
・線形回帰
DeZeroのモジュールとして実装した線形変換のクラスLinearと平均2乗誤差のクラスMeanSquaredErrorを利用して、勾配降下法によりパラメータ$\mathbf{W},\ \mathbf{b}$を推定します。
次のライブラリを利用します。
# 利用するライブラリ import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation
animationモジュールは、アニメーション(gif画像)を作成するためのモジュールです。最後に推移をアニメーションで確認するのに利用します。
また、これまでに実装済したクラスを利用します。dezeroフォルダの親フォルダまでのパスをsys.path.append()に指定します。
# 実装済みモジュールの読込用設定 import sys sys.path.append('..') # 利用する実装済みモジュール from dezero import Variable import dezero.functions as F
・ Linearクラスの利用
Linearは線形回帰
を計算するクラスです。順伝播と逆伝播の計算の詳細は、「ステップ42:線形変換の逆伝播の導出【ゼロつく3のノート(数学)】 - からっぽのしょこ」を参照してください。
実際に計算してみましょう。データ数と次元数を指定して、入力データxとパラメータW, bを作成します。
# データ数を指定 N = 100 # 入力データの次元数を指定 D = 3 # 出力データの次元数を指定 H = 4 # 入力データを作成 x = Variable(np.random.rand(N, D)) print(x.data[:5]) print(x.shape) # 重みを作成 W = Variable(np.random.randn(D, H)) print(W.data) print(W.shape) # バイアスを作成 b = Variable(np.random.randn(H)) print(b.data) print(b.shape)
[[0.3504918 0.67392164 0.07667619]
[0.03930807 0.52250659 0.3536131 ]
[0.09395481 0.80008115 0.43102346]
[0.74973155 0.66250096 0.88016759]
[0.79398932 0.15287064 0.66401706]]
(100, 3)
[[ 0.34316168 0.6148695 -0.77140733 -0.3405662 ]
[-2.03459893 -1.28885903 -1.38365704 -0.14615759]
[ 0.1775359 0.67282311 1.32689767 -0.43870435]]
(3, 4)
[-2.30985371 -0.44042832 0.19682787 1.49457893]
(4,)
線形変換の関数F.linear()で計算します。Linearクラスとlinear()関数については、ステップ43を参照してください。
# 出力データを計算 y = F.linear(x, W, b) print(y.data[:5]) print(y.shape)
[[-3.54712582 -1.04192208 -0.90427903 1.24307632]
[-3.29667701 -0.85177725 -0.08725619 1.24969202]
[-3.82893413 -1.12384764 -0.41076345 1.1565513 ]
[-3.24423696 -0.2411145 -0.13030233 0.75628281]
[-2.23053057 0.29750881 0.25390084 0.91052262]]
(100, 4)
$(N \times H)$の行列(2次元配列)yが出力されました。
出力の次元数が1の場合も$(N \times 1)$の2次元配列として出力されるので、作図時などにはflatten()で1次元配列に変換する必要があります。
F.mean_sqrared_error()の使い方は、簡易版のmean_sqrared_error()と(内部の処理は違いますが)変わらないので省略します。
・このステップでの問題設定
この例では、入力・出力ともに次元数を1とします。$D = 1,\ H = 1$のとき、バイアスを含む線形変換は次の式になります。
どちらのパラメータもスカラなので、$w = w_{0.0},\ b = b_0$とすると、$n$番目のデータは
傾き$w$、切片$b$の1次関数で計算できるのが分かります。
・データセットの作成
まずは、トイ・データセット$\mathbf{x},\ \mathbf{y}$を作成します。
この例では、入力$x_n$を0から1の一様乱数とします。また、出力$y_n$を$y_n = 2 x_n + 5$に更に0から1の一様乱数を加えたものとします。この場合、$w$の真の値は2、$b$の真の値は5.5です(だよね?)。
# データ数を指定 N = 100 # トイ・データセットを作成 x = np.random.rand(N, 1) y = 5 + 2 * x + np.random.rand(N, 1) # データを確認 print(x[:5]) print(x.shape) print(y[:5]) print(y.shape)
[[0.90518629]
[0.86438776]
[0.14821623]
[0.2202906 ]
[0.89278192]]
(100, 1)
[[7.28409679]
[7.32921031]
[5.34534916]
[6.09982576]
[7.09011907]]
(100, 1)
0から1の一様乱数はnp.random.rand()で生成できます。第1引数に行数、第2引数に列数を指定します。
作成したデータセットを散布図で確認しておきましょう。
# データセットの散布図を作成 plt.figure(figsize=(8, 6)) plt.scatter(x, y) # 散布図 plt.xlabel('x') # x軸ラベル plt.ylabel('y') # y軸ラベル plt.suptitle('dataset', fontsize=20) # 図全体のタイトル plt.title('N=' + str(len(x)), loc='left') # タイトル plt.grid() # グリッド線 plt.show()
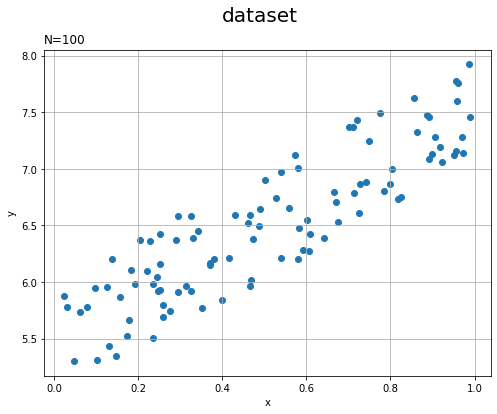
xがとり得る最小値は0、最大値は1です。yがとり得る最小値は5、最大値は8です。
・線形回帰の実装
では、勾配降下法による線形回帰を行います。
繰り返し回数をiters、学習率をlrとして値を指定します。また、重みWとバイアスbの初期値を指定します。
重みとバイアス、損失の推移を確認するために、学習を行う(値を更新する)ごとにリストtrace_*に値を格納していきます。
予測値の計算には線形変換の関数F.linear()、損失の計算には平均2乗誤差の関数F.mean_squared_error()を利用します。勾配降下法については、「ステップ29:勾配降下法とニュートン法の比較【ゼロつく3のノート(数学)】 - からっぽのしょこ」を参照してください。
# 試行回数を指定 iters = 100 # 学習率を指定 lr = 0.1 # パラメータの初期値を指定 W = Variable(np.zeros((1, 1))) # 重み b = Variable(np.zeros(1)) # バイアス # 推移の確認用のリストを初期化 trace_W = [W.data.item()] trace_b = [b.data.item()] trace_L = [] # 勾配降下法 for i in range(iters): # 予測値を計算 y_pred = F.linear(x, W, b) # 平均2乗誤差を計算 loss = F.mean_squared_error(y, y_pred) # 勾配を初期化 W.cleargrad() b.cleargrad() # 勾配を計算 loss.backward() # パラメータを更新 W.data -= lr * W.grad.data b.data -= lr * b.grad.data # パラメータを記録 trace_W.append(W.data.item()) trace_b.append(b.data.item()) trace_L.append(loss.data.item()) # i回目の結果を表示 print('iter:' + str(i + 1) + ', loss=' + str(loss.data))
iter:1, loss=42.7581529684914
iter:2, loss=23.76263039801906
iter:3, loss=13.232362445321503
iter:4, loss=7.394609396611447
iter:5, loss=4.158047821387347
(省略)
iter:96, loss=0.08954610031874527
iter:97, loss=0.08942441736304907
iter:98, loss=0.08930580356833545
iter:99, loss=0.08919018152237294
iter:100, loss=0.08907747576546791
(よく見ると式は$\hat{y} - y$なのにコードはy - y_predで違う?(わざわざ変える必要はありませんが)2乗をとると同じ結果になります。)
最後に更新したパラメータを使って損失を確認しておきます。
# 平均2乗誤差を計算 loss = F.mean_squared_error(y, F.linear(x, W, b)) trace_L.append(loss.data.item()) print(loss.data)
0.08896761274121708
0に近い値になっていることから、実際の値と予測値との誤差がほとんどなくなっているのが分かります。(ここで損失を計算した本当の目的は、trace_W, trace_bとtrace_Lの要素数を合わせるためです。アニメーション作成時に面倒になるので。)
・推定結果の確認
パラメータの推定値を用いて回帰直線を計算します。
# 作図用のxの点を作成 x_line = np.arange(0.0, 1.1, 0.1) print(x_line[:5]) # 作図用のxに対する予測値を計算 y_line = F.linear(x_line.reshape((len(x_line), 1)), W, b).data.flatten() print(y_line[:5])
[0. 0.1 0.2 0.3 0.4]
[5.39348674 5.61081304 5.82813934 6.04546564 6.26279194]
データxの最小値から最大値までを範囲として、作図用の$x$の値を作成します。作成した値ごとに予測値$\hat{y}$を計算します。
F.linear()の第1引数に渡すx_lineを縦に要素を並べた2次元配列に変換しています。また、出力を1次元配列に変換しています。
回帰直線を散布図と重ねて作図します。
# 回帰直線を作図 plt.figure(figsize=(8, 6)) plt.scatter(x, y, label='データセット') # データセット plt.plot(x_line, y_line, color='red', label='回帰直線') # 回帰直線 plt.xlabel('x') # x軸ラベル plt.ylabel('y') # y軸ラベル plt.suptitle('Linear Regression', fontsize=20) # 図全体のタイトル plt.title('iter:' + str(iters) + ', loss=' + str(np.round(loss.data, 3)) + ', N=' + str(len(x)) + ', W=' + str(np.round(W.data.item(), 2)) + ', b=' + str(np.round(b.data.item(), 2)), loc='left') # タイトル plt.legend(prop={"family":"MS Gothic"}) # 凡例 plt.grid() # グリッド線 plt.show()
prop={"family":"MS Gothic"}はmatplotlibで日本語を表示するためのおまじないです。
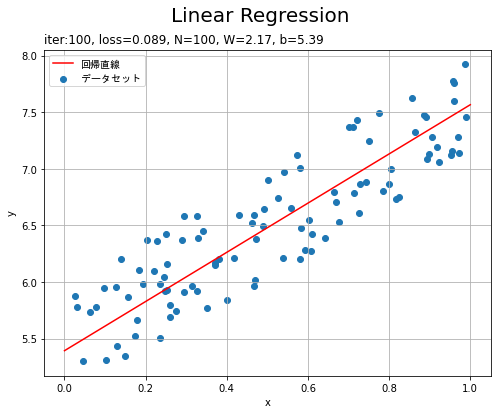
データへの当てはまりのよい直線を引けています。
損失(平均2乗誤差)の推移を確認します。
# 平均2乗誤差の推移を作図 plt.figure(figsize=(8, 6)) plt.plot(np.arange(len(trace_L)), trace_L, label='loss') plt.xlabel('iteration') # x軸ラベル plt.ylabel('value') # y軸ラベル plt.suptitle('Linear Regression', fontsize=20) # 図全体のタイトル plt.title('N=' + str(len(x)), loc='left') # タイトル plt.legend() # 凡例 plt.grid() # グリッド線 #plt.ylim(0.0, 0.2) # y軸の表示範囲 plt.show()
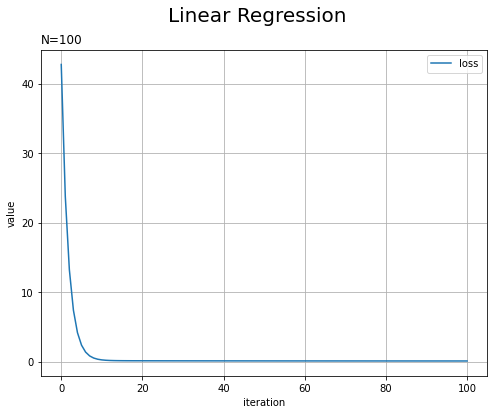
試行回数が増えるにしたがって損失が下がっています。表示範囲を狭めてみます。
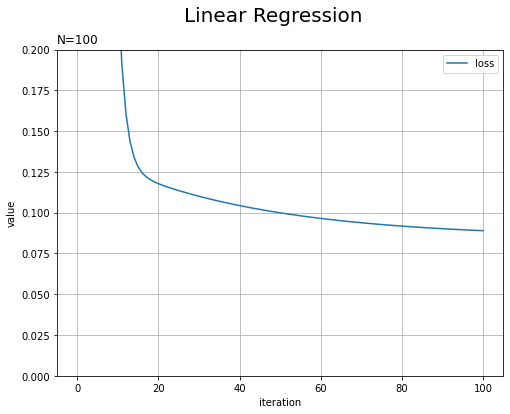
まだ少しずつ下がっています。
パラメータの推移も確認しておきましょう。
# 重みの推移を作図 plt.figure(figsize=(8, 6)) plt.plot(np.arange(iters + 1), trace_W, label='W') plt.xlabel('iteration') # x軸ラベル plt.ylabel('value') # y軸ラベル plt.suptitle('Linear Regression', fontsize=20) # 図全体のタイトル plt.title('N=' + str(len(x)), loc='left') # タイトル plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()
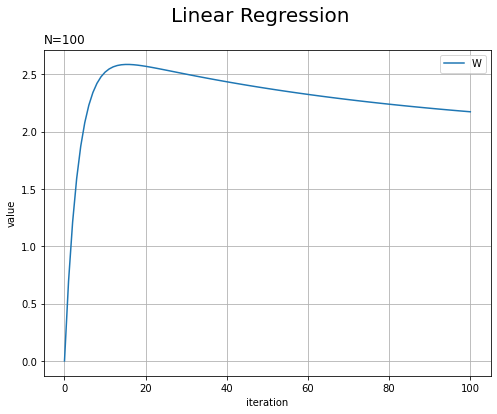
# バイアスの推移を作図 plt.figure(figsize=(8, 6)) plt.plot(np.arange(iters + 1), np.array(trace_b), label='b') plt.xlabel('iteration') # x軸ラベル plt.ylabel('value') # y軸ラベル plt.suptitle('Linear Regression', fontsize=20) # 図全体のタイトル plt.title('N=' + str(len(x)), loc='left') # タイトル plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()
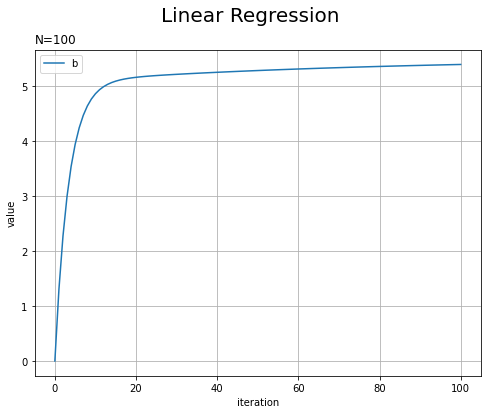
徐々に真の値に近付いていきます。
最後に、回帰直線の推移をアニメーションで確認します。
・コード(クリックで展開)
# 画像サイズを指定 fig = plt.figure(figsize=(8, 6)) # 作図処理を関数として定義 def update(i): # i回目のパラメータを用いて回帰直線を計算 y_line = trace_W[i] * x_line + trace_b[i] # 前フレームのグラフを初期化 plt.cla() # 作図 plt.scatter(x, y, label='データ') # 散布図 plt.plot(x_line, y_line, color='red', label='回帰直線') # 回帰直線 plt.xlabel('x') # x軸ラベル plt.ylabel('y') # y軸ラベル plt.suptitle('Linear Regression', fontsize=20) # 図全体のタイトル plt.title('iter:' + str(i) + ', loss=' + str(np.round(trace_L[i], 5)) + ', N=' + str(len(x)) + ', W=' + str(np.round(trace_W[i], 2)) + ', b=' + str(np.round(trace_b[i], 2)), loc='left') # タイトル plt.ylim(0.0, 10.0) # y軸の表示範囲 plt.legend(prop={"family":"MS Gothic"}) # 凡例 plt.grid() # グリッド線 # gif画像を作成 reg_anime = animation.FuncAnimation(fig, update, frames=iters + 1, interval=100) # gif画像を保存 reg_anime.save("step42_LinearRegression.gif")
F.linear()を使って計算すると出力の扱いが少し面倒なので、直接$y = w x_i + b$を計算しています。

試行回数が増えるにしたがって、データへの当てはまりが良くなっていきます。
以上で、LinearとMeanSquaredErrorを用いて線形回帰を行えました。次のステップからは、いよいよニューラルネットを実装していきます。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning 3 ――フレームワーク編』オライリー・ジャパン,2020年.
おわりに
さて、満を持してNN組んでくぞー。
特に理由はないですけど、この歌が最高なのでぜひ聞いてください♪
【次ステップの内容】