はじめに

　『トピックモデル』(MLPシリーズ)の勉強会資料のまとめです。各種モデルやアルゴリズムを「数式」と「プログラム」を用いて解説します。
　本の補助として読んでください。

　この記事では、混合ユニグラムモデル(混合カテゴリモデル)の生成モデルをPythonでスクラッチ実装します。

【前節の内容】

www.anarchive-beta.com

【他の節の内容】

www.anarchive-beta.com

【この節の内容】

はじめに
3.1 混合ユニグラムモデルの生成モデルの実装
- 文書データの簡易生成
  - パラメータの設定
  - 文書データの生成
- データの可視化
  - 文書データの作図
  - 真の分布の作図
参考書籍
おわりに

3.1 混合ユニグラムモデルの生成モデルの実装

　混合ユニグラムモデル(mixture of unigram models)の生成モデル(generative model)・生成過程(generative process)を実装して、簡易的な文書データ(トイデータ)を作成する。
　混合ユニグラムモデルについては「3.1-2：混合ユニグラムモデル【『トピックモデル』の勉強ノート】 - からっぽのしょこ」を参照のこと。

　利用するライブラリを読み込む。

# 利用ライブラリ
import numpy as np
import matplotlib.pyplot as plt

文書データの簡易生成

　まずは、混合ユニグラムモデルの生成モデルに従って、文書集合に対応するデータを生成する。

　真の分布や真のトピックなど本来は得られない情報についてはオブジェクト名に true を付けて表す。

パラメータの設定

　文書集合に関する値を設定する。

# 文書数を指定
D = 30

# 語彙数を指定
V = 100

# トピック数を指定
true_K = 10

　文書数 $D$ 、語彙(単語の種類)数 $V$ 、トピック数 $K$ を指定する。

　トピック分布のハイパーパラメータを設定する。

# トピック分布のハイパーパラメータを指定
true_alpha   = 1.0
true_alpha_k = np.repeat(true_alpha, repeats=true_K) # 一様なパラメータの場合
#true_alpha_k = np.random.uniform(low=1, high=2, size=true_K) # 多様なパラメータの場合
print(true_alpha_k[:5]) # 非負の値
print(true_alpha_k.shape) # トピック数

[1. 1. 1. 1. 1.]
(10,)

　 $K$ 個の値(ベクトル) $\boldsymbol{\alpha} = (\alpha_1, \cdots, \alpha_K)$ を指定する。各値は0より大きい値 $\alpha_k \gt 0$ を満たす必要がある。全てを同じ値 $\alpha_1 = \cdots = \alpha_K = \alpha$ とする場合は、1個の値(スカラ) $\alpha$ で表す。

　トピック分布のパラメータを生成する。

# トピック分布のパラメータを生成
true_theta_k = np.random.dirichlet(alpha=true_alpha_k, size=1).reshape(true_K)
print(true_theta_k[:5].round(2)) # 0から1の値
print(true_theta_k.sum()) # 総和が1の値
print(true_theta_k.shape) # トピック数

[0.16 0.19 0.03 0.07 0.01]
0.9999999999999999
(10,)

　トピック分布のパラメータ $\boldsymbol{\theta}$ を作成する。パラメータは $K$ 個の値(ベクトル) $\boldsymbol{\theta} = (\theta_1, \cdots, \theta_K)$ であり、各値は0から1の値 $0 \leq \theta_k \leq 1$ で、総和が1になる値 $\sum_{k=1}^K \theta_k = 1$ を満たす必要がある。
　ディリクレ分布の乱数は、np.random.dirichlet() で生成できる。パラメータの引数 alpha にハイパーパラメータ $\boldsymbol{\alpha}$ 、サンプルサイズの引数 size に文書数 1 を指定する。

　単語分布のハイパーパラメータを設定する。

# 語彙分布のハイパーパラメータを指定
true_beta   = 1.0
true_beta_v = np.repeat(true_beta, repeats=V) # 一様なパラメータの場合
#true_beta_v = np.random.uniform(low=1, high=2, size=V) # 多様なパラメータの場合
print(true_beta_v[:5]) # 非負の値
print(true_beta_v.shape) # 語彙数

[1. 1. 1. 1. 1.]
(100,)

　 $V$ 個の値(ベクトル) $\boldsymbol{\beta} = (\beta_1, \cdots, \beta_V)$ を指定する。各値は0より大きい値 $\beta_v \gt 0$ を満たす必要がある。全てを同じ値 $\beta_1 = \cdots = \beta_V = \beta$ とする場合は、1個の値(スカラ) $\beta$ で表す。

　単語分布のパラメータを生成する。

# 語彙分布のパラメータを生成
true_phi_kv = np.random.dirichlet(alpha=true_beta_v, size=true_K)
print(true_phi_kv[:5, :5].round(2)) # 0から1の値
print(true_phi_kv[:5].sum(axis=1)) # 総和が1の値
print(true_phi_kv.shape) # トピック数, 語彙数

[[0.03 0.01 0.   0.   0.01]
 [0.01 0.04 0.01 0.   0.  ]
 [0.03 0.01 0.01 0.   0.  ]
 [0.02 0.   0.   0.02 0.  ]
 [0.   0.04 0.   0.03 0.  ]]
[1. 1. 1. 1. 1.]
(10, 100)

　 $K$ 個の単語分布(語彙分布)のパラメータ $\boldsymbol{\Phi} = \{\boldsymbol{\phi}_1, \cdots, \boldsymbol{\phi}_K\}$ を生成する。各パラメータは $V$ 個の値(ベクトル) $\boldsymbol{\phi}_k = (\phi_{k1}, \cdots, \phi_{kV})$ であり、各値は0から1の値 $0 \leq \phi_{kv} \leq 1$ で、総和が1になる値 $\sum_{v=1}^V \theta_{kv} = 1$ を満たす必要がある。
　np.random.dirichlet() の alpha 引数にハイパーパラメータ $\boldsymbol{\beta}$ 、size 引数にトピック数 $K$ を指定する。

文書データの生成

　設定したパラメータに従う文書集合を作成する。

# 文書ごとの各単語の語彙を初期化
w_dic = {}

# 各文書のトピックを初期化
true_z_d = np.tile(np.nan, reps=D)

# 各文書の単語数を初期化
N_d = np.zeros(shape=D, dtype='int')

# 文書ごとの各語彙の単語数を初期化
N_dv = np.zeros(shape=(D, V), dtype='int')

# 文書データを生成
for d in range(D): # 文書ごと
    
    # トピックを生成
    onehot_k = np.random.multinomial(n=1, pvals=true_theta_k, size=1).reshape(true_K) # one-hot符号
    k, = np.where(onehot_k == 1) # トピック番号
    k  = k.item()
    
    # トピックを割当
    true_z_d[d] = k

    # 単語数を生成
    N_d[d] = np.random.randint(low=100, high=200, size=1) # 下限・上限を指定

    # 各単語の語彙を初期化
    tmp_w_n = np.repeat(np.nan, repeats=N_d[d]) # 各単語の語彙

    for n in range(N_d[d]): # 単語ごと

        # 語彙を生成
        onehot_v = np.random.multinomial(n=1, pvals=true_phi_kv[k], size=1).reshape(V) # one-hot符号
        v, = np.where(onehot_v == 1) # 語彙番号
        v  = v.item()
        
        # 語彙を割当
        tmp_w_n[n] = v

        # 頻度をカウント
        N_dv[d, v] += 1
    
    # データを記録
    w_dic[d] = tmp_w_n.copy()
    
    # 途中経過を表示
    print(f'document: {d+1}, words: {N_d[d]}, topic: {k+1}')

document: 1, words: 182, topic: 1
document: 2, words: 186, topic: 6
document: 3, words: 104, topic: 7
document: 4, words: 159, topic: 9
document: 5, words: 103, topic: 1
(省略)
document: 26, words: 167, topic: 7
document: 27, words: 199, topic: 1
document: 28, words: 185, topic: 6
document: 29, words: 181, topic: 6
document: 30, words: 174, topic: 7

個の文書について、順番に単語を生成していく。
- 文書 $d$ のトピック $z_d$ に、トピック分布(カテゴリ分布) $p(k | \boldsymbol{\theta})$ に従い、 $K$ 個のトピック $k = 1, \dots, K$ からトピック番号を割り当てる。
- 文書 $d$ の単語数 $N_d$ をランダムに決める。この例では、上限数・下限数を指定して一様乱数を生成する。
- 個の単語について、順番に語彙を生成していく。
  - 割り当てられたトピック $k$ の語彙分布(カテゴリ分布) $p(v | \boldsymbol{\phi}_k)$ に従い、 $V$ 個の語彙 $v = 1, \dots, V$ から語彙番号を割り当てる。

　文書間で単語数が異なる(2次元配列として扱えない)ので、単語集合 $\mathbf{W} = \{\mathbf{w}_1, \cdots, \mathbf{w}_D\}$ については、ディクショナリで扱う。

　カテゴリ分布の乱数は、np.random.multinomial() で生成できる。試行回数の引数 n に 1、パラメータの引数 pvals にトピック分布 $\boldsymbol{\theta}$ または語彙分布 $\boldsymbol{\phi}_k$ 、サンプルサイズの引数 size に 1 を指定する。
　one-hotベクトルが生成されるので、np.where() で値が 1 の要素番号を得る。np.argmax() でも抽出できる。
　または、np.random.choice() で直接番号を得られる。

　文書ごとに全ての語彙で和をとると各文書の単語数に一致する。

# 単語数を確認
print(N_d[:5]) # 各文書の単語数
print(N_dv[:5].sum(axis=1)) # 各文書の単語数

[182 186 104 159 103]
[182 186 104 159 103]

データの可視化

　次は、生成した文書データと真の分布のグラフを作成する。

　カラーマップを設定する。

# 作図用に変換
true_z_d = true_z_d.astype('int')

# 配色の共通化用のカラーマップを作成
cmap = plt.get_cmap('tab10')

# カラーマップの色数を設定:(カラーマップに応じて固定)
color_num = 10

　トピックごとに共通の配色をするために、カラーマップを指定して配色用のオブジェクト cmap を作成する。また、カラーマップで扱える色数を color_num とする。
　この記事では、トピック番号 k に応じて色付けする。その際に、トピック番号を色数で割った整数部分 k % color_num を使うことで、トピック番号が色数を超える場合にカラーマップの配色がサイクルして割り当てられる。

文書データの作図

　各トピックの割り当て文書数を集計する。

# 各トピックの文書数を集計
true_D_k = np.zeros(shape=true_K)
for d in range(D):
    k = true_z_d[d]
    true_D_k[k] += 1
print(true_D_k)

[8. 4. 0. 2. 0. 9. 4. 0. 3. 0.]

　各文書に割り当てられたトピック $z_d$ からトピック番号 $k$ を取り出して、各トピックの文書数 $D_k$ をカウントする(対応する要素に 1 を加えていく)。

　全てのトピックで和をとると文書数に一致する。

# 文書数を確認
print(D)
print(true_D_k.sum())

30
30.0

　描画する文書の数を指定して、文書データのグラフを作成する。

# 描画する文書数を指定
#doc_num = D
doc_num = 10

# グラフサイズを設定
u = 5
axis_Ndv_max = np.ceil(N_dv[:doc_num].max() /u)*u # u単位で切り上げ
axis_Dk_max  = np.ceil(true_D_k.max() /u)*u # u単位で切り上げ

# サブプロットの列数を指定:(1 < 列数 < D+1)
col_num = 3

# サブプロットの行数を計算:(1行or1列だとエラー)
row_num = np.ceil((doc_num+1) / col_num).astype('int')

# 文書データを作図
fig, axes = plt.subplots(nrows=row_num, ncols=col_num, constrained_layout=True, 
                         figsize=(30, 20), dpi=100, facecolor='white')

for d in range(doc_num):
    
    # サブプロットのインデックスを計算
    r = d // col_num
    c = d % col_num
    
    # サブプロットを抽出
    ax = axes[r, c]

    # トピック番号を取得
    k = true_z_d[d]
    
    # 語彙頻度を描画
    ax.bar(x=np.arange(stop=V)+1, height=N_dv[d], 
           color=cmap(k%color_num)) # 単語数
    ax.set_ylim(ymin=0, ymax=axis_Ndv_max)
    ax.set_xlabel('vocabulary ($v$)')
    ax.set_ylabel('frequency ($N_{dv}$)')
    ax.set_title(f'$d = {d+1}, k = {k+1}$', loc='left')
    ax.grid()

# 残りのサブプロットを非表示
if c == col_num-1: # (最後の文書が右端の列の場合)
    r = row_num - 1
    c = -1 
for c in range(c+1, col_num-1):
    axes[r, c].axis('off')
    
# トピックの割当を描画
ax = axes[row_num-1, col_num-1]
ax.bar(x=np.arange(stop=true_K)+1, height=true_D_k, 
        color=[cmap(k%color_num) for k in range(true_K)]) # 文書数
ax.set_ylim(ymin=0, ymax=axis_Dk_max)
ax.set_xlabel('topic ($k$)')
ax.set_ylabel('count ($D_k$)')
ax.set_title(f'$D = {D}$', loc='left')
ax.grid()

fig.supxlabel('document ($d$)')
fig.supylabel('document ($d$)')
fig.suptitle('document data (true topic)', fontsize=20)
plt.show()

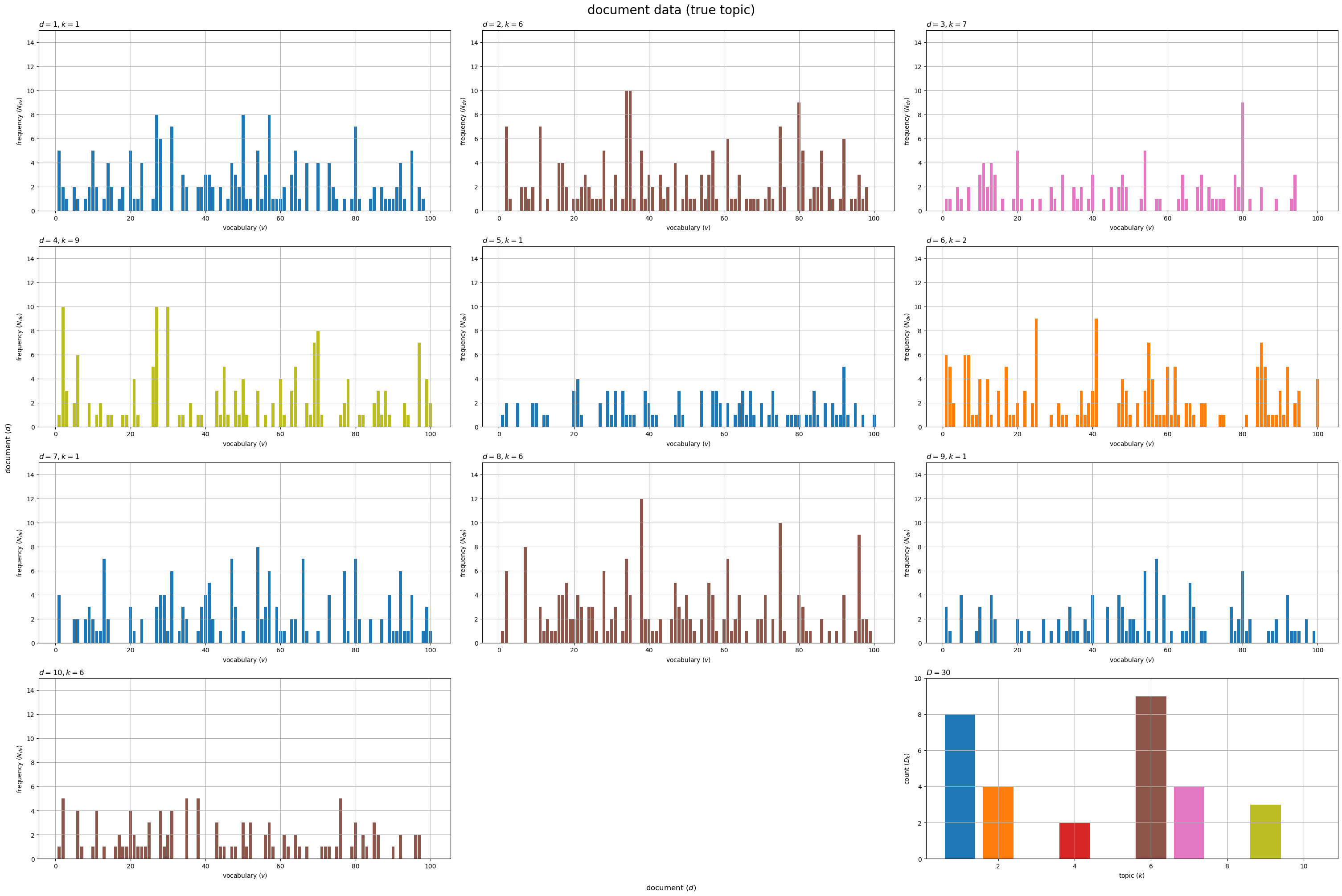
　文書ごとに各語彙の出現回数 $N_{dv}$ を棒グラフとして縦横に並べて描画する。各グラフは割り当てられたトピック $z_d$ で色付けしている。

　最後(右下)の図は、各トピックが割り当てられた文書数 $D_k$ を棒グラフで表している。

　データ数が増えると、最後の図はトピック分布、それ以外の図は対応するトピックの単語分布の形状に近付く。

真の分布の作図

　トピック分布のグラフを作成する。

# グラフサイズを設定
u = 0.1
axis_size = np.ceil(true_theta_k.max() /u)*u # u単位で切り上げ

# トピック分布を作図
fig, ax = plt.subplots(figsize=(8, 6), dpi=100, facecolor='white')
ax.bar(x=np.arange(stop=true_K)+1, height=true_theta_k, 
       color=[cmap(k%color_num) for k in range(true_K)]) # 確率
ax.set_ylim(ymin=0, ymax=axis_size)
ax.set_xlabel('topic ($k$)')
ax.set_ylabel('probability ($\\theta_k$)')
ax.set_title(f'$\\alpha = {true_alpha}$', loc='left') # (一様パラメータ用)
#ax.set_title('$\\alpha_k = ({})$'.format(', '.join([str(val.round(2)) for val in true_alpha_k])), loc='left') # (多様パラメータ用)
fig.suptitle('topic distribution (truth)', fontsize=20)
ax.grid()
plt.show()

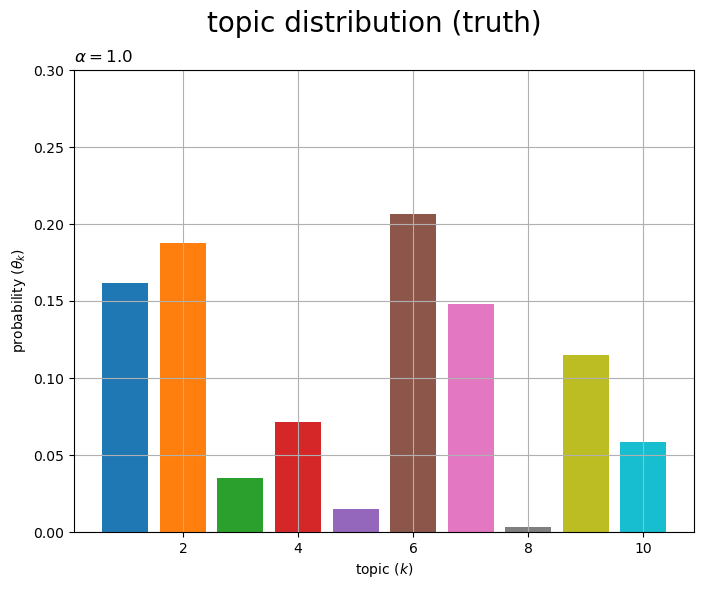
　トピック分布 $\mathrm{Categorical}(\boldsymbol{\theta})$ を棒グラフとして描画する。各トピックの割り当て確率 $\theta_k$ がバーに対応する。
　各グラフの値(バーの高さ)の総和が1になる。

　描画するトピックの数を指定して、単語分布のグラフを作成する。

# 描画するトピック数を指定
#topic_num = true_K
topic_num = 9

# グラフサイズを設定
u = 0.01
axis_size = np.ceil(true_phi_kv[:topic_num].max() /u)*u # u単位で切り上げ

# サブプロットの列数を指定:(1 < 列数 < K)
col_num = 3

# サブプロットの行数を計算:(1行or1列だとエラー)
row_num = np.ceil(topic_num / col_num).astype('int')

# 語彙分布を作図
fig, axes = plt.subplots(nrows=row_num, ncols=col_num, constrained_layout=True, 
                         figsize=(30, 15), dpi=100, facecolor='white')

for k in range(topic_num):
    
    # サブプロットのインデックスを計算
    r = k // col_num
    c = k % col_num

    # サブプロットを抽出
    ax = axes[r, c]

    # 語彙分布を描画
    ax.bar(x=np.arange(stop=V)+1, height=true_phi_kv[k], 
           color=cmap(k%color_num)) # 確率
    ax.set_ylim(ymin=0, ymax=axis_size)
    ax.set_xlabel('vocabulary ($v$)')
    ax.set_ylabel('probability ($\phi_{kv}$)')
    ax.set_title(f'$k = {k+1}, \\beta = {true_beta}$', loc='left') # (一様パラメータ用)
    #ax.set_title('$k = {}, \\beta_v = ({}, ...)$'.format(k+1, ', '.join([str(true_beta_v[v].round(2)) for v in range(5)])), loc='left') # (多様パラメータ用)
    ax.grid()

# 残りのサブプロットを非表示
for c in range(c+1, col_num):
    axes[r, c].axis('off')

fig.supxlabel('topic ($k$)')
fig.supylabel('topic ($k$)')
fig.suptitle('word distribution (truth)', fontsize=20)
plt.show()

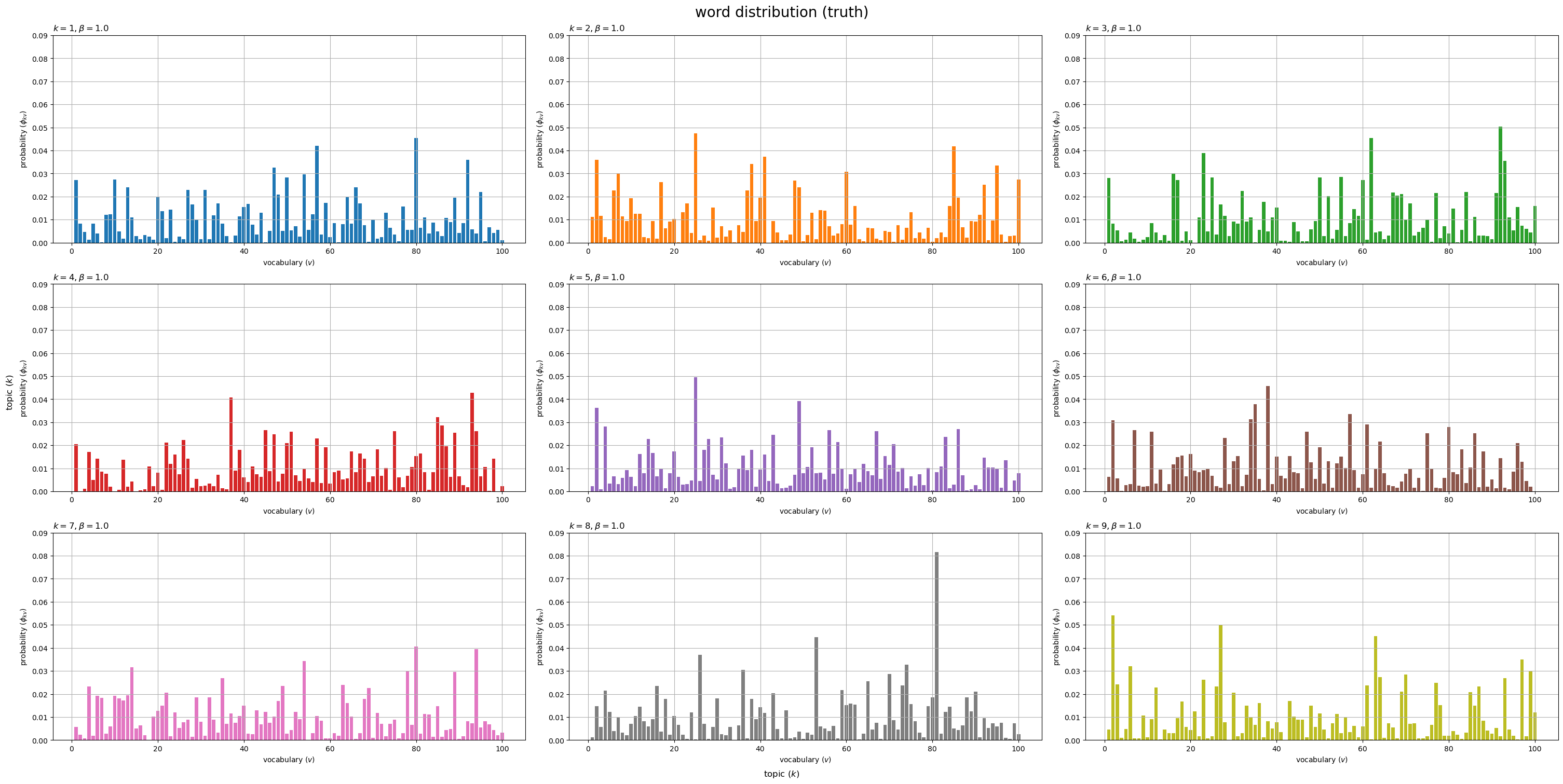
　トピックごとの単語分布(語彙分布) $\mathrm{Categorical}(\boldsymbol{\phi}_k)$ をそれぞれ棒グラフとして縦横に並べて描画する。各トピックにおける各語彙の出現確率 $\phi_{kv}$ がバーに対応する。
　各グラフの値(バーの高さ)の総和が1になる。

　この記事では混合ユニグラムモデルの生成モデルを実装して、各種アルゴリズムに用いる人工データを作成した。次からの記事では、推論処理を実装する。

参考書籍

岩田具治(2015)『トピックモデル』(機械学習プロフェッショナルシリーズ)講談社

おわりに

　Python実装編の執筆順で言うと「トピックモデルの生成モデル」に続く2つ目の記事です。現状では順番がハチャメチャになっています。記事が揃えば構成順で4つ目か5つ目の記事になると思います。
　Python編を始めた経緯は1つ目の記事で書きました。日記としてその補足なんぞ書いておきます。

　LDAに関して質問が来たことをきっかけに8章の内容の実装を試みました。撃沈しました。復習も兼ねて3・4章の対応するモデルをRで組んだものを参考にPythonでも組んでみました。3・4・8章に関して組めたり組めなかったりしたので、全部完成したらブログにしようとコードを放置しました。
　ところでこのブログは、ハロプロ時々スタプラのグループやメンバーの記念日駆動執筆ブログです。記事のストックが無い状態(有る状態はほとんどない)で誕生日などが近付く(あるいは当日に気付く)と放置しているコードを見繕って急遽記事を書き上げることが多々あります。
　前回と今回はまぁそういうことです。ネタ自体は面白いと思ってますよ！面白くないと完成しないので。
　つまり、記事ごとに1回は曲を聴いてください！

　2024年3月29日は、元エビ中(私立恵比寿中学)の柏木ひなたさんの25歳のお誕生日です。