はじめに
「プログラミング」学習初手『ゼロから作るDeep Learning』民のための実装攻略ノートです。『ゼロつく1』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
関数やクラスとして実装される処理の塊を細かく分解して、1つずつ処理を確認しながらゆっくりと組んでいきます。
この記事は、7.5節「CNNの実装」の内容になります。畳み込みニューラルネットワークをPythonで実装し、MNISTデータセットで学習します。
【前節の内容】
【他の節の内容】
【この節の内容】
7.5 CNNの実装
この節では簡単な畳み込みニューラルネットワークを実装します。前節までの前結合のニューラルネットワークとは、入力データを4次元としConvolutionレイヤとPoolingレイヤを用いる点が大きく異なりますが、処理の流れや実装方法は同じです。
## この節で利用するライブラリ # マスターデータの読み込み用の設定 import sys sys.path.append('C:\\Users\\「ユーザー名」\\Documents\\・・・\\deep-learning-from-scratch-master') # MNISTデータセット読み込み関数 from dataset.mnist import load_mnist # これまで実装してきたクラス(classの定義を実行済みなら不要) from common.layers import * from common.optimizer import * # 順番付きディクショナリ from collections import OrderedDict # 画像の保存 import pickle # NumPy import numpy as np # Matplotlib import matplotlib.pyplot as plt
5章で作成した各種レイヤのクラス定義と、6章で作成した各種最適化手法のクラス定義を実行済みであれば、それぞれlayers、optimizerの読み込みは不要です。
ただし「5.6.2:Affineレイヤの実装【ゼロつく1のノート(実装)】 - からっぽのしょこ」で実装したAffineレイヤは、2次元配列しか処理できません。そこで4次元データを入力した場合に、2次元配列に変形する処理を加えます。
# 4次元配列対応版Affineレイヤの実装 class Affine: # インスタンス変数の定義 def __init__(self, W, b): self.W = W # 重み self.b = b # バイアス self.x = None # 入力データ self.original_x_shape = None # 入力データのサイズ self.dW = None # 重みに関する勾配 self.db = None # バイアスに関する勾配 # 順伝播メソッドの定義 def forward(self, x): # 入力データのサイズを保存 self.original_x_shape = x.shape # バッチサイズ行の2次元配列に変形 x = x.reshape(x.shape[0], -1) self.x = x # 重み付きバイアスの和の計算 out = np.dot(self.x, self.W) + self.b return out # 逆伝播メソッドの定義 def backward(self, dout): # 勾配を計算 dx = np.dot(dout, self.W.T) self.dW = np.dot(self.x.T, dout) self.db = np.sum(dout, axis=0) # 入力データのサイズに変形 dx = dx.reshape(*self.original_x_shape) return dx
2次元配列を受け取った場合も0次元はバッチサイズなので、形状は変わりません。
・実装
- インスタンス作成時の引数
input_dimは、入力データのサイズです。(チャンネル数, 高さ, 横幅)の形式(タプル型)で指定します。MNISTデータセットの場合は(1, 28, 28)を指定します。conv_paramは、第1層の畳み込みレイヤのパラメータです。{'filter_num':フィルター数, 'filter_size':フィルター縦横, 'pad':パディング, 'stride':ストライド}の形式(ディクショナリ型)で指定します。hidden_sizeは、第2層のAffineレイヤのニューロン数です。任意の値を指定できます。output_sizeは、第3層(出力層)のAffineレイヤのニューロン数です。MNISTデータセットの場合は10を指定します。weight_init_stdは重みの初期値の標準偏差です。値を指定します。
- インスタンス変数
- パラメータやレイヤ、勾配をディクショナリ型のインスタンス変数に格納する方法は、5.7.2項と同様です。
- メソッド
- メソッドの定義もこれまでと同じです。ただし認識精度メソッドの処理がバッチデータで処理するように実装します。
.accuracy()のbtch_size引数に指定したデータ数ごとに認識精度を測定し、結果をacc加算していきます。
- メソッドの定義もこれまでと同じです。ただし認識精度メソッドの処理がバッチデータで処理するように実装します。
# CNNの実装 class SimpleConvNet: # インスタンス変数の定義 def __init__(self, input_dim=(1, 28, 28), conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1}, hidden_size=100, output_size=10, weight_init_std=0.01): filter_num = conv_param['filter_num'] # フィルター数 filter_size = conv_param['filter_size'] # フィルタの縦横 filter_pad = conv_param['pad'] # パディング filter_stride = conv_param['stride'] # ストライド input_size = input_dim[1] # 入力データの縦横 conv_output_size = (input_size - filter_size + 2 * filter_pad) / filter_stride + 1 # Convレイヤの出力の縦横 pool_output_size = int(filter_num * (conv_output_size / 2) * (conv_output_size / 2)) # Poolレイヤの出力の縦横 # パラメータの初期値を設定 self.params = {} # 初期化 self.params['W1'] = weight_init_std * np.random.randn(filter_num, input_dim[0], filter_size, filter_size) self.params['b1'] = np.zeros(filter_num) self.params['W2'] = weight_init_std * np.random.randn(pool_output_size, hidden_size) self.params['b2'] = np.zeros(hidden_size) self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size) self.params['b3'] = np.zeros(output_size) ## レイヤを格納したディクショナリ変数を作成 self.layers = OrderedDict() # 順番付きディクショナリ変数を初期化 # 第1層 self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'], conv_param['stride'], conv_param['pad']) self.layers['Relu1'] = Relu() self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2) # 第2層 self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2']) self.layers['Relu2'] = Relu() # 第3層 self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3']) self.last_layer = SoftmaxWithLoss() # 最終層の活性化レイヤと損失関数レイヤは別のインスタンス変数とする # 推論メソッドの定義 def predict(self, x): # レイヤごとに順伝播の処理:(未正規化) for layer in self.layers.values(): x = layer.forward(x) return x # 損失関数メソッドの定義 def loss(self, x, t): # CNNの処理:(未正規化) y = self.predict(x) # ソフトマックス関数による正規化と交差エントロピー誤差の計算 return self.last_layer.forward(y, t) # 認識精度測定メソッドの定義 def accuracy(self, x, t, batch_size=100): # 正解データのインデックスを取得 if t.ndim != 1 : # one-hot表現のとき t = np.argmax(t, axis=1) # 認識精度を初期化 acc = 0.0 # バッチデータごとに測定 for i in range(int(x.shape[0] / batch_size)): # バッチデータに切り分け tx = x[i*batch_size:(i+1)*batch_size] tt = t[i*batch_size:(i+1)*batch_size] # 推論処理:(未正規化) y = self.predict(tx) y = np.argmax(y, axis=1) # 認識精度を計算・記録 acc += np.sum(y == tt) return acc / x.shape[0] # 勾配計算メソッドの定義 def gradient(self, x, t): # 交差エントロピー誤差を計算:順伝播 self.loss(x, t) ## 各パラメータに関する勾配を計算:逆伝播 dout = 1 # 逆伝播の入力 dout = self.last_layer.backward(dout) # 最終層の出力 # 各レイヤを逆順に処理 layers = list(self.layers.values()) layers.reverse() for layer in layers: dout = layer.backward(dout) # 各パラメータに関する勾配を保存 grads = {} # 初期化 grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db grads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db grads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db return grads # 学習後のパラメータを書き出し def save_params(self, file_name="params.pkl"): # パラメータを格納 params = {} for key, val in self.params.items(): params[key] = val # 書き出し with open(file_name, 'wb') as f: pickle.dump(params, f) # 学習済みパラメータを読み込み def load_params(self, file_name="params.pkl"): # 読み込み with open(file_name, 'rb') as f: params = pickle.load(f) # インスタンス変数に格納 for key, val in params.items(): self.params[key] = val # 各レイヤのインスタンス変数に格納 for i, key in enumerate(['Conv1', 'Affine1', 'Affine2']): self.layers[key].W = self.params['W' + str(i+1)] self.layers[key].b = self.params['b' + str(i+1)]
最後に、パラメータの書き出しメソッド.save_params()と読み込みメソッド.load_params()の処理を少しだけ確認しておきます。
with構文を用いて、open()でファイルにアクセスすることができます。
with open('ファイルパス', mode) as 変数名: ファイルに対する処理
open()のmode引数にwbを指定すると書き出し、rbを指定すると読み込みとして、第1引数に指定したパスのファイルを開きます。開いたファイルに対してpickle.dump()で書き出し、pickle.load()で読み込みます。バイナリファイルとかpickle化とか詳しくはググってください。。。
以上でCNNを実装できました。では学習を行いましょう!
・MNISTデータセットで学習
これまでと同様にMNISTデータセットを使って学習を行います。
load_mnist()で手書き文字画像を読み込みます。この例では4次元データとして読み込むため、flatten引数にFalseを指定します。one_hot_label引数はTrue・Falseどちらでも処理できます。
# MNISTデータセットデータを取得 (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=False, one_hot_label=True) print(x_train.shape) # 訓練画像 print(t_train.shape) # 訓練ラベル print(x_test.shape) # テスト画像 print(t_test.shape) # テストラベル
(60000, 1, 28, 28)
(60000, 10)
(10000, 1, 28, 28)
(10000, 10)
これまでとは違い、画像データが4次元配列になっています。
全データ(エポック)に対する試行回数とミニバッチサイズを指定します。それなりに時間がかかるのでまずは小さい値で試してみましょう。処理に時間がかかりすぎる場合は、データセットを削減しましょう。
# 全データに対する試行回数を指定 max_epochs = 10 # ミニバッチサイズを指定 batch_size = 100 # 訓練データ数 train_size = x_train.shape[0] # 全データに対するミニバッチデータの割合 iter_per_epoch = max(train_size / batch_size, 1) print(iter_per_epoch) # ミニバッチデータに対する試行回数を計算 max_iters = int(max_epochs * iter_per_epoch) + 1 print(max_iters)
600.0
6001
CNNのインスタンスと、最適化手法(確率的勾配降下法)のインスタンスを作成します。この例ではAdamによってパラメータの更新を行います。
# CNNのインスタンスを作成 network = SimpleConvNet( input_dim=(1, 28, 28), conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1}, hidden_size=100, output_size=10, weight_init_std=0.01 ) # 最適化手法のインスタンスを作成 optimizer = Adam(lr=0.001)
学習の処理もこれまでと同様です。
# エポックあたりの試行回数のカウントを初期化 epoch_cnt = 0 # 精度記録用リストを初期化 train_acc_list = [] test_acc_list = [] train_loss_list = [] # ミニバッチデータごとに学習 for i in range(max_iters): # ランダムにバッチデータ抽出 batch_mask = np.random.choice(train_size, batch_size) x_batch = x_train[batch_mask] t_batch = t_train[batch_mask] # 勾配を計算 grads = network.gradient(x_batch, t_batch) # パラメータを更新 optimizer.update(network.params, grads) # 交差エントロピー誤差を記録 train_loss = network.last_layer.loss train_loss_list.append(train_loss) # (動作確認も兼ねて)交差エントロピー誤差を表示 if i % 100 == 0: print("iter:" + str(i) + ", train loss:" + str(np.round(train_loss, 3))) # 1エポックごとに認識精度を測定 if i % iter_per_epoch == 0: # 精度を測定 train_acc = network.accuracy(x_train, t_train) test_acc = network.accuracy(x_test, t_test) # 値を記録 train_acc_list.append(train_acc) test_acc_list.append(test_acc) # (動作確認も兼ねて)認識精度を表示 print( "===========" + "epoch:" + str(epoch_cnt) + "===========" + "\ntrain acc:" + str(np.round(train_acc, 3)) + "\ntest acc :" + str(np.round(test_acc, 3)) ) # エポックあたりの試行回数をカウント epoch_cnt += 1
iter:0, train loss:2.303
===========epoch:0===========
train acc:0.181
test acc :0.176
iter:100, train loss:0.483
iter:200, train loss:0.341
iter:300, train loss:0.136
iter:400, train loss:0.169
iter:500, train loss:0.148
iter:600, train loss:0.19
===========epoch:1===========
train acc:0.955
test acc :0.955
(省略)
===========epoch:9===========
train acc:0.996
test acc :0.988
iter:5500, train loss:0.006
iter:5600, train loss:0.113
iter:5700, train loss:0.001
iter:5800, train loss:0.002
iter:5900, train loss:0.064
iter:6000, train loss:0.002
===========epoch:10===========
train acc:0.996
test acc :0.989
訓練データとテストデータに対する認識精度の推移をグラフ化します。
# x軸の値を生成 epochs = np.arange(len(train_acc_list)) # 作図 plt.plot(epochs, train_acc_list, label='train') # 訓練データ plt.plot(epochs, test_acc_list, label='test') # テストデータ plt.xlabel("epochs") # x軸ラベル plt.ylabel("accuracy") # y軸ラベル plt.ylim(0, 1.1) # y軸の範囲 plt.legend() # 凡例 plt.title("Accuracy", fontsize=20) # タイトル plt.show()
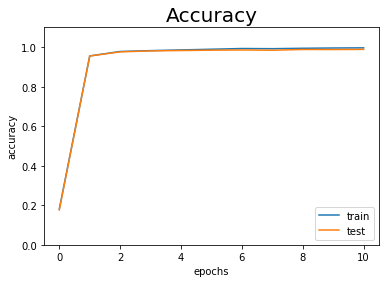
どちらもほぼ100%認識しています。
交差エントロピー誤差の推移も確認しましょう。
# x軸の値を生成 iters = np.arange(len(train_loss_list)) # 作図 plt.plot(iters, train_loss_list, label='train') # 訓練データ plt.xlabel("iters") # x軸ラベル plt.ylabel("loss") # y軸ラベル plt.title("Cross Entropy Error", fontsize=20) # タイトル plt.show()
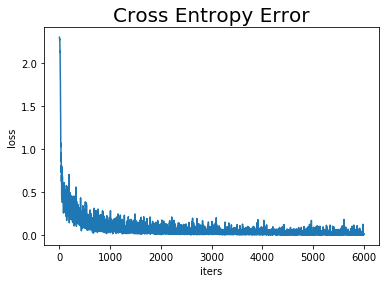
当然ですが、ほぼ0まで下がっています。
以上で簡単なCNNを実装し、MNISTデータセットの学習を行えました!
参考文献
- 斎藤康毅『ゼロから作るDeep Learning』オライリー・ジャパン,2016年.
おわりに
レジュメ的にはこれで終了です!!!!!お疲れ様でしたあああ。途中何度も想定レベルを落とし過ぎたと後悔しましたが、何とかやり切れました。良くも悪くも、Python歴1か月だったからこそ書けた内容だと思います。この資料を作ったおかげで、Python歴5か月レベルまで成長できました。
ところで、ここで止めるとDeep Learningを作れてないんですよね。
是非とも8.1節の実装までやりましょう!この節の内容で理解できるはずです。解説記事は、この節ですらろくに書くことがなかったので省略しました!
最後まで読んでいただきありがとうございました。
エンディング曲です♪♪Juice=Juiceで「Goal~明日はあっちだよ~」
配信リリース曲でMVがないのでLIVE版で。私は2巻へ進むぞ~
【次の内容】