はじめに
『ゼロから作るDeep Learning 4 ――強化学習編』の独学時のまとめノートです。初学者の補助となるようにゼロつくシリーズの4巻の内容に解説を加えていきます。本と一緒に読んでください。
この記事は、7.3.5項の内容です。DeZeroを利用して最適化手法を比較します。
【前節の内容】
【他の記事一覧】
【この記事の内容】
7.3.5 オプティマイザ(最適化手法)
DeZeroライブラリを使って、3つのベース関数(ローゼンブロック関数・ヒンメルブラウ関数・ビール関数)に対して5つの最適化手法(SGD・Momentum・AdaDelta・AdaGrad・Adam)による最適化(最小値の探索)を行い、各手法を比較します。DeZeroフレームワークについては「『ゼロから作るDeep Learning 3』の学習ノート:記事一覧 - からっぽのしょこ」、最適化手法については「『ゼロから作るDeep Learning』の学習ノート:記事一覧 - からっぽのしょこ」を参照してください。
利用するライブラリを読み込みます。
# ライブラリを読み込み import numpy as np from dezero import Model, Parameter from dezero import optimizers # 追加ライブラリ import matplotlib.pyplot as plt from matplotlib.colors import LogNorm from matplotlib.animation import FuncAnimation
更新推移をアニメーションで確認するのにmatplotlibのモジュールを利用します。不要であれば省略してください。
ベンチマーク関数の準備
まずは、ベンチマーク関数と作図用の配列を用意します。ローゼンブロック関数については「ステップ28:ローゼンブロック関数の可視化【ゼロつく3のノート(メモ)】 - からっぽのしょこ」を参照してください。
作図用に、ベンチマーク関数の計算を関数として定義します。
# ベンチマーク関数を作成 def benchmark(x0, x1): # Rosenbrock関数を計算 y = 100.0 * (x1 - x0**2)**2 + (x0 - 1.0)**2 # Himmelblau関数の計算 #y = (x0**2 + x1 - 11.0)**2 + (x0 + x1**2 - 7.0)**2 # Beale関数の計算 #y = (1.5 - x0 + x0 * x1)**2 + (2.25 - x0 + x0 * x1**2)**2 + (2.625 - x0 + x0 * x1**3)**2 return y
ローゼンブロック関数
や、ヒンメルブラウ関数
や、ビール関数
などを設定します。
作図用の配列を作成します。
# x軸・y軸の値を作成 x0_vals = np.linspace(-2.0, 2.0, num=250) x1_vals = np.linspace(-1.0, 3.0, num=250) # 格子点を作成 x0_grid, x1_grid = np.meshgrid(x0_vals, x1_vals) # ベンチマーク関数を計算 y_grid = benchmark(x0_grid, x1_grid) # z軸の最大値を指定 z_max = 900 # 表示範囲外をマスク y_mask_grid = np.ma.masked_where(y_grid >= z_max, y_grid) # 対数をとった最小値・最大値を取得 y_log10_min = np.floor(np.log10(y_grid.min()) - 1.0) y_log10_max = np.ceil(np.log10(y_grid.max()) + 1.0) # 等高線を引く値を作成 lev_log10 = np.linspace(y_log10_min, y_log10_max, num=50)[25:40] levs = np.power(10, lev_log10)
x軸($x_0$)とy軸($x_1$)の値x*_valsを指定して、np.meshgrid()で格子点x*_gridに変換して、z軸($y$)の値y_gridを計算します。
また、z軸の最大値を指定して、それ以上の値をマスクしてy_mask_gridとします。
対数をとったy_gridの最小値と最大値を使って、等高線を引く値levsを作成します。
ベンチマーク関数の等高線図と曲面図を作成します。
# ベンチマーク関数の等高線図を作成 plt.figure(figsize=(9, 8), facecolor='white') cnt = plt.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs) # 等高線 plt.xlabel('$x_0$', fontsize=15) plt.ylabel('$x_1$', fontsize=15) plt.suptitle('Rosenbrock function', fontsize=20) plt.colorbar(cnt, label='f(x)') plt.grid() plt.axis('equal') plt.show()
# ベンチマーク関数の曲面図を作成 fig = plt.figure(figsize=(9, 9), facecolor='white') ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs, offset=0.0) # 等高線 ax.plot_surface(x0_grid, x1_grid, y_grid, norm=LogNorm(), cmap='viridis', alpha=0.8) # 曲面 ax.set_xlabel('$x_0$', fontsize=15) ax.set_ylabel('$x_1$', fontsize=15) ax.set_zlabel('f(x)', fontsize=15) fig.suptitle('Rosenbrock function', fontsize=20) ax.set_box_aspect(aspect=(1, 1, 1)) plt.show()






それぞれ変数や等高線の値を変更しています。
各ベンチマーク関数が最小値となる点$\mathbf{x} = (x_0, x_1)$を求めます。
最適化
学習用に、DeZeroライブラリのModelクラスを継承して、ベンチマーク関数のクラスとして定義します。
# ベンチマーク関数のクラスを作成 class Benchmark(Model): # 初期化メソッドの定義 def __init__(self, x0, x1): # 親クラスのメソッドを継承 super().__init__() # パラメータとして値を保存 self.x0 = Parameter(np.array([x0])) self.x1 = Parameter(np.array([x1])) # 推移の確認用のリストを初期化 self.trace_x0 = [] self.trace_x1 = [] self.trace_y = [] # 順伝播メソッドの定義 def forward(self): # 値を取得 x0, x1 = self.x0, self.x1 # Rosenbrock関数を計算 y = 100.0 * (x1 - x0**2)**2 + (1.0 - x0)**2 # Himmelblau関数を計算 #y = (x0**2 + x1 - 11.0)**2 + (x0 + x1**2 - 7.0)**2 # Beale関数の計算 #y = (1.5 - x0 + x0 * x1)**2 + (2.25 - x0 + x0 * x1**2)**2 + (2.625 - x0 + x0 * x1**3)**2 # 値を保存 self.trace_x0.append(x0.data.item()) self.trace_x1.append(x1.data.item()) self.trace_y.append(y.data.item()) return y
$x_0, x_1$をParameterクラスのインスタン化して、インスタンス変数x0, x1とします。
また、順伝播を計算する度にリストtrace_*に$x_0, x_1, y$の値を格納します。
最適化手法ごとに、モデルとオプティマイザのインスタンスを作成して、それぞれ学習します。
# 試行回数を指定 iters = 1000 # 初期値を指定 x0 = 0.0 x1 = 2.0 # モデルのインスタンスを作成 model_SGD = Benchmark(x0, x1) model_Momentum = Benchmark(x0, x1) model_AdaDelta = Benchmark(x0, x1) model_AdaGrad = Benchmark(x0, x1) model_Adam = Benchmark(x0, x1) # 最適化手法のインスタンスを作成 optimizer_SGD = optimizers.SGD(lr=0.001) optimizer_Momentum = optimizers.MomentumSGD(lr=0.0001) optimizer_AdaDelta = optimizers.AdaDelta(rho=0.95) optimizer_AdaGrad = optimizers.AdaGrad(lr=0.5) optimizer_Adam = optimizers.Adam(alpha=0.5) # オプティマイザを設定 optimizer_SGD.setup(model_SGD) optimizer_Momentum.setup(model_Momentum) optimizer_AdaDelta.setup(model_AdaDelta) optimizer_AdaGrad.setup(model_AdaGrad) optimizer_Adam.setup(model_Adam) # インスタンスをリストに格納 model_lt = [model_SGD, model_Momentum, model_AdaDelta, model_AdaGrad, model_Adam] optimizer_lt = [optimizer_SGD, optimizer_Momentum, optimizer_AdaDelta, optimizer_AdaGrad, optimizer_Adam] # 繰り返し学習 for i in range(iters): # オプティマイザごとに処理 for model, optimizer in zip(model_lt, optimizer_lt): # 順伝播(ベンチマーク関数)を計算 y = model.forward() # 勾配を初期化 model.cleargrads() # 逆伝播(勾配)を計算 y.backward() # 値を更新 optimizer.update() # 一定回数ごとに結果を表示 if (i+1) % 100 == 0: print('----- iter ' + str(i+1) + ' -----') for model, optimizer in zip(model_lt, optimizer_lt): print( optimizer.__class__.__name__ + ' : y=' + str(np.round(model.trace_y[-1], 3)) )
----- iter 100 -----
SGD : y=0.589
MomentumSGD : y=0.809
AdaDelta : y=0.137
AdaGrad : y=0.008
Adam : y=0.403
----- iter 200 -----
SGD : y=0.436
MomentumSGD : y=0.559
AdaDelta : y=0.137
AdaGrad : y=0.008
Adam : y=0.066
(省略)
----- iter 800 -----
SGD : y=0.134
MomentumSGD : y=0.151
AdaDelta : y=0.122
AdaGrad : y=0.005
Adam : y=0.0
----- iter 900 -----
SGD : y=0.116
MomentumSGD : y=0.129
AdaDelta : y=0.113
AdaGrad : y=0.004
Adam : y=0.0
----- iter 1000 -----
SGD : y=0.1
MomentumSGD : y=0.111
AdaDelta : y=0.104
AdaGrad : y=0.004
Adam : y=0.0
モデルのインスタンスmodel_***とオプティマイザのインスタンスoptimizer_***をそれぞれリストに格納しておき、試行ごとにfor文で順番に取り出して学習を行います。
学習処理については本を参照してください。
ベンチマーク関数のグラフに、更新値の推移を重ねて描画します。
# ハイパーパラメータの表示用のリストを指定 lr_name_lt = ['lr', 'lr', 'rho', 'lr', 'alpha'] # ベンチマーク関数の等高線図を作成 plt.figure(figsize=(12, 10), facecolor='white') cnt = plt.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs) # 等高線 # オプティマイザごとに処理 for model, optimizer, lr_name in zip(model_lt, optimizer_lt, lr_name_lt): # 最適化手法名を取得 opt_name = optimizer.__class__.__name__ # ハイパーパラメータを取得 lr = getattr(optimizer, lr_name) # 更新値の推移を描画 plt.plot(model.trace_x0, model.trace_x1, marker='o', alpha=0.5, label=str(opt_name)+': '+lr_name+'='+str(lr)) plt.xlabel('$x_0$', fontsize=15) plt.ylabel('$x_1$', fontsize=15) plt.suptitle('Rosenbrock function', fontsize=20) plt.title('iter:'+str(iters), loc='left') plt.colorbar(cnt, label='f(x)') plt.legend() plt.grid() plt.axis('equal') #ax.set_xlim(x0_vals.min(), x0_vals.max()) #ax.set_ylim(x1_vals.min(), x1_vals.max()) plt.show()
# ハイパーパラメータの表示用のリストを指定 lr_name_lt = ['lr', 'lr', 'rho', 'lr', 'alpha'] # ベンチマーク関数の曲面図を作成 fig = plt.figure(figsize=(12, 10), facecolor='white') ax = fig.add_subplot(projection='3d') # 3D用の設定 # オプティマイザごとに処理 for model, optimizer, lr_name in zip(model_lt, optimizer_lt, lr_name_lt): # 最適化手法名を取得 opt_name = optimizer.__class__.__name__ # ハイパーパラメータを取得 lr = getattr(optimizer, lr_name) # 更新値の推移を描画 ax.plot(model.trace_x0, model.trace_x1, model.trace_y, marker='o', alpha=0.5, label=str(opt_name)+': '+lr_name+'='+str(lr), zorder=50) ax.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs, offset=0.0, zorder=0) # 等高線 ax.plot_surface(x0_grid, x1_grid, y_mask_grid, norm=LogNorm(), cmap='viridis', alpha=0.8, zorder=1) # 曲面 ax.set_xlabel('$x_0$', fontsize=15) ax.set_ylabel('$x_1$', fontsize=15) ax.set_zlabel('f(x)', fontsize=15) fig.suptitle('Rosenbrock function', fontsize=20) ax.set_title('iter:'+str(iters), loc='left') ax.legend() ax.set_box_aspect(aspect=(1, 1, 0.5)) #ax.set_xlim(x0_vals.min(), x0_vals.max()) #ax.set_ylim(x1_vals.min(), x1_vals.max()) ax.set_zlim(-z_max*0.1, z_max) ax.view_init(elev=30, azim=250) plt.show()



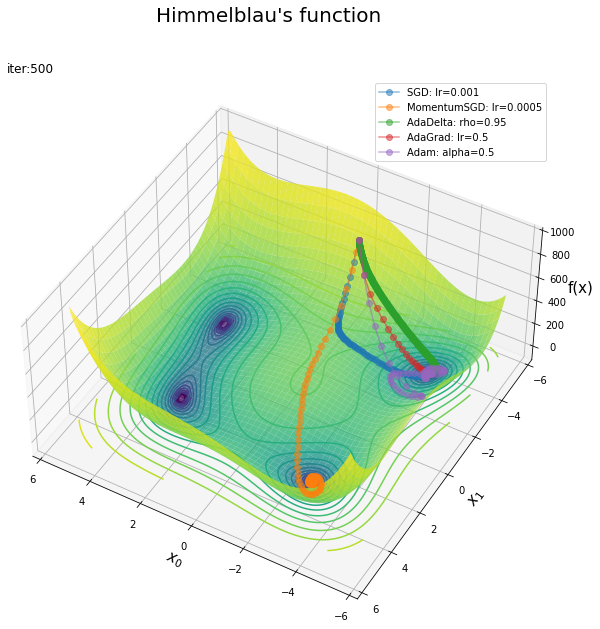


手法ごとに更新の様子が異なるのが分かります。それぞれ適切にハイパーパラメータ(学習率など)を設定する必要があります。
更新値の推移をアニメーションで確認します。
・作図コード(クリックで展開)
# フレーム数を指定 frame_num = 101 # 図を初期化 fig = plt.figure(figsize=(12, 10), facecolor='white') fig.suptitle('Rosenbrock function', fontsize=20) # カラーバー tmp = plt.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs) # カラーバー用のダミー fig.colorbar(tmp, label='f(x)') # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # オプティマイザごとにi番目までの更新値を描画 plt.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs) # 等高線 # オプティマイザごとに処理 for model, optimizer, lr_name in zip(model_lt, optimizer_lt, lr_name_lt): # 最適化手法名を取得 opt_name = optimizer.__class__.__name__ # ハイパーパラメータを取得 lr = getattr(optimizer, lr_name) # 更新値の推移を描画 plt.plot(model.trace_x0[:(i+1)], model.trace_x1[:(i+1)], marker='o', alpha=0.5, label=str(opt_name)+': '+lr_name+'='+str(lr)) plt.xlabel('$x_0$', fontsize=15) plt.ylabel('$x_1$', fontsize=15) plt.suptitle("Himmelblau's function", fontsize=20) plt.title('iter:'+str(i), loc='left') plt.legend() plt.grid() plt.axis('equal') ax.set_xlim(x0_vals.min(), x0_vals.max()) ax.set_ylim(x1_vals.min(), x1_vals.max()) # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # gif画像を保存 ani.save('Rosenbrock_cnf.gif')
# フレーム数を指定 frame_num = 101 # 図を初期化 fig = plt.figure(figsize=(12, 10), facecolor='white') ax = fig.add_subplot(projection='3d') # 3D用の設定 fig.suptitle('Rosenbrock function', fontsize=20) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # オプティマイザごとにi番目までの更新値を描画 for model, optimizer, lr_name in zip(model_lt, optimizer_lt, lr_name_lt): # 最適化手法名を取得 opt_name = optimizer.__class__.__name__ # ハイパーパラメータを取得 lr = getattr(optimizer, lr_name) # 更新値の推移を描画 ax.plot(model.trace_x0[:(i+1)], model.trace_x1[:(i+1)], model.trace_y[:(i+1)], marker='o', alpha=0.5, label=str(opt_name)+': '+lr_name+'='+str(lr), zorder=50) ax.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs, offset=0.0, zorder=0) # 等高線 ax.plot_surface(x0_grid, x1_grid, y_mask_grid, norm=LogNorm(), cmap='viridis', alpha=0.8, zorder=1) # 曲面 ax.set_xlabel('$x_0$', fontsize=15) ax.set_ylabel('$x_1$', fontsize=15) ax.set_zlabel('f(x)', fontsize=15) ax.set_title('iter:'+str(i), loc='left') ax.legend() ax.set_box_aspect(aspect=(1, 1, 0.5)) ax.set_xlim(x0_vals.min(), x0_vals.max()) ax.set_ylim(x1_vals.min(), x1_vals.max()) ax.set_zlim(-z_max*0.1, z_max) ax.view_init(elev=30, azim=240) # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # gif画像を保存 ani.save('Rosenbrock_srf.gif')
フレームごとにtrace_*からi番目までの値を取り出して点を描画する処理を関数update()として定義して、FuncAnimation()でアニメーション(gif画像)を作成します。






初期値の比較
最適化手法とハイパーパラメータを固定して、初期値を変更します。
初期値を指定します。
# 初期値を指定 x0_i = np.array([0.0, -5.0, 0.0, 5.0, 0.0, -5.0, -5.0, 5.0, 5.0]) x1_i = np.array([0.0, 0.0, -5.0, 0.0, 5.0, -5.0, 5.0, -5.0, 5.0])
x軸・y軸の値をx0_i, x1_iとして指定します。
格子点を指定する場合は、次のように処理できます。
# 初期値として利用する値を指定 x0_init_vals = np.arange(-5.0, 5.1, step=1.0) x1_init_vals = np.arange(-5.0, 5.1, step=1.0) # 格子点を作成 x0_init_grid, x1_init_grid = np.meshgrid(x0_init_vals, x1_init_vals) # 初期値を設定 x0_i = x0_init_grid.flatten() x1_i = x1_init_grid.flatten() print(len(x0_i))
121
初期値の点ごとに、モデルとオプティマイザのインスタンスを作成して、それぞれ学習します。
# 試行回数を指定 iters = 250 # リストを初期化 model_lt = [] optimizer_lt = [] # 初期値の点ごとにインスタンスを作成 for x0, x1 in zip(x0_i, x1_i): # モデルのインスタンスを作成 model = Benchmark(x0, x1) # 最適化手法のインスタンスを作成 optimizer = optimizers.Adam(alpha=0.5) # オプティマイザを設定 optimizer.setup(model) # インスタンスをリストに格納 model_lt.append(model) optimizer_lt.append(optimizer) # 繰り返し学習 for i in range(iters): # オプティマイザごとに処理 for model, optimizer in zip(model_lt, optimizer_lt): # 順伝播(ベンチマーク関数)を計算 y = model.forward() # 勾配を初期化 model.cleargrads() # 逆伝播(勾配)を計算 y.backward() # 値を更新 optimizer.update() # 一定回数ごとに結果を表示 if (i+1) % 100 == 0: print('----- iter ' + str(i+1) + ' -----') for model, optimizer in zip(model_lt, optimizer_lt): print( optimizer.__class__.__name__ + ', y=' + str(np.round(model.trace_y[-1], 3)) )
----- iter 100 -----
Adam, y=0.001
Adam, y=0.004
Adam, y=0.015
Adam, y=0.003
Adam, y=0.004
Adam, y=0.006
Adam, y=0.004
Adam, y=0.03
Adam, y=0.016
----- iter 200 -----
Adam, y=0.0
Adam, y=0.0
Adam, y=0.0
Adam, y=0.0
Adam, y=0.0
Adam, y=0.0
Adam, y=0.0
Adam, y=0.0
Adam, y=0.0
for文で初期値の組み合わせごとにインスタンスを作成して、リストに格納します。学習処理は先ほどと同じです。
作図処理も同様です。ラベル用の処理が異なります。
・作図コード(クリックで展開)
# ハイパーパラメータのインスタンス変数名を指定 lr_name = 'alpha' # ハイパーパラメータを取得 lr = getattr(optimizer_lt[0], lr_name) # 最適化手法名を取得 opt_name = optimizer_lt[0].__class__.__name__ # ベンチマーク関数の等高線図を作成 plt.figure(figsize=(12, 10), facecolor='white') cnt = plt.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs) # 等高線 # 初期値の点ごとに更新値の推移を描画 for model, optimizer in zip(model_lt, optimizer_lt): plt.plot(model.trace_x0, model.trace_x1, marker='o', alpha=0.5) plt.xlabel('$x_0$', fontsize=15) plt.ylabel('$x_1$', fontsize=15) plt.suptitle("Himmelblau's function", fontsize=20) plt.title('optimizer:'+opt_name + ', '+lr_name+'='+str(lr) + ', iter:'+str(iters), loc='left') plt.colorbar(cnt, label='f(x)') plt.grid() plt.axis('equal') #plt.xlim(x0_vals.min(), x0_vals.max()) #plt.ylim(x1_vals.min(), x1_vals.max()) plt.show()
# ベンチマーク関数の曲面図を作成 fig = plt.figure(figsize=(12, 10), facecolor='white') ax = fig.add_subplot(projection='3d') # 3D用の設定 # 初期値の点ごとに更新値の推移を描画 for model, optimizer in zip(model_lt, optimizer_lt): ax.plot(model.trace_x0, model.trace_x1, model.trace_y, marker='o', alpha=0.5, zorder=50) ax.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs, offset=0.0, zorder=0) # 等高線 ax.plot_surface(x0_grid, x1_grid, y_mask_grid, norm=LogNorm(), cmap='viridis', alpha=0.8, zorder=1) # 曲面 ax.set_xlabel('$x_0$', fontsize=15) ax.set_ylabel('$x_1$', fontsize=15) ax.set_zlabel('f(x)', fontsize=15) fig.suptitle("Himmelblau's function", fontsize=20) ax.set_title('optimizer:'+opt_name + ', '+lr_name+'='+str(lr) + ', iter:'+str(iters), loc='left') ax.set_box_aspect(aspect=(1, 1, 0.5)) #ax.set_xlim(x0_vals.min(), x0_vals.max()) #ax.set_ylim(x1_vals.min(), x1_vals.max()) ax.set_zlim(-z_max*0.1, z_max) ax.view_init(elev=45, azim=120) plt.show()


それぞれの点または軌跡のアニメーションを作成します。
・作図コード(クリックで展開)
# フレーム数を指定 frame_num = 101 # ハイパーパラメータのインスタンス変数名を指定 lr_name = 'alpha' # ハイパーパラメータを取得 lr = getattr(optimizer_lt[0], lr_name) # 最適化手法名を取得 opt_name = optimizer_lt[0].__class__.__name__ # 図を初期化 fig = plt.figure(figsize=(12, 10), facecolor='white') fig.suptitle("Himmelblau's function", fontsize=20) # カラーバー tmp = plt.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs) # カラーバー用のダミー fig.colorbar(tmp, label='f(x)') # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # 初期値の点ごとに更新値の推移を描画 plt.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs) # 等高線 # 初期値の点ごとに処理 for model, optimizer in zip(model_lt, optimizer_lt): # i番目までの点を描画 #plt.plot(model.trace_x0[:(i+1)], model.trace_x1[:(i+1)], # marker='o', alpha=0.5) # i番目の点を描画 plt.plot(model.trace_x0[i], model.trace_x1[i], marker='o') plt.xlabel('$x_0$', fontsize=15) plt.ylabel('$x_1$', fontsize=15) plt.title('optimizer:'+opt_name + ', '+lr_name+'='+str(lr) + ', iter:'+str(i), loc='left') #plt.legend() plt.grid() plt.axis('equal') plt.xlim(x0_vals.min(), x0_vals.max()) plt.ylim(x1_vals.min(), x1_vals.max()) # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # gif画像を保存 ani.save('Adam_cnf.gif')
# フレーム数を指定 frame_num = 101 # ハイパーパラメータのインスタンス変数名を指定 lr_name = 'alpha' # ハイパーパラメータを取得 lr = getattr(optimizer_lt[0], lr_name) # 最適化手法名を取得 opt_name = optimizer_lt[0].__class__.__name__ # 図を初期化 fig = plt.figure(figsize=(12, 10), facecolor='white') ax = fig.add_subplot(projection='3d') # 3D用の設定 fig.suptitle("Himmelblau's function", fontsize=20) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # 初期値の点ごとに更新値の推移を描画 for model, optimizer in zip(model_lt, optimizer_lt): # i番目までの点を描画 #ax.plot(model.trace_x0[:(i+1)], model.trace_x1[:(i+1)], model.trace_y[:(i+1)], # marker='o', alpha=0.5, zorder=50) # i番目の点を描画 ax.plot(model.trace_x0[i], model.trace_x1[i], model.trace_y[i], marker='o', zorder=50) ax.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs, offset=0.0, zorder=0) # 等高線 ax.plot_surface(x0_grid, x1_grid, y_mask_grid, norm=LogNorm(), cmap='viridis', alpha=0.8, zorder=1) # 曲面 ax.set_xlabel('$x_0$', fontsize=15) ax.set_ylabel('$x_1$', fontsize=15) ax.set_zlabel('f(x)', fontsize=15) ax.set_title('optimizer:'+opt_name + ', '+lr_name+'='+str(lr) + ', iter:'+str(i), loc='left') ax.set_box_aspect(aspect=(1, 1, 0.5)) ax.set_xlim(x0_vals.min(), x0_vals.max()) ax.set_ylim(x1_vals.min(), x1_vals.max()) ax.set_zlim(-z_max*0.1, z_max) ax.view_init(elev=45, azim=120) # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # gif画像を保存 ani.save('Adam_srf.gif')




この項では、最適化手法を比較しました。またこの節では、ニューラルネットワークを実装しました。次節は、ニューラルネットワークとしてQ学習を実装します。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning 4 ――強化学習編』オライリー・ジャパン,2022年.
- サポートページ:GitHub - oreilly-japan/deep-learning-from-scratch-4
おわりに
3巻のときにやりたかった内容なのですが、その時(1年前)は等高線に1つの手法をプロットするのがやっとでした。作図が面倒だったりまだ気になる点はありますが、満足の出来です。これがSGDsというやつか。テンション上がって、別の関数もやってみようとか次々と図が増えていきました。さて本編に戻りましょうか。ところで本当にビール関数って呼ぶのですか?
この記事のエンディングにぴったりな「Goal~明日はあっちだよ~」を聴きましょう!MVがないのでLIVE映像をどうぞ♪
ゴールが見えたと笑って~
【次節の内容】