4.2.2-4：交差エントロピー誤差の実装【ゼロつく1のノート(実装)】

はじめに

　「プログラミング」初学者のための『ゼロから作るDeep Learning』攻略ノートです。『ゼロつくシリーズ』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。

　関数やクラスとして実装される処理の塊を細かく分解して、1つずつ実行結果を見ながら処理の意図を確認していきます。

　この記事は、4.2.2「交差エントロピー誤差」から4.2.4項「バッチ対応版交差エントロピー誤差の実装」の内容です。他クラス分類の損失関数として用いられる交差エントロピー誤差をPythonで実装します。

【前節の内容】

www.anarchive-beta.com

【他の節の内容】

www.anarchive-beta.com

【この節の内容】

4.2.2 交差エントロピー誤差

　多クラス(多値)分類問題の損失関数として用いられる交差エントロピー誤差を実装します。

# 4.2.2項で利用するライブラリ
import numpy as np
import matplotlib.pyplot as plt

・数式の確認

　まずは、交差エントロピー誤差の定義式を確認します。

　最終層の活性化関数にソフトマックス関数を用いたニューラルネットワークの出力を$\mathbf{y} = (y_0, y_1, \cdots, y_9)$、one-hot表現の教師データ(ラベルデータ)を$\mathbf{t} = (t_0, t_1, \cdots, t_9)$とすると、交差エントロピー誤差は次の式で定義されます。ただし、0から9の数字に合わせてクラス数を$K = 10$とし、またPythonのインデックスに合わせて添字を0から割り当てています。

$$ E = - \sum_{k=0}^9 t_k \log y_k \tag{4.2} $$

　ソフトマックス関数の出力$\mathbf{y}$は、各要素$y_k$が0から1の値をとり、全ての要素の和が1になるため、ニューラルネットワークの入力(手書き数字)$\mathbf{x}$がどのラベル(数字・クラス)$k = 0, 1, \cdots, 9$なのかを表す確率分布として解釈できるのでした。
　また、one-hot表現の教師データ$\mathbf{t}$は、正解のラベル(書かれている数字)が1で、それ以外は0をとるのでした。つまり、$t_i = 1$のときの$i$が正解のラベルです。

　教師データ$\mathbf{t}$も、各要素$t_k$が0から1の値をとり、全ての要素の和が1になると言えますね。そこで、$\mathbf{t}$も確率分布として解釈すると、正解のラベルに対する確率が1(100%)でそれ以外の確率が0(0%)であると言えます。
　出力$\mathbf{y}$が、正解のラベルの確率が1(100%)でそれ以外の確率が0(0%)のとき、完全に予測できたと言えます。つまり、$\mathbf{y}$と$\mathbf{t}$は同じ値になります。よって、出力$\mathbf{y}$と教師データ(理想形)$\mathbf{t}$とのズレを誤差と考えます。

　交差エントロピー誤差では、正解のラベルに対応する出力に注目します。正解のラベルが$i$のとき($t_i = 1$のとき)、「ラベル$i$に関する出力($i$番目の出力)$y_i$」の符号を反転させた対数$-\log y_i$が交差エントロピー誤差$E$です(次で確認します)。

　$\log 1 = 0$なので、$\mathbf{y}$と$\mathbf{t}$が同じ値のとき($y_k = t_k = 1$のとき)最小値$E = 0$になります。また、$\log 0 = -\infty$なので、正解のラベルに関する出力が0のとき($t_k = 1,\ y_k = 0$のとき)最大値$E = \infty$になります。

・処理の確認

　次に、交差エントロピー誤差で行う処理を確認します。

　ニューラルネットワーク(ソフトマックス関数)の出力$\mathbf{y}$と教師データ$\mathbf{t}$を作成します。

# 仮の出力データを設定
y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])

# 仮の教師データを設定
t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])

　この例では、それぞれ次の値とします。

$$ \begin{aligned} \mathbf{y} &= \begin{pmatrix} 0.1 & 0.05 & 0.6 & 0 & 0.05 & 0.1 & 0 & 0.1 & 0 & 0 \end{pmatrix} \\ \mathbf{t} &= \begin{pmatrix} 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix} \end{aligned} $$

　$\mathbf{y},\ \mathbf{t}$を使って交差エントロピー誤差を計算していきますが、ここで1つ問題があります。

　$e^x = 0$を満たす$x$は存在しないので、$\log 0$は計算できません。

# log 0の計算
np.log(0)

-inf

　エラーとはならず、$-\infty$が返ってきます。

　そこで$\mathbf{y}$の各要素に、結果に影響しないような小さな値を加えてから対数をとることにします。微小な値をdeltaとします。

# 微小な値を設定
delta = 1e-7

# log 0対策
print(np.log(0 + delta))

-16.11809565095832

　ここでは微小な値として1e-7を加えることにします。(このeはネイピア数ではなく10のことで、)1e-7は$10^{-7} = \frac{1}{10^7} = 0.0000001$を意味します。

　これで対数を計算できました。

　出力yの各要素にdeltaを加えて対数をとります。

# 出力の対数をとる
log_y = np.log(y + delta)
print(np.round(log_y, 2))

[ -2.3   -3.    -0.51 -16.12  -3.    -2.3  -16.12  -2.3  -16.12 -16.12]

$$ \begin{aligned} \log \mathbf{y} &= \begin{pmatrix} \log y_0 & \log y_1 & \log y_2 & \cdots & \log y_9 \end{pmatrix} \\ &= \begin{pmatrix} \log 0.1 & \log 0.05 & \log 0.6 & \cdots & \log 0 \end{pmatrix}\\ &= \begin{pmatrix} -2.3 & -3 & -0.51 & \cdots & -16.12 \end{pmatrix} \end{aligned} $$

　$\mathbf{y}$の各要素は0から1の値のため、対数をとると0以下の値になります。

　教師データtと対数をとった出力log_yを掛けます。

# 教師データと出力の対数の積を計算
tmp = t * np.log(y + delta)
print(tmp)

[-0.         -0.         -0.51082546 -0.         -0.         -0.
 -0.         -0.         -0.         -0.        ]

$$ \begin{aligned} &\begin{pmatrix} t_0 \log y_0 & t_1 \log y_1 & t_2 \log y_2 & \cdots & t_9 \log y_9 \end{pmatrix} \\ &= \begin{pmatrix} 0 * (-2.3) & 0 * (-3) & 1 * (-0.51) & \cdots & 0 * (-16.12) \end{pmatrix} \\ &= \begin{pmatrix} 0 & 0 & -0.51 & \cdots & 0 \end{pmatrix} \end{aligned} $$

　教師データの各要素$t_k$は、正解のラベルが1でそれ以外は0でした。よって、正解のラベルに関する値はそのままで、それ以外は0になります。

　全ての要素の和を計算します。

# 教師データと出力の対数の積の総和を計算
tmp = np.sum(t * np.log(y + delta))
print(tmp)

-0.510825457099338

$$ \begin{aligned} \sum_{k=0}^9 t_k \log y_k &= t_0 \log y_0 + t_1 \log y_1 + t_2 \log y_2 + \cdots + t_9 \log y_9 \\ &= 0 + 0 * -0.51 + \cdots + 0 \\ &= -0.51 \end{aligned} $$

　(対数をとった)出力に教師データを掛けて総和をとることで、正解のラベルに関する要素を取り出せました。教師データとの積の総和の計算は、2乗和誤差のように全てのラベルにおける誤差を考慮するためではなく、正解のラベルに関する出力を抽出する操作を数式で表現したものと言えます。

　最後に、符号を反転させます($-1$を掛けます)。

# 交差エントロピー誤差を計算
E = -np.sum(t * np.log(y + delta))
print(E)

0.510825457099338

$$ - \sum_{k=0}^9 t_k \log y_k = 0.51083 = E $$

　ここまでの計算は常に0以下の値になるので、符号を反転させることで交差エントロピー誤差$E$は常に0以上の値をとるようになります。(あるいは、対数をとった出力の各要素$\log y_k\ (k = 0, 1, \cdots, 9)$が常に0以下の値になるので、最初の段階で符号を反転させて$- \log y_k$とし、$\mathbf{t}$との積の和$\sum_{k=0}^9 - t_k \log y$とも言えます。$-1$は定数なので$\sum$の外に出せます。)

　交差エントロピー誤差$E$が求まりました。正解のラベルが$i$のとき、$E = - \log y_i$なのを確認できました。

　以上が交差エントロピー誤差で行う処理です。

・実装

　処理の確認ができたので、交差エントロピー誤差を関数として実装します。

# 交差エントロピー誤差をの実装
def cross_entropy_error(y, t):
    # log 0回避用の微小な値を作成
    delta = 1e-7
    
    # 交差エントロピー誤差を計算:式(4.2)
    return - np.sum(t * np.log(y + delta))

　実装した関数を試してみましょう。

# (仮の)出力と教師データを指定
y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])

# 交差エントロピー誤差を計算
E = cross_entropy_error(y, t)
print(E)

0.510825457099338

# (仮の)出力と教師データを指定
y = np.array([0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0])
t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])

# 交差エントロピー誤差を計算
E = cross_entropy_error(y, t)
print(E)

2.302584092994546

　ただし、この関数では1つのデータ(1次元配列)かつone-hot表現の教師データしか処理できません。

・グラフの確認

　最後に、交差エントロピー誤差をグラフで確認します。

　ニューラルネットワーク(ソフトマックス関数)の出力$\mathbf{y}$の正解のクラスに関する要素$y_k$がとり得る値を作成します。

# 出力を作成
y = np.arange(0.0, 1.01, 0.01)
print(y)

[0.   0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1  0.11 0.12 0.13
 0.14 0.15 0.16 0.17 0.18 0.19 0.2  0.21 0.22 0.23 0.24 0.25 0.26 0.27
 0.28 0.29 0.3  0.31 0.32 0.33 0.34 0.35 0.36 0.37 0.38 0.39 0.4  0.41
 0.42 0.43 0.44 0.45 0.46 0.47 0.48 0.49 0.5  0.51 0.52 0.53 0.54 0.55
 0.56 0.57 0.58 0.59 0.6  0.61 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69
 0.7  0.71 0.72 0.73 0.74 0.75 0.76 0.77 0.78 0.79 0.8  0.81 0.82 0.83
 0.84 0.85 0.86 0.87 0.88 0.89 0.9  0.91 0.92 0.93 0.94 0.95 0.96 0.97
 0.98 0.99 1.  ]

　0から1までの値を作成してyとします。この例では、値を0.01間隔とします。yがx軸の値になります。

　ここでは、 正解のラベルに対応する出力のみを扱っているので、簡易的に交差エントロピー誤差$E = - \log y_k$を計算します。

# 交差エントロピー誤差を計算
E = - np.log(y)
print(np.round(E, 3))

[   inf  4.605  3.912  3.507  3.219  2.996  2.813  2.659  2.526  2.408
  2.303  2.207  2.12   2.04   1.966  1.897  1.833  1.772  1.715  1.661
  1.609  1.561  1.514  1.47   1.427  1.386  1.347  1.309  1.273  1.238
  1.204  1.171  1.139  1.109  1.079  1.05   1.022  0.994  0.968  0.942
  0.916  0.892  0.868  0.844  0.821  0.799  0.777  0.755  0.734  0.713
  0.693  0.673  0.654  0.635  0.616  0.598  0.58   0.562  0.545  0.528
  0.511  0.494  0.478  0.462  0.446  0.431  0.416  0.4    0.386  0.371
  0.357  0.342  0.329  0.315  0.301  0.288  0.274  0.261  0.248  0.236
  0.223  0.211  0.198  0.186  0.174  0.163  0.151  0.139  0.128  0.117
  0.105  0.094  0.083  0.073  0.062  0.051  0.041  0.03   0.02   0.01
 -0.   ]

　最初の要素は、値が0なので計算結果がinfになっています。

　交差エントロピー誤差のグラフを作成します。　

# 交差エントロピー誤差のグラフを作成
plt.figure(figsize=(8, 6)) # 図の設定
plt.plot(y, E) # 折れ線グラフ
plt.xlabel('$y_k$') # x軸ラベル
plt.ylabel('E') # y軸ラベル
plt.title('Cross Entropy Error', fontsize=20) # タイトル
plt.grid() # グリッド線
plt.show()

交差エントロピー誤差のグラフ

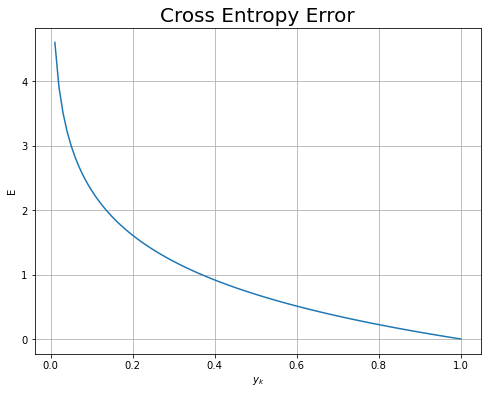
　$t_k = 1$のとき、$y_k$が1に近付くほど交差エントロピー誤差が小さくなる(ニューラルネットワークの性能が良い)のが分かります。また、$y_k = 1$のとき、最小値$E = 0$です。

　この項では、1データに対する交差エントロピー誤差を実装しました。次は、複数のデータに対する交差エントロピー誤差を実装します。

4.2.4 バッチ対応版交差エントロピー誤差の実装

　4.2.2項では、1データに対する交差エントロピー誤差について解説しました。この項では、複数データ(バッチデータ)に対する交差エントロピー誤差を実装します。

　利用するライブラリを読み込みます。

# 4.2.4項で利用するライブラリ
import numpy as np

・数式の確認

　まずは、複数のデータに対する交差エントロピー誤差の定義式を確認します。

　最終層の活性化関数にソフトマックス関数を用いたニューラルネットワークの出力$\mathbf{Y}$とone-hot表現の教師データ$\mathbf{T}$をそれぞれ次の$N \times K$の行列とします。

$$ \mathbf{Y} = \begin{pmatrix} y_{0,0} & y_{0,1} & \cdots & y_{0,9} \\ y_{1,0} & y_{1,1} & \cdots & y_{1,9} \\ \vdots & \vdots & \ddots & \vdots \\ y_{N-1,0} & y_{N-1,1} & \cdots & y_{N-1,9} \\ \end{pmatrix} ,\ \mathbf{T} = \begin{pmatrix} t_{0,0} & t_{0,1} & \cdots & t_{0,9} \\ t_{1,0} & t_{1,1} & \cdots & t_{1,9} \\ \vdots & \vdots & \ddots & \vdots \\ t_{N-1,0} & t_{N-1,1} & \cdots & t_{N-1,9} \\ \end{pmatrix} $$

　$N$はデータ数(バッチサイズ)です。また、0から9の数字に合わせてクラス数を$K = 10$とし、Pythonのインデックスに合わせて添字を0から割り当てています。
　複数データに対する交差エントロピー誤差は、次の式で定義されます。

$$ E = - \frac{1}{N} \sum_{n=0}^{N-1} \sum_{k=0}^9 t_{n,k} \log y_{n,k} \tag{4.3} $$

　この式について、$n$番目のデータに関する交差エントロピー誤差を$E_n$で表すと

$$ E_n = - \sum_{k=0}^9 t_{n,k} \log y_{n,k} $$

1つのデータに対する交差エントロピー誤差(4.2)と同じ式なのが分かります。
　また、式(4.3)を各データの交差エントロピー誤差$E_n$に置き換えると

$$ E = \frac{1}{N} \sum_{n=0}^{N-1} E_n = \frac{E_0 + E_1 + \cdots + E_{N-1}}{N} $$

複数データに対する交差エントロピー誤差$E$は、$N$個の交差エントロピー誤差の平均なのが分かります。

　データ数$N$で割り、1データ当たりの交差エントロピー誤差とすることで、データ数が異なる別の結果と学習の良し悪しを比較できます。
　また、1データに対する交差エントロピー誤差と同様に、$\mathbf{Y} = \mathbf{T}$のとき最小値$E = 0$になります。

・処理の確認

　次に、複数データ(2次元配列)に対応した交差エントロピー誤差で行う処理を確認します。

　ニューラルネットワーク(ソフトマックス関数)の出力$\mathbf{Y}$を作成します。

# (仮の)出力を作成
y = np.array([
    [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0], 
    [0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1], 
    [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
])
print(y)
print(y.shape)

[[0.1  0.05 0.6  0.   0.05 0.1  0.   0.1  0.   0.  ]
 [0.1  0.1  0.1  0.1  0.1  0.1  0.1  0.1  0.1  0.1 ]
 [0.1  0.05 0.1  0.   0.05 0.1  0.   0.6  0.   0.  ]]
(3, 10)

　one-hot表現の教師データ$\mathbf{t}$を作成します。

# (仮の)教師データを作成
t = np.array([
    [0, 0, 1, 0, 0, 0, 0, 0, 0, 0], 
    [0, 0, 0, 0, 0, 0, 0, 0, 1, 0], 
    [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
])
print(t)
print(t.shape)

[[0 0 1 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 1 0]
 [0 0 1 0 0 0 0 0 0 0]]
(3, 10)

　y, tを使って、one-hot表現の教師データの場合とスカラの教師データの場合の交差エントロピー誤差の処理を確認していきます。

・教師データがone-hot表現の場合

　まずは、教師データがone-hot表現の場合の処理を確認します。

　1データのときと同様に、全ての要素に微小な値を加えてから対数をとります。

# 微小な値を設定
delta = 1e-7

# 出力の対数をとる
log_y = np.log(y + delta)
print(np.round(log_y, 2))

[[ -2.3   -3.    -0.51 -16.12  -3.    -2.3  -16.12  -2.3  -16.12 -16.12]
 [ -2.3   -2.3   -2.3   -2.3   -2.3   -2.3   -2.3   -2.3   -2.3   -2.3 ]
 [ -2.3   -3.    -2.3  -16.12  -3.    -2.3  -16.12  -0.51 -16.12 -16.12]]

　$\log y_{n,k}$の計算を行うことで、全ての要素が0以下の値になりました。

　教師データtと対数をとった出力log_yの対応する要素を掛けます。

# 教師データと出力の対数の積を計算
tmp = t * log_y
print(np.round(tmp, 2))

[[-0.   -0.   -0.51 -0.   -0.   -0.   -0.   -0.   -0.   -0.  ]
 [-0.   -0.   -0.   -0.   -0.   -0.   -0.   -0.   -2.3  -0.  ]
 [-0.   -0.   -2.3  -0.   -0.   -0.   -0.   -0.   -0.   -0.  ]]

　$t_{n,k} \log y_{n,k}$の計算を行うことで、正解のラベルに関する値が残り、それ以外の要素は0になりました。

　全ての要素の和を計算します。

# 教師データと出力の対数の積の和を計算
tmp = np.sum(t * np.log(y + delta))
print(tmp)

-5.11599364308843

　$\sum_{n=0}^{N-1} \sum_{k=0}^9 t_{n,k} \log y_{n,k}$の計算によって、各データの正解ラベルに関する対数をとった出力の和が求まりました。

　最後に、バッチサイズ(データ数)$N$で割り、符号を反転させます($-N$で割ります)。

# バッチサイズを取得
batch_size = y.shape[0]
print(batch_size)

# 交差エントロピー誤差を計算:式(4.3)
E = - np.sum(t * np.log(y + delta)) / batch_size
print(E)

3
1.70533121436281

　変数名.shapeで各軸(各次元)の要素数を返します。この例では2次元配列(行列)を扱っているので、0番目の軸の要素数y.shape[0]は行数であり、またバッチサイズです。

　複数データに対する交差エントロピー誤差が求まりました。

　1データの場合も同様に処理できるように、次元数を変更するメソッド変数名.reshape()を使って、1次元配列のデータを2次元配列に変換します。

# 1次元配列(バッチサイズ1の出力)を作成
a = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
print(a)
print(a.shape) # 各軸の要素数
print(a.size) # 配列の要素数

[0.1  0.05 0.6  0.   0.05 0.1  0.   0.1  0.   0.  ]
(10,)
10

　要素数が10の1次元配列aを作成しました。

　aを$1 \times 10$の2次元配列に変換します。

# 2次元配列に変換
A = a.reshape(1, a.size)
print(A)
print(A.shape) # 各軸の要素数
print(A.size) # 配列の要素数

[[0.1  0.05 0.6  0.   0.05 0.1  0.   0.1  0.   0.  ]]
(1, 10)
10

　この処理を最初に行うことで、データ数に関わらず同じ処理で計算できます。

　以上の処理が、本に載っている1つ目の実装例に対応しています。

・教師データがスカラの場合

　続いて、教師データがone-hot表現ではなく正解ラベルを数値(スカラ)で示す場合の交差エントロピー誤差を実装します。

　交差エントロピー誤差に影響する「正解のラベルに関する出力」を取り出して計算することで、効率よく処理します。

　まずは、2次元配列から指定した要素を取り出す方法を確認しましょう。

# 2次元配列を作成
A = np.arange(50).reshape(5, 10)
print(A)
print(A.shape)

[[ 0  1  2  3  4  5  6  7  8  9]
 [10 11 12 13 14 15 16 17 18 19]
 [20 21 22 23 24 25 26 27 28 29]
 [30 31 32 33 34 35 36 37 38 39]
 [40 41 42 43 44 45 46 47 48 49]]
(5, 10)

　スライス機能を使って、指定した要素を取り出せます。

# 行を抽出
print(A[2, :])

# 列を抽出
print(A[:, 3])

# 要素を抽出
print(A[2, 3])

[20 21 22 23 24 25 26 27 28 29]
[ 3 13 23 33 43]
23

　:は、全ての要素を表します。

　行番号と列番号をそれぞれNumPy配列にまとめて指定することで、列と行が異なる複数の要素を取り出せます。

# 抽出する行番号を指定
row_idx = np.array([2, 1, 4, 3, 2])

# 抽出する列番号を指定
col_idx = np.array([4, 8, 2, 5, 0])

# 要素を抽出
print(A[row_idx, col_idx])

[24 18 42 35 20]

　出力yに対してこの機能を使うことで、各データの正解ラベルに関する要素を取り出します。

　「one-hot表現の教師データ」から「正解ラベルをスカラで表す教師データ」に変換します。

# 各データの正解ラベルを抽出
t = np.argmax(t, axis=1)
print(t)

[2 8 2]

　0か1の要素の内、1のインデックスが正解ラベルなのでした。そこで、np.argmax()で最大値1のインデックスを抽出します。axis=1を指定することで、行(データ)ごとに最大値のインデックスを調べられます。

　出力yから正解ラベルに対応する要素を抽出します。行番号には、0からバッチサイズまでの整数np.arange(batch_size)を指定します。列番号には、正解ラベルtを指定します。

# バッチサイズを抽出
batch_size = y.shape[0]

# 出力から各データの正解ラベルに関する要素を抽出
print(y[np.arange(batch_size), t])

[0.6 0.1 0.1]

　交差エントロピー誤差に影響する要素のみを抽出できました。

　抽出した出力に対して、対数をとり符号を反転させると、各データの交差エントロピー誤差を計算できます。

# 各データの交差エントロピー誤差を計算
E_n = - np.log(y[np.arange(batch_size), t] + delta)
print(E_n)

[0.51082546 2.30258409 2.30258409]

　$E_n = \sum_{k=1}^9 t_{nk} \log y_{nk}$の計算に対応します。

　E_nの総和をバッチサイズbatch_sizeで割ることで、1データ当たりの交差エントロピー誤差を計算します。

# 交差エントロピー誤差を計算:式(4.2)
E = - np.sum(np.log(y[np.arange(batch_size), t] + delta)) / batch_size
print(E)

1.70533121436281

　複数データに対する交差エントロピー誤差が求まりました。この方法だと、結果に影響しない要素に対する計算を行わずに済みます。

　以上の処理が、本に載っている2つ目の実装例に対応しています。

・実装

　処理の確認ができたので、バッチデータに対応した交差エントロピー誤差を関数として実装します。

# 交差エントロピー誤差の実装
def cross_entropy_error(y, t):
    # 2次元配列に変換
    if y.ndim == 1: # 1次元配列の場合
        # 1×Nの配列に変換
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
        
    # 教師ラベルを取得
    if t.size == y.size: # one-hot表現の場合
        # データごとに最大値を抽出
        t = t.argmax(axis=1)
    
    # データ数を取得
    batch_size = y.shape[0]
    
    # 交差エントロピー誤差を計算:式(4.3)
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size

　1データ(1次元配列)の場合は、2次元配列に変換します。
　また、教師データがone-hot表現の場合は、スカラに変換します。yとtの要素数が同じ場合は、one-hot表現です。
　2つ目に確認した処理方法で交差エントロピー誤差を計算して、出力します。

　これはcommonフォルダ内のfunctions.pyにある実装例です。

　実装した関数を試してみましょう。

# (仮の)出力を作成
y = np.array([
    [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0], 
    [0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1], 
    [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
])

# (仮の)教師データ(one-hot表現)を作成
t = np.array([
    [0, 0, 1, 0, 0, 0, 0, 0, 0, 0], 
    [0, 0, 0, 0, 0, 0, 0, 0, 1, 0], 
    [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
])

# 交差エントロピー誤差を計算
E = cross_entropy_error(y, t)
print(E)

1.70533121436281

# (仮の)教師データ(スカラ)を作成
t = np.array([2, 8, 2])

# 交差エントロピー誤差を計算
E = cross_entropy_error(y, t)
print(E)

1.70533121436281

# (仮の)出力を作成
y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])

# (仮の)教師データ(one-hot表現)を作成
t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])

# 交差エントロピー誤差を計算
E = cross_entropy_error(y, t)
print(E)

0.510825457099338

# (仮の)出力を作成
y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])

# (仮の)教師データ(スカラ)を作成
t = np.array(2)

# 交差エントロピー誤差を計算
E = cross_entropy_error(y, t)
print(E)

0.510825457099338

　この関数で、1次元配列と2次元配列のどちらでも、またone-hot表現とスカラのどちらでも処理できます。

　以上で、交差エントロピー誤差を実装できました。交差エントロピー誤差を小さくするようにパラメータを学習します。次節では、学習を行うのに必要な微分について解説します。

参考文献

• 斎藤康毅『ゼロから作るDeep Learning』オライリー・ジャパン,2016年.
• サポートページ：交差エントロピー誤差のコード(https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/common/functions.py)

おわりに

　現在の重み$\mathbf{W}$があり、その重みによって出力$\mathbf{Y}$が決まります。その出力$\mathbf{Y}$と教師データ$\mathbf{T}$から、損失関数によって誤差$E$を求めます。重み$\mathbf{W}$に関する誤差$E$の勾配を使って(=勾配降下法によって)、誤差が小さくなるように重みの値を少しだけ調整します。
　値を更新した重み$\mathbf{W}$によって出力$\mathbf{Y}$が決まり・・・

　このように、パラメータの値を少しずつ繰り返し更新することを「学習」と呼びます。深層「学習」と言うくらいですから、この一連の流れが大きな目的の1つです。
　4章では、微分やなんやと色々登場しますが(また入力$\mathbf{X}$と混同するかもしれませんが)、全ては重み$\mathbf{W}$と(省略しましたが)バイアス$\mathbf{B}$の学習のための道具だと思えば対応関係を整理できるかと思います。ちなみに入力$\mathbf{X}$は画像データのことなので既に決まった値です(変数ではありません)。

　なんかURLの埋め込みがうまくいかないことがある、、、

• 2021.08.04：加筆修正しました。

　JupyterLabの出力(半角スペースによる記法？)をそのままにしておくと、URLの埋め込みがうまくいかないことがあるようです(根本的な原因は未だ不明)。URLを張りたい場所の前後？をバッククオート3つで挟む記法に変えたらうまくいきました。

【次節の内容】

www.anarchive-beta.com