はじめに
「プログラミング」初学者のための『ゼロから作るDeep Learning』攻略ノートです。『ゼロつくシリーズ』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
関数やクラスとして実装される処理の塊を細かく分解して、1つずつ実行結果を見ながら処理の意図を確認していきます。
この記事は、4.2.1項「2乗和誤差」の内容です。2乗和誤差をPythonで実装します。
【前節の内容】
【他の記事一覧】
【この記事の内容】
4.2.1 2乗和誤差
多クラス(多値)分類問題の損失関数として用いられる2乗和誤差を実装します。
利用するライブラリを読み込みます。
# 4.2.1項で利用するライブラリ import numpy as np import matplotlib.pyplot as plt
・数式の確認
まずは、2乗和誤差の定義式を確認します。
最終層の活性化関数にソフトマックス関数を用いたニューラルネットワークの出力を$\mathbf{y} = (y_0, y_1, \cdots, y_9)$、one-hot表現の教師データ(ラベルデータ)を$\mathbf{t} = (t_0, t_1, \cdots, t_9)$とすると、2乗和誤差は次の式で定義されます。ただし、0から9の数字に合わせてクラス数を$K = 10$とし、またPythonのインデックスに合わせて添字を0から割り当てています。
ソフトマックス関数の出力$\mathbf{y}$は、各要素$y_k$が0から1の値をとり、全ての要素の和が1になるため、ニューラルネットワークの入力(手書き数字)$\mathbf{x}$がどのラベル(数字・クラス)$k = 0, 1, \cdots, 9$なのかを表す確率分布として解釈できるのでした。
また、one-hot表現の教師データ$\mathbf{t}$は、正解のラベル(書かれている数字)が1で、それ以外は0をとるのでした。つまり、$t_i = 1$のときの$i$が正解のラベルです。
教師データ$\mathbf{t}$も、各要素$t_k$が0から1の値をとり、全ての要素の和が1になると言えますね。そこで、$\mathbf{t}$も確率分布として解釈すると、正解のラベルに対する確率が1(100%)でそれ以外の確率が0(0%)であると言えます。
出力$\mathbf{y}$が、正解のラベルの確率が1(100%)でそれ以外の確率が0(0%)のとき、完全に予測できたと言えます。つまり、$\mathbf{y}$と$\mathbf{t}$は同じ値になります。よって、出力$\mathbf{y}$と教師データ(理想形)$\mathbf{t}$とのズレを誤差と考えます。
2乗和誤差では、ラベルごとの出力$y_k$と教師データ$t_k$の差に注目します。「各要素の差$y_k - t_k$」を2乗して、全ての要素の和をとったものが2乗和誤差です。(2で割ることで、$y_k$に関する微分が$\frac{\partial E}{\partial y_k} = y_k - t_k$という綺麗な形になります。2で割らない場合は、$\frac{\partial E}{\partial y_k} = 2 (y_k - t_k)$となります。詳しくは、4.4節や5章で扱います。)
$\mathbf{y}$が$\mathbf{t}$と同じ値のとき最小値$E = 0$になり、正解以外の要素の1つが1で(正解も含めた)それ以外が0のとき最大値$E = 1$になります。
・処理の確認
次に、2乗和誤差で行う処理を確認します。
ニューラルネットワーク(ソフトマックス関数)の出力$\mathbf{y}$と教師データ$\mathbf{t}$を作成します。
# (仮の)ニューラルネットワークの出力を作成 y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]) # (仮の)教師データを作成 t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])
この例では、それぞれ次の値とします。
出力yと教師データtの差を計算します。
# 各要素の差を計算 tmp = y - t print(tmp)
[ 0.1 0.05 -0.4 0. 0.05 0.1 0. 0.1 0. 0. ]
出力の各要素$y_k$は、0から1の値をとるのでした。また、教師データの各要素$t_k$は、正解のラベルでは1、それ以外では0でした。よって$y_k - t_k$は、正解のラベルでは-1から0、それ以外のラベルでは0から1の値になります。
では各要素の差の合計を全体の誤差としようと言いたいところですが、このまま足すと正の値と負の値が相殺されてしまいます。そこで、各要素を2乗してから合計することにします。(分散の考え方と同じですね。)
y - tの2乗を計算します。
# 各要素の差の2乗を計算 tmp = (y - t)**2 print(tmp)
[0.01 0.0025 0.16 0. 0.0025 0.01 0. 0.01 0. 0. ]
2乗したことで、全ての要素が0以上の値になりました。
yとtの差の2乗の総和を計算します。
# 各要素の差の2乗の総和を計算 tmp = np.sum((y - t)**2) print(tmp)
0.19500000000000006
最後に、2で割ります(0.5を掛けます)。
# 2乗和誤差を計算:式(4.1) E = 0.5 * np.sum((y - t)**2) print(E)
0.09750000000000003
2乗和誤差$E$が求まりました。
以上が2乗和誤差で行う処理です。
・実装
処理の確認ができたので、2乗和誤差を関数として実装します。
# 2乗和誤差の実装 def sum_squared_error(y, t): # 2乗和誤差を計算:式(4.1) return 0.5 * np.sum((y - t)**2)
(ちなみに、mean squared errorとなっている場合は、サポートページの正誤表「errata · oreilly-japan/deep-learning-from-scratch Wiki · GitHub」を参照してください。)
実装した関数を試してみましょう。
# (仮の)出力と教師データを作成 y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]) t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0]) # 2乗和誤差を計算 E = sum_squared_error(y, t) print(E)
0.09750000000000003
# (仮の)出力と教師データを作成 y = np.array([0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]) t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0]) # 2乗和誤差を計算 E = sum_squared_error(y, t) print(E)
0.5975
教師データがone-hot表現でない場合は、この関数では処理できません。
・グラフで確認
最後に、2乗和誤差をグラフで確認します。
グラフ化できるように、$K = 2$の場合を考えます。またこの例では、$t_1 = 1$(正解ラベルが1)とします。
ソフトマックス関数の出力$\mathbf{y} = (y_0, y_1)$がとり得る値の組み合わせを作成します。
# 出力を作成 y0 = np.arange(0.0, 1.01, 0.01) y1 = 1 - y0 print(y0) print(y1)
[0. 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11 0.12 0.13
0.14 0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22 0.23 0.24 0.25 0.26 0.27
0.28 0.29 0.3 0.31 0.32 0.33 0.34 0.35 0.36 0.37 0.38 0.39 0.4 0.41
0.42 0.43 0.44 0.45 0.46 0.47 0.48 0.49 0.5 0.51 0.52 0.53 0.54 0.55
0.56 0.57 0.58 0.59 0.6 0.61 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69
0.7 0.71 0.72 0.73 0.74 0.75 0.76 0.77 0.78 0.79 0.8 0.81 0.82 0.83
0.84 0.85 0.86 0.87 0.88 0.89 0.9 0.91 0.92 0.93 0.94 0.95 0.96 0.97
0.98 0.99 1. ]
[1. 0.99 0.98 0.97 0.96 0.95 0.94 0.93 0.92 0.91 0.9 0.89 0.88 0.87
0.86 0.85 0.84 0.83 0.82 0.81 0.8 0.79 0.78 0.77 0.76 0.75 0.74 0.73
0.72 0.71 0.7 0.69 0.68 0.67 0.66 0.65 0.64 0.63 0.62 0.61 0.6 0.59
0.58 0.57 0.56 0.55 0.54 0.53 0.52 0.51 0.5 0.49 0.48 0.47 0.46 0.45
0.44 0.43 0.42 0.41 0.4 0.39 0.38 0.37 0.36 0.35 0.34 0.33 0.32 0.31
0.3 0.29 0.28 0.27 0.26 0.25 0.24 0.23 0.22 0.21 0.2 0.19 0.18 0.17
0.16 0.15 0.14 0.13 0.12 0.11 0.1 0.09 0.08 0.07 0.06 0.05 0.04 0.03
0.02 0.01 0. ]
$y_0$をy0として、0から1の値を持つように作成します。この例では、値の間隔を0.01とします。
また、$y_1$をy1として作成します。ただし、$y_0 + y_1 = 1$なので、$y_1 = 1 - y_0$の計算結果をy1とします。
y0[0], y1[0]が$\mathbf{y} = (0, 1)$であり、0.01刻みで$(0.01, 0.99), \cdots, (1, 0)$に対応しています。
教師データ$\mathbf{t} = (t_0, t_1) = (0, 1)$を作成します。この例では、正解ラベルを1とします。(1の手書き数字を入力して、0か1のどちらであるかを予測するイメージです。)
# 教師データを作成 t = np.array([0, 1]) print(t)
[0 1]
こちらは、$\mathbf{t}$をtとします。
y0とy1の対応する要素ごとに、2乗和誤差$E$を計算します。
# 2乗和誤差を計算 E = np.array([sum_squared_error(y, t) for y in zip(y0, y1)]) print(np.round(E, 3))
[0. 0. 0. 0.001 0.002 0.003 0.004 0.005 0.006 0.008 0.01 0.012
0.014 0.017 0.02 0.023 0.026 0.029 0.032 0.036 0.04 0.044 0.048 0.053
0.058 0.062 0.068 0.073 0.078 0.084 0.09 0.096 0.102 0.109 0.116 0.123
0.13 0.137 0.144 0.152 0.16 0.168 0.176 0.185 0.194 0.202 0.212 0.221
0.23 0.24 0.25 0.26 0.27 0.281 0.292 0.303 0.314 0.325 0.336 0.348
0.36 0.372 0.384 0.397 0.41 0.423 0.436 0.449 0.462 0.476 0.49 0.504
0.518 0.533 0.548 0.562 0.578 0.593 0.608 0.624 0.64 0.656 0.672 0.689
0.706 0.722 0.74 0.757 0.774 0.792 0.81 0.828 0.846 0.865 0.884 0.903
0.922 0.941 0.96 0.98 1. ]
リスト内包表記のfor文とzip()を使って、y0, y1から順番に要素を取り出して2乗和誤差を求めます。(本の内容と離れているので、この処理の解説は省略します。本で登場するタイミングで解説します。)
Eは0から1の値になります。
ラベル0に関する出力$y_0$と2乗和誤差$E$のグラフを作成します。
# 2乗和誤差のグラフを作成 plt.figure(figsize=(6, 6)) # 図の設定 plt.plot(y0, E) # 折れ線グラフ plt.xlabel('$y_0$') # x軸ラベル plt.ylabel('Error') # y軸ラベル plt.suptitle('Sum of Squared Error', fontsize=20) # 全体のタイトル plt.title('$t = (0, 1)$', loc='left') # タイトル plt.grid() # グリッド線 plt.show()
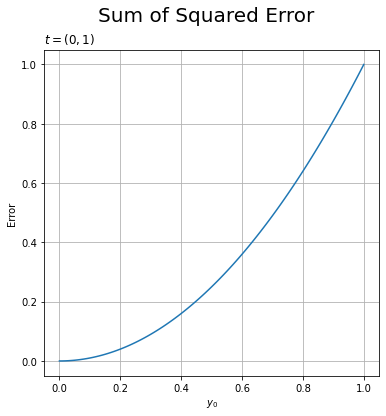
0は不正解のラベルなので、$y_0$の値が大きいほど2乗和誤差も大きくなる(ニューラルネットワークの性能が悪いと言える)のが分かります。$\mathbf{y} = (0, 1)$のとき最小値の$E = 0$で、$\mathbf{y} = (1, 0)$のとき最大値の$E = 1$になります。
同様に、$y_1$と$E$の関係をグラフで見ます。
# 2乗和誤差のグラフを作成 plt.figure(figsize=(6, 6)) # 図の設定 plt.plot(y1, E) # 折れ線グラフ plt.xlabel('$y_1$') # x軸ラベル plt.ylabel('Error') # y軸ラベル plt.suptitle('Sum of Squared Error', fontsize=20) # 全体のタイトル plt.title('$t = (0, 1)$', loc='left') # タイトル plt.grid() # グリッド線 plt.show()
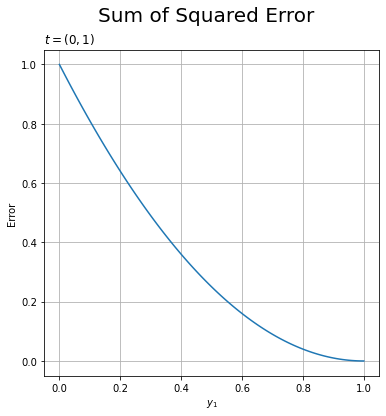
こちらは正解のラベルに対する予測なので、$y_1$の値が大きいほど2乗和誤差が小さくなる(性能が良い)のが分かります。当然、$\mathbf{y} = (0, 1)$のとき最小値の$E = 0$で、$\mathbf{y} = (1, 0)$のとき最大値の$E = 1$になるのは変わりません。
おまけとして、$\mathbf{y}$と$\mathbf{t}$の関係を3Dのグラフで確認しましょう。
・コード(クリックで展開)
# 3D散布図を作成 fig = plt.figure(figsize=(8, 6)) # 図の準備 ax = fig.add_subplot(projection='3d') # 3Dプロットの準備 sctr = ax.scatter(y0, y1, E, c=E, cmap='jet') # 散布図 ax.set_xlabel('$y_0$') # x軸ラベル ax.set_ylabel('$y_1$') # y軸ラベル ax.set_zlabel('E') # z軸ラベル ax.set_title('$t = (0, 1)$', loc='left') # グラフタイトル fig.suptitle('Sum of Squared Error', fontsize=20) # 図全体のタイトル fig.colorbar(sctr, shrink=0.5, aspect=10, label='E') # カラーバー ax.view_init(elev=20, azim=245) # 表示アングル plt.show()

1枚目のグラフはこの図を$y_0$側から、2枚目のグラフは$y_1$側から(奥行きを無視して)見たものです。
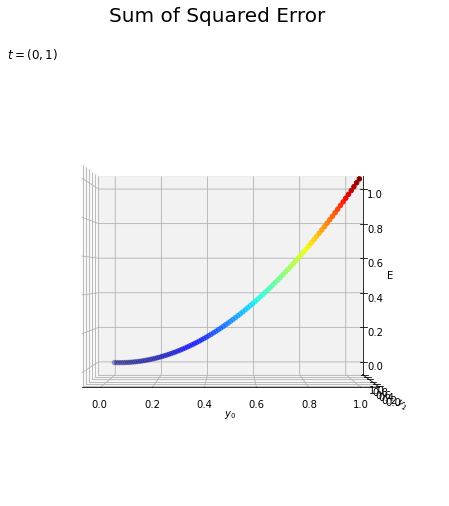
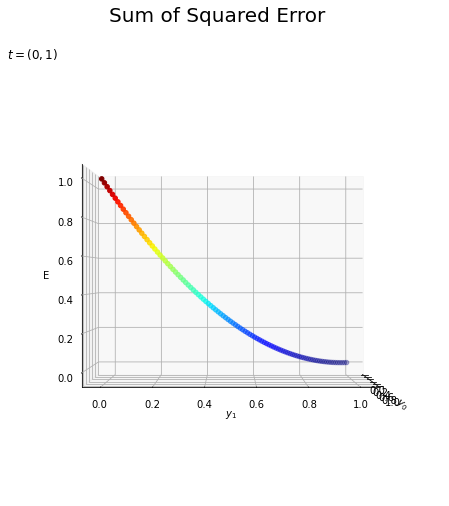
作図方法が気になる方は「3Dプロットの作図【ゼロつく1のノート(Python)】 - からっぽのしょこ」を参照してください。
以上で、2乗和誤差を実装できました。次項では、交差エントロピー誤差を実装します。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning』オライリー・ジャパン,2016年.
- サポートページ:2乗和誤差のコード(https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/common/functions.py)
おわりに
4章の内容の勉強会資料が書き終わりました!10日くらいかかりましたかね。また暫く続けてブログ記事化していきます。
その勉強会は6月の頭から始まるはずだったのですが、まだ本格的には始まっていません。それどころか4章分を書いている間に、かなり規模縮小しそうで(そもそもが数人だけど)すごーくモチベーションが下がっております。でも既に全体の半分以上を書いてしまっているので、最後まで質を下げることなくやりきるつもりです。頑張ります。よろしくお願いします。
何がどうなろうとそも自分の勉強ですしね。早く2巻やりたーーい。
- 2021.08.04:加筆修正しました。
結局勉強会は2か月もたずに自然消滅しました。。。あと、2巻と3巻の記事も書きました。
ところで、2乗和誤差を調べてもこの本関連の記事ばかりなんだけど、何に・どういう場合に使うんだ?あと、バッチデータの場合は平均をとるのかな。
【次節の内容】