はじめに
『ゼロから作るDeep Learning 4 ――強化学習編』の独学時のまとめノートです。初学者の補助となるようにゼロつくシリーズの4巻の内容に解説を加えていきます。本と一緒に読んでください。
この記事は、1.5節の始めの内容です。非定常問題に対応したスロットマシンを実装します。
【前節の内容】
【他の記事一覧】
【この記事の内容】
1.5.0 非定常問題のスロットマシンの実装
非定常問題のバンディット(スロットマシン)の機能を持つNonStatBanditクラスの処理を確認します。
利用するライブラリを読み込みます。
# 利用するライブラリ import numpy as np import matplotlib.pyplot as plt
・処理の確認
NonStatBanditクラスの内部で行われる処理を確認します。基本的な処理はBanditクラスと同様です。「1.4.1:スロットマシンの実装【ゼロつく4のノート】 - からっぽのしょこ」参照してください。
各マシンの当たりの確率の初期値をランダムに設定して、繰り返しランダムノイズを加えます。
# 試行回数を指定 steps = 100 # マシンの数を指定 arms = 10 # 記録用の配列を初期化 trace_rates = np.zeros((arms, steps+1)) # 各マシンの確率の初期値を設定 rates = np.random.rand(arms) print(np.round(rates, 3)) # 初期値を記録 trace_rates[:, 0] = rates # 繰り返し試行 for step in range(steps): # 各マシンの確率にランダムノイズを加算 rates += 0.1 * np.random.randn(arms) # 更新値を記録 trace_rates[:, step+1] = rates # 最終結果を確認 print(np.round(trace_rates[:, steps], 3))
[0.959 0.456 0.188 0.03 0.017 0.631 0.973 0.839 0.178 0.366]
[ 2.549 -1.076 -0.293 -0.196 -0.7 1.151 -0.623 2.439 0.678 -1.161]
np.random.rand()で0から1の一様乱数を生成して、各マシンの確率ratesの初期値とします。
np.random.randn()で平均0・標準偏差1のガウスノイズを生成して、0.1倍した値を各マシンの確率に加えていきます。
結果を見ると、0未満や1より大きい要素があります。確率の定義を満たしませんが、負の値であれば常に外れ、1より大きければ常に当たりになります。
各マシンの当たりの確率の推移をグラフで確認します。
# 確率の推移のグラフを作成 plt.figure(figsize=(8, 6)) for arm in range(arms): plt.plot(trace_rates[arm]) # 各マシンの確率 plt.xlabel('steps') plt.ylabel('rates') plt.suptitle('Non-Stationary Problem', fontsize=20) plt.grid() plt.show()
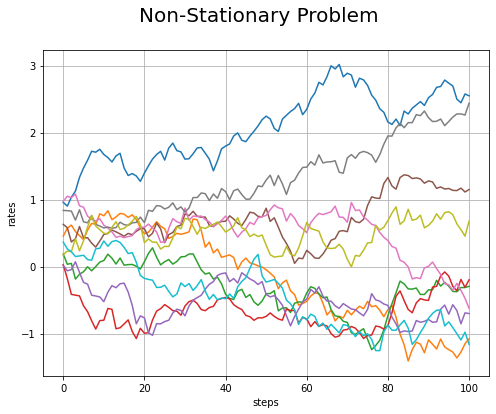
ステップが離れた値との関連は弱いですが、ステップが近い値との関連は見えます。
以上が、NonStatBanditクラスで行う処理です。
np.random.randn()で生成できる乱数をヒストグラムで確認します。
# データ数を指定 N = 10000 # ガウス乱数を生成 r_vals = np.random.randn(N) # 乱数のヒストグラムを作成 plt.figure(figsize=(8, 6)) plt.hist(r_vals, bins=20) # ガウス乱数 plt.xlabel('value') plt.ylabel('count') plt.title('N=' + str(N), loc='left') # データ数 plt.suptitle('np.random.randn(N)', fontsize=20) plt.grid() plt.show()
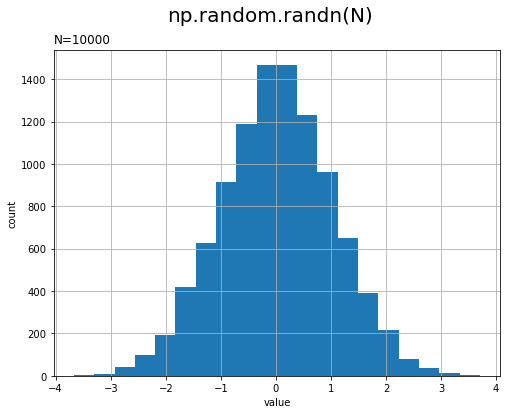
0付近の値が多く生成されるのが分かります。
・実装
NonStatBanditクラスの実装は、次のページを参照してください。
実装したクラスを試してみます。
バンディットクラスのインスタンスを作成します。
# マシンの数を指定 arms = 10 # インスタンスを作成 bandit = NonStatBandit(arms) # 各マシンの確率を確認 print(np.round(bandit.rates, 3))
[0.021 0.061 0.821 0.763 0.034 0.549 0.128 0.635 0.436 0.023]
インスタンスを作成する度に、ランダムに値が設定されるので、各マシンの確率が変わります。
マシンのプレイ回数と、プレイするマシン番号を指定して、マシンをプレイします。
# 試行回数を指定 steps = 5 # マシン番号を指定 arm = 0 # 繰り返し試行 for step in range(steps): # arm番目のマシンをプレイ reward = bandit.play(arm) print(reward) # 各マシンの確率を確認 print(np.round(bandit.rates, 3))
0
[ 0.013 0.092 0.795 0.787 0.087 0.557 -0.021 0.453 0.269 -0.079]
0
[ 0.05 -0.045 0.796 0.685 -0.066 0.444 -0.086 0.458 0.479 -0.01 ]
0
[ 0.235 -0.093 0.908 0.81 -0.091 0.438 -0.166 0.366 0.498 0.018]
0
[ 0.229 -0.196 0.709 1.022 -0.091 0.493 -0.173 0.238 0.596 -0.038]
1
[ 0.007 -0.196 0.586 1.056 -0.133 0.313 -0.235 0.133 0.702 0.019]
play()メソッドを実行する度に各マシンの当たりの確率が変化します。
当たりなら報酬が1、外れなら報酬が0で、試行の度に確率が少しずつ変化するスロットマシンの実行結果が得られました。
以上で、スロットマシンの機能を持つクラスを実装できました。次節では、エージェントの機能を持つクラスを実装します。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning 4 ――強化学習編』オライリー・ジャパン,2022年.
- サポートページ:GitHub - oreilly-japan/deep-learning-from-scratch-4
おわりに
今更ですが、スロットマシンの当たりの確率と表現していましたが、本だと勝率となっていますね。
【次節の内容】