はじめに
『ゼロから作るDeep Learning 4 ――強化学習編』の独学時のまとめノートです。初学者の補助となるようにゼロつくシリーズの4巻の内容に解説を加えていきます。本と一緒に読んでください。
この記事は、1.5.2節の内容です。非定常な多腕バンディット問題の学習を行います。
【前節の内容】
【他の記事一覧】
【この記事の内容】
1.5.2 非定常バンディット問題の学習
1.5.0項で実装したNonStatBanditクラスと1.5.1項で実装したAlphaAgentクラスを使って、非定常な多腕バンディット問題を解きます。
利用するライブラリを読み込みます。
# 利用するライブラリ import numpy as np import matplotlib.pyplot as plt
・標本平均と指数移動平均の比較
NonStatBanditクラスとAlphaAgentクラスのインスタンスを使って、繰り返しプレイし学習を行います。さらに、それぞれ複数の学習結果の平均を求めます。
# 実験回数を指定 runs = 200 # 実験1回当たりの試行回数を指定 steps = 1000 # マシンの数を指定 action_size = 10 # ランダムにマシンを選ぶ確率を指定 epsilon = 0.1 # 減衰率を指定 alpha = 0.8 # エージェントの切り替え用の設定 agent_types = ['sample average', 'alpha const update'] # 実験結果の平均の記録用のディクショナリを初期化 results = {} # エージェントクラスを切り替え for agent_type in agent_types: print(agent_type) # 実験結果の記録用の配列を初期化 all_rates = np.zeros((runs, steps)) # 繰り返し試行 for run in range(runs): # インスタンスを作成(マシンの確率・推定価値を初期化) bandit = NonStatBandit(action_size) if agent_type == 'sample average': # 定常問題版 agent = Agent(epsilon, action_size) else: # 非定常問題版 agent = AlphaAgent(epsilon, alpha, action_size) # 平均報酬の記録用のオブジェクトを初期化 total_reward = 0 rates = [] # 繰り返し試行 for step in range(steps): # マシンをプレイ action = agent.get_action() reward = bandit.play(action) # マシンの推定価値を更新 agent.update(action, reward) # 平均報酬を記録 total_reward += reward rates.append(total_reward / (step + 1)) # 実験結果を記録 all_rates[run] = rates # 試行ごとに平均を計算 avg_rates = np.average(all_rates, axis=0) # エージェントごとに実験結果の平均を記録 results[agent_type] = avg_rates print(avg_rates[-1])
sample average
0.8895099999999998
alpha const update
0.9187250000000001
基本的な処理は定常問題のときと同様です。「1.4.3-4：バンディット問題の学習【ゼロつく4のノート】 - からっぽのしょこ」も参照してください。
1つ目のfor文とagent_typesとif文を使って、「標本平均を用いるエージェントのクラスAgent」と「指数移動平均を用いるエージェントのクラスAlphaAgent」を切り替えます。
それぞれの実験結果の平均をディクショナリ型のオブジェクトresultに格納します。
1回の実験における平均報酬の推移をratesに格納して、各実験における平均報酬の推移をall_ratesに格納します。all_ratesの各行が各実験、各列が各試行に対応します。
all_ratesを試行ごとに(列ごとに)平均をとりavg_ratesとします。avg_ratesが推移の平均になります。最後に、avg_ratesをresultに格納します。
2つのエージェントの平均推移をグラフで確認します。
# 実験結果を作図 plt.figure(figsize=(8, 6)) for key, avg_rates in results.items(): plt.plot(avg_rates, label=key) # 実験ごとの平均報酬の推移 plt.xlabel('Steps') plt.ylabel('Average Rates') plt.title('$runs:'+str(runs) + ', \epsilon='+str(epsilon)+ ', \\alpha='+str(alpha)+'$', loc='left') # 実験の設定 plt.suptitle('Average reward', fontsize=20) plt.grid() plt.legend() plt.ylim(0, 1) plt.show()
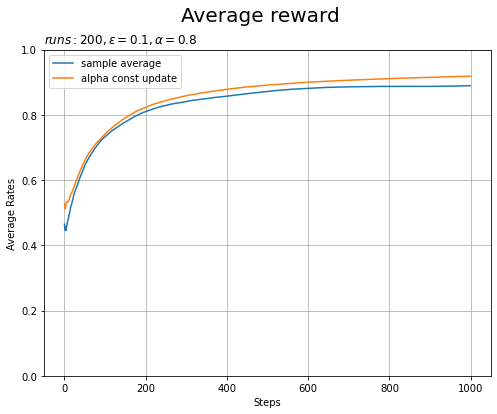
指数移動平均を用いたエージェント(オレンジ色の線)の方が当たりの割合が大きくなっていることから、より学習できているのが分かります。
・減衰率の影響
先ほどは、減衰率を$\alpha = 0.8$として学習の推移を確認しました。今度は、減衰率の値を変更して比較します。
# 実験回数を指定 runs = 200 # 実験1回当たりの試行回数を指定 steps = 10000 # ランダムにマシンを選ぶ確率を指定 epsilon = 0.1 # 減衰率を指定 alpha_list = [0.01, 0.05, 0.1, 0.2, 0.4, 0.8] # マシンの数を指定 action_size = 10 # 平均報酬の記録用の配列を初期化 all_rates = np.zeros((runs, steps)) all_avg_rates = np.zeros((len(alpha_list), steps)) # 割引率を切り替え for i, alpha in enumerate(alpha_list): # 実験の設定を表示 print('alpha =', alpha) # 繰り返し実験 for run in range(runs): # インスタンスを作成:(マシンの確率を初期化) bandit = NonStatBandit(action_size) agent = AlphaAgent(epsilon, alpha, action_size) # 記録用の配列を初期化 total_reward = 0 rates = [] # 繰り返し試行 for step in range(steps): # マシンをプレイ action = agent.get_action() reward = bandit.play(action) # 値を更新 agent.update(action, reward) total_reward += reward rates.append(total_reward / (step + 1)) # 実験結果を記録 all_rates[run] = rates # 試行ごとの平均を計算 avg_rates = np.average(all_rates, axis=0) print(avg_rates[-1]) # alphaごとの実験結果を記録 all_avg_rates[i] = avg_rates
alpha = 0.01
0.8971904999999996
alpha = 0.05
0.9359095000000001
alpha = 0.1
0.9402190000000004
alpha = 0.2
0.9426115000000003
alpha = 0.4
0.9447975
alpha = 0.8
0.9466104999999995
比較する減衰率の値をalpha_listに指定します。
for文を使って、alpha_listの値を取り出して1.4.4項の実験を行います。
減衰率ごとの実験結果の平均をグラフで確認します。
# 実験結果を作図 plt.figure(figsize=(8, 6)) for i, alpha in enumerate(alpha_list): plt.plot(all_avg_rates[i], label='$\\alpha='+str(alpha)+'$') # 実験ごとの平均報酬 plt.xlabel('Steps') plt.ylabel('Rates') plt.title('$runs:'+str(runs)+ ', \epsilon='+str(epsilon)+'$', loc='left') # 実験回数 plt.suptitle('Bandit Algorithms', fontsize=20) plt.grid() plt.legend() plt.ylim(0, 1) plt.show()
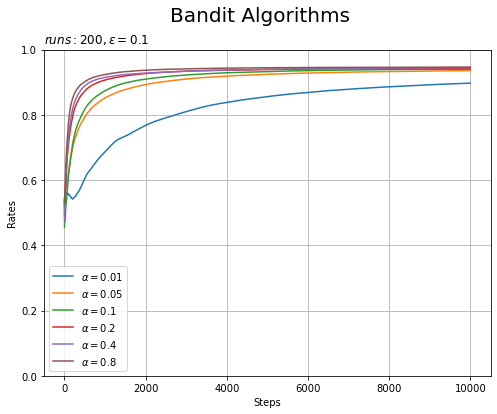
値が大きいほど早く学習が進んでいます(問題の設定によるかもしれません)。
以上で、非定常な多腕バンディット問題の学習を行えました。
参考文献
おわりに
これで1章が完了です。2章は問題設定(考え方)の話です。本ではプログラミングが少ないので、ブログでは無理やりにでもねじ込めたらと思います。
そして、2022年5月7日は元モーニング娘。の佐藤優樹さんの23歳のお誕生日です！
まーちゃんのソロ活動も楽しい日々でありますよーに♪
私は佐藤優樹さんをきっかけにハロプロにハマりまして、さらにハロプロ楽曲をテキスト分析したいというモチベーションでこのブログをやってます。なのでこの方がいなければこのブログはなかったわけで、このブログを読まれた方はぜひぜひ一度はハロプロ楽曲を聴いてくださいっ！モーニング娘。以外にも色んな魅力あふれるグループがいますよ♬
【次節の内容】
