はじめに
機械学習で登場する確率分布について色々な角度から理解したいシリーズです。
カテゴリ分布の計算とグラフの作成をR言語で行います。
【前の内容】
【他の記事一覧】
【目次】
カテゴリ分布
カテゴリ分布(Categorical Distribution)の計算と作図を行います。
利用するパッケージを読み込みます。
# 利用するパッケージ library(tidyverse) library(gganimate)
分布の変化をアニメーション(gif画像)で確認するのにgganimateパッケージを利用します。不要であれば省略してください。
定義式の確認
まずは、カテゴリ分布の定義式を確認します。
カテゴリ分布は、次の式で定義されます。詳しくは「カテゴリ分布の定義式 - からっぽのしょこ」を参照してください。
ここで、$x_v$はクラス$v$が出現した回数、$\phi_v$はクラス$v$の出現確率です。
確率変数の値$\mathbf{x} = (x_1, \cdots, x_V)$はone-hotベクトルで、$x_v \in \{0, 1\}$、$\sum_{v=1}^V x_v = 1$となります。パラメータ$\boldsymbol{\phi} = (\phi_1, \cdots, \phi_V)$は、$\phi_v \in (0, 1)$、$\sum_{v=1}^V \phi_v = 1$を満たす必要があります。
この式の対数をとると、次の式になります。
カテゴリ分布のクラス$v$における平均と分散は、次の式で計算できます。詳しくは「カテゴリ分布の平均と分散の導出 - からっぽのしょこ」を参照してください。
これらの計算を行いグラフを作成します。
確率の計算
カテゴリ分布に従う確率を計算する方法をいくつか確認します。
パラメータを設定します。
# パラメータを指定 phi_v <- c(0.2, 0.4, 0.1, 0.3) # 確率変数の値を指定 x_v <- c(0, 1, 0, 0)
カテゴリ分布のパラメータ$\boldsymbol{\phi} = (\phi_1, \cdots, \phi_V)$、$0 \leq \phi_v \leq 1$、$\sum_{v=1}^V \phi_v = 1$を指定します。
確率変数がとり得る値$\mathbf{x} = (x_1, \cdots, x_V)$、$x_v \in \{0, 1\}$、$\sum_{v=1}^V x_v = 1$を指定します。
まずは、定義式から確率を計算します。
# 定義式により確率を計算 prob <- prod(phi_v^x_v) prob
## [1] 0.4
カテゴリ分布の定義式
で計算します。
対数をとった定義式から確率を計算します。
# 対数をとった定義式により確率を計算 log_prob <- sum(x_v * log(phi_v)) prob <- exp(log_prob) prob; log_prob
## [1] 0.4 ## [1] -0.9162907
対数をとった定義式
を計算します。計算結果の指数をとると確率が得られます。
指数と対数の性質より$\exp(\log x) = x$です。
次は、関数を使って確率を計算します。
多項分布の確率関数dmultinom()を使って計算します。
# 多項分布の関数により確率を計算 prob <- dmultinom(x = x_v, size = 1, prob = phi_v) prob
## [1] 0.4
試行回数の引数sizeに1を指定することで、カテゴリ分布の確率を計算できます。
出現頻度の引数xにx_v、出現確率の引数probにphi_vを指定します。
log = TRUEを指定すると対数をとった確率を返します。
# 多項分布の対数をとった関数により確率を計算 log_prob <- dmultinom(x = x_v, size = 1, prob = phi_v, log = TRUE) prob <- exp(log_prob) prob; log_prob
## [1] 0.4 ## [1] -0.9162907
計算結果の指数をとると確率が得られます。
最後に、スライス機能を使って確率を取り出します。
# インデックスにより確率を抽出 v <- which(x_v == 1) prob <- phi_v[v] prob
## [1] 0.4
which()を使って、x_vから値が1の要素のインデックスを検索してvとします。
phi_vのv番目の要素を抽出します。
統計量の計算
カテゴリ分布の平均と分散を計算します。
クラス$v$の平均を計算します。
# クラス番号を指定 v <- 1 # 平均を計算 E_x <- phi_v[v] E_x
## [1] 0.2
カテゴリ分布の平均は、次の式で計算できます。
クラス$v$の分散を計算します。
# 分散を計算 V_x <- phi_v[v] * (1 - phi_v[v]) V_x
## [1] 0.16
カテゴリ分布の分散は、次の式で計算できます。
グラフの作成
ggplot2パッケージを利用してカテゴリ分布のグラフを作成します。
カテゴリ分布の確率変数がとり得るクラス$v$と対応する確率をデータフレームに格納します。
# パラメータを指定 phi_v <- c(0.2, 0.4, 0.1, 0.3) # クラス数を取得 V <- length(phi_v) # カテゴリ分布の情報を格納 prob_df <- tidyr::tibble( v = 1:V, # クラス probability = phi_v # 確率 ) head(prob_df)
## # A tibble: 4 x 2 ## v probability ## <int> <dbl> ## 1 1 0.2 ## 2 2 0.4 ## 3 3 0.1 ## 4 4 0.3
$\mathbf{x}$によって表されるクラス番号1:Vと、各クラスに対応する確率phi_vをデータフレームに格納します。
カテゴリ分布のグラフを作成します。
# カテゴリ分布のグラフを作成 ggplot(data = prob_df, mapping = aes(x = v, y = probability)) + # データ geom_bar(stat = "identity", position = "dodge", fill = "#00A968") + # 棒グラフ scale_x_continuous(breaks = 0:V, labels = 0:V) + # x軸目盛 labs(title = "Categorical Distribution", subtitle = paste0("phi=(", paste0(phi_v, collapse = ", "), ")")) # ラベル
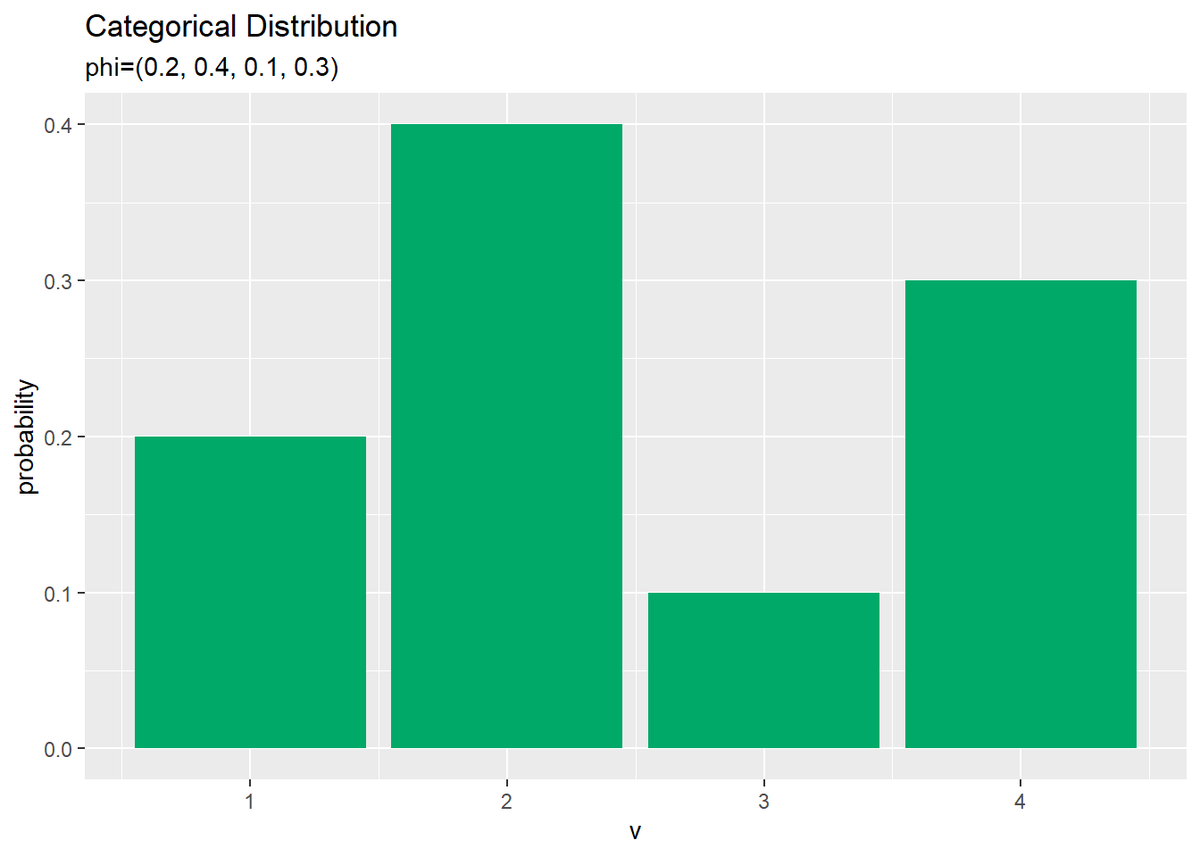
パラメータの値そのままですが、これがカテゴリ分布のグラフです。
パラメータと分布の形状の関係
続いて、パラメータ$\phi_v$の値を少しずつ変更して、分布の変化をアニメーションで確認します。
・作図コード(クリックで展開)
# 作図用のphi_1の値を作成 phi_vals <- seq(from = 0, to = 1, by = 0.01) # クラス数を指定 V <- 3 # phiの値ごとに分布を計算 anime_prob_df <- tidyr::tibble() for(phi in phi_vals) { # phi_1以外の割り当てを指定 phi_v <- c(phi, (1 - phi) * 0.6, (1 - phi) * 0.4) # カテゴリ分布の情報を格納 tmp_prob_df <- tidyr::tibble( v = 1:V, # クラス probability = phi_v, # 確率 parameter = paste0("phi=(", paste0(round(phi_v, 2), collapse = ", "), ")") %>% as.factor() # フレーム切替用のラベル ) # 結果を結合 anime_prob_df <- rbind(anime_prob_df, tmp_prob_df) } head(anime_prob_df)
## # A tibble: 6 x 3 ## v probability parameter ## <int> <dbl> <fct> ## 1 1 0 phi=(0, 0.6, 0.4) ## 2 2 0.6 phi=(0, 0.6, 0.4) ## 3 3 0.4 phi=(0, 0.6, 0.4) ## 4 1 0.01 phi=(0.01, 0.59, 0.4) ## 5 2 0.594 phi=(0.01, 0.59, 0.4) ## 6 3 0.396 phi=(0.01, 0.59, 0.4)
$\phi_1$がとり得る値を作成してphi_valsとします。
for()ループを使ってphi_valsの値ごとにphi_vを更新して、anime_prob_dfに追加していきます。$\phi_1$以外の確率の和$1 - \phi_1$を他のクラスの確率として割り振ります。
gif画像を作成します。
# アニメーション用のカテゴリ分布を作図 anime_prob_graph <- ggplot(data = anime_prob_df, mapping = aes(x = v, y = probability)) + # データ geom_bar(stat = "identity", position = "dodge", fill = "#00A968") + # 分布 scale_x_continuous(breaks = 0:V, labels = 0:V) + # x軸目盛 gganimate::transition_manual(parameter) + # フレーム labs(title = "Categorical Distribution", subtitle = "{current_frame}") # ラベル # gif画像を作成 gganimate::animate(anime_prob_graph, nframes = length(phi_vals), fps = 100)
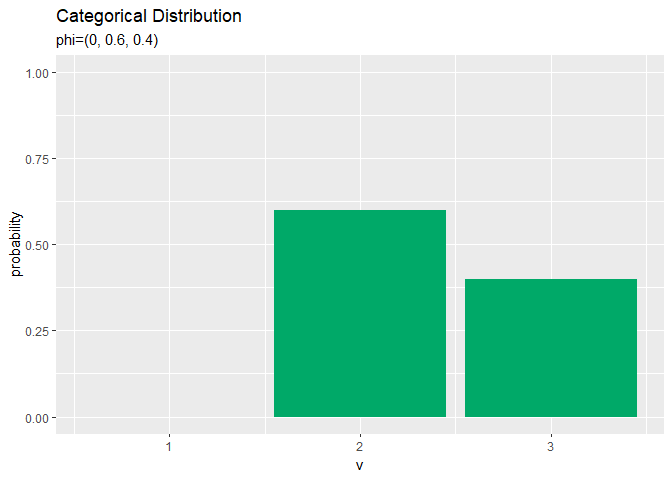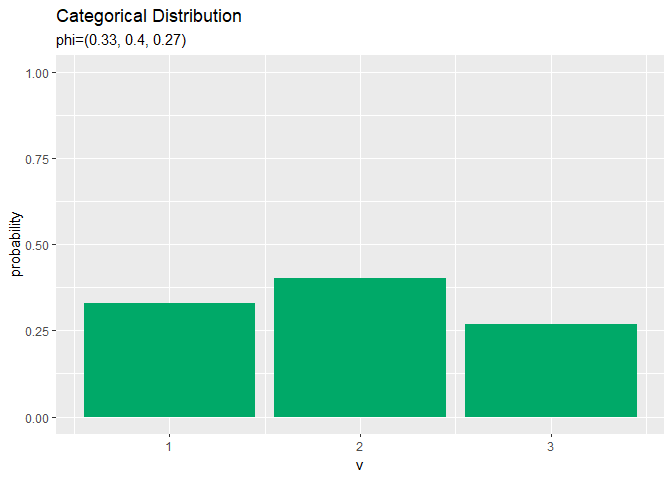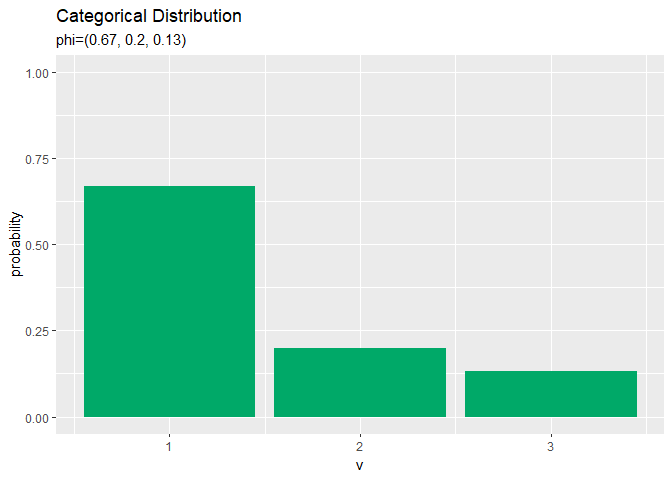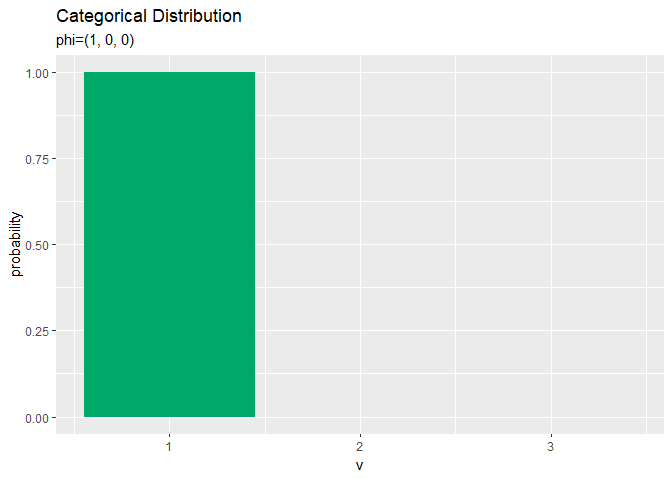
(定義のままですが、)パラメータ$\phi_1$の値が大きいほど、$x_1 = 1$となる確率が高く、他のクラスとなる確率が低いを確認できます。
乱数の生成
カテゴリ分布の乱数を生成してヒストグラムを確認します。
パラメータを指定して、カテゴリ分布に従う乱数を生成します。
# パラメータを指定 phi_v <- c(0.2, 0.4, 0.1, 0.3) # クラス数を取得 V <- length(phi_v) # データ数を指定 N <- 1000 # カテゴリ分布に従う乱数を生成 x_nv <- rmultinom(n = N, size = 1, prob = phi_v) %>% t() x_nv[1:5, ]
## [,1] [,2] [,3] [,4] ## [1,] 1 0 0 0 ## [2,] 0 1 0 0 ## [3,] 1 0 0 0 ## [4,] 1 0 0 0 ## [5,] 0 0 1 0
多項分布の乱数生成関数rmultinom()の試行回数の引数sizeに1を指定することで、カテゴリ分布に従う乱数を生成できます。
データ数(サンプルサイズ)の引数nにN、成功確率の引数probにphi_vを指定します。
各データに割り当てられたクラス番号を抽出します。
# インデックスを抽出 x_n <- which(x = t(x_nv) == 1, arr.ind = TRUE)[, "row"] x_n[1:5]
## [1] 1 2 1 1 3
which()を使って、x_nvの各行から値が1の列番号を抽出できます。ここではx_nは使いません。
サンプルの値を集計します。
# 乱数を集計して格納 freq_df <- tidyr::tibble( v = 1:V, # クラス frequency = colSums(x_nv), # 頻度 proportion = frequency / N ) head(freq_df)
## # A tibble: 4 x 3 ## v frequency proportion ## <int> <dbl> <dbl> ## 1 1 211 0.211 ## 2 2 411 0.411 ## 3 3 108 0.108 ## 4 4 270 0.27
x_nvの列ごとに和をとると、各クラスの出現頻度(各クラスが割り当てられたデータ数)を得られます。
また、得られた頻度frequencyをデータ数Nで割り、1からVの構成比を計算します。
ヒストグラムを作成します。
# サンプルのヒストグラムを作成 ggplot(data = freq_df, mapping = aes(x = v, y = frequency)) + # データ geom_bar(stat = "identity", position = "dodge", fill = "#00A968") + # 棒グラフ scale_x_continuous(breaks = 0:V, labels = 0:V) + # x軸目盛 labs(title = "Categorical Distribution", subtitle = paste0("phi=(", paste0(phi_v, collapse = ", "), ")", ", N=", N, "=(", paste0(colSums(x_nv), collapse = ", "), ")")) # ラベル
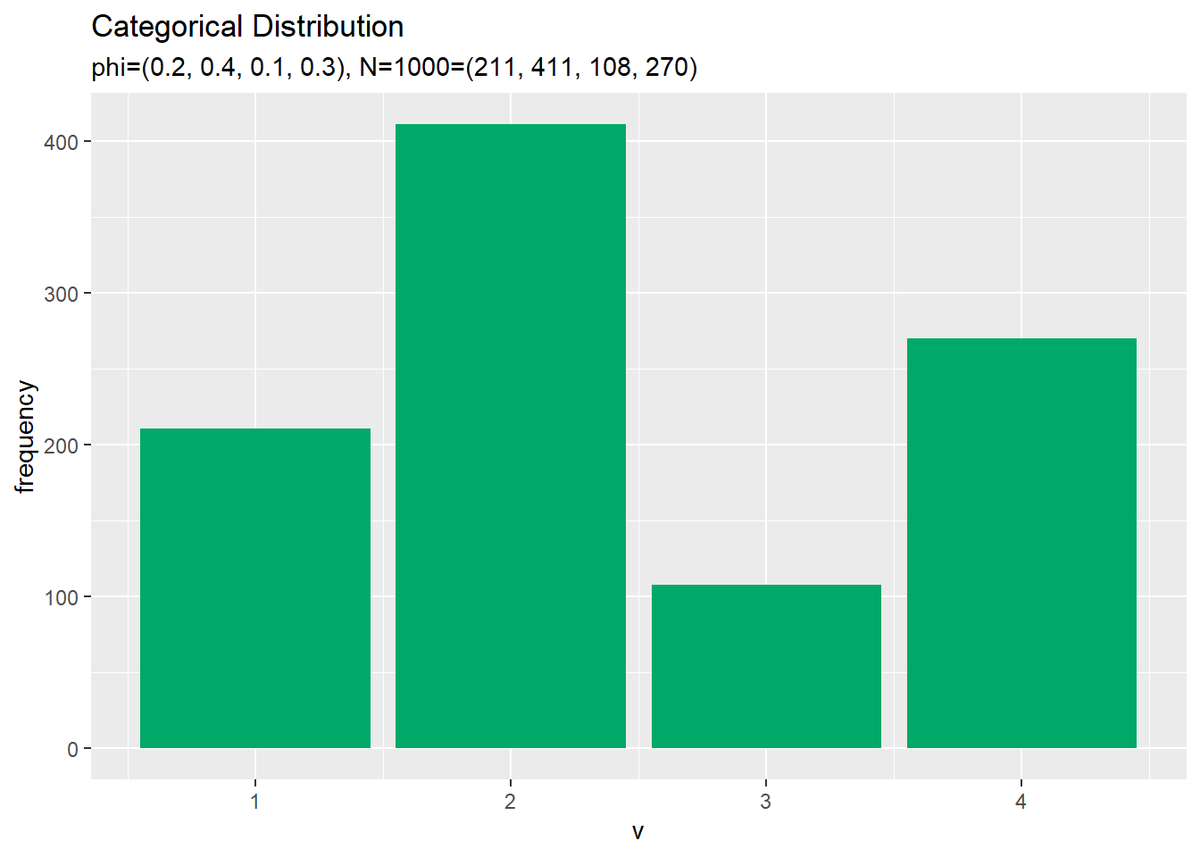
構成比を分布と重ねて描画します。
# サンプルの構成比を作図 ggplot() + geom_bar(data = freq_df, mapping = aes(x = v, y = proportion), stat = "identity", position = "dodge", fill = "#00A968") + # 構成比 geom_bar(data = prob_df, mapping = aes(x = v, y = probability), stat = "identity", position = "dodge", alpha = 0, color = "darkgreen", linetype = "dashed") + # 真の分布 scale_x_continuous(breaks = 0:V, labels = 0:V) + # x軸目盛 labs(title = "Categorical Distribution", subtitle = paste0("phi=(", paste0(phi_v, collapse = ", "), ")", ", N=", N, "=(", paste0(colSums(x_nv), collapse = ", "), ")")) # ラベル
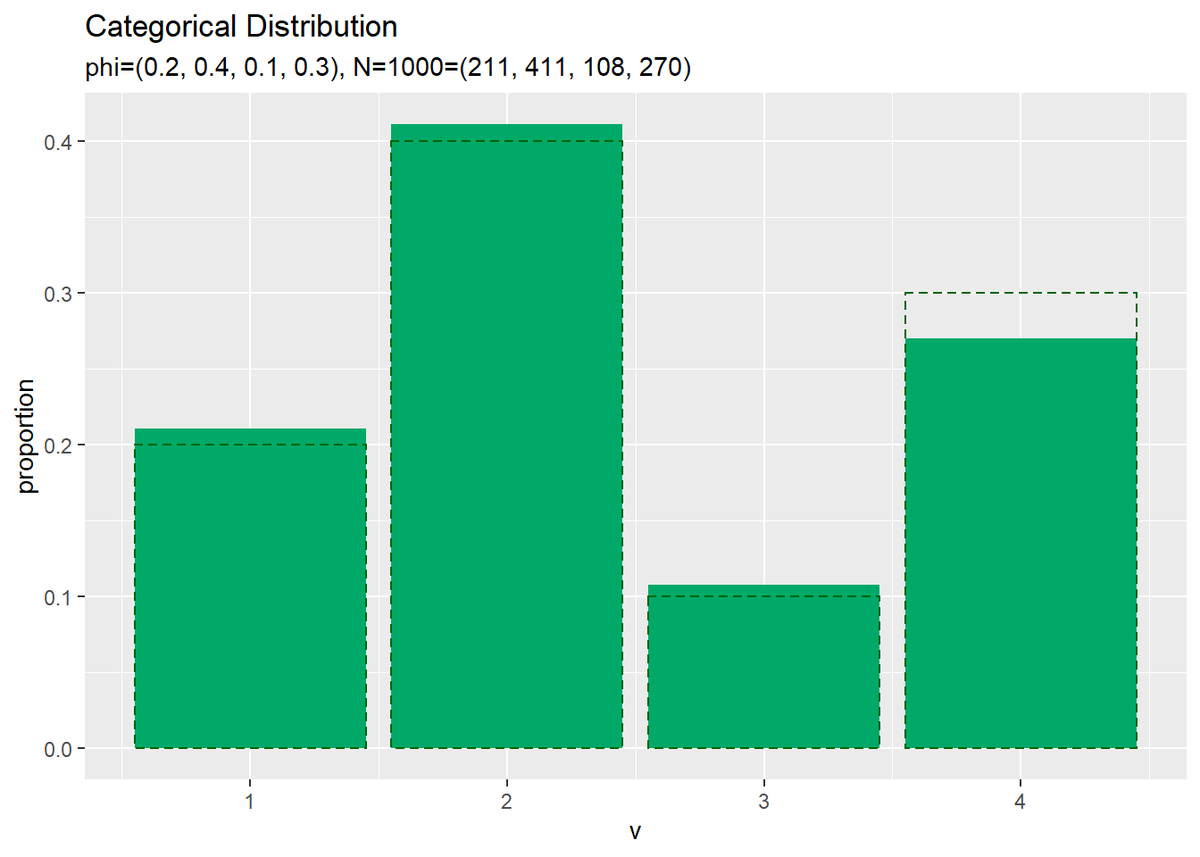
データ数が十分に増えると分布のグラフに形が近づきます。
サンプルサイズとヒストグラムの変化をアニメーションで確認します。
・作図コード(クリックで展開)
# データ数を指定 N <- 100 # 乱数を1つずつ生成 x_nv <- matrix(NA, nrow = N, ncol = V) anime_freq_df <- tidyr::tibble() anime_data_df <- tidyr::tibble() anime_prob_df <- tidyr::tibble() for(n in 1:N) { # カテゴリ分布に従う乱数を生成 x_nv[n, ] <- rmultinom(n = 1, size = 1, prob = phi_v) %>% as.vector() # ラベル用のテキストを作成 label_text <- paste0( "phi=(", paste0(phi_v, collapse = ", "), ")", ", N=", n, "=(", paste0(colSums(x_nv, na.rm = TRUE), collapse = ", "), ")" ) # n個の乱数を集計して格納 tmp_freq_df <- tidyr::tibble( v = 1:V, # クラス frequency = colSums(x_nv, na.rm = TRUE), # 頻度 proportion = frequency / n, # 割合 parameter = as.factor(label_text) # フレーム切替用のラベル ) # n番目の乱数を格納 tmp_data_df <- tidyr::tibble( v = which(x_nv[n, ] == 1), # サンプルのクラス番号 parameter = as.factor(label_text) # フレーム切替用のラベル ) # n回目のラベルを付与 tmp_prob_df <- prob_df %>% dplyr::mutate(parameter = as.factor(label_text)) # 結果を結合 anime_freq_df <- rbind(anime_freq_df, tmp_freq_df) anime_data_df <- rbind(anime_data_df, tmp_data_df) anime_prob_df <- rbind(anime_prob_df, tmp_prob_df) } head(anime_freq_df)
## # A tibble: 6 x 4 ## v frequency proportion parameter ## <int> <dbl> <dbl> <fct> ## 1 1 0 0 phi=(0.2, 0.4, 0.1, 0.3), N=1=(0, 1, 0, 0) ## 2 2 1 1 phi=(0.2, 0.4, 0.1, 0.3), N=1=(0, 1, 0, 0) ## 3 3 0 0 phi=(0.2, 0.4, 0.1, 0.3), N=1=(0, 1, 0, 0) ## 4 4 0 0 phi=(0.2, 0.4, 0.1, 0.3), N=1=(0, 1, 0, 0) ## 5 1 0 0 phi=(0.2, 0.4, 0.1, 0.3), N=2=(0, 2, 0, 0) ## 6 2 2 1 phi=(0.2, 0.4, 0.1, 0.3), N=2=(0, 2, 0, 0)
乱数を1つず生成して、結果をanime_***_dfに追加していきます。
ヒストグラムのアニメーションを作成します。
# アニメーション用のサンプルのヒストグラムを作成 anime_freq_graph <- ggplot() + # データ geom_bar(data = anime_freq_df, mapping = aes(x = v, y = frequency), stat = "identity", position = "dodge", fill = "#00A968") + # ヒストグラム geom_point(data = anime_data_df, mapping = aes(x = v, y = 0), color = "orange", size = 5) + # サンプル scale_x_continuous(breaks = 0:V, labels = 0:V) + # x軸目盛 gganimate::transition_manual(parameter) + # フレーム labs(title = "Categorical Distribution", subtitle = "{current_frame}") # ラベル # gif画像を作成 gganimate::animate(anime_freq_graph, nframes = N, fps = 100)
構成比のアニメーションを作成します。
# アニメーション用のサンプルの構成比を作図 anime_prop_graph <- ggplot() + # データ geom_bar(data = anime_freq_df, mapping = aes(x = v, y = proportion), stat = "identity", position = "dodge", fill = "#00A968") + # 構成比 geom_bar(data = anime_prob_df, mapping = aes(x = v, y = probability), stat = "identity", position = "dodge", alpha = 0, color = "darkgreen", linetype = "dashed") + # 真の分布 geom_point(data = anime_data_df, mapping = aes(x = v, y = 0), color = "orange", size = 5) + # 乱数 scale_x_continuous(breaks = 0:V, labels = 0:V) + # x軸目盛 gganimate::transition_manual(parameter) + # フレーム labs(title = "Categorical Distribution", subtitle = "{current_frame}") # ラベル # gif画像を作成 gganimate::animate(anime_prop_graph, nframes = N, fps = 100)
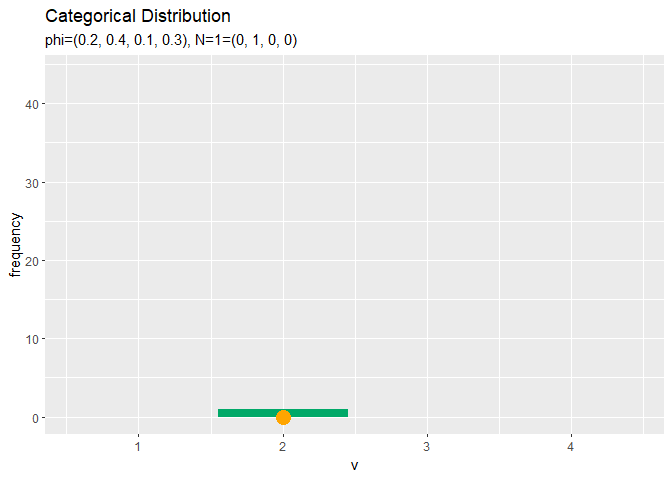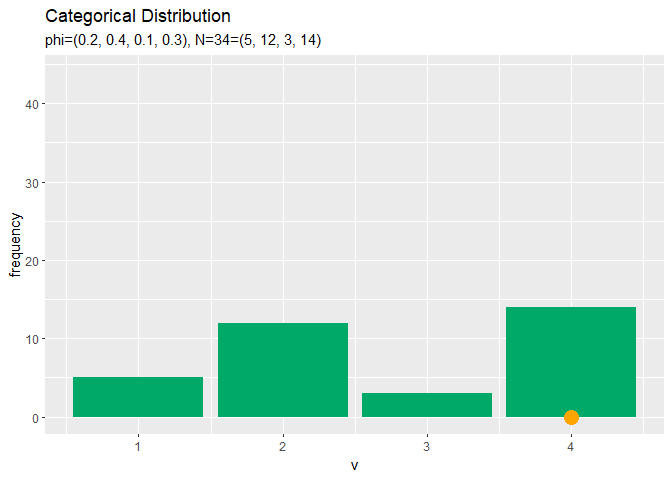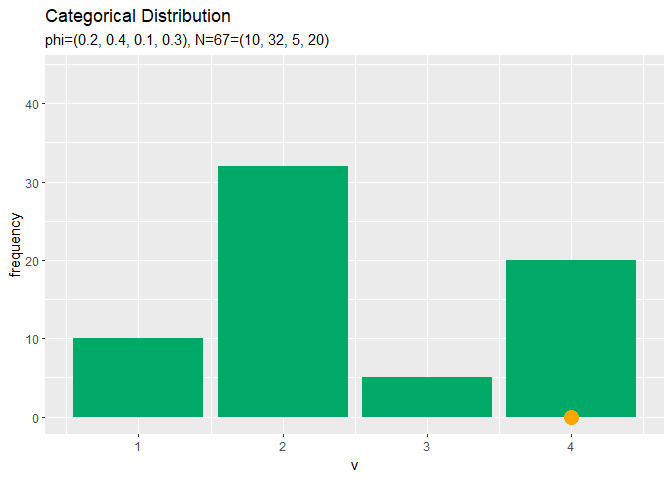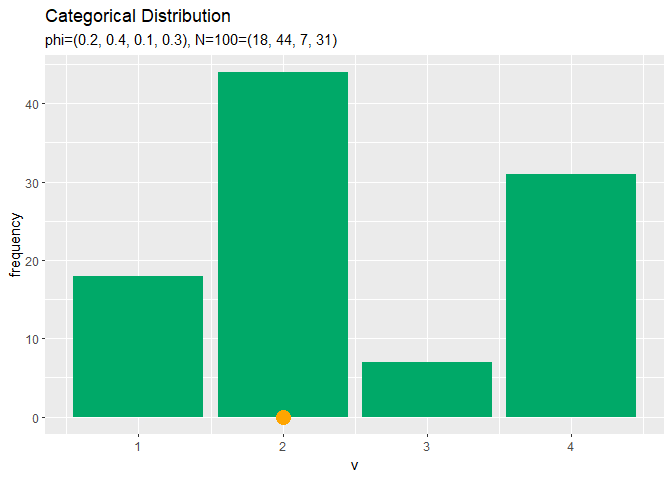
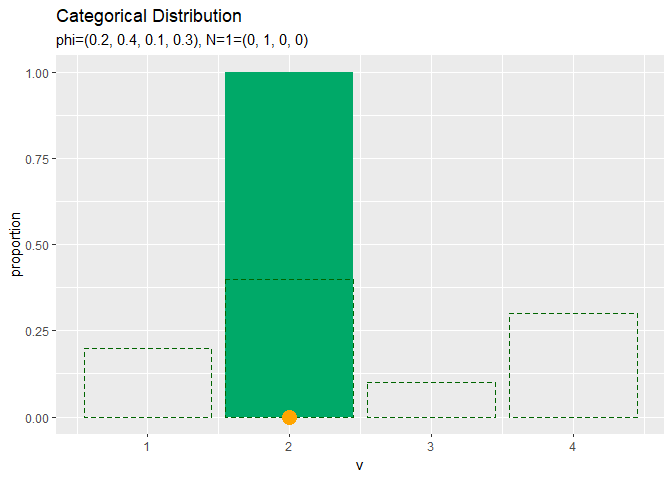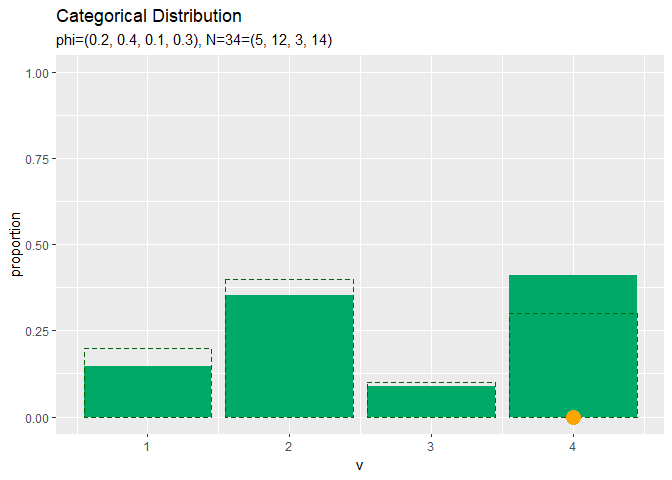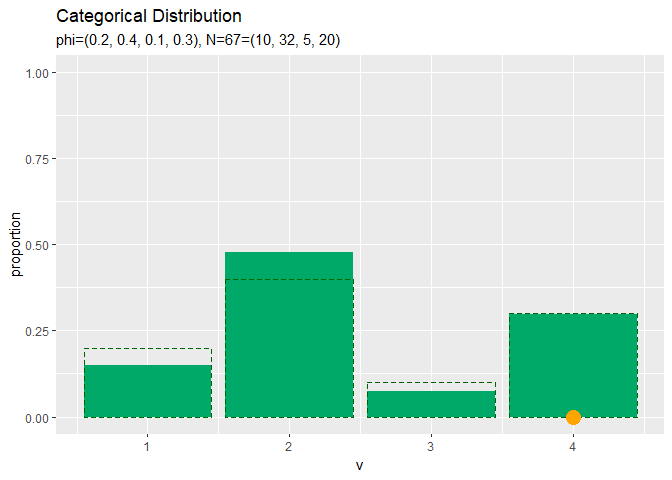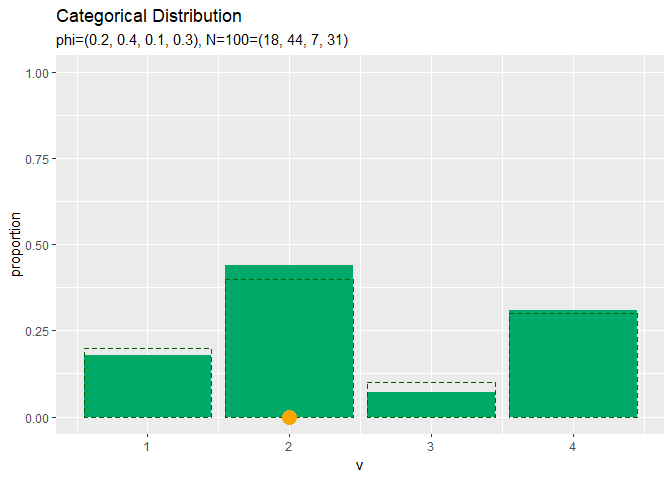
サンプルが増えるに従って、真の分布に近付いていくのを確認できます。
以上で、カテゴリ分布を確認できました。
参考文献
- 岩田具治『トピックモデル』(機械学習プロフェッショナルシリーズ)講談社,2015年.
- 須山敦志『ベイズ推論による機械学習入門』(機械学習スタートアップシリーズ)杉山将監修,講談社,2017年.
おわりに
トピックモデルと言えばカテゴリ分布とディリクレ分布!まだディリクレ分布まで結構あるけどモチベが。
加筆修正の際に青トピシリーズから独立させました。
【次の内容】