はじめに
『パターン認識と機械学習』の独学時のまとめです。一連の記事は「数式の行間埋め」または「R・Pythonでのスクラッチ実装」からアルゴリズムの理解を補助することを目的としています。本とあわせて読んでください。
この記事は、3.1.4項「正則化最小二乗法」を補足する内容です。LpノルムをPythonで作図します。
【他の節一覧】
【この節の内容】
3.1.4.0 Lpノルムの作図
3.1.4項の正則化で利用するLpノルム($L^p$ノルム)をグラフで確認します。
利用するライブラリを読み込みます。
# 3.1.4項で利用するライブラリ import numpy as np import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation
Lpノルムのグラフをアニメーションで確認するのにMatplotlibライブラリのanimationモジュールを利用します。不要であれば省略してください。
・定義式の確認
$M$次元ベクトル$\mathbf{w} = (w_1, w_2, \cdots, w_M)^{\top}$のLpノルム$\|\mathbf{w}\|_p$は、次の式で定義されます。
ベクトルを$\|$で挟んでそのベクトルのノルムを表します。$\sqrt[n]{x} = x^{\frac{1}{n}}$であり、$(\sqrt[n]{x})^n = (x^{\frac{1}{n}})^n = x$です。
本では$q$を使っていますが、(Lpノルムと呼ぶくらいなので)この記事では$p$を使うことにします。
・L1ノルム
$q = 1$のときL1ノルム($L^1$ノルム)と呼びます。L1ノルムのグラフを確認します。
$q = 1$のとき、$x^{\frac{1}{1}} = x$なので累乗根$\sqrt{}$が外れ、次の式になります。
つまり、L1ノルム$\|\mathbf{w}\|_1$は、$\mathbf{w}$の各要素の絶対値$|w_j|$の総和です。
作図用の$\mathbf{w}$の点を作成して、L1ノルムを計算します。2次元のグラフで描画するため$M = 2$とします。
# 値を指定 p = 1 # wの値を指定 w_vals = np.arange(-10.0, 10.1, 0.1) # 作図用のwの点を作成 W1, W2 = np.meshgrid(w_vals, w_vals) # Lpのノルムを計算 Lp = (np.abs(W1)**p + np.abs(W2)**p)**(1.0 / p) # 確認 print(Lp) print(Lp.shape)
[[20. 19.9 19.8 ... 19.8 19.9 20. ]
[19.9 19.8 19.7 ... 19.7 19.8 19.9]
[19.8 19.7 19.6 ... 19.6 19.7 19.8]
...
[19.8 19.7 19.6 ... 19.6 19.7 19.8]
[19.9 19.8 19.7 ... 19.7 19.8 19.9]
[20. 19.9 19.8 ... 19.8 19.9 20. ]]
(201, 201)
グラフとして描画する$w_j$の値をnp.arange()で作成してw_valsとします。処理が重い場合は、この値を調整してください。
w_valsとして作成した値に対して、全ての組み合わせを持つように$\mathbf{w} = (w_1, w_2)$の値をnp.meshgrid()で作成します。W1, W2の各要素が、1つの点$\mathbf{w}$に対応します。
絶対値はnp.abs()で計算できます。
L1ノルムの3Dグラフを作成します。
# Lpノルムの3Dグラフを作成 fig = plt.figure(figsize=(8, 8)) ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_surface(W1, W2, Lp, cmap='jet') # 曲面図 ax.contour(W1, W2, Lp, cmap='jet', offset=0) # 等高線図 ax.set_xlabel('$w_1$') ax.set_ylabel('$w_2$') ax.set_zlabel('$||w||_p$') ax.set_title('p=' + str(np.round(p, 1)), loc='left') fig.suptitle('$||w||_p = {}^p\sqrt{\sum_{j=1}^M |w_j|^p}$') #ax.view_init(elev=90, azim=270) # 表示アングル plt.show()
axes.plot_surface()で3Dプロットを描画できます。


右の図は真上から見た図です。
L1ノルムの等高線グラフを作成します。
# Lpノルムの2Dグラフを作成 plt.figure(figsize=(9, 8)) plt.contour(W1, W2, Lp, cmap='jet') # 等高線図 #plt.contour(W1, W2, Lp, cmap='jet', levels=1) # 等高線図:(値を指定) #plt.contourf(W1, W2, Lp, cmap='jet') # 塗りつぶし等高線図 plt.xlabel('$w_1$') plt.ylabel('$w_2$') plt.title('p=' + str(np.round(p, 1)), loc='left') plt.suptitle('$||w||_p = {}^p\sqrt{\sum_{j=1}^M |w_j|^p}$') plt.colorbar(label='$||w||_p$') plt.grid() plt.gca().set_aspect('equal') plt.show()
pyplot.contour()で等高線を描画できます。levels引数に等高線を描く値を指定できます。
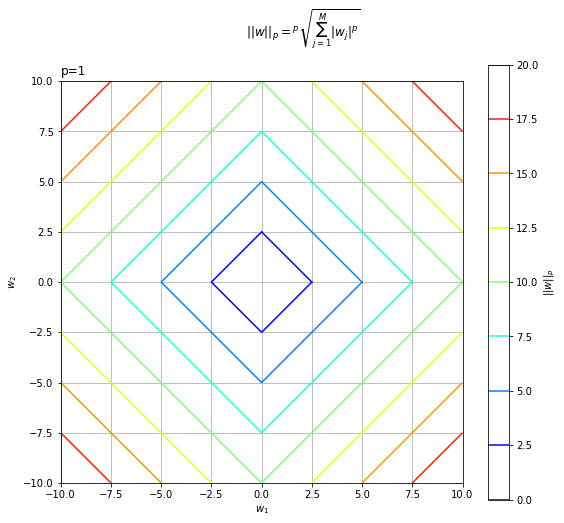

右の図は、L1ノルムの値(z軸の値)が1の線だけ描画した図です。
L1ノルムは、$M = 2$のとき3Dグラフを水平に切断した断面を上から見ると、ひし形になります。
・L2ノルム
$p = 2$のときL2ノルム($L^2$ノルム)と呼びます。L2ノルムのグラフを確認します。
$p = 2$のとき、$|x|^2 = x^2$なので絶対値が外れ、次の式になります。
つまり、L2ノルム$\|\mathbf{w}\|_2$は、$\mathbf{w}$の各要素の二乗和の平方根です。
$p = 2$の3Dグラフと等高線グラフを確認します。pに2を代入すると、先ほどのコードで処理できます。
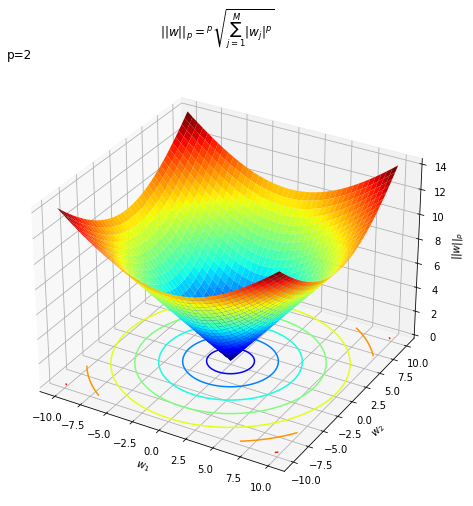
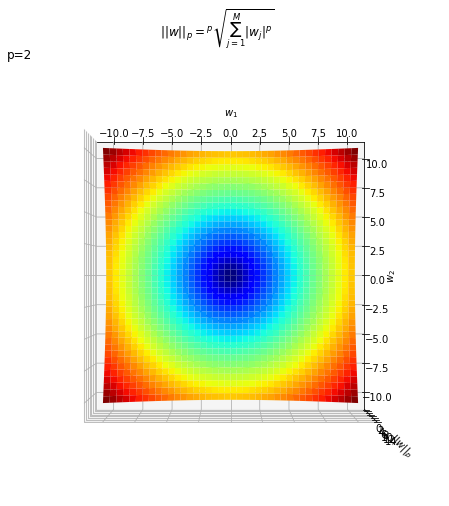
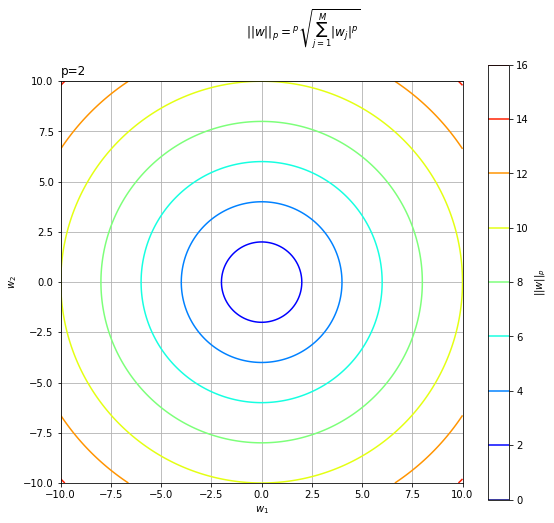
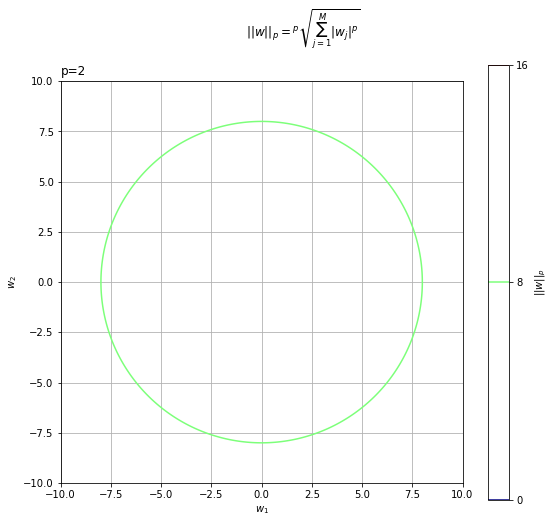
L2ノルムは、$M = 2$のとき3Dグラフを水平に切断した断面を上から見ると、円形になります。
・正則化項
正則化では累乗根の計算を行わず、次の式で計算します。
正則化項のグラフも確認しましょう。
# 値を指定 p = 1 # 正則化項を計算 E_W = (np.abs(W1)**p + np.abs(W2)**p) / p # 正則化項の3Dグラフを作成 fig = plt.figure(figsize=(8, 8)) ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_surface(W1, W2, E_W, cmap='jet') # 曲面図 ax.contour(W1, W2, Lp, cmap='jet', offset=0) # 等高線図 ax.set_xlabel('$w_1$') ax.set_ylabel('$w_2$') ax.set_zlabel('$E_W(w)$') ax.set_title('p=' + str(np.round(p, 1)), loc='left') fig.suptitle('$E_W(w) = \\frac{1}{p} \sum_{j=1}^M |w_j|^p$') #ax.view_init(elev=90, azim=270) # 表示アングル plt.show()
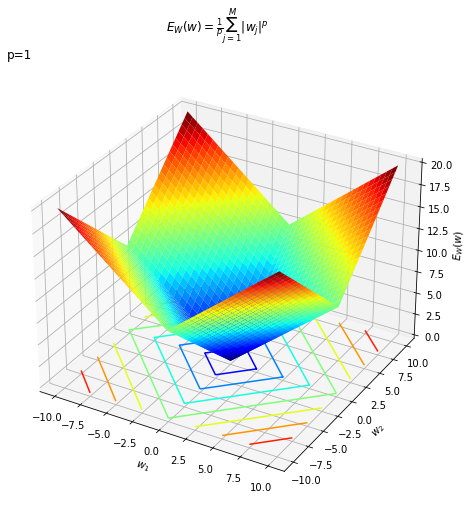

値は変わりますが、形状は変化していません。
・おまけ:pとグラフの形状の関係
最後に、$p$の値とグラフの形状の関係をアニメーションで確認します。
・作図コード(クリックで展開)
animationモジュールを利用して、3Dグラフと等高線グラフのアニメーション(gif画像)を作成します。
3Dプロットのアニメーションを作成します。
# 使用するpの値を指定 p_vals = np.arange(0.1, 10.1, 0.1) # 図を初期化 fig = plt.figure(figsize=(8, 8)) ax = fig.add_subplot(projection='3d') # 3D用の設定 fig.suptitle('Lp-Norm', fontsize=20) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i回目の値を取得 p = p_vals[i] # Lpノルムを計算 Lp = (np.abs(W1)**p + np.abs(W2)**p)**(1.0 / p) # Lpノルムの3Dグラフを作成 ax.plot_surface(W1, W2, Lp, cmap='jet') # 曲面図 ax.contour(W1, W2, Lp, cmap='jet', offset=0) # 等高線図 ax.set_xlabel('$w_1$') ax.set_ylabel('$w_2$') ax.set_zlabel('$||w||_p$') ax.set_title('p=' + str(np.round(p, 1)), loc='left') # gif画像を作成 anime_norm3d = FuncAnimation(fig, update, frames=len(p_vals), interval=100) # gif画像を保存 anime_norm3d.save('ch3_1_4_LpNorm_3d.gif')
等高線グラフのアニメーションを作成します。
# 図を初期化 fig = plt.figure(figsize=(8, 8)) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i回目の値を取得 p = p_vals[i] # Lpノルムを計算 Lp = (np.abs(W1)**p + np.abs(W2)**p)**(1.0 / p) # Lpノルムの2Dグラフを作成 plt.contour(W1, W2, Lp, cmap='jet') # 等高線図 #plt.contourf(W1, W2, Lp, cmap='jet') # 塗りつぶし等高線図 plt.xlabel('$w_1$') plt.ylabel('$w_2$') plt.title('p=' + str(np.round(p, 1)), loc='left') plt.suptitle('Lp-Norm', fontsize=20) plt.grid() plt.axes().set_aspect('equal') # gif画像を作成 anime_norm2d = FuncAnimation(fig, update, frames=len(p_vals), interval=100) # gif画像を保存 anime_norm2d.save('ch3_1_4_LpNorm_2d.gif')


この項では、Lpノルムを確認しました。次項では、L1ノルムとL2ノルムを利用して正則化を行います。
参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上下』,丸善出版,2012年.
おわりに
とりあえず3Dでプロットした方がいいのをPythonでやっていきます。