はじめに
『パターン認識と機械学習』の独学時のまとめです。一連の記事は「数式の行間埋め」または「R・Pythonでの実装」からアルゴリズムの理解を補助することを目的としています。本とあわせて読んでください。
この記事は、10.1.3項の内容です。平均と精度が未知の1次元ガウス分布(正規分布)に対する変分推論(変分ベイズ)をR言語で実装します。
【数式読解編】
【他の節一覧】
【この節の内容】
・Rで実装
人工データを用いて、簡単な変分推論を行ってみましょう。
利用するパッケージを読み込みます。
# 10.1.3で利用するパッケージ library(tidyverse)
・真の分布の設定
まずは、真の分布を設定します。この項では、真の分布を平均$\mu$、精度$\tau$の1次元ガウス分布$\mathcal{N}(x | \mu, \tau^{-1})$とします。
真の分布のパラメータを設定します。
# 真の平均パラメータを指定 mu_truth <- 5 # 真の精度パラメータを指定 tau_truth <- 0.5
真の平均パラメータ$\mu$をmu_truthとして値を指定します。
真の精度パラメータ$\tau$をtau_truthとして0より大きい値$\tau > 0$を指定します。精度は分散の逆数$\sigma^2 = \frac{1}{\tau}$です。値が大きいほど、散らばり具合が小さくなります。
この例では、この2つのパラメータの値を分布推定するのが目的です。
真の分布をグラフで確認しましょう。作図用の点を作成します。
# 作図用のxの値を作成 x_vec <- seq( mu_truth - 4 * sqrt(1 / tau_truth), mu_truth + 4 * sqrt(1 / tau_truth), length.out = 1000 )
作図用に、ガウス分布に従う変数$x$がとり得る値をseq()で作成してx_vecとします。この例では、平均値を中心に標準偏差の4倍を範囲とします。length.out引数を使うと指定した要素数で等間隔に切り分けます。by引数を使うと切り分ける間隔を指定できます。処理が重い場合は、この値を調整してください。
真の分布を計算します。
# 真の分布を計算 model_df <- tibble( x = x_vec, density = dnorm(x = x, mean = mu_truth, sd = sqrt(1 / tau_truth)) )
x_vecの値ごとに確率密度を計算します。1次元ガウス分布の確率密度は、dnorm()で計算できます。値の引数xにx_vec、平均の引数meanにmu_truth、標準偏差の引数sdにtauの逆数の平方根sqrt(1 / tau_truth)を指定します。精度$\tau$は分散の逆数なので、その平方根が真の標準偏差$\sigma = \sqrt{\frac{1}{\tau}}$になります。
作成したデータフレームは次のようになります。
# 確認 head(model_df)
## # A tibble: 6 x 2 ## x density ## <dbl> <dbl> ## 1 -0.657 0.0000946 ## 2 -0.646 0.0000977 ## 3 -0.634 0.000101 ## 4 -0.623 0.000104 ## 5 -0.612 0.000108 ## 6 -0.600 0.000111
真の分布を作図します。
# 真のを作図 ggplot(model_df, aes(x = x, y = density)) + geom_line(color = "blue") + # 真の分布 labs(title = "Gaussian Distribution", subtitle = paste0("mu=", mu_truth, ", tau=", tau_truth))
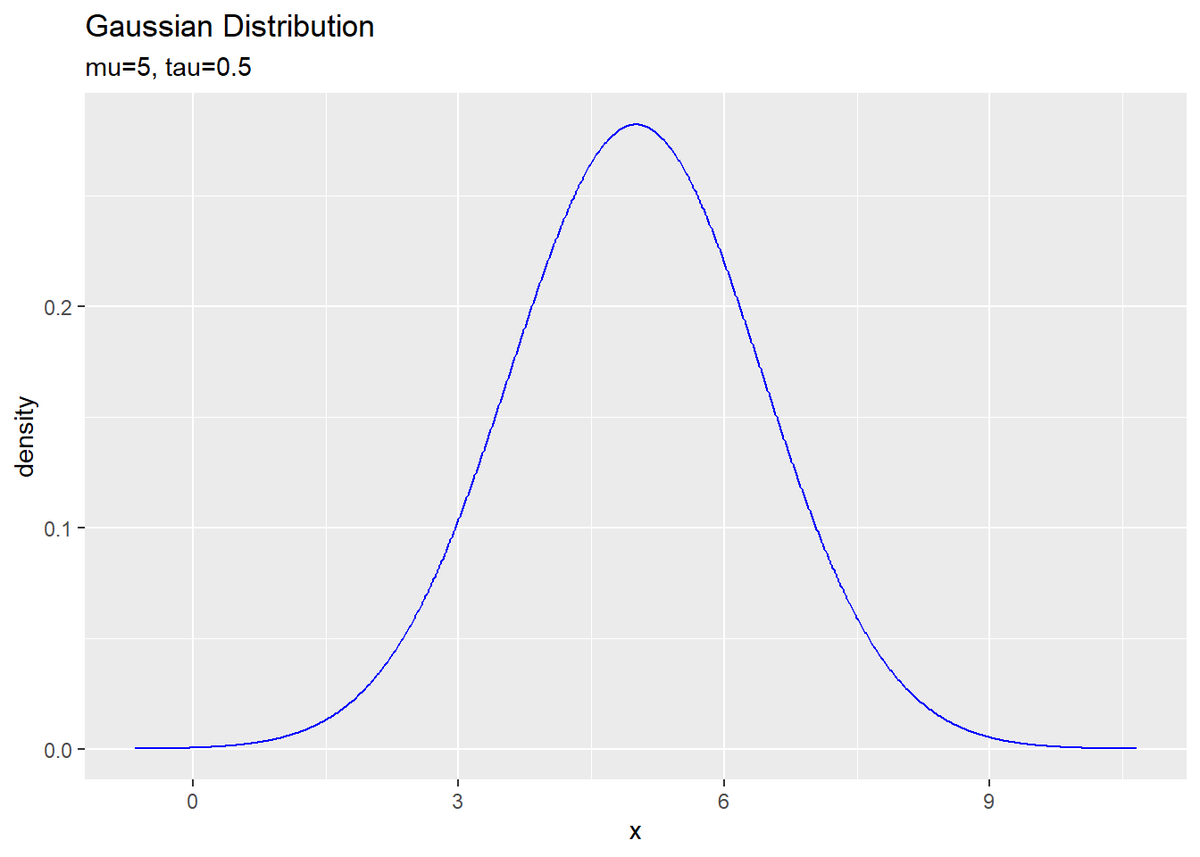
・観測データの生成
続いて、設定した真の分布に従って観測データ$\mathcal{D} = \{x_1, x_2, \cdots, x_N\}$を生成します。
ガウス分布に従う$N$個のデータをランダムに生成します。
# (観測)データ数を指定 N <- 50 # ガウス分布に従うデータを生成 x_n <- rnorm(n = N, mean = mu_truth, sd = sqrt(1 / tau_truth))
生成するデータ数$N$をNとして値を指定します。
ガウス分布に従う乱数は、rnorm()で生成できます。データ数の引数nにNを指定します。他の引数についてはdnorm()と同じです。生成したN個のデータをx_nとします。
観測したデータをグラフで確認しましょう。作図用のデータフレームを作成します。
# 観測データをデータフレームに格納 data_df <- tibble(x_n = x_n) # 確認 head(data_df)
## # A tibble: 6 x 1 ## x_n ## <dbl> ## 1 4.46 ## 2 5.56 ## 3 3.76 ## 4 3.48 ## 5 4.76 ## 6 6.16
観測データのヒストグラムを作成します。
# 観測データのヒストグラムを作成 ggplot() + geom_histogram(data = data_df, aes(x = x_n), binwidth = 0.5) + # 観測データ:(度数) #geom_histogram(data = data_df, aes(x = x_n, y = ..density..), binwidth = 1) + # 観測データ:(相対度数) #geom_line(data = model_df, aes(x = x, y = density), # color = "red", linetype = "dashed") + # 真の分布:(相対度数用) labs(title = "Gaussian Distribution", subtitle = paste0("N=", N, ", mu=", mu_truth, ", tau=", tau_truth), x = "x")
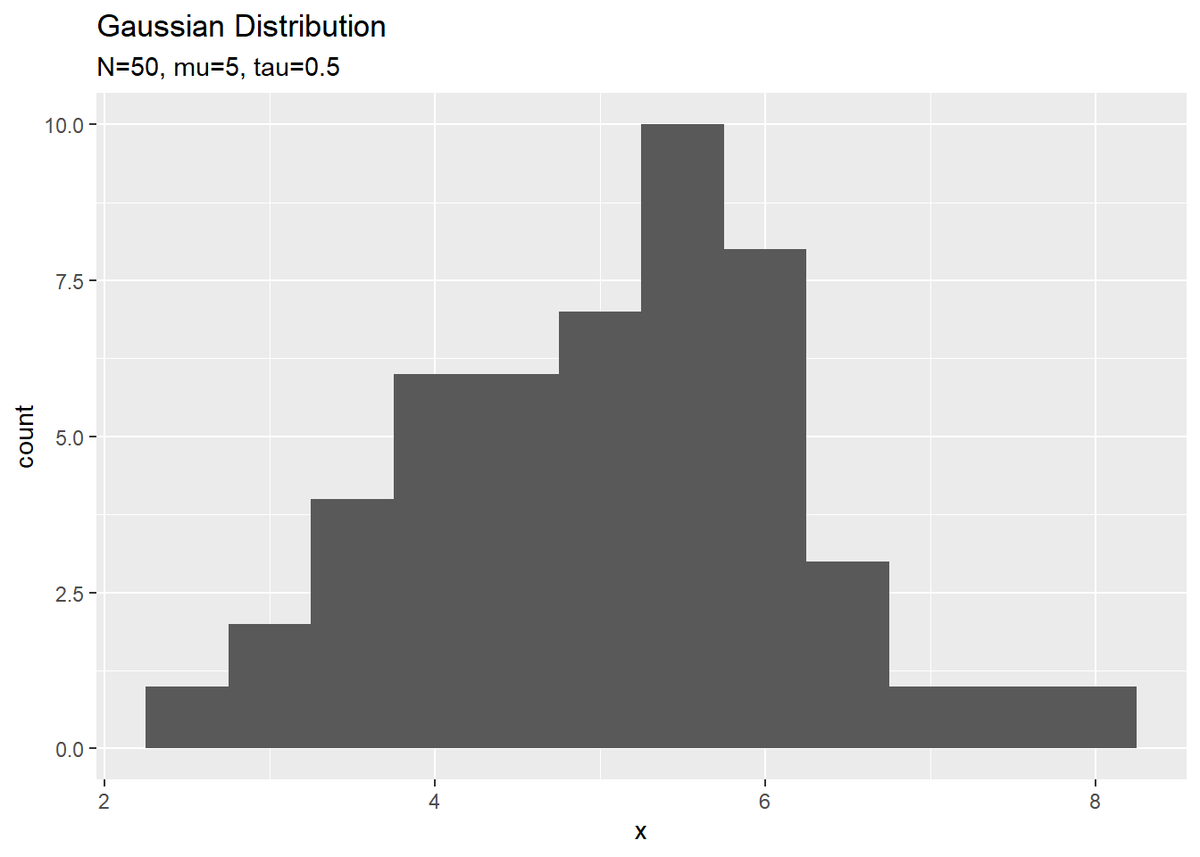
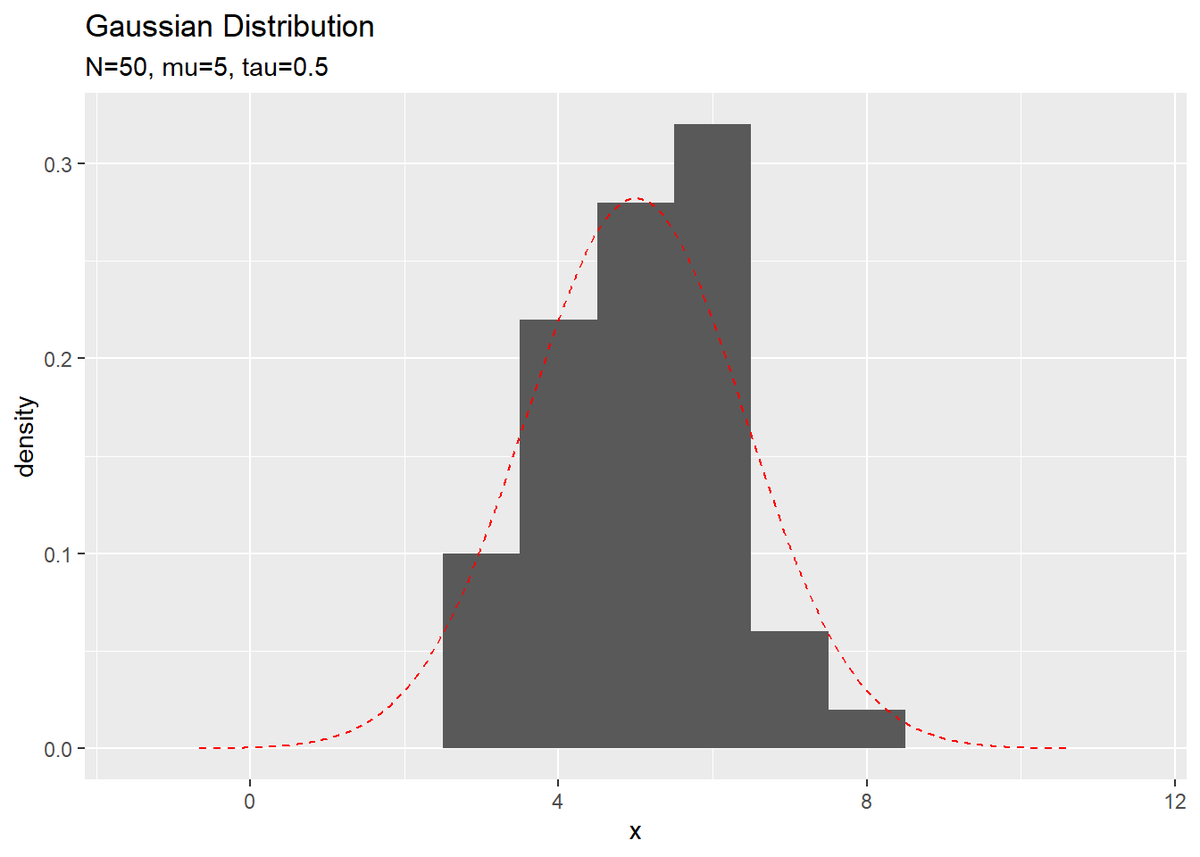
左の図のy軸はデータ数です。カウントする間隔はbinwidthで調整できます。右の図のy軸は相対度数です。y = ..density..を指定すると相対度数のヒストグラムになります。
・事前分布の設定
次に、尤度に対する共役事前分布を設定します。1次元ガウス分布の平均・精度パラメータ$\mu,\ \tau$の同時事前分布$p(\mu, \tau)$として、ガウス-ガンマ分布$\mathrm{NG}(\mu, \tau | \mu_0, \lambda_0, a_0, b_0)$を設定します。
$\mu$と$\tau$の事前分布のパラメータ(超パラメータ)を指定します。
# muの事前分布のパラメータを指定 mu_0 <- 0 lambda_0 <- 1 # tauの事前分布のパラメータを指定 a_0 <- 1 b_0 <- 1
$\mu$の事前分布$\mathcal{N}(\mu | \mu_0, (\lambda_0 \tau)^{-1})$の平均パラメータ$\mu_0$と精度パラメータの係数$\lambda_0$をそれぞれmu_0, lambda_0として$\lambda_0 > 0$の値を指定します。
$\tau$の事前分布$\mathrm{Gam}(\tau | a_0, b_0)$のパラメータ$a_0,\ b_0$をa_0, b_0として$a_0 > 0,\ b_0 > 0$の値を指定します。
$\mu,\ \tau$の事前分布をグラフで確認しましょう。作図用の点を作成します。
# 作図用のmuの値を作成 mu_vec <- seq( mu_truth - 4 * sqrt(1 / tau_truth), mu_truth + 4 * sqrt(1 / tau_truth), length.out = 500 ) # 作図用のtauの値を作成 tau_vec <- seq(0, tau_truth + 2, length.out = 500)
1次元ガウス分布に従う変数$\mu$がとり得る値を作成してmu_vecとします。この例では、真の平均値を中心に真の標準偏差の4倍を範囲とします。
ガンマ分布に従う変数$\tau$がとり得る値を作成してtau_vecとします。この例では、0からtau + 2を範囲とします。
格子状の点を作成します。
# 作図用の点を作成 mu_tau_point_mat <- cbind( mu = rep(mu_vec, times = length(tau_vec)), tau = rep(tau_vec, each = length(mu_vec)) )
mu_vecとtau_vecの要素の全ての組み合わせを持つようにマトリクスを作成してmu_tau_point_matとします。これは、ガウス-ガンマ分布の確率密度を等高線図にする際に格子状の点(2軸の全ての値が直交する点)を渡す必要があるためです。
作成した$\mu$と$\tau$の点は次のようになります。
# 確認 mu_tau_point_mat[1:5, ]
## mu tau ## [1,] -0.6568542 0 ## [2,] -0.6341815 0 ## [3,] -0.6115087 0 ## [4,] -0.5888360 0 ## [5,] -0.5661632 0
1列目が$\mu$、2列目が$\tau$の値です。
$\mu,\ \tau$の事前分布を計算します。
# 同時事前分布を計算 prior_df <- tibble( mu = mu_tau_point_mat[, 1], tau = mu_tau_point_mat[, 2], N_dens = dnorm(x = mu, mean = mu_0, sd = sqrt(1 / lambda_0 / tau)), # muの事前分布 Gam_dens = dgamma(x = tau, shape = a_0, rate = b_0), # tauの事前分布 density = N_dens * Gam_dens )
ガウス-ガンマ分布の確率密度は、次のガウス分布とガンマ分布の確率密度の積です。
真の分布のときと同様に、ガウス分布の確率密度をdnorm()で計算します。引数xには格子状の点に変換した$\mu$の値mu_tau_point_mat[, 1]を指定します。また、標準偏差は$\sqrt{\frac{1}{\lambda_0 \tau}}$です。$\tau$として格子状の点に変換した$\tau$の値mu_tau_point_mat[, 2]を使います。
ガンマ分布の確率密度は、dgamma()で計算できます。値の引数xにmu_tau_point_mat[, 2]、パラメータの引数shapeにa_0、rateにb_0を指定します。
作成したデータフレームは次のようになります。
# 確認 head(prior_df)
## # A tibble: 6 x 5 ## mu tau N_dens Gam_dens density ## <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 -0.657 0 0 1 0 ## 2 -0.634 0 0 1 0 ## 3 -0.612 0 0 1 0 ## 4 -0.589 0 0 1 0 ## 5 -0.566 0 0 1 0 ## 6 -0.543 0 0 1 0
$\mu,\ \tau$の事前分布を作図します。
# 真のパラメータをデータフレームに格納 true_params_df <- tibble(mu = mu_truth, tau = tau_truth) # 事前分布を作図 ggplot() + geom_contour(data = prior_df, aes(x = mu, y = tau, z = density, color = ..level..)) + # 事前分布 geom_point(data = true_params_df, aes(x = mu, y = tau), color = "red", shape = 4, size = 5) + # 真の値 labs(title = "Gaussian-Gamma Distribution", subtitle = paste0("mu_0=", mu_0, ", lambda_0=", lambda_0, ", a_0=", a_0, ", b_0=", b_0), x = expression(mu), y = expression(tau))
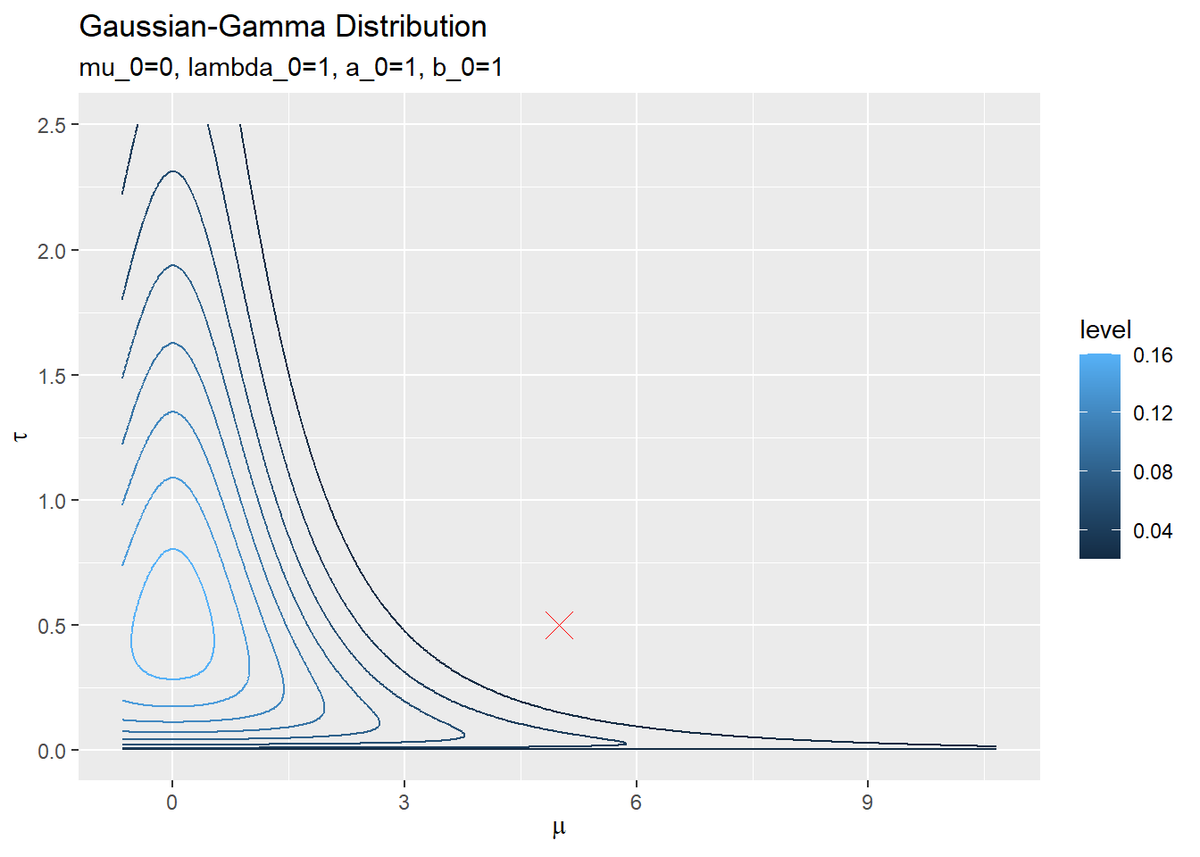
等高線図はgeom_contour()で描画します。また、真のパラメータをデータフレームに格納して、事前分布と重ねてプロットしています。
・真の事後分布の計算
この項では、変分推論により事後分布の近似分布$q(\mu, \tau)$を求めます。ただし、この問題は解析的に求められます。解析的に求めた真の事後分布$p(\mu, \tau | \mathcal{D})$を確認します。事後分布もガウス-ガンマ分布$\mathrm{NG}(\mu, \tau | \hat{\mu}, \hat{\lambda}, \hat{a}, \hat{b})$になります。
$\mu$の真の事後分布のパラメータを計算します。
# muの真の事後分布のパラメータを計算 lambda_hat <- lambda_0 + N mu_hat <- (lambda_0 * mu_0 + sum(x_n)) / lambda_hat
解析的に求めた$\mu$の事後分布の平均パラメータ$\hat{\mu}$、精度パラメータの係数$\hat{\lambda}$を次の式で計算します。
計算結果は次のようになります。
# 確認
mu_hat
lambda_hat
## [1] 4.976428 ## [1] 51
$\tau$の真の事後分布のパラメータを計算します。
# lambdaの真の事後分布のパラメータを計算 a_hat <- a_0 + 0.5 * N b_hat <- b_0 + 0.5 * (sum(x_n^2) + lambda_0 * mu_0^2 - lambda_hat * mu_hat^2)
解析的に求めた$\tau$の事後分布のパラメータ$\hat{a},\ \hat{b}$を次の式で計算します。
計算結果は次のようになります。
# 確認
a_hat
b_hat
## [1] 26 ## [1] 47.89597
$\mu,\ \tau$の真の事後分布を作図します。
# 真の同時事後分布を計算 true_posterior_df <- tibble( mu = mu_tau_point_mat[, 1], tau = mu_tau_point_mat[, 2], N_dens = dnorm(x = mu, mean = mu_hat, sd = sqrt(1 / lambda_hat / tau)), # muの真の事後分布 Gam_dens = dgamma(x = tau, shape = a_hat, rate = b_hat), # tauの真の事後分布 density = N_dens * Gam_dens ) # 真の事後分布を作図 ggplot() + geom_contour(data = true_posterior_df, aes(x = mu, y = tau, z = density, color = ..level..)) + # 真の事後分布 geom_point(data = true_params_df, aes(x = mu, y = tau), color = "red", shape = 4, size = 5) + # 真の値 labs(title = "Gaussian-Gamma Distribution", subtitle = paste0("N=", N, ", mu_hat=", round(mu_hat, 1), ", lambda_hat=", lambda_hat, ", a_hat=", a_hat, ", b_hat=", round(b_hat, 1)), x = expression(mu), y = expression(tau))
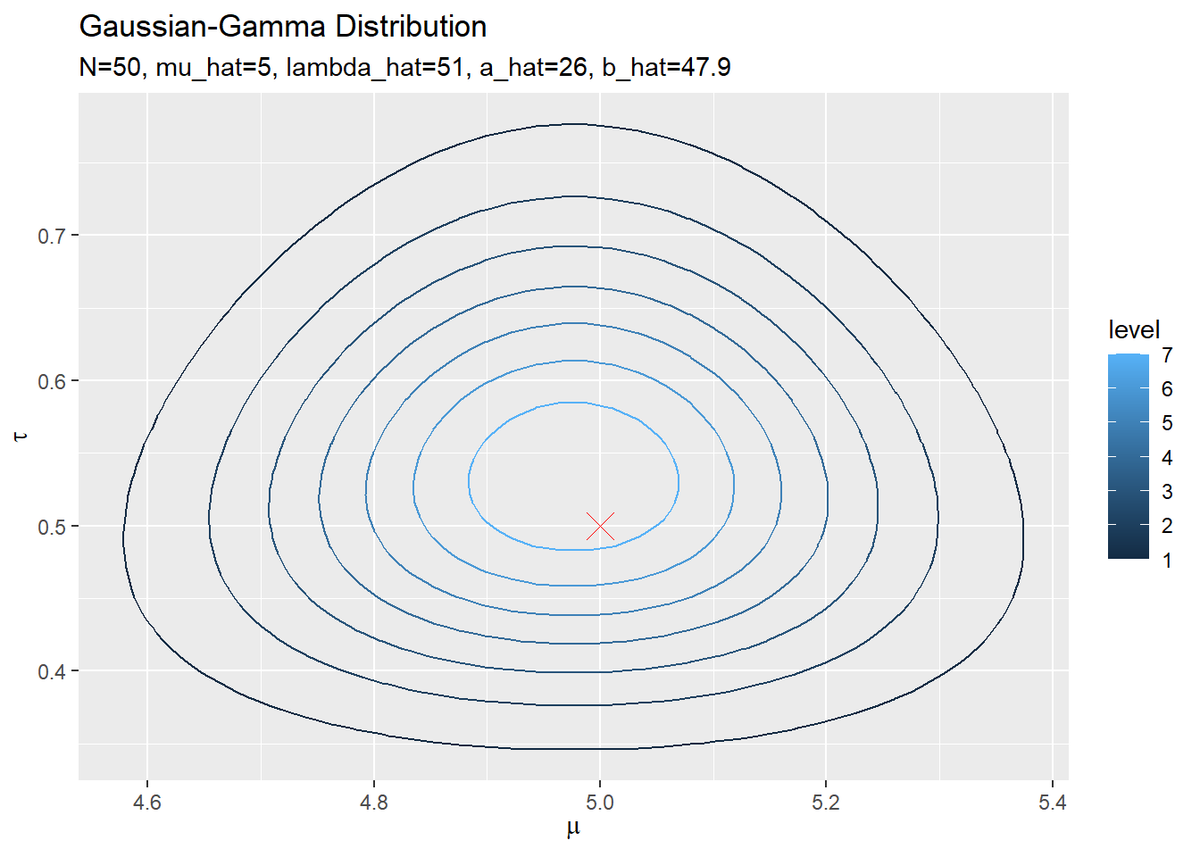
事前分布のときと同様に計算して作図します。
各パラメータの真の事後分布も確認しておきましょう。
・コード(クリックで展開)
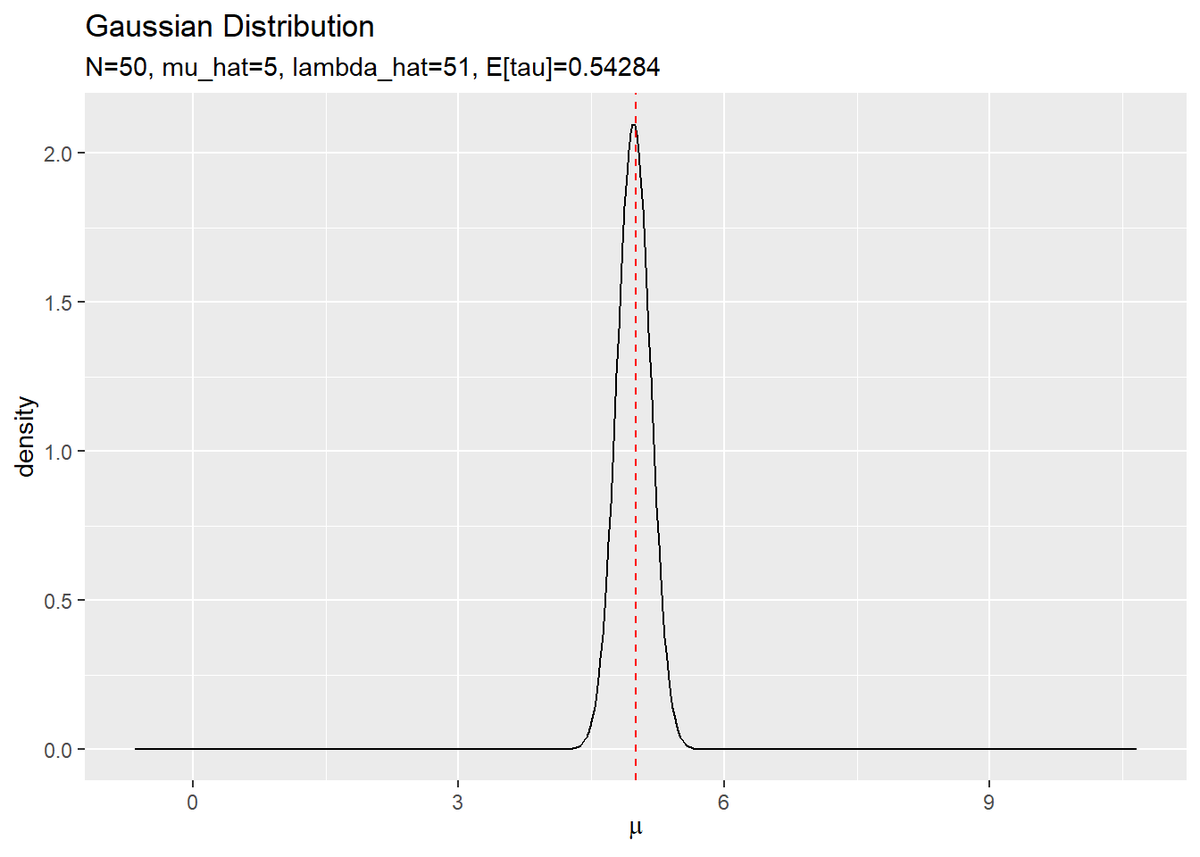
$\mu$の真の事後分布を作図します。
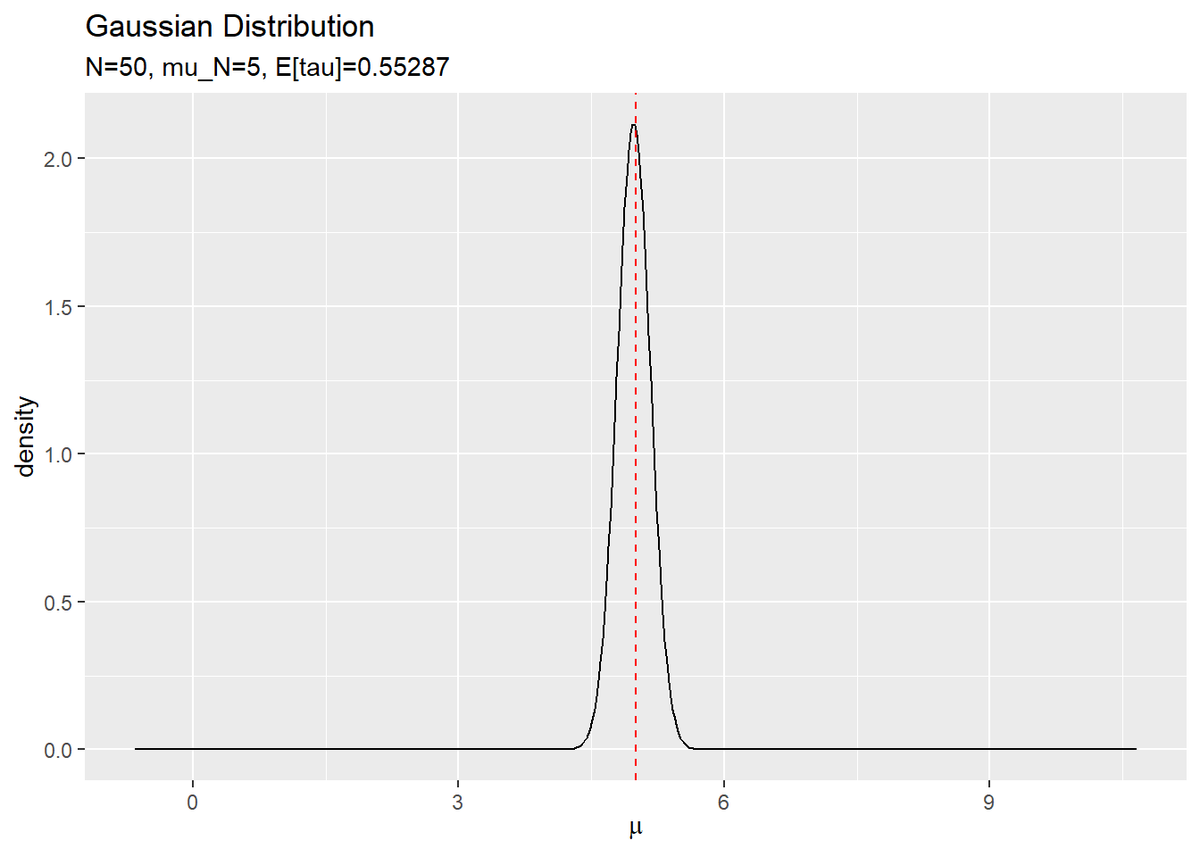
# muの真の事後分布を作図 tibble( mu = mu_vec, N_dens = dnorm(x = mu, mean = mu_hat, sd = sqrt(1 / (lambda_hat * a_hat / b_hat))) ) %>% ggplot(aes(x = mu, y = N_dens)) + geom_line() + # muの真の事後分布 geom_vline(xintercept = mu_truth, color = "red", linetype = "dashed") + # muの真の値 labs(title = "Gaussian Distribution", subtitle = paste0("N=", N, ", mu_hat=", round(mu_hat, 1), ", lambda_hat=", lambda_hat, ", E[tau]=", round(a_hat / b_hat, 5)), x = expression(mu), y = "density")
重複していない$\mu$の値mu_vecの要素ごとに確率密度を計算します。ただし、$\tau$の代わりに、ガンマ分布の期待値(B.27)より、$\tau$の期待値$\mathbb{E}[\tau] = \frac{\hat{a}}{\hat{b}}$を用いて確率密度を計算します。
真の値を垂直線geom_vline()で示しています。
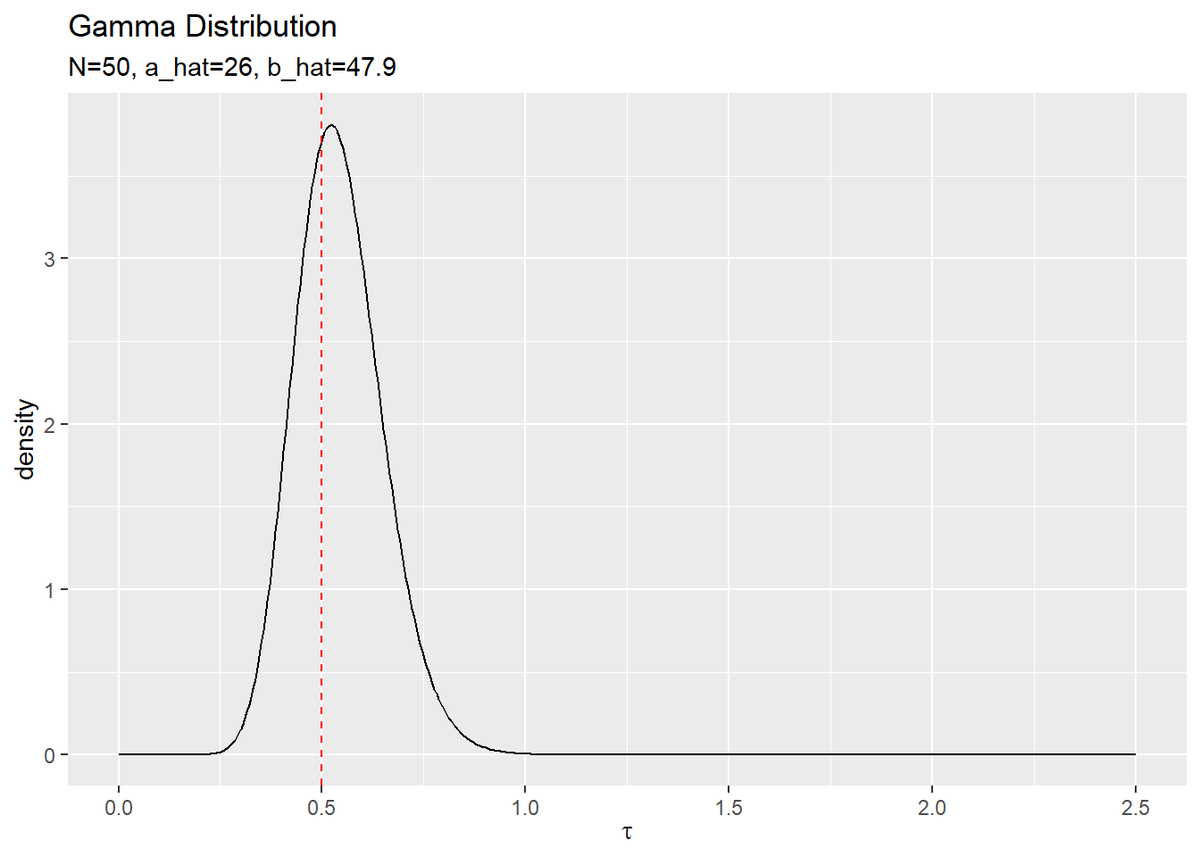
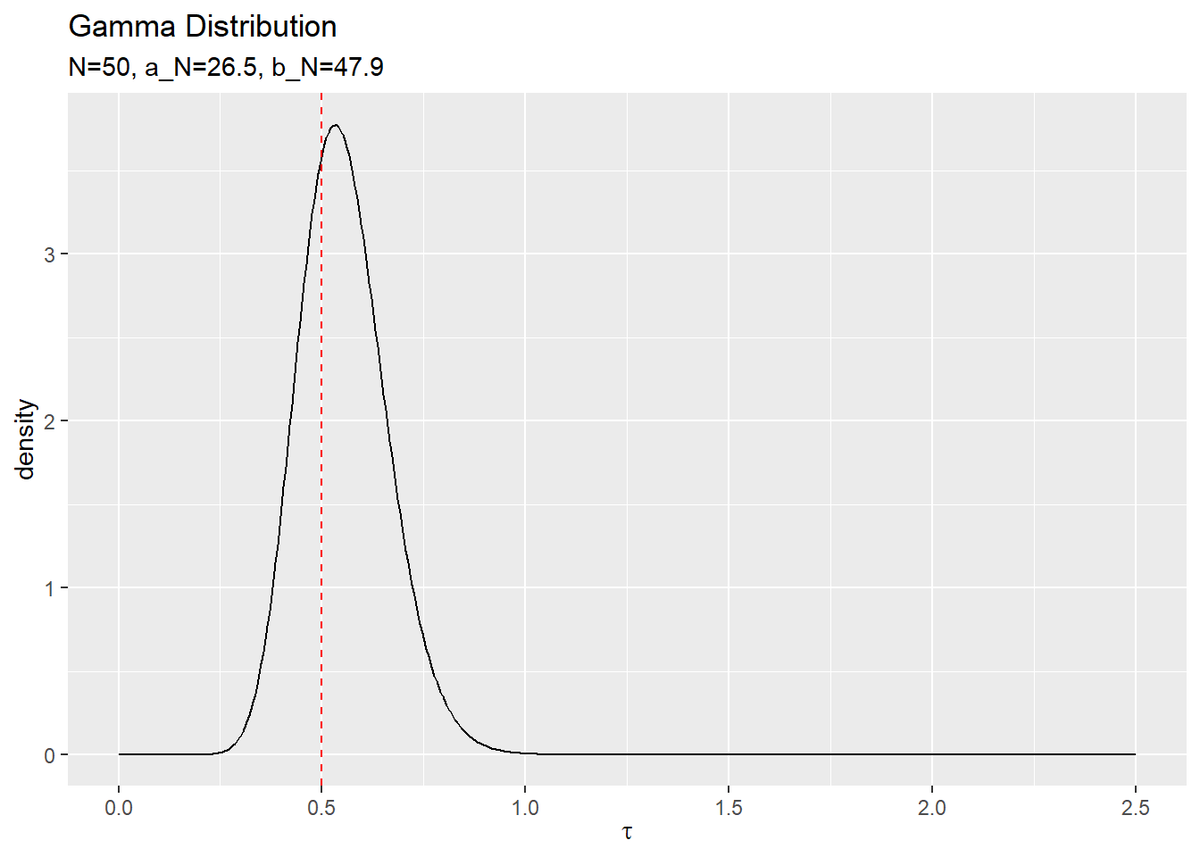
同様に、$\tau$の真の事後分布を作図します。
# tauの真の事後分布を作図 tibble( tau = tau_vec, Gam_dens = dgamma(x = tau, shape = a_hat, rate = b_hat) ) %>% ggplot(aes(x = tau, y = Gam_dens)) + geom_line() + # tauの真の事後分布 geom_vline(xintercept = tau_truth, color = "red", linetype = "dashed") + # tauの真の値 labs(title = "Gamma Distribution", subtitle = paste0("N=", N, ", a_hat=", a_hat, ", b_hat=", round(b_hat, 1)), x = expression(tau), y = "density")
こちらも重複していない$\tau$の値tau_vecの要素ごとに確率密度を計算します。
以上でモデルの構築ができたので、次は推論処理を行います。
・変分推論
変分推論により$\mu,\ \tau$の近似事後分布$q(\mu, \tau)$を求めます。近似事後分布もガウス-ガンマ分布$\mathrm{NG}(\mu, \tau | \mu_N, \lambda_N, a_N, b_N)$になります。
変分推論では、$\mu$の近似事後分布$q_{\mu}(\mu)$(のパラメータ$\mu_N,\ \lambda_N$)と$\tau$の近似事後分布$q_{\tau}(\tau)$(のパラメータ$a_N,\ b_N$)の更新を交互に行います。
・コード全体
事前分布のパラメータの値を初期値として持つように近似事後分布のパラメータを作成しておきます。
また、後で各パラメータの更新値や分布の推移を確認するために、それぞれ試行ごとにtrace_***に値を保存していきます。ただし、この例はすぐに収束してしまうので、$q_{\mu}(\mu)$と$q_{\tau}(\tau)$をそれぞれ更新する度に値を記録することにします。
# 試行回数を指定 MaxIter <- 5 # 初期値を代入 mu_N <- mu_0 lambda_N <- lambda_0 * a_0 / b_0 a_N <- a_0 b_N <- b_0 # 推移の確認用の受け皿を作成 trace_mu_i <- rep(0, MaxIter * 2 + 1) trace_lambda_i <- rep(0, MaxIter * 2 + 1) trace_a_i <- rep(0, MaxIter * 2 + 1) trace_b_i <- rep(0, MaxIter * 2 + 1) # 初期値を記録 trace_mu_i[1] <- mu_0 trace_lambda_i[1] <- lambda_0 trace_a_i[1] <- a_0 trace_b_i[1] <- b_0 # 変分推論 for(i in 1:MaxIter) { # muの近似事後分布のパラメータを計算:式(10.26)(10.27) mu_N <- (lambda_0 * mu_0 + sum(x_n)) / (lambda_0 + N) lambda_N <- (lambda_0 + N) * a_N / b_N # i回目のmuの近似事後分布の更新後の結果を記録 trace_mu_i[i * 2] <- mu_N trace_lambda_i[i * 2] <- lambda_N trace_a_i[i * 2] <- a_N trace_b_i[i * 2] <- b_N # lambdaの近似事後分布のパラメータを計算:式(10.29)(10.30) a_N <- a_0 + 0.5 * (N + 1) term_x <- 0.5 * (lambda_0 * mu_0^2 + sum(x_n^2)) term_mu2 <- 0.5 * (lambda_0 + N) * (mu_N^2 + 1 / lambda_N) term_mu <- (lambda_0 * mu_0 + sum(x_n)) * mu_N b_N <- b_0 + term_x + term_mu2 - term_mu # i回目のlambdaの近似事後分布の更新後の結果を記録 trace_mu_i[i * 2 + 1] <- mu_N trace_lambda_i[i * 2 + 1] <- lambda_N trace_a_i[i * 2 + 1] <- a_N trace_b_i[i * 2 + 1] <- b_N # 動作確認 #print(paste0(i, ' (', round(i / MaxIter * 100, 1), '%)')) }
・処理の解説
続いて、変分推論で行う処理を確認していきます。
・平均パラメータの近似事後分布の更新
先に、$q_{\tau}(\tau)$を固定した下での$\mu$の近似事後分布の最適解$q_{\mu}^{*}(\mu)$を計算します。
$\mu$の近似事後分布のパラメータを計算します。
# muの近似事後分布のパラメータを計算:式(10.26)(10.27) mu_N <- (lambda_0 * mu_0 + sum(x_n)) / (lambda_0 + N) lambda_N <- (lambda_0 + N) * a_N / b_N
変分推論により求めた$\mu$の事後分布の平均パラメータ$\mu_N$、精度パラメータ$\lambda_N$を次の式で計算します。
$\lambda_N$は、これまでのように精度パラメータの係数ではなく、精度パラメータそのものであることに注意してください。
計算結果は次のようになります。
# 確認
mu_N
lambda_N
## [1] 4.976428 ## [1] 28.19653
・精度パラメータの近似事後分布の更新
続いて、$q_{\mu}(\mu)$を固定した下での$\tau$の近似事後分布の最適解$q_{\tau}^{*}(\tau)$を計算します。
$\tau$の近似事後分布のパラメータを計算します。
# lambdaの近似事後分布のパラメータを計算:式(10.29)(10.30) a_N <- a_0 + 0.5 * (N + 1) term_x <- 0.5 * (lambda_0 * mu_0^2 + sum(x_n^2)) term_mu2 <- 0.5 * (lambda_0 + N) * (mu_N^2 + 1 / lambda_N) term_mu <- (lambda_0 * mu_0 + sum(x_n)) * mu_N b_N <- b_0 + term_x + term_mu2 - term_mu
変分推論により求めた$\tau$の事後分布のパラメータを$a_N,\ b_N$を次の式で計算します。
計算結果は次のようになります。
# 確認
a_N
b_N
## [1] 26.5 ## [1] 47.93144
これで超パラメータ$\mu_N,\ \lambda_N$と$a_N,\ b_N$を更新できました。
以上が変分推論で行う個々の処理です。繰り返し行うことで、徐々に真の事後分布に近付けていきます。閾値に達するまでループすることもできますが、この例では簡単に、試行回数を設定してループすることにします。
・推論結果の確認
推論結果を確認していきます。
・近似事後分布の確認
mu_N, lambda_N、a_N, b_Nの最後の更新値を用いて、$\mu,\ \tau$の近似事後分布を計算します。
# 同時近似事後分布を計算 posterior_df <- tibble( mu = mu_tau_point_mat[, 1], tau = mu_tau_point_mat[, 2], N_dens = dnorm(x = mu, mean = mu_N, sd = sqrt(1 / (lambda_N * b_N / a_N * tau))), # muの近似事後分布 Gam_dens = dgamma(x = tau, shape = a_N, rate = b_N), # tauの近似事後分布 density = N_dens * Gam_dens )
事前分布のときと同様に計算します。ただし、$\mu$の近似事後分布の精度パラメータ$\lambda_N$には、既に$\tau$の情報が期待値$\mathbb{E}[\tau]$として含まれています。そこで、$\mathbb{E}[\tau] = \frac{a_N}{b_N}$の逆数を掛けて打ち消してから、$\tau$の値mu_tau_point_mat[, 2]を掛けて確率密度を計算します。(本当にこんなことをしていいのかよく分かっていません。やるにしてももう少し納得できる理由が欲しい。)
$\mu,\ \tau$の同時近似事後分布を作図します。
# 近似事後分布を作図 ggplot() + geom_contour(data = posterior_df, aes(x = mu, y = tau, z = density, color = ..level..)) + # 近似事後分布 geom_contour(data = true_posterior_df, aes(x = mu, y = tau, z = density, color = ..level..), alpha = 0.5, linetype = "dashed") + # 真の事後分布 geom_point(data = true_params_df, aes(x = mu, y = tau), color = "red", shape = 4, size = 5) + # 真の値 labs(title = "Gaussian-Gamma Distribution", subtitle = paste0("N=", N, ", mu_N=", round(mu_N, 1), ", lambda_N=", round(lambda_N, 5), ", a_N=", a_N, ", b_N=", round(b_N, 1)), x = expression(mu), y = expression(tau))
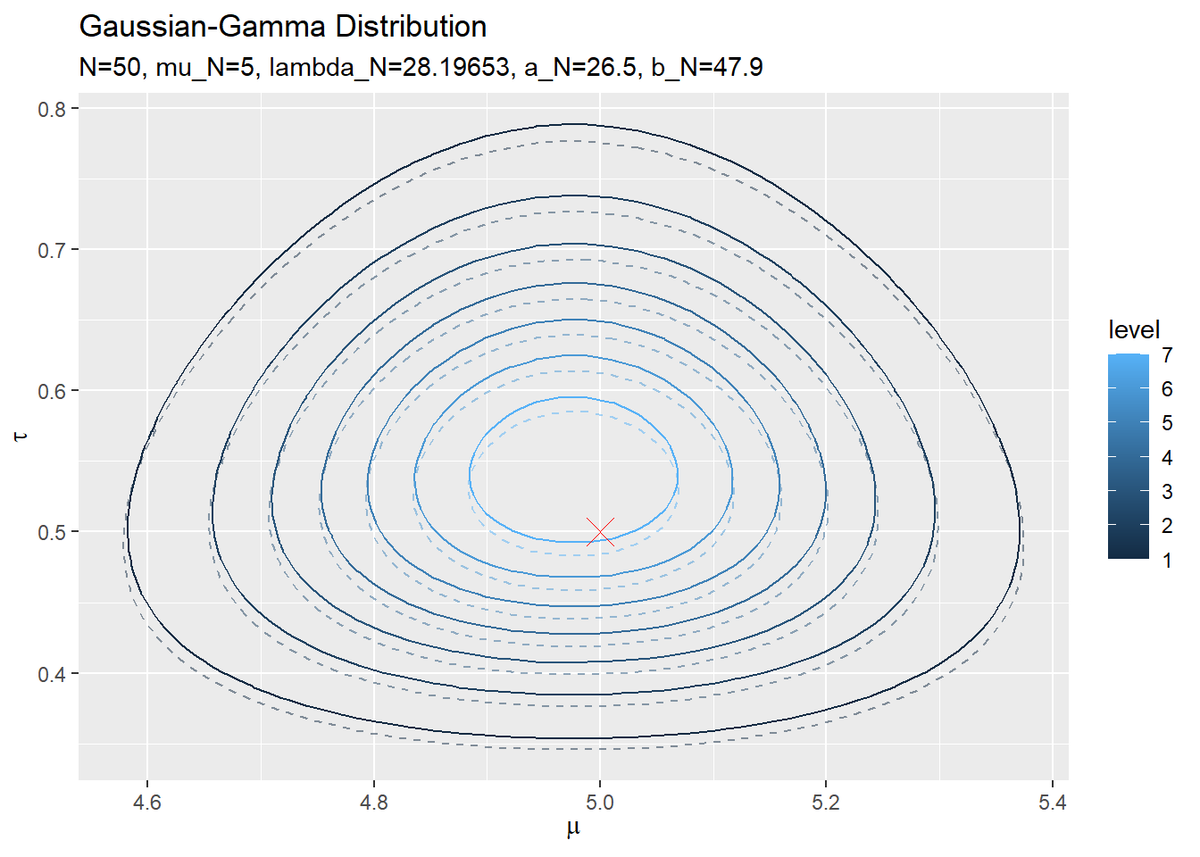
事前分布のときと同様に作図できます。真の事後分布と重ねて描画しています。
真の事後分布を近似できています。
各パラメータの近似事後分布も確認しましょう。
・コード(クリックで展開)
$\mu$の近似事後分布を作図します。
# muの近似事後分布を作図 tibble( mu = mu_vec, N_dens = dnorm(x = mu, mean = mu_N, sd = sqrt(1 / lambda_N)) ) %>% ggplot(aes(x = mu, y = N_dens)) + geom_line() + # muの近似事後分布 geom_vline(xintercept = mu_truth, color = "red", linetype = "dashed") + # muの真の値 labs(title = "Gaussian Distribution", subtitle = paste0("N=", N, ", mu_N=", round(mu_N, 1), ", E[tau]=", round(a_N / b_N, 5)), x = expression(mu), y = "density")
こちらは、lambda_Nをそのまま精度パラメータとして用います。
$\tau$の近似事後分布を作図します。
# tauの近似事後分布を作図 tibble( tau = tau_vec, Gam_dens = dgamma(x = tau, shape = a_N, rate = b_N) ) %>% ggplot(aes(x = tau, y = Gam_dens)) + geom_line() + # tauの近似事後分布 geom_vline(xintercept = tau_truth, color = "red", linetype = "dashed") + # tauの真の値 labs(title = "Gamma Distribution", subtitle = paste0("N=", N, ", a_N=", a_N, ", b_N=", round(b_N, 1)), x = expression(tau), y = "density")
真の事後分布のときと同様に作図できます。
・超パラメータの推移の確認
超パラメータの更新値の推移を確認します。
・コード(クリックで展開)
学習ごとの値を格納した各パラメータの配列trace_***をtidyr::pivot_longer()で縦長のデータフレームに変換して作図します。
# mu_Nの推移を作図 tibble( iteration = 0:(MaxIter * 2) * 0.5, value = trace_mu_i ) %>% ggplot(aes(x = iteration, y = value)) + geom_line() + labs(title = "Variational Inference", subtitle = expression(mu[N]))
# lambda_Nの推移を作図 tibble( iteration = 0:(MaxIter * 2) * 0.5, value = trace_lambda_i ) %>% ggplot(aes(x = iteration, y = value)) + geom_line() + labs(title = "Variational Inference", subtitle = expression(lambda[N]))
# a_Nの推移を作図 tibble( iteration = 0:(MaxIter * 2) * 0.5, value = trace_a_i ) %>% ggplot(aes(x = iteration, y = value)) + geom_line() + labs(title = "Variational Inference", subtitle = expression(a[N]))
# b_Nの推移を作図 tibble( iteration = 0:(MaxIter * 2) * 0.5, value = trace_b_i ) %>% ggplot(aes(x = iteration, y = value)) + geom_line() + labs(title = "Variational Inference", subtitle = expression(b[N]))
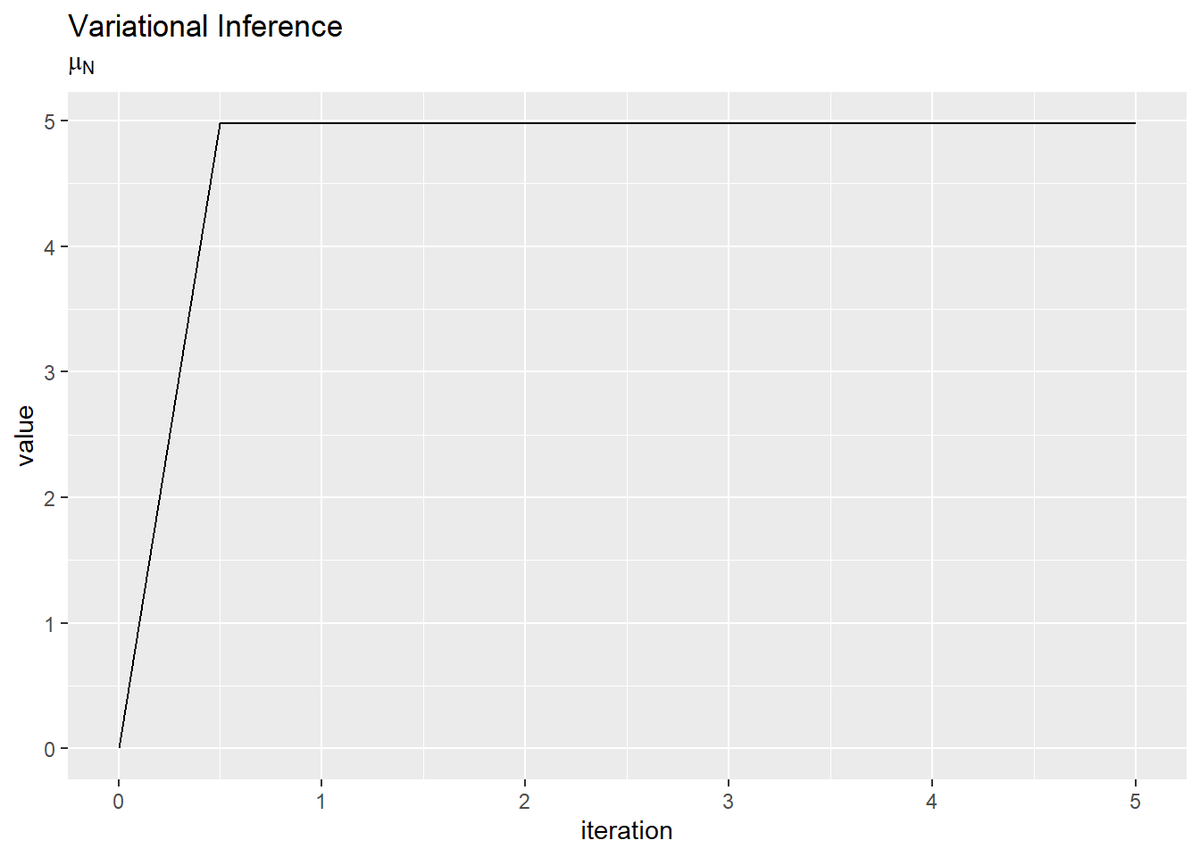
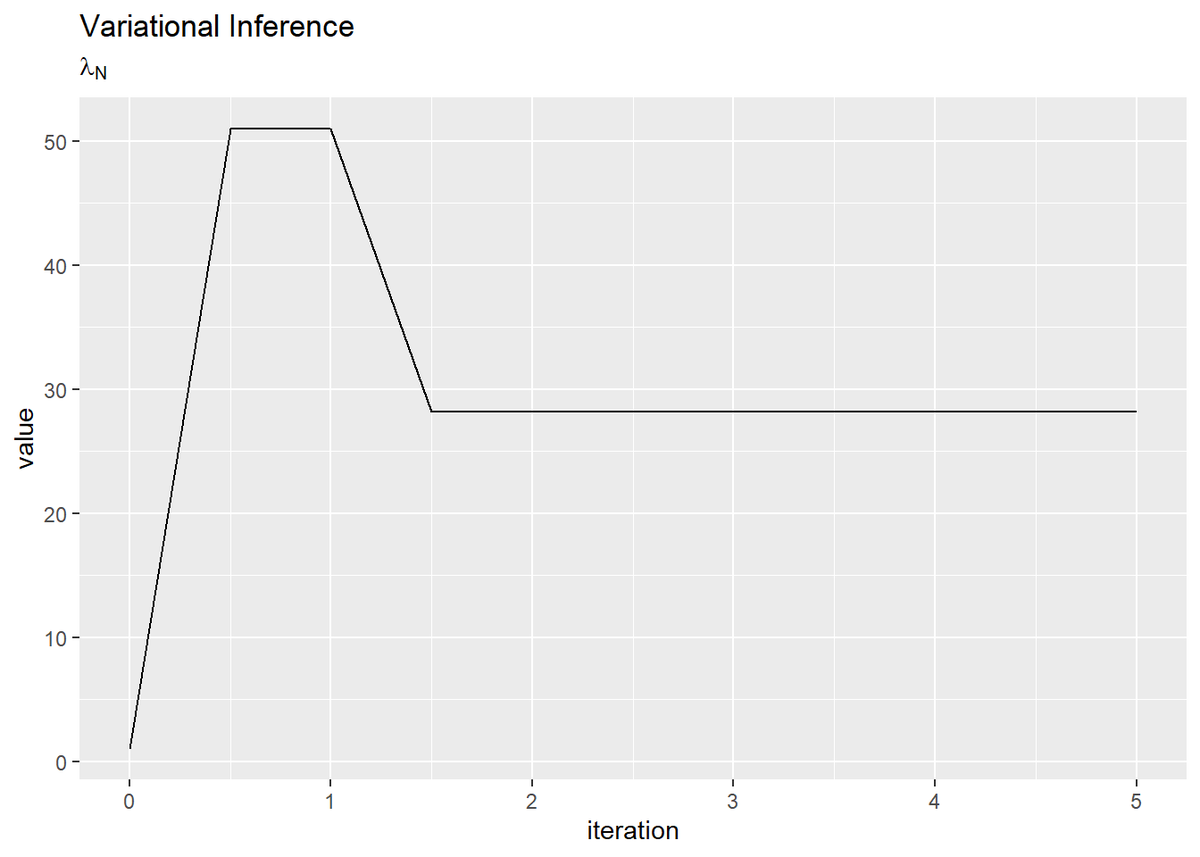
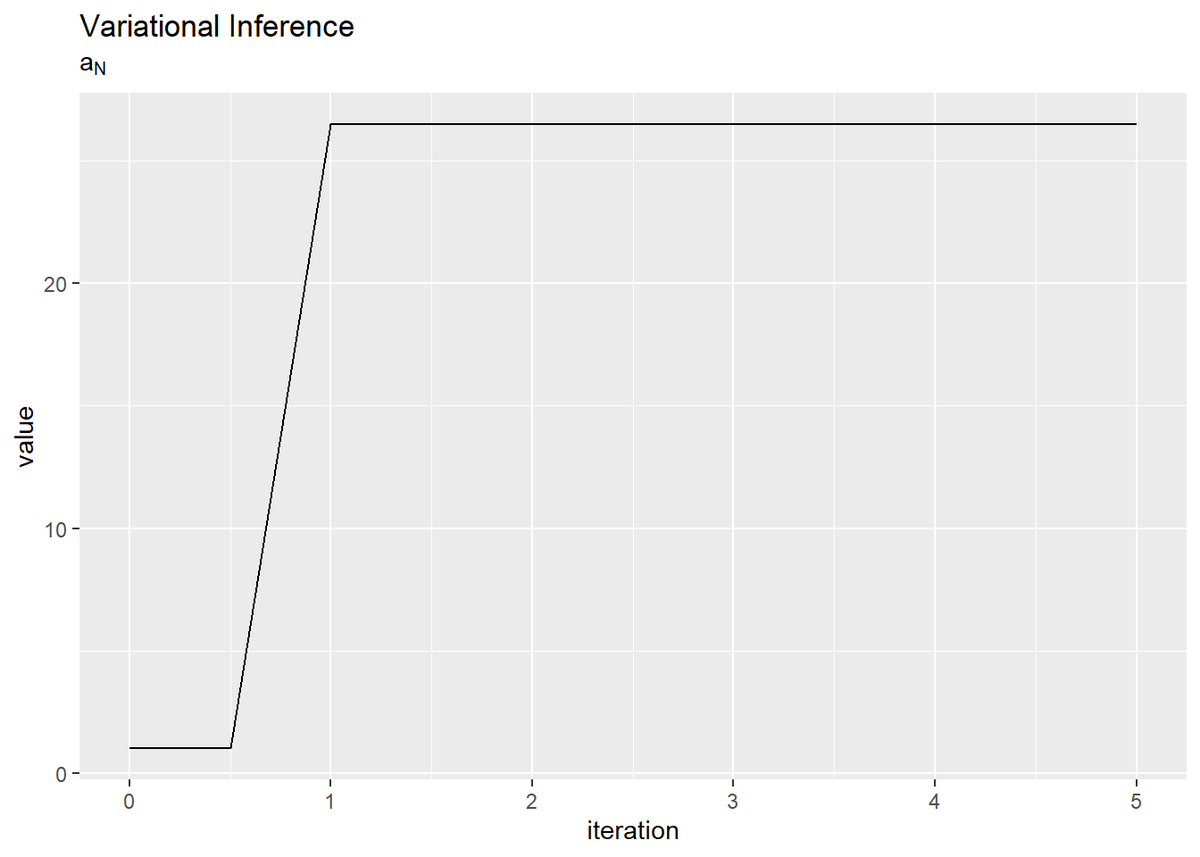
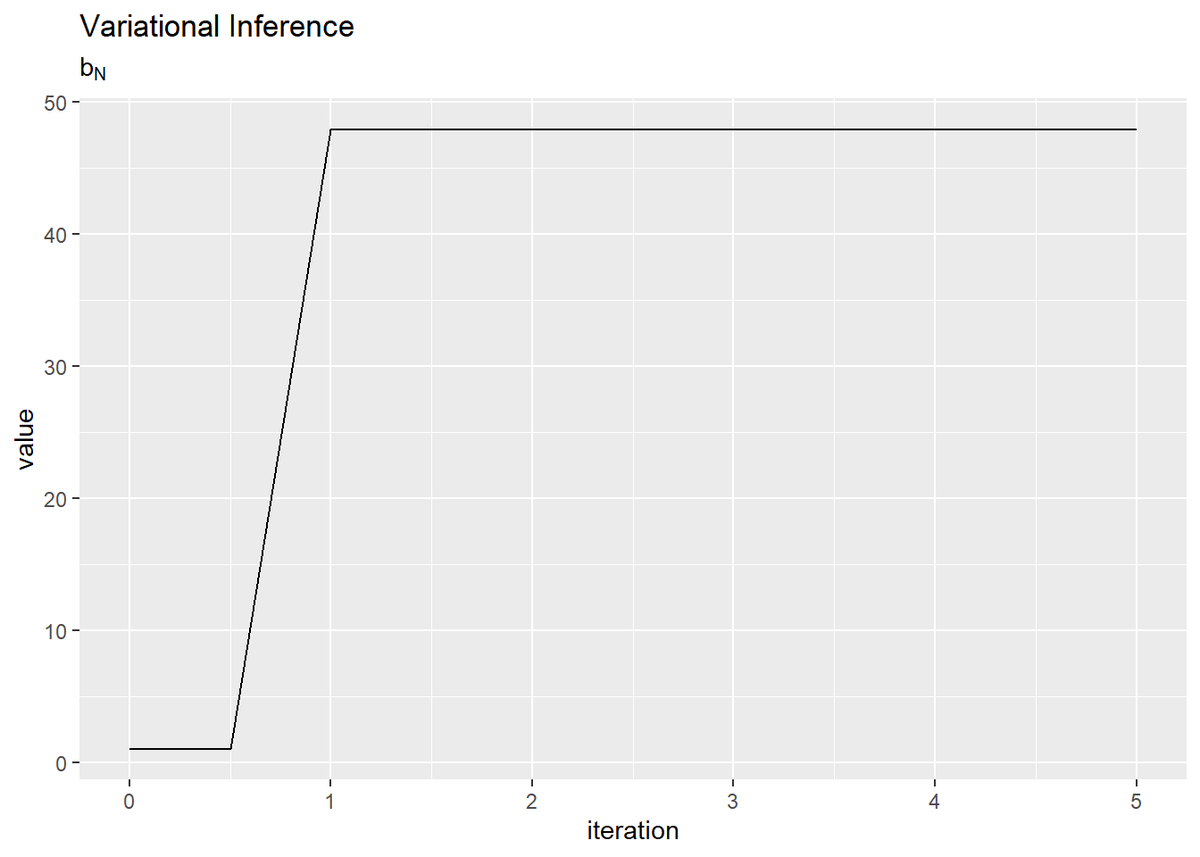
平均パラメータに関しては1回目の試行で、精度パラメータに関しては2回目の試行で収束しているのが確認できます。
・おまけ:アニメーションによる推移の確認
gganimateパッケージを利用して、分布の推移のアニメーション(gif画像)を作成するためのコードです。
・コード(クリックで展開)
# 追加パッケージ library(gganimate)
事後分布の推移を確認します。作図用のデータフレームを作成します。
# 作図用のデータフレームを作成 trace_posterior_df <- tibble() for(i in 1:(MaxIter * 2 + 1)) { # i回目の近似事後分布を計算 tmp_posterior_df <- tibble( mu = mu_tau_point_mat[, 1], tau = mu_tau_point_mat[, 2], N_dens = dnorm( x = mu, mean = trace_mu_i[i], sd = sqrt(1 / (trace_lambda_i[i] * trace_b_i[i] / trace_a_i[i] * tau)) ), # muの近似事後分布 Gam_dens = dgamma(x = tau, shape = trace_a_i[i], rate = trace_b_i[i]), # tauの近似事後分布 density = N_dens * Gam_dens, label = as.factor( paste0("iter:", (i - 1) * 0.5, ", N=", N, ", mu_N=", round(trace_mu_i[i], 1), ", lambda_N=", round(trace_lambda_i[i], 5), ", a_N=", trace_a_i[i], ", b_N=", round(trace_b_i[i], 1)) ) # フレーム切替用のラベル ) # 結合 trace_posterior_df <- rbind(trace_posterior_df, tmp_posterior_df) # 動作確認 #print(paste0((i - 1) * 0.5, ' (', round((i - 1) * 0.5 / MaxIter * 100, 1), '%)')) }
各試行における計算結果を同じデータフレームに格納していく必要があります。処理に時間がかかる場合は、mu_tau_point_matの範囲や間隔を調整してください。
作成したデータフレームは次のようになります。
# 確認 head(trace_posterior_df)
## # A tibble: 6 x 6 ## mu tau N_dens Gam_dens density label ## <dbl> <dbl> <dbl> <dbl> <dbl> <fct> ## 1 -0.657 0 0 1 0 iter:0, N=50, mu_N=0, lambda_N=1, a_N=1,~ ## 2 -0.634 0 0 1 0 iter:0, N=50, mu_N=0, lambda_N=1, a_N=1,~ ## 3 -0.612 0 0 1 0 iter:0, N=50, mu_N=0, lambda_N=1, a_N=1,~ ## 4 -0.589 0 0 1 0 iter:0, N=50, mu_N=0, lambda_N=1, a_N=1,~ ## 5 -0.566 0 0 1 0 iter:0, N=50, mu_N=0, lambda_N=1, a_N=1,~ ## 6 -0.543 0 0 1 0 iter:0, N=50, mu_N=0, lambda_N=1, a_N=1,~
フレーム切替用のラベルの列labelをパラメータの値を使って作成していますが、ややこしければas.factor(paste0("iter:", (i - 1) * 0.5))だけにして試行回数を表示するだけでもそれっぽくなります。
分布の推移をgif画像で出力します。
# 近似事後分布を作図 trace_graph <- ggplot() + geom_contour(data = trace_posterior_df, aes(x = mu, y = tau, z = density, color = ..level..)) + # 近似事後分布 geom_contour(data = true_posterior_df, aes(x = mu, y = tau, z = density, color = ..level..), alpha = 0.5, linetype = "dashed") + # 真の事後分布 geom_point(data = true_params_df, aes(x = mu, y = tau), color = "red", shape = 4, size = 5) + # 真の値 gganimate::transition_manual(label) + # フレーム labs(title = "Gaussian-Gamma Distribution", subtitle = "{current_frame}", x = expression(mu), y = expression(tau)) # gif画像を作成 gganimate::animate(trace_graph, nframes = MaxIter * 2 + 1, fps = 5)
各フレームの順番を示す列をgganimate::transition_manual()に指定します。初期値を含み各試行で2回記録しているため、フレーム数はMaxIter * 2 + 1です。
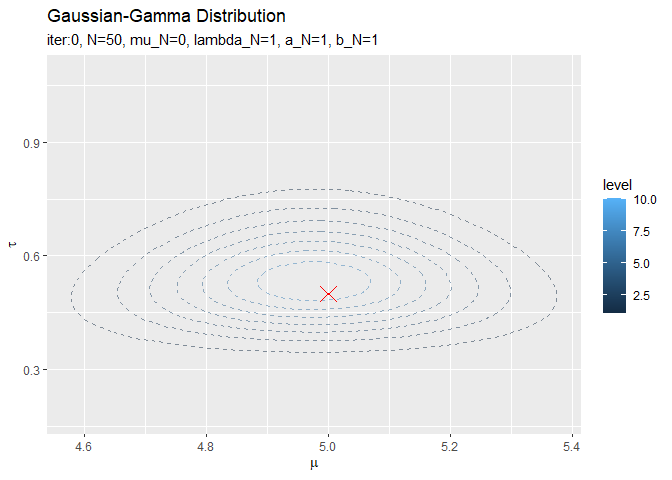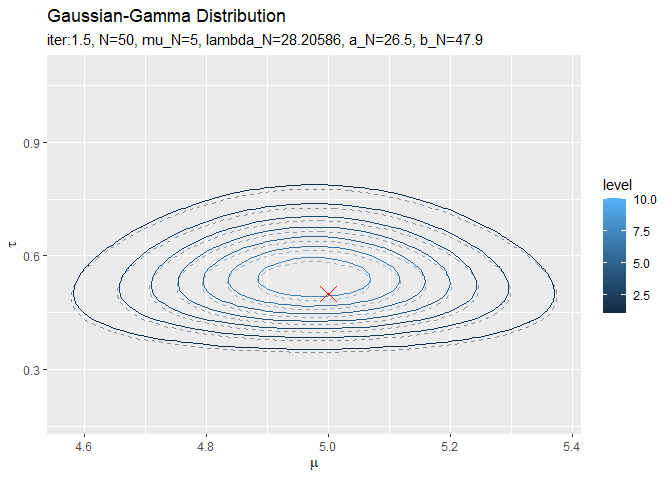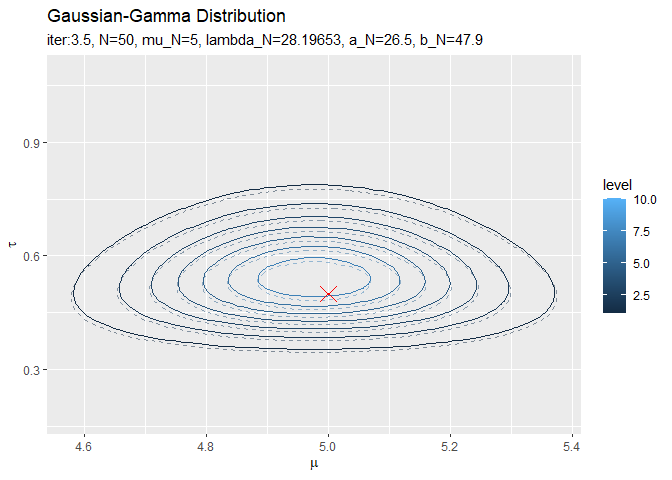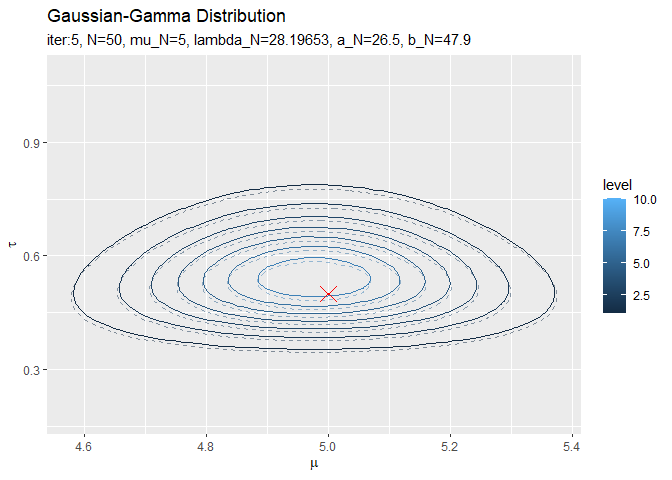
初期値(事前分布)は分散が大きく確率密度が小さいため表示されていません。平均は初期値が0なので、0.5回目の試行で収束しています。精度は2回目の試行で収束しているのが分かります。
参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上下』,丸善出版,2012年.
おわりに
本では無情報事前分布として全ての超パラメータを0にすると書いてあるけど0はダメなのでは?それに初期値が0だと図10.4の(a)のグラフにはならないと思うし。それとは別に、(あんまり努力はしてないけど)図10.4を再現できなかった。今回は色々ちょっと自信ない。
そんなことよりこのブログを投稿する数時間前に、元つばきファクトリーの小片リサさんの活動再開が発表されました!ソロデビューおめでとう!!
同時に公開されたカバー動画です♪何はともあれ良かった良かった。
【関連する内容】
解析的に解く(真の事後分布を求める)はこちらの記事でやりました。