はじめに
『パターン認識と機械学習』の独学時のまとめです。一連の記事は「数式の行間埋め」または「R・Pythonでの実装」からアルゴリズムの理解を補助することを目的としています。本とあわせて読んでください。
この記事は、9.2.2項の内容です。多次元混合ガウス分布(多変量混合正規分布)に対するEMアルゴリズムによる最尤推定をPythonで実装します。
【他の節一覧】
【この節の内容】
・Pythonでやってみる
人工データを用いて、EMアルゴリズムによる最尤推定を行ってみましょう。
利用するライブラリを読み込みます。
# 9.2.2項で利用するライブラリ import numpy as np from scipy.stats import multivariate_normal # 多次元ガウス分布 import matplotlib.pyplot as plt
scipyライブラリのstatsから、多次元ガウス分布multivariate_normalのクラスを利用します。確率密度の計算にpdf()を使います。
・真の分布の設定
まずは、データを生成する真の分布を設定します。この節では、$K$個の$D$次元ガウス分布からなる混合ガウス分布$\sum_{k=1}^K \pi_k \mathcal{N}(\mathbf{x}_n | \boldsymbol{\mu}_k, \boldsymbol{\Lambda}_k^{-1})$とします。また、各データに対するクラスタの割り当てをカテゴリ分布$\mathrm{Cat}(\mathbf{z}_n | \boldsymbol{\pi})$によって行います。
真の分布のパラメータを設定します。この実装例では2次元のグラフで表現するため、$D = 2$のときのみ動作します。
# 次元数を設定:(固定) D = 2 # クラスタ数を指定 K = 3 # K個の真の平均を指定 mu_truth_kd = np.array( [[5.0, 35.0], [-20.0, -10.0], [30.0, -20.0]] ) # K個の真の共分散行列を指定 sigma2_truth_kdd = np.array( [[[250.0, 65.0], [65.0, 270.0]], [[125.0, -45.0], [-45.0, 175.0]], [[210.0, -15.0], [-15.0, 250.0]]] ) # 真の混合係数を指定 pi_truth_k = np.array([0.45, 0.25, 0.3])
$K$の平均パラメータ$\boldsymbol{\mu} = \{\boldsymbol{\mu}_1, \boldsymbol{\mu}_2, \cdots, \boldsymbol{\mu}_K\}$、$\boldsymbol{\mu}_k = (\mu_{k1}, \mu_{k2}, \cdots, \mu_{kD})$をmu_truth_kd、共分散行列パラメータ$\boldsymbol{\Sigma} = \{\boldsymbol{\Sigma}_1, \boldsymbol{\Sigma}_2, \cdots, \boldsymbol{\Sigma}_K\}$、$\boldsymbol{\Sigma}_k = (\sigma_{k11}^2, \cdots, \sigma_{kDD}^2)$をsigma2_truth_kddとして、値を指定します。$\boldsymbol{\Sigma}_k$は正定値行列です。
設定したパラメータは次のようになります。
# 確認 print(mu_truth_kd) print(sigma2_truth_kdd)
[[ 5. 35.]
[-20. -10.]
[ 30. -20.]]
[[[250. 65.]
[ 65. 270.]]
[[125. -45.]
[-45. 175.]]
[[210. -15.]
[-15. 250.]]]
混合係数を設定します。
# 真の混合比率を指定 pi_truth_k = np.array([0.45, 0.25, 0.3])
混合係数パラメータ$\boldsymbol{\pi} = (\pi_1, \pi_2, \cdots, \pi_K)$をpi_true_kとして、$\sum_{k=1}^K \pi_k = 1$、$\pi_k \geq 0$の値を指定します。ここで、$\pi_k$は各データがクラスタ$k$となる($z_{nk} = 1$となる)確率を表します。
この3つのパラメータの値を観測データから求めるのがここでの目的です。
設定した真の分布をグラフで確認しましょう。作図用の点を作成します。
# 作図用のx軸のxの値を作成 x_1_line = np.linspace( np.min(mu_truth_kd[:, 0] - 3 * np.sqrt(sigma2_truth_kdd[:, 0, 0])), np.max(mu_truth_kd[:, 0] + 3 * np.sqrt(sigma2_truth_kdd[:, 0, 0])), num=300 ) # 作図用のy軸のxの値を作成 x_2_line = np.linspace( np.min(mu_truth_kd[:, 1] - 3 * np.sqrt(sigma2_truth_kdd[:, 1, 1])), np.max(mu_truth_kd[:, 1] + 3 * np.sqrt(sigma2_truth_kdd[:, 1, 1])), num=300 ) # 作図用の格子状の点を作成 x_1_grid, x_2_grid = np.meshgrid(x_1_line, x_2_line) # 作図用のxの点を作成 x_point_arr = np.stack([x_1_grid.flatten(), x_2_grid.flatten()], axis=1) # 作図用に各次元の要素数を保存 x_dim = x_1_grid.shape print(x_dim)
(300, 300)
作図用に、2次元ガウス分布に従う変数$\mathbf{x}_n = (x_{n1}, x_{n2})$がとり得る点(値の組み合わせ)を作成します。$x_{n1}$がとり得る値(x軸の値)をnp.linspace()で作成してx_1_lineとします。この例では、$K$個のクラスタそれぞれで平均値から標準偏差の3倍を引いた値と足した値を計算して、その最小値から最大値までを範囲とします。
np.linspace()を使うと指定した要素数で等間隔に切り分けます。np.arange()を使うと切り分ける間隔を指定できます。処理が重い場合は、この値を調整してください。
同様に、$x_{n2}$がとり得る値(y軸の値)も作成してx_2_lineとします。
np.meshgrid()を使って、x_1_lineとx_2_lineの要素の全ての組み合わせを持つような2次元配列に変換してそれぞれx_1_grid, x_2_gridとします。
これは、確率密度を等高線図にする際に格子状の点(2軸の全ての値が直交する点)を渡す必要があるためです。
また、x_1_grid, x_2_gridの要素を列として持つ2次元配列を作成してx_point_arrとします。これは、確率密度の計算に使います。
計算結果の確率密度は1次元配列になります。作図時にx_1_grid, x_2_gridと同じ形状にする必要があるため、形状をx_dimとして保存しておきます。
作成した$\mathbf{x}$の点は次のようになります。
# 確認 print(x_point_arr[:5])
[[-53.54101966 -67.4341649 ]
[-53.11621983 -67.4341649 ]
[-52.69142 -67.4341649 ]
[-52.26662017 -67.4341649 ]
[-51.84182033 -67.4341649 ]]
1列目がx軸の値、2列目がy軸の値に対応しています。
真の分布の確率密度を計算します。
# 真の分布を計算 model_dens = 0 for k in range(K): # クラスタkの分布の確率密度を計算 tmp_dens = multivariate_normal.pdf( x=x_point_arr, mean=mu_truth_kd[k], cov=sigma2_truth_kdd[k] ) # K個の分布を線形結合 model_dens += pi_truth_k[k] * tmp_dens
$K$個のパラメータmu_truth_kd, sigmga2_truth_kddを使って、x_point_arrの点ごとに、次の式で混合ガウス分布の確率密度を計算します。
$K$個の多次元ガウス分布に対して、$\boldsymbol{\pi}$を使って加重平均をとります。
多次元ガウス分布の確率密度は、SciPyライブラリのmultivariate_normal.pdf()で計算できます。$k$番目の分布の場合は、データの引数xにx_point_arr、平均の引数muにmu_truth_kd[k]、分散共分散行列の引数sigmaにsigma2_truth_kdd[k]を指定します。
この計算をfor文でK回繰り返し行います。各パラメータによって求めた$K$回分の確率密度をそれぞれpi_truth_k[k]で割り引いてmodel_densに加算していきます。
計算結果は次のようになります。
# 確認 print(model_dens[:5])
[9.06768334e-13 1.07345258e-12 1.27033352e-12 1.50260830e-12
1.77630256e-12]
真の分布を作図します。
# 真の分布を作図 plt.figure(figsize=(12, 9)) plt.contour(x_1_grid, x_2_grid, model_dens.reshape(x_dim)) # 真の分布 plt.suptitle('Mixture of Gaussians', fontsize=20) plt.title('K=' + str(K), loc='left') plt.xlabel('$x_1$') plt.ylabel('$x_2$') plt.colorbar() # 等高線の色 plt.show()

等高線グラフはplt.contour()で描画します。
$K$個の分布を重ねたような分布になります。ただし、積分して1となるようにしているため、$K$個の分布そのものよりも1つ1つの山が小さく(確率密度が小さく)なっています。
・データの生成
続いて、設定した真の分布に従ってデータを生成します。先に、潜在変数$\mathbf{Z} = \{\mathbf{z}_1, \mathbf{z}_2, \cdots, \mathbf{z}_N\}$、$\mathbf{z}_n = (z_{n1}, z_{n2}, \cdots, z_{nK})$を生成し、各データにクラスタを割り当てます。次に、割り当てられたクラスタに従い観測データ$\mathbf{X} = \{\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_N\}$、$\mathbf{x}_n = (x_{n,1}, x_{n,2}, \cdots, x_{n,D})$を生成します。
$N$個の潜在変数$\mathbf{Z}$を生成します。
# (観測)データ数を指定 N = 250 # 潜在変数を生成 z_truth_nk = np.random.multinomial(n=1, pvals=pi_truth_k, size=N)
生成するデータ数$N$をNとして値を指定します。
カテゴリ分布に従う乱数は、多項分布に従う乱数生成関数np.random.multinomial()のn引数を1にすることで生成できます。また、確率(パラメータ)の引数probにpi_truth_k、試行回数の引数sizeにNを指定します。生成した$N$個の$K$次元ベクトルをz_truth_nkとします。
結果は次のようになります。
# 確認 print(z_truth_nk[:5])
[[1 0 0]
[0 0 1]
[0 0 1]
[0 0 1]
[1 0 0]]
これが本来は観測できない潜在変数であり、真のクラスタです。各行がデータを表し、値が1の列番号が割り当てられたクラスタ番号を表します。
s_truth_nkから各データのクラスタ番号を抽出します。
# クラスタ番号を抽出 _, z_truth_n = np.where(z_truth_nk == 1) # 確認 print(z_truth_n[:5])
[0 2 2 2 0]
np.where()を使って行(データ)ごとに要素が1の列番号を抽出します。
各データに割り当てられたクラスタに従い$N$個のデータを生成します。
# (観測)データを生成 x_nd = np.array([ np.random.multivariate_normal( mean=mu_truth_kd[k], cov=sigma2_truth_kdd[k], size=1 ).flatten() for k in z_truth_n ])
各データ$\mathbf{x}_n$に割り当てられたクラスタ($s_{nk} = 1$である$k$)のパラメータ$\boldsymbol{\mu}_k,\ \boldsymbol{\Sigma}_k$を持つ多次元ガウス分布に従いデータ(値)を生成します。多次元ガウス分布の乱数は、np.random.multivariate_normaln()で生成できます。
データごとにクラスタが異なるので、for文(リスト内包表記)で1データずつ処理します。$n$番目のデータのクラスタ番号z_true_n[n]を取り出してkとします。そのクラスタに従ってデータ$\mathbf{x}_n$を生成します。平均の引数meanにmu_true_kd[k]、共分散行列の引数covにsigma2_true_kdd[k]を指定します。また1データずつ生成するので、データ数の引数sizeは1です。2次元配列で出力されるため、flatten()で1次元配列に変換しておきます。
生成した観測データは次のようになります。
# 確認 print(x_nd[:5])
[[-11.4749068 1.79448484]
[ 58.91279813 -24.22527427]
[ 28.76001222 -22.15901677]
[ 26.20324628 -7.82181246]
[ 13.93898498 29.94545891]]
観測データの散布図を真の分布に重ねて作図します。
# 観測データの散布図を作成 plt.figure(figsize=(12, 9)) for k in range(K): k_idx, = np.where(z_truth_n == k) # クラスタkのデータのインデック plt.scatter(x=x_nd[k_idx, 0], y=x_nd[k_idx, 1], label='cluster:' + str(k + 1)) # 観測データ plt.contour(x_1_grid, x_2_grid, model_dens.reshape(x_dim), linestyles='--') # 真の分布 plt.suptitle('Mixture of Gaussians', fontsize=20) plt.title('$N=' + str(N) + ', K=' + str(K) + ', \pi=(' + ', '.join([str(pi) for pi in pi_truth_k]) + ')$', loc='left') plt.xlabel('$x_1$') plt.ylabel('$x_2$') plt.colorbar() # 等高線の色 plt.show()
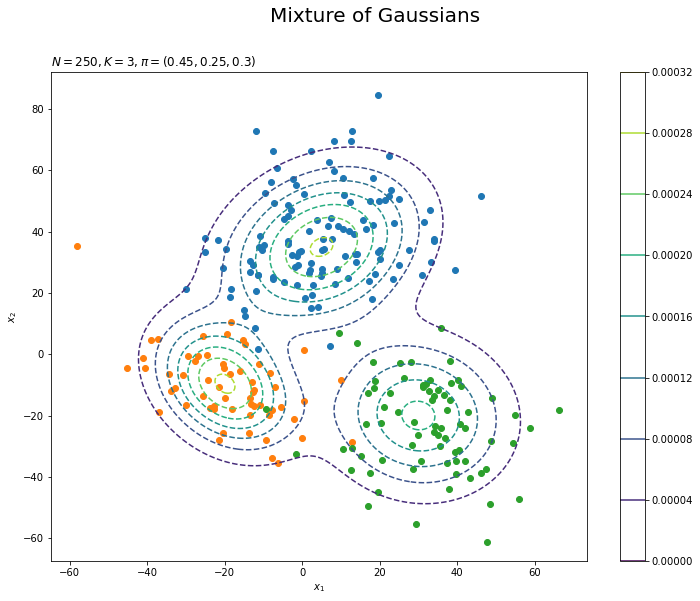
散布図はplt.scatter()で描画します。各クラスタが割り当てられたデータのインデックスをnp.where(z_true_n == k)で抽出してk_idxとします。k_idxを使ってクラスタ$k$が割り当てられたデータを取り出して、クラスタごとに色を変えた散布図を描きます。
観測データから各データのクラスタも推定します。
・初期値の設定
パラメータ$\boldsymbol{\mu},\ \boldsymbol{\Lambda},\ \boldsymbol{\pi}$の初期値を設定します。
ランダムに値を生成してパラメータを初期化します。
# 平均パラメータの初期値を生成 mu_kd = np.array([ np.random.uniform( low=np.min(x_nd[:, d]), high=np.max(x_nd[:, d]), size=K ) for d in range(D) ]).T # 共分散行列の初期値を指定 sigma2_kdd = np.array([np.identity(D) * 1000 for _ in range(K)]) # 混合係数の初期値を生成 pi_k = np.random.rand(3) pi_k /= np.sum(pi_k) # 正規化
$K$個の平均パラメータ$\boldsymbol{\mu}$をmu_kdとして値を生成します。この例では、次元ごとに観測データx_ndの最小値から最大値を範囲とする一様乱数を設定します。一様乱数はnp.random.uniform()で生成できます。
$K$個の共分散行列$\boldsymbol{\mu}$をsigma2_kddとして値を指定します。(ランダムに共分散行列を作成するのは少し手間なので)この例では、全てのクラスタを分散1000、共分散0とします。$D \times D$の単位行列をnp.identity(D)で作成して1000を掛けます。それをfor文でK個作成します。
混合係数$\boldsymbol{\pi}$をpi_kとして値を生成します。この例では、0以上の一様乱数を$K$個生成して、総和で割ることで$\sum_{k=1}^K \pi_k = 1,\ \pi_k \geq 0$となるように正規化します。
生成したパラメータは次のようになります。
# 確認 print(mu_kd) print(sigma2_kdd) print(pi_k)
[[-19.97009022 74.34371918]
[-36.79811568 26.31334054]
[ 12.19569363 -4.21029473]]
[[[1000. 0.]
[ 0. 1000.]]
[[1000. 0.]
[ 0. 1000.]]
[[1000. 0.]
[ 0. 1000.]]]
[0.30091715 0.10675321 0.59232964]
パラメータmu_kd, sigma2_ddkとpi_kの初期値を用いて、混合分布を計算します。
# 初期値による混合分布を計算 init_dens = 0 for k in range(K): # クラスタkの分布の確率密度を計算 tmp_dens = multivariate_normal.pdf( x=x_point_arr, mean=mu_kd[k], cov=sigma2_kdd[k] ) # K個の分布線形結合 init_dens += pi_k[k] * tmp_dens
# 初期値による分布を作図 plt.figure(figsize=(12, 9)) plt.contour(x_1_grid, x_2_grid, model_dens.reshape(x_dim), alpha=0.5, linestyles='dashed') # 真の分布 #plt.contour(x_1_grid, x_2_grid, init_dens.reshape(x_dim)) # 推定値による分布:(等高線) plt.contourf(x_1_grid, x_2_grid, init_dens.reshape(x_dim), alpha=0.6) # 推定値による分布:(塗りつぶし) plt.suptitle('Mixture of Gaussians', fontsize=20) plt.title('iter:' + str(0) + ', K=' + str(K), loc='left') plt.xlabel('$x_1$') plt.ylabel('$x_2$') plt.colorbar() # 等高線の色 plt.show()

真の分布のときと同様に計算して作図します。更新を繰り返すことで真の分布に近付けていきます。
初期値による対数尤度を計算します。
# 初期値による対数尤度を計算:式(9.14) term_dens_nk = np.array( [multivariate_normal.pdf(x=x_nd, mean=mu_kd[k], cov=sigma2_kdd[k]) for k in range(K)] ).T L = np.sum(np.log(np.sum(term_dens_nk, axis=1)))
次の式で対数尤度を計算します。
計算結果は次のようになります。
# 確認 print(L)
-2216.4456546901756
以上でモデルが整いました。次は、推論を行います。
・最尤推定
最尤推定では、EステップとMステップを交互に繰り返します。Eステップでは、負担率$\gamma(\mathbf{Z})$を更新します。Mステップでは、対数尤度が最大化されるようにパラメータ$\boldsymbol{\mu},\ \boldsymbol{\Sigma},\ \boldsymbol{\pi}$を更新します。
まずは、パラメータの初期値を用いて負担率を更新します。続いて、更新した負担率を用いて各パラメータを更新します。ここまでが1回の試行です。
次の試行では、前回更新したパラメータを用いて負担率を更新となります。この処理を指定した回数繰り返します。
・コード全体
後で各パラメータの更新値や分布の推移を確認するために、それぞれ試行ごとにtrace_***に値を保存していきます。関心のあるパラメータを記録してください。
# 試行回数を指定 MaxIter = 100 # 推移の確認用の受け皿を作成 trace_L_i = [L] trace_gamma_ink = [np.tile(np.nan, reps=(N, K))] trace_mu_ikd = [mu_kd.copy()] trace_sigma2_ikdd = [sigma2_kdd.copy()] trace_pi_ik = [pi_k.copy()] # 最尤推定 for i in range(MaxIter): # 負担率を計算:式(9.13) gamma_nk = np.array( [multivariate_normal.pdf(x=x_nd, mean=mu_kd[k], cov=sigma2_kdd[k]) for k in range(K)] ).T gamma_nk /= np.sum(gamma_nk, axis=1, keepdims=True) # 正規化 # 各クラスタとなるデータ数の期待値を計算:式(9.18) N_k = np.sum(gamma_nk, axis=0) for k in range(K): # 平均パラメータの最尤解を計算:式(9.17) mu_kd[k] = np.dot(gamma_nk[:, k], x_nd) / N_k[k] # 共分散行列の最尤解を計算:式(9.19) term_x_nd = x_nd - mu_kd[k] sigma2_kdd[k] = np.dot(gamma_nk[:, k] * term_x_nd.T, term_x_nd) / N_k[k] # 混合係数の最尤解を計算:式(9.22) pi_k = N_k / N # 対数尤度を計算:式(9.14) tmp_dens_nk = np.array( [multivariate_normal.pdf(x=x_nd, mean=mu_kd[k], cov=sigma2_kdd[k]) for k in range(K)] ).T L = np.sum(np.log(np.sum(tmp_dens_nk, axis=1))) # i回目の結果を記録 trace_L_i.append(L) trace_gamma_ink.append(gamma_nk.copy()) trace_mu_ikd.append(mu_kd.copy()) trace_sigma2_ikdd.append(sigma2_kdd.copy()) trace_pi_ik.append(pi_k.copy()) # 動作確認 #print(str(i + 1) + ' (' + str(np.round((i + 1) / MaxIter * 100, 1)) + '%)')
・処理の解説
続いて、EMアルゴリズムで行う処理を確認していきます。
・Eステップ
Eステップでは、負担率$\gamma(\mathbf{Z})$を更新(最尤解を計算)します。
前回のパラメータを用いて、負担率を計算します。
# 負担率を計算:式(9.13) gamma_nk = np.array( [multivariate_normal.pdf(x=x_nd, mean=mu_kd[k], cov=sigma2_kdd[k]) for k in range(K)] ).T gamma_nk /= np.sum(gamma_nk, axis=1, keepdims=True) # 正規化
次の式で負担率を計算します。
処理上は、全てのクラスタで分子の計算をして、行(データ)ごとに和をとったもので割る(正規化する)ことで、式(9.13)の計算になります。
計算結果は次のようになります。
# 確認 print(np.round(gamma_nk[:5], 3)) print(np.sum(gamma_nk[:5], axis=1))
[[0.106 0.891 0.003]
[0. 0. 1. ]
[0. 0.001 0.999]
[0.002 0. 0.997]
[0.998 0. 0.002]]
[1. 1. 1. 1. 1.]
行(データ)ごとの和が1になります。
各クラスタが割り当てられたデータ数の期待値を計算します。
# 各クラスタとなるデータ数の期待値を計算:式(9.18) N_k = np.sum(gamma_nk, axis=0)
次の式を計算してN_kとします。
# 確認 print(N_k)
[115.23815311 63.46617725 71.29566964]
これは次のパラメータの更新に使います。
・Mステップ
Mステップでは、対数尤度を最大にするパラメータ$\boldsymbol{\pi},\ \boldsymbol{\Sigma},\ \boldsymbol{\pi}$を更新(最尤解を計算)します。
平均パラメータを更新します。
k in range(K): # 平均パラメータの最尤解を計算:式(9.17) mu_kd[k] = np.dot(gamma_nk[:, k], x_nd) / N_k[k]
$\boldsymbol{\mu}_k$の最尤解をクラスタごとに次の式で更新します。
# 確認 print(mu_kd)
[[ 5.35629799 37.56788909]
[-18.1429256 -10.80318895]
[ 33.17084836 -22.73661902]]
共分散行列を更新します。
# 共分散行列の最尤解を計算:式(9.19)
term_x_nd = x_nd - mu_kd[k]
sigma2_kdd[k] = np.dot(gamma_nk[:, k] * term_x_nd.T, term_x_nd) / N_k[k]
$\boldsymbol{\Sigma}_k$の最尤解をクラスタごとに次の式で更新します。
ただし、$\sum_{n=1}^N$の計算を効率よく処理するために、$\tilde{\mathbf{X}} = \mathbf{x}_n - \boldsymbol{\mu}_k$として、$\tilde{\mathbf{X}}^{\top} \tilde{\mathbf{X}}$で計算しています。
# 確認 print(sigma2_kdd)
[[[ 221.73278714 44.59345633]
[ 44.59345633 233.5097042 ]]
[[ 187.86543726 -110.50844675]
[-110.50844675 187.09562851]]
[[ 155.41983497 -46.56668818]
[ -46.56668818 217.42368047]]]
混合係数を更新します。
# 混合係数の最尤解を計算:式(9.22)
pi_k = N_k / N
$\boldsymbol{\pi}$の最尤解を次の式で計算します。
# 確認 print(pi_k) print(np.sum(pi_k))
[0.46095261 0.25386471 0.28518268]
1.0
これでパラメータ$\boldsymbol{\mu},\ \boldsymbol{\Sigma},\ \boldsymbol{\pi}$を更新できました。更新したパラメータを用いて、対数尤度を計算して記録しておきます。計算方法は「初期値の設定」のときと同じです。
以上がEMアルゴリズムで行う個々の処理です。これを繰り返し行うことで、徐々にパラメータを真の値に近付けていきます。
・推論結果の確認
推論結果を確認していきます。
・最後のパラメータの確認
パラメータmu_kd, sigma2_ddkとpi_kの最後の更新値を用いて、混合分布を計算します。
# 最後の更新値による混合分布を計算 res_dens = 0 for k in range(K): # クラスタkの分布の確率密度を計算 tmp_dens = multivariate_normal.pdf( x=x_point_arr, mean=mu_kd[k], cov=sigma2_kdd[k] ) # K個の分布を線形結合 res_dens += pi_k[k] * tmp_dens
変数名以外は「初期値の設定」のときと同じコードです。
負担率を用いて、各データにクラスタを割り当てます。
# 負担率が最大のクラスタ番号を抽出 z_n = np.argmax(gamma_nk, axis=1) # 割り当てられたクラスタとなる負担率(確率)を抽出 prob_z_n = gamma_nk[np.arange(N), z_n]
各データにおいて負担率(確率)が最大のクラスタをそのデータのクラスタとします。np.argmax()を使って、gamma_nkの行(データ)ごとに値が最大の列番号(クラスタ番号)を抽出してz_nとします。また、その値を取り出してprob_z_nとします。
結果は次のようになります。
# 確認 print(z_n[:5]) print(prob_z_n[:5])
[1 2 2 2 0]
[0.8906079 0.99999988 0.99875865 0.99746493 0.99755678]
最後の更新値による分布とクラスタの散布図を重ねて作図します。
# K個のカラーマップを指定 colormap_list = ['Blues', 'Oranges', 'Greens'] # 負担率が最大のクラスタ番号を抽出 z_n = np.argmax(gamma_nk, axis=1) # 割り当てられたクラスタとなる負担率(確率)を抽出 prob_z_n = gamma_nk[np.arange(N), z_n] # 最後の更新値による混合分布を計算 res_dens = 0 for k in range(K): # クラスタkの分布の確率密度を計算 tmp_dens = multivariate_normal.pdf( x=x_point_arr, mean=mu_kd[k], cov=sigma2_kdd[k] ) # K個の分布を線形結合 res_dens += pi_k[k] * tmp_dens # 最後の更新値による分布を作図 plt.figure(figsize=(12, 9)) plt.contour(x_1_grid, x_2_grid, model_dens.reshape(x_dim), alpha=0.5, linestyles='dashed') # 真の分布 plt.scatter(x=mu_truth_kd[:, 0], y=mu_truth_kd[:, 1], color='red', s=100, marker='x') # 真の平均 plt.contourf(x_1_grid, x_2_grid, res_dens.reshape(x_dim), alpha=0.5) # 推定値による分布:(塗りつぶし) for k in range(K): k_idx, = np.where(z_n == k) # クラスタkのデータのインデックス cm = plt.get_cmap(colormap_list[k]) # クラスタkのカラーマップを設定 plt.scatter(x=x_nd[k_idx, 0], y=x_nd[k_idx, 1], c=[cm(p) for p in prob_z_n[k_idx]], label='cluster:' + str(k + 1)) # 負担率によるクラスタ #plt.contour(x_1_grid, x_2_grid, res_density.reshape(x_dim)) # 推定値による分布:(等高線) #plt.colorbar() # 等高線の値:(等高線用) plt.suptitle('Mixture of Gaussians:Maximum Likelihood', fontsize=20) plt.title('$iter:' + str(MaxIter) + ', L=' + str(np.round(L, 1)) + ', N=' + str(N) + ', \pi=[' + ', '.join([str(pi) for pi in np.round(pi_k, 3)]) + ']$', loc='left') plt.xlabel('$x_1$') plt.ylabel('$x_2$') plt.legend() plt.show()

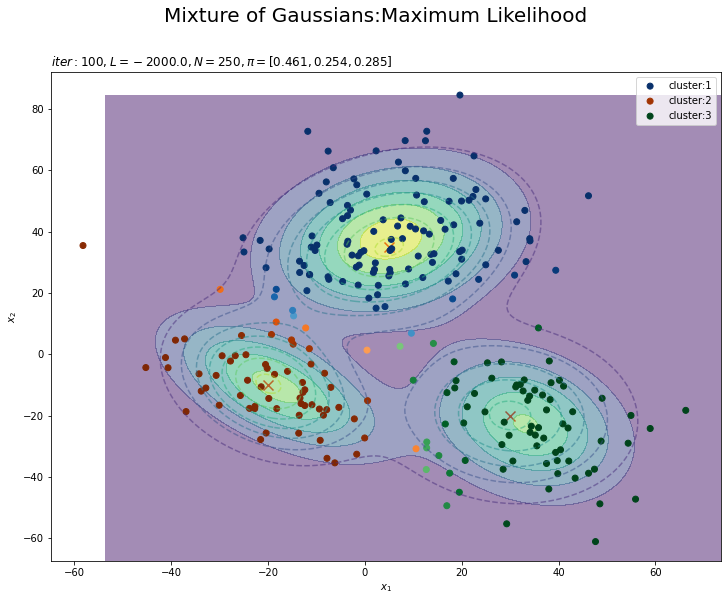
データの生成のときと同様に、各データに割り当てられたクラスタに従って色分けします。ただしここでは、そのクラスタとなる確率に従って濃淡を付けることにします。plt.get_cmap()によって確率値を色コードに変換したもの(よく分かってない…)を、plt.scatter()の色の引数cに指定します。
上の図はplt.contour()で、下の図はplt.contourf()で作成したものです。
対数尤度の推移を作図します。
## 対数尤度の推移を作図 plt.figure(figsize=(12, 9)) plt.plot(np.arange(MaxIter + 1), np.array(trace_L_i)) plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('Maximum Likelihood', fontsize=20) plt.title('Log Likelihood', loc='left') plt.grid() # グリッド線 plt.show()

更新を繰り返すごとに対数尤度が増加しているのを確認できます。
・パラメータの推移の確認
パラメータの更新値の推移を確認します。
・コード(クリックで展開)
初期値とMaxIter個の値を格納した各パラメータのリストtrace_***をnp.arange()でNumPy配列に変換して作図します。それぞれ真の値***_truthを水平線plt.hlines()で描画しておきます。
# muの推移を作図 plt.figure(figsize=(12, 9)) plt.hlines(y=mu_truth_kd, xmin=0, xmax=MaxIter + 1, label='true val', color='red', linestyles='--') # 真の値 for k in range(K): for d in range(D): plt.plot(np.arange(MaxIter+1), np.array(trace_mu_ikd)[:, k, d], label='k=' + str(k + 1) + ', d=' + str(d + 1)) plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('Maximum Likelihood', fontsize=20) plt.title('$\mu$', loc='left') plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()
# lambdaの推移を作図 plt.figure(figsize=(12, 9)) plt.hlines(y=sigma2_truth_kdd, xmin=0, xmax=MaxIter + 1, label='true val', color='red', linestyles='--') # 真の値 for k in range(K): for d1 in range(D): for d2 in range(D): plt.plot(np.arange(MaxIter + 1), np.array(trace_sigma2_ikdd)[:, k, d1, d2], alpha=0.5, label='k=' + str(k + 1) + ', d=' + str(d1 + 1) + ', d''=' + str(d2 + 1)) plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('Maximum Likelihood', fontsize=20) plt.title('$\Sigma$', loc='left') plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()
# piの推移を作図 plt.figure(figsize=(12, 9)) plt.hlines(y=pi_truth_k, xmin=0, xmax=MaxIter + 1, label='true val', color='red', linestyles='--') # 真の値 for k in range(K): plt.plot(np.arange(MaxIter + 1), np.array(trace_pi_ik)[:, k], label='k=' + str(k + 1)) plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('Maximum Likelihood', fontsize=20) plt.title('$\pi$', loc='left') plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()



更新を繰り返すに従って真の値に近付いているのを確認できます。
・おまけ:アニメーションによる推移の確認
animationモジュールを利用して、各分布の推移のアニメーション(gif画像)を作成するためのコードです。
# 追加ライブラリ import matplotlib.animation as animation
・サンプルしたパラメータによる分布とクラスタの推移
・コード(クリックで展開)
# K個のカラーマップを指定 colormap_list = ['Blues', 'Oranges', 'Greens'] # 画像サイズを指定 fig = plt.figure(figsize=(9, 9)) # 作図処理を関数として定義 def update_model(i): # i回目の更新値による混合分布を計算 res_dens = 0 for k in range(K): # クラスタkの分布の確率密度を計算 tmp_dens = multivariate_normal.pdf( x=x_point_arr, mean=trace_mu_ikd[i][k], cov=trace_sigma2_ikdd[i][k] ) # K個の分布を線形結合 res_dens += trace_pi_ik[i][k] * tmp_dens # 前フレームのグラフを初期化 plt.cla() # i回目の負担率を取得 gamma_nk = trace_gamma_ink[i] # i回目のサンプルによる分布を作図 plt.contour(x_1_grid, x_2_grid, model_dens.reshape(x_dim), alpha=0.5, linestyles='dashed') # 真の分布 #plt.contour(x_1_grid, x_2_grid, res_dens.reshape(x_dim)) # 推定値による分布:(等高線) plt.contourf(x_1_grid, x_2_grid, res_dens.reshape(x_dim), alpha=0.5) # 推定値による分布:(塗りつぶし) plt.scatter(x=mu_truth_kd[:, 0], y=mu_truth_kd[:, 1], color='red', s=100, marker='x') # 真の平均 for k in range(K): k_idx, = np.where(np.argmax(gamma_nk, axis=1) == k) cm = plt.get_cmap(colormap_list[k]) # クラスタkのカラーマップを設定 plt.scatter(x=x_nd[k_idx, 0], y=x_nd[k_idx, 1], c=[cm(p) for p in gamma_nk[k_idx, k]], label='cluster:' + str(k + 1)) # 負担率によるクラスタ plt.suptitle('Mixture of Gaussians:Maximum Likelihood', fontsize=20) plt.title('$iter:' + str(i) + ', L=' + str(np.round(trace_L_i[i], 1)) + ', N=' + str(N) + ', \pi=(' + ', '.join([str(pi) for pi in np.round(trace_pi_ik[i], 3)]) + ')$', loc='left') plt.xlabel('$x_1$') plt.ylabel('$x_2$') plt.legend() # gif画像を作成 model_anime = animation.FuncAnimation(fig, update_model, frames=MaxIter + 1, interval=100) model_anime.save("ch9_2_2_Model_f.gif")
(よく理解していないので、animationの解説は省略…とりあえずこれで動きます……)


上の図はplt.contour()で、下の図はplt.contourf()で作成したものです。
参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上下』,丸善出版,2012年.
おわりに
次はどれしよっかな。
【関連する内容】