はじめに
『ベイズ推論による機械学習入門』の学習時のノートです。基本的な内容は「数式の行間を読んでみた」とそれを「RとPythonで組んでみた」になります。「数式」と「プログラム」から理解するのが目標です。
この記事は、3.2.2項の内容です。尤度関数をカテゴリ分布、事前分布をディリクレ分布とした場合のパラメータの事後分布と未観測値の予測分布の計算をPythonで実装します。
省略してある内容等ありますので、本とあせて読んでください。初学者な自分が理解できるレベルまで落として書き下していますので、分かる人にはかなりくどくなっています。同じような立場の人のお役に立てれば幸いです。
【数式読解編】
【他の節の内容】
【この節の内容】
・Pythonでやってみよう
人工的に生成したデータを用いて、ベイズ推論を行ってみましょう。
利用するパッケージを読み込みます。
# 3.2.2項で利用するライブラリ import numpy as np import math # 対数ガンマ関数:lgamma() from scipy.stats import dirichlet # ディリクレ分布 import matplotlib.pyplot as plt
この例では、ディリクレ分布の確率密度を求めるのにガンマ関数$\Gamma(\cdot)$の計算を行います。ガンマ関数の計算には、mathライブラリの対数をとったガンマ関数lgamma()を使います。または、SciPyライブラリのderichlet.pdf()で直接ディリクレ分布の確率密度を計算することもできます。
・モデルの構築
まずは、モデルの設定を行います。
尤度(カテゴリ分布)$p(\mathbf{S} | \boldsymbol{\pi})$のパラメータ$\boldsymbol{\pi} = (\pi_1, \pi_2, \cdots, \pi_K)$を設定します。
# 次元数:(固定) K = 3 # 真のパラメータを指定 pi_truth_k = np.array([0.3, 0.5, 0.2])
次元数$K$をKとします。この例では三角図で可視化するため、一部のプログラムは$K = 3$の場合だけ動作します。超パラメータの推定自体は、3以外でも動作します。
$\pi_k$は、各データ$\mathbf{s}_n = (s_{n,1}, s_{n,2}, \cdots, s_{n,K})$において$s_{n,k} = 1$となる確率です。$\boldsymbol{\pi}$をpi_truth_kとして、$0 \leq \pi_k \leq 1$、$\sum_{k=1}^K \pi_k = 1$の値を指定します。これが真のパラメータであり、この値を求めるのがここでの目的です。
作図用に、尤度の次元番号$k = 1, 2, \cdots, K$の配列を作成します。
# x軸の値を作成 k_line = np.arange(1, K + 1)
尤度の各次元に対応する確率は、カテゴリ分布の定義式
や、scipyライブラリの多項分布の確率計算関数multinomial.pmf()で計算できます。
# 全てのパターンのデータを作成 s_kk = np.identity(K) # 確率を計算:式(2.29) print(np.prod(pi_truth_k**s_kk, axis=1)) # 確率を計算:SciPy ver from scipy.stats import multinomial # 多項分布 print(multinomial.pmf(x=s_kk, n=1, p=pi_truth_k))
[0.3 0.5 0.2]
[0.3 0.5 0.2]
ただし、$\mathbf{s}_n$における$s_{n,k} = 1$以外の$s_{n,1}, \cdots, s_{n,k-1}, s_{n,k+1}, \cdots, s_{n,K}$は0であり、$x^0 = 1$なので、計算結果はpi_truth_kになります。
よって、パラメータpi_truth_kをそのまま使って尤度を作図します。
# 画像サイズを指定 fig = plt.figure(figsize=(12, 9)) # 尤度を作図 plt.bar(x=k_line, height=pi_truth_k, color='purple') # 真のモデル plt.xlabel('k') plt.ylabel('prob') plt.xticks(ticks=k_line, labels=k_line) # x軸目盛 plt.suptitle('Categorical Distribution', fontsize=20) plt.title('$\pi=(' + ', '.join([str(k) for k in pi_truth_k]) + ')$', loc='left') plt.ylim(0, 1) plt.show()
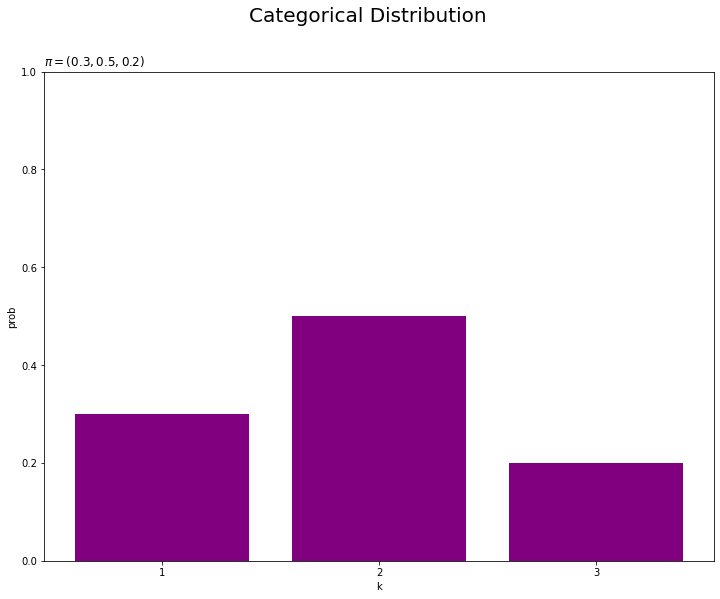
真のパラメータを求めることは、この真の分布を求めることを意味します。
・データの生成
続いて、構築したモデルに従って観測データ$\mathbf{S} = \{\mathbf{s}_1, \mathbf{s}_2, \cdots, \mathbf{s}_N\}$を生成します。
カテゴリ分布に従う$N$個のデータをランダムに生成します。
# データ数を指定 N = 50 # (観測)データを生成 s_nk = np.random.multinomial(n=1, pvals=pi_truth_k, size=N)
生成するデータ数$N$をNとして、値を指定します。
カテゴリ分布に従う乱数は、多項分布に従う乱数生成関数np.random.multinomial()のn引数を1にすることで生成できます。また、確率の引数pvalsにpi_truth_k、試行回数の引数sizeにNを指定します。生成したN個のデータをs_nkとします。
観測したデータ$\mathbf{S}$を確認しましょう。
# 観測のデータを確認 print(s_nk[:5]) print(np.sum(s_nk, axis=0))
[[0 1 0]
[1 0 0]
[0 1 0]
[0 1 0]
[0 1 0]]
[17 22 11]
各データ$\mathbf{s}_n = (s_{n,1}, s_{n,1}, \cdots, s_{n,K})$は、1つの項を1、それ以外の項を0とする$K$次元ベクトルです。$k$番目の次元において1となったデータ数は、$\sum_{n=1}^N s_{n,k}$で得られます。
$\mathbf{S}$をヒストグラムでも確認します。
# 画像サイズを指定 fig = plt.figure(figsize=(12, 9)) # 観測データのヒストグラムを作図 plt.bar(x=k_line, height=np.sum(s_nk, axis=0)) # 観測データ plt.xlabel('k') plt.ylabel('count') plt.xticks(ticks=k_line, labels=k_line) # x軸目盛 plt.suptitle('Observation Data', fontsize=20) plt.title('$N=' + str(N) + ', \pi=(' + ', '.join([str(k) for k in pi_truth_k]) + ')$', loc='left') plt.show()
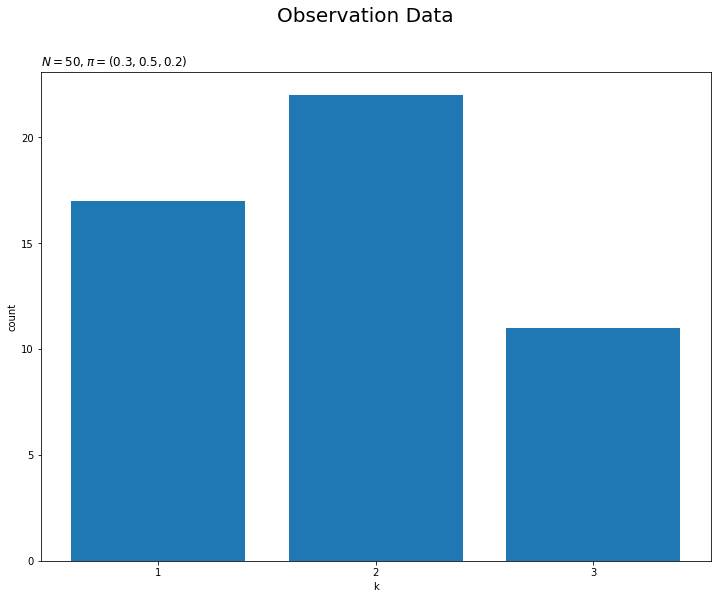
データ数が十分に大きいと、分布の形状が真の分布に近づきます。
・事前分布の設定
尤度に対する共役事前分布を設定します。
事前分布(ディリクレ分布)$p(\boldsymbol{\pi} | \boldsymbol{\alpha})$のパラメータ(超パラメータ)を設定します。
# 事前分布のパラメータを指定 alpha_k = np.array([1.0, 1.0, 1.0])
ディリクレ分布のパラメータ$\boldsymbol{\alpha} = (\alpha_1, \alpha_2, \cdots, \alpha_K)$をalpha_kとして、$\alpha_k > 0$の値を指定します。
事前分布の作図用に、$\boldsymbol{\pi}$がとり得る値を用意します。
# 作図用の点を設定 point_vec = np.arange(0.0, 1.001, 0.02) # 格子状の点を作成 X, Y, Z = np.meshgrid(point_vec, point_vec, point_vec) # 確率密度の計算用にまとめる pi_point = np.array([list(X.flatten()), list(Y.flatten()), list(Z.flatten())]).T pi_point = pi_point[1:, :] # (0, 0, 0)の行を除去 pi_point /= np.sum(pi_point, axis=1, keepdims=True) # 正規化 pi_point = np.unique(pi_point, axis=0) # 重複を除去
np.arange()で、$\pi_k$がとり得る0から1までの値を用意してpoint_vecとします。第3引数で間隔を指定できるので、グラフが粗かったり処理が重かったりする場合はこの値を調整してください。
事前分布(と事後分布)を三角図で描画するために、パラメータは3次元$\boldsymbol{\pi} = (\pi_1, \pi_2, \pi_3)$に限ります。point_vecの要素を使ってnp.meshgrid()で、3つの次元で全ての組み合わせを作成しX, Y, Zとします。
X, Y, Zをflatten()で1列に並べ直して2次元配列に格納します。その際、最初の行が$\boldsymbol{\pi} = (0, 0, 0)$になってしまうので取り除き、各行の総和が1になるように正規化します。最後に、正規化したことで重複した行を取り除きます。
簡単な例にすると次のような処理です。
# 作図用の点を作成 vec = np.array([1, 2]) X, Y, Z = np.meshgrid(vec, vec, vec) arr = np.array([list(X.flatten()), list(Y.flatten()), list(Z.flatten())]).T print(arr)
[[1 1 1]
[1 1 2]
[2 1 1]
[2 1 2]
[1 2 1]
[1 2 2]
[2 2 1]
[2 2 2]]
事前分布の確率密度を計算します。
# 事前分布(ディリクレ分布)の確率密度を計算:式(2.41) ln_C_dir = math.lgamma(np.sum(alpha_k)) - np.sum([math.lgamma(a) for a in alpha_k]) # 正規化項(対数) prior = np.exp(ln_C_dir) * np.prod(pi_point**(alpha_k - 1), axis=1) # 事前分布(ディリクレ分布)の確率密度を計算:SciPy ver prior = np.array([ dirichlet.pdf(x=pi_point[i], alpha=alpha_k) for i in range(len(pi_point)) ])
pi_pointの各行に対して確率密度を計算します。ディリクレ分布の確率密度は、定義式
で計算します。ここで、$\Gamma(\cdot)$はガンマ関数です。
ガンマ関数の計算はmath.gamma()で行えますが、値が大きくなると発散してしまします。そこで、対数をとったガンマ関数math.lgamma()で計算した後に、np.exp()で戻します。
または、SciPyライブラリのdirichlet.pdf()でも計算できます。(たぶん上の方が早い?)
計算結果は次のようになります。
# 確認 print(prior)
[2. 2. 2. ... 2. 2. 2.]
事前分布を作図します。
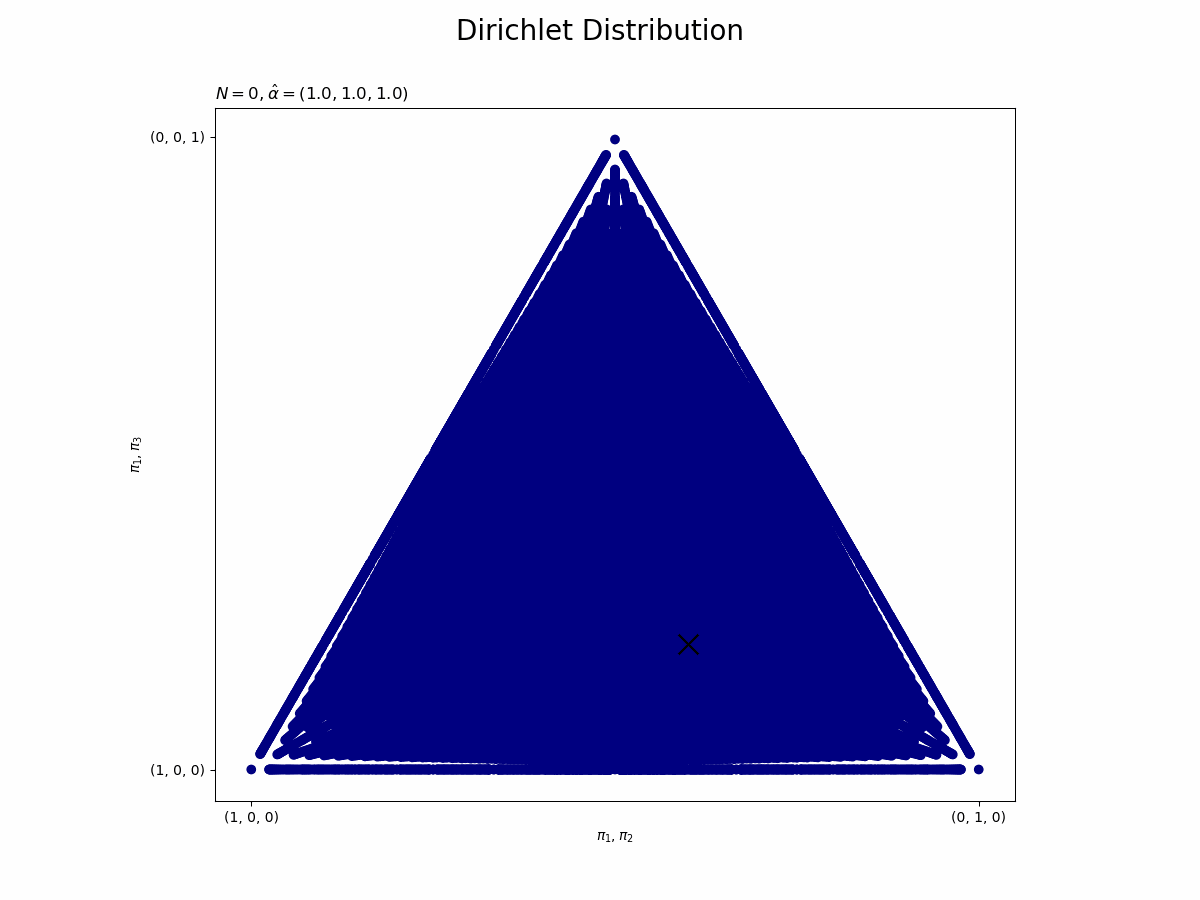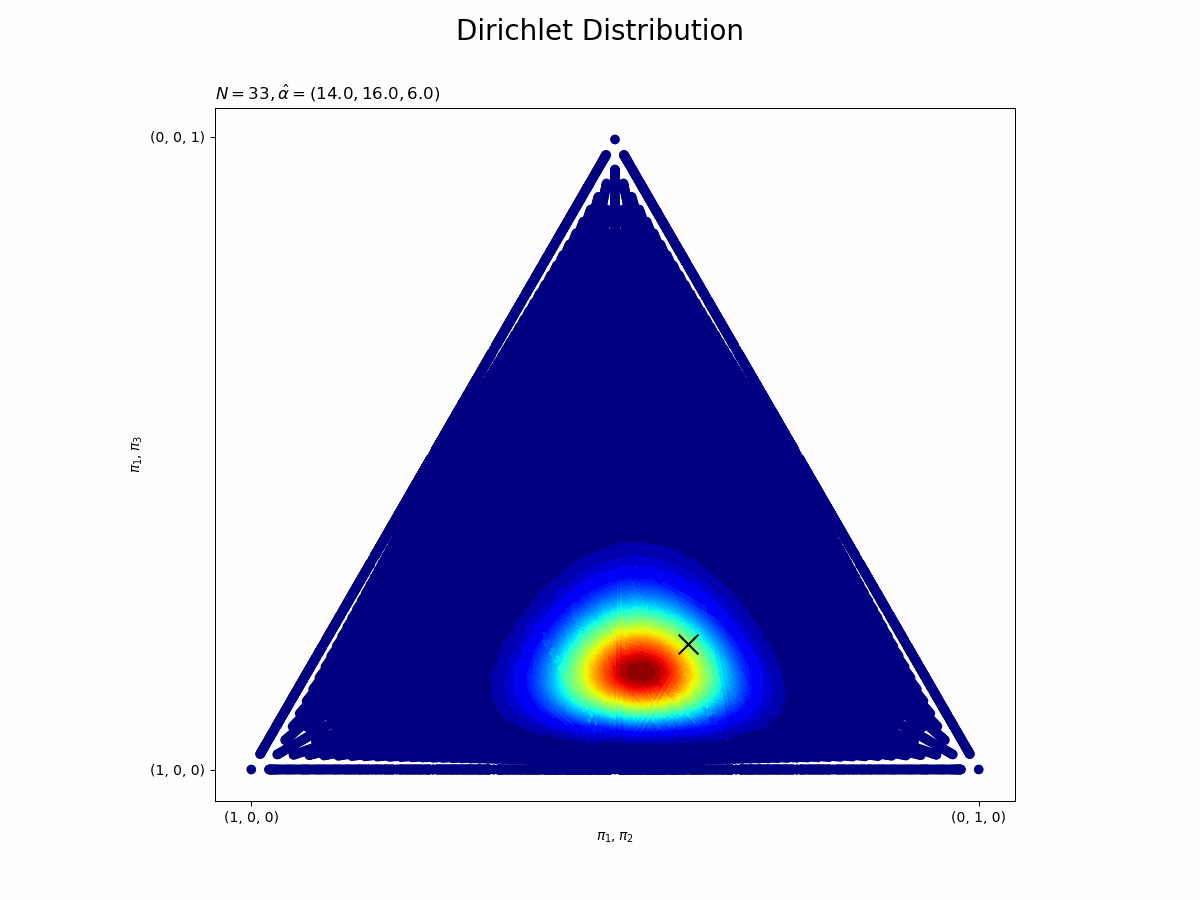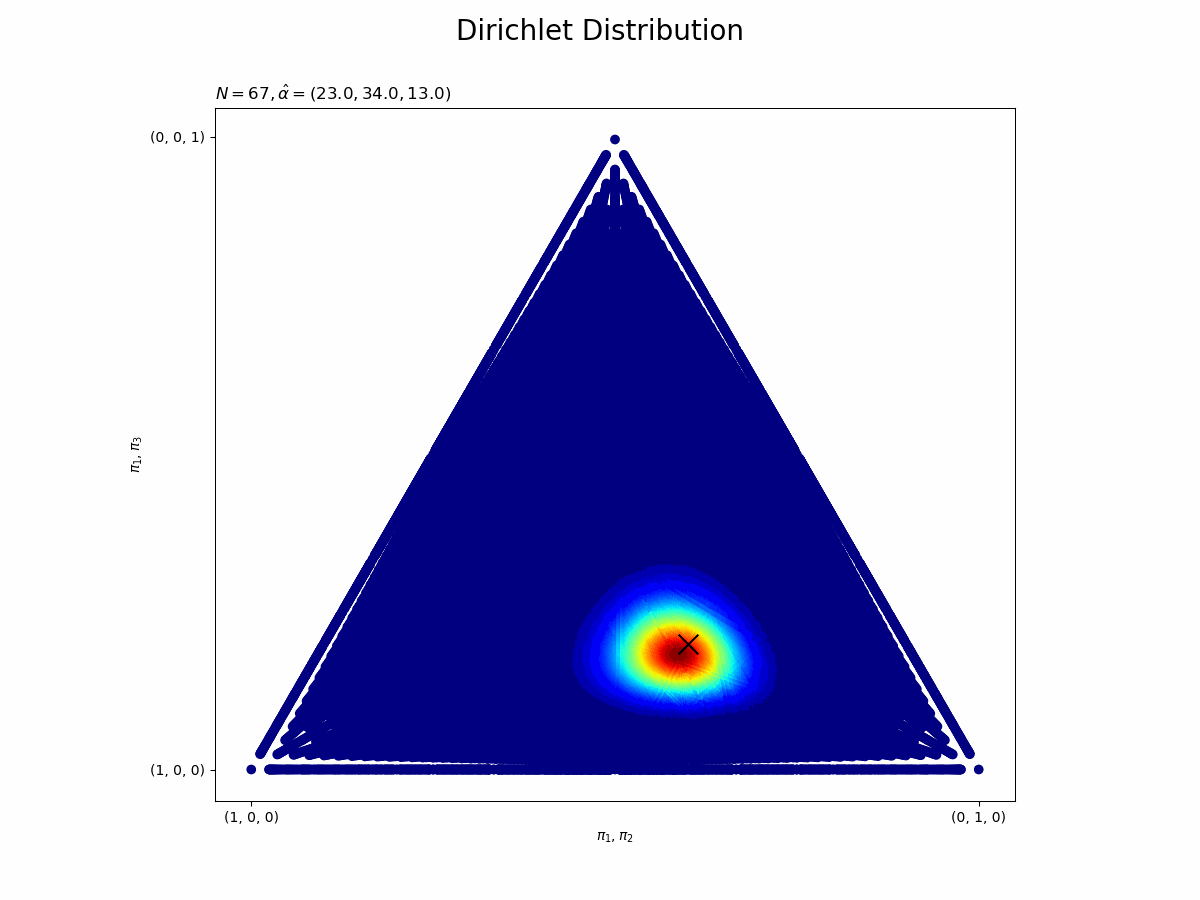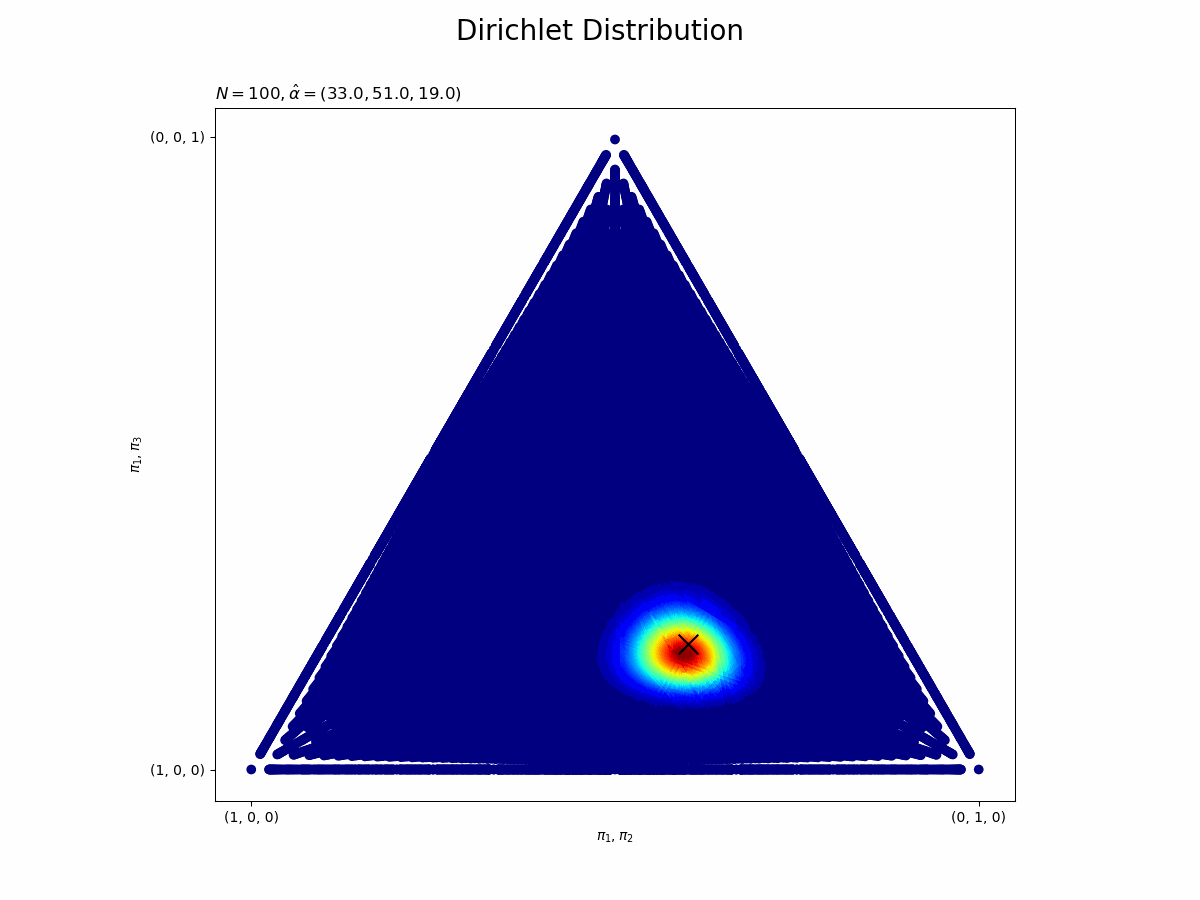
# 三角座標に変換 tri_x = pi_point[:, 1] + pi_point[:, 2] / 2 tri_y = np.sqrt(3) * pi_point[:, 2] / 2 # 画像サイズを指定 fig = plt.figure(figsize=(12, 9)) # 事前分布を作図 plt.scatter(tri_x, tri_y, c=prior, cmap='jet') # 事前分布 plt.xlabel('$\pi_1, \pi_2$') # x軸ラベル plt.ylabel('$\pi_1, \pi_3$') # y軸ラベル plt.xticks(ticks=[0.0, 1.0], labels=['(1, 0, 0)', '(0, 1, 0)']) # x軸目盛 plt.yticks(ticks=[0.0, 0.87], labels=['(1, 0, 0)', '(0, 0, 1)']) # y軸目盛 plt.suptitle('Dirichlet Distribution', fontsize=20) plt.title('$\\alpha=(' + ', '.join([str(k) for k in alpha_k]) + ')$', loc='left') plt.colorbar() # 凡例 plt.gca().set_aspect('equal') # アスペクト比 plt.show()

3次元の値を2次元の図に落とし込むために、三角図に落とし込みます。
alpha_kの値を変更することで、ディリクレ分布におけるパラメータと形状の関係を確認できます。
・事後分布の計算
観測データ$\mathbf{S}$からパラメータ$\boldsymbol{\pi}$の事後分布を求めます(パラメータ$\boldsymbol{\pi}$を分布推定します)。
観測データs_nkを用いて、事後分布(ディリクレ分布)のパラメータを計算します。
# 事後分布のパラメータを計算:式(3.28) alpha_hat_k = np.sum(s_nk, axis=0) + alpha_k
事後分布のパラメータは
で計算して、結果をalpha_hat_kとします。
# 確認 print(alpha_hat_k)
[18. 23. 12.]
事前分布のパラメータ$\alpha_1, \cdots, \alpha_K$に、それぞれs_nkの次元ごとに1となったデータ数を加えています。
事後分布の確率密度を計算します。
# 事後分布(ディリクレ分布)の確率密度を計算:式(2.41) ln_C_dir = math.lgamma(np.sum(alpha_hat_k)) - np.sum([math.lgamma(a) for a in alpha_hat_k]) # 正規化項(対数) posterior = np.exp(ln_C_dir) * np.prod(pi_point**(alpha_hat_k - 1), axis=1) # 事後分布(ディリクレ分布)の確率密度を計算:SciPy ver posterior = np.array([ dirichlet.pdf(x=pi_point[i], alpha=alpha_hat_k) for i in range(len(pi_point)) ])
更新した超パラメータalpha_hat_kを用いて、事前分布のときと同様にして計算します。
計算結果は次のようになります。
# 確認 print(posterior)
[0. 0. 0. ... 0. 0. 0.]
真のパラメータの位置を表示するために、三角図上のx軸とy軸の値を計算します。
# 真のパラメータの値を三角座標に変換 tri_x_truth = pi_truth_k[1] + pi_truth_k[2] / 2 tri_y_truth = np.sqrt(3) * pi_truth_k[2] / 2
事後分布を作図します。
# 画像サイズを指定 fig = plt.figure(figsize=(12, 9)) # 事後分布を作図 plt.scatter(tri_x, tri_y, c=posterior, cmap='jet') # 事後分布 plt.xlabel('$\pi_1, \pi_2$') # x軸ラベル plt.ylabel('$\pi_1, \pi_3$') # y軸ラベル plt.xticks(ticks=[0.0, 1.0], labels=['(1, 0, 0)', '(0, 1, 0)']) # x軸目盛 plt.yticks(ticks=[0.0, 0.87], labels=['(1, 0, 0)', '(0, 0, 1)']) # y軸目盛 plt.suptitle('Dirichlet Distribution', fontsize=20) plt.title('$\\alpha=(' + ', '.join([str(k) for k in alpha_hat_k]) + ')$', loc='left') plt.colorbar() # 凡例 plt.gca().set_aspect('equal') # アスペクト比 plt.scatter(tri_x_truth, tri_y_truth, marker='x', color='black', s=200) # 真のパラメータ plt.show()

パラメータ$\mu$の真の値付近をピークとする分布を推定できています。
・予測分布の計算
最後に、$\mathbf{S}$から未観測のデータ$\mathbf{s}_{*}$の予測分布を求めます。
事後分布のパラメータalpha_hat_k、または観測データs_nkと事前分布のパラメータalpha_kを用いて予測分布(カテゴリ分布)のパラメータを計算します。
# 予測分布のパラメータを計算 pi_hat_star_k = alpha_hat_k / np.sum(alpha_hat_k) pi_hat_star_k = (np.sum(s_nk, axis=0) + alpha_k) / np.sum(np.sum(s_nk, axis=0) + alpha_k)
予測分布のパラメータの計算式
の結果をpi_hat_star_kとします。
上の式だと、事後分布のパラメータalpha_hat_kを使って計算できます。下の式だと、観測データs_nkと事前分布のパラメータalpha_kを使って計算できます。
# 確認 print(pi_hat_star_k)
[0.33962264 0.43396226 0.22641509]
$\hat{\pi}_{*}$は、$s_{*,k} = 1$となる確率を表し、$\mathbf{S}$から学習しているのが式からも分かります。
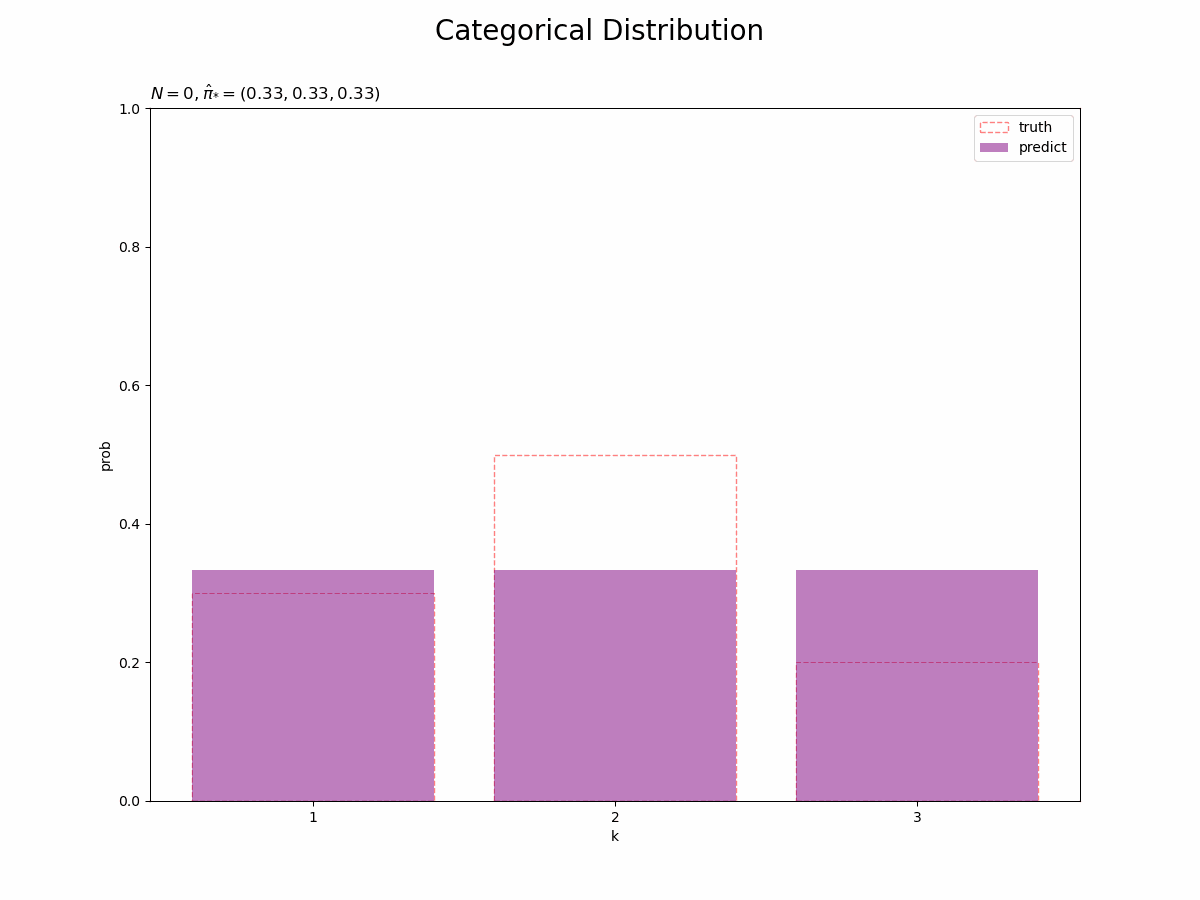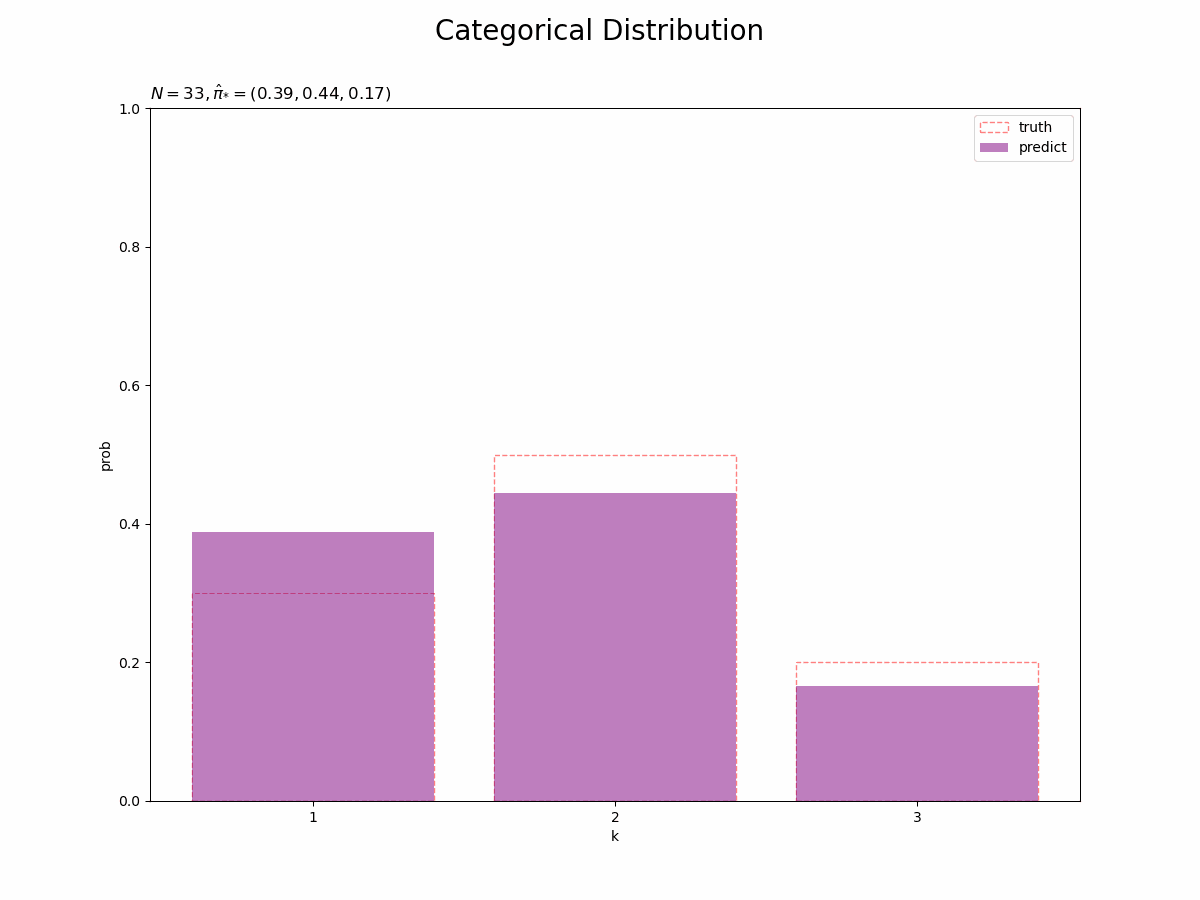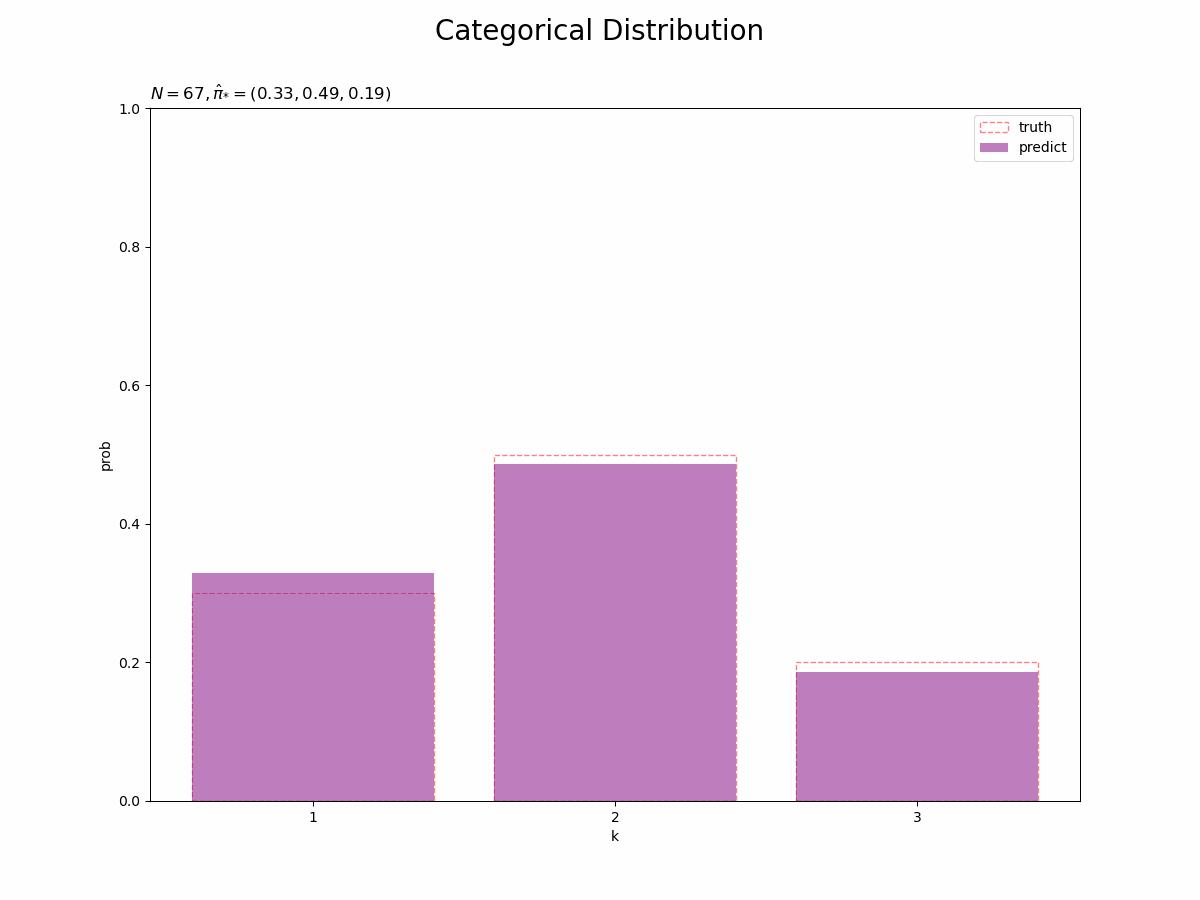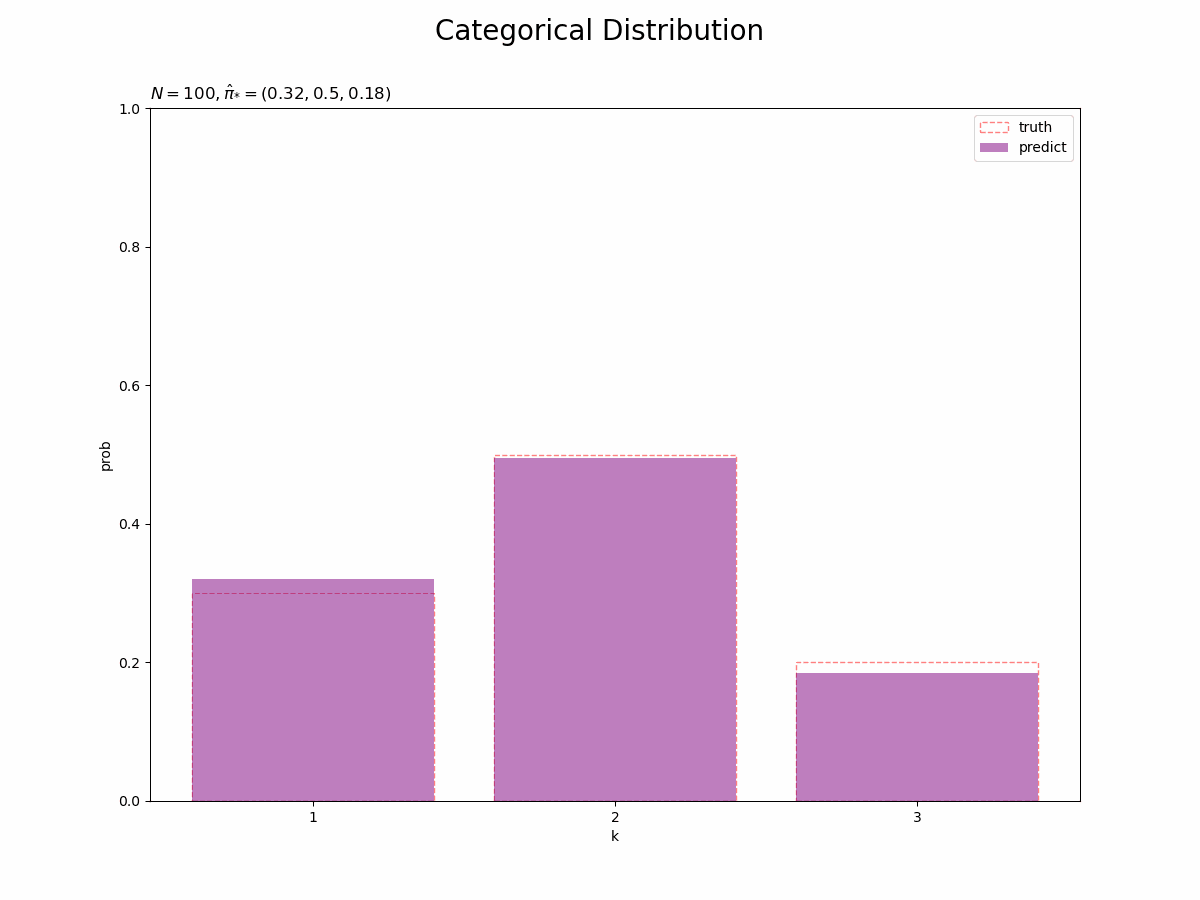
予測分布を真のモデルと重ねて作図します。
# 画像サイズを指定 fig = plt.figure(figsize=(12, 9)) # 予測分布を作図 plt.bar(x=k_line, height=pi_truth_k, label='truth', alpha=0.5, color='white', edgecolor='red', linestyle='dashed') # 真のモデル plt.bar(x=k_line, height=pi_hat_star_k, label='predict', alpha=0.5, color='purple') # 予測分布 plt.xlabel('k') plt.ylabel('prob') plt.xticks(ticks=k_line, labels=k_line) # x軸目盛 plt.suptitle('Categorical Distribution', fontsize=20) plt.title('$N=' + str(N) + ', \hat{\pi}_{*}=(' + ', '.join([str(k) for k in np.round(pi_hat_star_k, 2)]) + ')$', loc='left') plt.ylim(0, 1) plt.show()
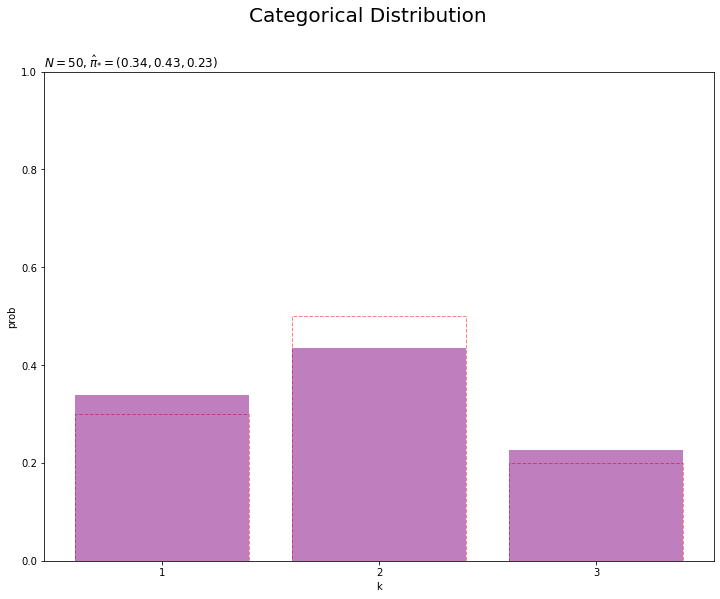
観測データが増えると、予測分布が真の分布に近づきます。
・おまけ:推移の確認
animationモジュールを利用して、パラメータの推定値の推移のアニメーション(gif画像)を作成するためのコードです。
・コード(クリックで展開)
# 利用するライブラリ import numpy as np from scipy.stats import dirichlet # ディリクレ分布 import matplotlib.pyplot as plt import matplotlib.animation as animation
異なる点のみ簡単に解説します。
# 作図用の点を設定 point_vec = np.arange(0.0, 1.001, 0.025) # 格子状の点を作成 X, Y, Z = np.meshgrid(point_vec, point_vec, point_vec) # 確率密度の計算用にまとめる pi_point = np.array([list(X.flatten()), list(Y.flatten()), list(Z.flatten())]).T pi_point = pi_point[1:, :] # (0, 0, 0)の行を除去 pi_point /= np.sum(pi_point, axis=1, keepdims=True) # 正規化 pi_point = np.unique(pi_point, axis=0) # 重複を除去 # 三角座標に変換 tri_x = pi_point[:, 1] + pi_point[:, 2] / 2 tri_y = np.sqrt(3) * pi_point[:, 2] / 2
# 次元数:(固定) K = 3 # 真のパラメータを指定 pi_truth_k = np.array([0.3, 0.5, 0.2]) # 事前分布のパラメータを指定 alpha_k = np.array([1.0, 1.0, 1.0]) # 初期値による予測分布のパラメータを計算 mu_star_k = alpha_k / np.sum(alpha_k)
試行ごとの結果をtrace_***に格納していきます。それぞれ初期値の結果を持つように作成しておきます。
# データ数を指定 N = 100 # 記録用の受け皿を初期化 s_nk = np.empty((N, K)) trace_alpha = [list(alpha_k)] trace_posterior = [[dirichlet.pdf(x=pi_point[i], alpha=alpha_k) for i in range(len(pi_point))]] trace_predict = [list(mu_star_k)] # ベイズ推論 for n in range(N): # (観測)データを生成 s_nk[n] = np.random.multinomial(n=1, pvals=pi_truth_k, size=1)[0] # 事後分布のパラメータを更新:式(3.28) alpha_k += s_nk[n] # 値を記録 trace_alpha.append(list(alpha_k)) # 事後分布(ディリクレ分布)の確率密度を計算:式(2.41) trace_posterior.append( [dirichlet.pdf(x=pi_point[i], alpha=alpha_k) for i in range(len(pi_point))] ) # 予測分布のパラメータを更新 mu_star_k = alpha_k / np.sum(alpha_k) # 予測分布(カテゴリ分布)の確率を記録 trace_predict.append(list(mu_star_k)) # 途中経過を表示 print('n=' + str(n + 1) + ' (' + str(np.round((n + 1) / N * 100, 1)) + '%)')
n=1 (1.0%)
n=2 (2.0%)
n=3 (3.0%)
n=4 (4.0%)
n=5 (5.0%)
(省略)
n=96 (96.0%)
n=97 (97.0%)
n=98 (98.0%)
n=99 (99.0%)
n=100 (100.0%)
観測された各データによってどのように学習する(分布が変化する)のかを確認するため、for文で1データずつ処理します。よって、データ数Nがイタレーション数になります。
パラメータの推定値に関して、$\hat{\boldsymbol{\alpha}}$に対応するalpha_hat_kを新たに作るのではなく、alpha_kをイタレーションごとに更新していきます。
それに伴い、事後分布のパラメータの計算式(3.28)の$\sum_{n=1}^N$の計算は、forループによってN回繰り返しs_nk[n]を加えることで行います。n回目のループ処理のときには、n-1回分のs_nk[n]が既にalpha_kに加えられているわけです。
結果は次のようになります。
# 確認 print(np.sum(s_nk, axis=0)) print(trace_alpha[:5]) print(np.round(trace_posterior[:5], 2)) print(np.round(trace_predict[:5], 2))
[24. 51. 25.]
[[1.0, 1.0, 1.0], [2.0, 1.0, 1.0], [2.0, 2.0, 1.0], [2.0, 2.0, 2.0], [3.0, 2.0, 2.0]]
[[2. 2. 2. ... 2. 2. 2. ]
[0. 0. 0. ... 5.88 5.88 6. ]
[0. 0. 0. ... 0. 0.46 0. ]
[0. 0. 0. ... 0. 0. 0. ]
[0. 0. 0. ... 0. 0. 0. ]]
[[0.33 0.33 0.33]
[0.5 0.25 0.25]
[0.4 0.4 0.2 ]
[0.33 0.33 0.33]
[0.43 0.29 0.29]]
・事後分布の推移
## 事後分布の推移をgif画像化 # 真のパラメータの値を三角座標に変換 tri_x_truth = pi_truth_k[1] + pi_truth_k[2] / 2 tri_y_truth = np.sqrt(3) * pi_truth_k[2] / 2 # 画像サイズを指定 fig = plt.figure(figsize=(12, 9)) # 作図処理を関数として定義 def update_posterior(n): # 前フレームのグラフを初期化 plt.cla() # nフレーム目の事後分布を作図 plt.scatter(tri_x, tri_y, c=trace_posterior[n], cmap='jet') # 事後分布 plt.scatter(tri_x_truth, tri_y_truth, marker='x', color='black', s=200) # 真のパラメータ plt.xlabel('$\pi_1, \pi_2$') # x軸ラベル plt.ylabel('$\pi_1, \pi_3$') # y軸ラベル plt.xticks(ticks=[0.0, 1.0], labels=['(1, 0, 0)', '(0, 1, 0)']) # x軸目盛 plt.yticks(ticks=[0.0, 0.87], labels=['(1, 0, 0)', '(0, 0, 1)']) # y軸目盛 plt.suptitle('Dirichlet Distribution', fontsize=20) plt.title('$N=' + str(n) + ', \hat{\\alpha}=(' + ', '.join([str(a) for a in trace_alpha[n]]) + ')$', loc='left') plt.gca().set_aspect('equal') # アスペクト比 # gif画像を作成 posterior_anime = animation.FuncAnimation(fig, update_posterior, frames=N + 1, interval=100) posterior_anime.save("ch3_2_2_Posterior.gif")
・予測分布の推移
## 予測分布の推移をgif画像化 # x軸の値を作成 k_line = np.arange(1, K + 1) # 画像サイズを指定 fig = plt.figure(figsize=(12, 9)) # 作図処理を関数として定義 def update_predict(n): # 前フレームのグラフを初期化 plt.cla() # nフレーム目の予測分布を作図 plt.bar(x=k_line, height=pi_truth_k, label='truth', alpha=0.5, color='white', edgecolor='red', linestyle='dashed') # 真の分布 plt.bar(x=k_line, height=trace_predict[n], label='predict', alpha=0.5, color='purple') # 予測分布 plt.xlabel('k') plt.ylabel('prob') plt.xticks(ticks=k_line, labels=k_line) # x軸目盛 plt.suptitle('Categorical Distribution', fontsize=20) plt.title('$N=' + str(n) + ', \hat{\pi}_{*}=(' + ', '.join([str(k) for k in np.round(trace_predict[n], 2)]) + ')$', loc='left') plt.ylim(0.0, 1.0) plt.legend() # 凡例 # gif画像を作成 predict_anime = animation.FuncAnimation(fig, update_predict, frames=N + 1, interval=100) predict_anime.save("ch3_2_2_Predict.gif")
(よく理解していないので、animationの解説は省略...)
参考文献
- 須山敦志『ベイズ推論による機械学習入門』(機械学習スタートアップシリーズ)杉山将監修,講談社,2017年.
おわりに
とりあえず装飾より内容ということで自力で三角図を作成しましたが、三角図用のライブラリがあるようなので、一通り実装できたら3Dプロットと合わせて追加したいと思います。
2021年2月22日は、モーニング娘。'21の横山玲奈さんの二十歳のお誕生日です!
(センター曲がまだない、、左の方です。)よこやーん、にゃんにゃんにゃーん
【次節の内容】